目前,空间拦截轨道优化问题的解法主要是结合不同的优化指标要求建立轨道优化数学模型,将其转化为最优控制问题,再通过直接法或间接法求取最优解[1].其中直接法是指通过参数化方法,将轨迹优化问题转化为参数优化问题,然后采用优化算法进行参数优化求解的方法.直接法中采用的优化算法的计算效率直接影响了轨道优化效率,因此高效的轨道优化算法是国内外研究的热点[2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13].目前已提出的方法包括图解法、遗传算法、模拟退火算法、蚁群算法、粒子群优化算法以及各种方法的混合智能算法.
关于直接法求解轨道优化问题,文献[2]讨论了用Lambert法求解固定位置、固定时间的双脉冲轨道转移问题,并用图解法获得了多圈Lambert转移的燃料最优解.文献[3]研究了椭圆轨道飞行器固定时间最小能量拦截问题,分析得到了有限推力一次机动作用下的点火时刻.事实上,对于这种多变量的优化问题,传统的优化方法很难得到全局最优解.遗传算法作为一种全局寻优算法,能较好地解决这类实际问题.文献[4]采用遗传算法求解燃料最优转移问题,但只考虑了圆轨道间、目标位置固定的情况.文献[5]提出一种遗传算法和迭代法相结合的混合算法求解优化问题,但遗传参数采用二进制编码,二进制与浮点数之间的频繁转换降低了优化结果的精确度.文献[6]先使用引物矢量理论求得轨道优化问题的局部最优解,并将此作为初始猜测值,然后使用遗传算法求取全局最优解,加快了从局部最优解到全局最优解的收敛速度,但该方法依赖于初始猜测值的准确度且时间消耗也较多.
本文提出一种基于遗传算法(Genetic Algorithm,GA)和改进高斯法(Improved Gauss Method,IGM)混合算法的空间拦截轨道优化方法.改进高斯法为改进的轨道生成方法,具有收敛域大、收敛速度快的优点,遗传算法为性能优越的优化算法,本文将两种算法的优点结合在一块,解决空间拦截轨道优化问题.在求解初始位置和转移时间均不固定的空间拦截轨道优化问题时,通过改进高斯法对遗传过程中产生的种群进行选择,去除不满足约束条件的个体,提高遗传算法的计算效率,从而达到提高轨道优化效率的目的.仿真结果证明本文提出的混合优化算法比文献[5]中混合算法求解精度高,收敛速度快.本文组织如下:首先,引入牛顿-拉夫逊迭代法对原始高斯法进行改进,根据转移角的大小选择不同方法,解决原始高斯法收敛速度慢、转移角不能过大等问题.然后,给出基于遗传算法和改进高斯法的混合优化算法.以初始转移时刻、转移时间为优化设计变量,用混合优化算法求解燃料和转移时间的综合最优解.最后,通过仿真验证本文所给出的优化算法的有效性.
1 空间拦截问题所谓空间拦截问题,就是给定空间两点相对引力中心的位置矢量与转移时间,求解固定时间、过这两个端点的转移轨道问题.
如图 1所示,空间拦截问题可描述为:初始时刻t0,拦截器位于点A,目标航天器位于点C,rI和rT分别为点A和点C的矢径.经过一段时间t1,拦截器飞行至点B,此时施加速度增量Δv,经过转移时间Δt,目标航天器和拦截器同时到达拦截点D.根据Δt,可求解出在转移轨道上变轨点B的速度矢量vt,进而可得到拦截器的速度增量:

式中:vi为拦截器在变轨前的速度矢量.
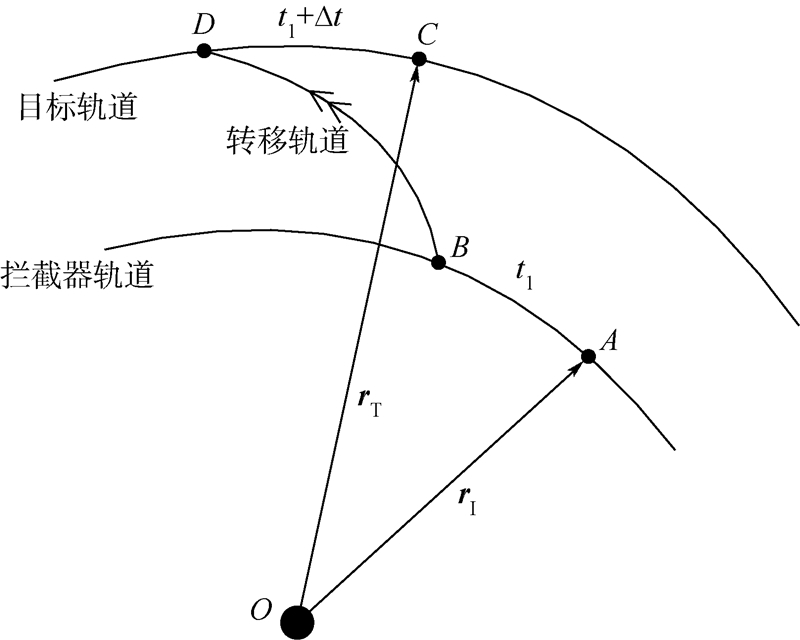 |
| 图 1 空间拦截问题示意图Fig. 1 Schematic diagram of space interception |
| 图选项 |
2 改进高斯法由文献[14]所述,原始高斯法(不同于用于轨道优化的高斯伪谱法)在求解空间拦截问题时精度高,但存在3个问题:
1) 当转移角大于π/2时,方法失效.
2) 原始高斯法的迭代初值可能不在函数迭代收敛域内.
3) 函数迭代收敛时,线性收敛速度慢.
为了使高斯法保持求解高精度,同时在收敛域上和收敛速度上都能有提高,下面对原始高斯法进行改进.
由高斯第一方程和高斯第二方程[14],可令函数

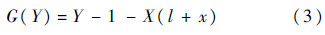
式中:
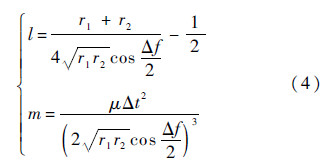

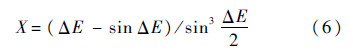
其中:ΔE为转移轨道上两固定点的偏近点角之差,0<ΔE<π;Δf为两固定点的转移角;r1和r2分别为图 1中点B和点D的矢径的模;Y为图 1中扇形OBD与三角形OBD的面积之比.
将ΔE对x、X对ΔE、Y对x分别求导有
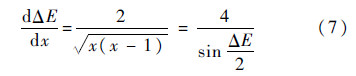
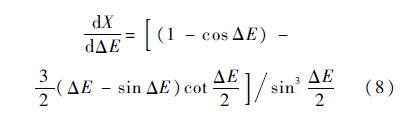
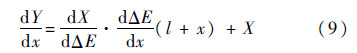
根据转移角Δf是否大于π/2,分别给出改进高斯法求解空间拦截问题的x迭代和y迭代的计算步骤,解决了由于转移角Δf>π/2时原始高斯法无法求解的问题,扩大了高斯法的收敛域;进一步引入牛顿-拉夫逊迭代法,对原始高斯法进行改进,使改进后算法更快收敛.具体步骤如图 2所示.图中ε为误差容许值.
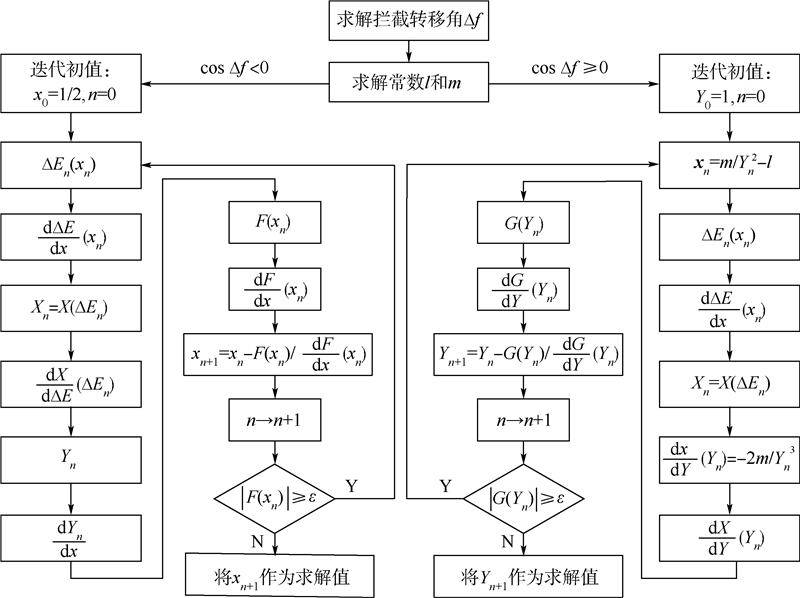 |
| 图 2 改进高斯法流程图Fig. 2 low chart of IGM |
| 图选项 |
解收敛后,按原始高斯法步骤[14]计算拦截器所需的速度增量Δv.
为了验证改进高斯法的优越性,设置初始轨道根数如表 1所示,转移开始时刻为16188.47s,转移结束时刻为20235.59s,在配置为3.2GHz、内存1.25GB的计算机上分别使用改进高斯法和原始高斯法计算1000次拦截器所需速度增量Δv.统计它们的求解时间如表 2所示.
表 1 目标器及拦截器的初始轨道根数Table 1 Initial orbit elements of target and interceptor
| 航天器 | a/km | e | i/rad | Ω/rad | κ/rad | f/rad |
| 目标器 | 15000 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 拦截器 | 8000 | 0.0 | 0.0 | 0.0 | π | 0.0 |
表选项
表 2 求解时间比较Table 2 Comparison of consuming time
| 比较参数 | 原始高斯法 | 改进高斯法 |
| 求解时间/ms | 54.4 | 44.8 |
表选项
从表 2中求解时间比较结果可知,改进高斯法相比原始高斯法大约减少了20%的求解用时.由于在轨道优化时,所采用的混合优化算法在寻优过程中需要计算速度增量几千次,因此可以说改进高斯法对轨道优化时间的节省是可观的;同时由前述可知,改进高斯法较原始高斯法有更大的收敛域,更适用于大范围寻优,避免了混合优化算法收敛到局部最优.综上所述,改进后的高斯算法收敛域扩大,收敛速度加快.
3 迭代方程有唯一解的充要条件为了使改进高斯法与遗传算法更好地混合,提高混合后算法的收敛速度,本文给出了改进高斯法迭代方程式(2)、式(3)有唯一解的充分必要条件.当转移轨道为椭圆时,可以在混合算法开始计算阶段,去除一些不满足充分必要条件的情况.
对式(2)、式(3)求导,代入式(7)~式(9)化简得
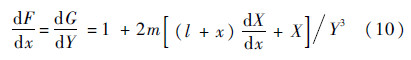
由式(10)可知,如果X在0<x<1区间上连续单调非负,则F(x)、G(Y)分别在它们的定义域上单调增.因此如果F(x)、G(Y)函数曲线分别只穿越x轴、y轴一次,则方程F(x)=0和G(Y)=0有唯一解.下面证明X在0<x <1区间上连续单调非负.令U(ΔE)=ΔE-sin ΔE,在ΔE∈(0,2π)区间上,由
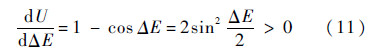
可知U(ΔE)非负且是单调增函数.
同理,在0 < x<1区间上,由式(12)可知U(ΔE(x))非负且是单调增函数.
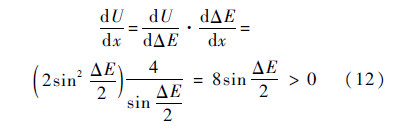
由式(7)和式(8)可得
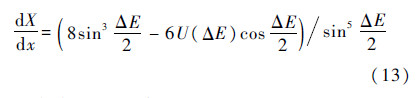
由洛比达法则

当x∈[1/2,1)时,由式(13)可知dXdx>0.
当x∈[0,1/2],ΔE∈[0,π]时,令
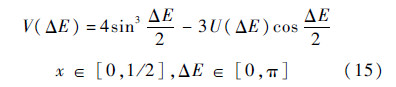
对其进行求导
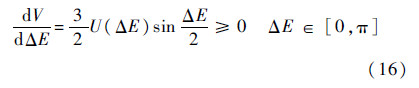
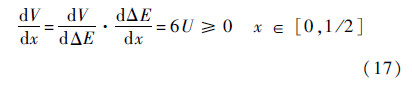
可知V≥0,x∈[0,1/2],即dXdx≥0.
由X(0)=4/3和dXdx≥0,可知X(x)≥4/3,x∈[0,1).经过前面分析可知,F(x)、G(Y)分别在它们的定义域上单调增.
定理1 迭代方程式(2)、式(3)有唯一解的充分必要条件为

证明
必要性:假设F(x*)=0,x*∈(0,1].由F(x)的单调性和x*>0可知
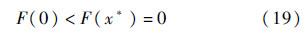
这样Y(0)=1+4l/3,结合式(19)
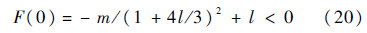
假设G(Y*)=0,Y*∈([m/(l+1)]1/2,[m/l]1/2).
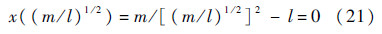
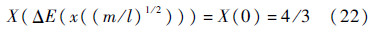
由G(Y)的单调性可知
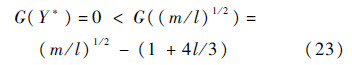
以上证明了式(18)是方程有唯一解的必要条件.
充分性:由式(20)知F(0)<0,

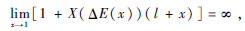 ,所以
,所以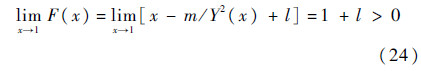
再由F(x)的单调性和连续性可知方程有唯一解.同理可由
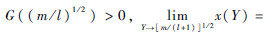
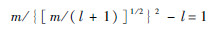 ,所以
,所以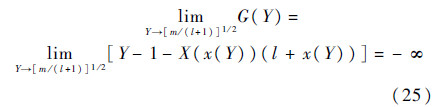
再由G(Y)的单调性和连续性可知方程有唯一解.定理的充分性得到证明.证毕4 混合优化算法设计遗传算法作为一种搜索算法,它的寻优结果可能陷入局部最优解,当优化变量增多时更是如此.由于改进高斯法收敛范围大、收敛速度快,为减少遗传算法的寻优变量,提高其寻优速度和准确性,本文设计了一种将遗传算法与前述的改进高斯法相结合的混合优化算法.
4.1 约束条件在轨道转移过程中,需要满足一定的约束条件,如参数的取值范围及工程实际的限制.本文主要考虑:
1) 开始转移时刻应小于目标轨道周期的1/2,即tk<1/2tp,拦截时刻应小于目标轨道周期,即te<tp,从而使目标航天器预警机动的时间减少,提高命中概率.
2) 拦截器变轨是在一次速度脉冲的作用下瞬间完成的.轨道转移能量消耗应有上限约束,即Δv≤vmax,本文将拦截器最大变轨脉冲限制为vmax=8.5km/s.
4.2 变量的编码编码是应用遗传算法时要解决的首要问题,编码的方法很大程度上决定了遗传算法的计算效率,常用的有二进制编码和浮点数编码.浮点数编码与二进制编码相比,具有表示范围大、求解精度高、运算速度快、更能反映实际问题等优点,同时也便于与改进高斯法混合使用,虽然二进制编码比浮点数编码搜索能力强一些,但浮点数编码比二进制编码在变异操作上能够保持更好的种群多样性.因此本文采用浮点数编码.
4.3 适应度函数由于很难达到理论边界条件,假设在拦截点,目标航天器的位置与拦截器的位置偏差在1%范围内即满足边界条件.给出适应度函数为
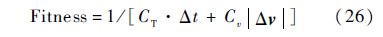
式中:CT和Cv分别为时间和能量的权重因子,它们的选取由战场态势决定.若较看重打击时间,则取CT稍大一些,若较看重能量的节省,则取Cv稍大一些.
4.4 混合优化算法设计步骤图 3所示,首先,初始化目标航天器和拦截器的轨道参数,初始化种群(tk,Δt),得到开始转移时刻tk和转移时间Δt.接着,计算开始转移时刻拦截器的速度矢量和位置矢量、目标航天器在拦截点的位置矢量.继而使用改进高斯法的求解步骤,求解拦截器的变轨脉冲.当转移轨道为椭圆时,可以在混合算法开始计算阶段,去除一些不满足充分必要条件的个体,提高算法速度.最后以适应度函数为准则,用轮盘赌的方法选择父代,经过交叉、变异产生新种群,从而得到新的开始转移时刻和转移时间.如此往复,直到第N代或者代与代之间没有进化时为止.
 |
| 图 3 混合优化算法流程图Fig. 3 Flow chart of hybrid optimal algorithm |
| 图选项 |
遗传算法运行过程中,交叉概率Pc和变异概率Pm直接影响算法的收敛性.本文使用文献[15]提出的自适应遗传算法,即Pc和Pm的选取能够随适应度函数值自适应调整,使算法更快更准确地达到全局最优解,其表达式为

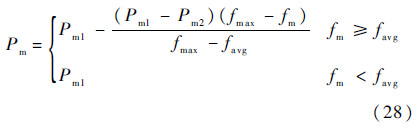
式中:Pc1取为0.8;Pc2取为0.5;fmax为种群最大适应度值;favg为每代种群的平均适应度值;f*为交叉的两个个体中较大的适应度值;Pm1取为0.15;Pm2取为0.1;fm为变异个体的适应度值.
5 仿真算例下面采用数值仿真的方法验证混合优化算法的性能.遗传参数设定如下:种群数目为20,遗传代数为180.
算例1 目标航天器和拦截器的初始轨道根数使用文献[5]中的数据,如表 1所示,两者均为圆轨道.CT=0,Cv=1,求燃料最优解.
对于轨道半径之比小于15.58的两共面圆轨道之间的转移,霍曼转移是燃料最省的.下面分析证明,对于两共面圆轨道的单脉冲拦截问题,霍曼转移所求得的转移脉冲也是燃料最省的.图 4为航天器从低轨道1到较高轨道3的霍曼转移轨道.航天器在原轨道1上瞬间加速后,进入一个椭圆转移轨道2.航天器由此椭圆轨道的近拱点开始,抵达远拱点后再瞬间加速,进入另一个圆轨道3,此即为目标轨道.由前述可知,第1次瞬间加速后,航天器最远能达到的高度为轨道3的高度.若第1次加速脉冲变小后,可知椭圆轨道2最远能达到的高度将小于轨道3的高度,不能满足要求.因此可知,对于单脉冲拦截问题,霍曼转移是最小能量拦截轨道.
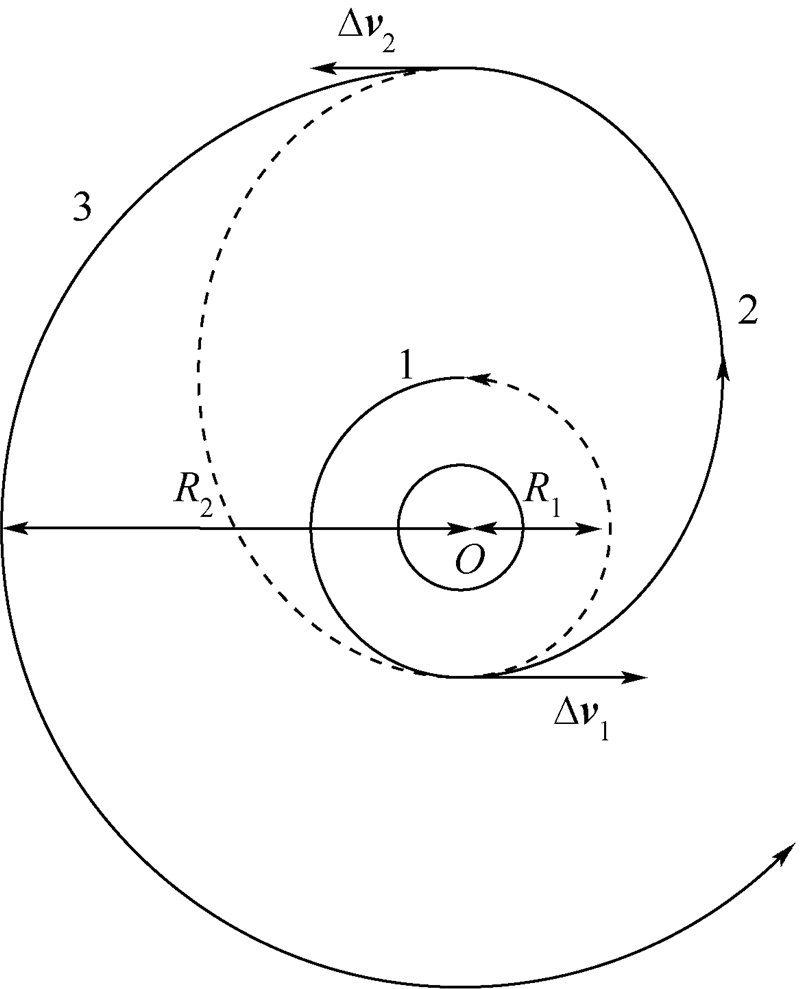 |
| 图 4 霍曼转移示意图Fig. 4 Schematic diagram of Homan transfer |
| 图选项 |
将霍曼转移、文献[5]中算法和混合优化算法所得到的结果进行对比如表 3所示.结果表明,本文优化算法更有效,求解结果更接近霍曼转移解算出的燃料最优解.
表 3 不同算法下的性能Table 3 Performance of different methods
| 算法 | Δt/s | Δf/(°) | Δv/(km·s-1) |
| 霍曼转移 | 6136.6 | 180.0 | 1.0029 |
| 文献[5]算法 | 6102.8 | 178.9 | 0.9961 |
| 本文算法 | 6124.8 | 179.8 | 1.00291 |
表选项
图 5为种群适应度值随遗传代数变化的过程.由图可知,种群的最优适应度值随着遗传代数的增加而逐渐收敛;群体的适应度均值也随着遗传代数的增加,逐渐向最小适应度值逼近.这表明群体中适应度值较小的个体逐渐被淘汰,较优个体逐渐被保留,群体中的个体差异不断减小并趋于最优值.与文献[5]算法相比,本文算法的最优适应度值在第10代后就趋于平稳,更快收敛到最优解.图 6为目标航天器和拦截器在地心惯性坐标系下的运动轨迹.
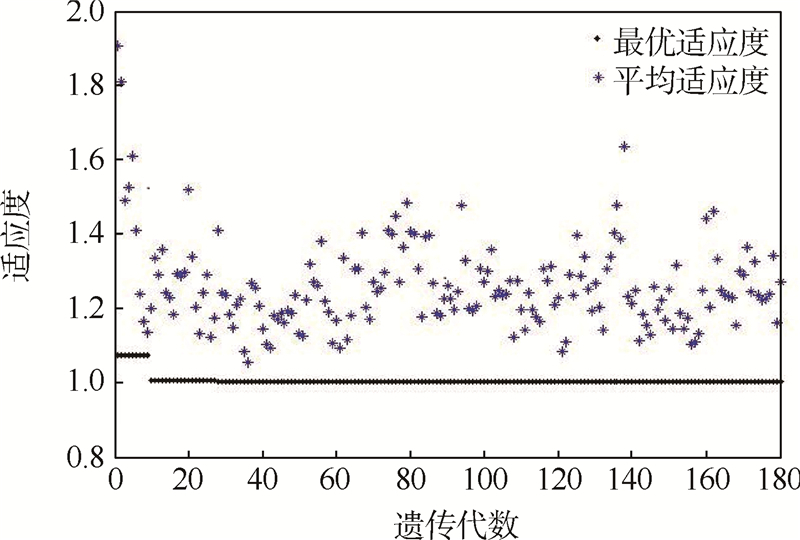 |
| 图 5 适应度值随遗传代数的变化Fig. 5 Variation of fitness value via generation |
| 图选项 |
 |
| 图 6 共面圆间转移的运动轨迹Fig. 6 Trajectory of coplanar transfer |
| 图选项 |
算例2 目标航天器和拦截器的初始轨道根数如表 4所示,两者在异面椭圆轨道上.表中ω为近地点幅角.
卫星变轨多采用能量最省方案,这是由于其对时间消耗并无要求,耗时可长可短.本文所涉及的空间拦截器在所携带燃料有限的前提下,对时间要求也较高,因此提出了燃料和时间的线性组合优化指标.在非攻击模式下,拦截器轨道维护、作战部署等可采用能量最省方案;在攻击模式下,则要综合考虑两个优化指标,在满足有限燃料的情况下,设置指标权重因子.例如攻击目标时一般原则是先攻为快,要求拦截器攻击时间尽量少,将CT设置为1,Cv设置为0,则为时间最优情况.但是时间最优情况的所需燃料有可能大于燃料上限,此时就需要适当减小时间的权重因子CT,增加燃料的权重因子Cv,直到满足燃料限制为止.而在拦截器轨道维护、作战部署时,要求其消耗燃料尽量少,将燃料的权重因子Cv设置为1,CT设置为0,为燃料最优情况.因此,选取3组不同的CT、Cv对算例2进行仿真,表 5为仿真结果.其中,第1组为燃料最优解,第2组为燃料和转移时间综合最优解,第3组为时间最优解.
表 4 算例2的目标器与拦截器轨道根数Table 4 Ex.2 orbit elements of target and interceptor
| 航天器 | a/km | e | i/rad | Ω/rad | ω/rad | f/rad |
| 目标器 | 20000 | 0.3 | 0.3 | 2.1 | 0.0 | 0.0 |
| 拦截器 | 8000 | 0.1 | 0.1 | 0.3 | π | 0.0 |
表选项
表 5 不同权重因子下的结果Table 5 Results of different weight factors
| 组别 | 权重因子 | Δt/s | |Δf|/(°) | Δv/(km·s-1) | e |
| 1 | CT=0,Cv=1 | 13697.1 | 241.3 | 1.4853 | 0.465 |
| 2 | CT=0.3,Cv=0.7 | 4272.9 | 112.4 | 2.5007 | 0.806 |
| 3 | CT=1,Cv=0 | 2685.4 | 24.3 | 8.1571 | 0.958 |
表选项
图 7~图 9分别为目标航天器和拦截器在3组不同情况下的运动轨迹.从优化结果可以看出,随着Cv减小、CT增大,时间在优化指标中所占比重增大,而燃料所占比重减小.故最优解中脉冲增量增大、转移时间减小,且转移轨道的偏心率增大,这是符合常理的.需要指出的是,第3组时间
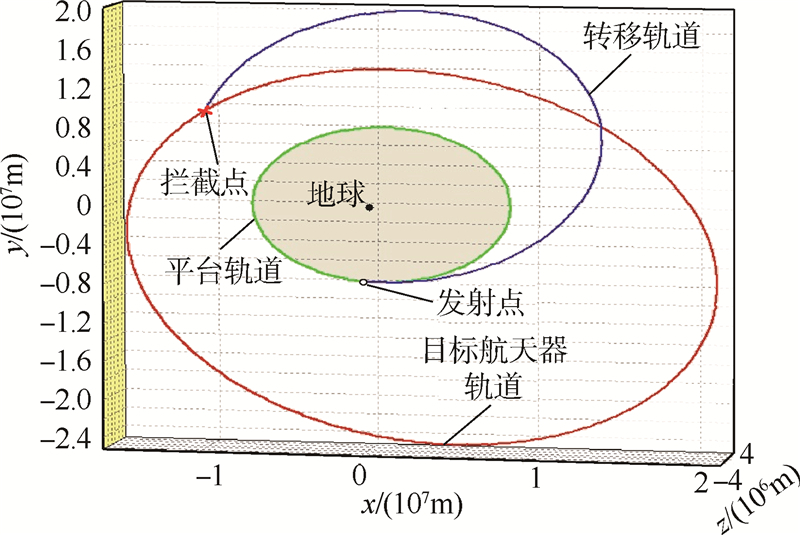 |
| 图 7 CT=0,Cv=1时目标器与拦截器的运动轨迹Fig. 7 Trajectory of target and interceptor when |
| 图选项 |
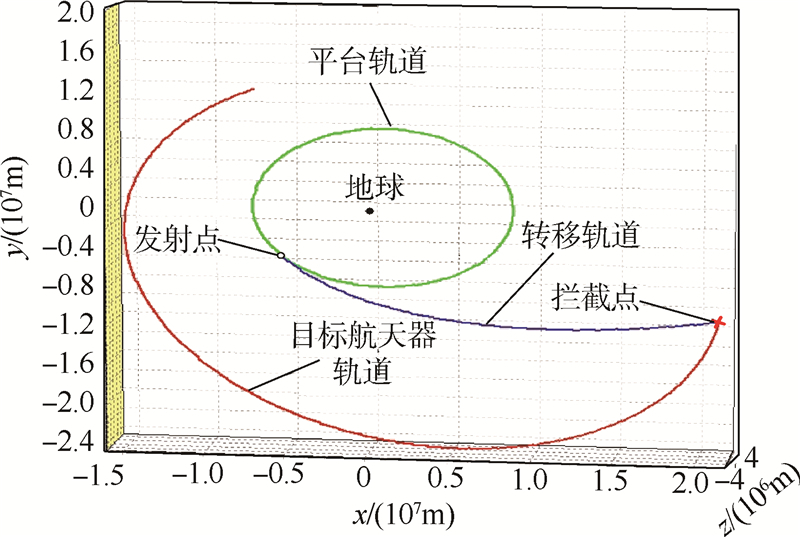 |
| 图 8 CT=0.3,Cv=0.7时目标器与拦截器的运动轨迹Fig. 8 Trajectory of target and interceptor when CT=0.3,Cv=0.7 |
| 图选项 |
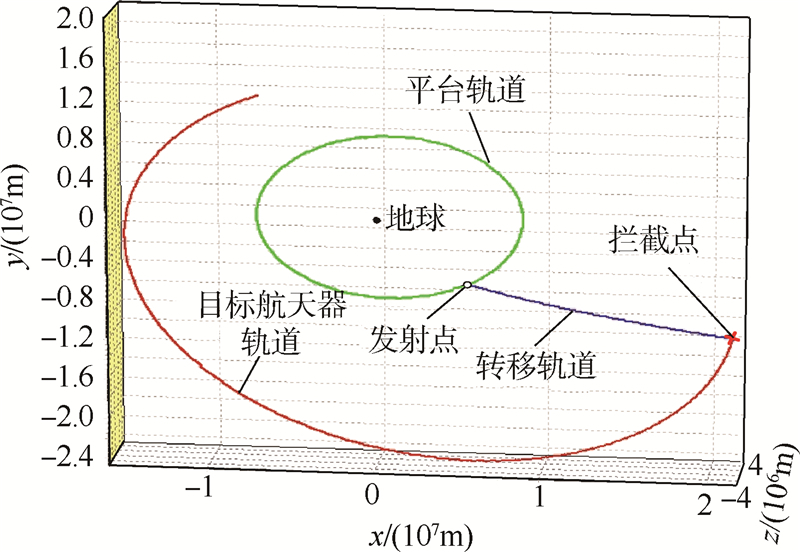 |
| 图 9 CT=1,Cv=0时目标器与拦截器的运动轨迹Fig. 9 Trajectory of target and interceptor when CT=1,Cv=0 |
| 图选项 |
最优解,算得的偏心率e接近1,转移轨道近似为抛物线,所需要的变轨脉冲增量较大,一般在执行紧急任务,需要争取时间的情况下使用.
6 结 论对于初始位置和转移时间不固定的拦截转移轨道优化问题,引入牛顿-拉夫逊迭代法对经典高斯算法进行改进,继而提出了遗传算法和改进高斯法相结合的混合优化算法,并给出了混合优化算法求解此优化问题的设计步骤.该算法具有以下优点:
1) 此方法不需要初始猜测,避免了传统轨道优化方法中初始猜测的困难.
2) 可以求得全局最优解,克服了某些传统优化方法容易收敛于局部最优解的困难.
3) 与传统优化方法相比,收敛精度和收敛速度有所提高.
本文适应度函数的权重因子通过人工选取得到,实际上权重因子关系到遗传算法的精度,适宜的权重因子能使遗传算法更有效,本文下一步工作可考虑在权重因子的选取方面努力.
参考文献
| [1] | 晁涛, 王松艳, 王子才, 等.基于组合优化算法的临近空间飞行器轨迹优化[J].宇航学报, 2012, 33(2):183-188. Chao T, Wang S Y, Wang Z C, et al.Near space vehicle trajectory optimization approach based on hybrid SVM and GA algorithm[J].Journal of Astronautics, 2012, 33(2):183-188(in Chinese). |
| Cited By in Cnki | |
| [2] | Shen H J, Tsiotras P.Optimal two-impulse rendezvous using multiple-revolution Lambert solutions[J].Journal of Guidance, Control, and Dynamics, 2003, 26(1):50-61. |
| Click to display the text | |
| [3] | 周荻, 张刚, 孙胜.有限推力椭圆轨道近距离拦截方法[J].宇航学报, 2010, 31(7):1763-1767. Zhou D, Zhang G, Sun S.A thrust-limited short-distance interception scheme on elliptical orbit[J].Journal of Astronautics, 2010, 31(7):1763-1767(in Chinese). |
| Cited By in Cnki (2) | |
| [4] | Spencer D B, Kim Y H.Optimal spacecraft rendezvous using genetic algorithms[J].Journal of Spacecraft and Rockets, 2002, 39(6):859-865. |
| Click to display the text | |
| [5] | 黄勇, 李小将, 张东来, 等.混合遗传算法在最优Lambert轨道转移设计中的应用[J].飞行力学, 2013, 31(3):269-272. Huang Y, Li X J, Zhang D L, et al.Application of hybrid genetic algorithm in optimal Lambert orbital transfer design[J].Flight Dynamics, 2013, 31(3):269-272(in Chinese). |
| Cited By in Cnki (1) | |
| [6] | Kim D Y, Woo B, Park S Y, et al.Hybrid optimization for multiple-impulse reconfiguration trajectories of satellite formation flying[J].Advances in Space Research, 2009, 44(1):1257-1269. |
| Click to display the text | |
| [7] | Battin R H.An introduction to the mathematics and methods of astrodynamics[M].Revised Edition.New York:AIAA, 1999. |
| Click to display the text | |
| [8] | 邓泓, 仲惟超, 孙兆伟, 等.基于遗传算法的卫星攻击路径规划方法研究[J].宇航学报, 2009, 30(4):1587-1592. Deng H, Zhong W C, Sun Z W, et al.Method research of satellite attacking path planning based on genetic algorithm[J].Journal of Astronautics, 2009, 30(4):1587-1592(in Chinese). |
| Cited By in Cnki (2) | |
| [9] | 陈统, 徐世杰.基于遗传算法的最优Lambert双脉冲转移[J].北京航空航天大学学报, 2007, 33(3):273-277. Chen T, Xu S J.Optimal Lambert two-impulse transfer using genetic algorithm[J].Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(3):273-277(in Chinese). |
| Cited By in Cnki (37) | |
| [10] | 高怀, 朱战霞, 刘剑.基于遗传算法的连续推力最短时间转移轨道设计[J].西北工业大学学报, 2012, 30(2):187-191. Gao H, Zhu Z X, Liu J.An effective minimum-time orbital transfer design under continuous thrust[J].Journal of Northwestern Polytechnical University, 2012, 30(2):187-191(in Chinese). |
| Cited By in Cnki | |
| [11] | Danchick R.Gauss meets newton again: How to make Gauss orbit determination from two position vectors more efficient and robust with Newton-Raphson iterations[J].Applied Mathematics and Computation, 2008, 195(2):364-375. |
| Click to display the text | |
| [12] | Abdelkhalik O, Mortari D.N-impulse orbit transfer using genetic algorithms[J].Journal of Spacecraft and Rockets, 2007, 44(2):456-460. |
| Click to display the text | |
| [13] | 齐映红, 曹喜滨.基于遗传算法的最优多脉冲交会轨道设计[J].哈尔滨工业大学学报, 2008, 40(9):1345-1348. Qi Y H, Cao X B.Design of multiple-impulsive rendezvous trajectory using genetic algorithms[J].Journal of Harbin Institute of Technology, 2008, 40(9):1345-1348(in Chinese). |
| Cited By in Cnki (7) | |
| [14] | 王威, 于志坚.航天器轨道确定-模型与算法[M].北京:国防工业出版社, 2007:76-87. Wang W, Yu Z J.Orbit determination-modeling and algorithm[M].Beijing:Defense Industry Press, 2007:76-87(in Chinese). |
| [15] | Srinivas M, Patnaik L M.Adaptive probabilities of crossover and mutation in genetic algorithm[J].IEEE Transaction on Systems, Man and Cybernetics, 1994, 24(4):656-666. |
| Click to display the text |
