切削力仿真是虚拟数控加工的重要研究内容,同时也是进一步研究切削加工过程和优化切削参数的基础.而切屑厚度的计算精度和效率又对最终的切削力仿真结果具有重要影响.在传统的立铣刀加工过程模型中,Martellotti指出铣刀齿的轨迹为次摆线,并得到了较为精确的方程[6, 7].然而为应用方便,通常采用简化公式fz×cosφ(fz为每齿进给，φ为接触角)来计算未变形切屑厚度[8];对于球头刀加工过程,人们则采用公式fz×cosφ×cosγ(γ为余偏角)来近似计算其未变形切屑厚度[9],上述公式既清楚了揭示了切屑厚度与相关参数的物理关系,同时给出了满足精度要求的较简便的计算切屑厚度的方法因而在铣削过程仿真中得到了大量的应用.Zhu等通过用刀具形状代替切削刃轨迹,对球头刀加工曲面过程的切屑厚度进行求解,并在此基础上实现了切削力的仿真[10].Montgomery和Altintas在进行铣削加工过程仿真时,用一系列离散的点来表示工件表面,并根据切削刃和工件表面的位置来计算切屑厚度[11].另一类应用较多的方法则是通过列出刀刃轨迹方程,再通过数值解法求出每个瞬时的切屑厚度[12],这种方法具有更高的计算精度,然而应用这种方法进行仿真需要占用更多的时间,同时也很难看出切屑厚度公式的物理意义,一般用在多轴加工仿真中.针对正交车铣加工过程,姜增辉和贾春德实现了切屑形状的计算机仿真,并研究了不同工艺参数对切屑形状的影响[13].在正交车铣加工中,刀具切削刃通常被划分成圆周刃和端面刃两部分,姜增辉和贾春德对无偏心正交车铣加工过程进行了建模,并分别研究了每部分切削刃的切削厚度[14].朱立达等通过理论分析的方法建立了正交车铣加工三维切屑的模型[15].闫蓉等对正交车铣加工过程切削力仿真进行了研究[16].他们考虑了刀具切出过程对圆周刃切屑厚度的影响.
面铣刀适于进行大余量去除,有着较高的加工效率,这些优点使其同样适用于车铣复合加工过程,以降低零件的加工成本、提高企业的生产效率.但现有文献中很少见到关于面铣刀正交车铣加工切屑厚度的研究.本文首先分析了正交车铣加工过程刀具、工件运动关系；接下来针对主偏角为γ的面铣刀,通过假设瞬时刀刃轨迹为圆台回转体,考虑其空间运动推导了正交车铣加工过程切削厚度的计算公式,并进一步将推导的公式拓展到了应用圆刀片铣刀进行加工的情形,并与通过数值方法得到的结果进行了对比分析；最后,应用本文所建立的切屑厚度计算公式,并采用机械力学模型实现了对正交车铣加工过程切削力的仿真,并在车铣复合机床上进行了切削力的验证实验.
1 正交车铣运动关系的描述1.1 正交车铣概述正交车铣复合加工是随着制造业的进步而逐渐发展起来的一种相对较新的切削加工技术.正交车铣加工中铣刀回转轴线与刀具回转轴线相互垂直,刀具以nT转速高速旋转,并以速度fv沿着工件轴向作直线进给运动;工件则以较低的转速nW旋转.这样的运动关系使其适合于外圆柱表面的加工.工件旋转速度、工件直径、刀具旋转速度以及刀具沿工件轴向进给速度共同决定着每个刀齿周期切除材料的多少.当两条轴线之间距离e=0时为无偏心车铣,e>0时为偏心车铣(见图 1).偏心距离的大小对于正交车铣加工过程具有重要影响[17].
 |
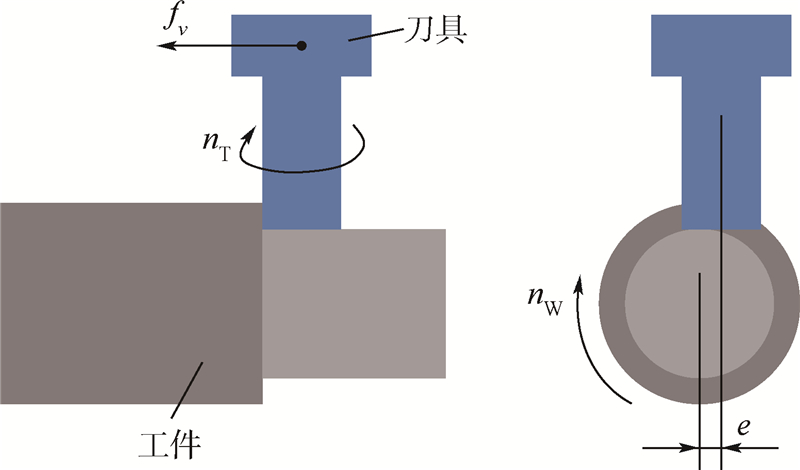| 图 1 正交车铣示意图Fig. 1 Orthogonal turn-milling process |
| 图选项 |
正交车铣加工中用到的面铣刀多为镶片刀,主要有图 2所示的几种.其中,图 2(a)所示刀具的余偏角为0°(即主偏角为90°),图 2(b)所示刀具的余偏角为γ,而图 2(c)为圆刀片面铣刀.图 2(a)铣刀适合用来清根部,图 2(b)和图 2(c)铣刀则适合用在高进给速度的切削过程中.
 |
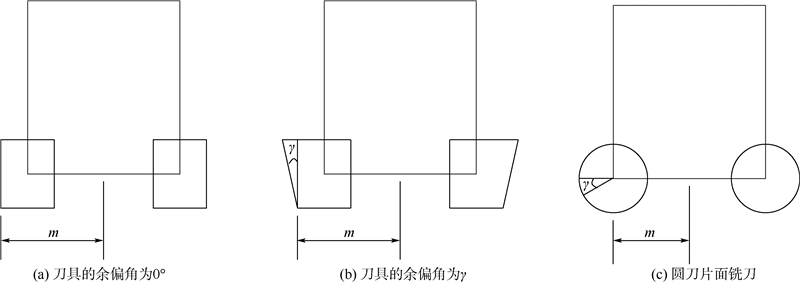| 图 2 不同形状的面铣刀Fig. 2 Inserted cutters with different shapes |
| 图选项 |
1.2 切屑厚度计算公式的推导通过分析正交车铣加工过程可知,当用图 2(a)或图 2(b)所示铣刀进行加工时,铣刀的侧刃和底刃同时参与切削.其中,底刃所对应的切屑厚度可以由文献[14]给出的公式计算得到.因此本文主要研究铣刀侧刃所对应的切屑厚度的计算方法.
下面以图 2(b)所示余偏角为γ的面铣刀为例推导切屑厚度的计算公式.为了描述正交车铣加工过程中刀刃相对于工件的运动关系,需要分别建立刀具坐标系和工件坐标系.如图 3所示,以铣刀底面中心OT为原点,以铣刀轴线方向为zT轴建立笛卡儿直角坐标系,即刀具坐标系,其中,xT轴被定义为与工件轴线平行的方向.工件坐标系的原点定义在工件端面的中心,工件轴线方向定义为xW轴,该坐标系与工件固定在一起,在实际加工中与工件一同绕着xW轴(即工件轴线)转动.然而为了方便分析,可以假设工件是静止的,刀具在自转的同时绕着工件轴线公转,同时沿着工件轴线方向作进给运动.对于切削刃j上任意一点P,该点在刀具坐标系中的坐标可以由式(1)表示:
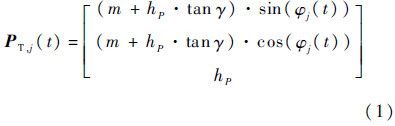
式中:hP为P点距离刀具底面的高度;φj(t)为接触角,其表达式由式(2)给出,式(2)中N为刀具齿数(忽略刀片方位角对切削刃点接触角的影响).
 |
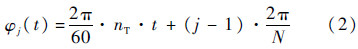
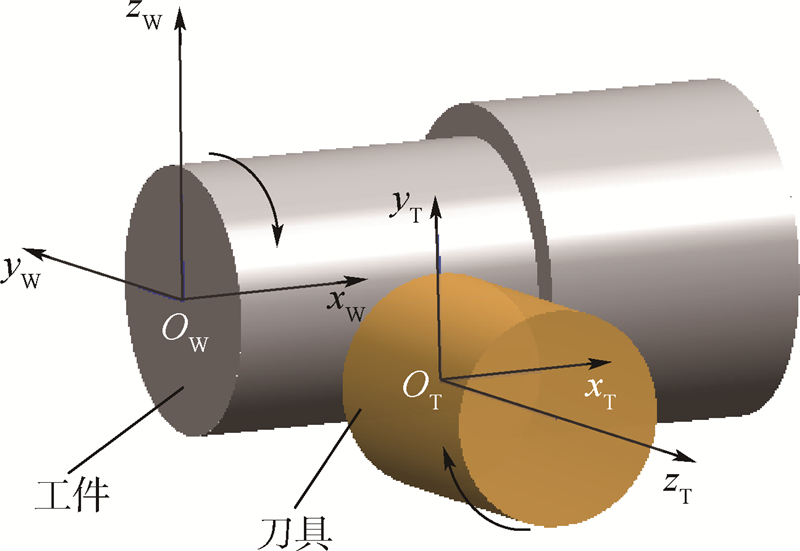| 图 3 刀具坐标系和工件坐标系Fig. 3 Tool coordinate system and workpiece coordinate system |
| 图选项 |
有了P点在刀具坐标系中的表达式,再进一步对其进行旋转变换(乘以矩阵TTW(t))和平移变换(加上向量OTW(t))便可以得到P点在工件坐标系中的坐标表达式PW,j(t).
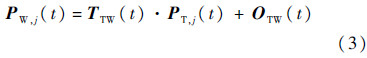
式中：
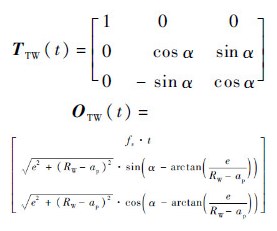
其中:α为刀具绕着工件转过的角度,rad;RW和ap分别为工件半径和切深.
切屑厚度的求解过程直接影响着切削力仿真的效率和精度.尽管通过数值解法能够获得切屑厚度的精确值,但其计算过程需要迭代,会耗费较长的时间.本文给出一种通过用刀具形状包络即圆台体侧面代替刀刃实际轨迹曲面来近似计算切屑厚度的方法.如图 4所示,假设直线
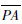与上一个刀齿的轨迹曲面的交点是H,那么线段
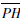的长度即为切削刃点P所对应的切屑厚度. |
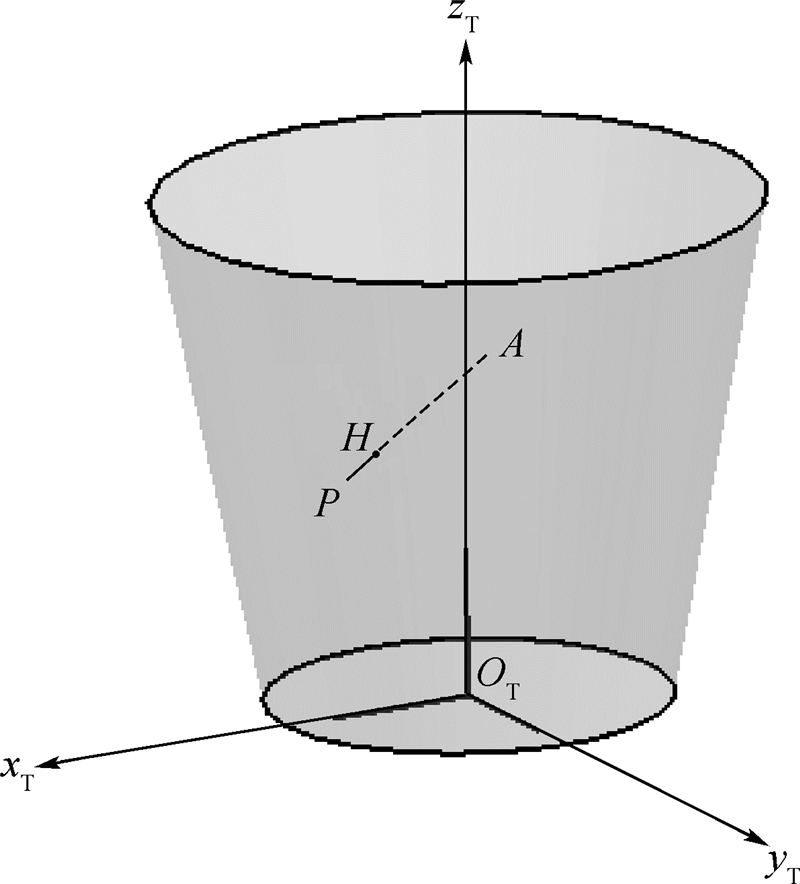| 图 4 切屑厚度的示意图Fig. 4 Schematic diagram of uncut chip thickness |
| 图选项 |
点A在刀具坐标系中的坐标表达式可以写成式(4)的形式,如同前面介绍的点P一样,通过对式(4)进行旋转变换和平移变换便可得到点A在工件坐标系中的表达式.
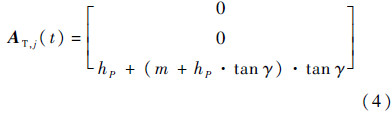
根据P、H、A三点共线可知,在工件坐标系中,三点的坐标值满足如式(5)所示的关系:
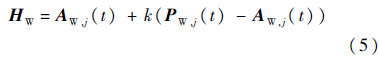
进一步代入各项的表达式可以得到式(6),其中,HT′表示点H在t-Td时刻的刀具坐标系(记为T′)中的坐标值.将式(6)等号两侧同时乘以矩阵TTW(t-Td)的逆,并整理便得到式(7).
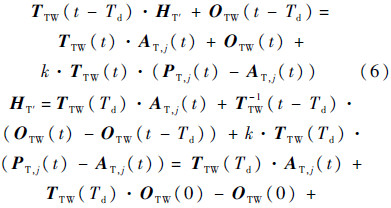
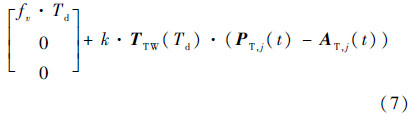
若令
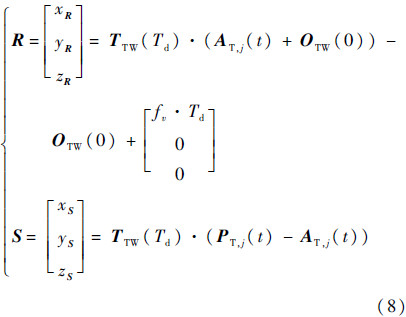
那么,H点的3个坐标值可以表示成式(9)的形式：
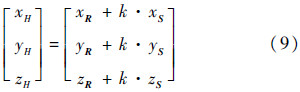
根据前面的假设,点H位于圆台体的侧面上,因此它的3个坐标值满足:
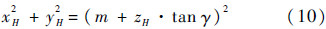
将式(9)代入式(10)中,有
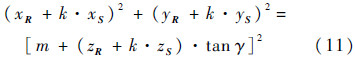
式(11)是关于未知数k的一元二次方程,可以整理成式(12)的形式:
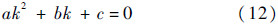
式中:
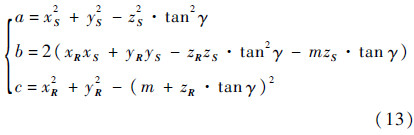
应用一元二次方程的求根公式可以很容易求得方程(12)的解.将求得的k的值代入式(14)便能够求得切屑厚度.
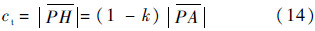
令γ=0,上面所推导的公式便可以用来计算图 2(a)所示铣刀正交车铣加工时的切屑厚度.
1.3 圆刀片铣刀的情形对于圆刀片铣刀切削刃上的任意一点P,其在刀具坐标系中的表达式为
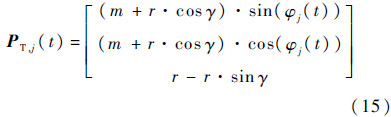
假设点P与刀片圆心Or的连线与前一个刀齿周期的轨迹曲面的交点为H,那么,点P和点H之间的距离即为P点的切屑厚度.根据P、H、Or三点之间的共线关系以及通过和前文类似的推导过程,同样可以将H点在坐标系T′中的3个轴的坐标表示成k的一次多项式的形式.若仍然以刀具形状包络来近似轨迹曲面的话,H点的坐标值之间将满足式(16)的关系:
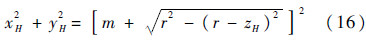
此时,式(16)不再是关于k的一元二次方程,其求解过程比较复杂.针对这个问题,本文采用以过P点的圆台来进一步简化轨迹曲面的方法.这样做的优点是一方面简化了计算过程,另一方面也使得图 2所示3种形状铣刀的切屑厚度的计算公式具有一致的形式,这将有利于仿真算法的实现.
如图 5所示,根据几何关系,可以求得
 |
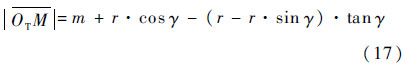
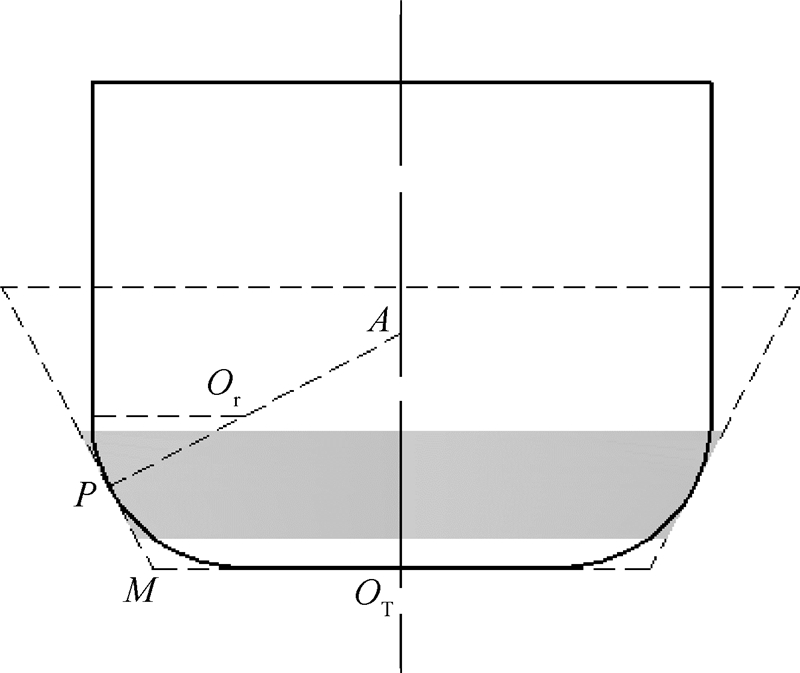| 图 5 圆刀片铣刀几何包络的近似Fig. 5 Approximation of geometry envelop of round insert cutter |
| 图选项 |
通过与上面相同的推导过程,同样可以得到关于k的一元二次方程,此时方程的系数由式(18)给出.求出k后,便可以进一步求得切屑厚度.
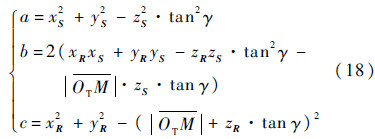
2 仿真实例验证为了验证本文所给出的切屑厚度计算方法,同时采用数值方法[12]和本文方法针对几组实例进行仿真并比较二者的结果.数值计算方法采用真实的刀刃轨迹,需要用迭代的方法进行求解.仿真结果如图 6～图 8所示,其中,横坐标表示所分析的切削刃点的转角,即前文所提到的接触角.每张图的上半部分为得到的切屑厚度的对比,图的下半部分给出的是相对误差的情况,其计算公式为
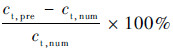
式中:ct,pre为用本文方法计算所得结果；ct,num为用数值方法所得结果.
 |
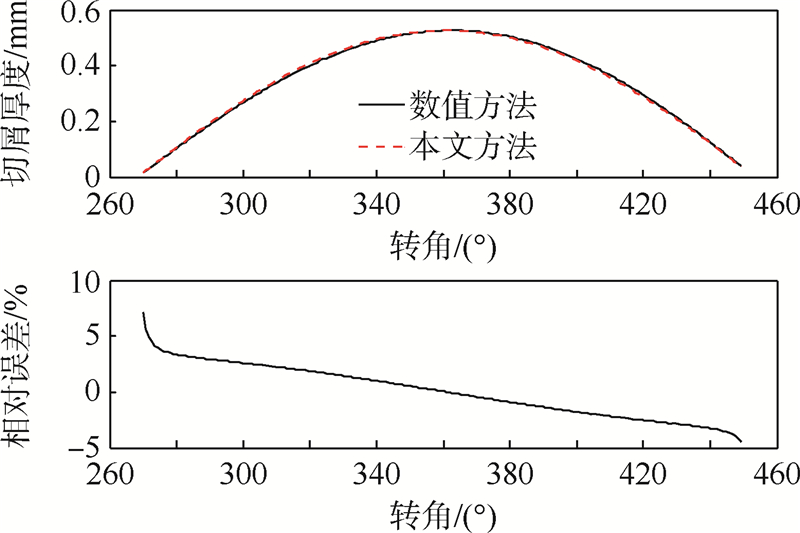| 图 6 γ为0°的铣刀切屑厚度的仿真实例Fig. 6 Simulation example of uncut chip thickness for cutter with γ being 0° |
| 图选项 |
 |
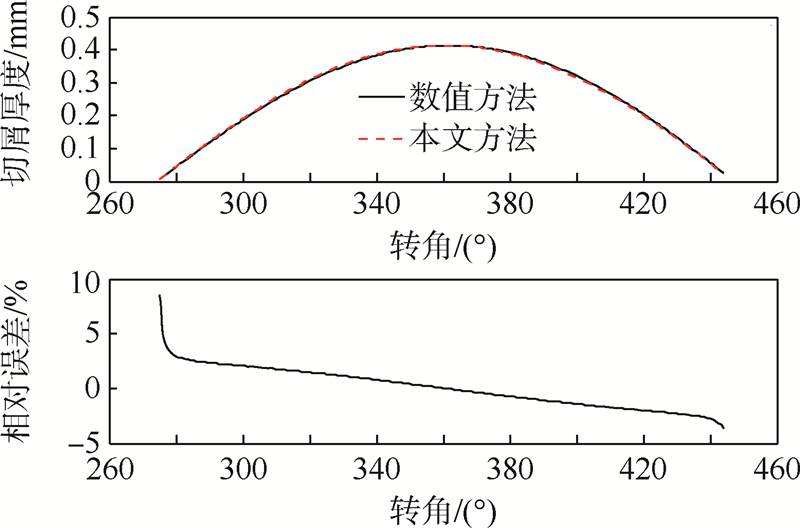| 图 7 γ为45°的铣刀切屑厚度的仿真实例Fig. 7 Simulation example of uncut chip thickness for cutter with γ being 45° |
| 图选项 |
 |
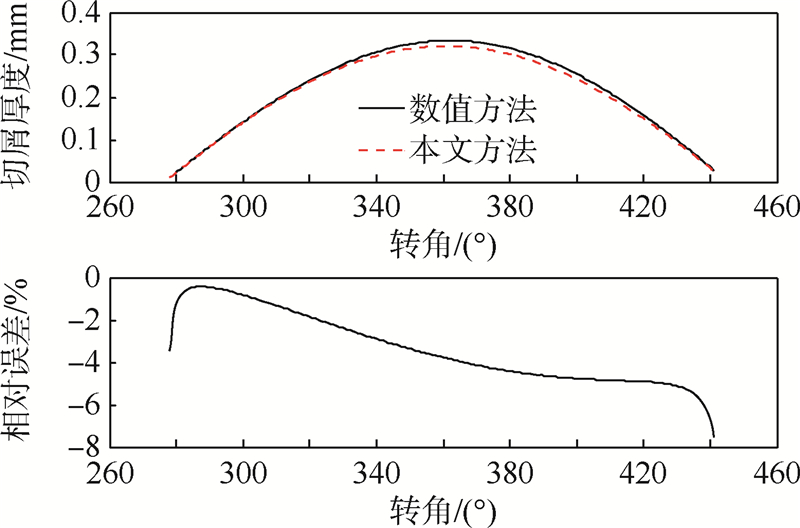| 图 8 圆刀片铣刀切屑厚度的仿真实例Fig. 8 Simulation example of uncut chip thickness for round insert cutter |
| 图选项 |
图 6和图 7为余偏角γ分别为0°和45°的面铣刀正交车铣加工切屑厚度的计算实例.γ=0°的铣刀采用的加工方式为无偏心加工,γ=45°的铣刀采用偏心加工方式,偏心为4mm.两种铣刀采用的其余的切削参数同为:工件直径为70mm,刀具底面半径m为6mm、齿数为2,切深为3mm,刀具转速和工件转速分别为3000r/min和15r/min,刀具沿着工件轴向进给速度为45mm/min.所选取的切削刃点距离刀具底面高度为1.5mm.从图中可以看出采用本文所推导的公式计算得到的结果与数值方法所得结果十分接近,相对误差值很小.
图 8为圆刀片面铣刀正交车铣加工切屑厚度的计算实例.所采用的参数为:工件直径为60mm,刀片半径为4mm,刀片圆心距离刀具轴线m为4mm,齿数为2,偏心为4mm,切深为2.5mm,刀具转速和工件转速分别为2000r/min和10r/min,刀具沿着工件轴向进给速度为35mm/min.所选取的切削刃点的位置角为50°.从图中能够看到两种方法得到的切屑厚度随着转角的变化曲线基本吻合,相对误差值也能够满足一般工程计算的需要.
为了进一步分析两种方法的计算效率,本文针对前文所述的γ=45°的铣刀正交车铣加工仿真实例,计算了所分析的切削刃点(即距刀具底面高度1.5mm处的切削刃点)在400个主轴周期时间内的切屑厚度,并进行计时.所用计算机的处理器为:Intel(R) Core(TM) i5-3210M CPU 2.50GHz.结果显示,应用数值方法进行计算需要约5.6s,而应用本文所推导的公式则仅需要约1.4s.从中可以看到,应用本文方法求解正交车铣加工过程中的切屑厚度具有更高的效率.
刀具工件转速比是正交车铣加工过程区别于传统铣削加工过程的一个重要参数,其对切削过程具有很大的影响.图 9给出了转速比λ的改变对本文所给出的切屑厚度计算方法的误差的影响情况(通过对前文所述的γ=45°的铣刀加工实例进行仿真得到).从图中可以看出,随着转速比λ的减小,误差将会增大.
 |
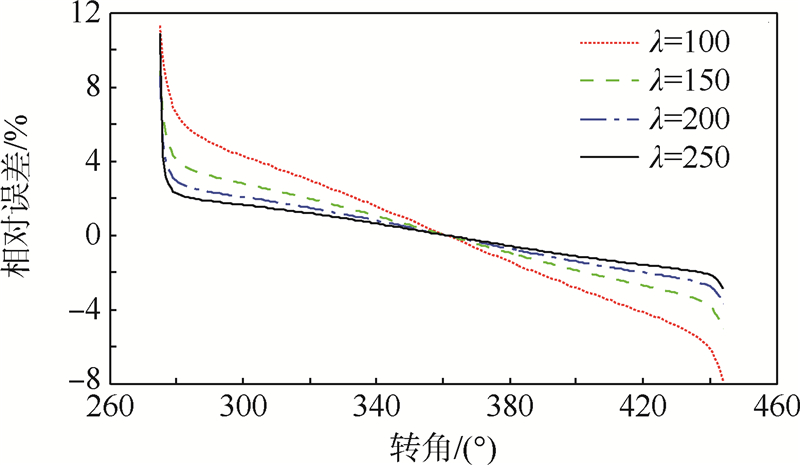| 图 9 转速比对切屑厚度仿真误差的影响Fig. 9 Influence of speed ratio on simulation error of uncut chip thickness |
| 图选项 |
3 实验验证为了进一步验证本文所推导的切屑厚度计算公式,在车铣复合机床上针对铝合金7050进行了切削力测试实验(见图 10).工件直径为47.8mm,采用的刀具为山特维克镶齿刀,刀具直径为16mm,加工时安装一个刀片.所使用的测力仪为Kistler9123C旋转测力仪,所测得的三向切削力是在固定在刀具上、与刀具共同旋转的旋转坐标系内测量得到的结果.所采用的切削参数为:刀具转速为1000r/min,工件转速为1r/min,切深为2mm,刀具沿着工件轴向进给速度为2.5mm/min,加工方式为无偏心切削.应用本文得到的公式计算侧刃上的切屑厚度,同时采用文献[14]中的公式计算底刃上的切屑厚度,并在此基础上对切削力进行仿真.仿真结果与实验测试结果对比情况如图 11所示.其中,实线为实验过程中测得的原始切削力数据,点划线为对实验数据进行滤波处理后得到的结果,虚线为仿真得到的切削力结果.通过旋转测力仪测得的切削力信号存在明显的波动,对其进行了滤波处理,从图中可以看出,仿真得到的切削力波形和幅值与滤波后的实验数据基本一致,从而证明了本文所推导的切屑厚度计算公式的正确性.
 |
| 图 10 切削力测试实验设置Fig. 10 Experimental setup of cutting force test |
| 图选项 |
 |
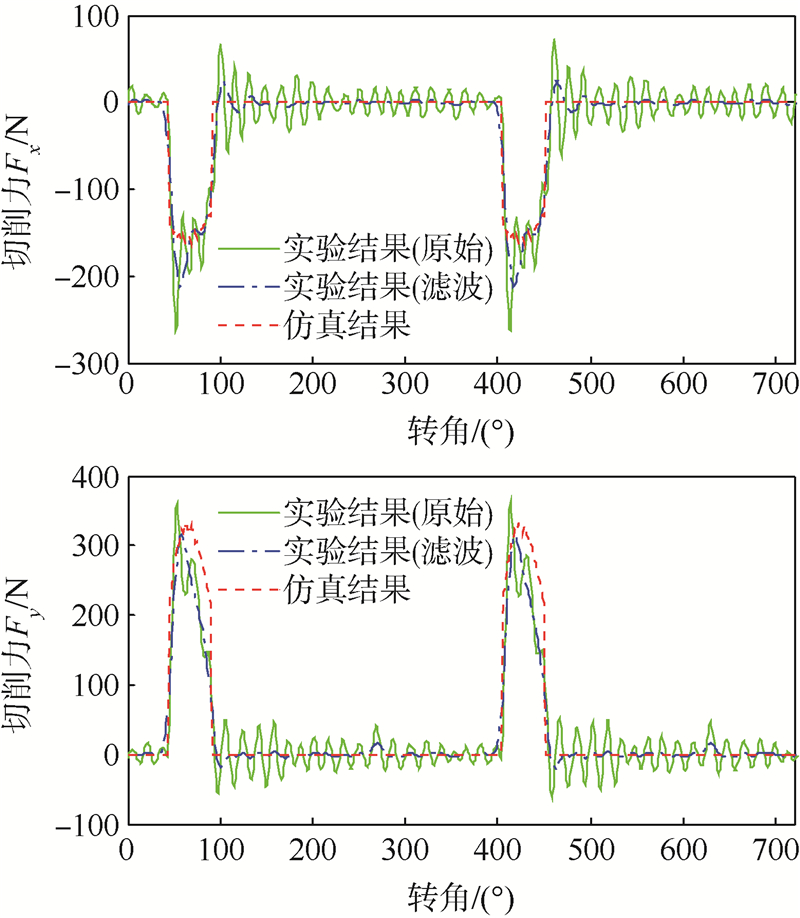| 图 11 切削力仿真结果与实验对比Fig. 11 Comparison of simulation results of cutting forces and experimental results |
| 图选项 |
4 结论1) 本文在对切削刃轨迹进行近似的基础上,给出了一种计算面铣刀正交车铣加工过程侧刃切屑厚度的统一模型.
2) 结合几组实例,应用本文所提出的模型对切屑厚度进行了仿真,并与数值方法的计算结果进行了对比分析.结果显示,在仿真的接触角范围内,二者的相对误差在10%以内.
3) 在本文切屑厚度模型的基础上对切削力进行了仿真,并在车铣复合机床上进行了实验验证.数据对比显示,仿真得到的切削力曲线的波形和幅值均能够与实验结果较好地吻合.
4) 仿真分析及切削力实验验证结果显示,在一定的参数范围内,本文所提出的方法能够正确地计算正交车铣加工中刀具侧刃的切屑厚度,并且具有良好的精度;同时省去了数值方法中的迭代运算,具有较高的计算效率和较大的实际应用价值.
参考文献
| [1] | KopačJ, Pogačnik M.Theory and practice of achieving quality surface in turn milling[J].International Journal of Machine Tools and Manufacture, 1997, 37(5):709-715. |
| Click to display the text | |
| [2] | Choudhury S, Bajpai J.Investigation in orthogonal turn-milling towards better surface finish[J].Journal of Materials Processing Technology, 2005, 170(3):487-493. |
| Click to display the text | |
| [3] | 王凡, 喻红婕, 姜增辉.正交车铣运动轨迹的研究[J].哈尔滨工业大学学报, 2004, 36(8):1038-1040.Wang F, Yu H J, Jiang Z H.Research on movement track of orthogonal turn-milling[J].Journal of Harbin Institute of Technology, 2004, 36(8):1038-1040(in Chinese). |
| Cited By in Cnki (17) | |
| [4] | 蔡永林, 黄超, 李建勇.基于切削接触状况的车铣复合加工刀具磨损分析[J].北京交通大学学报, 2013, 37(1):162-165.Cai Y L, Huang C, Li J Y.Analysis of cutter wear based on contact conditions in turn-milling[J].Journal of Beijing Jiaotong University, 2013, 37(1):162-165(in Chinese). |
| Cited By in Cnki | |
| [5] | 金成哲, 隋连香, 徐骣.正交车铣复合加工的切削用量优化[J].沈阳理工大学学报, 2010, 29(5):60-63.Jin C Z, Sui L X, Xu C.The optimization of cutting regime for orthogonal turn-milling[J].Journal of Shenyang Ligong University, 2010, 29(5):60-63(in Chinese). |
| Cited By in Cnki (5) | |
| [6] | Martellotti M E.An analysis of the milling process[J].Transactions of the ASME, 1941, 63:677-700. |
| Click to display the text | |
| [7] | Martellotti M E.An analysis of the milling process.Part 2 down milling[J].Transactions of the ASME, 1945, 67:233-251. |
| Click to display the text | |
| [8] | Wei Z C, Wang M J, Han X G.Cutting forces prediction in generalized pocket machining[J].International Journal of Advanced Manufacturing Technology, 2010, 50(5-8):449-458. |
| Click to display the text | |
| [9] | Cao Q Y, Xue D Y, Zhao J, et al.A cutting force model considering influence of radius of curvature for sculptured surface machining[J].International Journal of Advanced Manufacturing Technology, 2011, 54(5-8):821-835. |
| Click to display the text | |
| [10] | Zhu R, Kapoor S G, Devor R E.Mechanistic modeling of the ball end milling process for multi-axis machining of free-form surfaces[J].Journal of Manufacturing Science and Engineering, 2001, 123(3):369-379. |
| Click to display the text | |
| [11] | Montgomery D, Altintas Y.Mechanism of cutting force and surface generation in dynamic milling[J].Journal of Engineering for Industry, 1991, 113(2):160-168. |
| Click to display the text | |
| [12] | Sun Y W, Guo Q.Numerical simulation and prediction of cutting forces in five-axis milling processes with cutter runout[J].International Journal of Machine Tools and Manufacture, 2011, 51(10-11):806-815. |
| Click to display the text | |
| [13] | 姜增辉, 贾春德.正交车铣切屑仿真的研究[J].兵工学报, 2002, 23(4):525-528.Jiang Z H, Jia C D.A study on the emulation of orthogonal turn-milling chips[J].Acta Armamentarii, 2002, 23(4):525-528(in Chinese). |
| Cited By in Cnki (18) | |
| [14] | 姜增辉, 贾春德.无偏心正交车铣理论切削力[J].机械工程学报, 2006, 42(9):23-28.Jiang Z H, Jia C D.Theoretical cutting force of non-eccentricity orthogonal turn-milling[J].Chinese Journal of Mechanical Engineering, 2006, 42(9):23-28(in Chinese). |
| Cited By in Cnki (13) | |
| [15] | 朱立达, 李虎, 杨建宇, 等.正交车铣三维切屑理论建模研究[J].东北大学学报:自然科学版, 2012, 33(1):111-115.Zhu L D, Li H, Yang J Y, et al.Research on theoretical modeling of 3D chip of orthogonal turn-milling[J].Journal of Northeastern University:Natural Science, 2012, 33(1):111-115(in Chinese). |
| Cited By in Cnki (4) | |
| [16] | 闫蓉, 邱锋, 彭芳瑜, 等.螺旋立铣刀正交车铣轴类零件切削力建模分析[J].华中科技大学学报:自然科学版, 2014, 42(5):1-5.Yan R, Qiu F, Peng F Y, et al.Modeling and analysis of cutting forces in orthogonal turn-milling shaft parts with helical end mills[J].Journal of Huazhong University of Science and Technology:Natural Science Edition, 2014, 42(5):1-5(in Chinese). |
| Cited By in Cnki | |
| [17] | Uysal E, Karaguzel U, Budak E, et al.Investigating eccentricity effects in turn-milling operations[C]//6th CIRP International Conference on High Performance Cutting.Amsterdam:Elsevier, 2014, 14:176-181. |
| Click to display the text |
