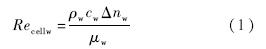
式中,Recellw为基于壁面参数的网格雷诺数;ρw为壁面密度;cw为壁面声速;μw为壁面流体黏性系数;Δnw为壁面法向第1层网格尺度.Men’shov等通过研究[5]发现,网格雷诺数的大小对高超声速气动热环境预测尤为重要,网格雷诺数即使为10,计算结果也可能产生100%的误差.其研究还认为网格雷诺数应不大于3才能保证热流计算结果的准确性.由于在计算前无法完全确定壁面参数,因此只能通过多套网格进行测试.为了解决上述问题,本文提出了针对基于壁面参数网格雷诺数的网格尺度预估方法.由于热流峰值一般位于驻点附近,驻点附近网格尺度一般最小,所以只需得到驻点附近壁面参数即可用上述准则确定壁面网格法向尺度.首先确定驻点附近壁面密度,对于完全气体壁面密度可采用状态方程计算:

式中,ps为驻点壁面压强;Tw为等温壁面条件中设置的壁面温度;R为气体常数.临近空间飞行器高马赫数飞行时头部往往产生脱体激波,可近似认为驻点壁面压强等于驻点线上激波波后总压:

式中,p02为驻点线上波后总压.驻点线上波后总压可根据正激波前后总压关系式获得:
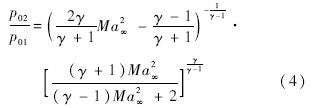
式中,p01为自由来流总压;Ma∞为自由来流马赫数;γ为比热比.自由来流总压p01可根据一维定常绝热流驻点总参数关系式获得:
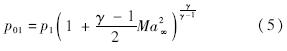
式中,p1为自由来流压强.在已知自由来流马赫数、静压或总压以及壁面温度的情况下可根据驻点壁面估算公式快速估算出驻点壁面密度值.对于存在真实气体效应的流动,若给定完全催化冷壁条件,壁面附近原子完全复合成自由来流气体分子,气体常数R可认为与自由来流值相同,因此上述壁面密度估算方法同样可适用于此种情况.而完全非催化壁面条件下,上述公式是否适用将在随后进行数值验证.式(1)中的壁面声速cw和壁面流体黏性系数μw采用声速公式及Sutherland公式给出:

式中,T0为参考温度;μ0为参考温度所对应的黏性系数;C为常数.由式(2)~式(7)及式(1)可估算出基于壁面参数的网格雷诺数,进而可根据需要控制网格雷诺数大小确定出壁面法向第1层网格高度Δnw.由上述分析可以看出,基于壁面参数网格雷诺数确定的壁面法向网格尺度与自由来流马赫数、压强和壁面温度有关,在这些条件给定的情况下,与来流静温无关.1.2 基于自由来流参数的网格雷诺数准则为了避免使用壁面参数计算网格雷诺数,很多****[6, 7]采用了自由来流参数计算网格雷诺数,并通过研究发现某些条件下当网格雷诺数接近于1时,热流计算结果与实验值吻合得较好.自由来流网格雷诺数由式(8)给出:
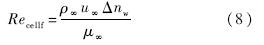
式中,ρ∞为自由来流密度;u∞为自由来流速度;μ∞为自由来流黏性系数;Recellf为基于自由来流参数的网格雷诺数.使用该准则时,先根据自由来流参数计算出单位长度雷诺数:

之后基于自由来流参数的网格雷诺数为1来获得壁面法向第1层网格高度:

由式(8)~式(10)可以看出,基于自由来流参数网格雷诺数确定的壁面法向网格尺度与自由来流马赫数、温度和密度相关,在这些条件给定的情况下,与壁面温度无关.2 壁面法向网格尺度MFP准则程晓丽等摒弃了网格雷诺数的概念,引入气体分子平均自由程分析网格尺度,提出了一种新的壁面网格法向尺度确定方法[8].该方法按照气体动力学的观点,认为壁面传热是大量微观气体分子通过热运动与壁面碰撞进行能量交换的宏观反映,只有当壁面法向第1层网格高度不小于一个分子平均自由程时,才能包含所有与壁面碰撞的气体分子.基于上述分析,建立了基于平均自由程(MFP)的壁面网格法向尺度确定准则.MFP准则壁面法向第1层网格高度Δnw根据式(11)确定:

式中,cw为修正参数;λw为壁面附近气体分子平均自由程,可由式(12)进行计算:
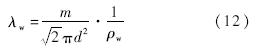
式中,m为气体分子质量;d为气体分子有效直径.取式(11)中cw等于1,即认为壁面法向网格尺度为一个分子平均自由程,式(11)和式(12)可进一步简化为
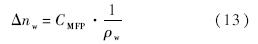
对于空气,分子量M=28.9 kg/kmol,分子有效直径d=3.5×10-10 m,因此可近似计算出式(13)中的系数CMFP,近似为
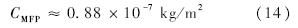
壁面法向网格尺度MFP准则形式简单,但在计算前无法准确获得壁面密度,程晓丽等采用的策略为先进行粗网格计算,得到壁面密度,再重新在由MFP准则确定的密网格上进行数值计算.这种方式针对复杂外形网格量较大时实用性较差.本文采用式(2)~式(5)提出的壁面密度估算方法,与上述MFP准则结合能够在计算之前预估高超声速热环境模拟中壁面网格法向尺度.此外,MFP准则确定的壁面法向网格尺度与自由来流压强、马赫数以及壁面温度相关,在这些条件给定的情况下,与来流静温无关,这一点与基于壁面参数的网格雷诺数有相同的特性.3 壁面网格准则研究的数值实验本节将针对上述3种壁面网格准则分别在完全气体以及考虑真实气体效应的条件下开展数值实验,并对本文提出的壁面密度估算公式进行数值验证.根据阎超等的研究[9],AUSM(Advection Upstream Splitting Method)格式在热流计算精确性方面具有优势,所以验证算例均采用AUSM格式进行计算.此外,本文是基于国家计算流体力学实验室ACANS(Aerodynamic Combustion and Aerothermodynamics Numerical Simulation)有限差分程序开展数值计算研究,该程序已经得到相关研究者[10, 11]的验证.3.1 完全气体壁面网格准则数值实验研究3.1.1 完全气体壁面参数估算公式验证为验证本文提出的壁面密度估算公式的准确性,本文选取了Holden等[12]的高超声速圆柱绕流实验作为验证算例,圆柱直径D=0.076 m.实验条件为:自由来流马赫数Ma∞=16.34,静温T∞=52 K,静压p∞=82.95 Pa,壁面温度Tw=294.4 K,雷诺数Re=3.94×106 /m.由上述条件根据自由来流参数网格雷诺数准则确定壁面法向第1层网格高度约为2.57×10-7 m;根据驻点壁面密度估算公式得到的驻点壁面密度为0.338 kg/m3,由MFP准则确定壁面法向第1层网格高度约为2.6×10-7 m;在该壁面法向网格尺度条件下,根据式(1)得到基于壁面参数的网格雷诺数约为1.66,满足小于3的要求.在此算例条件下,3种网格准则给出的壁面法向第1层网格高度恰好一致.此外,为比较不同壁面法向网格尺度对热流计算结果的影响,另取其他5种不同的壁面法向网格尺度,各网格尺度及基于壁面参数的网格雷诺数如表 1所示.表 1 算例1:壁面法向网格尺度及网格雷诺数 Table 1 Wall normal grid scale and cell Reynolds number for Case 1
| 网格编号 | 壁面法向第1层网格高度/m | 网格雷诺数 |
| Grid 1 | 1.0×10-5 | 63.90 |
| Grid 2 | 6.0×10-6 | 38.34 |
| Grid 3 | 3.0×10-6 | 19.17 |
| Grid 4 | 1.2×10-6 | 9.58 |
| Grid 5 | 6.0×10-7 | 3.83 |
| Grid 6 | 2.6×10-7 | 1.66 |
表选项
图 1给出了不同壁面法向网格尺度得到的热流qw计算结果,其中0°位置为驻点.由图 1可以看到,粗网格计算所得热流与实验值存在较大的偏差,Grid 5和Grid 6计算结果与实验值吻合较好,Grid 5壁面参数网格雷诺数略大于3.上述3个壁面网格准则在此算例条件下确定的壁面法向网格尺度均满足了热流计算精度要求.
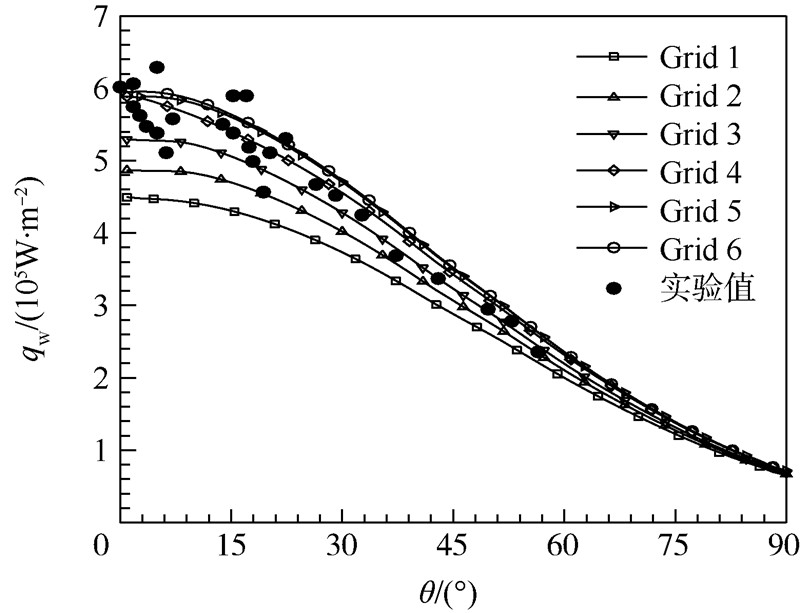 |
| 图 1 不同壁面法向网格尺度热流计算结果Fig. 1 Comparison between experimental and computational heat flux values with different wall normal grid scales |
| 图选项 |
根据图 1计算结果,Grid 6计算结果与实验值最为吻合,表 2给出了Grid 6驻点壁面密度计算值与估算值的对比.可以看出本文提出的驻点密度估算值与数值计算误差约为1.8%,表明本文提出的由驻点壁面密度估算公式结合MFP准则的策略在完全气体条件下是适用的.表 2 完全气体驻点壁面密度估算与计算值对比Table 2 Comparison between estimated and computational density value of stagnation point in ideal gas conditionkg/m3
| 参数 | 估算值 | 计算值 |
| 数值 | 0.338 | 0.332 |
表选项
3.1.2 来流静温变化对网格准则影响由基于自由来流及壁面参数的网格雷诺数准则和MFP准则确定的壁面法向网格尺度在3.1.1节Holden等实验条件下基本一致.然而,是否在所有情况下3种网格准则给出的壁面法向网格尺度均一致则需要进一步分析,本节将在3.1.1节实验条件下,改变来流静温,研究分析来流静温变化对网格准则的影响.将上述实验条件提高来流静温至145 K,其他条件不变.基于自由来流参数网格雷诺数准则确定的壁面法向第1层网格高度约为1.27×10-6 m,与静温变化前相比明显增大,该尺度下基于壁面参数的网格雷诺数约为8.10;由MFP准则确定的壁面法向第1层网格高度仍为2.6×10-7 m,该网格尺度在此条件下的壁面法向网格雷诺数仍为1.66.此外,由于本节主要针对来流静温和壁面温度变化对网格准则的影响开展研究,虽然该条件下可能发生真实气体效应,计算模型中并未进行考虑,真实气体效应影响将在后续内容进行研究.图 2给出了表 1中6种不同壁面法向网格尺度在来流静温提高至145 K条件下的热流计算结果.与图 1相比,来流静温提高后,热流显著提高,Grid 5与Grid 6计算结果也出现较大差异,根据Men’shov等的研究[5],壁面参数网格雷诺数应小于3才可能保证热流计算精度要求,此时Grid 5可能不再满足热流计算精度要求.在等温壁面条件下,自由来流温度提高后,物理推理认为由于壁面附近温度梯度增加,应对网格进行适当加密才能保证获得足够精确的热流计算结果.
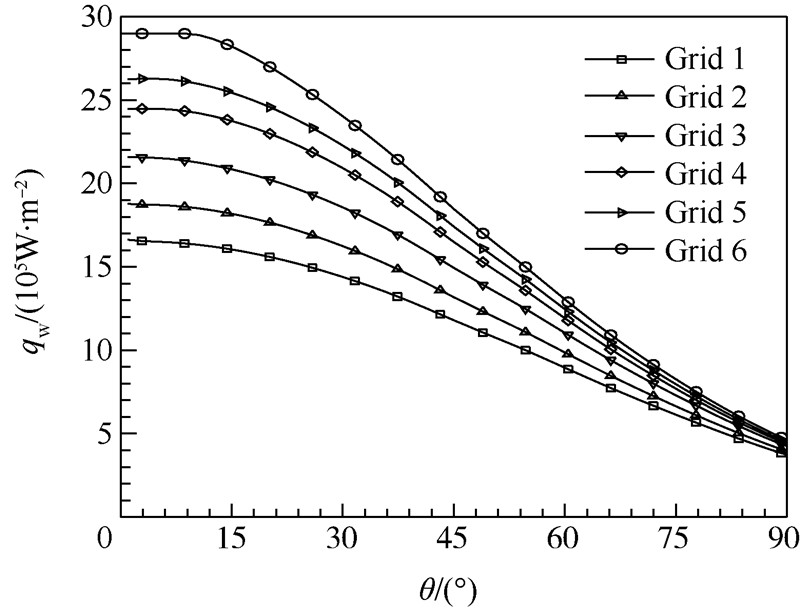 |
| 图 2 提高来流静温后不同壁面法向网格尺度热流计算结果Fig. 2 Result of heat flux values with different wall normal grid scales when the wall temperature increasesnormal grid scales |
| 图选项 |
基于自由来流参数的网格雷诺数准则在自由来流温度提高后,其确定的壁面法向第1层网格高度反而由2.57×10-7 m稀疏至1.27×10-6 m,其壁面参数网格雷诺数由1.66增大至8.10.鉴于该准则确定的网格尺度随来流静温的变化与物理推理趋势相反,不建议将其作为高超声速热环境模拟壁面法向网格尺度确定的准则.3.2 真实气体效应下壁面网格准则数值实验研究真实气体效应对热环境预测模拟有重要影响,本节开展上述3个壁面网格准则在真实气体效应条件下适用性的研究.算例选取了Klaus等的高超声速圆柱绕流实验[13],圆柱直径D=0.09 m.实验条件为:自由来流马赫数Ma∞=8.78,自由来流静温T∞=694 K,静压p∞=687 Pa,密度ρ∞=0.003 26 kg/m3,自由来流总温约为11 393.8 K,壁面温度Tw=300 K.自由来流空气由N2,O2,NO,N和O这5种组分组成,其质量分数分别为ξN2=0.735 55,ξO2=0.134,ξNO=0.050 9,ξN=1.0×10-9,ξO=0.079 55.各反应组分及混合气体的输运系数、热力学函数等均由文献[14]给出,化学反应动力学模型采用其中的5组分6化学反应模型.由上述条件根据自由来流参数网格雷诺数准则确定的壁面法向网格尺度约为2×10-6 m,基于壁面参数的网格雷诺数约为30.99;根据驻点壁面密度估算公式得到的估算值为0.796 kg/m3,由MFP准则确定的壁面法向网格尺度约为1.1×10-7 m,基于壁面参数的网格雷诺数约为1.65.取介于二者之间的一个壁面法向网格尺度,以对比真实气体效应下不同壁面法向网格尺度对热流计算结果影响(Grid 2),基于壁面参数网格的雷诺数如表 3所示.表 3 算例2:壁面法向网格尺度及网格雷诺数Table 3 Wall normal grid scale and cell Reynolds number for Case 2
| 网格编号 | 壁面法向第1层网格高度/m | 网格雷诺数 |
| Grid 1 | 2.0×10-6 | 30.99 |
| Grid 2 | 8.0×10-7 | 11.97 |
| Grid 3 | 1.1×10-7 | 1.65 |
表选项
根据文献[13]可知,此算例数值计算中应采用完全催化壁面条件.为研究驻点壁面估算公式是否适用于完全非催化壁面条件下驻点壁面密度估算,算例中分别给定了完全催化和完全非催化壁面条件进行计算,得到驻点壁面密度计算值.图 3给出了表 3中不同壁面法向网格尺度的网格热流计算结果,其中0°位置为驻点.由MFP准则确定的网格(Grid 3)也满足基于壁面参数网格雷诺数小于3的要求,其热流计算结果与实验值吻合较好,说明MFP准则和壁面参数网格雷诺数准则对发生真实气体效应现象的流动有较好的适应性.而自由来流参数网格雷诺数准则确定的网格(Grid 1)热流计算结果与实验值出现较大的偏差,其壁面参数网格雷诺数也远大于3.由3.1节分析可知,基于自由来流参数的网格雷诺数准则不再适用,主要是由于本算例来流静温较高造成的.
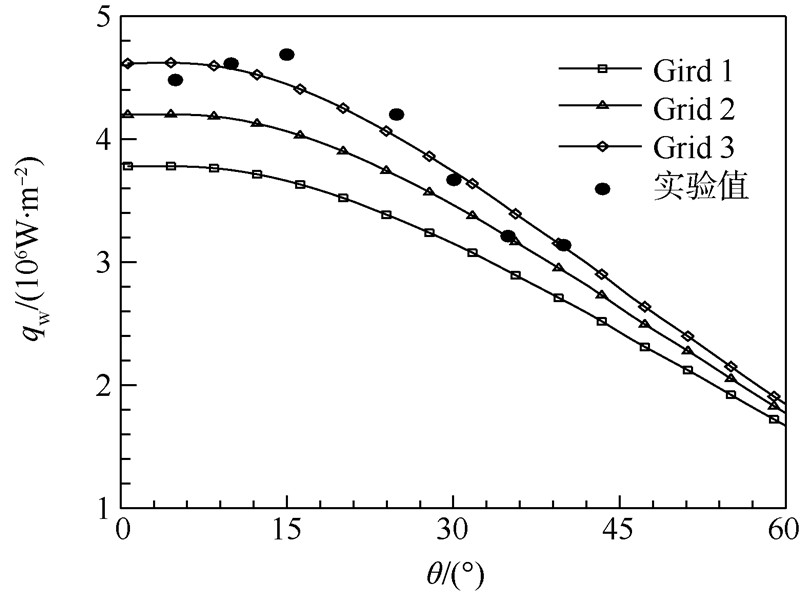 |
| 图 3 不同壁面法向网格尺度下考虑化学反应的热流对比Fig. 3 Comparison between experimental and computational heat flux values with different wall normal grid scales considering chemical reactionnormal grid scales |
| 图选项 |
图 4和图 5分别给出了Grid 3网格驻点线上温度T与氧气质量分数变化曲线.其中,自由来流方向为x轴正方向,驻点位置为x=-0.045 m.可以看出,自由来流空气经过激波后温度迅速升高,氧气分子发生离解,其质量分数迅速降低至0左右,由于壁面为完全催化条件,氧原子在壁面附近复合成气体分子,所以氧气分子质量分数在壁面附近升高,说明化学反应模型对真实气体效应进行了正确的模拟.
 |
| 图 4 驻点线上温度变化曲线Fig. 4 Temperature variation along the stagnation point line |
| 图选项 |
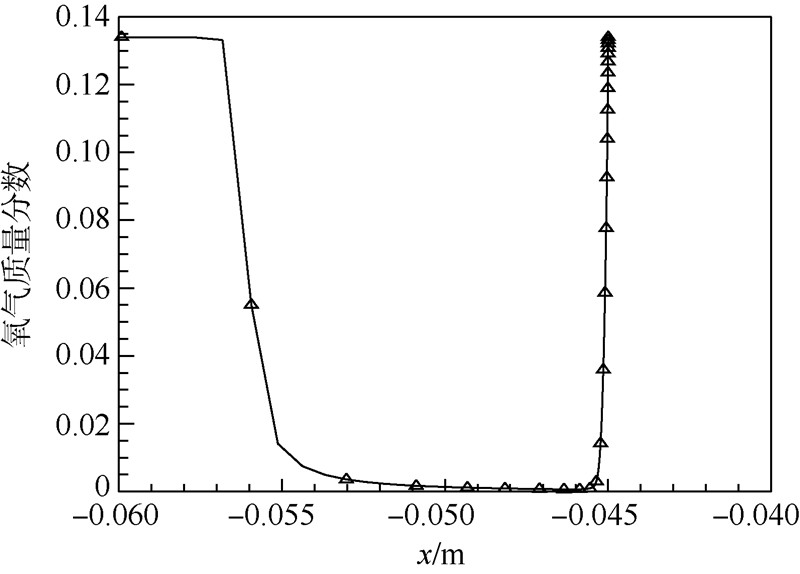 |
| 图 5 驻点线上氧气质量分数变化曲线Fig. 5 Mass fraction variation of oxygen molecules along the stagnation point line |
| 图选项 |
表 4给出了Grid 3网格分别在完全催化和完全非催化壁面条件下驻点壁面密度计算值与估算值对比.由驻点壁面密度估算公式所估算的值与完全催化壁面条件计算得到的结果误差约为3.9%,与完全非催化壁条件计算结果误差约为12.7%.驻点壁面密度估算公式在产生真实气体效应并给定完全壁面催化条件下可获得较准确的驻点壁面密度,在完全非催化壁面条件下,误差略大于10%.因此,真实气体效应条件下采用本文提出的驻点壁面密度估算公式并进一步由相应准则确定壁面法向网格尺度是一种可行的方法.表 4 驻点壁面密度估算值与完全催化和非催化壁面条件下的计算值对比Table 4 Comparison between estimated and computational density values of stagnation point in fully catalytic and equilibrium catalytic wall condition kg/m3
| 参数 | 估算值 | 计算所得密度值 | |
| 完全催化壁面 | 完全非催化壁面 | ||
| 数值 | 0.796 | 0.766 | 0.706 |
表选项
3.3 复杂外形适用性由前述算例验证可知,MFP准则确定的壁面法向网格尺度也满足壁面参数网格雷诺数小于3的要求,这两种准则在二维问题中有较好的表现,接下来选取了高超声速钝双锥实验[15]研究其三维复杂外形问题适用性.该钝锥体前缘半径为3.835 mm,前锥半锥角为12.84°,后锥半锥角为7°,前锥距头部距离Lf=69.55 mm,后锥距头部距离即锥体全长L=122.24 mm.实验条件为:自由来流马赫数Ma∞=9.86,来流静温T∞=48.88 K,静压p∞=89.92 Pa,密度ρ∞=0.004 27 kg/m3,壁面温度Tw=300 K,攻角为0°.根据驻点密度估算公式以及MFP准则确定的壁面法向第1层网格高度约为1.0×10-6 m,壁面参数网格雷诺数约为1.65,MFP准则确定的壁面法向网格尺度满足壁面参数网格雷诺数小于3的要求.图 6给出了钝双锥轴向热流分布.其横纵坐标进行了无量纲化处理,由Fay-Riddell公式估算得到参考热流qws=3.69×105 W/m2,特征长度为锥体总长L=122.24 mm.计算结果表明该壁面法向网格尺度能够满足热环境模拟中热流计算精度的要求,说明MFP准则和壁面参数网格雷诺数准则对复杂外形流动仍然具有良好的适用性.
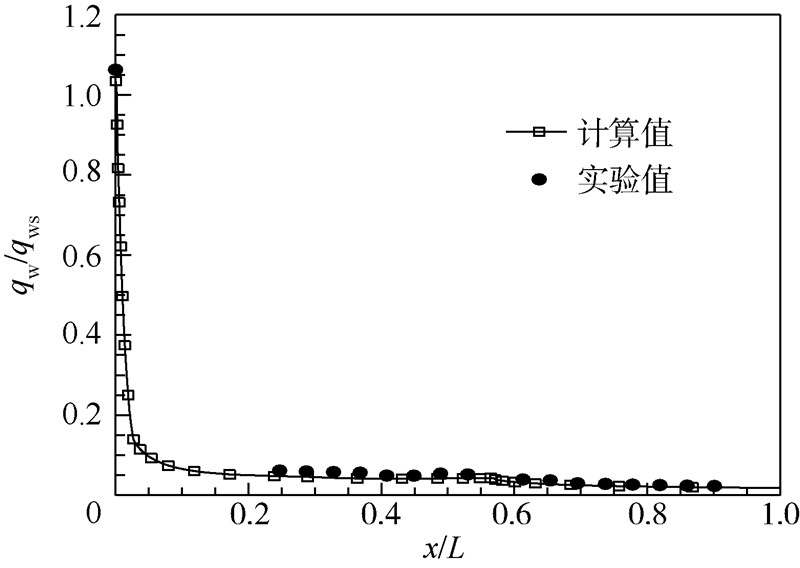 |
| 图 6 钝双锥表面热流轴向分布Fig. 6 Heat flux distribution along axial direction of blunt bicone |
| 图选项 |
4 结 论1) 针对基于壁面参数网格雷诺数和MFP两种准则无法在计算前确定壁面密度的问题,提出了驻点壁面密度估算方法,数值模拟结果显示其在不同流动条件下均可给出可接受的驻点壁面密度估算值,从而使得壁面参数网格雷诺数和MFP两种准则无需进行多套网格或粗网格试算而直接预估出壁面法向网格尺度,增加了此两种准则的实用性.2) 数值实验及理论分析表明:基于自由来流参数的网格雷诺数准则确定的壁面法向网格尺度与壁面温度无关;在给定条件下,提高来流静温而增大壁面附近温度梯度时,其确定的壁面法向网格尺度反而增大,这与物理推理相悖.数值模拟与实验数据的对比也证明在来流静温较高时该准则所确定的壁面法向网格尺度无法给出准确的气动热结果.因此,不建议使用该准则来确定高超声速气动热环境数值计算中壁面法向网格尺度.3) 基于壁面参数网格雷诺数和MFP两种准则确定的壁面法向网格尺度与自由来流温度无关,主要受壁面温度影响.并且不同条件下这两种准则所确定的壁面法向网格尺度基本一致.本文开展的高超声速二维完全气体及真实气体效应算例、三维钝双锥算例的数值模拟结果均显示,这两种准则确定的壁面法向网格尺度满足热环境模拟的精度要求.4) 最后,结合本文提出的壁面参数预估方法,可将壁面参数网格雷诺数和MFP两种准则作为高超声速气动热数值计算中壁面法向网格尺度的确定方法.
参考文献
| [1] | Olynick D R, Henline W D.Numerical benchmarks for Navier-Stokes heating calculations on access to space vehicles,AIAA-1995-2078[R].Reston:AIAA,1995. |
| Click to display the text | |
| [2] | Siddiqui M S, Hoffman K A,Chiang S T,et al.A comparative study of the Navier-Stokes solvers with emphasis on the heat transfer computations of high speed flows,AIAA-1992-0835[R].Restion:AIAA,1992. |
| Click to display the text | |
| [3] | Hoffman K A, Siddiqui M S,Chiang S T.Difficulties associated with the heat flux computations of high speed flows by the Navier-Stokes equations,AIAA-1991-0457[R].Reston:AIAA,1991. |
| Click to display the text | |
| [4] | Papadopoulos P, Venkatapathy E,Prabhu D,et al.Current grid-generation strategies and future requirements in hypersonic vehicle design,analysis and testing[J].Applied Mathematical Modelling,1999,23(9):705-735. |
| Click to display the text | |
| [5] | Men'shov I S, Nakamura Y.Numerical simulations and experimental comparison for high-speed nonequilibrium air flows[J].Fluid Dynamics Research,2000,27(5):305-334. |
| Click to display the text | |
| [6] | Klopfer G H, Yee H C.Viscous hypersonic shock-on-shock interaction on blunt cowl lips,AIAA-1988-0233[R].Reston:AIAA, 1988. |
| Click to display the text | |
| [7] | 潘沙,冯定华, 丁国昊,等.气动热数值模拟中的网格相关性及收敛[J].航空学报,2010,31(3):493-499. Pan S,Feng D H,Ding G H,et al.Grid dependency and convergence of hypersonic aerothermal simulation[J].Acta Aeronautica et Astronautica Sinica,2010,31(3):493-499(in Chinese). |
| Cited By in Cnki (12) | |
| [8] | 程晓丽,艾邦成, 王强.基于分子平均自由程的热流计算壁面网格准则[J].力学学报,2010,42(6):1083-1089. Cheng X L,Ai B C,Wang Q.A wall grid scale criterion based on the molecule mean free path for the wall heat flux computations by the Navier-Stokes equations[J].Chinese Journal of Theoretical and Applied Mechanics,2010,42(6):1083-1089(in Chinese). |
| Cited By in Cnki (6) | |
| [9] | 阎超,禹建军, 李君哲.热流CFD计算中格式和壁面法向网格尺度若干问题研究[J].空气动力学学报,2006,24(1):125-130. Yan C,Yu J J,Li J Z.Scheme effect and grid dependency in CFD computations of heat transfer[J].Acta Aerodynamica Sinica,2006,24(1):125-130(in Chinese). |
| Cited By in Cnki (45) | |
| [10] | Gao Z X, Jiang C W,Lee C H.Improvement and application of wall function boundary condition for high-speed compressible flows[J].Science China Technological Sciences,2013,56(10): 2501-2515. |
| Click to display the text | |
| [11] | Gao Z X, Lee C H.A numerical study of turbulent combustion characteristics in a combustion chamber of a scramjet engine[J].Science China Technological Sciences,2010,53(8):2111-2121. |
| Click to display the text | |
| [12] | Holden M S, Wieting A R,Moselle J R,et al.Studies of aerothermal loads generated in regions of shock/shock interaction in hypersonic flow,AIAA-1988-0477[R].Reston:AIAA,1988. |
| Click to display the text | |
| [13] | Klaus H, Jan M S,Sebastian K,et al.Cylinder shock layer density profiles measured in high enthalpy flows in HEG,AIAA-2002-2913[R].Reston:AIAA,2002. |
| [14] | Gupta R N, Yos J M,Thompson R A,et al.A review of reaction rates and thermodynamic and transport properties for the 11 species air model for chemical and thermal nonequilibrium calculations to 30000 K,NASA-TM-101528[R].Washington,D.C.:NASA,1989. |
| Click to display the text | |
| [15] | Miler C G III. Experimental and predicted heating distributions for biconics at incidence in air at Mach 10,NASA-TP-2334[R].Washington,D.C.:NASA,1984. |
| Click to display the text |
