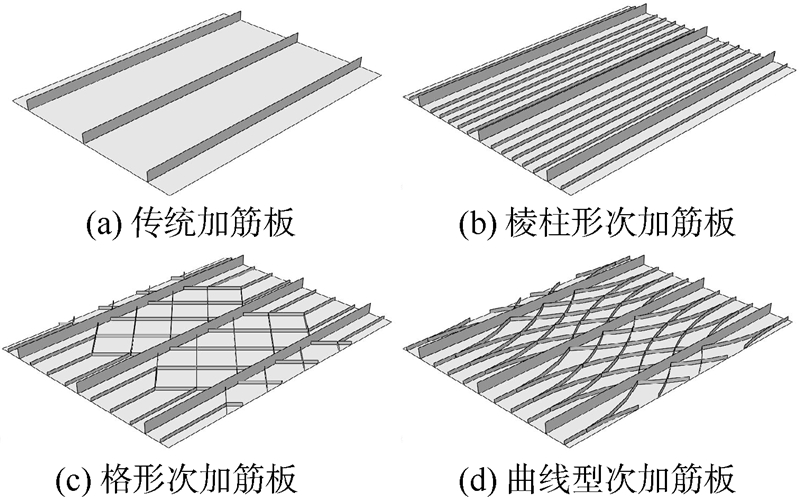
 |
| 图 1 传统加筋板和次加筋板的比较Fig. 1 Comparison between traditional stiffened panel and sub-stiffened panels |
| 图选项 |
 |
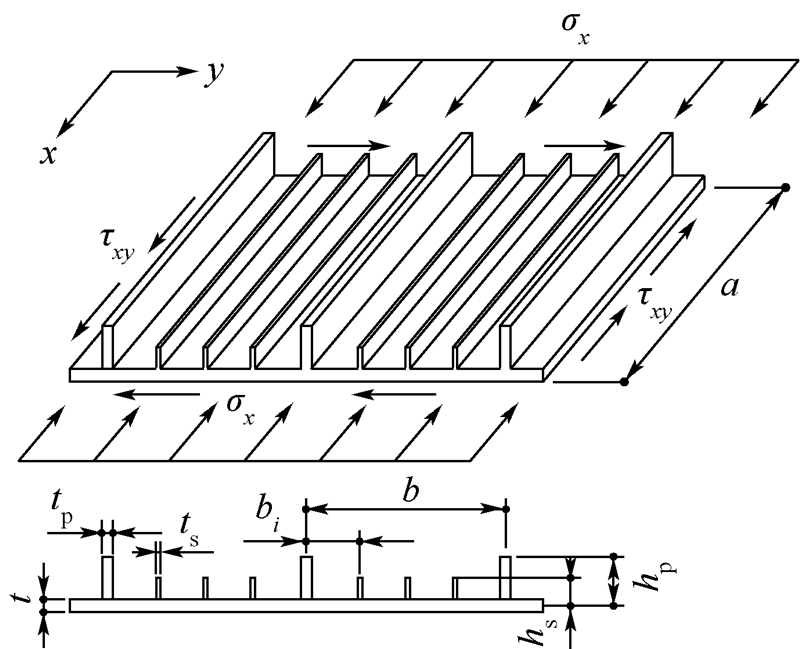| t—平板厚度；a—次加筋板长度； b—带板宽度；bi—次筋条之间平板宽度; hp,hs—主、次加筋的高度;tp,ts—主、次加筋条的厚度. 图 2 次加筋板的主要尺寸与载荷的示意图 Fig. 2 Schematic diagram of primary dimensions and load of sub-stiffened panel |
| 图选项 |
假设平板部分作用有正应力σx和切应力τxy.在厚度方向上应力是均匀分布的,单位长度的压缩和剪切内力分别为:Nx=σx·t,Nxy=τxy·t.主、次筋条的端面应力与平板的端面应力σx相同,主、次筋条端面合力分别为:Np=hp·tp·σx,Ns=hs·ts·σx.1.2 基本假设和失稳载荷近似计算方法为了简化问题,采取如下假设:忽略材料非线性的影响,只研究次加筋薄壁板弹性稳定性问题;采用Kirchhoff板假设和小变形假设;主筋条不会发生失稳,即次加筋板不会发生整体失稳;不考虑筋条对板的扭转约束限制,即筋板连接处看作简支约束.文献[5]和有限元数值仿真表明,棱柱形次加筋板主要可能发生3种失稳情况:①次筋条之间的板发生失稳.②次筋条发生局部失稳.③主筋条之间,由次筋条和平板组成的带板发生整体失稳.当其中之一的情况出现时就认为棱柱形次加筋板发生了失稳.失稳模式示意图如图 3所示.
 |
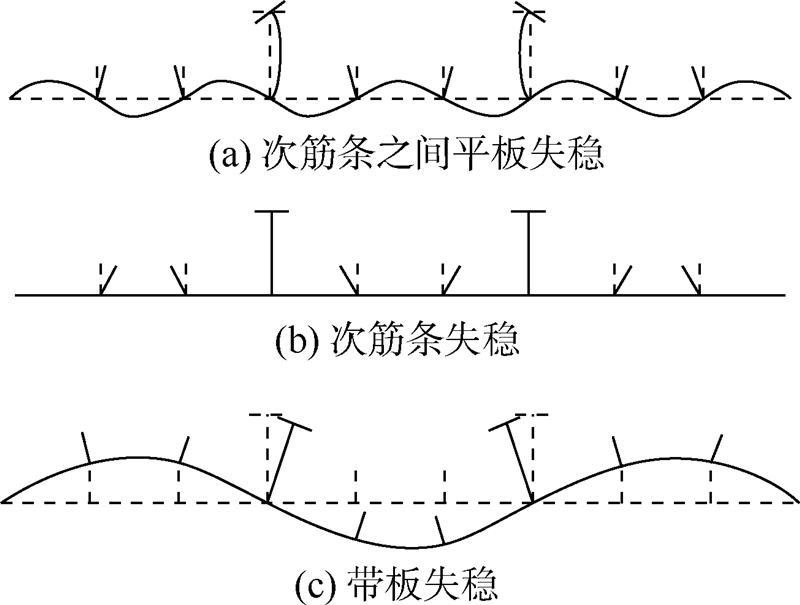| 图 3 次加筋板失稳模式示意图Fig. 3 Schematic diagram of buckling forms of sub-stiffened panel |
| 图选项 |
1.2.1 次筋条之间的平板失稳[11]当次筋条与它们之间平板的弯曲刚度比值较大时,容易发生该种失稳.特征是次筋条与板连接处保持为直线,次筋条之间的板在y轴方向呈现出一个半波,x轴方向呈现若干个半波.此时,次筋条之间的平板可看作是四边简支的弹性板.当仅在纵向压缩载荷Nx或剪切载荷Nxy作用下,可使用经典的矩形板屈曲载荷计算公式:
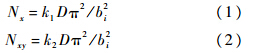
式中,D为板的弯曲刚度;k1,k2为稳定系数.对于大多数情况,面板的长宽比远大于4,可近似看作为无限长板,k1可以近似取为4.k2可由拟合公式得:k2=(5.34+4(bi/a)2),a,bi分别为次筋条之间的平板的长度和宽度.当受到均布压剪组合载荷作用时,次加筋板的屈曲载荷可用下式计算:
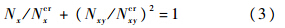
式中,Nxcr为仅在纵向压缩载荷作用时屈曲载荷;Nxycr为仅在剪切载荷作用时屈曲载荷.1.2.2 次加筋条发生局部屈曲当次筋条高厚比很大的时候,会发生此类失稳.特征是筋条与板相连接处仍保持为直线,自由端在筋条面外方向产生若干个半波.因此,次筋条可以看作长宽比很大、三边简支、一边自由的板条.在失稳发生时,次筋条端面应力与平板端面应力相同.由于筋条承受面外横向载荷能力很弱,因此忽略筋条承受该方向外载的能力.用经典矩形板屈曲载荷理论可以得到次筋条在该边界条件下的屈曲载荷[12]:
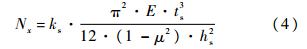
式中ks为稳定系数.次筋条长宽比很大,稳定系数可取为ks=0.425[13].1.2.3 带板发生整体屈曲当主筋条与带板的弯曲刚度之比较大,且次筋条的弯曲刚度和高厚比较小时,容易发生此类失稳.特点是主筋条间的带板发生了整体失稳,对于一般的航空薄壁结构,在y轴方向有一个半波,在x轴方向有若干半波.这一结构可看作四边简支的加筋板.当次筋条的数目比较密(大于2)时,带板可进一步看作正交各向异性板.带板的等效各向异性板厚度可表示为
式中ns为次筋条个数.当该等效性板仅在纵向压缩载荷作用下,屈曲载荷计算公式为[11]
式中,
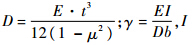为次筋条的惯性矩.计算临界屈曲载荷时,m可能取为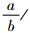
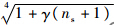向下取整和向上取整的两个整数,且真实的m应使屈曲载荷取最小.当该等效各向异性板仅在剪切载荷作用下,可通过下式计算得到屈曲载荷[11]: 
式中,p±m=奇数；q±n=奇数,m,n,p,q均为正整数；D1=D(1+γ(ns+1)).当Amn取A11，A13，A31，A33，A22这5项进行计算时,得到5个方程组成的方程组,令其系数行列式为零,从而得到屈曲载荷Nxy,且得到的结果已经足够精确[11].本文后面的计算均取这5项进行计算.当该等效各向异性板在压剪组合载荷作用下,重新改写式(3),得到屈曲载荷计算公式:
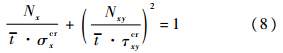
式中,σxcr为纵向压缩载荷单独作用时的临界屈曲应力值；σxycr为剪切载荷单独作用时的临界应力值. 1.2.4 小 结在计算次筋条数大于2的次加筋板的临界屈曲载荷时,综合以上3种失效情况,取它们中的最小值为屈曲载荷.同时,最小值所对应的失稳模态,即为次加筋板的屈曲模态.该计算方法没有考虑主筋条对次加筋壁板稳定性的影响,在使用时应注意满足假设条件.2 公式准确度的有限元验证若要上述计算方法能够计算次加筋板失稳载荷,首先要求理论公式在计算各个失稳形式时有较高的准确度,因此有必要对它们的计算结果准确性进行有限元验证.2.1 用于验证准确度的有限元模型采用ABAQUS软件进行有限元分析.材料为2024-T351铝合金,弹性模量E=73.8 GPa,泊松比μ=0.33,密度ρ=2 780 kg/m3.根据有关文献的建议[14, 15],计算加筋板屈曲时,宜采用四节点四边形壳单元S4R,每个屈曲的半波之间至少设计6个网格.针对1.2节提出的3种失稳形式,分别建立了3个有限元模型,如图 4所示.图 4(a)模型：四边简支,a=590 mm,bi=27.8 mm,t=2 mm;图 4(b)模型：三边简支,一边自由,a=590 mm,hs=10 mm,ts=1.5 mm;图 4(c)模型：四边简支,a=590 mm,b=167 mm,t=2 mm,均匀分布着5根次筋条,高度和宽度与图 4(b)尺寸相同.
 |
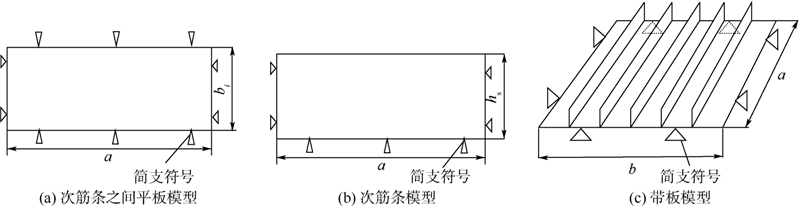| 图 4 准确度验证有限元模型Fig. 4 Finite element models for accuracy verification |
| 图选项 |
2.2 结果与讨论对上述模型分别在纵向压缩载荷和压剪载荷比例1∶0.5的组合载荷作用下进行计算.由于筋条不能承受剪切载荷,因此在压剪组合载荷作用时不考虑失效形式2.计算结果见表 1.表 1 有限元模型计算结果Table 1 Calculation results of finite element models
| 失效形式 | 压剪载荷比例 | 有限元计算/ 105 Pa | 理论计算/ 105 Pa | 误差/% | ||
| Nx | Nxy | Nx | Nxy | |||
| 1 | 1 : 0 | 28.0 | 0 | 28.1 | 0 | 0.4 |
| 2 | 8.92 | 0 | 9.77 | 0 | 9.5 | |
| 3 | 1.96 | 0 | 2.10 | 0 | 6.9 | |
| 1 | 1 : 0.5 | 25.4 | 12.7 | 25.3 | 12.6 | 0.4 |
| 2 | 1.69 | 0.85 | 1.74 | 0.87 | 2.7 | |
表选项
当受载情况为纵向压缩载荷时,失效形式1的结果准确度很高,失效形式3准确度适中,失效形式2结果稍差,但仍有足够的准确度(不超过10%).结果稍差的原因可能是由于文献中失效形式2的稳定系数ks值存在一定误差.当受载情况为压剪组合载荷时,失效形式1和3均有较高的准确度.从两种工况中的相应结果可以看出剪力的存在对失效形式1的误差影响很小,而对失效形式3,剪力的存在使误差减小.综合以上结论,3种失效形式理论公式具有较高的准确度.3 计算方法适用性的有限元验证3.1 整体次加筋壁板有限元模型材料属性和网格划分方法均与第2节一致.为保证主筋条不易发生弯曲失稳,选用了弯曲刚度较大的T字形筋条.次筋条为刀片形,均匀布置在主筋条之间.为了较为准确地模拟真实结构边界条件,模型在平行x轴的边向外延伸了一定的长度,结构形式如图 5所示.模型在x轴方向的两端面处简支,另两端面处自由.
 |
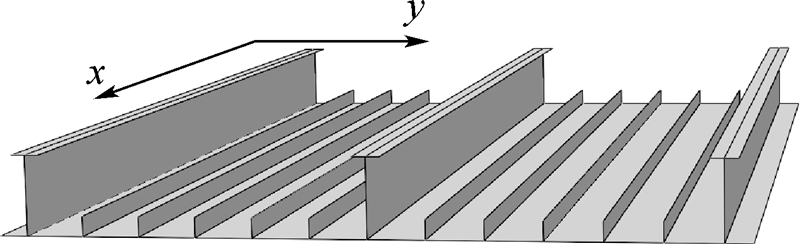| 图 5 次加筋板的有限元模型(次筋条数可以不同)Fig. 5 Finite element model of sub-stiffened panel (sub-stiffener numbers may be different) |
| 图选项 |
为了不失一般性,针对不同的次加筋带板的长宽比,次筋条的高厚比,压剪载荷比例建立了9个有限元模型.这些模型中相同的基本参数是:t=2 mm,hp=40 mm,tp=2 mm,ts=1.50 mm.模型其他参数以及受载情况见表 2.表 2 整体次加筋板模型参数Table 2 Model parameters of integral sub-stiffened panel
| 模型编号 | 板长/mm | 带板宽度 | 次筋条数 | 次筋高度/mm |
| 1 | 300 | 300 | 5 | 10 |
| 2 | 500 | 300 | 5 | 10 |
| 3 | 700 | 300 | 5 | 10 |
| 4 | 1 200 | 300 | 5 | 10 |
| 5 | 590 | 167 | 5 | 8 |
| 6 | 590 | 167 | 5 | 10 |
| 7 | 590 | 167 | 5 | 20 |
| 8 | 590 | 167 | 3 | 10 |
| 9 | 590 | 167 | 7 | 10 |
表选项
3.2 结果与讨论对模型1~4分别在纵向压缩载荷和压剪比例1∶0.5的组合载荷作用下进行计算,结果见表 3.由于压剪载荷比例已知,因此下面的所有表格中理论结果均为Nx值. 表 3 模型1~4计算结果Table 3 Calculation results of model 1-4
| 压剪 载荷比 | 模型编号 | 有限元 结果/kPa | 理论 结果/kPa | 失效形式 | 误差/% |
| 1∶0 | 1 | 99.2 | 93.5 | 3 | 5.8 |
| 2 | 57.0 | 53.5 | 3 | 6.0 | |
| 3 | 55.1 | 54.3 | 3 | 1.5 | |
| 4 | 54.8 | 51.6 | 3 | 5.7 | |
| 1∶0.5 | 1 | 96.3 | 89.8 | 3 | 6.8 |
| 2 | 53.6 | 49.3 | 3 | 8.2 | |
| 3 | 49.7 | 46.7 | 3 | 6.0 | |
| 4 | 40.3 | 44.5 | 3 | 10.4 |
表选项
模型1~4长宽比不同,当压剪载荷比为1∶0时,最大误差出现在模型2,仅为6%.当压剪载荷比为1∶0.5时,所有模型误差均比纵向压缩载荷作用时的误差大,除模型4的结果外,其他模型误差均可接受.进一步检查模型4,发现造成误差过大的原因是长宽比过大时,主筋条抑制板剪切失稳的能力不足,结构发生了整体失稳(如图 6),这与理论公式假设的主筋条不发生弯曲失稳不符,造成了误差增大.
 |
| 图 6 模型8的屈曲模态Fig. 6 Buckling modal of model 8 |
| 图选项 |
对模型5~7分别在纵向压缩载荷和压剪比例1∶0.5的组合载荷作用下进行计算,结果见表 4. 表 4 模型5~7计算结果Table 4 Calculation results of model 5-7
| 压剪 载荷比 | 模型 编号 | 有限元 结果/kPa | 理论 结果/kPa | 失效 形式 | 误差/% |
| 1∶0 | 5 | 163 | 155 | 3 | 4.6 |
| 6 | 200 | 210 | 3 | 4.7 | |
| 7 | 265 | 244 | 2 | 8.0 | |
| 1∶0.5 | 5 | 139 | 135 | 3 | 2.4 |
| 6 | 169 | 174 | 3 | 2.8 | |
| 7 | 248 | 244 | 2 | 1.4 |
表选项
模型5~7次筋条的高厚比不同,表 4显示,在两种工况下,结果的误差都在8%以内,理论公式结果与有限元结果符合得较好.其中,模型7由于次筋条过高,发生了第2种失效形式(次筋条失稳).由2.2节可知,失效形式2的理论计算公式比其他失效形式的理论公式误差更大,因而模型7在纵向压缩载荷作用时相对于其他模型的误差稍大.对模型8和9分别在纵向压缩载荷和压剪比例1∶0.5的组合载荷作用下进行计算,并将计算结果与模型6结果一同记录在表 5. 表 5 模型6,8,9计算结果Table 5 Calculation results of model 6,8,9
| 压剪 载荷比 | 模型 编号 | 有限元 结果/kPa | 理论 结果/kPa | 失效 形式 | 误差/% |
| 1∶0 | 6 | 200 | 210 | 3 | 4.7 |
| 8 | 168 | 182 | 3 | 8.5 | |
| 9 | 199 | 233 | 3 | 17.4 | |
| 1∶0.5 | 6 | 169 | 174 | 3 | 2.8 |
| 8 | 142 | 130 | 3 | 8.0 | |
| 9 | 179 | 190 | 3 | 6.4 |
表选项
模型6,8,9次筋条数目不同,结果显示除在压缩载荷作用下的模型9数据异常外,其他的误差都在8.5%以内,理论公式结果与有限元结果符合得较好.模型9误差较大的原因是次筋条个数过多,造成带板的弯曲刚度过高,导致主筋条抑制带板弯曲的能力变弱,主筋条发生了弯曲,这与第2节的基本假设不符.为验证分析是否正确且希望对模型的改动最小,仅将主筋条的翼板增加1倍,以增加主筋条抗弯刚度,有限元计算结果变为222 kPa,误差减小到5.21%.对模型6分别在压剪比例1∶0.2和1∶0.8的组合载荷作用下进行计算,并将计算结果与模型6在其他载荷比例下的结果记录在表 6. 表 6 模型6在不同压剪载荷比计算结果Table 6 Calculation results of model 6 under different compression and shear load ratios
| 压剪 载荷比 | 有限元 结果/kPa | 理论 结果/kPa | 失效 模式 | 误差/% |
| 1∶0 | 200 | 210 | 3 | 4.7 |
| 1∶0.2 | 194 | 202 | 3 | 4.2 |
| 1∶0.5 | 169 | 174 | 3 | 2.8 |
| 1∶0.8 | 143 | 145 | 3 | 1.7 |
表选项
计算结果显示误差均在5%以内,理论与有限元结果符合得较好.剪力的存在对误差有一定影响,但是影响的效果不确定:表 3的结果显示剪力的存在增大了误差,表 6的结果显示剪力的存在减小了误差,从各个模型的计算结果来看,剪力的影响都不是很大.从上述的讨论中可以得到,在满足理论公式假设的前提下,即主筋条不发生弯曲失稳时,提出的计算方法适用于计算次加筋板屈曲载荷,且有一定准确度.4 结 论1) 本文提出的棱柱形整体次加筋板计算公式仅适用于主筋条间次筋条个数大于2个的情况,且次加筋板不会发生整体失稳.否则,将会产生较大误差.2) 针对3种失效形式而提出的计算公式,无论在纵向压缩载荷作用下还是压剪组合载荷作用下,公式计算结果与有限元结果的误差都不大于10%,有较高的准确度.3) 针对不同的次加筋带板的长宽比、次筋条的高厚比,以及不同压剪载荷比例,本文提出的计算方法与有限元仿真的结果符合得较好,反映出该方法具有较为广泛的适用性,非常适合用于结构的初步设计阶段进行近似计算,以及加快棱柱形次加筋板的优化速度.
参考文献
| [1] | Mulani S B, Slemp W C H,Kapania R K.EBF3PanelOpt:an optimization framework for curvilinear blade-stiffened panels[J].Thin-Walled Structures,2013,63:13-26. |
| Click to display the text | |
| [2] | Murphy A, Quinn D,Mawhinney P,et al.Tailoring static strength performance of metallic stiffened panels by selective local sub-stiffening[C]//Proceedings of the Forty Seventh AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference.Reston:AIAA,2006:1-4. |
| Click to display the text | |
| [3] | Farley G L. Selective reinforcement to enhance the structural performance of metallic compression panels[C]//45th AIAA/ASME/ASCE/AHS/ASCSDM Conference.Reston:AIAA,2004. |
| Click to display the text | |
| [4] | Bushnell D, Rankin C.Optimum design of stiffened panels with substiffeners[C]//46th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference.Reston:AIAA,2005:1-54. |
| [5] | Watson A, Featherston C A,Kennedy D.Optimization of postbuckled stiffened panels with multiple stiffener sizes[C]//Proceedings of the Forty Eighth AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference.Reston: AIAA,2007:23-26. |
| Click to display the text | |
| [6] | Quinn D, Murphy A,Mcewan W,et al.Non-prismatic sub-stiffening for stiffened panel plates-stability behaviour and performance gains[J].Thin-Walled Structures,2010,48(6):401-413. |
| Click to display the text | |
| [7] | Quinn D, Murphy A,Mcewan W,et al.Stiffened panel stability behaviour and performance gains with plate prismatic sub-stiffening[J].Thin-Walled Structures,2009,47(12):1457-1468. |
| Click to display the text | |
| [8] | Özakça M, Murphy A,Van der Veen S.Buckling and post-buckling of sub-stiffened or locally tailored aluminium panels[C]//25th International Congress of the Aeronautical Sciences.Bonn:ICAS,2006:3-8. |
| Click to display the text | |
| [9] | Khvyiuzov A, Xu Y M.Initial buckling of compressed rectangular panels with variable stiffener sizes[J].Advanced Materials Research,2014,915:150-164. |
| Click to display the text | |
| [10] | 王博,田阔, 郝鹏,等.多级加筋板结构承载性能与缺陷敏感度研究[J].固体火箭技术,2014,37(3):408-412. Wang B,Tian K,Hao P,et al.Load-carrying capacity and imperfection-sensitivity analysis of hierarchical stiffened panels[J].Journal of Solid Rocket Technology,2014,37(3):408-412(in Chinese). |
| Cited By in Cnki | |
| [11] | 肖明心. 板的稳定理论[M].1版.成都:四川科学技术出版社,1993:61-87. Xiao M X.Stability theory of plate[M].1st ed.Chengdu: Sichuan Science and Technology Press,1993:61-87(in Chinese). |
| [12] | Timoshenko S. Theory of elastic stability[M].2nd ed.Dover:Dover Publications Inc,2009:348-356. |
| [13] | Bleich F. Buckling strength of metal structures[M].New York:McGraw-Hill,1952:349-385. |
| [14] | Lynch C, Murphy A,Price M,et al.The computational post buckling analysis of fuselage stiffened panels loaded in compression[J].Thin-Walled Structures,2004,42(10):1445-1464. |
| Click to display the text | |
| [15] | Murphy A, Price M,Lynch C,et al.The computational post-buckling analysis of fuselage stiffened panels loaded in shear[J].Thin-Walled Structures,2005,43(9):1455-1474. |
| Click to display the text |
