按适航要求^[1],在民用飞机结构定型阶段,要全面考虑各种分散性因素评定机群的可靠性寿命,影响飞机结构寿命分散性的因素主要分为结构特性分散性和载荷谱分散性^{[2, 3, 4, 5, 6]}.关于结构特性分散性,国内外已经有大量理论以及试验研究,形成了比较成熟的分析方法^{[7, 8, 9, 10, 11]}.载荷分散性指的是由于机群内飞机的结构特性、飞行员水平、天气情况、跑道质量等存在差异,导致机群内飞机实际经历的载荷-时间历程分散,即规定使用方法或相同的使用方法下导致的载荷差异性^[12].相对于结构分散性而言,研究载荷分散性需要获取机群足够数量的载荷数据,这一过程需要耗费大量的物力和财力,因此载荷分散性研究相对较少.载荷谱分散性的描述方法很多,其中一个非常重要的方面是机群载荷谱损伤的分散性.随着载荷监控设备的广泛使用,载荷谱损伤分散性对飞机结构寿命的影响受到越来越多的关注.在军用飞机领域,文献^[13]以202架F-15E飞机的载荷数据为基础,通过疲劳计算分析讨论了载荷谱损伤的分散性,文献^[14]给出了我国某型军用飞机载荷谱损伤服从对数正态分布的结论,文献^[15]选取5个单机谱,进行了疲劳试验,验证了载荷损伤可取对数正态分布的结论,为军用飞机在综合载荷和结构分散的机群可靠性寿命分析奠定了良好的基础.在民用飞机领域,文献^[16]利用飞行距离以B747-400为例给出使用情况差异对地-空-地载荷损伤分散性的影响,文献^[17]针对通用类飞机进行了机群飞机载荷因子-超越数曲线的分散性研究,文献^[18]采用“Damage Index”模型对Fokker F27飞机的载荷谱分散性进行了计算分析,但是损伤评估方法不具有通用性,也未给出载荷损伤的描述模型.由于民用飞机的使用特点与军用飞机明显不同,机群载荷谱损伤分散形式和分散程度也不一定相同,必须对其进行深入研究.因此,本文以拥有大量载荷数据的小型民用运输机Fokker F27为例,通过计算分析,研究载荷谱损伤分散性的描述方法.1 单机载荷谱编制1.1 机群载荷因子-超越数曲线筛选1) 载荷因子-超越数曲线族.文献^[18]给出了63架Fokker F27飞机的每次飞行载荷因子-超越数数据,其峰值载荷因子分别为1.25g,1.55g,1.95g和2.35g,谷值载荷因子分别为0.75g,0.45g,0.05g和-0.35g.上述63架飞机来自于5个地区29名飞行员的使用经历,飞机的使用地域见文献^[18]表 4.2) 数据筛选.进行机群寿命评定时,分析对象是按相同的使用方法进行使用的飞机,为了保证载荷因子-超越数曲线来源于同一个母体,需要对文献^[18]中飞机的载荷因子-超越数曲线进行筛选.①筛选原则:飞机的使用方法基本相同,每次飞行时间基本相当,飞行次数和飞行时间比较接近^[19].②筛选结果文献^[18]指出澳大利亚编号分别为10131，10132，10444和10445的4架飞机使用情况偏严重,认为使用情况不同.将上述4架飞机删除后,对剩余的59架飞机的载荷因子-超越数曲线族进行分析,发现非洲编号为10193、欧洲编号为10116以及澳大利亚编号为10135的3架飞机平均每次飞行所有测量载荷因子的超越数增量均小于1,使用情况偏轻,有理由认为上述7架飞机的使用情况与其他飞机不同,从而删除上述7架飞机的载荷数据.对剩余56架飞机的载荷-超越数数据、飞行时间和飞行次数进行检查后,将56架飞机作为按相同使用情况使用的同类飞机,认为其载荷因子-超越数数据属于同一母体.1.2 外推峰谷值累积超越数Fokker F27载荷因子数据记录于1961年至1976年间,采用英国Mechanism Ltd的“Fatigue meter”按“Peak between mean”方法进行计数,这种计数方法会造成峰、谷值累积超越数不相等.文献^[18]给出的Fokker F27飞机的谷值累积超越数低于峰值累积超越数,为了编制飞机的载荷谱,需要将谷值对应的载荷超越数曲线外推至与峰值累积超越数相同.为此,参考文献^[20]采用一般对数多项式方程拟合谷值-累积超越数曲线.
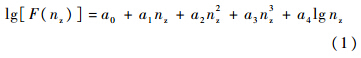
式中,F(n_z)为各级重心载荷n_z的累积频数,n_z为重心法向载荷因子;a₀，a₁，a₂，a₃和a₄为拟合曲线系数.将谷值-累积超越数曲线进行处理前后的56架飞机载荷因子-累积超越数曲线族见图 1.

图 1 Fokker F27飞机载荷因子-超越数曲线族Fig. 1 Load factor-exceedence curves of Fokker F27 airplanes

图选项

1.3 地-空-地循环对民用飞机结构而言,地-空-地循环为每次飞行过程中的最小和最大应力构成的循环,对应地面滑跑和着陆过程中的最小谷值载荷因子和空中飞行最大峰值载荷因子构成的完整循环,其中最大峰值载荷因子为每次飞行仅出现1次的峰值载荷因子n_z,once,其确定方法为:记峰值载荷因子按由大到小的顺序为n_zP,i(i=1,2,3,4),对应的超越数分别为ΔN_i(i=1,2,3,4),认为超越数对数与载荷因子呈线性关系,通过插值得到峰值载荷因子n_z,once^[18].由于上述飞机的ΔN₁>1,ΔN₂<1,从而取(n_zP,1,ln ΔN₁)和(n_zP,2,ln ΔN₂)两点线性插值确定n_z,once,计算公式为
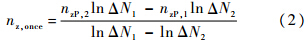
文献^[18]中未给出地面载荷数据,从而根据典型的民用运输机Boeing 737以及Airbus A320飞机的实际使用载荷数据,统一取地-空-地循环的谷值载荷因子为-0.2g^{[21, 22]}.1.4 载荷谱编制方法参考文献^[20]提出的载荷谱编制方法,根据每架飞机的载荷因子-累积超越数曲线,按如下步骤编制Fokker F27飞机的单机载荷谱:1) 分级离散.峰值曲线按照记录的载荷因子等级进行分级离散,即1.25g,1.55g,1.95g和2.35g.谷值曲线按照记录载荷因子等级和外推载荷因子值进行分级离散,即-0.35g,0.05g,0.45g,0.75g和外推载荷因子值.2) 分配载荷.将一架飞机各级载荷因子超越数增量取整后分配到每次飞行,对剩余的载荷因子随机分配到各次飞行,使得每次飞行谷值载荷因子与峰值载荷因子数目相匹配.保证每架飞机分配后的各级载荷因子数目之和与实际记录的各级载荷因子超越数相匹配.由此对每架飞机而言,最终编制形成一个包含多次飞行的长谱.3) 随机配对.每架飞机各次飞行的峰值载荷因子与谷值载荷因子按照谷值-峰值的顺序随机配对,并连接形成一个多次飞行的飞行载荷长谱,检验在该谱中各级载荷超越数与分级离散结果是否相同.4) 关于地-空-地循环载荷的考虑.将1.3节求得的每架飞机的地-空-地循环谷值载荷因子与峰值载荷因子,按照谷值-峰值的顺序插入到每次飞行的末尾,得到飞机实际使用载荷谱.由此编制得到的典型单机载荷谱局部构成见图 2.

图 2 Fokker F27飞机载荷谱(局部)Fig. 2 Load spectrum of Fokker F27 (part)

图选项

2 损伤计算2.1 损伤计算方法不考虑结构特性的分散,避免材料和结构部位的影响,采用基于由Smith，Watson和Topper等为反映平均应力的影响推出的SWT公式^[23]和线性累积损伤理论的方法计算载荷谱损伤.指定应力比下的S-N曲线用幂函数式来表示,即
S-N曲线参数m的值与材料、结构特性以及载荷情况相关.文献^[8]给出了综合考虑飞机结构多个关键部位不同材料及细节形式可能的m值范围的m值优化方法.并且给出了对应一般飞机载荷历程下的m值在4左右的结论,在本文计算中取m=4.按线性累积损伤理论,单个循环损伤为
式中,S_i，C_i为第i次应力循环下的S-N曲线参数;N_i为给定循环下的寿命.累积各次循环损伤得到全部循环损伤D的计算公式为
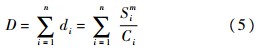
为了考虑载荷谱中的循环应力比的影响,取SWT公式将所有的载荷循环转换为对称循环(应力比为-1).其形式为
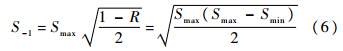
式中,S_max与S_min为一次载荷循环的最大值与最小值；R=S_max/S_min表示应力比；S_－1表示转换为应力比R=－1的对称循环后的峰值.根据文献^[14]中假设,在飞机对称飞行占主导地位的情况下,可以假定关键部位的应力与载荷因子呈线性的关系,即
式中,σ_1g为单位载荷因子对应的关键部位名义应力,并且认为全部载荷循环的σ_1g是相同的.将式(5)代入式(4)，将载荷因子转换为对称循环,整理得
式中,n_z,max和n_z,min为载荷因子的峰值与谷值;n_z,－1为R=－1时的对称循环载荷因子峰值.SWT公式转换载荷循环应力比R=－1后,S-N曲线的参数C为定值.式(8)可以进一步整理得
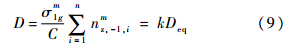
式中,k为常数；D_eq为与D呈线性关系的当量损伤.
本文编制的载荷谱为多次飞行的长谱,则每架飞机每次飞行当量损伤为
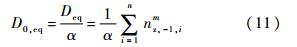
式中,D_0,eq为每次飞行当量损伤；α为每个载荷谱所包含的飞行次数.2.2 损伤计算过程1) 对载荷因子谱进行雨流计数^[24],抽取全循环和半循环.2) 按2.1中的方法对每个循环进行当量损伤计算.3) 按线性累积损伤理论计算得到总的当量损伤.2.3 损伤计算结果每架飞机每次飞行的飞行损伤、地-空-地载荷损伤(简记为GAG损伤)和总损伤见表 1.表 1 损伤计算结果Table 1 Result of damage calculation

序号	飞行损伤	GAG损伤	总损伤	R′		序号	飞行损伤	GAG损伤	总损伤	R′
1	2.260 92	4.738 67	7.150 82	0.66		29	2.640 20	4.966 72	7.819 87	0.64
2	2.022 64	4.712 97	6.929 74	0.68		30	2.433 92	4.921 53	7.576 96	0.65
3	2.433 09	4.981 41	7.635 89	0.65		31	2.544 55	5.051 28	7.847 18	0.64
4	3.676 21	5.161 59	8.987 90	0.57		32	3.015 15	5.391 84	8.705 04	0.62
5	1.334 38	4.306 19	5.816 38	0.74		33	3.226 22	5.355 06	8.843 99	0.61
6	2.684 09	5.143 76	8.091 34	0.64		34	2.570 67	4.957 39	7.743 86	0.64
7	3.248 09	5.053 99	8.474 81	0.60		35	2.340 00	4.841 22	7.403 33	0.65
8	3.507 96	5.227 79	8.944 08	0.58		36	1.673 27	4.532 24	6.352 54	0.71
9	1.763 95	4.506 14	6.446 32	0.70		37	2.295 39	4.770 95	7.227 62	0.66
10	2.060 88	4.759 31	7.075 14	0.67		38	2.406 23	5.055 34	7.740 25	0.65
11	3.702 98	5.666 42	9.817 19	0.58		39	1.102 17	4.101 38	5.491 29	0.75
12	1.650 95	4.557 20	6.377 79	0.71		40	2.961 40	5.308 64	8.576 66	0.62
13	2.624 21	5.651 72	8.559 10	0.66		41	3.489 28	5.483 19	9.253 54	0.59
14	3.384 38	5.526 41	9.211 39	0.60		42	1.964 93	4.720 67	6.907 48	0.68
15	2.978 24	5.205 65	8.433 29	0.62		43	1.192 81	4.173 51	5.557 14	0.75
16	1.615 05	4.467 83	6.185 25	0.72		44	2.042 37	4.692 49	6.940 91	0.68
17	0.917 87	3.933 00	4.969 60	0.79		45	3.505 12	5.888 97	9.845 06	0.60
18	2.229 95	4.767 07	7.171 19	0.66		46	4.081 16	6.103 99	10.599 20	0.58
19	2.087 41	4.702 72	6.945 58	0.68		47	2.238 77	4.782 61	7.212 73	0.66
20	2.364 34	4.921 53	7.487 62	0.66		48	2.206 49	5.059 39	7.545 02	0.67
21	3.918 71	5.934 56	10.133 10	0.59		49	2.084 56	4.665 70	6.915 85	0.67
22	2.483 73	4.950 74	7.633 31	0.65		50	1.722 51	4.475 22	6.314 65	0.71
23	2.042 92	4.839 91	7.108 22	0.68		51	2.651 47	5.901 11	9.020 28	0.65
24	1.877 10	4.825 54	6.891 29	0.70		52	2.176 73	5.212 57	7.756 22	0.67
25	0.865 69	3.897 28	4.860 94	0.80		53	2.811 87	5.593 17	8.857 28	0.63
26	2.727 74	5.255 57	8.227 59	0.64		54	2.364 71	4.974 73	7.689 75	0.65
27	1.999 03	4.677 17	6.829 86	0.68		55	1.917 98	5.037 79	7.208 01	0.70
28	2.537 31	4.948 08	7.699 73	0.64		56	1.275 48	4.389 49	5.855 79	0.75

表选项


按照式(12)计算每架飞机地-空-地载荷损伤占总损伤的比例,范围在0.57~0.80.计算结果一并列入表 1.
式中,D_GAG为地-空-地循环的损伤；D_T为总损伤,R′为GAG损伤占总损伤比例系数.2.4 编谱方法对载荷谱损伤的影响为研究在单机载荷谱编制中,随机配对和随机排序对载荷谱损伤的影响,依据机群每架飞机的载荷因子-累积超越数曲线,抽样5次,随机生成了5组载荷谱,并对每组载荷谱的当量损伤进行计算.比较5组载荷谱计算得到的当量损伤发现,当量损伤的误差范围在±1.82%,并且机群载荷谱损伤大小顺序未改变.因此认为利用本文采用的载荷谱编制方法随机生成一组载荷谱可以反映机群飞机间的差异性.3 机群载荷损伤分布特性分析3.1 分布特性检验方法考虑到飞机损伤的非负性,选择工程中常用的非负样本分布形式：对数正态分布、威布尔分布和指数分布.其分布函数为1) 对数正态分布:
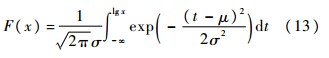
式中,μ为对数正态期望；σ为对数正态分布标准差.2) 威布尔分布(双参数):
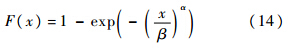
式中，α，β为威布尔分布参数.3) 指数分布:
式中,λ>0为常数.通常进行分布特性检验的方法有:χ²检验、克尔莫格洛夫检验、概率坐标纸检验等方法,本文采用概率坐标回归方法进行检验,其原理为将56架飞机的当量损伤按照从小到大的顺序排列x₁,x₂,x₃,…,x₅₆.按秩序统计理论,经验检验频率函数f依据国家标准GB/T4882—2001推荐采用
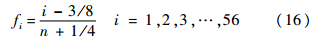
式中n表示样本的数量,在本文中n=56,i表示样本从小到大排列后该样本的序号.对于上述3种分布,根据其分布形式,将分布函数线性化后得到线性的检验方程.1) 标准正态分布:
式中,u_p为标准正态分布p分位点.2) 威布尔分布(双参数):
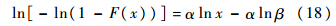
3) 指数分布:
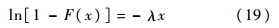
将56架飞机载荷谱当量损伤数据利用上述线性方程进行拟合,并进行回归分析.以相关系数高、拟合效果好作为选取准则,并综合考虑分布函数与散点图的逼近程度,选取最佳分布形式.3.2 机群载荷谱损伤分布特性检验1) 飞行载荷损伤分布特性.将机群飞行载荷当量损伤作为随机变量进行分布特性拟合优度检验,检验结果如表 2所示.表 2 机群飞行载荷谱损伤分布拟合优度Table 2 Goodness fit of fleet flight load spectrum damage distribution

分布	相关系数
对数正态	0.980 42
威布尔	0.990 76
指数	0.948 95

表选项


机群飞行载荷当量损伤拟合图和散点分布图分别见图 3，P为损伤累积概率.综合考虑,取威布尔分布作为最佳分布.

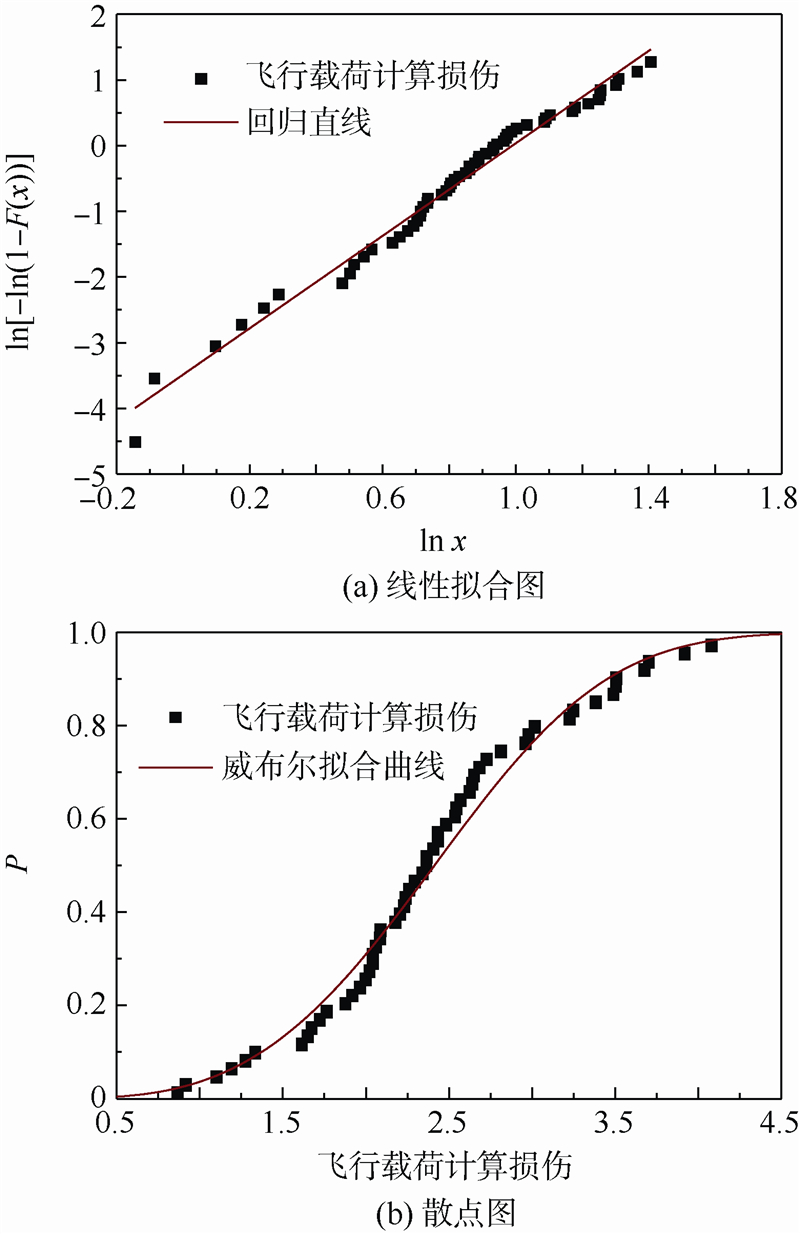图 3 飞行载荷损伤威布尔分布Fig. 3 Weibull distribution of flight load damage

图选项

利用最大似然估计方法估计威布尔分布参数.最大似然函数为
经过整理后得到最大似然估计方程组:
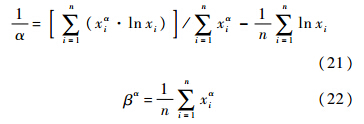
根据上述方程组选取α初值为α₀=1.2 x / s进行迭代求解分布参数.其中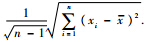飞行载荷当量损伤的概率分布函数为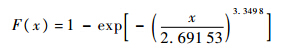
式中,x为机群飞行载荷当量损伤.2) 地-空-地载荷损伤分布.将机群地-空-地载荷损伤作为随机变量进行分布特性拟合优度检验,检验结果如表 3所示.表 3 机群地-空-地循环损伤分布拟合优度Table 3 Goodness fit of GAG cycle damage distribution

分布	相关系数
对数正态	0.991 82
威布尔	0.971 78
指数	0.947 98

表选项


机群地-空-地循环当量损伤线性拟合图与散点分布图分别见图 4.同理,取对数正态分布为最佳分布.

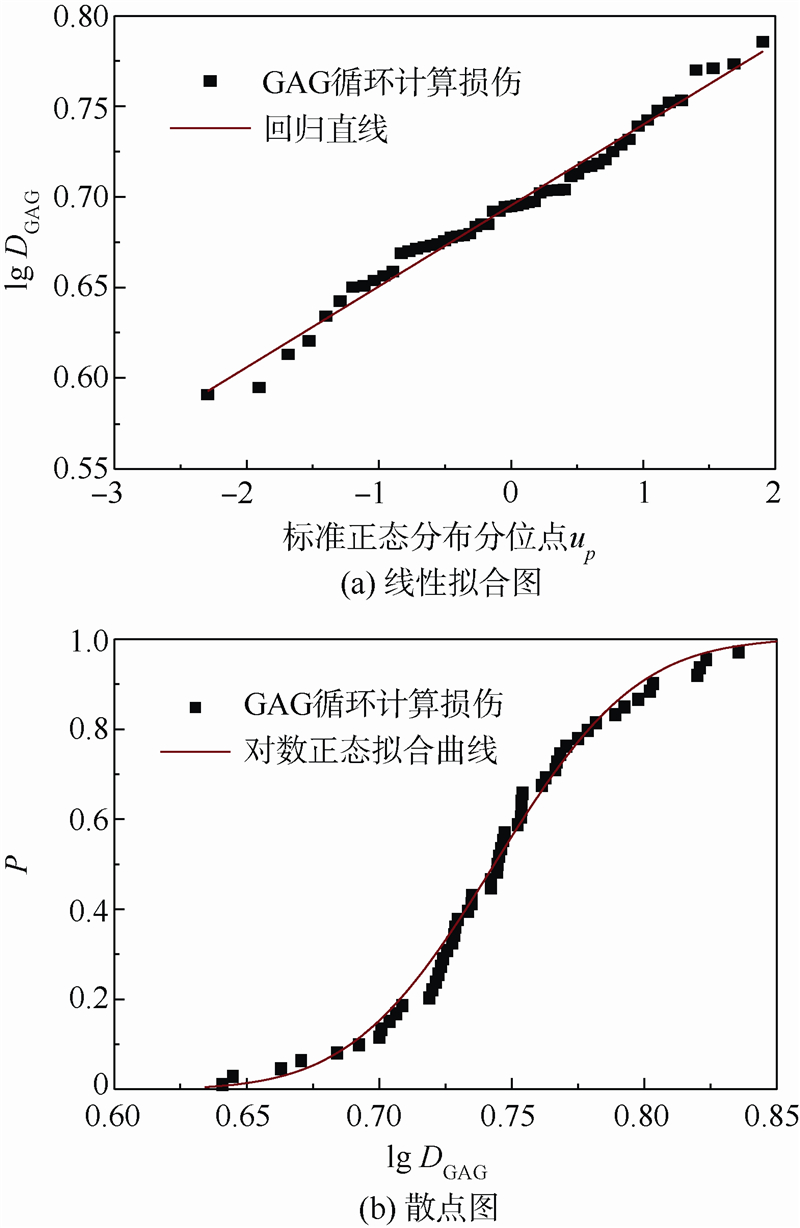图 4 GAG损伤对数正态分布Fig. 4 Lognormal distribution of GAG load damage

图选项

对数正态分布最大似然估计方程为
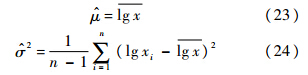
根据式(23)和式(24)计算出分布参数.机群地-空-地循环当量损伤的概率分布函数为
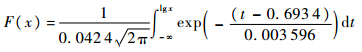
3) 每次飞行载荷损伤分布.将机群每次飞行载荷当量损伤作为随机变量进行分布特性拟合优度检验,检验结果如表 4所示.表 4 机群载荷谱损伤拟合优度Table 4 Goodness fit of fleet load spectrum damage distribution

分布	相关系数
对数正态	0.992 31
威布尔	0.982 82
指数	0.944 54

表选项


机群每架飞机每次飞行当量损伤线性拟合图与散点分布图如图 5所示.同理,取对数正态分布为最佳分布.

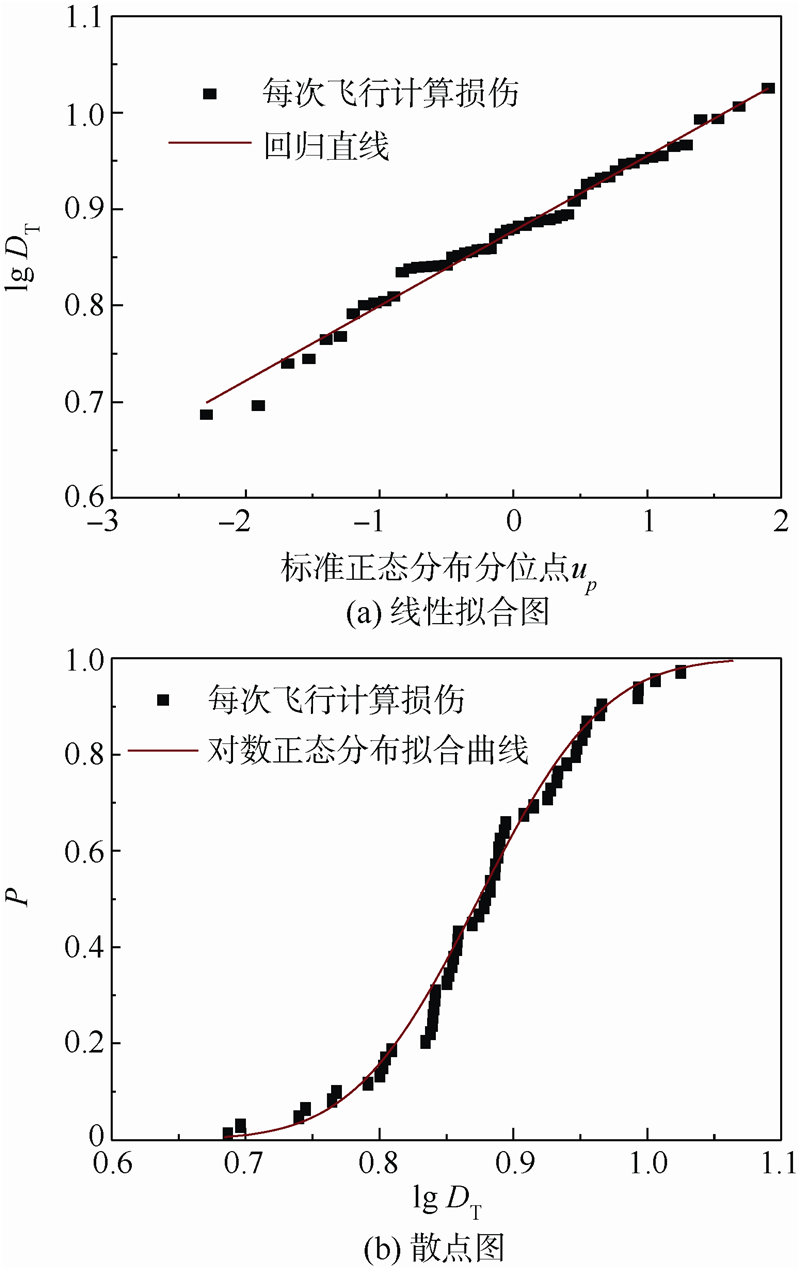图 5 机群载荷谱损伤对数正态分布Fig. 5 Lognormal distribution of fleet load spectrum damage

图选项

根据式(23)与式(24)估计对数正态分布参数,得到机群每架飞机每次飞行当量损伤的概率分布函数为
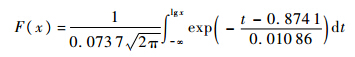
3.3 对比分析根据以上分析得出机群每次飞行的损伤样本与地-空-地循环损伤样本均服从对数正态分布,机群飞行载荷损伤样本服从威布尔分布.机群平均每次飞行载荷损伤样本的对数正态标准差为0.073 7,地-空-地循环损伤的对数正态标准差为0.042 4.机群地-空-地损伤占总损伤比例在0.57~0.80,与文献^[20]中给出的范围相当.由于Fokker F27为小型的民用运输机,跑道质量以及每架飞机起落时的速度等差异并不明显.空中飞行由于受到阵风、天气等因素的影响,则本文得出空中飞行的标准差较地-空-地载荷损伤更大是合理的.每次飞行损伤对数标准差已与结构特性分散性基本相当^[25],在民用飞机结构定寿阶段对载荷谱损伤分散性的考虑是十分必要的.4 结 论1) Fokker F27机群飞机每次飞行的飞行载荷当量损伤服从威布尔分布,Fokker F27机群飞机每次飞行的损伤与地-空-地循环的损伤服从对数正态分布.2) Fokker F27机群每次飞行损伤的对数正态标准差为0.073 7.3) Fokker F27飞机机群地-空-地循环损伤占总损伤的比例在57%~80%的范围.
参考文献

[1]	CCAR-25-R4 中国民用航空条例第25部运输类飞机适航标准[S].北京:中国民用航空局,2011:1-4. CCAR-25-R4 China civil aviation regulations Part 25 transport category aircraft airworthiness standards[S].Beijing:Civil Aviation Administration of China,2011:1-4(in Chinese).
[2]	Schijve J. Statistical distribution functions and fatigue of structures[J].International Journal of Fatigue,2005,27(9):1031-1039.
	Click to display the text
[3]	Tovo R. On the fatigue reliability evaluation of structural components under service loading[J].International Journal of Fatigue,2001,23(7):587-598.
	Click to display the text
[4]	de Jonge J B. Load experience variability of fighter aircraft[C]//Australian Aeronautical Conference of Australia.Canberra:The Institution of Engineers,1989:102.
	Click to display the text
[5]	Freudenthal A M, Gumbel E J.On the statistical interpretation of fatigue tests[J].Proceedings of the Royal Society A:Mathematical and Physical Sciences,1953,216(1126):309-332.
	Click to display the text
[6]	陈志伟. 载荷谱差异对疲劳寿命影响的研究[C].//第七届全国疲劳会议文集.北京:中国力学学会,1995. Chen Z W.Effect of spectrum difference on fatigue life[C]//Proceedings of the 7th Chinese National Fatigue Conference.Beijing:The Chinese Society of Theoretical and Applied Mechanics,1995(in Chinese).
[7]	Freudenthal A M. The scatter factor in the reliability assessment of aircraft structures[J].Journal of Aircraft,1977,14(2):202-208.
	Click to display the text
[8]	高镇同. 飞机结构疲劳分散系数,BH-B884[R].北京:北京航空学院,1982. Gao Z T.The fatigue scatter for aircraft structures, BH-B884[R].Beijing:Beijing Institute of Aeronautics,1982(in Chinese).
[9]	施耐康. 规范疲劳寿命及其标准差[J].航空学报,1987,8(10): 467-474. Shi N K.Normalize the fatigue life and standard variation[J].Acta Areonautica et Astronautica Sinica,1987,8(10):467-474(in Chinese).
	Cited By in Cnki (5)
[10]	Cardrick A W, Mew A B.Scatter considerations in the interpretation of major fatigue tests[C]//Proceedings of the ICAF Symposium.Seattle:International Committee on Aeronautical Fatigue,1999.
[11]	Hoffman M E, Hoffman P C.Corrosion and fatigue research-structural issues and relevance to naval aviation[J].International Journal of Fatigue,2001,23(Sup.1):1-10.
	Click to display the text
[12]	贺小帆,刘家曦, 王强,等.基于载荷损伤分散的严重谱选取准则初探[J/OL].北京:工程力学,2011(2012-05-11)[2014-05-21].http://gclx.tsinghua.edu.cn/CN/10.6052/j.issn.1000-4750.2011.11.0755. He X F,Liu J X,Wang Q,et al.Primary analysis on the selection method of severe load pectrum based on the fleet lod damage variation[J/OL].Beijing:Engineering Mechanics,2011(2012-05-11)[2014-05-21].http://gclx.tsinghua.edu.cn/CN/10.6052/j.issn.1000-4750.2011.11.0755(in Chinese).
[13]	Lincoln J W, Melliere R A.Economic life determination for a military aircraft[J].Journal of Aircraft,1999,36(5):737-742.
	Cited By in Cnki | Click to display the text
[14]	王智,刘文珽, 王磊.单机结构疲劳分散系数研究[J].机械强度,2009,31(1):150-154. Wang Z,Liu W T,Wang L.Study on the fatigue scatter factor for individual aircraft structure[J].Journal of Mechanical Strength,2009,31(1):150-154(in Chinese).
	Cited By in Cnki (7)
[15]	He X F, Sui F C,Zhai B,et al.Probabilistic and testing analysis for the variability of load spectrum damage in a fleet[J].Engineering Fatigue Analysis,2013,33:419-429.
	Click to display the text
[16]	王长江,姚卫星. 使用情况差异对民机载荷谱地空地损伤分散性的影响[J].机械强度,2013,35(5):668-673. Wang C J,Yao W X.GAG damage scatter of civil aircraft load spectra due to variation in aircraft usage[J].Journal of Mechanical Strength,2013,35(5):668-673(in Chinese).
	Cited By in Cnki
[17]	Locke J E, Smith H W,Gabriel E A,et al.General aviation aircraft-normal acceleration data analysis and collection project,KU-FRL-926-1[R].Kansas:Kansas University Lawrence Flight Research Lab,1993.
	Click to display the text
[18]	de Jonge J B, Hol P A.Variation in load factor experience:a re-analysis of Fokker F27 and F28 operational acceleration data[M].Amsterdam:National Aerospace Laboratory,1996:1-51.
[19]	贺小帆,王强, 刘文珽.基于Fokker 27飞机过载-超越数曲线族的严重超越数包线选取[J].航空学报,2013,34(4):840-845. He X F,Wang Q,Liu W T.A method for determining the exceedance envelope of severe spectrum based on the acceleration-exceedance curves of Fokker 27 airplanes[J].Acta Aeronautica et Astronautica Sinica,2013,34(4):840-845(in Chinese).
	Cited By in Cnki
[20]	蒋祖国,田丁栓, 周占廷.飞机结构载荷/环境谱[M].北京:电子工业出版社,2012:98. Jiang Z G Tian D Q,Zhou Z T.The aircraft structure load and environment spectra[M].Beijing:Publishing House of Electronics Industry,2012:98(in Chinese).
[21]	Rustenburg J, Skinn D,Tipps D O.Statistical loads data for boeing 737-400 aircraft in commercial operations,DOT/FAA/AR-98/28[R].Alexander:American Institute of Aeronautics and Astronautics,1998.
	Click to display the text
[22]	Rustenburg J W, Skinn D A,Tipps D O.Statistical loads data for the airbus a-320 aircraft in commercial operations,UDR-TR-2001-80[R].Alexander:American Institute of Aeronautics and Astronautics,2002.
	Click to display the text
[23]	Smith K N, Watson P,Topper T H.A stress-strain function for the fatigue of metals[J].Journal of Materials,1970,5(4):767-778.
[24]	刘文珽, 郑旻仲,费斌军,等.概率断裂力学与概率损伤容限/耐久性[M].北京:北京航空航天大学出版社,1998:38-41. Liu W T,Zheng M Z,Fei B J,et al.The probability fracture mechanics and probability damage tolerance/durability[M].Beijing:Beihang University Press,1998:38-41(in Chinese).
[25]	Parish H E. Fatigue test results and analysis 42 piston provost wings,3474[R].London:Her Majesty's Stationery Office,1967.
	Click to display the text