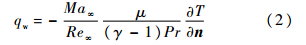高超声速飞行器气动热的精确预测是计算流体力学(CFD)最具挑战性的难题之一
[1].热流是由黏性起主导作用的物理现象,它的计算精度与物理模型、数值格式、计算网格、收敛过程、热流后处理等密切相关,这些多重因素的交错影响导致了热流计算的复杂性
[2].壁面热流依赖温度梯度在壁面上的精确计算,而高超声速边界层内的温度分布具有强非线性,要想获得准确的温度分布需要在边界层内布置大量的计算网格
[3],以往的文献均将网格雷诺数
[2](
Recell)作为衡量网格因素的重要参数,并研究了保证热流计算精度所需要的网格雷诺数条件
[3, 4, 5, 6].对于计算格式和收敛判别方面,姜振华和阎超
[2]研究了目前广泛使用的两类上风格式:Roe的FDS(Flux Difference Splitting)和AUSM(Advection Upstream Splitting Method)系列搭配不同限制器以及高阶格式对热流计算精度的影响;潘沙等
[3]研究了热流计算收敛性的判别标准;李君哲和阎超
[4]研究了几类上风格式对热流计算精度的影响.而高超声速流动的雷诺数很大,在一般的飞行器上均会发生转捩
[7],当流动从层流转变为湍流时,壁面摩阻和热流会迅速增大,壁面热流可以增大一个量级
[8].可以肯定的是,尽管DNS(Direct Numerical Simulation)能够给出简单流动问题的计算结果,但对于工程常见的复杂外形,DNS高昂的计算成本和时间成本让人望而生畏.本文结合已有文献对计算网格、数值格式以及限制器选取的研究结果,分析了4种工程常用的湍流模型:BL,SA,
k-ω,SST对热流计算精度的影响,并验证了计算精度较高的两方程模型(
k-ω与SST)搭配耗散性小的AUSMPW格式与混合限制器时对网格的依赖性.另外,对于一般的吸气式高超声速飞行器,由于飞行高度较低,控制舵处流态大多已发展为湍流,此时舵前缘的气动加热异常严峻
[9].文献
[10]中详细介绍了平板钝舵模型的研究现状,分析了不同因素对钝舵热流的影响.本文依据对湍流模型的评价结果,研究了不同后掠角对钝舵热流的影响,得到了钝舵前缘最大热流随后掠角的变化趋势. 1 数值计算方法 1.1 控制方程本文热流通过求解Reynolds平均N-S方程,守恒形式为
[11]
式中
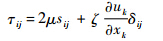
各参数的意义详见文献
[11].为了使式(1)封闭,需要对式(1)中的雷诺应力
τij做出各种假设.从对模式处理的出发点不同,一般可将湍流模式分为雷诺应力模型和涡黏性模型两类.受计算条件的约束,雷诺应力模型计算量巨大,使其应用范围受到限制,在工程湍流问题中广泛应用的是涡黏性模型
[12].因此本文选取4种涡黏性湍流模型进行计算.壁面热流
qw由下式计算:
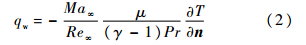
式中,
Ma∞和
Re∞为来流马赫数和雷诺数;
μ为气体动力黏性系数;普朗特数
Pr=0.72;两者比热之比
γ=1.4;
n 为壁面法向. 1.2 数值离散方法采用有限体积法求解雷诺平均可压缩N-S方程和模型输运方程;无黏通量采用Roe的FDS格式和AUSMPW格式,并通过限制器
[13]来抑制振荡;黏性通量采用二阶中心差分格式;时间推进采用LU-SGS(Lower-Upper Symmetric Gauss-Seidel)隐式方法. 2 湍流模型对热流计算的影响对文献
[10]中的双椭球风洞实验进行了数值模拟.该模型在低焓高超声速风洞中测得了详实的气动力及热流数据,且其流动不受真实气体效应的影响.由于实验雷诺数较高,因此可将其作为验证高超声速湍流模型性能的标准算例.计算条件为:
Ma∞=7.8,
T∞=56K,壁温
Tw=288K,来流雷诺数
Re∞=1.67×10
7m
-1,攻角为0°.计算网格共267万,壁面法向第1层网格雷诺数
Recell为10.采用耗散较小的AUSMPW格式和混合限制器计算.图 1给出了双椭球对称面上下表面处的压力分布与实验值的比较,其中压力分布通过来流静压
Pinf无量纲化.可以看出4种湍流模型均可给出正确的压力分布,并且与实验结果吻合良好.图 2给出了双椭球对称面上下表面的热流沿轴向的分布.由图可以看到,无论上下表面,BL模型与实验值相差较大,这是由于BL模型为零方程模型,它完全由当时、当地的平均流动参数的函数来决定,对存在较大逆压梯度以及分离再附等流动,该模式不能给出合理的结果.SA模型虽然能较好地模拟下表面的热流分布,但对上表面两椭球相贯处的激波-边界层干扰模拟不足.两种两方程湍流模型:Wilcox
k-ω模型和Menter SST模型对上下表面的热流分布模拟较好,但
k-ω模型对流动分离处的热流计算较大.SST模型计算结果与实验吻合较好,这是由于SST模型是
k-ε模型和
k-ω模型的混合模型,同时保持了
k-ω模型近壁面特性和
k-ε在尾迹区的特性,其借鉴了J-K模型的思想,对雷诺剪切应力进行了经验式的约束,计算效果较好
[14].
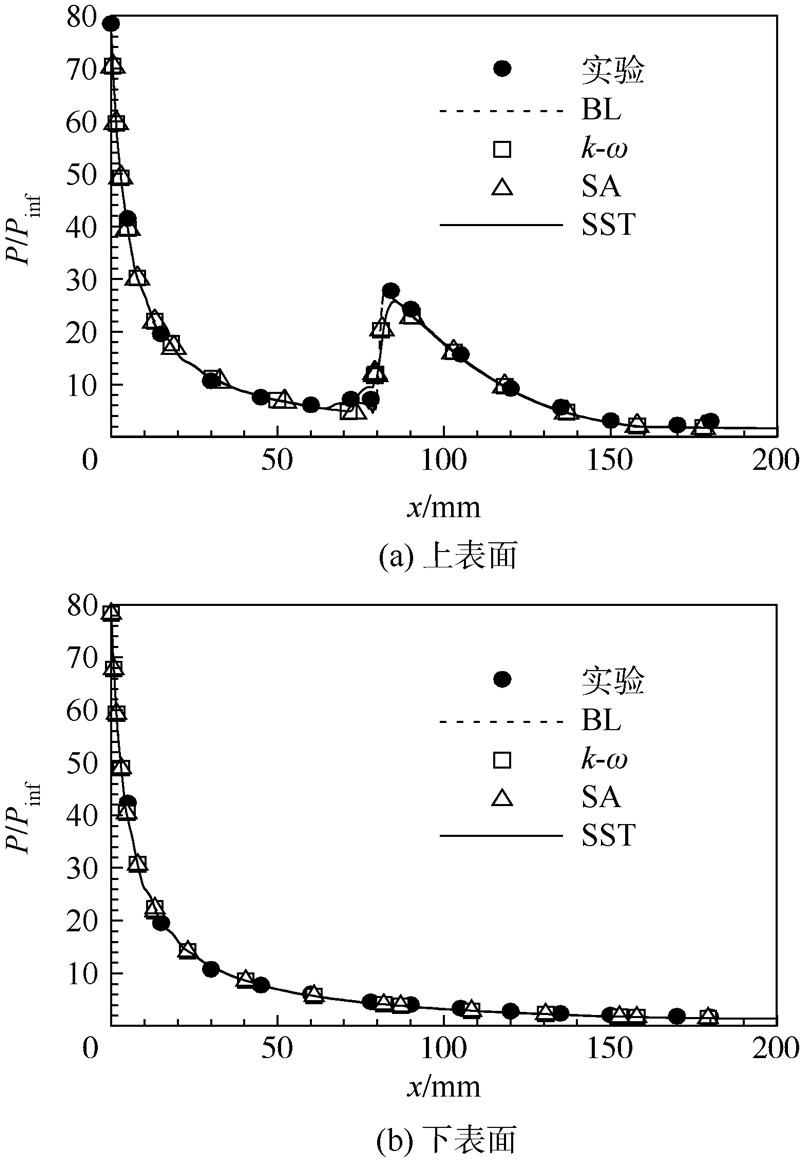 |
| 图 1 对称面上下表面压力分布Fig. 1 Pressure distribution on upper and lower symmetrical surface |
|
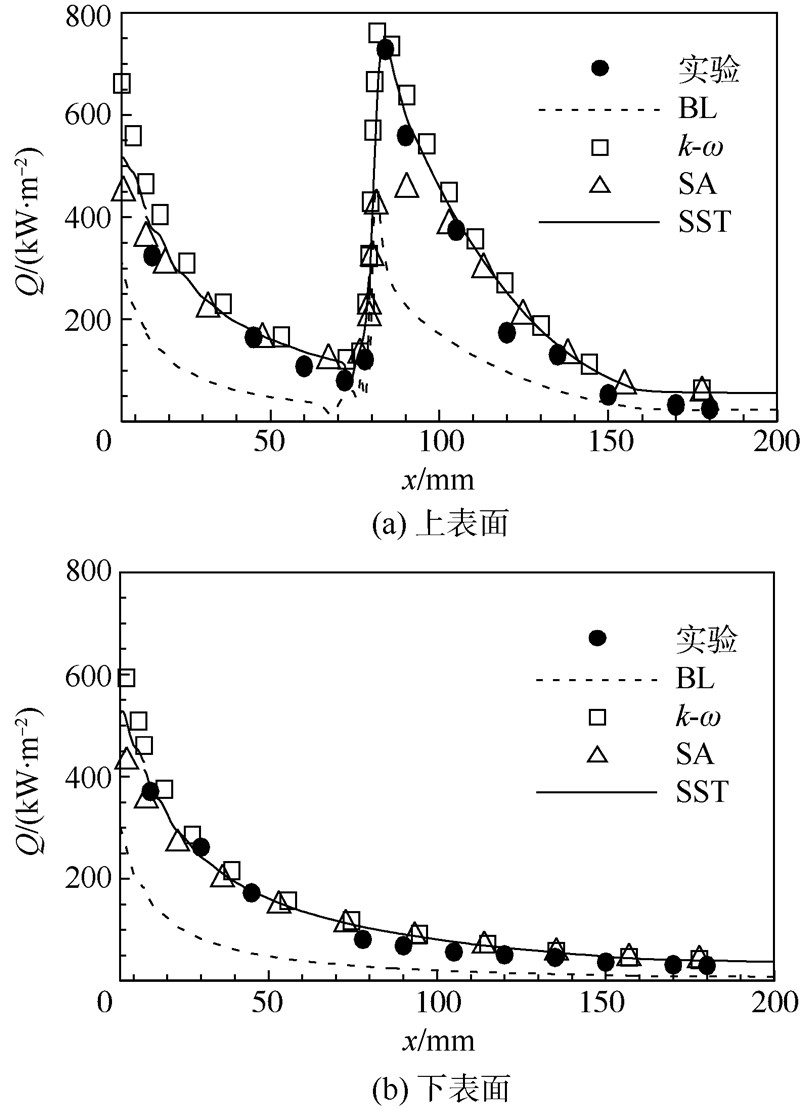 |
| 图 2 对称面上下表面热流分布Fig. 2 Heat flow distribution on upper and lower symmetrical surface |
|
3 网格雷诺数对热流计算的影响 由以上分析可知,两方程模型对热流计算具有较高的精度.为考察湍流模型下热流计算精度与网格雷诺数的关系,依旧选取双椭球模型,取网格雷诺数
Recell依次为30,10,5进行计算.
Recell为30的计算网格法向共80个点,为保证法向的过度小于1.1,
Recell为10和5的计算网格在法向上依次增加到100和120.并且,这3种网格雷诺数下
y+(平板自由来流结果预估)均小于1.依旧选取耗散较小的AUSMPW格式和混合限制器,湍流模型选取前文计算结果较好的Wilcox
k-ω模型和Menter SST模型.图 3给出了3种网格雷诺数
Recell下
k-ω模型对称面上下表面热流分布.可以看出对于上、下表面,3种不同
Recell下热流计算结果几乎相同.这是由于:首先,无论哪种
Recell,
y+均小于1;其次,文献
[2]认为,用耗散性较大的格式和限制器会导致网格依赖性较小、较稳定的、略大于实验值的热流结果,尽管计算格式和限制器选取了耗散性较小的格式,但是由于湍流模型较大的耗散性,导致热流计算结果较稳定,特别在
y+<1时,对网格雷诺数的敏感性较弱.而且可以看到,CFD计算结果总是略高于实验值.
 |
| 图 3 k-ω模型上下表面热流分布Fig. 3 Heat flow distribution on upper and lower surface of k-ω model |
|
图 4给出了3种网格雷诺数
Recell下SST模型的计算结果与实验数据的对比.同样,3种不同网格雷诺数下的热流计算结果相近且均较实验值偏大.另外,相比
k-ω模型,SST模型对双椭球相贯处,流动分离后再附时的热流峰值预测能力依旧优秀.由图 3(a)与图 4(a)对比看出,
k-ω模型对分离流动再附后的热流峰值预测偏高,而SST模型的热流峰值计算结果与实验值吻合非常好,这两种湍流模型计算的热流分布在
y+<1时均不随网格雷诺数的变化而改变.图 5给出了在网格雷诺数10的情况下,SST模型计算的对称面等马赫线图及双椭球壁面极限流线图.整体来看,流场等马赫线清晰无抖动,可以清晰看到激波-边界层干扰引起的流动分离,以及两球相贯处的二次激波与头部弓形激波的相交.
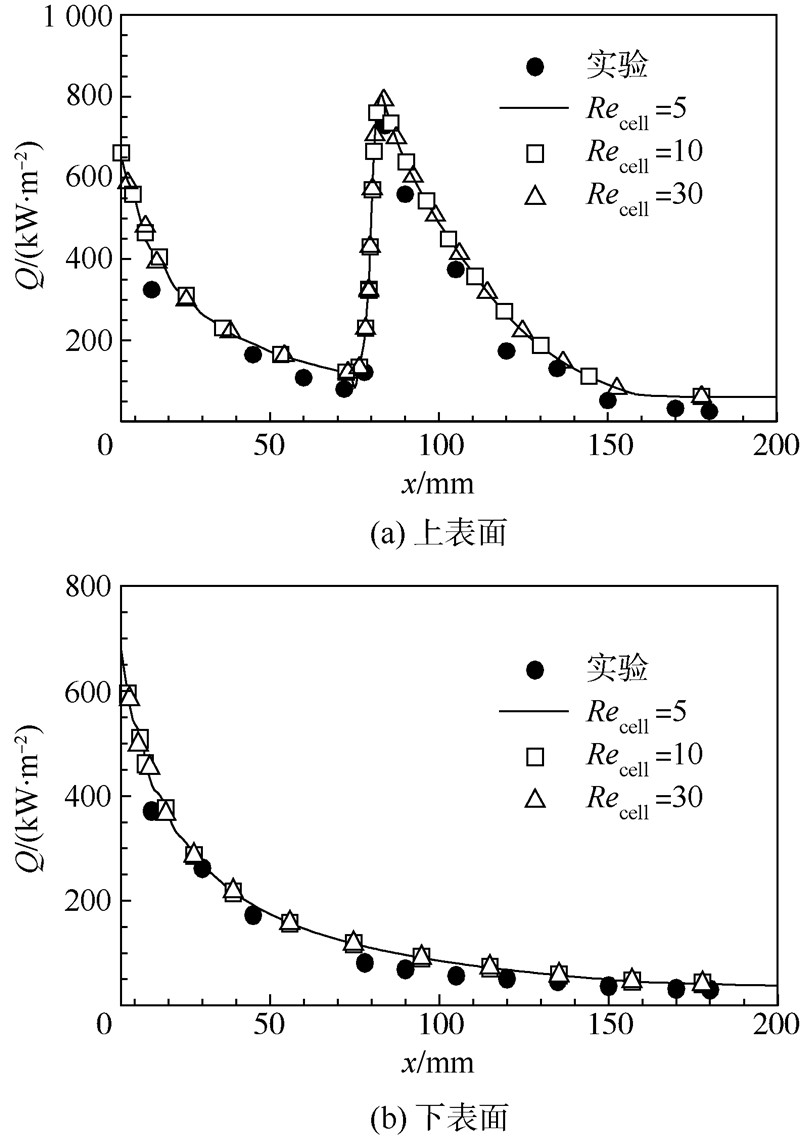 |
| 图 4 SST模型上下表面热流分布Fig. 4 Heat flow distribution on upper and lower surface of SST model |
|
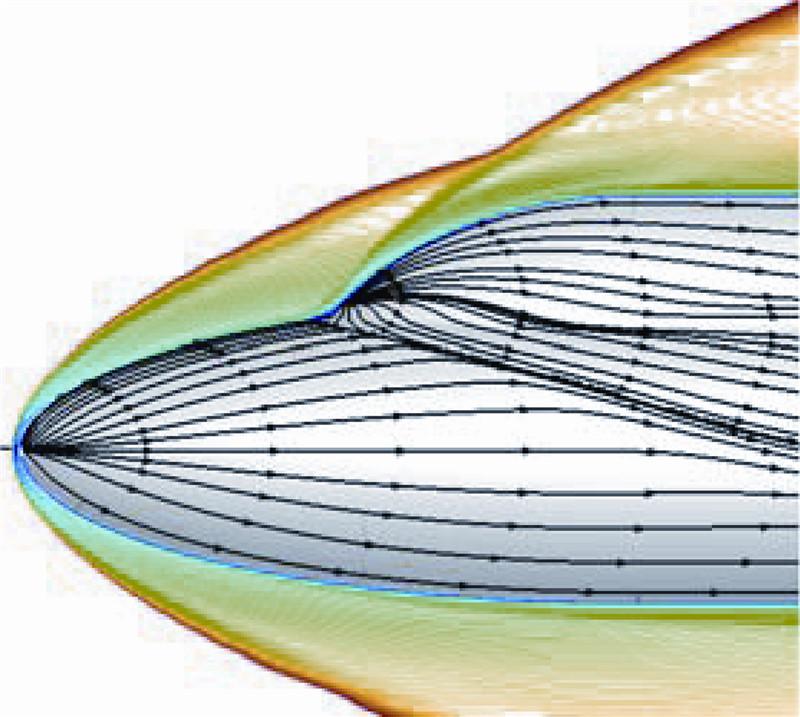 |
| 图 5 双椭球等马赫线图和壁面极限流线图Fig. 5 Lines counter of equal Mach number and limit stream lines on wall of double ellipsoid model |
|
4 后掠角对钝舵热流峰值的影响 通过第2节和第3节对气动热计算中湍流模型性能和网格雷诺数影响的研究,将其结论应用于下文中平板钝舵热流的计算,以揭示舵前缘热流峰值随后掠角的变化趋势.钝舵前缘半径为5mm,高40mm,后掠角从0°每隔10°~60°,共7种模型.计算条件为来流马赫数
Ma∞=5,自由来流参数取15km高度处的美国标准大气参数,壁温
Tw=300K,攻角为0°,计算网格约210万,保证
Recell小于5,同时网格过度小于1.1.采用Roe的FDS和AUSMPW格式搭配混合限制器,湍流模型选取Menter SST模型.图 6给出了30°后掠角钝舵壁面热流等值线.可以看出舵前缘受热严重,尤其是流动再附处.这表明钝舵前缘驻点线的热流是衡量飞行器热环境的重要标杆.图 7给出了在各后掠角情况下,前缘驻点线热流随
z轴的变化趋势.计算格式选取AUSMPW格式.可以看到驻点线热流均在10
6量级,其中,分离区处驻点的热流达到最大值,20°后掠角的热流峰值约是流动非分离处的3倍.并且,热流峰值的位置随后掠角的增加而单调下降.这是由于后掠角的增大导致流动滞止点下移,进而使驻点线最大热流下移.
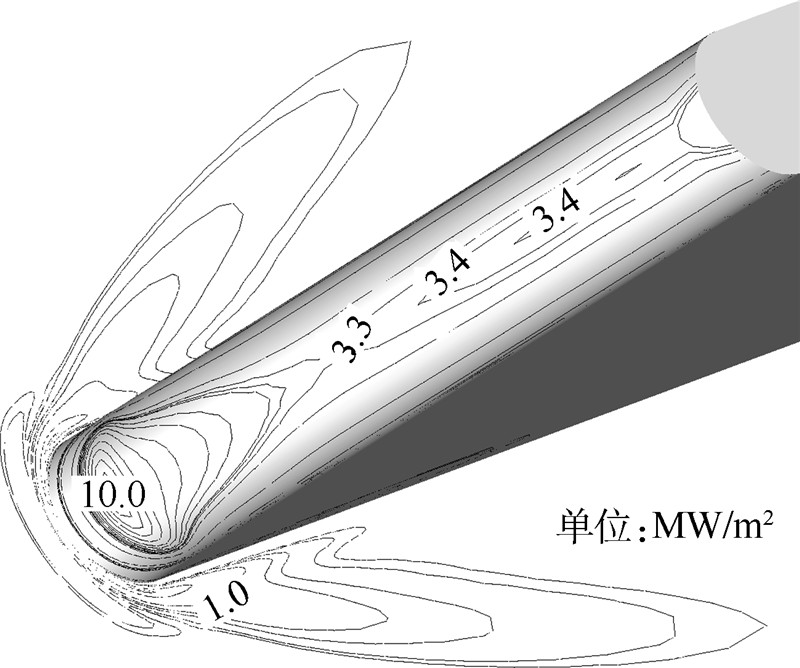 |
| 图 6 壁面热流等值线Fig. 6 LinesHeat flow equal lines on the wall |
|
 |
| 图 7 不同后掠角钝舵前缘热流分布Fig. 7 Heat flow distribution on leading edge of different angles |
|
图 8给出了驻点线上热流峰值随后掠角的变化规律.计算分别采用Roe格式和AUSMPW格式配合SST模型,以及层流Roe格式.可以看出,湍流模型下,驻点线的热流峰值随后掠角的变化不是单调的,先随后掠角的增大而增大,到后掠角大概为22°时达到最大值,然后热流又随后掠角的增大而逐渐下降.
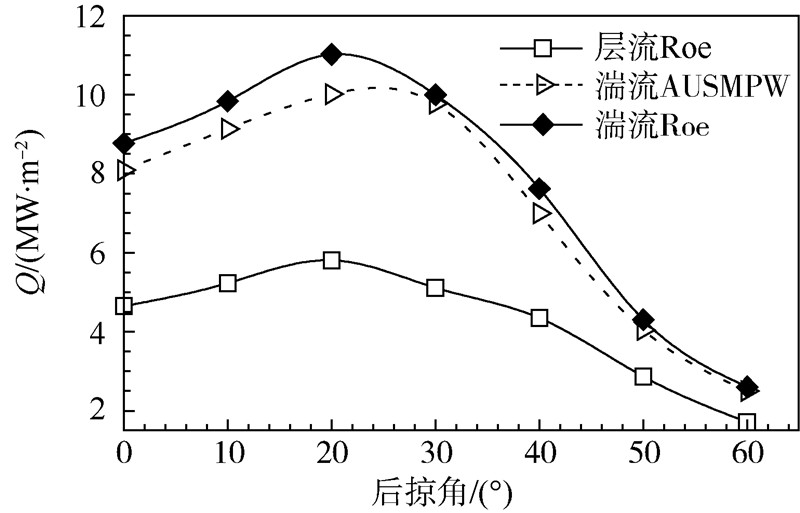 |
| 图 8 不同后掠角下钝舵热流峰值Fig. 8 Peak heat of blunt fin in different sweep angles |
|
按文献
[2]的观点,Roe格式的数值耗散要大于AUSM系列格式的,较大的耗散会导致计算的热流值偏高,并且这一偏高的规律不随计算网格的变化而改变.图 8中湍流模型计算结果表明,采用Roe格式计算的热流在所有后掠角下均大于AUSM格式,在小后掠角情况下,这一表现更为显著. 由于湍动能加热的原因,湍流流态下热流要远大于层流流态下的热流.图 8也给出了湍流结果与层流结果的比较.可以看出,层流流态下热流峰值随后掠角的变化较平缓,随后掠角的增大,热流峰值呈现缓慢的增加趋势,后掠角达到22°时,热流达到最大值,随后又缓慢减小.并且,湍流热流峰值约为层流热流峰值的2倍.5 结 论 1) 对于双椭球类存在激波-边界层干扰流动的模型,4种湍流模型均能准确模拟壁面的压力分布,但BL模型无法正确模拟壁面的热流分布,SA模型虽能较正确刻画下表面的热流分布,但是对上表面的激波-边界层干扰处流动分离刻画能力表现不足.两方程模型表现优秀,
k-ω和SST模型的计算结果与实验结果吻合较好,但是
k-ω模型高估了流动再附处的热流.SST模型总体表现优异.2) 在
y+<1时,热流计算对壁面法向网格的依赖性较小,网格雷诺数满足10以内即可得到与实验值吻合较好的热流结果.3) 钝舵驻点线热流峰值随后掠角呈现先增大后减小的趋势.因此,在防热设计中,可以考虑选择较大的后掠角来减小钝舵驻点线上的热流峰值.
参考文献 | [1] | Bertin J J, Cummings R M.Critical hypersonic aerothermodynamic phenomena[J].Annual Review of Fluid Mechanics, 2006,38:129-157. |
| Click to display the text |
| [2] | 姜振华, 阎超.高超声速热流高精度数值模拟方法[J].北京航空航天大学学报,2011,37(12):1529-1533. Jiang Z H,Yan C. High order accurate methods in numerical simulation of hypersonic heat transfer[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(12):1529-1533(in Chinese). |
| Cited By in Cnki (3) |
| [3] | 潘沙,冯定华, 丁国昊,等.气动热数值模拟中的网格相关性及收敛[J].航空学报,2010,31(3):493-499. Pan S,Feng D H,Ding G H,et al.Grid dependency and convergence of hypersonic aerothermal simulation[J].Acta Aeronautica et Astronautica Sinica, 2010,31(3):493-499(in Chinese). |
| Cited By in Cnki (9) |
| [4] | 李君哲, 阎超.气动热CFD计算的格式效应研究[J].北京航空航天大学学报,2003,29(11):1022-2025. Li J Z,Yan C.Research on scheme effect of computational fluid dynamics in aerothermal[J].Journal of Beijing University of Aeronautics and Astronautics,2003,29(11):1022-2025(in Chinese). |
| Cited By in Cnki (33) |
| [5] | Klopfer G H, Yee H C.Viscous hypersonic shock/shock interaction on blunt line cowl lips,AIAA-1988-0233[R].Reston:AIAA,1988. |
| |
| [6] | Hoffmann K A, Siddiqui M S,Chiang S T.Difficulties associated with the heat flux computations of high speed flow by the Navier-Stokes equations,AIAA-1991-0457[R].Reston:AIAA,1991. |
| |
| [7] | Benard E, Cooper R K,Sidorenko A.Transitional and turbulent heat transfer of swept cylinder attachment line in hypersonic flow[J].International Journal of Heat and Mass Transfer,2006,49(5-6): 836-843. |
| Click to display the text |
| [8] | 朱辉玉, 王刚, 孙泉华, 等.高超声速飞行器气动热数值模拟的几个关键因素[C]//第三届高超声速科技学术会议会议文集.北京:中国力学学会, 2010:0056-1-8. Zhu H Y,Wang G,Sun Q H,et al.Some critical factors in hypersonic aerothermal simulation[C]//Proceedings of Third Hypersonic Technology Academic Conference.Beijing:CSTAM,2010:0056-1-8(in Chinese). |
| |
| [9] | 贺旭照, 赵慧勇,乐嘉陵.吸气式高超声速飞行器气动力气动热的数值模拟方法及应用[J].计算物理,2008,25(5):555-560. He X Z,Zhao H Y,Le J L.Aerodynamic force and heat of hypersonic laminar and turbulent flow[J].Chinese Journal of Computational Physics, 2008,25(5):555-560(in Chinese). |
| Cited By in Cnki (5) |
| [10] | 李素循. 激波与边界层主导的复杂流动[M].北京:科学出版社,2007:11-51, 146-148. Li S X.The complex flow caused by shock/boundary interaction[M].Beijing:Science Press,2007:11-51, 146-148(in Chinese). |
| |
| [11] | Wilcox D C. Turbulence modeling for CFD[M].3rd ed.California:DCW Industries Inc,2006:243-249. |
| |
| [12] | 阎超. 计算流体力学方法与应用[M].北京:北京航空航天大学出版社,2006:221-223. Yan C.The methods and application of computational fluid dynamics[M].Beijing:Beihang University Press,2006:221-223(in Chinese). |
| |
| [13] | van Leer B. Towards the ultimate conservative difference scheme.V.A second-order sequel to Godunov's method[J].Journal of Computational Physics,1997,135(2):227-248. |
| Click to display the text |
| [14] | 耿云飞, 阎超,徐晶磊,等.高超声速流动湍流模式评估[J].北京航空航天大学学报,2011,37(8):907-911. Geng Y F,Yan C,Xu J L,et al.Turbulent modeling validation in hypersonic flow[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(8):907-911(in Chinese). |
| Cited By in Cnki (4) |

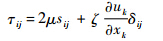 各参数的意义详见文献[11].为了使式(1)封闭,需要对式(1)中的雷诺应力τij做出各种假设.从对模式处理的出发点不同,一般可将湍流模式分为雷诺应力模型和涡黏性模型两类.受计算条件的约束,雷诺应力模型计算量巨大,使其应用范围受到限制,在工程湍流问题中广泛应用的是涡黏性模型[12].因此本文选取4种涡黏性湍流模型进行计算.壁面热流qw由下式计算:
各参数的意义详见文献[11].为了使式(1)封闭,需要对式(1)中的雷诺应力τij做出各种假设.从对模式处理的出发点不同,一般可将湍流模式分为雷诺应力模型和涡黏性模型两类.受计算条件的约束,雷诺应力模型计算量巨大,使其应用范围受到限制,在工程湍流问题中广泛应用的是涡黏性模型[12].因此本文选取4种涡黏性湍流模型进行计算.壁面热流qw由下式计算: