脉冲雷达测速通常采用细谱线跟踪技术,导弹等高动态目标的加速度和加加速度会使回波多普勒谱线展宽甚至出现混叠,导致雷达测速系统很难正确跟踪.因此为了提高脉冲雷达多普勒测速精度,估计目标的加速度和加加速度并进行相位补偿至关重要^{[1, 2]}.当目标作加速运动时,回波信号为相位具有高阶项的非平稳信号.目标加速度和加加速度分别对应于回波信号的二阶相位系数和三阶相位系数.常用非平稳信号参数估计的方法有时频分析和基于Hilbert-Huang变换(HHT)^[3]参数估计方法.Wigner-Hough^[4]变换、Radon-Wigner^[5]变换、Radon-Ambiguity变换^{[6, 7]}、分级傅里叶变换^{[8, 9]}等时频分析方法需要进行一维搜索或二维搜索,计算量较大.经验模式分解(EMD)^{[10, 11]}是一种适用于非平稳信号处理的新方法.信号通过EMD可分解为不同的本征模态函数(IMF).IMF是Huang^[10]提出的一种调幅调频(AM-FM)信号,其目的是为了对IMF作Hilbert变换得到有意义的瞬时频率(IF).对分解得到的各级IMF作Hilbert变换即可得到对应的瞬时频率,再利用直接型主成分提取方法(DPCE)^[12]或能量型主成分提取方法(EPCE)^[13]就能从得到的各组瞬时频率中得到调频信号的频率主成分.在EMD的基础上,Wu等人提出了一种叫作总体经验模式分解(EEMD)^[14]的噪声辅助数据分析方法.EEMD能解决EMD的模态混叠(mode mixing)问题,同时对分解的IMF求总体平均,使分解更具有鲁棒性,但由于要进行多次EMD分解,也会有计算量大的问题.结合EMD的自适应性和小波分析的理论框架,Gilles提出了一种称为经验小波变换(EWT)^[15]的自适应信号处理方法.其核心思想是通过对信号的Fourier谱进行自适应划分,建立合适的小波滤波器组来提取信号不同的AM-FM成分.对不同的信号成分作Hilbert变化可以得到有意义的瞬时频率,利用类似于EMD的EPCE方法就能提取到调频信号的瞬时频率.EWT方法是在小波框架下建立的方法,所以其计算量远小于EMD方法,而且具有较强的鲁棒性.1 经验小波变换 经验小波本质上是根据信号频谱特性选择的一组带通滤波器.为了确定带通滤波器的频率范围,对信号的Fourier谱进行分割.假设将Fourier支撑[0,π]分割成N个连续的部分Λ_n=[w_n-1,w_n],n=1,2，…,N(w0=0,w_N=π),w_n选择为信号Fourier谱相邻两个极大值点之间的中点,那么∪_n-1^NΛ_n=[0,π]，如图 1所示.图中的过渡区域以w_n为中心,宽度为2τ_n.确定分割区间Λ_n后,根据Meyer小波确定的经验尺度函数和小波函数分别如式(1)和式(2)所示.

图 1 Foureier坐标系的分割 Fig. 1 Partitioning of the Fourier axis

图选项

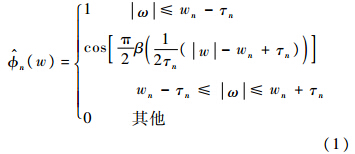
式中，τ_n=γw_n;γ<min_n[(ω_n-1-ω_n)∕(ω_n+1+ω_n)];β(x)=x⁴(35-84x+70x²-20x3).原始信号可被重构为
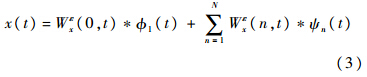
式中:*为卷积符号;W^ε_x(0,t)为逼近系数;W^ε_x(n,t)为x(t)的经验小波变换,经验模式x_k(t)可定义为
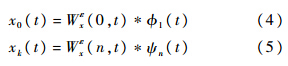
2 基于EWT速度与加速度估计方法 2.1 问题分析设脉冲雷达发射的单载频脉冲串信号为
式中,T_r为脉冲持续时间;f_c为载波频率;φ₀为初始相位.对应的回波信号为
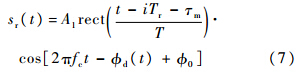
式中,φ_d=2π∫ f_d(t)dt; f_d(t)=2v(t)/λ为多普勒频率,λ为信号波长.通过正交解调得到的输出信号为
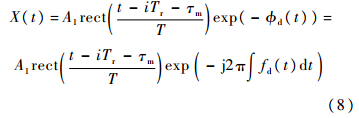
假设积累N个脉冲,每个脉冲采样一个点来求多普勒速度：
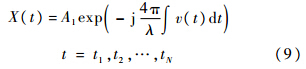
若在t1~t_N内目标作加速运动,速度近似为v(t)≈v₀+at+j_a/2t2,则
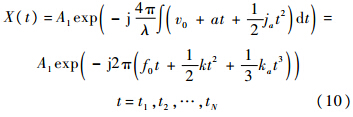
式中,f₀=2v₀/λ；k=2a/λ；k_a=j_a/λ,a为加速度,j_a为加加速度,此时回波的相位具有三阶相位系数.2.2 频率主成分提取 令含噪回波信号的模型为
式中,A为幅度;f₀为初始频率;k为二次相位系数;k_a为三次相位稀疏;w(t)为引入FM信号中的高斯白噪声.文中仿真信号设置A=1,f₀=100Hz,k=400,k_a=300,采样率f_s=2500Hz.对X(t)作EWT变换得到不同的经验模式X_k(t),即X(t)=∑kX_k(t).对X_k(t)作Hilbert变换,可得
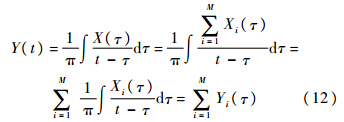
各经验模式的解析函数为
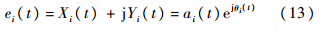
式中,a_i(t)为瞬时幅度;θ_i(t)为瞬时相位；且
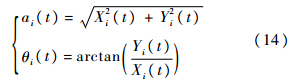
则原信号可表示为
式中f_j(t)为第j个经验模式的瞬时频率.得到M组瞬时频率f_j(t)后,可利用基于能量型主成分提取方法来提取信号的频率主成分.对于同一时刻τ,选出各IMF在时刻τ对应的瞬时幅度最大值a_k对应的经验模式的瞬时频率作为频率主成分,即
则信号的瞬时频率为f(t)=f_k(t)(t). 2.3 基于EWT的参数估计性能分析在利用EWT变换进行FM信号参数估计时,实际得到的是一组信号的瞬时频率点f(t):
式中e(t)为频率噪声.EWT变换等价于一组带通滤波器,EWT变换得到的不同IMF的瞬时频率分属不同的频率区间.通过频率主成分提取方法可将不同频率区间内的瞬时频率点提取出来,频率噪声仅与信号的信噪比相关.利用最小二乘方法可以对参数α=(f₀,k,k_a)进行估计,因此参数的估计精度仅与回波信号的信噪比相关.由最小二乘估计的性质可知,估计量α^为参数α的线性无偏估计.根据式(13)确定待估参数的C-R下界^[16]为
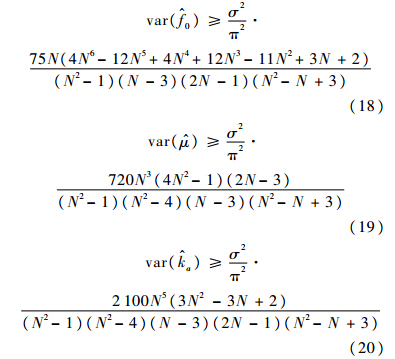
EWT方法是一种小波分析算法,利用Mallat算法^[17]可实现快速计算.而传统的FRFT方法是二维搜索算法,其计算量远大于EWT算法,导致数据处理速度较慢.因此,EWT算法比FRFT算法更适用于实时数据处理.3 仿真与分析 3.1 理论数据仿真理论仿真分为2部分.第1部分仅考虑信号具有二次相位项.
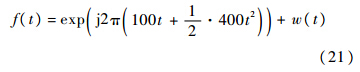
式中w(t)为加性高斯白噪声.图 2(a)为信号经EWT变换后得到的各个经验模式,图 2(b)为信噪比等于10dB时用EWT方法提取的频率主成分.从图 2(b)可以看出利用EWT方法提取的频率主成分受噪声干扰较小,绝大部分瞬时频率点都分布在瞬时频率直线两端.图 3、图 4分别为5dB<信噪比<15dB时,分别用EWT，EEMD-PCA和分数阶傅里叶变换(FRFT)方法Monte Carlo仿真50次得到的一次、二次相位系数估计均方根误差(RMSE)图,并将各参数估计误差与C-R下界作比较.从图 3、图 4中可以看出,基于EWT的参数估计方法估计精度要远远高于传统的FRFT方法和EEMD-PCA方法.传统的FRFT方法在估计线性调频(LFM)信号初始频率和高阶相位系数时,其估计精度主要受采样点数N和旋转角度搜索间隔决定,受信噪比影响不大,因此图中FRFT方法估计的参数误差随信噪比变化不大.EWT方法估计的参数误差最为接近C-R下界,且随着信噪比的增大,EWT逐渐逼近于C-R下界.同等硬件条件下EWT方法运行一次的计算时长为0.0079s,FRFT方法的计算时长为2.711s,EEMD方法的计算时长为6.328s.EWT算法由于采用了Mallat小波快速算法,计算速度要远远快于FRFT方法和EEMD方法.

图 2 利用经验小波变换(EWT)算法得到的经验模式和瞬时频率 Fig. 2 Estimated intrinsic mode functions (IMF) and instantaneous frequency (IF) using empirical wavelet transform (EWT) method

图选项

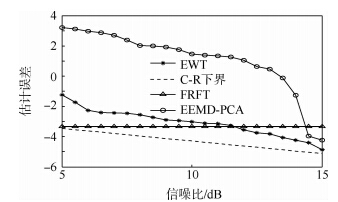图 3 一次相位系数f0估计误差 Fig. 3 Estimating error of coefficient f0

图选项

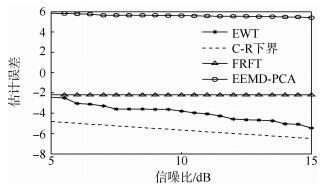图 4 二次相位系数k估计误差 Fig. 4 Estimating error of coefficient k

图选项

考虑三阶相位项时,假设k_a=300,则
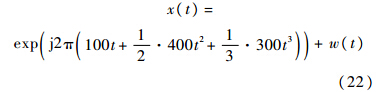
用本文的方法提取得到的瞬时频率如图 5所示,对获取的频率点用抗差最小二乘拟合可估计各阶相位系数.对具有三阶相位项非平稳信号,传统的FRFT方法不再适用.因此,将基于EWT方法的参数估计的估计误差与EEMD-PCA方法和各待估参数的C-R下界作比较.一二阶相位系数估计误差与3.1节类似,三次相位项的估计误差如图 6所示.信号的瞬时频率为二次曲线,从图 5可以看出,提取的瞬时频率集中点分布在二次曲线两侧.从图 6中可以看出,利用本文提出的方法估计得到的信号的三次相位系数估计精度最接近C-R下界,且随着信噪比的提高,逐渐逼近于C-R下界.

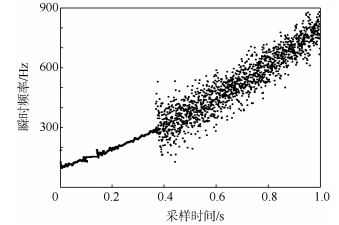图 5 具有三阶相位系数信号的瞬时频率 Fig. 5 Estimated instantaneous frequency (IF) of signal with the third order phase coefficients

图选项

图 6 三阶相位系数估计误差 Fig. 6 Estimating error of the third order phase coefficient

图选项

3.2 实测数据仿真利用某C波段窄带脉冲雷达测量得到的飞行器主动段数据进行仿真.为了满足目标作加速运动或加加速度运动的假设,仅积累50个回波的I/Q数据作为滑动窗口,每个回波采一个点,窗口每次滑动一个点.利用本文的加速度估计算法得到的加速度作相位补偿估计的速度误差如图 7所示.利用真实速度作21点中心平滑得到的加速度均方根误差为0.03m/s²,将本文得到的加速度与速度中心平滑得到加速度误差如图 8所示.从图中可以看出,利用本文的方法估计的加速度进行相位补偿效果很好,使估计的速度误差小于0.05m/s,最大加速度误差小于0.4m/s².

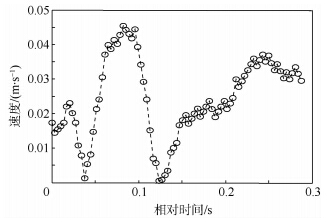图 7 加速度补偿后的速度误差 Fig. 7 Velocity error after acceleration compensation

图选项

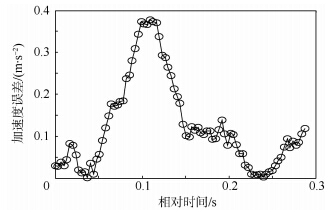图 8 实测数据加速度误差 Fig. 8 Estimated acceleration error of measured data

图选项

4 结 论 本文在经验小波变换的基础上,提出EWT方法对目标径向加速度进行估计,仿真和理论数据对该算法进行验证表明:1) 仿真表明该算法在不同的信噪比条件下均能以较高的精度估计信号的参数,估计精度高于传统FRFT算法和EEMD算法,且估计误差逼近于C-R下界;2) 计算速度要远远快于传统算法;3) 脉冲雷达实测I/Q数据表明,该算法估计的加速度误差小于0.4m/s²,加速度的补偿后估计的速度误差小于0.05m/s.
参考文献

[1]	袁斌,陈曾平,徐世友,等.基于距离单元筛选快速最小熵的含旋转部件目标相位补偿方法[J].电子与信息学报,2013,35(5):1128-1134.Yuan B,Chen Z P,Xu S Y,et al.Phase compensation for targets with rotating parts based on range bins selection in fast minimum entropy[J].Journal of Electronics & Information Technology,2013,35(5):1128-1134(in Chinese).
	Cited By in Cnki
[2]	夏猛,杨小牛.基于三次相位补偿的运动目标参数估计[J].电子科技大学学报,2013,42(4):559-564.Xia M,Yang X N.Parameter estimation for moving target based on three-phase compensation[J].Journal of University of Electronic Science and Technology of China,2013,42(4):559-564(in Chinese).
	Cited By in Cnki
[3]	Cao S,Bing P,Lu J,et al.Seismic data time-frequency analysis by the improved Hilbert-Huang transform[J].Oil Geophysical Prospecting,2013,48(2):246-254.
[4]	Wang Z Z,Liu F,Huang Y,et al.Digitized periodic wigner-hough transform and its performance analysis[J].Telecommunications Engineering,2012,52(9):1452-1458.
[5]	欧国建,陈玲珑,何俞璟.一种多分量LFM信号参数估计的快速仿真算法[J].重庆邮电大学学报:自然科学版,2013,25(4):459-463.Ou G J,Chen L L,He Y J.A simulation fast algorithm for parameters estimationof the multicomponent LFM signals[J].Journal of Chongqing University of Posts and Telecommunications,2013,25(4):459-463(in Chinese).
	Cited By in Cnki
[6]	Yu Y.Detection and parameter estimation of linear frequency modulated signals based on radon transform[J].Journal of Modern Defence Technology,2013,41(1):136-141.
[7]	Zhu Y W,Zhao Y J,Jia W G.Fast parameter estimation method for LFM signal based on ambiguity function slice and FrFT[J].Journal of Information Engineering University,2012,13(2):218-223.
[8]	Mohindru P,Khanna R K R,Bhatia S S.Analysis of chirp signal with fractional Fourier transform[J].Majlesi Journal of Multimedia Processing,2013,2(1):314-322.
[9]	Dinç E,Duarte F B,Machado J A T,et al.Application of continuous wavelet transform to the analysis of the modulus of the fractional Fourier transform bands for resolving two component mixture[J].Signal,Image and Video Processing,2013,21(10):1-7.
	Click to display the text
[10]	Huang N E.The empirical modedecomposition and the Hilbert spectrum for nonlinear andnon-stationary time series analysis[J].Proceedings of Royal Society of London,1998,A4(54):903-995.
	Click to display the text
[11]	Flandrin P,Rilling G,Goncalves P.Empirical mode decomposition as a filter bank[J].Signal Processing Letters,IEEE,2004,11(2):112-114.
	Click to display the text
[12]	崔华.一种新的线性调频信号的瞬时频率估计方法[J].计算机应用研究,2008,25(8):2532-2533.Cui H.New method for instantaneous frequency estimations of LFM signals[J].Application Research of Computers,2008,25(8):2532-2533(in Chinese).
	Cited By in Cnki (8)
[13]	王燕,邹男,付进,等.基于局部瞬时能量密度级的瞬态信号检测方法[J].电子与信息学报,2013,35(7):1720-1724.Wang Y,Zou N,Fu J,et al.Transient signal detection method based on partial instantaneous energy density level[J].Journal of Electronics & Information Technology,2013,35(7):1720-1724(in Chinese).
	Cited By in Cnki (4)
[14]	Wu Z H,Huang N E.Ensemble empirical mode decomposition:a noise assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.
	Click to display the text
[15]	Gilles J.Empirical wavelet transform[J].IEEE Transactions in Signal Processing,2013,61(16):3999-4010.
	Click to display the text
[16]	Steven M K.Fundamentals of statistical signal processing, Volume I:estimation theory[M].Beijing:Publishing House of Electronics Industry,2006:25-39.
[17]	成礼智.小波的理论与应用[M].北京:科学出版社,2009:75-88.Cheng L Z.Theories and applications of wavelet[M].Beijing:Science Press,2009:75-88(in Chinese)