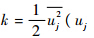为脉动速度);耗散率 
为瞬时变形率张量,ν为运动黏度)与RANS(Reynolds-Averaged Navier-Stokes)计算结果匹配.涡方法的主要目的是通过漩涡场生成湍流脉动速度场,基本原理构图如图 1所示. |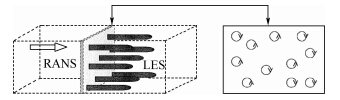
| 图 1 涡方法基本原理构图 Fig. 1 Configuration of vortex method |
| 图选项 |
二维情况下,涡方法是基于涡量的动力学方程:
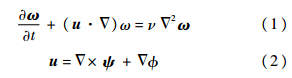
式中,ω为涡量;Ψ为二维情况下流体的流函数;为速度势.对式(2)求旋度,可以得到:
理想中的漩涡在空间中的分布方式为狄拉克分布,那么式(3)的解析解可以通过对涡量进行卷积运算得到:
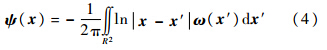
将式(4)代入到式(2),就可以得到速度场和漩涡场的关系表达式[4](毕奥-萨伐尔定律):
式(5)为卷积计算,可以简写为
式中,表示卷积计算;K为卷积计算的核,在简单的二维涡方法中,K=zz2.在实际的三维情况下,漩涡在空间中的分布不可能像理想中的狄拉克分布那样,漩涡在空间中的分布由形状方程ξσ和环量值Γ来定义,其中σ是漩涡的作用半径.在任意一个位置x由漩涡i得到的旋量:
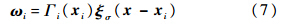
由式(6)，得到相应的脉动速度场为
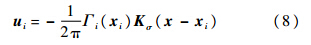
式中
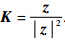全场的速度和漩涡可以用以下的关系式给出: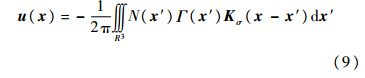
式中,N(x′)为在任意一个位置x′的漩涡场的密度.1.2 运用涡方法的基本流程 这个方法最早是由Sergent提出的,并使用商用计算流体力学软件Fluent进行了验证[7].涡方法的使用流程具体如下.在进口界面上随机分布一个漩涡场.针对所添加的每一个漩涡,确定其环量值以及作用半径(σ和Γ).在数值模拟计算的每一个网格上,计算出由漩涡场生成的脉动速度场,然后将其叠加到平均速度的剖面上.控制漩涡的运动.例如,在进口界面上平移或者使其绕着某一轴旋转.每隔一段时间(例如k/ε),可以调转漩涡的方向.通过漩涡场计算出相应的脉动速度场.2 改进后的涡方法的参数设定 2.1 漩涡的形状函数 漩涡的形状函数采用式(11)给出的形式,这种形状函数是改进的高斯函数型,与原始的涡方法中对形状函数的设定保持一致.
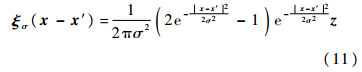
2.2 漩涡的作用半径 原始的涡方法中,Sergent用式(12)来给出漩涡的作用半径σ,这个表达式基于k和ε:
式中，k为当地的湍动能；Cμ为湍流模型常数.在改进后的涡方法中,对漩涡半径的参数设定是基于均匀各向同性湍流的假设.通过匹配由速度场表达的湍动能以及由漩涡场来表达的耗散率,可以得到近似于泰勒尺度的漩涡半径:
2.3 漩涡的环量和密度分布 基于均匀各向同性湍流的假设所得到的漩涡的环量与密度的关系表达式为
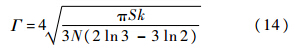
式中,N为漩涡的数量.原始的涡方法中,漩涡的分布方式是随机的,N个漩涡随机的分布在进口处.这种随机分布漩涡的方式有一定缺陷,可能导致局部的漩涡数量远大于或者远小于实际需要的漩涡数量.为了更为精确地确定在不同位置添加漩涡的数量,当地的漩涡数量应该和当地的湍动能和耗散率相关联.由此提出漩涡场的密度分布方式:
2.4 对漩涡场的运动的控制原始的涡方法中,漩涡的移动是完全随机的.这样产生的一个副作用是,它会打乱脉动速度场在时间和空间的相关性.因此改进后的涡方法通过Langevin方程[8, 9]来控制漩涡的运动:
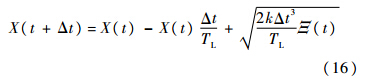
式中，X(t)为漩涡中心在t时刻的位置;Δt为时间步长；TL为该过程的时间尺度,也叫作释放时间,
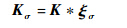,Cμ=0.09;Ξ(t)为一个白噪信号.实质上,这个过程是模仿实验方法中的蜂窝器来生成湍流[10].蜂窝器通过网格来扰动平均速度场,进而生成脉动速度,这与添加的漩涡场的作用是一样的.蜂窝器的网格所具备的分形结构与通过控制方程来控制漩涡场的运动具有相似性.以Langevin方程控制漩涡的运动,来重构流场在时间和空间的相关关系,以便尽快地生成湍流,这与蜂窝器的网格的分形结构所起的作用是一样的. 3 数值模拟实验通过一个雷诺数为395的槽道湍流算例来检验改进后的涡方法.数值模拟使用的程序为法国里昂流体与声学实验室(LMFA)开发的Turb’Flow.槽道的大小为2πh×2h×πh,h是槽道半高(h=0.01m).3个方向的网格数为49×89×41.流向和展向网格均匀分布,y方向的网格分布如下: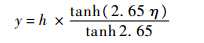 
式中,
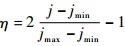为沿y方向的网格编号值.具体网格分布如图 2所示. |
| 图 2 槽道的网格分布示意图 Fig. 2 Meshes of channel |
| 图选项 |
为了加速计算,整个槽道并行分配为8个网格块.槽道y方向的两个面是无滑移壁面,x方向是流向,进口处的边界条件通过涡方法添加,出口处为压力边界.z方向采用周期性边界条件.数值模拟计算所需要的平均场由RANS计算得到,所采用的RANS模型是Wilcox k-ω模型[11].大涡模拟中使用的亚格子模型为WALE模型[12, 13].为了和原始的涡方法进行对比,第1种模拟计算采用了在进口界面随机分布的800个漩涡来生成漩涡场,所有漩涡在进口界面的平移也是随机的,按照式(11)、式(13)和式(14)来设定漩涡的形状函数、作用半径和环量值,这与原始的涡方法是一致的.第2种计算采用了改进后的涡方法,按照式(11)、式(13)和式(14)设定漩涡的形状函数、作用半径和环量值,但漩涡场采用式(15)的密度分布方式,总的漩涡数目依然为800个,并且运用Langevin方程(16)来控制漩涡场的运动.试验结果的参考数据来自于DNS(Direct Numerical Simulation)的计算结果[14, 15, 16]. 4 计算结果及分析4.1 平均速度场 实验所得到的平均速度场的结果由图 3和图 4给出.在进口处,由于平均速度场是根据RANS的计算结果给定,所以无论是在平均速度的线性区还是对数区,它都比较符合直接数值模拟的结果.在出口处,平均速度也能和直接数值模拟的数据相吻合.因为湍流沿着流向不断发展过程中,脉动速度越来越符合湍流的脉动统计特性,对平均速度场统计的影响越来越小.
 |
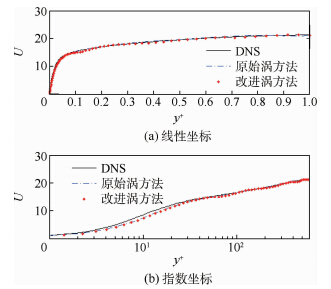| 图 3 进口平均速度场的统计结果 Fig. 3 Mean velocity of inlet |
| 图选项 |
 |
| 图 4 出口平均速度场的统计结果 Fig. 4 Mean velocity of outlet |
| 图选项 |
4.2 涡 量脉动涡量ω′的结果由图 5和图 6给出.很容易观察到,在进口处,传统的涡方法不能够得到准确的统计结果.而采用密度分布方式并且由Langevin方程来控制漩涡运动的改进涡方法能够生成与DNS统计数据相吻合的脉动涡量场,这是由于采用密度分布漩涡的方式能准确地根据不同位置的需求量来分布漩涡的数目,从而得到更接近真实湍流的脉动速度场.
 |
| 图 5 进口处的涡量统计结果 Fig. 5 Vorticity of inlet |
| 图选项 |
 |
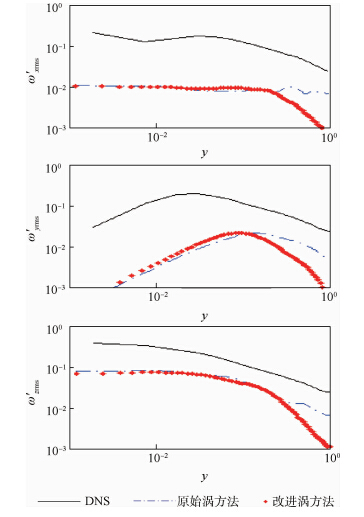| 图 6 出口处的涡量统计结果 Fig. 6 Vorticity of outlet |
| 图选项 |
流体向下游流动的过程中,湍动能在不同尺度的脉动间传递,直至传递到Kolmogorov尺度并耗散掉,这个过程中能量会衰减.并且由于进口处添加的漩涡场产生的脉动速度场在统计上不能完全符合湍流的统计特性,这种初始场在通过Navier-Stokes方程求解的过程中,会摧毁掉初始场所包含的流场信息.但从曲线的走势来看,出口处,曲线更加平滑,更加趋近于DNS的统计曲线.对比DNS数据,在大小上约有一个量级的误差. 4.3 雷诺应力图 7和图 8给出了进出口处的雷诺应力的统计结果.进口处,改进后的涡方法中,漩涡场的分布跟当地的湍动能和耗散率相关,所以得到的脉动速度的统计更接近DNS结果.在出口处,由于脉动场得到了一定程度的发展,所以雷诺应力的统计曲线更为平滑,改进后的涡方法得到的〈uu〉和〈uv〉的统计曲线更为接近DNS结果.同时从统计结果可以看出,流体在向下游流动的过程中,湍动能有所衰减,初始场所包含的信息在通过Navier-Stokes方程求解的过程中在慢慢丢失,流体更加符合湍流真实的统计特性.
 |
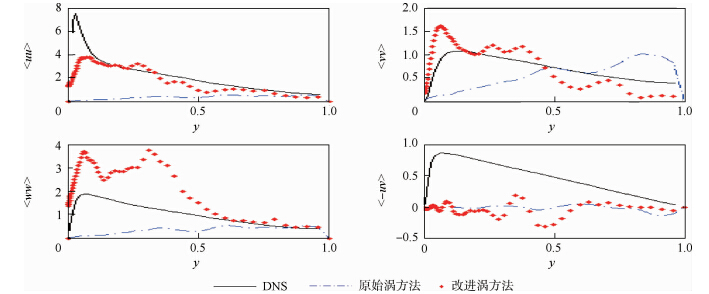| 图 7 进口处的雷诺应力统计结果 Fig. 7 Reynolds stress of inlet |
| 图选项 |
 |
| 图 8 出口处的雷诺应力统计结果 Fig. 8 Reynolds stress of outlet |
| 图选项 |
5 结 论 实验证明,涡方法能够通过RANS的结果来生成脉动场.改进后的涡方法采用密度分布方式来分布进口漩涡场并通过Langevin方程控制漩涡的运动.1) 相比于原始的涡方法,对比涡量和雷诺应力的统计结果,不论是在槽道的进口处,还是出口处,改进后的涡方法生成的脉动速度场更加接近真实的湍流.2) 在出口处,湍流得到一定程度的发展,从统计结果来看,更加符合真实湍流的统计特性,这个过程中,湍流所需要的流向发展长度约为10h,对比传统的使用循环条件[2]来生成大涡模拟进口条件的方法,涡方法显得更加有效.3) 另一方面,从进出口处雷诺应力的统计数据来看(〈w′w′〉和〈v′v′〉),改进后的涡方法所生成的脉动速度场还不能完全和DNS数据契合,这方面还需要进一步的探索和改进.致谢 感谢北京航空航天大学的方乐老师以及法国里昂流体与声学实验室的高峰博士对我的帮助和指导.
参考文献
| [1] | Nilsen K M, Kong B,Fox R O,et al.Effect of inlet conditions on the accuracy of large eddy Simulations of a turbulent rectangular wake[J].Chemical Engineering Journal,2014,250:175-189. |
| Click to display the text | |
| [2] | Payri R, Gimeno J,Marti-Aldaravi P,et al.Study of the influence of the inlet boundary conditions in a LES simulation of internal flow in a diesel injector[J].Mathematical and Computer Modelling,2013,57(7):1709-1715. |
| Click to display the text | |
| [3] | Tabor G R, Baba-Ahmadi M H.Inlet conditions for large eddy simulation:a review[J].Computers & Fluids,2010,39(4):553-567. |
| Click to display the text | |
| [4] | Sergent E. Vers une methodologie de couplage entre la simulation des grandes echelles et les modeles statistiques[D].Lyon:Ecole Centrale de Lyon,2002. |
| Click to display the text | |
| [5] | Yokota R, Barba L A.FMM-based vortex method for simulation of isotropic turbulence on GPUs,compared with a spectral method[J].Computers & Fluids,2013,80(1):17-27. |
| Click to display the text | |
| [6] | Leonard A. Vortex methods for flow simulation[J].Journal of Computational Physics,1980,37(3):289-335. |
| Click to display the text | |
| [7] | Mathey F, Cokljat D,Bertoglio J P,et al.Assessment of the vortex method for large eddy simulation inlet conditions[J].Progressin Computational Fluid Dynamics,2006,6(1-3):58-67. |
| Click to display the text | |
| [8] | Chorin A J, Hald O H.Generalized Langevin equations[C]//Stochastic Tools in Mathematics and Science.New York:Springer,2013:171-198. |
| Click to display the text | |
| [9] | Kursawe J, Schulz J,Metzler R.Transient aging in fractional Brownian and Langevin-equation motion[J].Physical Review E:Statistical,Nonlinear,and Soft Matter Physics,2013,88(6): 062124. |
| Click to display the text | |
| [10] | Djenidi L, Tardu S F,Antonia R A.Relationship between temporal and spatial averages in grid turbulence[J].Journal of Fluid Mechanics,2013,730:593-606. |
| Click to display the text | |
| [11] | Parent B, Sislian J P.Validation of the Wilcox k-ω model for flows characteristic to hypersonic airbreathing propulsion[J].AIAA Journal,2004,42(2):261-270. |
| Click to display the text | |
| [12] | Ducros F, Nicoud F,Poinsot T.Wall-adapting local eddy-viscosity models for simulations in complex geometries[C]//Proceedings of 6th ICFD Conference on Numerical Methods for Fluid Dynamics.Oxford:Oxford University Computing Laboratory 1998:293-299. |
| Click to display the text | |
| [13] | Schumann U. Subgrid scale model for finite difference simulations of turbulent flows in plane channel and annuli[J].Journal of Computational Physics,1975,18(4):3762404. |
| Click to display the text | |
| [14] | del Alamo J C, Jimenez J.Direct numerical simulation of the very large anisotropic scales in a turbulent channel[J].In CTR Annual Research Briefs,2001:329-341. |
| Click to display the text | |
| [15] | Moser R D,Kim J, Mansour N N.Direct numerical simulation of turbulent channel flow up to Re=590[J].Physics of Fluids,1999,11(4):943-945. |
| Click to display the text | |
| [16] | Grotzbach G. Direct numerical and large eddy simulation of turbulent channel flows[J].Encyclopedia of Fluid Mechanics,1987,6:1337-1391. |
