上述研究都是基于大量的产品失效数据,而在快速响应制造模式下,加工完成后的产品很难获得大量失效数据.而在产品的设计、生产和使用阶段积累了各种来源的信息,充分挖掘和利用这些信息可以有效提高产品的质量和可靠性.谷振宇等[5]基于设备加工运行状态信息融合设计开发了大型设备视情维修系统.在进行多源可靠性信息融合的研究中,冯静和周经伦[6]等通过引入模糊逻辑算子对多源可靠性先验信息进行融合,获得了较为合理的融合先验分布;Savchuk和Martz[7]结合最大熵方法和最大后验风险方法对不同的先验信息进行了融合;Smets[8]将证据理论引入可靠性评估工作中,对专家意见等信息进行了融合.
针对当前快速响应制造模式下很难获得大量产品失效数据的问题,论文提出基于制造过程信息融合的方法,通过评价产品的早期失效率来评估特定工艺的质量,进而为选取合适的工艺提供理论依据.论文首先建立产品早期失效率的模型,并给出参数估计的方法;其次通过分析形成产品可靠性的制造过程,确定合理的信息源;再次利用信息熵得到当前加工完成的产品与类似产品的相似程度;最后确定产品早期失效率的融合分布函数,对产品的可靠性进行评估;并以雷达移相单元为评估对象,验证论文所提方法的可行性.
1 早期失效建模及参数估计实践证明大多数机电产品的失效率λ(t)是时间t的函数,典型失效曲线为一种类似于“浴盆”形状的曲线,如图 1所示.不同的失效机理造成产品的失效阶段大致可以分为早期失效阶段、偶然失效阶段和耗损失效阶段.在产品投入使用的初期,设计和制造中的缺陷很容易暴露出来,造成在早期失效阶段产品的失效率较高,且随着时间的增加迅速下降.实际生产中经常采用温度循环、随机振动等方法来消灭早期失效.
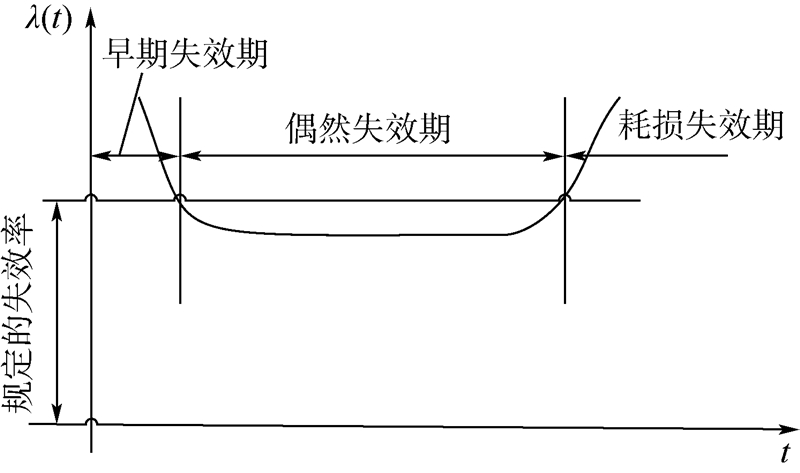 |
| 图 1 产品失效率曲线Fig. 1 Product failure rate curve |
| 图选项 |
威布尔分布[9, 10, 11]被广泛用于刻画机电产品失效的分布形式,其失效密度函数为
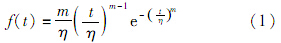
式中:m为形状参数;η为尺度参数.
相应的可靠度函数为
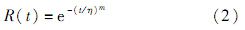
失效率函数为
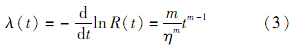
因为在早期故障期和偶然故障期造成产品故障的失效机理不同,若直接采用单一形式的分布对产品失效数据进行拟合可能会出现较大误差,所以需要判断产品失效数据的失效阶段.文献[12]表明,若产品失效数据在威布尔概率纸上反映为没有拐点的直线,则说明收集到的产品失效数据主要由一种失效机理造成,可选用单阶段威布尔分布进行拟合,反之则需采用两重威布尔分段 模型来拟合产品失效率分布曲线.本文假设首 先对收集的失效产品进行失效原因分析,剔除偶然失效阶段的失效数据,然后选用单阶段威布尔模型表示产品失效率.此时,若投入n个样本产品进行试验,至有r个失效时停止试验,整理失效时间的顺序统计量为t(1)≤t(2)≤…≤t(r).对其似然函数取对数并求导,整理化简后可得
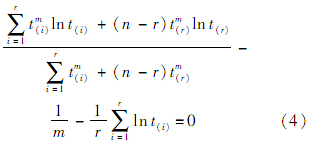
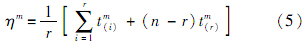
联立式(4)和式(5),利用数值方法迭代求解,可以得到参数m和η的值.
参数估计所需要的数据一般来自产品的可靠性试验,但在快速响应制造模式下,很难得到大量失效数据,而在实际工作中,存在一些可用于辅助产品可靠性估计的信息,对这些信息的有效融合可以使得评估结果更为准确,下文将通过分析制造过程中影响产品早期失效率的因素,确定可靠性评估的信息.
2 固有可靠性评估的多源信息 2.1 制造过程的信息源产品的固有可靠性是由设计和加工过程决定的,产品加工过程中的质量特性符合工艺规范要求的程度,反映了产品的固有可靠性与设计可靠性的差距.而质量特性通常是在多道工序过程中形成,且每道工序都有对其产生影响的工艺因素.对产品进行故障机理分析和故障模式影响分析(Failure Model Effect Analysis,FMEA),可以确定相应的关键质量特性和关键工艺因素.产品的可靠度可以通过关键质量特性满足工艺规范要求的程度来反映,也可以通过关键工艺因素满足工艺要求的程度来反映.另外,在产品加工完成后,为了剔除早期失效,并在较短时间内获得必要信息,通常会进行加速应力筛选试验.而且设计和装配相同,仅存在工艺差异的同类产品可靠性信息也可以通过历史数据得到.因此,在可靠性评估中,确定其信息来源为关键工艺因素、关键质量特性和产品可靠性3个方面,其中,产品可靠性信息包括当前产品可靠性信息和类似产品可靠性信息.这三者之间的关系如图 2所示.
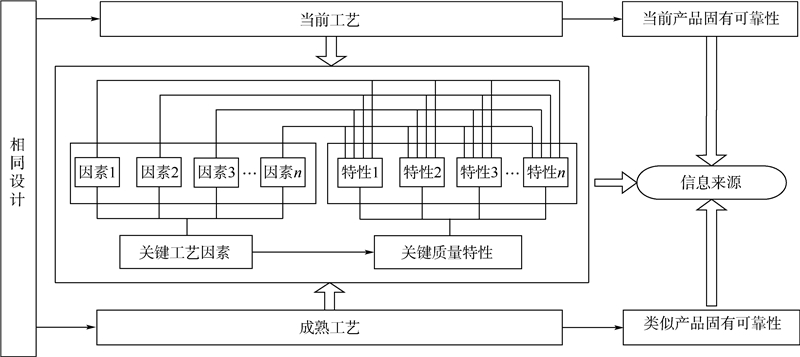 |
| 图 2 制造过程的信息源Fig. 2 Information source of manufacturing process |
| 图选项 |
2.2 过程信息的相似度通过比较当前加工完成的产品与类似产品制造过程信息的相似程度来估计当前产品的可靠性.通过上文的分析可知,产品在设计完成后主要是由加工过程决定其固有可靠性,而产品的可靠性水平可以通过加工过程中那些决定产品可靠性指标的关键质量特性和关键工艺因素来反映.因此,影响其可靠性的关键质量特性和关键工艺因素,可以通过评定当前产品和类似产品的加工过程中上述因素满足要求的水平,来反映产品可靠性之间的相似程度.
在加工过程中用于评价加工质量水平的指标通常选用工序能力指数.而产品的不同质量特性通常是由不同的工序加工得到,因此论文使用关键质量特性加工工序的工序能力指数来衡量产品的可靠性水平,通过评定两种产品的关键质量特性的工序能力指数的差异来衡量它们之间的相似程度.根据产品的FMEA分析,确定对产品可靠性有显著影响的关键质量特性为Ki(i=1,2,…,n),令Cpm,A(i)和Cpm,B(i)(i=1,2,…,n)分别代表当前产品和类似产品n个关键质量特性的相应工序的工序能力指数.从当前产品中抽取样本量为N的产品,对其关键质量特性的参数进行测量后可得相应的工序能力指数为Cpm,A(i).同理,抽取相同数量的类似产品,可以获得类似产品n个关键质量特性相应的工序能力指数Cpm,B(i).假定各关键质量特性对产品可靠性的影响权重为wi(i=1,2,…,n).因此定义基于关键质量特性的当前产品与类似产品的相似度为
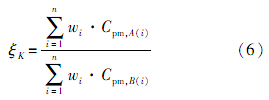
式中:wi为关键质量特性对产品可靠性的影响权重,
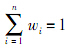 .
.假设对产品可靠性有显著影响的关键工艺因素为Yj(j=1,2,…,m),其对产品可靠性的影响权重为ρj(j=1,2,…,m),且满足∑ m i=1 ρi = 1.因为加工过程中对产品可靠性有影响的工艺因素种类很多,故对于关键工艺因素Yj满足工艺要求的程度,可以由专家根据生产经验和实际生产情况来评定.在将定性信息转化为定量信息时,模糊方法是应用较广的方法.Tillmann和Robert[13]及蒋平[14]使用梯形模糊数来表示专家意见,蒋平[14]通过一组专家的判断定量表示影响因素对机械制造过程加工产品孔位特征的影响程度.本文利用梯形模糊数方法给出当前产品和类似产品的关键工艺因素满足工艺要求程度的分值分别为MYj和M*Yj,则基于关键工艺因素的当前产品和类似产品之间的相似程度为
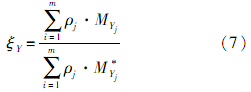
3 基于过程相似信息的融合分布为了通过衡量当前产品和类似产品之间的相似程度来评定当前产品的可靠性水平,还必须获得各关键质量特性和各关键工艺因素对产品可靠性的影响权重.下文在给出信息熵定义的基础上,利用基于距离的熵给出影响权重的确定方法,并利用信息熵公式给出融合先验分布的确定方法.
3.1 信息熵的定义信息熵是对随机事件不确定的度量,假设随机变量 X =(x1,x2,…,xn),若 X =(x1,x2,…,xn) 为离散型随机变量,则其信息熵定义为
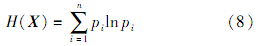
式中:pi=p( X =xi)(i=1,2,…,n) 表示随机变量取值的概率.若 X =(x1,x2,…,xn) 为连续型随机变量,则其信息熵定义为
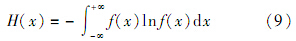
式中:f(x)为随机变量的概率密度函数.
为了利用信息熵公式求出随机变量的概率密度函数,通常会给出相应的约束条件,而在所有满足给定的约束条件的众多概率密度函数中,取其中信息熵最大的为最佳概率密度函数,称之为最大熵原理.
3.2 不同信息源下的早期故障率分布为了求出各wi的取值,本文使用基于距离的熵[15]:
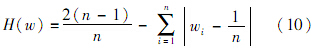
为了利用最大熵原理求出wi的值,需要给出约束条件.在判定每种影响因素的权重wi时,根据工程经验往往可以给出各权重的取值范围.建立优化模型为
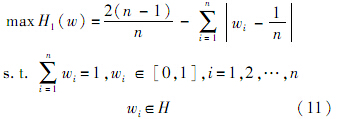
式中:H为各权重的取值范围.
通过求解式(11),可以得到各权重wi的取值.若类似产品寿命数据为 X 0=(x1,x2,…,xn),则通过关键质量特性信息源得到的当前产品寿命数据可表示为
X K=(ξKx1,ξKx2,…,ξKxn)
将数据 X K 代入式(4)和式(5)可以确定基于关键质量特性的产品可靠度RK(t).
为了得到ρj的取值,首先假设关键工艺因素Yj对关键质量特性Ki的影响权重为 μij(i=1,2,…,n;j=1,2,…,m),且∑ m i=1 μij = 1,其中,j=1,2,…,n.并给出权重矩阵:

然后根据生产经验给出各μij的取值范围,并利用式(11)得到各关键工艺因素对各关键质量特性影响权重μij的具体取值;最后根据式(12)求出各ρj的取值.
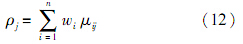
此时,若另一批类似产品寿命数据为 X *0=(x*1,x*2,…,x*n),则通过关键工艺因素信息源得到的当前产品寿命数据可表示为
X Y=(ξYx*1,ξYx*2,…,ξYx*n)
通过将数据 X Y 代入式(4)和式(5)可以确定基于关键工艺因素的产品可靠度RY(t).
3.3 早期故障率的融合分布若 D =(D1,D2,…,Dn) 表示n个不同信息,由信息Di(i=1,2,…,n)可以求出相应分布Ri(t)(i=1,2,…,n),根据式(9)可以得到信息Di(i=1,2,…,n)的信息熵为
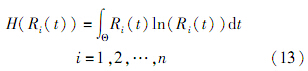
式(13)可以表示信息 D =(D1,D2,…,Dn) 的随机性大小,若信息熵越大,则表示该信息的随机性越大,即求出的分布更加符合真实分布.在多源信息条件下,不同信息对融合分布的贡献大小程度不同,且信息Di(i=1,2,…,n)的权重可以表示为
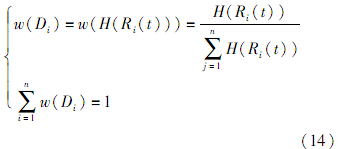
式中:w(Di)(i=1,2,…,n)表示信息Di(i=1,2,…,n)在所有信息中对融合分布贡献大小的比重,则融合分布可以表示为
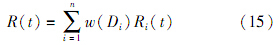
通过产品加工完成后进行的小样本寿命试验获得的数据,可以得到基于当前产品可靠性信息的产品可靠度R0(t).故产品可靠度的融合分布表示为
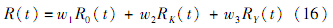
式中:w1+w2+w3=1.
依据式(3),可以得到早期失效率的分布函数,进而进行相应的可靠性评估.
4 案例研究 4.1 问题描述移相单元是相控阵雷达的核心器件,其早期失效率通常服从威布尔分布.通过对移相单元进行故障机理分析和FMEA分析,确定影响其早期失效率的关键质量特性和关键工艺因素如表 1所示.在移相单元粘接镀膜工艺完成后,通常会对其进行温度循环、随机振动试验.并选取移相单元的磁通率低于规定的阈值以及在加速应力筛选试验中发生脱胶、膜层破损、崩边等现象作为其失效判据.为了获取优化后的粘接镀膜工艺A下产品的早期失效率,选取两种成熟粘接镀膜工艺(B、C)下的移相单元为研究对象,利用工艺B和工艺C下产品的历史数据来估计工艺A下产品的早期失效率,以此验证论文所提方法的可行性.
表 1 关键质量特性和关键工艺因素Table 1 Key quality characteristics and key process factors
| 编号 | 工序 | 关键工艺因素 | 关键质量特性 |
| 1 | 磨外圆 | 砂轮粒度(Y1)、进刀量(Y2)、导轮转速(Y3) | 直线度(K1) |
| 2 | 磨端面 | 砂轮粒度(Y4)、工作台平面度(Y5)、工作台进给速度(Y6) | 垂直度(K2) |
| 3 | 胶接 | 固化温度(Y7)、固化时间(Y8)、固化压力(Y9) | 胶接强度(K3) |
| 4 | 精磨外圆 | 砂轮粒度(Y10)、进刀量(Y11)、导轮转速(Y12) | 粗糙度(K4) |
| 5 | 镀膜 | 腔内温度(Y13)、镀膜时间(Y14)、溅射功率(Y15) | 膜厚(K5) |
表选项
4.2 结果分析对A工艺加工的整批产品进行温度循环、随机振动试验,至有10个产品失效时停止试验,收集样品的失效时间序列为 (0.19,0.78,0.96,1.31,2.78,3.16,4.15,4.67,4.85,6.5)(单位:d). 收集B和C工艺加工产品的失效数据各100个.根据实际测量数据,得到工艺A和B下产品的各关键质量特性相应工序的工序能力指数如表 2所示;根据生产经验对A和C工艺加工产品的各关键工艺因素满足工艺要求的程度打分如表 3所示.将试验数据代入式(4)和式(5)可以得到 R0(t) = exp[-(t/9.4)0.9]
表 2 关键质量特性的工序能力指数Table 2 Process capability index of key quality characteristics
| 工艺 | K1 | K2 | K3 | K4 | K5 |
| A | 1.29 | 1.3 | 1.31 | 1.36 | 1.33 |
| B | 1.35 | 1.25 | 1.36 | 1.39 | 1.4 |
表选项
表 3 关键工艺因素的符合程度Table 3 Degree of compliance of key process factors
| 工艺 | Y1 | Y2 | Y3 | Y4 | Y5 |
| A | 0.85 | 0.86 | 0.85 | 0.82 | 0.83 |
| C | 0.92 | 0.89 | 0.91 | 0.86 | 0.86 |
| 工艺 | Y6 | Y7 | Y8 | Y9 | Y10 |
| A | 0.82 | 0.84 | 0.81 | 0.80 | 0.76 |
| C | 0.85 | 0.82 | 0.85 | 0.84 | 0.80 |
| 工艺 | Y11 | Y12 | Y13 | Y14 | Y15 |
| A | 0.82 | 0.81 | 0.84 | 0.81 | 0.82 |
| C | 0.87 | 0.83 | 0.89 | 0.84 | 0.87 |
表选项
为了得到基于关键质量特性的失效数据和基于关键工艺因素的失效数据,需要先确定关键质量特性对产品寿命的影响权重wi(i=1,2,3,4)和关键工艺因素对产品寿命的影响权重ρj(j=1,2,3,4).
根据生产经验给出各wi的取值范围分别为
0.18≤w1≤0.5
0.25≤w2≤0.55
0.16≤w3≤0.4
0.15≤w4≤0.25
0.12≤w5≤0.2
依据式(11)得到wi的取值为
w1=0.1939
w2=0.25
w3=0.19
w4=0.1913
w5=0.1748
为了得到各ρj的取值,根据生产经验先给出了各关键工艺因素对各关键质量特性的影响权重μij(i=1,2,…,5;j=1,2,…,15),由表 1可知,每道工序的关键工艺因素仅对该工序的关键质量特性有影响,故给出影响权重的取值范围为
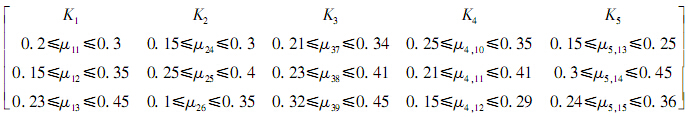
依据式(11)和式(12)可以得到各ρj的取值,如表 4所示.
表 4 各ρj的取值Table 4 Value of each ρj
| ρj | ρ1 | ρ2 | ρ3 | ρ4 | ρ5 |
| 数值 | 0.0232 | 0.0591 | 0.0677 | 0.0421 | 0.0836 |
| ρj | ρ6 | ρ7 | ρ8 | ρ9 | ρ10 |
| 数值 | 0.0743 | 0.0652 | 0.0813 | 0.0832 | 0.0627 |
| ρj | ρ11 | ρ12 | ρ13 | ρ14 | ρ15 |
| 数值 | 0.0574 | 0.0641 | 0.0842 | 0.0642 | 0.0877 |
表选项
依据式(6)和式(7)可以得到ξK=0.935,ξY=0.893.结合B和C工艺加工产品的失效数据,可以分别得到基于类似产品信息的当前产品寿命数据XK和XY.由此得到基于关键质量特性的产品可靠度分布和基于关键工艺因素的产品可靠度分布分别为
RK(t) = exp[-(t/8.7)0.93]
RY(t) = exp[-(t/8.1)0.94]
依据式(13)~式(16)可以确定产品可靠度的融合分布为
R(t) = 0.227RK(t)+0.141RY(t)+0.632R0(t)
由式(3)可以得到产品早期失效率的分布函数如图 3中A工艺所示,依据历史数据得到B和C工艺加工产品的早期失效率,如图 3所示.从图中可以明显看出3种工艺的优劣顺序.且优化后的A工艺加工产品的早期失效率在较短的时间内就迅速下降,可以保证后续使用过程中的可靠性要求.
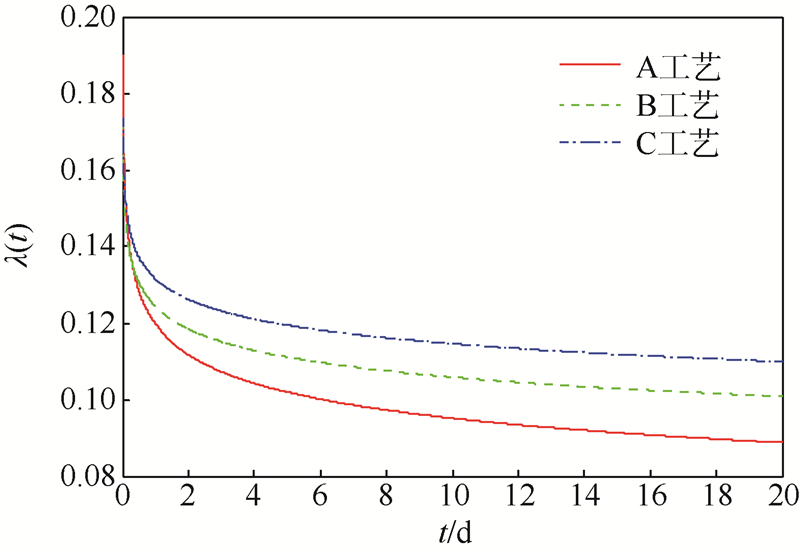 |
| 图 3 各工艺下产品的早期失效率Fig. 3 Early failure rates of products in every process |
| 图选项 |
5 结 论1) 在快速响应制造模式下很难获得大量产品失效数据时,可以充分利用制造过程多源信息,开展对产品早期失效率的评估研究.
2) 在产品的设计规范相同时,可以通过评定当前产品和类似产品的加工过程中影响其可靠性的关键质量特性和关键工艺因素满足要求的水平,来反映产品可靠性之间的相似程度.
参考文献
| [1] | 范秀君, 许静林,张根保,等.数控机床早期故障消除技术[J].中国机械工程,2013,24(16):2241-2247. Fan X J,Xu J L,Zhang G B,et al.Technology of eliminating early failures for NC machine tool[J].Chinese Mechanical Engineering,2013,24(16):2241-2247(in Chinese). |
| Cited By in Cnki (8) | |
| [2] | Keller A Z, Beng C.Further applications of fuzzy logic to reliability assessment and safty analysis[J].Microelectronics Reliability,1989,29(3):399-404. |
| Click to display the text | |
| [3] | Rao S S, Reddy C P.Reliability analysis of machine tool structures[J].Journal of Engineering for Industry,1977,99(4):882-888. |
| Click to display the text | |
| [4] | Nelson W. Accelerated life testing-step-stress models and data analyses[J].IEEE Transaction on Reliability,1980,29(2):103-108. |
| [5] | 谷振宇,何彦, 刘军.基于运行信息融合的大型设备视情维修系统[J].计算机集成制造系统,2010,16(10):2094-2100. Gu Z Y,He Y,Liu J.Condition-based maintenance system for large equipment based on running information fusion[J].Computer Integrated Manufacturing Systems,2010,16(10):2094-2100(in Chinese). |
| Cited By in Cnki (7) | |
| [6] | 冯静,周经伦. 基于Bayes-模糊逻辑算子的小子样可靠性信息融合方法[J].航空动力学报,2008,23(9):1633-1636. Feng J,Zhou J L.Small-sample reliability information fusion approach based on Bayes-fuzzy logistic operator[J].Journal of Aerospace Power,2008,23(9):1633-1636(in Chinese). |
| Click to display the text | |
| [7] | Savchuk V P, Martz H F.Bayes reliability estimation using multiple sources of prior information:Binomial sampling[J].IEEE Trans on Reliability,1994,43(1):138-144. |
| Click to display the text | |
| [8] | Smets P. The transferable belief model for expert judgments and reliability problems[J].Reliability Engineering and System Safety,1992,38(1-2):59-66. |
| Click to display the text | |
| [9] | Zhang Q, Hua C,Xu G.A mixture Weibull proportional hazard model for mechanical system failure prediction utilising lifetime and monitoring data[J].Mechanical Systems and Signal Processing,2014,43(1-2):103-112. |
| Click to display the text | |
| [10] | Jóźwiak I J. An introduction to the studies of reliability of systems using the Weibull proportional hazards model[J].Microelectronics Reliability,1997,37(6):915-918. |
| Click to display the text | |
| [11] | Jardine A K S, Anderson P M,Mann D S.Application of the Weibull proportional hazards model to aircraft and marine engine failure data[J].Quality and Reliability Engineering International,1987,3(2):77-82. |
| Click to display the text | |
| [12] | 张根保,唐贤进, 廖小波,等.数控机床故障率分布曲线定量化建模及应用[J].重庆大学学报,2013,36(6):119-123. Zhang G B,Tang X J,Liao X B,et al.Quantitative modeling and application of CNC machine failure distribution curve[J].Journal of Chongqing University,2013,36(6):119-123(in Chinese). |
| Cited By in Cnki (2) | |
| [13] | Tillmann S, Robert L K T.Quantifying qualitative information on risks:Development of the QQIR method[J].Journal of Construction Engineering and Management,2009,135(1):56-71. |
| Click to display the text | |
| [14] | 蒋平. 机械制造的工艺可靠性评估[D].长沙:国防科学技术大学,2010. Jiang P.Research on process reliability for manufacturing[D].Changsha:National University of Defense Technology,2010(in Chinese). |
| [15] | Yager R R. Measures of entropy and fuzziness related to aggregation operators[J].Information Sciences,1995,82(3-4):147-166. |
