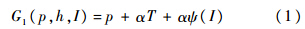
乘客不计划行程的一般成本为
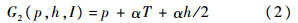
由式(1)和式(2)可知,计划行程与否主要取决于αψ(I)与αh/2之间的大小关系,令αψ(I)=αh/2的解为

其中Iω为使乘客进行计划行程的最差信息质量,是关于h的函数.式(3)两边对h求导,得

所以两公交车之间的时间间隔越大,即服务频率越小,乘客计划行程的最差信息质量越小.假设I∈(I-,I+),若Iω>I+,则没有人计划行程;若Iω<I-,则所有的人都计划行程,计划行程人数的比例可以表示为
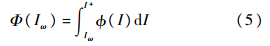
其中φ(I)是关于I的密度函数,上式两边分别对h求导,得
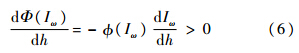
所以增加公交车之间的发车时间间隔,即降低服务频率可以增加计划行程的人数比例.则不计划行程人数的比例为

所以乘坐公交的期望一般成本为
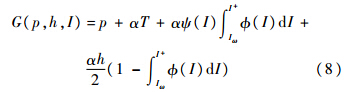
1.2 消费者剩余、公交公司收入和社会福利D(N)为当乘车人数为N时乘坐公交的一般成本,是反需求函数,D'(N)<0,即乘坐公交一般成本的减少会造成乘客数量的增加;N为乘车人数.由均衡条件
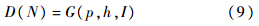
得

消费者剩余为
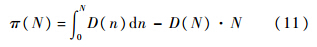
其中n∈(0,N).公交公司收入为

公交公司成本为
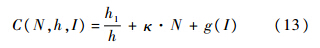
其中,h1为运行一辆公交车的系统固定成本,如司机费用等,为一常数;κ为乘客的平均变动成本,包括油耗费用、电费等,为一常数;g(I)为公交公司提供信息的成本.故公交公司的利润为
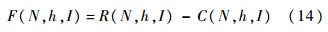
社会福利为
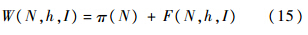
2 垄断最优与社会最优本节分析公司利润最大化与社会福利最大化2种情况下乘车人数、发车时间间隔和信息质量之间的关系以及公交价格的确定.2.1 垄断最优如果政府对公交不进行管制,那么公交公司将寻找最优的(N,h,I)使其自身利润最大化,即
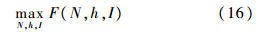
该数学规划的一阶条件为
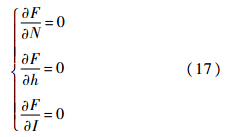
由
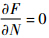 得
得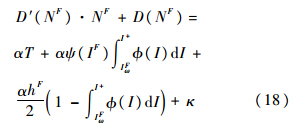
其中,上标F为利润最大化情况下变量的解;等号左边为公交公司的边际收入,第1部分反应了公交公司的市场垄断能力;等号右边为乘客的期望边际成本.由式(18)得
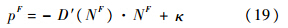
因为D′(N)<0,所以式(19)第1项为正.这说明垄断情况下,公交公司为了最大化其利润,将设定比平均乘客变动成本κ更大的公交价格,与经典的微观经济学市场结构理论中的垄断定价理论一致.2.2 社会最优政府的目的是使社会福利最大,即
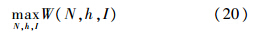
该数学规划的一阶条件为
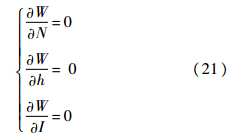
社会最优的目标函数比垄断最优的目标函数多了一个消费者剩余部分,即式(11),而式(11)是一个关于N的函数,因此,除了第1个一阶条件不同之外,另外2个一阶条件与垄断最优相等.由
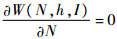 ,得
,得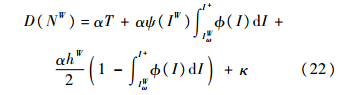
其中,上标W为社会最优情况下各个变量的解;等号左边为整个社会的边际收入;等号右边为整个社会系统的边际成本.由式(22)得

该价格的制定只弥补了乘客的平均变动成本,没有剥夺消费者的剩余,整个社会最优.3 管制策略本节主要分析在不同的管制策略下信息为整个公交系统的优化所产生的作用.管制策略主要包括收益率管制策略和数量管制策略.3.1 收益率管制策略在收益率管制策略下,公交公司可以自由改变其输入,即发车的频率和提供信息的质量,也可以改变自己的输出水平,即乘客数,但公交公司的经济利润是有一定的约束的,经济利润平摊到每位乘客时不能超过政府规定的每单位输出收益,用ε(ε>0)表示,那么收益率约束就是F(N,h,I)/N≤ε.该优化问题为

其一阶条件为

其中,ρ≥0,且ρ是收益率约束的拉格朗日乘子.由式(25)得,
 当
当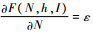 时,则
时,则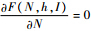 矛盾,故
矛盾,故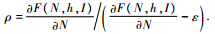 当边际利润大于约束收益率,且均大于0时,收益率约束为紧约束,此时ρ>1;当边际利润小于0,且小于约束收益率时,收益率约束为紧约束,此时0<ρ<1;当边际利润为0时,则收益率约束为松约束,不起作用,此时ρ=0.3.2 数量管制策略数量控制管制策略是为了保证整个公交系统有一定的输出能力,因此,政府会制定一个最小输出量N,那么数量约束就可以表示为N≥N,则该优化问题为
当边际利润大于约束收益率,且均大于0时,收益率约束为紧约束,此时ρ>1;当边际利润小于0,且小于约束收益率时,收益率约束为紧约束,此时0<ρ<1;当边际利润为0时,则收益率约束为松约束,不起作用,此时ρ=0.3.2 数量管制策略数量控制管制策略是为了保证整个公交系统有一定的输出能力,因此,政府会制定一个最小输出量N,那么数量约束就可以表示为N≥N,则该优化问题为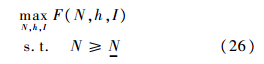
该优化问题的一阶条件为
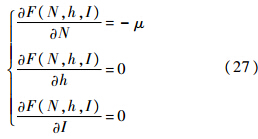
其中,μ≥0,且μ是数量约束的拉格朗日乘子,其经济含义是对乘车人数边际利润的负数.与垄断最优相比较,惟一不同的是
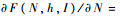 =-μ.若边际利润为0,即μ=0,此时数量约束为松约束,不起作用,其最优解与垄断最优解相同;若边际利润小于0,即μ>0,此时数量约束是紧约束,即N=N-,就相当于求解优化问题:
=-μ.若边际利润为0,即μ=0,此时数量约束为松约束,不起作用,其最优解与垄断最优解相同;若边际利润小于0,即μ>0,此时数量约束是紧约束,即N=N-,就相当于求解优化问题: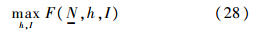
由一阶条件
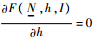 和
和 0所求得的解为最优解;不存在边际利润大于0的情况,因为即使存在边际利润大于0时的情况,也可以通过增加乘客人数提高利润,而且不用违背数量约束.3.3 公交管制策略的比较在不影响研究结论的前提下,为了方便解析推导,本文采用线性函数的形式来描述乘客需求和相关信息成本.假设反需求函数为D(N)=b-a·N,乘客查找信息的时间函数为ψ(I)=c/I,公交公司提供信息的成本函数为g(I)=d·I.信息质量I~U(0,1),则
0所求得的解为最优解;不存在边际利润大于0的情况,因为即使存在边际利润大于0时的情况,也可以通过增加乘客人数提高利润,而且不用违背数量约束.3.3 公交管制策略的比较在不影响研究结论的前提下,为了方便解析推导,本文采用线性函数的形式来描述乘客需求和相关信息成本.假设反需求函数为D(N)=b-a·N,乘客查找信息的时间函数为ψ(I)=c/I,公交公司提供信息的成本函数为g(I)=d·I.信息质量I~U(0,1),则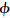 (I)=1,I∈(0,1).其中,a,b,c,d为参数,则收益率管制和数量管制策略起作用情况下优化的求解条件分别为
(I)=1,I∈(0,1).其中,a,b,c,d为参数,则收益率管制和数量管制策略起作用情况下优化的求解条件分别为
和

求得相应的收益率管制的解为

数量管制的解为

而完全无管制的垄断最优解为
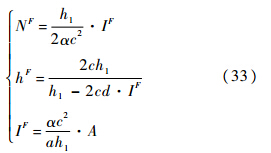
完全管制,即社会最优解为
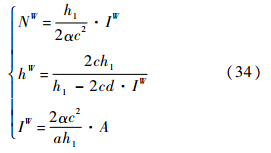
其中,
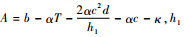 为分交车的系统固定成本.以上结果表明,任何情况下最优解的乘车人数N与信息质量I,发车时间间隔h与信息质量I都具有相同的关系,因为4种情况的最优解都有等价的2个一阶条件,即都有
为分交车的系统固定成本.以上结果表明,任何情况下最优解的乘车人数N与信息质量I,发车时间间隔h与信息质量I都具有相同的关系,因为4种情况的最优解都有等价的2个一阶条件,即都有 和
和
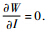 收益率管制可能存在2个解,公交公司将选择利润大的方案.数量管制能够有效保证乘车人数的下限.完全管制所提供的信息质量和乘车人数是完全无管制的2倍,这是因为假设的公交信息成本函数和反需求函数都是线性函数,信息质量也服从简单的均匀分布,实际中信息成本g(I)应该是关于I的凸函数.所以这里的IW=2IF只是在需求函数线性、信息成本函数线性时得出的结果,而NF=NW,hF=hW是由垄断最优与社会最优2个分别相同的一阶条件所得,虽然函数假设的局限性,但是这里反映了完全管制比完全无管制更能使资源合理分配.4 算 例4.1 垄断最优与社会最优令a=1,b=30,c=2,d=10,h1=100元,α=0.25元/min,T=30 min.将乘车时间T作为自变量,则垄断最优解与社会最优解的信息质量、乘车人数、发车时间间隔、公交公司利润或社会福利都随着乘客乘车时间的增加而降低,如图 1所示.
收益率管制可能存在2个解,公交公司将选择利润大的方案.数量管制能够有效保证乘车人数的下限.完全管制所提供的信息质量和乘车人数是完全无管制的2倍,这是因为假设的公交信息成本函数和反需求函数都是线性函数,信息质量也服从简单的均匀分布,实际中信息成本g(I)应该是关于I的凸函数.所以这里的IW=2IF只是在需求函数线性、信息成本函数线性时得出的结果,而NF=NW,hF=hW是由垄断最优与社会最优2个分别相同的一阶条件所得,虽然函数假设的局限性,但是这里反映了完全管制比完全无管制更能使资源合理分配.4 算 例4.1 垄断最优与社会最优令a=1,b=30,c=2,d=10,h1=100元,α=0.25元/min,T=30 min.将乘车时间T作为自变量,则垄断最优解与社会最优解的信息质量、乘车人数、发车时间间隔、公交公司利润或社会福利都随着乘客乘车时间的增加而降低,如图 1所示.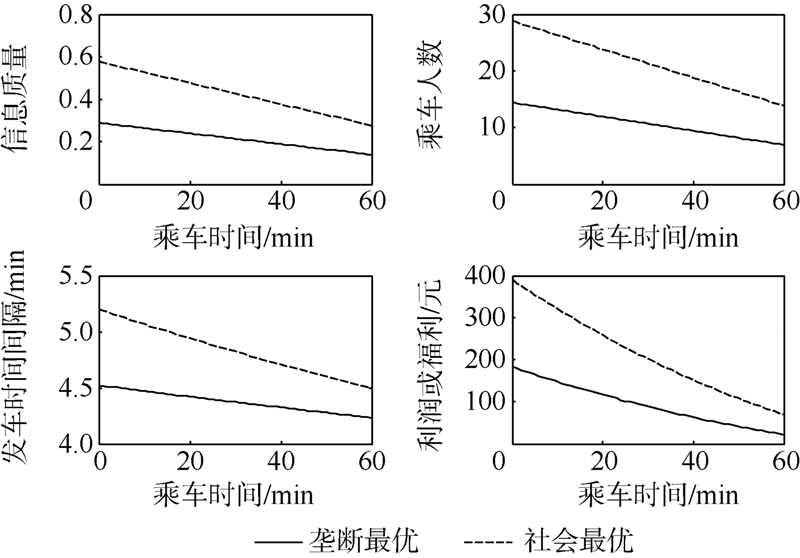 |
| 图 1 乘车时间对社会最优与垄断最优的影响Fig. 1 Trip duration on social and monopoly optima |
| 图选项 |
将乘客单位时间成本α作为自变量,当α从0开始增大时,垄断最优解与社会最优解的信息质量与发车时间间隔先增大后减小,乘车人数则一直减小,公交公司的利润或社会福利先减小后增大,如图 2所示.
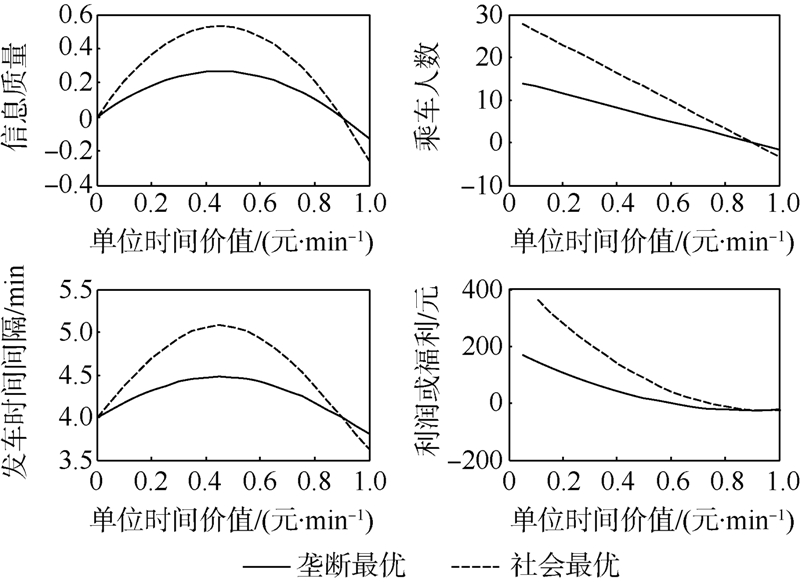 |
| 图 2 单位时间价值对社会最优与垄断最优的影响Fig. 2 Unit time cost on social and monopoly optima |
| 图选项 |
将h1作为自变量,当h1从0开始增大时,垄断最优解与社会最优解的信息质量减少,且减少的速度越来越慢,最后趋于一个稳定值;乘车人数逐渐增加,最后趋于一个稳定值;发车时间间隔先增加,后减小,最后趋于一个稳定值;公交公司利润或者社会福利先稍微增加,后一直减小,如图 3所示.
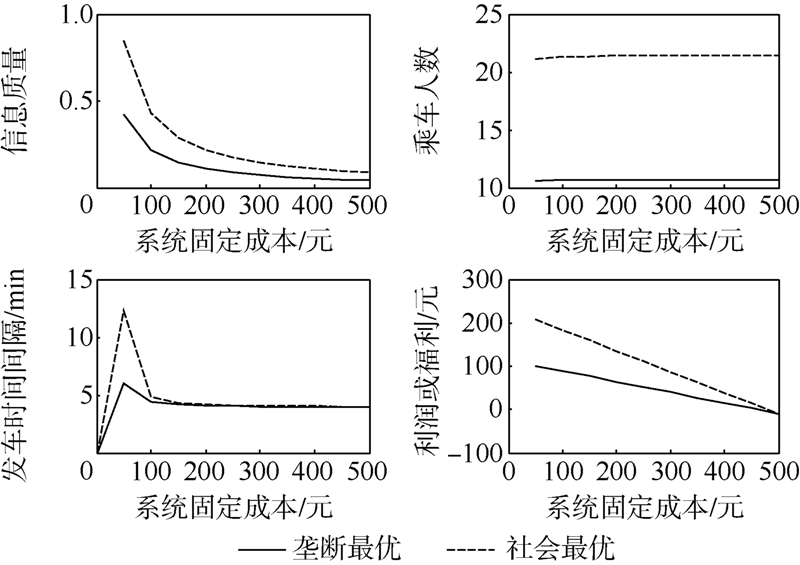 |
| 图 3 系统固定成本对社会最优与垄断最优的影响Fig. 3 System fixed cost on social and monopoly optima |
| 图选项 |
将平摊到乘车人身上的变动成本κ作为自变量,随着变动成本的增加,垄断最优解与社会最优解的信息质量、乘车人数、发车时间间隔、公交公司利润或者社会福利都减小,如图 4所示.
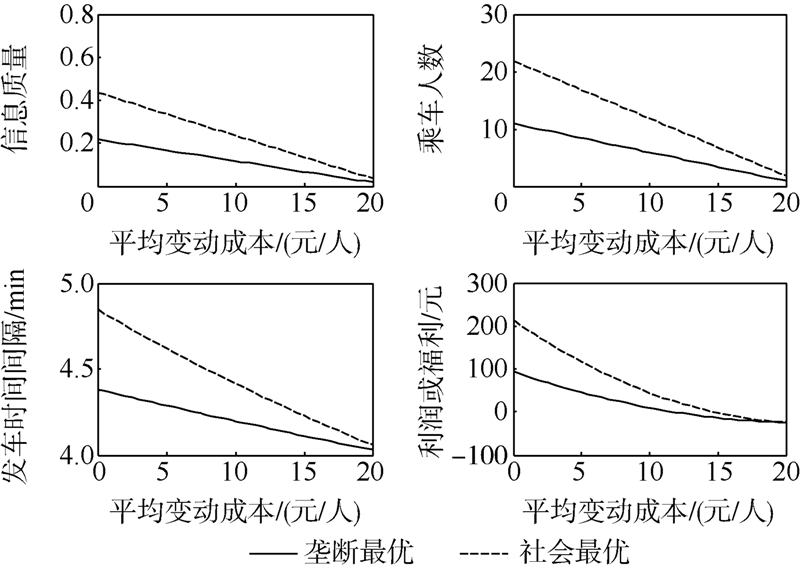 |
| 图 4 平均变动成本对社会最优与垄断最优的影响Fig. 4 Average variable cost on social and monopoly optima |
| 图选项 |
4.2 收益率管制与数量管制4.2.1 收益率管制将收益率ε作为自变量,最优解的信息质量、乘车人数、发车时间间隔以及公交公司利润的变化如图 5所示.
 |
| 图 5收益率管制的影响Fig. 5 The effects of rate-of-return regulation |
| 图选项 |
由图 5可知,当给定的收益率ε<11.3元/人时,满足该约束下的解有2个,根据利润最大原则,公交公司会选择利润大的解,即曲线OAB段,利润最大点为A点,此时收益率为8.302 6元/人,所以当ε≥8.3元/人时,约束不起作用,为垄断最优.因此,图 5中利润最大情况下会选择图形的OAB段.随着收益率的增加,信息质量、乘车人数、发车时间间隔均减小,公交公司利润增大,最后与垄断最优解相同.4.2.2 数量管制因为在无约束条件下的垄断最优解NF=10.65,所以当N<NF时,数量约束为松约束,没有作用,最优解就是垄断最优解;当N≥NF时,数量约束为紧约束,此时数量约束才会起作用.将N作为自变量,相关关系如图 6所示.
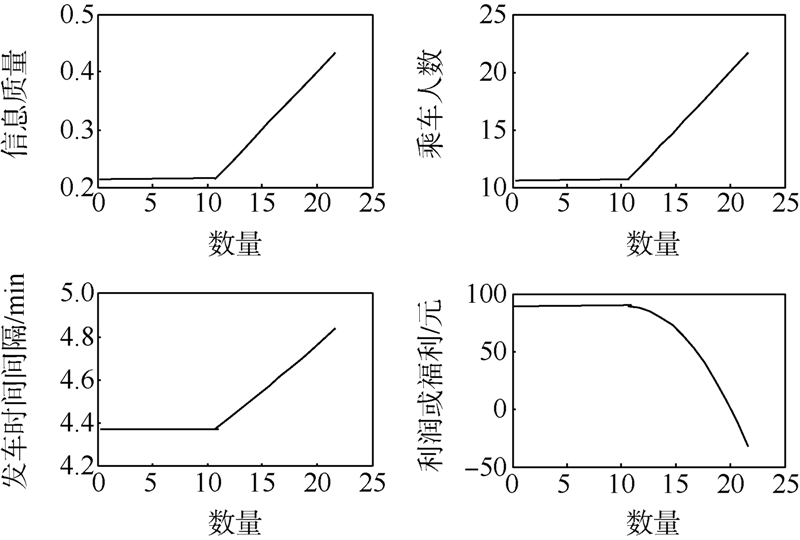 |
| 图 6数量管制的影响Fig. 6 The effects of quantity-control regulation |
| 图选项 |
由图 6可知,当数量约束N-≤10.65时,此时数量约束无作用,最优解为垄断最优解.当N->10.65时,随着N-的增加,公交公司利润在减小,信息质量在增加,发车时间间隔也在增加.此时的数量约束才是有效约束.5 结 论在考虑公交公司提供信息服务和乘客获取信息存在差异的条件下,将乘客分为计划行程与不计划行程2类,分析了公交公司在不同的公交管制策略下公交价格、发车时间间隔和信息提供之间的相互关系,并考察了3种主要的管制策略的影响,分别推导出在完全无管制、完全管制、收益率管制和数量管制下,公交公司所制定的发车时间间隔和所提供的信息质量的关系.研究发现:1) 完全管制情况下的信息质量和乘车人数是完全无管制情况下的2倍,具有更有效的资源配置.2) 在收益率管制下,随着约束收益率的增加,信息质量、乘车人数和发车时间间隔都在减小,公交公司利润则是在增加,直到约束约束收益率不起作用后达到垄断最优的情况.3) 在数量管制下,约束数量较小时,数量管制没有作用,此时与完全无管制结果相同;当约束数量达到一定的临界值之后,随着约束数量的增加,信息质量和发车时间间隔都在增加,但公交公司利润则一直在降低.
参考文献
| [1] | 黄海军, 吴文祥.交通信息对交通行为影响的评价模型[J].系统工程理论与实践,2002,10(3):81-84. Huang H J,Wu W X.Models for evaluating impacts by travel information system on travel behavior[J].Journal of Transportation Systems Engineering and Information Technology,2002,10(3): 81-84(in Chinese). |
| Cited By in Cnki (45) | |
| [2] | 杨晓光,安健, 刘好德,等.公交运行服务质量评价指标体系探讨[J].交通运输系统工程与信息,2010,10(4):13-21. Yang X G,An J,Liu H D,et al.Evaluation architecture discussion of route-level transit service quality[J].Journal of Transportation Systems Engineering and Information Technology,2010,10(4): 13-21(in Chinese). |
| Cited By in Cnki (35) | |
| [3] | 胡金星,刘允才. 公交信息智能化管理系统框架及其关键技术研究[J].交通运输系统工程与信息,2005,5(4):14-17. Hu J X,Liu Y C.Architecture and key technique of intelligent public transportation information management system[J].Journal of Transportation Systems Engineering and Information Technology,2005,5(4):14-17(in Chinese). |
| Cited By in Cnki (13) | |
| [4] | 杨兆升,胡坚明. 中国智能公共交通系统框架与实施方案研究[J].交通运输系统工程与信息,2001,1(1):39-43. Yang Z S,Hu J M.Research on the architecture and implementary scheme of intelligent public transportation system in China[J].Journal of Transportation Systems Engineering and Information Technology,2001,1(1):39-43(in Chinese). |
| Cited By in Cnki (115) | |
| [5] | De Borger B, Fosgerau M.Information provision by regulated public transport companies[J].Transportation Research Part B:Methodological,2012,46(4):492-510. |
| Click to display the text | |
| [6] | 孙连菊,高自友. 城市公交管理的Stackelberg博弈模型[J].交通运输系统工程与信息,2009,9(3):121-127. Sun L J,Gao Z Y.Stacklberg game management model of public transit[J].Journal of Transportation Systems Engineering and Information Technology,2009,9(3):121-127(in Chinese). |
| Cited By in Cnki (4) | |
| [7] | Tian Q, Huang H J,Yang H.Pareto efficient strategies for regulating public transit operations[J].Public Transport,2011,11(3): 199-212. |
| Click to display the text | |
| [8] | Mohring H. Optimization and scale economics in urban bus transportation[J].American Economic Review,1972,62(4):591-604. |
| Click to display the text | |
| [9] | Small K. The scheduling of consumer activities:work trips[J].American Economic Review,1982,72(3):467-479. |
| Click to display the text | |
| [10] | Arnott R, De Palma A,Lindsey R.A structural model of peak-period congestion:a traffic bottleneck with elastic demand[J].American Economic Review,1993,83(1):161-179. |
| Click to display the text | |
| [11] | Jansson K. Optimal public transport price and service frequency[J].Journal of Transport Economics and Policy,1993,27(1):33-50. |
| Click to display the text | |
| [12] | De Palma A, Lindsey R.Optimal timetables for public transportation[J].Transportation Research Part B:Methodological,2001,35(8):789-813. |
| Click to display the text | |
| [13] | Fosgerau M. The marginal social cost of headway[J].Transportation Research Part B:Methodological,2009,43(8-9):813-820. |
| [14] | 黄海军,田琼, 杨海,等.高峰期内公交车均衡乘车行为与制度安排[J].管理科学学报,2005,6(8):1-9. Huang H J,Tian Q,Yang H,et al.Equilibrium bus riding behavior in rush hours and system configuration for providing bus services[J].Journal of Management Sciences in China,2005,6(8): 1-9(in Chinese). |
| Cited By in Cnki (15) |
