图匹配算法在计算机视觉与模式识别领域的应用研究已经有40多年的历史[4].从算法的角度来看,一般将图匹配分为精准图匹配与非精准图匹配,其中精准图匹配是指图(或其一部分)之间满足严格的结构一致性,即匹配后图(或其一部分)的顶点标签、边的邻接关系及权重完全一致.非精准图匹配是指允许匹配后的图(或其一部分)存在一定的顶点标签,边的邻接关系及权重的误差,通过定义一种误差度量方式并最小化,来寻找最优的图(或其一部分)之间的对应关系.从应用角度讲,在计算机视觉应用中,由于物体形变、遮挡、视角变换、图像采集传输过程中的噪声等客观原因,从图像中提取的图结构之间往往不可避免地存在差异,因此在这些任务中非精准图匹配算法的应用更为普遍.
不同于早期的非精准图匹配算法,如基于树搜索并采用编辑距离作为误差度量的算法[5],近年来非精准图匹配算法的一个显著特点是基于一个良好定义的目标函数[6, 7, 8, 9, 10].具体来说,目标函数的形式可以分为基于邻接矩阵的目标函数[6, 8, 9, 11, 12]和基于相似矩阵的目标函数[7, 10, 13, 14].其中基于邻接矩阵的目标函数通常利用两个权重邻接矩阵分别存储两个待匹配权重图的边的邻接关系及权重,然后将图匹配问题转换成为两个权重邻接矩阵的匹配.采用这种形式的目标函数的一个主要优势在于较低的存储复杂度.与此不同,近年来很多算法采用基于相似矩阵的目标函数,其优势在于更为灵活的边的相似度量方式的定义,比如可以采用高斯核的形式.而且当待匹配的图较为稀疏时,采用基于相似矩阵的目标函数的图匹配算法同样具有可接受的存储复杂度与计算复杂度.此外,基于相似矩阵的目标函数更容易推广到高阶图匹配算法,事实上,现有高阶图匹配算法采用的目标函数均为基于相似矩阵的目标函数在高阶约束下的推广.
虽然目前主流的非精准图匹配算法采用的目标函数的具体形式不同,但是总的来说都属于二次组合优化问题.求取其全局最优解仍然是典型的NP难问题,具有阶乘复杂度.出于效率的考虑,大部分情况下并不直接求取全局最优解,而是采用近似算法求取一个较好的局部最优解.根据近似优化策略的不同,近似方法可以分为基于谱分解的优化算法[6, 7, 13]和基于梯度的优化算法[8, 9, 10, 11].基于谱分解的方法是指利用与待匹配的权重图相关联的矩阵的特征值与特征向量来求解顶点间对应关系的方法.Umeyama的算法[6]被认为是第一个谱分解图匹配算法,它采用基于邻接矩阵的目标函数,并证明了原问题放松到连续域后的最优解与两个权重邻接矩阵的特征向量间的关系,该算法仅适用于同规模的图匹配问题,而且实际效果并不鲁棒[8].Leordeanu和Hebert[7]提出另外一种著名的基于相似矩阵的谱分解算法,通过转变匹配约束,将原问题转换为连续域的Rayleigh商优化问题,继而通过求相似矩阵主特征值对应的特征向量得到连续解,最终根据匹配约束将连续解映射回离散域.基于梯度的优化算法中的著名的逐步分配算法[10]、利用半正定规划的图匹配算法[15]在优化过程中都利用目标函数的梯度信息,而且它们均采用基于相似矩阵的目标函数.其中逐步分配算法虽然已经提出了很多年,但是由于其鲁棒的匹配效果,至今仍被认为是最优秀的图匹配算法之一.利用线性规划的图匹配算法[11]同样利用了梯度信息,不同的是它采用了基于邻接矩阵的目标函数,其主要缺陷在于较高的运算复杂度和局限于同规模图匹配问题.最近提出的凸凹松弛过程[8, 9, 16]也是一种梯度方法,用以优化基于邻接矩阵的目标函数,并且通过引入原目标函数的凸松弛函数与凹松弛函数,在同规模的图匹配问题中取得了非常优异的匹配效果,但是该方法的主要问题在于凸松弛函数与凹松弛函数形式复杂,难以构建,无法推广到子图匹配问题.2014年,Liu等提出了一种可以隐式构建凸松弛与凹松弛函数的方法,称为渐非凸渐凹化过程(Graduated Nonconvexity and Concavity Procedure,GNCCP)[17, 18],证明了其严格实现了一种凸凹松弛过程,并将其成功应用于子图匹配问题.
但是,渐非凸渐凹化过程仅能应用在基于邻接矩阵的目标函数,而采用基于相似矩阵目标函数的算法往往能取得更优异的效果.因此,在本文中将渐非凸渐凹化过程推广到基于相似矩阵的目标函数,并因此提出一种新的子图匹配算法.该算法优势在于:①更加灵活的相似性度量定义;②它可以有效解决外点存在情况下的匹配问题;③不同于其他基于相似矩阵目标函数的图匹配算法通常仅能应用于无向图的匹配[7, 13],该算法还可以解决有向图的匹配问题.在人工数据与真实数据上的实验结果证实了算法的有效性.
1 公式化方法假定已经从每一幅图像中抽取出一个权重图G={VG,EG,LG,WG},其中VG={1,2,…,M}为顶点的集合(M为顶点的个数),指代物体中各个部分或者图像中提取出的特征点集,EG∈VG×VG为边的集合,指代物体各个部分或者特征点之间的邻接关系,LG∈Rdl×M为顶点标签的集合,用来描述每个顶点作为一个个体的外观特征,dl为外观描述子的维数,比如如果使用从每个特征点周围的小图像块中提取的128维SIFT直方图描述子作为该特征点的外观描述子,则有dl=128,WG∈Rdw×||EG||0为边的权重集合,用来描述顶点间的结构关系,dw为权重的维数,或者称为结构描述子的维数,比如如果同时使用距离和方向作为结构描述子,则有dw=2.
给定两个权重图G={VG,EG,LG,WG}和H={VH,EH,LH,WH},规模分别为M和N,图匹配就是寻找VG和VH之间的满足某种最优性条件的对应关系,这种对应关系可以通过一个分配矩阵X∈{0,1}M×N来表示,当Xia=1意味着将G中顶点i分配给H中的顶点a,
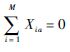意味着G中没有一个顶点与H中的顶点相a对应,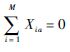也有类似定义.当进一步考虑一对一约束时,X就成为一个偏置换矩阵,即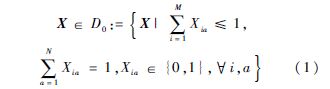
当M=N时,X退化为一个置换矩阵.
G和H的相似矩阵可以按照以下形式构建：
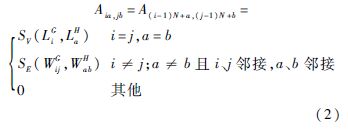
式中:i与j为G中的顶点;a与b为H中的顶点;SV(LiG,LaH)表示图G中的顶点i标签与图H中的顶点a标签之间的相似性度量;SE(WijG,WabH)表示图G中的边ij权重与图H中的边ab权重之间的相似性度量.SV(LiG,LaH)和SE(WijG,WabH)可以有多种灵活的定义方式,比如采用高斯核函数的形式:
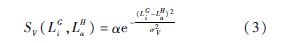
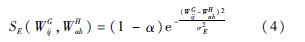
式中:σV和σE为核宽度参数;α为平衡两种相似性度量的权重系数.此外,构建相似矩阵时要同时考虑图结构,仅当两个图中相应的两条边都存在,即i、j邻接且a、b邻接才计算ij与ab的相似性,在这一点上,基于这样的相似矩阵的目标函数与基于邻接矩阵的目标函数也有区别.
基于偏置换矩阵X和相似矩阵A,可以构建目标函数为
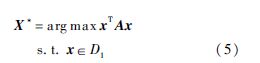
x是X按行抽取的复制,并同时以此更新离散域的定义D1为
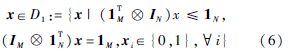
式中:⊗为矩阵间的Kronecker积;1M为长度为M全是1的列向量;IN∈RN×N为单位矩阵.目标函数式(5)的物理意义是给定分配矩阵X的情况,最大化对应顶点相似性度量和对应边相似性度量的加权和.
在给出优化目标函数式(5)的算法前,讨论基于邻接矩阵的目标函数和式(5)之间的区别和联系.文献[19]通过将相似矩阵分解并进一步进行矩阵的奇异值分解(Single Value Decomposition,SVD),证实了基于相似矩阵的目标函数可以写成基于邻接矩阵的目标函数的加权和形式.实际上,在某些情况下,这两种目标函数是等价的,比如在采用全连接图结构的情况下,当式(4)中SE(WijG,WabH)采用最小二乘方式的相似性度量时,即
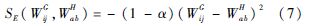
式(5)与如下基于邻接矩阵的目标函数[19]等价:
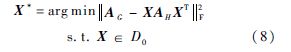
式(8)是一种广泛使用的基于邻接矩阵的目标函数[8, 9, 18],其中||·||F是矩阵的Frobenius范数,AG和AH是分别与G和H相关联的邻接矩阵.等价性可以通过将式(8)展开证实,因为式(8)同样是对应边的相似性度量的和.由此可见,基于邻接矩阵的目标函数可以看成基于相似矩阵的目标函数的一个特例,与前者相比,基于相似矩阵的目标函数可以更灵活地定义相似性度量,如式(4)所示的指数形式.另外,当图结构稀疏时,基于相似矩阵的目标函数往往更加鲁棒的原因是它直接计算两个图中边之间的相似性,而形如式(8)的基于邻接矩阵的目标函数不可避免地需要引入实际存在的边与不存在的边(权重为0)权重间的差异性,这在某种程度上引入了附加噪声,降低了模型的鲁棒性.
2 优化算法优化问题式(5)是一个典型的NP难问题,具有阶乘复杂度,出于运算效率的考虑,需要采用近似策略.目前主流思路是将原问题放松为一个连续优化问题,然后将得到的连续解映射回离散域.基于谱分解的算法[7, 13]是采用这种思路的重要一类算法,但为了使问题可解,这类算法往往对相关矩阵的形式进行限制并进而影响了应用范围,比如文献[7]基于相似矩阵的谱分解算法要求相似矩阵是非负且对称的,因而不能应用于有向图的匹配.渐非凸渐凹化过程研究的出发点是凸凹松弛过程[8, 9, 16],凸凹松弛过程同样将原离散问题先放松到连续域,具体来说是放松到原离散域的凸包,然后通过调整原目标函数的凸松弛函数与凹松弛函数的线性组合系数,逐步地将优化问题的连续解映射回离散域,这往往会得到比采用直接映射的方式更好的匹配结果.凸凹松弛过程在同规模的图匹配问题上表现优异,但其主要问题是凸松弛函数与凹松弛函数的形式复杂,很难推广到其他问题,比如子图匹配问题.文献[17, 18]提出一种隐式实现基于邻接矩阵目标函数的凸松弛函数与凹松弛函数线性组合的策略,从而可以解决子图匹配问题.本文进一步将渐非凸渐凹化过程推广到基于相似矩阵的目标函数.具体地,本文提出的算法采用以下形式：
式中:η为线性组合系数;C1为D1的凸包,定义为
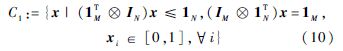
当线性组合系数η从-1逐步增加到1时,优化目标函数Fη(x)的问题会逐步从一个凸优化问题转变成一个凹优化问题,而且该凸优化问题与凹优化问题在离散域D1具有相同的局部最优解.凸优化理论已经比较成熟,存在很多快速有效的算法,比如内点法、牛顿法等,而凹优化问题在凸包C1的最优点取在其顶点集上,即D1上,所以当η从-1逐步增加到1时,在连续域内的最优解会沿着一条路径到达离散域,这样的逐步映射方法往往比直接映射得到更好的匹配结果,本算法总结在算法1中.
算法1 基于GNCCP的优化算法
输入：相似矩阵A
初始化：
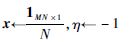
执行
x←Frank-Wolfe(x,A,η)
η←η+δη
直到η≥1 or x∈D1
输出：x
对于每一个η,采用Frank-Wolfe算法[20]来优化.Frank-Wolfe算法,又称为条件梯度算法,是一种非常有效的非线性优化算法,由于其易用且性能稳定,在机器学习领域一直得到广泛使用[21].该算法总结在算法2中.
算法2 Frank-Wolfe(x,A,η)
输入：相似矩阵A，当前x
执行
y←argmax yT▽Fη(x),s.t. y∈C1
λ←argmax Fη(x+λ(y-x)),
s.t. 0≤λ≤1
y←x+λ(y-x)
直到x收敛
输出：x
在算法2中,线性规划问题:
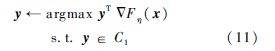
可通过匈牙利算法[22]解决,其中导数▽Fη(x)为
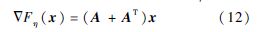
步长λ可以通过非精确线搜索得到,比如回溯法[23].x收敛的停机准则为：如果(y－x)TΔFη(x)≤0,则停止.
3 实验比较在本节中,分别在人工数据集与真实数据集上将提出的算法与几种有代表性的图匹配算法比较.用于比较的算法包括:谱分解算法(Spectral Method,SM)[7],步分配算法(Graduated Assignment,GA)[10],概率匹配算法(Probabilistic Graph Matching,PGM)[13],这些算法均采用基于相似矩阵的目标函数,本文提出的算法记为OUR.本实验中顶点标签相似度度量与边权重相似性度量分别采用式(3)和式(4)的形式,设定参数σV=0.15,σE=0.15.
3.1 人工数据集首先在人工数据集上验证提出的算法.随机产生两个空间点集,方式如下:首先通过均匀随机采样产生规模为M=20的空间点集G={gi}i=1M,gi～U[0-1]1×2,然后通过对G施加高斯噪声n～N(0,σ2)得到规模同样为20的点集H0,并进一步通过均匀随机采样得到规模为#outlier的外点集合H1={ha}a=1#outlier,ha～U[0-1]1×2,其中#outlier是使用的外点数目,将H0和H1组合形成规模为N的空间点集H,N=20+#outlier.采用空间点间的距离作为边的权重,并采用全连接的图结构.本实验中不使用外观描述子,即设定α=0,以便更好地比较算法二阶匹配的效果.
实验1:将噪声水平σ从0增加的0.1,步长为0.01,设定#outlier=10.
实验2:将#outlier从0增加到20,步长为2,设定σ=0.05.
实验结果如图 1所示,从图中可以观察到:①匹配准确度随着噪声水平的提高和外点数目的增加逐步降低;②本文提出的算法不管从匹配准确度还是从目标函数优化角度来看,取得的匹配效果最好;③PGM没有取得预想中的匹配效果,这可能是因为PGM并不适应于外点与真实关键点在空间上存在较大重叠的情况;④匹配准确度有时产生与目标函数不一致的情况,这很大程度是因为由于噪声的存在,标定的真实匹配点未必是实际最优的匹配点.
 |
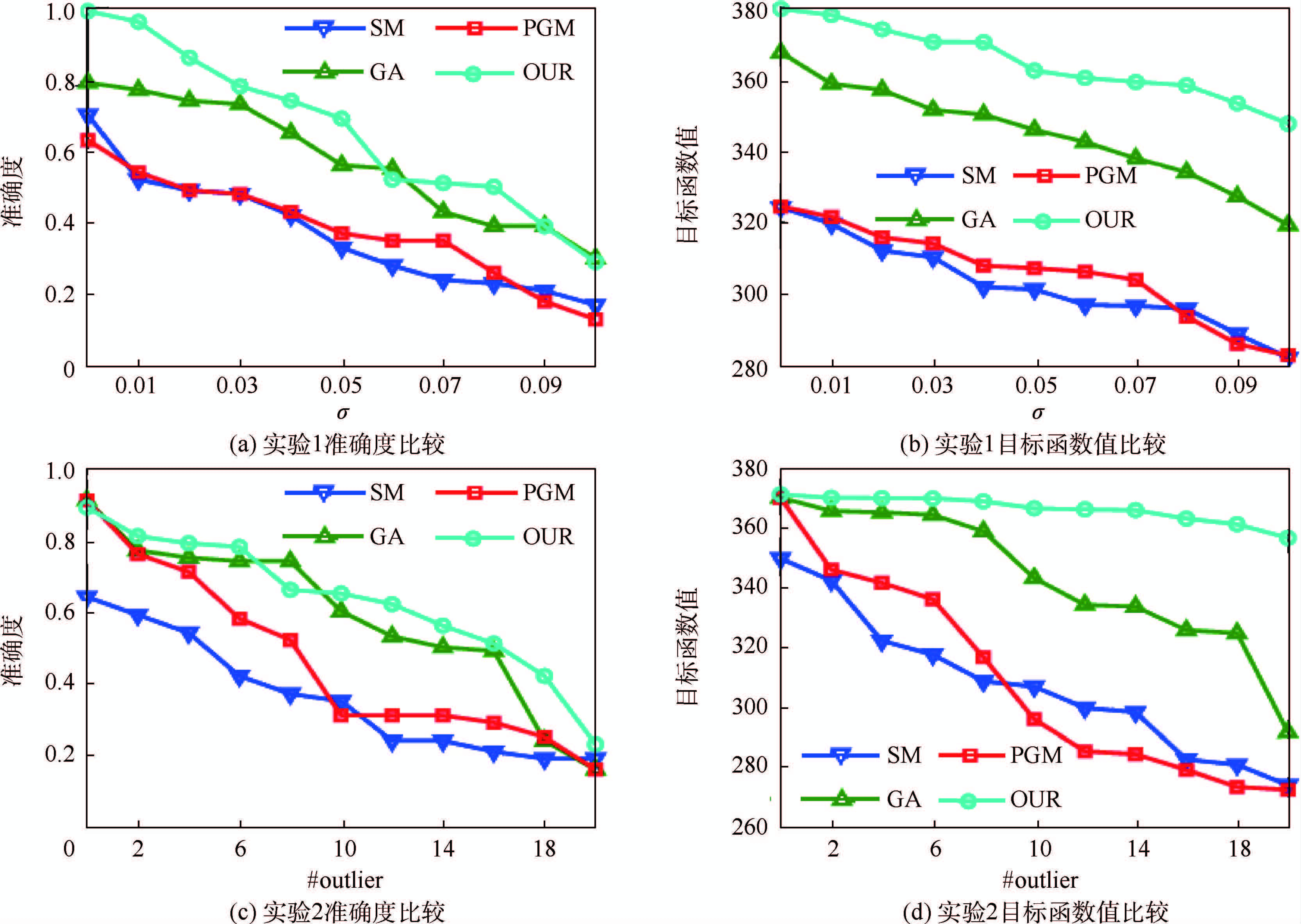| 图 1 人工数据集上的实验结果Fig. 1 Experimental results of artificial datasets |
| 图选项 |
3.2 真实数据集将提出的算法应用在标准的图像匹配数据集上[24].该图像数据集含有30对Car图像和20对Motorbike图像,每一对图像通过手动标注得到真实对应点,数目为15～52.实验中以特征点间的距离和方向作为结构描述子,其中OUR和GA采用有向图模型,而SM和PGM仅适用于无向图模型,故使用无向图.采用形状上下文特征作为外观描述子,系数α=0.5,此外采用Delaunay triangulation的形式构建图模型,如图 2所示.
 |
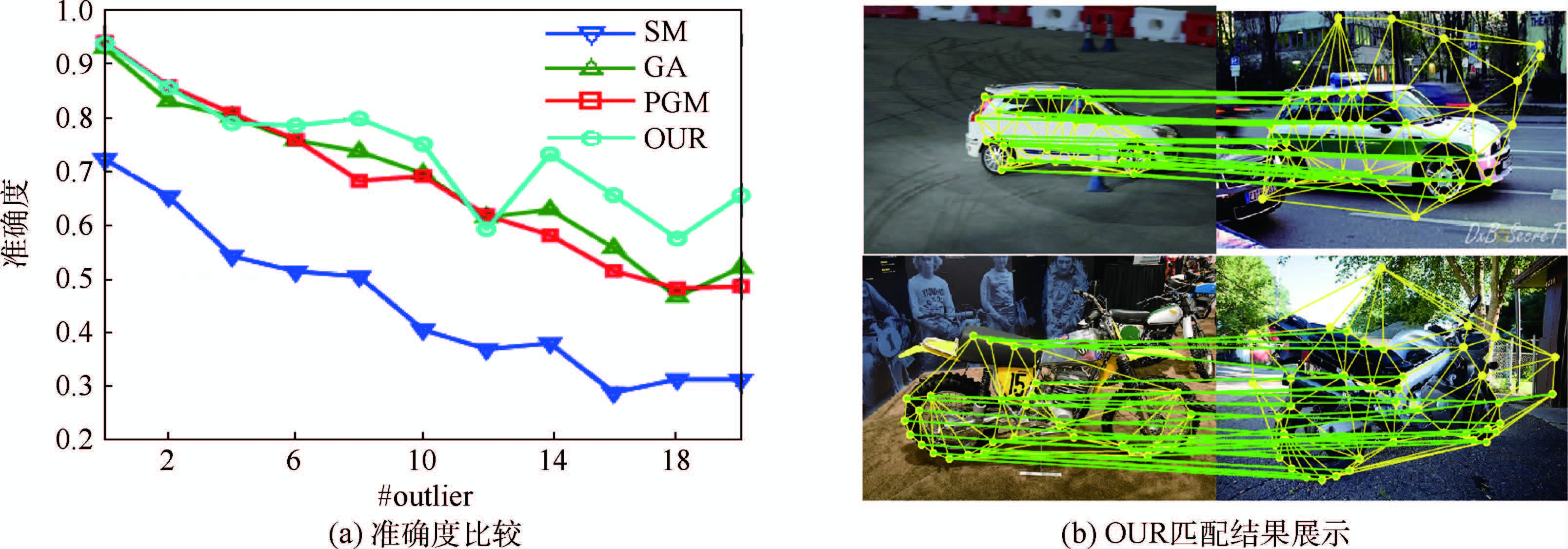| 图 2 真实数据集上的实验结果Fig. 2 Experimental results of real datasets |
| 图选项 |
随机加入外点,数目#outlier从0增加到20,步长为2,实验结果如图 2(a)所示,从图中可以观察到:①本文提出的算法得到最优的匹配结果;②PGM的匹配效果有了显著的提升,这可能是因为使用的数据集中外点的分布往往与真实点没有重合.OUR取得真实匹配结果如图 2(b)所示,左、右图之间的连线为通过算法求得的匹配关系.
4 结 论本文提出一种新的采用二阶约束的图匹配算法,具体来说,该算法采用基于相似矩阵的目标函数,并扩展渐非凸渐凹化过程来优化该问题.该算法优势在于:①更加灵活的相似性度量定义;②它可以有效解决外点存在情况下的匹配问题;③可以处理有向图的匹配问题.在人工数据与真实数据上的实验结果证实了算法的有效性.
参考文献
| [1] | Leordeanu M, Hebert M, Sukthankar R.Beyond local appearance: Category recognition from pairwise interactions of simple features[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE Press, 2007: 1-8. |
| Click to display the text | |
| [2] | Jiang H, Yu S X, Martin D R.Linear scale and rotation invariant matching[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(7): 1339-1355. |
| Click to display the text | |
| [3] | Brendel W, Todorovic S.Learning spatiotemporal graphs of human activities[C]//Proceedings of IEEE International Conference on Computer Vision.Piscataway, NJ: IEEE Press, 2011: 778-785. |
| [4] | Conte D, Foggia P, Sansone C, et al.Thirty years of graph matching in pattern recognition[J].International Journal of Pattern Recognition and Artificial Intelligence, 2004, 18(3): 265-298. |
| Click to display the text | |
| [5] | Tsai W H, Fu K S.Error-correcting isomorphisms of attributed relational graphs for pattern analysis[J].IEEE Transactions on Systems, Man and Cybernetics, 1979, 9(12): 757-768. |
| Click to display the text | |
| [6] | Umeyama S. An eigendecomposition approach to weighted graph matching problems[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 1988, 10(5): 695-703. |
| Click to display the text | |
| [7] | Leordeanu M, Hebert M.A spectral technique for correspondence problems using pairwise constraints[C]//Preceedings of the IEEE International Conference on Computer Vision.Piscataway, NJ: IEEE Press, 2005, II: 1482-1489. |
| Click to display the text | |
| [8] | Zaslavskiy M, Bach F, Vert J P.A path following algorithm for the graph matching problem[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(12): 2227-2242. |
| Click to display the text | |
| [9] | Liu Z Y, Qiao H, Xu L.An extended PATH following algorithm for graph matching problem[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(7): 1451-1456. |
| Click to display the text | |
| [10] | Gold S, Rangarajan A.A graduated assignment algorithm for graph matching[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 1996, 18(4): 377-388. |
| Click to display the text | |
| [11] | Almohamad H, Duffuaa S.A linear programming approach for the weighted graph matching problem[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 1993, 15(5): 522-525. |
| Click to display the text | |
| [12] | Liu Z Y. Graph matching: A new concave relaxation function and algorithm[J].Acta Automatica Sinica, 2012, 38(5): 725-731. |
| Click to display the text | |
| [13] | Egozi A, Keller Y, Guterman H.A probabilistic approach to spectral graph matching[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(1): 18-27. |
| Click to display the text | |
| [14] | Torresani L, Kolmogorov V, Rother C.A dual decomposition approach to feature correspondence[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(2): 259-271. |
| Click to display the text | |
| [15] | Torr P H S. Solving markov random fields using semi definite programming[C]//Proceedings of Artificial Intelligence and Statistics, 2003. |
| [16] | Liu Z Y, Qiao H.A convex-concave relaxation procedure based subgraph matching algorithm[J].Journal of Machine Learning Research: W&CP, 2012, 25: 237-252. |
| Click to display the text | |
| [17] | Liu Z Y, Qiao H.Graduated nonconvexity and concavity procedure for partial graph matching[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(6): 1258-1267. |
| Click to display the text | |
| [18] | Yang X, Qiao H, Liu Z Y.Partial correspondence based on subgraph matching[J].Neurocomputing, 2013, 122: 193-197. |
| Click to display the text | |
| [19] | Zhou F, De La Torre F.Factorized graph matching[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ: IEEE Press, 2012: 127-134. |
| [20] | Frank M, Wolfe P.An algorithm for quadratic programming[J].Naval Research Logistics Quarterly, 1956, 3(1-2): 95-110. |
| Click to display the text | |
| [21] | Jaggi M. Revisiting frank-wolfe: Projection-free sparse convex optimization[C]//Proceedings of the 30th International Conference on Machine Learning (ICML-13).[S.l.]: International Machine Learning Society, 2013: 427-435. |
| [22] | Kuhn H W. The Hungarian method for the assignment problem[J].Naval Research Logistics Quarterly, 1955, 2(1-2): 83-97. |
| Click to display the text | |
| [23] | Boyd S, Vandenberghe L.Convex optimization[M].Cambridge: Cambridge University Press, 2004: 464-466. |
| [24] | Leordeanu M, Sukthankar R, Hebert M.Unsupervised learning for graph matching[J].International Journal of Computer Vision, 2012, 96(1): 28-45. |
| Click to display the text |
