随着地球环境的不断恶化,人们的环保意识逐渐觉醒,减少能源消耗和污染气体的排放的呼声越来越高^[1].航空业也希望降低飞行器的燃料消耗以降低运营成本,提高飞行经济性.减少阻力是降低飞行器燃料消耗、提高经济性的重要手段之一.若保持航程不变,大型民用客机减少一个阻力点(ΔC_D=0.000 1,C_D为阻力系数)可以增加8名乘客;以B747为例,减少1%的阻力相当于每年减少10 000加仑(1加仑=3.78 L(美))的航空燃油消耗^[2].边界层吸气是目前研究比较广泛的减阻方法.边界层吸气可将边界层内低能量气体吸除,减少飞行器的压差阻力^[3].边界层吸气也可抑制边界层内的扰动发展,延迟边界层转捩,增加飞行器层流面积,减少飞行器摩擦阻力^[4].吸气位置与吸气质量是影响边界层吸气减阻效果的关键因素.然而边界层吸气位置的确定大多是靠经验或者实验,随意性很大.如果吸气位置设置不恰当,在相同的减阻目标下,吸气质量会大大增加,甚至边界层吸气技术根本没有减阻效果.大量吸气消耗过多的能量,阻碍了边界层吸气技术的实际应用.如何确定最适宜的吸气位置,提高吸气的利用效率,减少边界层吸气总量,成了一个亟待解决的问题.本文研究的目的是寻找最佳的吸气位置,在吸气质量最少的情况下使边界层吸气减阻效果最好,提高边界层吸气减阻的效率,减少吸气减阻技术的能量消耗,促进边界层吸气技术的实际应用.遗传算法是一类模拟生物界适者生存、优胜劣汰进化规律演化而来的随机化搜索算法.由于其寻优能力好、鲁棒性强等特点,遗传算法被广泛应用于多个领域.本文将多岛遗传算法与计算流体力学相结合,将吸气开口位置与吸气质量作为优化变量,以最小化翼型阻力系数与吸气质量为目标,对边界层吸气减阻技术优化进行数值研究.1 研究方法1.1 多岛遗传算法遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法^[5].遗传算法对决策变量的编码,即“染色体”,进行选择、交叉、变异等操作,搜索具有最佳目标值的遗传“个体”.由于遗传算法鲁棒性强和方便使用的优点,其被广泛应用于自动控制、图像处理及机器学习等领域.传统遗传算法流程图见图 1.

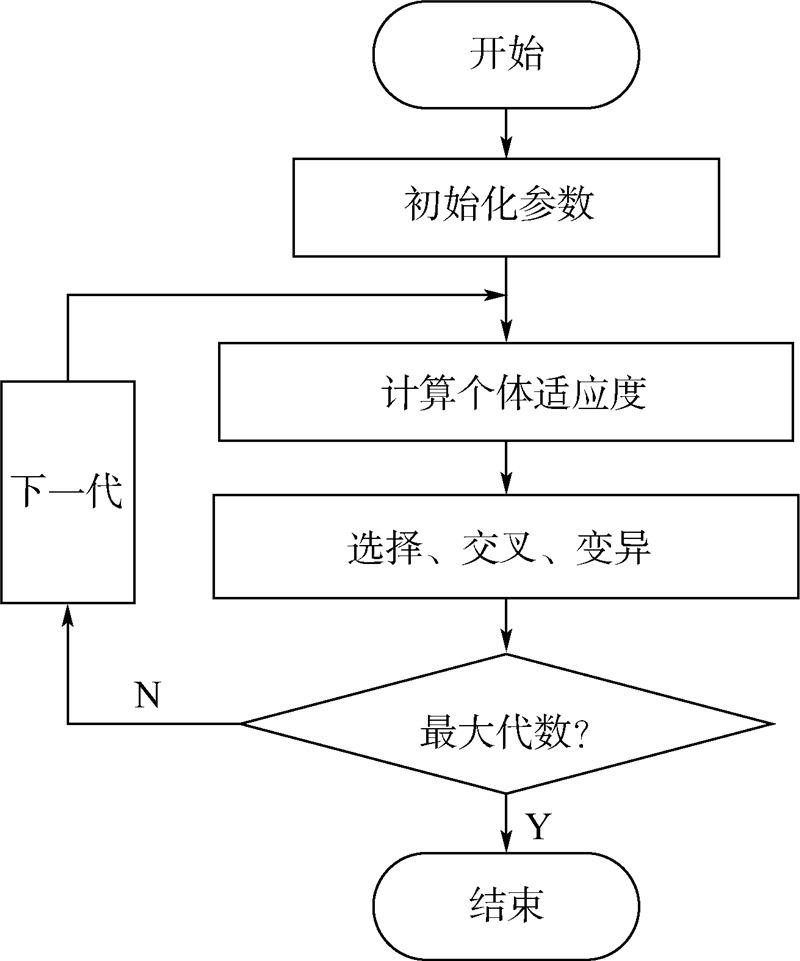
图 1 传统遗传算法流程图Fig. 1 Process of traditional genetic algorithm

图选项

多岛遗传算法是由传统遗传算法发展而来的一种基于群体分组的并行性遗传算法.与传统遗传算法的不同之处在于,多岛遗传算法将整个种群划分为若干子群,并将子群互相隔绝于不同的“岛屿”上,各个子群独立地进化,而不是全部种群采用相同的进化机制,并且各个“岛屿”间以一定的时间间隔进行“迁移”操作,使各个“岛屿”间进行信息交换.多岛遗传算法能够有效地提高运算速度,并且若干独立进化的子群提高了整个种群的遗传多样性,所以其还可以回避传统遗传算法的早熟现象,有利于找到全局最优解.在本文吸气减阻优化中,优化变量并不是单一的,而是存在两个优化变量,即吸气开口位置和吸气质量,翼型阻力随二者的变化规律会比单一优化变量时复杂得多.若使用传统遗传算法,极有可能使种群陷入局部最优解,从而无法找到全局最优解.为避免上述问题,将多岛遗传算法应用于本文吸气减阻优化中是十分必要的.1.2 物理模型与数值方法物理模型选用E387翼型,其弦长为6 m.吸气开口位于上翼面,宽度为61.5 mm.吸气开口位置由其与翼型后缘的相对距离L/S定义,其中L为吸气开口沿着上翼面到翼型后缘的曲线距离,S为整个上翼面曲线长度,W为吸气开口的宽度,见图 2.

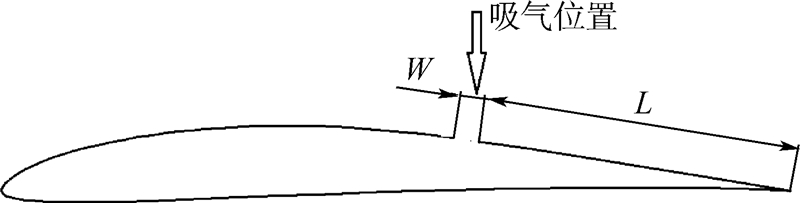图 2 E387翼型吸气减阻模型示意图Fig. 2 Schematic diagram of suction model for E387 airfoil

图选项

翼型的阻力包括压差阻力与摩擦阻力,为了准确预测翼型阻力,数值计算采用Transition SST转捩模型.Transition SST转捩模型由Menter等^[6]于2002年提出,其将k-ω SST湍流模型与基于两个转捩输运方程的γ-Re_θ转捩模型结合,实现对转捩现象的模拟.Transition SST转捩模型可以很好地融入现有的CFD程序,对并行计算及相对较为复杂的外形具有较好的适应性.关于Transition SST转捩方程的更多介绍,可参见文献^[7].离散方程采用有限体积法,扩散项采用中心差分格式,对流项采用二阶迎风格式,求解方法采用SIMPLE算法.远场采用压力远场条件,物面满足无滑移边界条件,吸气开口采用质量入口条件,指定吸气开口的质量通量,吸气方向垂直于壁面.计算风速为30 m/s,基于弦长的雷诺数为1.12×10⁶,翼型迎角为4°.为保证计算的准确性,第1层网格尺寸满足y⁺<1.2 数值方法验证E387翼型有比较丰富的实验数据,所以计算验证仍然采用此翼型.计算验证采用Selig^[8]的实验数据,实验条件为:机翼弦长为1ft,即0.304 8 m,基于弦长的雷诺数为2×10⁵,风洞湍流强度小于0.1%.图 3为翼型极曲线的计算结果(正方形)与实验结果(圆形)对比.由图中数据可见,计算结果与实验结果吻合较好,说明计算方法是可行的,Transition SST转捩模型对阻力预测结果可信.

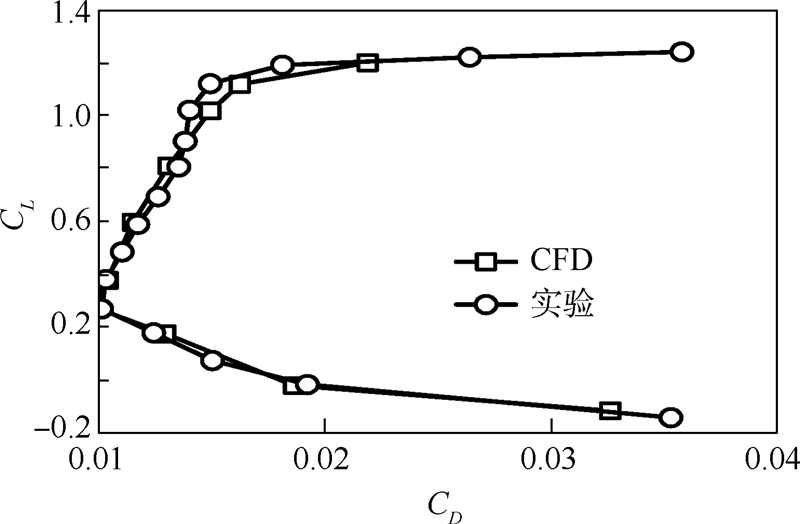图 3 E387翼型极曲线计算与实验结果对比(Re=2×105)Fig. 3 Comparison between CFD and experimental result for the drag polar of E387(Re=2×105)

图选项

3 优化算法设置3.1 变量的编码本次优化所采用的变量编码方法为格雷码.格雷码编码方法是二进制编码方法的一种变形,但其与二进制编码方法相比,能够增强遗传算法的局部搜索能力,便于对连续函数进行局部空间搜索.对于一个吸气开口,相应的变量总共有两个,即吸气开口的位置及吸气质量.吸气开口的位置由L/S定义,吸气质量则由其质量通量φ，kg·m^-2·s^-2定义.变量编码即将L/S与φ分别编码为16位的格雷码.3.2 优化目标与参数设置本次优化目的是既能减少翼型阻力也能降低吸气消耗,即
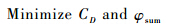
阻力系数C_D与吸气总量φ_sum同时最小化意味着多目标优化问题,而多岛遗传算法为单目标优化算法,故本文采用归一化方法对多目标适应度函数进行处理.加权法是多目标归一化算法的代表算法之一,把多个目标转化为单一目标,指定权重系数,即可通过成熟单目标优化方法求解,即
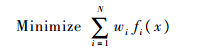
式中:w_i为权重因子;f_i(x)为优化目标参数.加权法归一化算法的好处在于可以通过调整权重因子的值突出某一参数在目标函数中的重要性.则本次优化的目标函数为
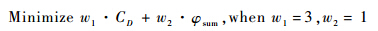
w₁=3 与w₂=1的取值原因,是由于在两个优化目标中优先考虑减阻效果,所以阻力系数的权重因子较大.在遗传算法中,适应度表示个体所代表解的优良程度,适应度越高,个体所对应的解越好.个体适应度定义为目标函数的倒数,即
可见,目标函数越小,适应度越大.本次优化中,吸气开口的数目只有一个,相应的变量包括两个：L/S和φ.优化目标为
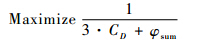
约束条件为
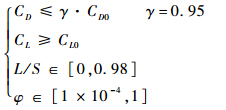
多岛遗传算法的参数选择见表 1.表 1 多岛遗传算法参数Table 1 Parameters of multi-island genetic algorithm

参数	数值
进化代数	45
岛屿个数	5
岛屿上的个体数	10
迁移间隔	4
交叉概率	0.8
变异概率	0.03
迁移概率	0.4

表选项


4 结果分析4.1 优化结果优化的最终结果见表 2,与没有吸气时相比,翼型阻力系数减小8.3%,吸气口的质量通量达到了1×10^-4,其为约束条件的下限,最优吸气开口位置L/S为47.28%.表 2 优化结果Table 2 Results of optimization

参数	CD	L/S	φ
数值	0.012 2	47.28%	1×10-4

表选项


适应度与进化代数关系曲线如图 4所示.当前最优适应度表示进化到当前代的种群中最优个体的适应度(图中三角形),而种群平均适应度则是进化到当前代的种群中全部个体的平均适应度(图中正方形).第1代种群中的个体是随机生成的,其种群平均适应度为1.73,而当前最优适应度为20.12,说明随机产生的种群整体适应度表现不好,且个体间适应度相差较大.由图可见,当前最优适应度在第2代突增到25.77,从第2代到第12代,当前最优适应度缓慢增加至26.18,与之相比,在前12代中种群平均适应度逐渐由1.73增大至5.52,说明种群整体在不断地进化中.在第13代时,当前最优适应度和种群平均适应度都出现突增,之后当前最优适应度缓慢地由27.49增加至27.83,增加了1.2%.虽然当前最优适应度变化不大,但种群平均适应度则出现剧烈波动,这说明种群没有停止进化,各个影响参数仍在进行优化.

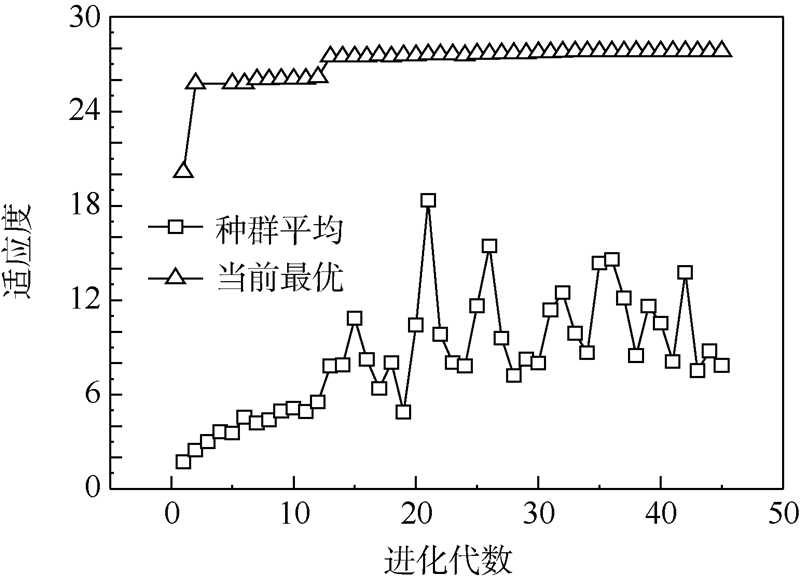图 4 种群进化收敛过程Fig. 4 Population evolve convergence history

图选项

当前最优吸气开口位置与进化代数的关系曲线如图 5所示.当前最优吸气质量与进化代数的关系曲线如图 6所示.当前最优阻力系数与进化代数的关系曲线如图 7所示.由图 5~图 7可见,当前最优个体分散在一定的范围内,并且吸气开口位置与阻力系数波动的幅度较大,这说明吸气开口位置与阻力系数是影响个体适应度的主要参数;也进一步说明相同吸气质量的情况下,吸气开口位置决定着吸气减阻的效果.在第25代之后,吸气开口位置(L/S)、吸气质量通量(φ)和阻力系数已经接近不变,说明种群在第25代之后已经基本成熟.

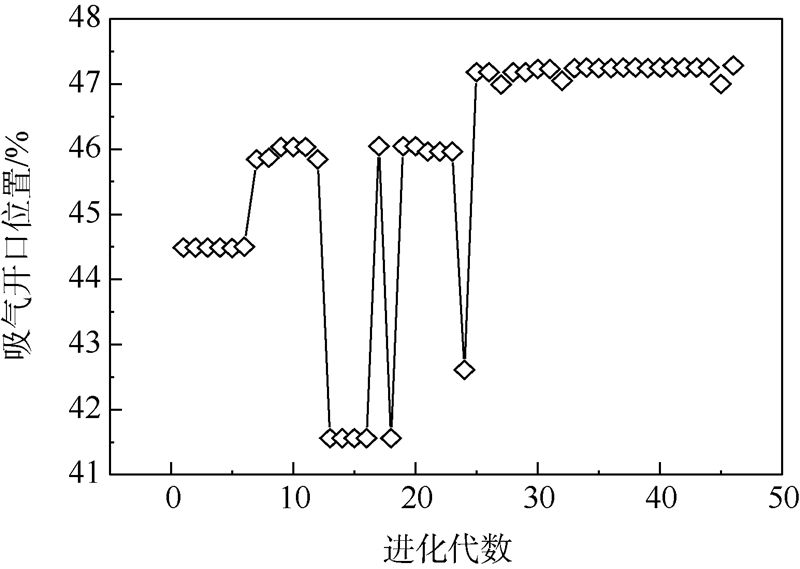图 5 最优个体吸气开口位置与进化代数曲线Fig. 5 Suction location of best individual versus population with generation

图选项

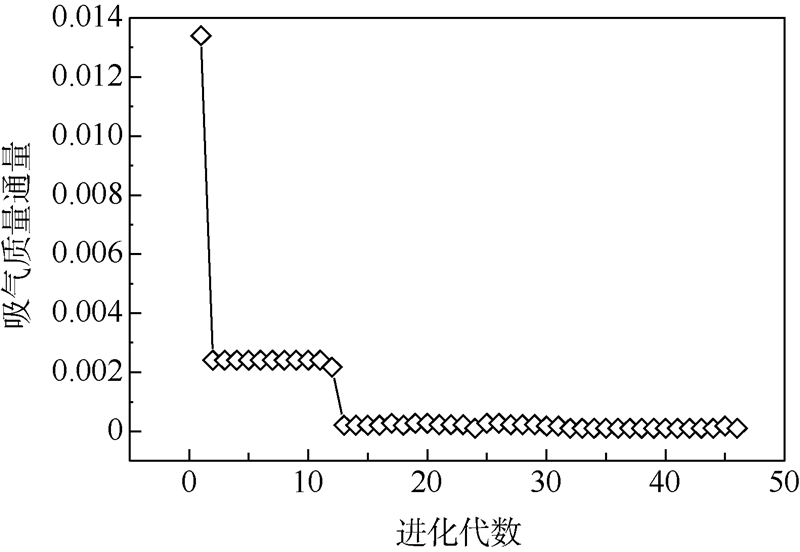图 6 最优个体吸气质量通量与进化代数曲线Fig. 6 Mass flux of best individual versus population with generation

图选项

图 7 最优个体阻力系数与进化代数曲线Fig. 7 Airfoil drag coefficient of best individual versus population with generation

图选项

4.2 流动分析表 3为吸气与未吸气时的翼型阻力组成.由表中数据可见,在吸气的情况下,压差阻力显著减少,而摩擦阻力基本不受影响,说明压差阻力的减少是翼型阻力减小的根本原因.表 3 翼型阻力组成Table 3 Components of the airfoil drag

情况	压差阻力/10-3	摩擦阻力/10-3
未吸气	5.24	8.06
吸气	4.14	8.05

表选项


翼型上翼面摩擦阻力系数和湍流强度分别见图 8和图 9.由图可见,除吸气开口附近,两种情况下的上翼面摩擦阻力系数C_f和湍流强度完全重合,均在弦向位置x/c=0.1时,开始转捩流动.这说明吸气所能影响的区域非常有限,没有延缓流动转捩的发生,也证明本次优化结果中翼型摩擦阻力没有减少.

图 8 上翼面摩擦阻力系数比较Fig. 8 Comparison of skin friction coefficient for upper airfoil

图选项

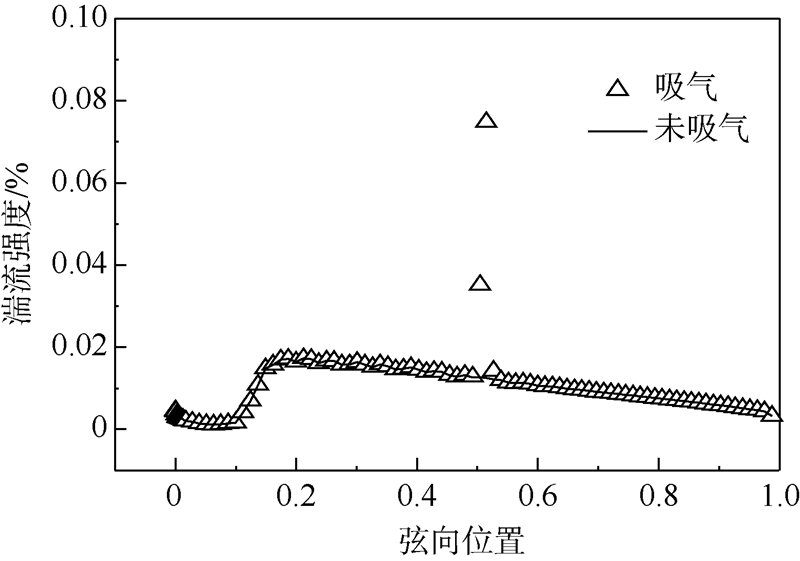图 9 上翼面湍流强度比较Fig. 9 Comparison of turbulent intensity for upper airfoil

图选项

图 10为吸气时翼面压力系数减去未吸气时翼面压力系数的差.可见,除前缘外,下翼面ΔC_p接近于0,说明吸气对下翼面没有影响;对于上翼面,吸气开口位置前ΔC_p相对较大,且在靠近吸气开口前缘的位置出现压差峰值.这说明吸气改变了翼型表面的压力分布,主要是吸气开口之前上翼面的压力分布,且距离吸气开口越近所受影响越大.

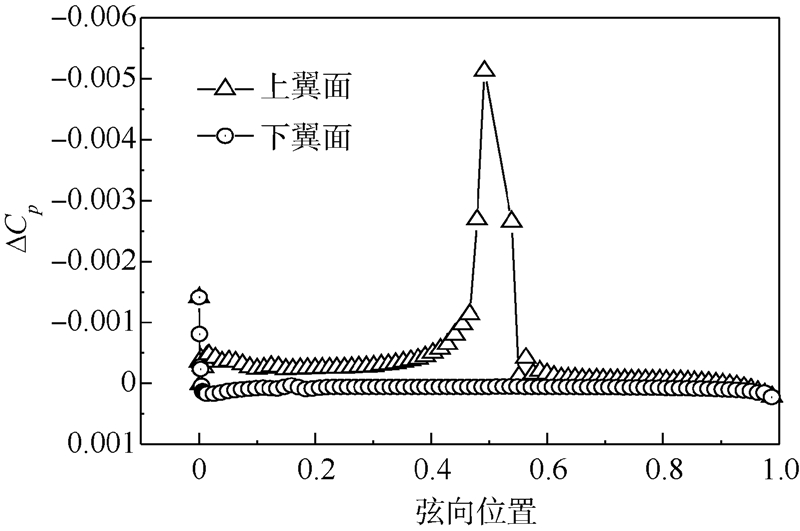图 10 翼型表面压力系数差分布曲线Fig. 10 Differential pressure coefficient distribution on airfoil

图选项

5 结 论1) 多岛遗传算法能够优化边界层吸气减阻技术的吸气位置参数和吸气量参数.吸气开口位置最优时,只需很少的吸气质量就能够达到很好的减阻效果.2) 优化结束后吸气开口位置为最优,此时吸气开口质量通量达到寻优区间下限,即1×10^-4,而吸气减阻效果可达8.3%.3) 优化后的吸气开口位于转捩点之后,吸气不能延缓流动转捩,翼型层流面积没有增加,故摩擦阻力没有减少,翼型阻力的减小主要是由于压差阻力的减小.
参考文献

[1]	Abbas A,de Vicente J,Valero E.Aerodynamic technologies to improve aircraft performance[J].Aerospace Science and Technology,2013,28(1):100-132.
	Click to display the text
[2]	马汉东,崔尔杰. 大型飞机阻力预示与减阻研究[J].力学与实践,2007,29(2):1-7. Ma H D,Cui E J.Drag prediction and reduction for civil transportation aircraft[J].Mechanics in Engineering,2007,29(2):1-7(in Chinese).
	Cited By in Cnki (16)
[3]	Schlichting H. Boundary layer theory[M].7th ed.New York:McGraw Hill Book Company,1979:380-381.
[4]	段会申,刘沛青,何雨薇,等.二维翼型微吸吹气减阻控制新技术数值研究[J].航空学报,2009,30(7):1220-1226. Duan H S,Liu P Q,He Y W,et al.Numerical investigation of drag-reduction control by micro-suction-blowing on airfoil[J].Acta Aeronautica et Astronautica Sinica,2009,30(7):1220-1226(in Chinese).
	Cited By in Cnki (6)
[5]	周明,孙树栋. 遗传算法原理及应用[M].北京:国防工业出版社,1999:4. Zhou M,Sun S D.Genetic algorithms:theory and applications[M].Beijing:National Defence Industry Press,1999:4(in Chinese).
[6]	Menter F R,Esch T,Kubacki S.Transition modelling based on local variables[C]//Proceedings of the 5th International Symposium on Engineering Turbulence Modelling and Measurements. Amsterdam:Elsevier,2002:555-564.
	Click to display the text
[7]	Langtry R B,Menter F R.Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes[J].AIAA Journal,2009,47(12):2894-2906.
	Click to display the text
[8]	Selig M S,McGranahan B D.Wind tunnel aerodynamic tests of six airfoils for use on small wind turbines,AIAA-2004-1188[R].Reston:AIAA,2004.
	Click to display the text