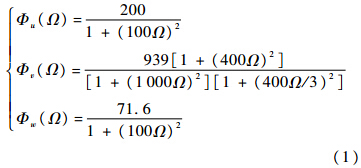
式中Ω为角频率.将式(1)的频谱函数根据分子分母的不同形式分为两类:第1类包括Φu(Ω)和Φw(Ω);第2类为Φv(Ω).两者的处理方法略为不同,下面分别进行讨论.1.1 第1类频谱函数因Φu(Ω)和Φw(Ω)之间存在线性关系,故以Φw(Ω)为例说明进行.Φw(Ω)共轭分解后得到的传递函数Gw(s)=8.461+100s,由Euler前向差分格式可得紊流速度:
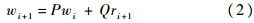
式中{r}表示均值为0、方差为1的Gauss白噪声序列.这里借鉴文献[7]中的思想加入修正系数,差分方程变为
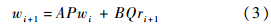
式中A,B为待定修正系数.由递推公式(3)可得
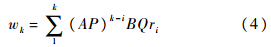
因为w均值为0[5],所以其方差为
由白噪声特性,
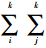(AP)2k－i－jrirj=0,σr=0,故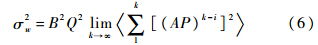
根据文献[5],可知AP<1,则式(6)的等比级数和收敛:
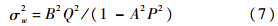
在随机过程中,频谱函数与相关函数之间存在Fourier变换对的关系.对Φw(Ω)作Fourier逆变换可得到该方向紊流序列以距离差ξ为自变量的距离相关函数:
取ξ=nh,有
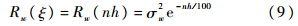
根据相关函数的定义,可知:
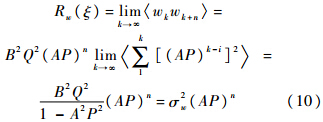
对比式(9)和式(10)可得
将式(11)代入紊流速度方差表达式(7)可得
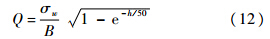
1.2 第2类频谱函数对于第2类频谱函数,可将其因式分解表示为两个独立频谱函数和的形式,之后采用同1.1节类似的方法分别处理.
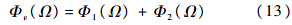
式中
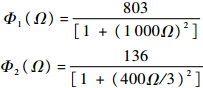
由此得到传递函数:
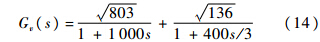
总的紊流序列{v}可先分别求出各自紊流序列{v1},{v2},再求和得到{v}={v1}+{v2}.类似式(3),有
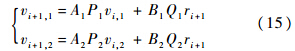
式中,P1=e－h/1 000/A1;P2=e－3h/400/A2;A1,B1,A2,B2为待定修正系数.取ξ=nh,总的相关函数:
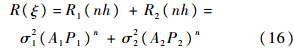
式中,σ21=2∫∞0Φ1(Ω)dΩ;σ22=2∫∞0Φ2(Ω)dΩ.紊流序列{v}的方差:
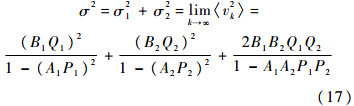
该频谱函数的相关函数为
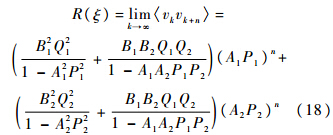
若式(16)和式(18)两者表示同样的衰减率,则比较可得
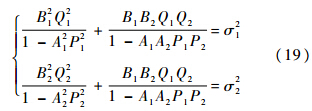
式(19)必然满足:
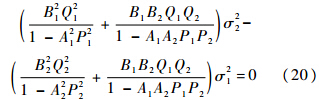
令η=
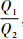,a=1－A21P21,b=1－A22P22,c=1－A1A2P1P2,可解出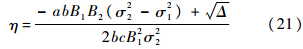
式中
Δ=[abB1B2(σ22-σ21)]2+4abc2B21B22σ21σ22另外由式(17)可得
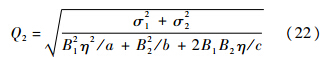
这样,若待定修正系数确定,即可根据不同形式的紊流频谱函数不断递推生成所需的紊流序列.2 待修正系数确定方法舰尾紊流作为大气紊流的一种特殊存在形式,它拥有大气紊流的所有特征.相关性函数因为能够反映出紊流的全部性状,所以一直以来多用为检验和分析紊流的主要指标[7, 8, 9].另外,舰尾紊流也是一个随机过程,需要用统计特性对其进行描述.而均方差作为随机过程重要的统计特性,它反映了随机过程的能量,同时也是反映数据离散程度最常用的一种量化形式,是检验仿真结果精确与否的重要指标.因此,为检验生成的紊流序列{x}是否正确,这里采取了两个验证准则:一是让{x}的均方差σx趋近理论值σx,th,即f1(x)=minσx－σx,th;二是通过对{x}进行相关性检验使相关函数Rx(ξ)贴近理论相关函数Rx,th(ξ),即f2(x)=min[maxRx(ξ)－Rx,th(ξ)].在两个准则之间函数关系不明确的情况下,不能通过权重关系将之合并为一个待优化函数用常规的单目标优化寻得最优解,因此采用多目标寻优的思想进行求解.则问题可描述为f(x)=min[f1(x),f2(x)],两个约束准则作为待优化的目标函数f1(x)=σx－σx,th
f2(x)=maxRx(ξ)－Rx,th(ξ),待修正系数为通过寻优最终得到的决策变量.2.1 改进的NSGA2算法遗传算法基于群体操作的特点使其能在一次运算后并行得到多个解,因此非常适合作为有多个解的多目标优化问题[10].目前,比较有代表性的多目标遗传算法包括向量估计遗传算法VEGA[11]、多目标进化算法MOGA[12]、小生境Pareto遗传算法NPGA[13]、非劣排序遗传算法NSGA[14]、强度Pareto进化算法SPEA[15]、NSGA2[16]等,其中NSGA2算法因其低时间复杂性、高鲁棒性等特点应用较为广泛.本文采用的寻优方法就是一种改进的NSGA2算法,在此将改进的部分加以说明.2.1.1 基于序值的交叉、变异操作将支配关系引入遗传机制中,位于不同前端的个体,序值越小表明该个体越优秀,也越有希望能遗传到下一代.因此在进行个体之间的交叉操作时,希望能有更多的低序值个体的基因参与,而自身变异时则希望能更多地保留低序值个体的基因.基于以上论断,标准模拟二进制交叉操作和多项式变异操作[17]可改进为以下形式.交叉操作:
式中rank为序值.
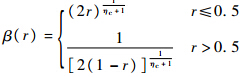
式中，r为[0,1]之间均匀分布的随机数；ηc为交叉分布指数.变异操作:
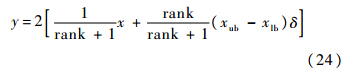
式中
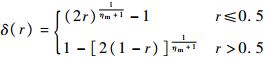ηm为变异分布指数.2.1.2 基于拥挤距离的修剪方法NSGA2中,采用的是精英选择的策略,低序值的个体会被优先保留.这样做存在一定的不足,一旦算法陷入了局部最优,因为修剪掉的都是高序值的个体,而自身种群没有新个体更新,因此很难跳出.为了保持种群的多样性,避免算法早熟现象,这里对修剪方法进行改进.假设每一前端的个体由两部分构成,其中原前端按拥挤距离保留一定比例的个体,其余的由下一前端的个体补上,候补的个体同样遵循按拥挤距离从大到小的选取方法.2.2 基于改进NSGA2算法的参数选择算法流程如图 1所示,具体步骤如下. |
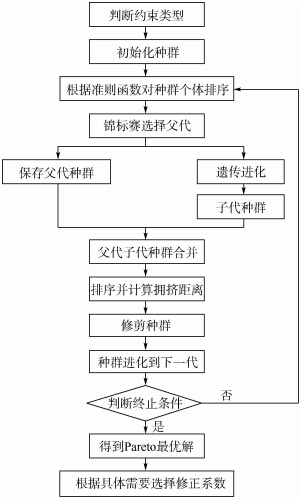| 图 1 修正系数选择流程图Fig. 1 Flow chart of correction coefficient selection |
| 图选项 |
步骤1 随机初始化种群,种群中每个个体由待修正系数xi(i=1,2,…,n)和其对应的待优化目标函数值fj(j=1,2)两部分组成.步骤2 根据目标函数值fj判断种群个体间的支配关系,通过非支配排序得到每个个体的序值和拥挤距离.步骤3 依据个体序值和拥挤距离,采用锦标赛选择方法得到父代种群.步骤4 保存父代种群到临时记忆库,同时开始遗传进化过程,对父代种群进行基于序值的交叉和变异操作,得到子代种群.步骤5 将临时记忆库中的父代与步骤4产生的子代合并为中间种群.步骤6 重复步骤2的操作,得到该中间种群个体的序值和拥挤距离.步骤7 采用改进的修剪方法整理中间种群并得到最终的种群.步骤8 判断是否达到最大遗传代数,若满足,结束优化,并根据需求选择修正系数;否则,返回步骤2,同时清空临时记忆库.3 计算结果及分析为方便比较,使用本文的改进NSGA2算法计算时所取的各向紊流采样步长为0.1 m,产生白噪声的随机数种子为23 341,修正系数限定在[0.5,2.5]之间,优化前的原始修正系数均为1.通过上述方法求出的Pareto非劣解分布如图 2所示,可以看出两个约束准则存在着此消彼长的关系,并不能同时达到最优,因此需根据实际工程需要选择其中的一个解作为该问题的最终解.
 |
| 图 2 x,y,z向Pareto解分布图Fig. 2 Distribution image of Pareto solution in x,y,z direction |
| 图选项 |
本文以相关性误差f2为主需求同时兼顾紊流方差误差f1为原则选取的优化值及对应的修正系数如表 1所示,图 3为相应的各向紊流相关性检验结果.可见,优化后的目标函数值均比未优化的结果小一个数量级以上,并且优化后紊流相关性函数与理论值基本吻合,达到了良好的效果.采用相应修正系数得出的各方向紊流速度如图 4所示,因为x向和z向频谱函数存在线性关系,所以结果也较类似.表 1 优化结果Table 1 Optimization results
| 参数 | 原始目标函数误差 | 优化后目标函数误差 | 对应的修正系数 |
| u | (1.557×10－1,7.216×10－3) | (1.113×10－2,7.433×10－5) | (0.989,1.974) |
| v | (3.031×10－2,2.134×10－1) | (1.012×10－3,5.576×10－3) | (1.002,0.993,0.982,2.402) |
| w | (5.573×10－2,4.318×10－3) | (3.772×10－3,2.613×10－4) | (0.989,1.958) |
表选项
 |
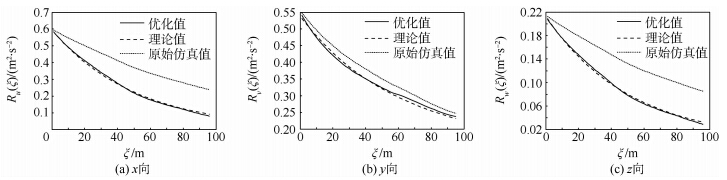| 图 3 x,y,z向相关性检验Fig. 3 Correlation tests in x,y,z direction |
| 图选项 |
 |
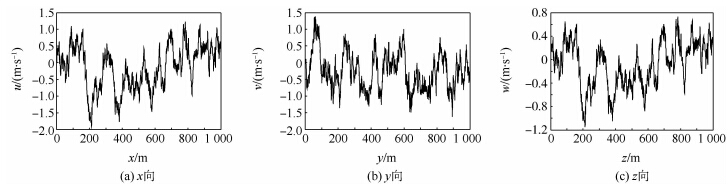| 图 4 x,y,z向紊流序列Fig. 4 changeswiththeinputangle |
| 图选项 |
4 结 论本文对标准NSGA2算法进行改进,提出了一种基于改进NSGA2算法的舰尾紊流数值模拟方法,通过仿真实验,得到了以下结论:1) 本文算法得到的Pareto非劣解集在解空间的分布均匀且连续,算法的分布性较好.2) 仿真得到的舰尾紊流序列的均方差误差和相关函数误差均在要求误差范围之内,满足该模型频谱函数的理论表达式,表明通过该方法生成的舰尾流紊流序列的准确性高,而且在小步长情况下也能够得到较精确的修正系数,验证了本文方法的正确性和合理性.
参考文献
| [1] | Moorhouse D J, Woodcock R J.Background information and user guide for MIL-F-8785C,military specification-flying qualities of piloted airplanes,AD-A11942[R].1982. |
| Click to display the text | |
| [2] | 胡国才, 王奇,刘湘一,等.舰尾流对舰载机着舰轨迹和动态响应的影响研究[J].飞行力学,2009,27(6):18-21. Hu G C,Wang Q,Liu X Y,et al.Influence of carrier airwake on carrier-based aircraft landing trajectory and dynamic response[J].Flight Dynamics,2009,27(6):18-21(in Chinese). |
| Cited By in Cnki (15) | |
| [3] | 蒋康博, 刘超,袁东.近舰区风场建模与着舰仿真分析[J].飞行力学,2010,28(6):11-15. Jiang K B,Liu C Yuan D.Close-carrier-area wind field modeling and carrier-landing simulation analysis[J].Flight Dynamics,2010,28(6):11-15(in Chinese). |
| Cited By in Cnki (4) | |
| [4] | 吕开东,李新飞, 姜迈,等.舰载机着舰过程的舰尾气流场数值仿真分析[J].飞行力学,2013,31(1):18-23. Lü K D,Li X F,Jiang M,et al.Simulation analysis on carrier landing disturbance model[J].Flight Dynamics,2013,31(1):18-23(in Chinese). |
| Cited By in Cnki | |
| [5] | 赵震炎,肖业伦, 施毅坚.Dryden大气紊流模型的数字仿真技术[J].航空学报,1986,7(5):433-443. Zhao Z Y,Xiao Y L,Shi Y J.A digital simulation technique for Dryden atmospheric turbulence model[J].Acta Aeronautica et Astronautica Sinica,1986,7(5):433-443(in Chinese). |
| Cited By in Cnki (39) | |
| [6] | 屈香菊,李勇. 一种改进的紊流风模型及其仿真算法[J].系统仿真学报,2004,16(1):10-13. Qu X J,Li Y.An improved model of atmospheric turbulence and its simulation algorithm[J].Journal of System Simulation,2004,16(1):10-13(in Chinese). |
| Cited By in Cnki (17) | |
| [7] | 马东立. 大气紊流数字仿真的改进方法[J].北京航空航天大学学报,1990,16(3):57-63. Ma D L.An improvement of the digital simulation method for atmospheric turbulence[J].Journal of Beijing University of Aeronautics and Astronautics,1990,16(3):57-63(in Chinese). |
| Cited By in Cnki (12) | |
| [8] | 吴扬,姜守达. 非质点飞行器模型的大气紊流仿真[J].沈阳工业大学学报,2010,32(1):22-26. Wu Y,Jiang S D.Simulation of atmospheric turbulence for non-particle aircraft model[J].Journal of Shenyang University of Technology,2010,32(1):22-26(in Chinese). |
| Cited By in Cnki (1) | |
| [9] | Reid L D. Correlation model for turbulence along the glide path[J].Journal of Aircraft,1978,15(1):13-20. |
| Click to display the text | |
| [10] | 申晓宁,郭毓, 陈庆伟,等.一种保持群体多样性的多目标遗传算法[J].控制与决策,2008,23(12):1435-1440. Shen X N,Guo Y,Chen Q W,et al.Multi objective optimization genetic algorithm keeping diversity of population[J].Control and Decision,2008,23(12):1435-1440(in Chinese). |
| Cited By in Cnki (11) | |
| [11] | Schaffer J D. Multiple objective optimizations with vector evaluated genetic algorithms[C]//Proceedings of the 1st International Conference on Genetic Algorithms.New Jersey:Lawrence Erlbaum Associates,1985:93-100. |
| Click to display the text | |
| [12] | Fonseca C M. Multi-objective genetic algorithms with application to control engineering problems[D].UK:The University of Shefield,1995. |
| Click to display the text | |
| [13] | Horn J, Nafpliotis N,Goldberg D E.A niched pareto genetic algorithm for multi-objective optimization[C]//Proceedings of the 1st IEEE Conference on Evolutionary Computation.New York:IEEE,1994:82-87. |
| Click to display the text | |
| [14] | Srinivas N, Deb K.Multi-objective function optimization using non-dominated sorting genetic algorithms[J].Evolutionary Computation,1995,2(2):221-248. |
| Click to display the text | |
| [15] | Zitzler E, Thiele L.Multi-objective evolutionary algorithms: a comparative case study and the strength Pareto approach[J].IEEE Trans on Evolutionary Computation,1999,3(4):257-271. |
| Click to display the text | |
| [16] | Deb K, Pratap A,Agarwal R B.A fast and elitist multi-objective genetic algorithms:NSGA2[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197. |
| Click to display the text | |
| [17] | Deb K, Agrawal R B.Simulated binary crossover for continuous search space[J].Complex Systems,1995,9(3):1-15. |
| Click to display the text |
