 |
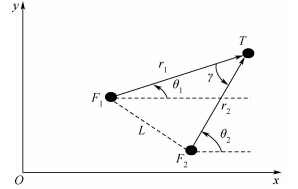
| F1,F2—己方飞机;T—目标飞机;L—己方飞机之间的距离;r1,r2—己方飞机与目标的距离;θ1,θ2—己方飞机对目标的方位角;γ—己方飞机相对目标的视线夹角. 图 1 飞机与目标的几何态势 Fig. 1 Geometric situation of aircrafts to target |
| 图选项 |
两架飞机对目标的方位角的测量值分别为
 1和
1和 2,分别存在相互独立的服从零均值高斯分布的角度测量误差δ(θ1)和δ(θ2),其方差分别为σ2θ1,σ2θ2,飞机自身定位系统得到的自身的位置测量值为(
2,分别存在相互独立的服从零均值高斯分布的角度测量误差δ(θ1)和δ(θ2),其方差分别为σ2θ1,σ2θ2,飞机自身定位系统得到的自身的位置测量值为(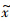 1,
1, 1)和(
1)和(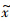 2,
2, 2),分别存在相互独立的服从零均值高斯分布的位置测量误差δ(x1),δ(y1)和δ(x2),δ(y2),其方差分别为σx12,σy12,σx22,σy22.则有
2),分别存在相互独立的服从零均值高斯分布的位置测量误差δ(x1),δ(y1)和δ(x2),δ(y2),其方差分别为σx12,σy12,σx22,σy22.则有 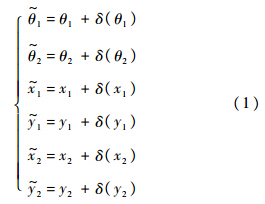
两架飞机相对目标的视线的夹角为

飞机的观测方位角满足以下方程:
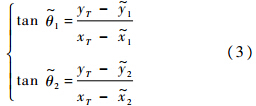
则可得出目标的位置:
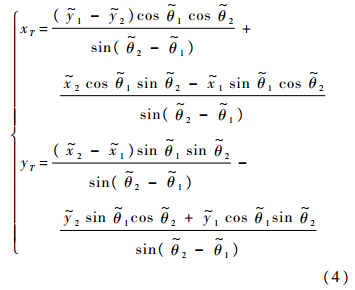
根据泰勒公式,可将xT,yT在真实值(θ1,θ2,x1,x2,y1,y2)处进行展开,并只保留一阶项,得到目标x方向和y方向估计误差:
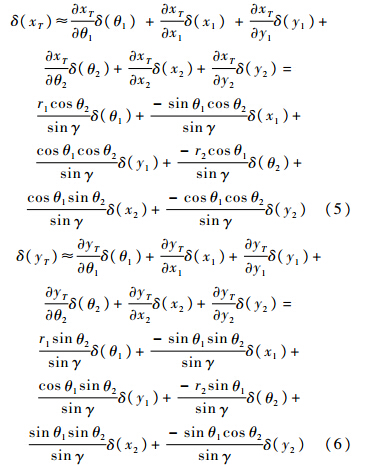
根据飞机与目标的几何关系,可得飞机距目标的距离为
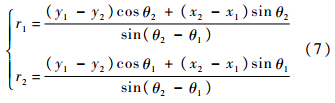
因为测量误差都为零均值高斯噪声,根据式(7),分别对式(5)和式(6)求方差:

对于双机协同探测跟踪系统,位置精度因子(PDOP)是一种常见的衡量探测精度的指标[1, 2, 3, 4, 15],在本文中,PDOP可表示为
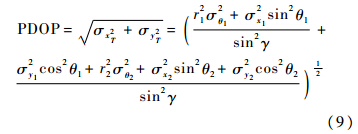
如果σ2x1=σ2x2=σ2y1=σ2y2=σ2r,σ2θ1=σ2θ2=σ2θ,即两飞机的角测量误差的方差和自身定位误差的方差分别相同,则有
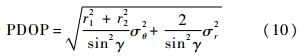
如果两架飞机的某种几何态势能使PDOP最小,则相应的目标估计精度也就达到最优[14].由式(10),在飞机红外搜索跟踪系统的角测量方差和飞机自身定位位置测量方差一定的情况下,PDOP的大小与飞机距目标的距离以及两架飞机相对目标的视线的夹角有关,双机协同无源探测的最优的飞机配置为
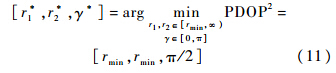
式中,rmin为飞机能够靠近目标的安全距离.式(11)说明为了提高探测精度,两架飞机应该尽可能地靠近目标,并保持π/2的视线夹角. 2 双机协同无源跟踪轨迹优化双机协同无源目标跟踪系统的控制结构如图 2所示.融合中心根据两架飞机传输的目标角度测量信息和自身定位信息,根据目标的运动模型以及系统的观测方程,采用一定的滤波方法,估算出目标的状态;指挥中心根据估算出的目标状态以及飞机的状态计算某种轨迹规划的性能指标,再根据优化算法对指标进行优化求解,解算出两架飞机各自的协同无源跟踪控制输入量,飞机再根据各自的控制输入来控制飞机的运动.
 |
| 图 2 双机协同无源目标跟踪系统的控制结构 Fig. 2 Control structure of two aircrafts’ collaborative passive target tracking system |
| 图选项 |
2.1 双机协同无源跟踪建模 系统的状态向量为X=[xT,x·T,yT,y·T]T.其中,(xT,yT)为目标的位置,(x·T,y·T)为目标的速度.则目标的运动模型为
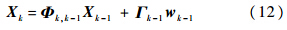
式中,Xk为k时刻的状态向量;Φk,k-1为k-1时刻到k时刻的状态转移矩阵;Xk-1为k-1时刻的状态向量;Γk-1为k-1时刻噪声输入矩阵.假设目标做匀速直线运动,在加速度方向上有过程噪声,采样时间间隔为ΔT,则
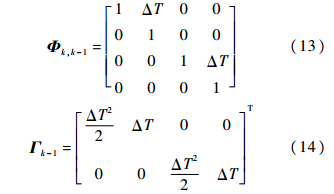
wk=[w1k,w2k]T为零均值不相关的高斯白噪声,其方差阵为
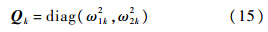
k时刻第i架飞机对目标的方位角的真实值为
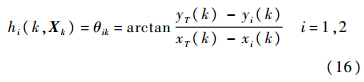
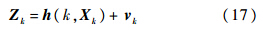
式中,Zk=[
 1k,
1k, 2k]T为k时刻的双机协同观测向量值;h(k,Xk)=[h1(k,Xk),h2(k,Xk)]T为k时刻的双机协同观测函数,这是一个非线性函数,对其进行线性化处理,得其Jacobian矩阵:
2k]T为k时刻的双机协同观测向量值;h(k,Xk)=[h1(k,Xk),h2(k,Xk)]T为k时刻的双机协同观测函数,这是一个非线性函数,对其进行线性化处理,得其Jacobian矩阵: 
vk=[v1k,v2k]T为零均值不相关的高斯白噪声,其方差阵为
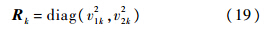
2.2 基于扩展信息滤波的目标状态估计 扩展信息滤波(EIF)是结合了扩展卡尔曼滤波(EKF)和信息滤波(IF)的优点的基础上发展起来的针对非线性系统的滤波方法[16],卡尔曼滤波中使用状态估计x^及方差P进行滤波计算,而信息滤波利用信息状态y^及费歇信息Y进行滤波计算,其中,y^=P-1x^,Y=P-1.扩展信息滤波的预测和估计过程如下:1) 预测过程.
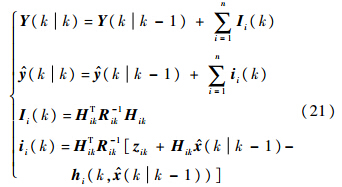
式中,x^(kk-1)=Y-1(kk-1)y^(kk-1)为k-1时刻到k时刻的状态预测值.2) 估计过程.
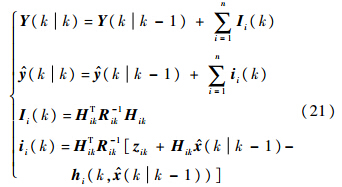
式中,zik为k时刻第i架飞机的观测向量;n为信息滤波节点个数,本文中,n=2.则k时刻目标状态的最终估计结果为
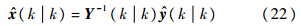
2.3 控制指标的选取双机协同无源跟踪的主要任务就是提高目标的估计精度,本文用信息熵作为双机协同轨迹控制的优化指标[14]:
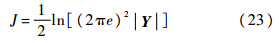
信息熵越大,则飞机的精度就越高,飞机的最优控制就是找到飞机最优速度和航向角输入,使得控制指标最大,即

式中,ψ=[ψ1,ψ2]T为飞机的航向角;v=[v1,v2]T为飞机的速度.同时,在对飞机进行控制时,还应该考虑飞机的性能约束:
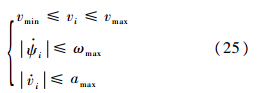
式中,vi为飞机速度;vmin为飞机的最小速度;vmax为飞机的最大速度;ψ·i为飞机的角速度;ωmax为飞机的最大角速度;v·i为飞机的加速度;amax为飞机的最大加速度.双机协同无源跟踪时还应该考虑飞机自身的安全,即飞机与目标的距离应不小于安全距离,本文取安全距离为目标的导弹的最大发射距离,则安全约束可表示为
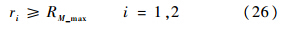
式中RM_max为目标的导弹的最大发射距离. 2.4 基于RHO的双机协同轨迹优化双机协同无源探测轨迹优化问题是一个多约束的单目标优化问题,本文采用了滚动时域优化来进行最优求解[8, 14].RHO来源于滚动时域控制(RHC),在每一个采样时刻,优化指标只考虑从该时刻起的未来某一段时间,根据系统运动模型来预测系统未来一段时间内的状态,并利用该状态来计算优化指标,从而建立一个优化问题,求解该优化问题,最终得到最优控制序列.当到了下一个采样时刻时,重复上一过程,随着时间的增加,整个过程如此反复滚动进行.双机协同无源目标跟踪所处的环境是动态不确定的,全程的轨迹优化设计是不切实际的,轨迹需要不断地更新优化设计,而滚动时域优化的优点表明其可以很好地满足这些要求.滚动时域优化方法步骤如下.1) 由k时刻目标的状态XT[k],对未来tr步内的目标状态进行预测,估计得到目标的状态序列:

由k时刻飞机的状态X[k],估计飞机的tr步控制序列:
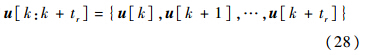
计算k+tr时间段内的最优控制序列:
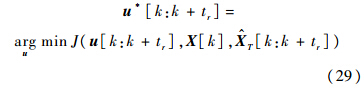
2) 取此最优控制序列的前τr段输入u*[k:k+τr](1≤τr≤tr)作为该τr时间段内的控制输入.3) k+τr时刻,重复步骤1)和2).本文中,tr=8,τr=2.3 仿真结果与分析 仿真假设:己方飞机的最小速度vmin=100m/s,最大速度vmax=300m/s,最大加速度amax=15m/s2,最大航向角速度ωmax=0.1rad/s,飞机的角测量均方差σθ=5mrad,飞机的自身定位均方差σr=5m;目标飞机的导弹最大发射距离为25km.仿真时间为1500s,采样时间为1s,过程噪声方差和测量方差分别为
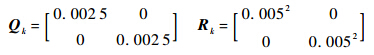
1) 情形1.飞机1和飞机2的初始位置分别为(-20,-80)km,(-70,-50)km,初始速度分别为(-120,160)m/s,(-160,-120)m/s;目标的初始位置和速度为(-60,-40)km,(150,150)m/s,且目标做匀速直线运动.EIF滤波器初值为X0=(-60010,151,-40010,151)T,滤波信息阵初值为Y0=diag([500, 100,500, 100])-1.飞机和目标的轨迹如图 3所示.在图中,每隔250s标注出3架飞机的位置,并将此时的目标与己方飞机用虚线连接起来,可以看出,飞机1一直靠近目标,由于飞机2与目标的初始距离小于最小距离,所以飞机2开始时的轨迹是远离目标的,之后将靠近目标,两架飞机与目标的视线之间的夹角也在π/2左右,直到达到最优几何配置.飞机与目标的视线夹角如图 4所示,两架飞机与目标的视线之间的夹角最终在π/2附近波动,且波动很小.双机协同无源跟踪目标的PDOP变化曲线如图 5所示,可以看出目标的PDOP减少并收敛于最小的PDOP.这说明基于RHO的双机轨迹优化设计能够使得飞机按双机协同无源跟踪的最优几何配置飞行.目标的位置估计均方根误差(RMSE)曲线如图 6所示,目标的均方根误差减少并收敛到一个较小水平.这说明基于RHO的双机轨迹优化设计能够减少估计误差,提高目标的估计精度.此情形下,该轨迹优化算法总耗时为139s,比仿真时间1500s的1/10还小,这说明该算法具有一定的实时性.
 |
| 图 3 情形1的飞机及目标轨迹 Fig. 3 Aircraft and target trajectory of case 1 |
| 图选项 |
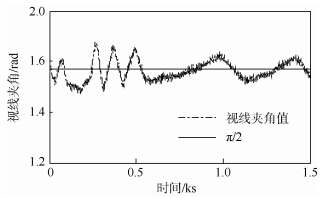 |
| 图 4 情形1飞机与目标的视线夹角 Fig. 4 The line of sight angle of aircraft and target of case 1 |
| 图选项 |
 |
| 图 5 情形1的位置精度因子曲线 Fig. 5 Position dilution of precision curve of case 1 |
| 图选项 |
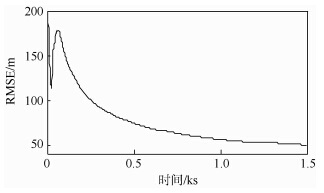 |
| 图 6 情形1的均方根误差曲线 Fig. 6 Root-mean-square error curve of case 1 |
| 图选项 |
2) 情形2.飞机1和飞机2的初始位置分别为(-30,-70)km,(-70,-30)km,初始速度分别为(-150,120)m/s,(-130,-140)m/s;目标的初始位置和速度为(-60,-40)km,(140,120)m/s,且开始目标做匀速直线运动,在800~1000s时做角速度为0.005rad/s的匀速左转弯机动,之后再做匀速直线运动.EIF滤波器初值为X0=(-60010,141,-40010,121)T,滤波信息阵初值为Y0=diag(500,100,500,100)-1.飞机和目标的轨迹如图 7所示,在图中,每隔250s标注出3架飞机的位置,并将此时目标与己方飞机用虚线连接起来,可以看出,飞机1一直靠近目标,飞机2开始远离目标,之后将靠近目标,两架飞机与目标的视线之间的夹角也在π/2左右,直到达到最优几何配置,在目标进行机动转弯之后,两架飞机也将相应地进行机动转弯.飞机与目标的视线夹角如图 8所示,两架飞机与目标的视线之间的夹角最终在π/2附近波动,且波动很小.双机协同无源跟踪目标的PDOP变化曲线如图 9所示,可以看出目标的PDOP减少并收敛于最小的PDOP.这说明基于RHO的双机轨迹优化设计能够使得飞机按双机协同无源跟踪的最优几何配置飞行.目标的位置估计均方根误差(RMSE)曲线如图 10所示,目标的均方根误差减少到一个较小水平.这说明基于RHO的双机轨迹优化设计能够减少估计误差,提高目标的估计精度.此情形下,该轨迹优化算法总耗时为147s,约为仿真时间1500s的1/10,这说明该算法具有一定的实时性.
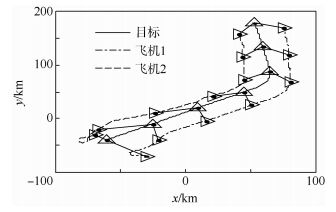 |
| 图 7 情形2的飞机及目标轨迹 Fig. 7 Aircraft and target trajectory of case 2 |
| 图选项 |
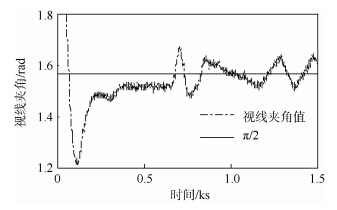 |
| 图 8 情形2飞机与目标的视线夹角 Fig. 8 The line of sight angle of aircraft and target of case 2 |
| 图选项 |
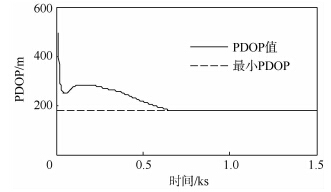 |
| 图 9 情形2的位置精度因子曲线 Fig. 9 Position dilution of precision curve of case 2 |
| 图选项 |
 |
| 图 10 情形2的均方根误差曲线 Fig. 10 Root-mean-square error curve of case 2 |
| 图选项 |
4 结 论本文在综合分析双机协同无源探测PDOP的基础上提出了一种基于RHO的双机协同无源探测轨迹跟踪算法,经实验验证表明:1) 双机协同无源定位中使得PDOP最小的双机的几何配置为双机与目标视线夹角为90°,双机与目标的距离为安全距离;2) 基于滚动时域优化的轨迹优化算法能保证双机在执行无源探测任务过程中保持最优几何配置.未来空战中,多机协同无源跟踪具有很强的实用价值,将双机跟踪的最优空间几何配置及误差模型推广到多机情况具有很重要的意义,是作者以后研究的一个重要方向.
参考文献
| [1] | 朱剑辉,方洋旺,张平,等.双机协同定位误差分析的研究[J].电光与控制,2012,19(6):21-25.Zhu J H,Fang Y W,Zhang P,et al.Error analysis in dual-aircraft cooperative locating[J].Electronics Optics & Control,2012,19(6):21-25(in Chinese). |
| Cited By in Cnki (3) | |
| [2] | 王伯生,王芳.空基平台无源定位的误差推导与精度分析[J].航空计算技术,2012,42(3):89-91.Wang B S,Wang F.Error calculation and accuracy analysis of two-fighter passive location[J].Aeronautical Computing Technique,2012,42(3):89-91(in Chinese). |
| Cited By in Cnki | |
| [3] | 武宜川,潘冠华,罗双喜.空基平台无源定位精度分析[J].指挥控制与仿真,2010,32(2):89-92.Wu Y C,Pan G H,Luo S X.Analysis of passive location accuracy by air-based platform[J].Command Control & Simulation,2010,32(2):89-92(in Chinese). |
| Cited By in Cnki (5) | |
| [4] | 张笑.无源二维交叉定位分析[J].电子科技,2013,26(2):54-56.Zhang X.Analysis of 2-D triangulation method[J].Electronic Sci & Tech,2013,26(2):54-56(in Chinese). |
| Cited By in Cnki | |
| [5] | Ousingsawat J,Campbell M E.On-line estimation and path planning for multiple vehicles in an uncertain environment[J].International Journal of Robust and Nonlinear Control,2004,14(8):741-766. |
| Click to display the text | |
| [6] | Pongpunwattana A,Rysdyk R.Real-time planning for multiple autonomous vehicles in dynamic uncertain environments[J].Journal of Aerospace Computing,Information,and Communication,2004,1(12):580-604. |
| Click to display the text | |
| [7] | Casbeer D W,Zhan P C,Swindlehurst A L.A non-search optimal control solution for a team of muavs in a reconnaissance mission[C]//Acoustics,Speech and Signal Processing,2006.Piscataway,NJ:IEEE,2006,4:1169-1172. |
| Click to display the text | |
| [8] | Frew E W.Receding horizon control using random search for UAV navigation with passive, non-cooperative sensing[C]//2005 AIAA Guidance,Navigation,and Control Conference and Exhibit.Reston,VA:AIAA,2005,5864:1-13. |
| Click to display the text | |
| [9] | 张胜祥,裴海龙,刘保罗,等.基于滚动时域优化的无人飞行器轨迹规划[J].计算机工程与应用,2008,44(35):237-239.Zhang S X,Pei H L,Liu B L,et al.Trajectory planning for unmanned vehicles based on receding horizon optimazafion[J].Computer Engineering and Applications,2008,44(35):237-239(in Chinese). |
| Cited By in Cnki (5) | |
| [10] | Frew E W,Lawrence D A.Cooperative stand-off tracking of moving targets by a team of autonomous aircraft[C]//2005 AIAA Guidance,Navigation,and Control Conference and Exhibit.Reston,VA:AIAA,2005,7:4885-4895. |
| Click to display the text | |
| [11] | Frew E W,Lawrence D A,Morris S.Coordinated standoff tracking of moving targets using Lyapunov guidance vector fields[J].Journal of Guidance,Control,and Dynamics,2008,31(2):290-306. |
| Click to display the text | |
| [12] | Summers T H,Akella M R,Mears M J.Coordinated standoff tracking of moving targets: control laws and information architectures[J].Journal of Guidance,Control,and Dynamics,2009,32(1):56-69. |
| Click to display the text | |
| [13] | Sinclair A J,Prazenica R J,Jeffcoat D E.Optimal and feedback path planning for cooperative attack[J].Journal of Guidance,Control,and Dynamics,2008,31(6):1708-1715. |
| Click to display the text | |
| [14] | 孙海波.多无人机协同目标跟踪与打击方法研究[D].北京:北京航空航天大学,2010.Sun H B. Research of multiple UAV's cooperative target tracking and attack[D].Beijing:Beihang University,2010(in Chinese). |
| [15] | Zhong E J,Huang T Z.Geometric dilution of precision in navigation computation[C]//Proceedings of the Fifth International Conference on Machine Learning and Cybernetics.Piscataway,NJ:IEEE,2006:4116-4119. |
| [16] | Gasparri A,Pascucci F.An interlaced extended information filter for self-localization in sensor networks[J].IEEE Transactions on Mobile Computing,2010,9(10):1491-1504 |
| Click to display the text |
