加筋板作为一种典型的薄壁结构形式,被广泛应用于飞机机身和机翼的盒段^[1]、运载火箭的舱段^[2],提高其在不同工况下的稳定性是工程设计的迫切需求.曲筋加筋板作为直筋加筋板的一种结构扩展,已经开始受到研究工作者的重视.目前,一些创新性的制造技术,如搅拌摩擦焊和电子束自由曲面成型技术已经可以使用铝合金与钛合金,从而使曲筋片型加筋板的整体加工成为了可能^[3].文献^{[3, 4, 5, 6, 7]}曾对曲筋加筋板的优化设计做过研究并提出了优化系统EBF3PanelOpt.研究表明,对于T型筋,直筋加筋板是最优方案,而对于曲线片型筋条,曲筋加筋板相比直筋加筋板获得了更好的稳定性.但由于EBF3PanelOpt框架中加筋板筋条设计参数数目固定,无法为曲筋加筋板提供更广阔的优化空间.另外,EBF3PanelOpt框架没有施加载荷于筋条上,这样便无法保证筋条的稳定性^[7].因此,本文提出了一套基于ModelCenter、Catia和Abaqus的曲线片型加筋板优化设计框架.一方面,筋条设计曲线采用设计参数数目可变的等距剖分三次B样条插值函数,为曲筋加筋板提供了足够大的优化空间.另一方面,由于筋条只能承受其本身面内的载荷,采用了2种方式来考虑曲线片型加筋板的筋条加载问题.第1种是2条或2条以上筋条加载端相聚的情况,并由此提出了一种新的曲筋布局形式;第2种是让筋条垂直于板边.1 优化框架优化平台基于PHX ModelCenter 9.0设计优化环境、Catia模型设计工具和Abaqus有限元分析系统.该平台能对一般的矩形板和筒状板进行稳定性或质量的优化设计.利用ModelCenter的二次开发功能,自主编写2个数据模块:优化算法模块Optimization和建模与分析模块CatiaAbaqusCOM.优化算法模块内部封装了粒子群算法(PSO)并提供了目标函数、约束条件和设计变量接口.建模与分析模块完成了从Catia建模到生成stp文件,再进行Abaqus有限元分析并获取数据的完整过程.曲线片型加筋板优化框架如图 1所示.

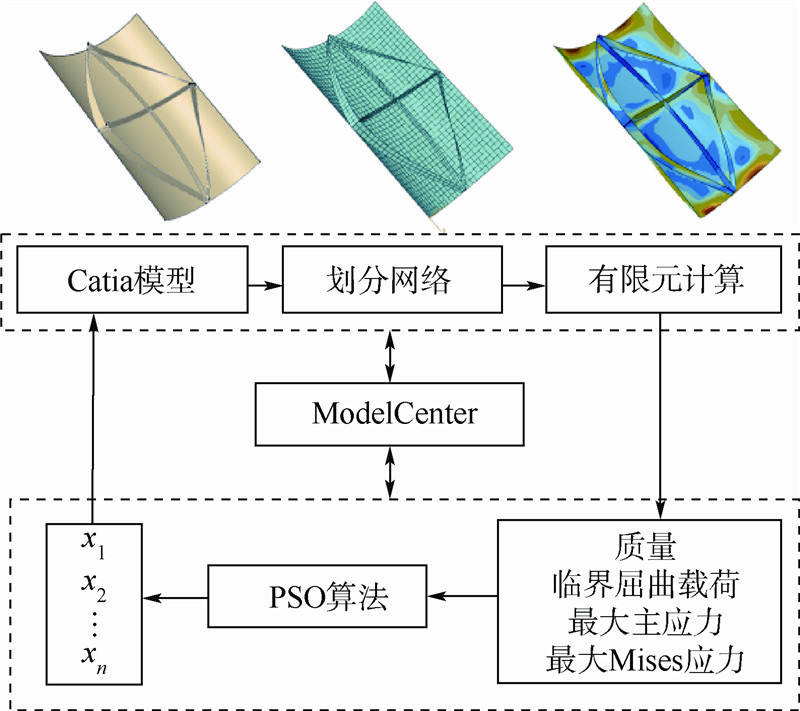
图 1 曲线片型加筋板优化框架Fig. 1 Optimization framework of curvilinear blade-stiffened panels

图选项

1.1 曲筋曲线生成方法采用三次等距剖分B样条插值方法生成曲线^[8].设f(x)为定义在区间[a,b]上的函数,f(x_i)=f_i(i=0,1,…,n),求三次样条函数s(x)使得:
在[a,b]上给定一个等距剖分:
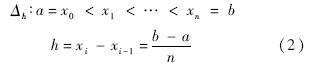
并记外节点x_-1=a－h,x_n+1=b+h.基于等距剖分三次B样条理论,可将插值问题解表示为
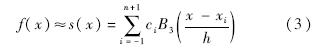
式中
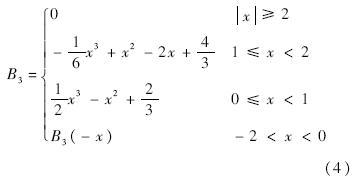
c_i由式(5)求得.
式中,为n+3阶矩阵.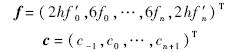
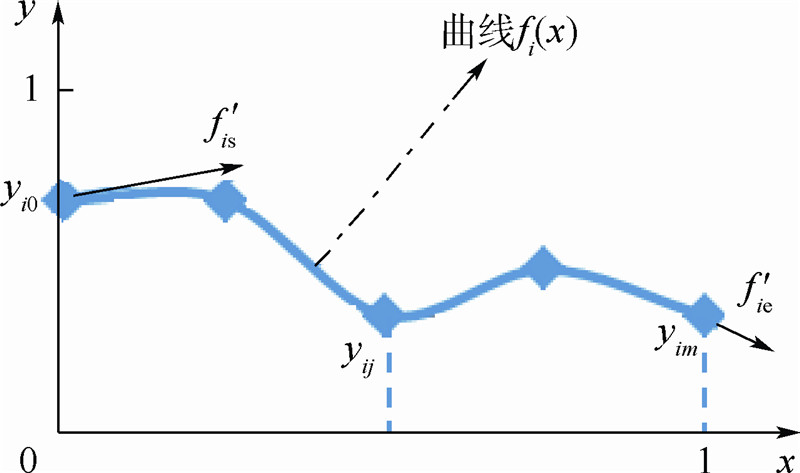
1.2 优化数学模型根据等距剖分下的三次B样条插值函数,每一条样条曲线由若干个等距剖分点和两端点处斜率唯一确定.等距剖分三次B样条曲线如图 2所示.

图 2 等距剖分三次B样条曲线Fig. 2 Equally-split cubic B-spline curve

图选项

实际的筋条曲线的两端可以在板的4条边自由移动.根据端点位于不同的板边,数学上可以通过定义坐标映射函数map(S_i,y_i0,y_im),产生6种基本布局形式(约定曲线两端点不位于同一板边),如图 3所示.这里S_i是布局形式的离散变量,取1~6.其中,1表示筋条在板宽对边连接,2表示板长对边连接,3~6分别表示板相邻边的4种连接方式.

图 3 曲筋布局形式(横向为板长、纵向为板宽)Fig. 3 Configurations of curvilinear blade-stiffened panels (horizontal edges represent plate length,longitudinal edges represent plate width)

图选项

1.2.1 设计变量在等质量条件下,将加筋板临界屈曲载荷作为优化目标.记第i条曲线第j个数据点坐标为(x_ij,y_ij),将y_ij及第i条曲线两端点的切线导数f ′_is和f ′_ie作为设计变量.另外,将第i条曲线的布局形式S_i、筋条高度hsi、筋条厚度tsi作为设计变量,则筋条数目为n、曲线数据点数目为m的加筋板共有(m+5)n个参数.若将加筋板质量作为优化目标,必须将板厚t_p也作为设计变量.1.2.2 约束条件1) 几何约束条件:
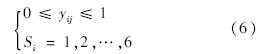
其中y_ij将根据S_i的不同进行坐标映射,变换为真实的坐标值.2) 考虑到工程需求:
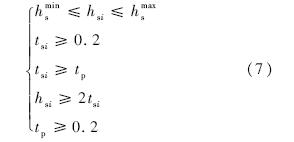
另外,若将临界屈曲载荷作为目标函数,需满足等质量约束:
式中,a为板长;b为板宽;ρ为密度;t_p0为初始板厚,优化过程中大小不变.3) 加筋板需要满足稳定性和强度要求.① 第三强度准则:von Mises等效应力最大值σ_vm小于材料屈服载荷σ_y，即
或者筋条的强度约束可采用式(10):
式中,σ_s为筋条的最大主应力;F_cc为片型筋条的最大允许主应力.F_cc由式(11)算出.
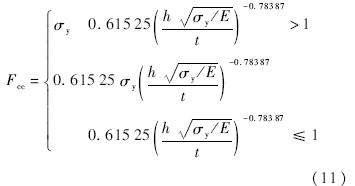
式中,E为弹性模量;h为筋条高度;t为筋条厚度.式(11)由文献^[9]中的曲线获得,适用于任何材料一般的挤压部件.② 稳定性条件:要求实际载荷小于临界屈曲载荷,在有限元特征分析里面,可表示为
式中，λ₀为加筋板一阶模态的特征值.1.2.3 目标函数若以临界屈曲载荷为目标函数,其值由Abaqus odb结果文件中获取.若以加筋板质量为目标函数,由式(13)求出.
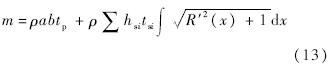
式中，R′(x)为样条插值函数一阶导.2 计算实例2.1 筋端相聚形式的曲筋优化所谓筋端相聚形式,是指2条或多条曲筋的加载边聚于一点的形式.由于筋条只能承受面内载荷,若2条筋条的加载边聚到一起,外载荷可以自动分配到2条曲筋面内.基于这种想法,提出了一种由2条曲筋构成的端点闭合的新构型.基本想法是用2条端点闭合的曲筋代替一条直筋,以此来获得更好的稳定性.端点闭合的曲筋构型如图 4所示.

图 4 端点闭合的曲筋构型Fig. 4 Configurations of collecting loaded edges of stiffeners

图选项

以图 5给定的矩形加筋板作为优化实例.优化目标选择临界屈曲载荷,初始板厚设为2.6 mm,材料选用2039铝合金.假设筋条中单位长度上的分布载荷与板边分布载荷相同.加筋板边界条件采用简支,如图 5所示,其中v为y向位移,w为z向位移.

图 5 加筋板几何尺寸与边界条件Fig. 5 Geometries and boundary conditions

图选项

2.1.1 单轴载荷下的优化结果设定x向载荷N_xx=1 N,y向载荷N_yy和剪切载荷N_xy为0.假定筋条端点给定,取筋条高度h_si,筋条厚度t_si,曲筋斜率f ′_1s和f ′_1e为设计变量,f ′_2s和f ′_2e根据对称性由f ′_1s和f ′_1e算出.2139铝合金材料属性如表 1所示，设计变量约束范围如表 2所示，单轴载荷下的优化结果如表 3所示.其中，ν为泊松比，σ为屈服强度，n为迭代次数.表 1 2139铝合金材料属性 Table 1 Material properties of 2139 aluminum

参数	数值
E/GPa	73.085
ν	0.33
σ/MPa	427.47
ρ/(kg·m-3)	2 700

表选项


表 2 设计变量约束范围Table 2 Range of design variables

设计变量	下界	上界
f ′is	-3	3
f ′ie	-3	3
hsi/mm	5	50
tsi/mm	0.2	10

表选项


表 3 单轴载荷下的优化结果Table 3 Optimization results for single-axial load

变量	光板	1条直筋	2条曲筋	2条直筋	4条曲筋
m/kg	1.179 36	1.179 36	1.179 36	1.179 36	1.179 36
σy/N	11 466	37 165	40 503	56 169	60 388
σvm/kPa	13 900	52 167	84 152	69 755	126 532
σs/kPa	0	16 828	43 502	21 357	99 348
n		435	2 004	328	1 693
hsi/mm		30.76	30.82	36.26	35.29
tsi/mm		2.343 2	2.122 2	2.221 4	1.718 1
tp/mm	2.6	2.342 6	2.112 5	2.024 7	1.710 4
f ′1s		0	-0.603 8	0	0.425 5
f ′1e		0	0.426 9	0	-0.390 4

表选项


单轴载荷下光板和单直筋的一阶模态如图 6所示，单轴载荷下双曲筋和双直筋的一阶模态如图 7所示.图 8所示为单轴荷下4条曲筋的一阶模态.由优化结果可看出,2条端点闭合的曲筋比单直筋板获得了8.98%的临界屈曲载荷提高;4条端点闭合的曲筋比双直筋板获得了7.51%的临界屈曲载荷提高.

图 6 单轴载荷下光板和单直筋的一阶模态Fig. 6 First step mode of bare board and one straight stiffener board for single-axial load

图选项

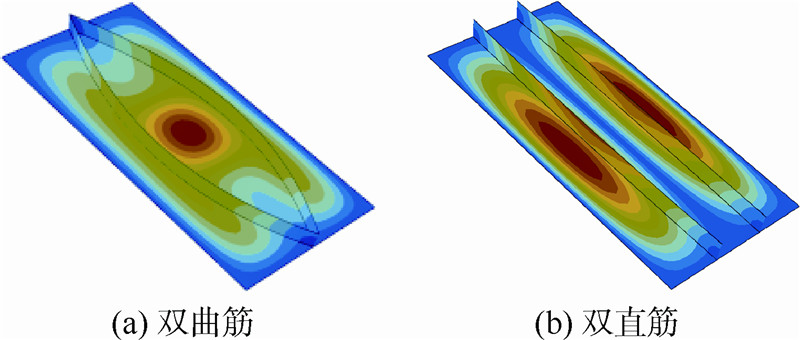图 7 单轴载荷下双曲筋和双直筋的一阶模态Fig. 7 First step mode of two curvilinear stiffeners board and two straight stiffeners board for single-axial load

图选项

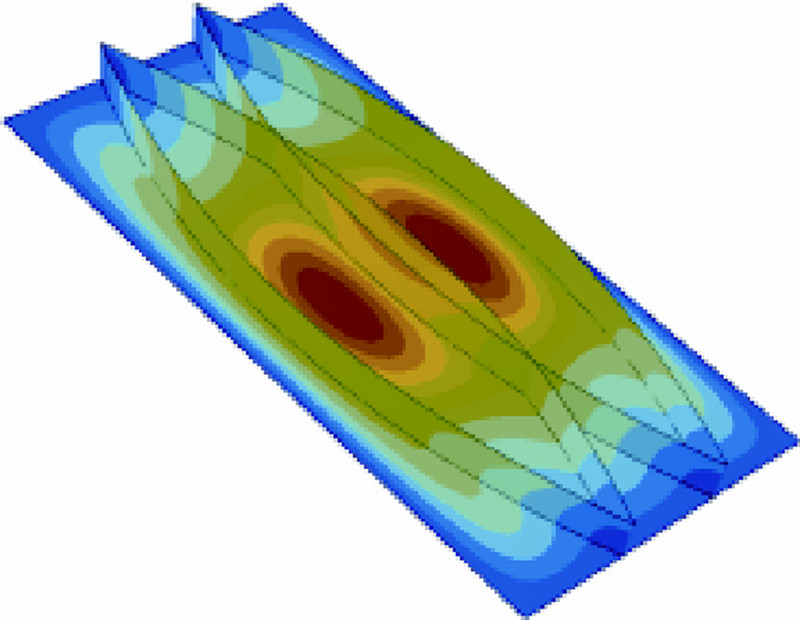图 8 单轴载荷下4条曲筋的一阶模态Fig. 8 First step mode of four curvilinear stiffeners board for single-axial load

图选项

2.1.2 组合载荷下的优化结果对于组合载荷的情况,设定x向载荷N_xx,y向载荷N_yy和剪切载荷N_xy比值为1∶1∶1.这时允许筋条端点在板边自由移动,因此增加了一个设计变量y₁₁,其他端点坐标值根据对称性由y₁₁算出.组合载荷下的优化结果如表 4所示.表 4 组合载荷下的优化结果Table 4 Optimization results for multi-axial load

变量	光板	1条直筋	2条曲筋	2条直筋	4条曲筋
m/kg	1.179 36	1.179 36	1.179 36	1.179 36	1.179 36
σy/N	5 021	12 995	15 635	17 109	21 935
σvm/kPa	13 793	41 041	82 583	63 069	114 560
σs/kPa	0	2 459	36 799	5 403	61 168
n		407	1 021	997	1 594
hsi/mm		32.27	27.91	43.82	26.39
tsi/mm		2.332 1	2.148	1.980 4	1.858 6
tp/mm	2.6	2.331 3	2.148	1.980 1	1.856 4
f ′1s		0	-0.593 6	0	-0.621 8
f ′1e		0	0.593 6	0	-0.621 8
y11/mm		150	150	205.54	116.67

表选项


组合载荷下光板和单直筋的一阶模态如图 9所示，组合载荷下双曲筋和双直筋的一阶模态如图 10所示.组合载荷下4条曲筋的一阶模态如图 11所示.由优化结果可以看出,提出的这种端点闭合的双曲筋板构型比单直筋板临界屈曲载荷增加了20.3%,四曲筋板构型比双直筋板临界屈曲载荷增加了28.2%,说明曲筋板更适用于复杂载荷.

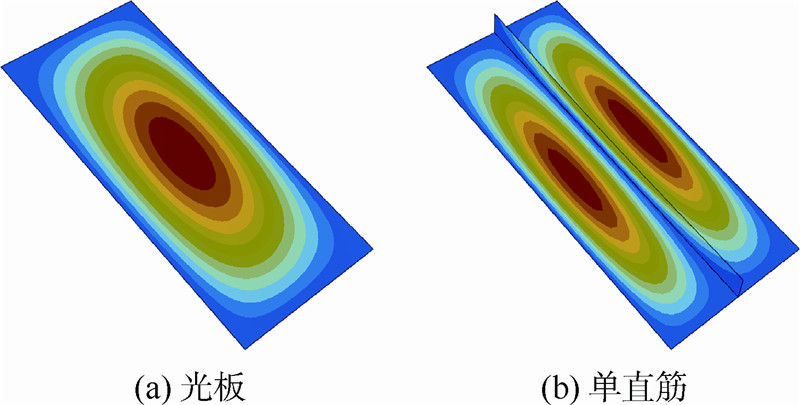图 9 组合载荷下光板和单直筋的一阶模态Fig. 9 First step mode of bare board and one straight stiffener board for multi-axial load

图选项

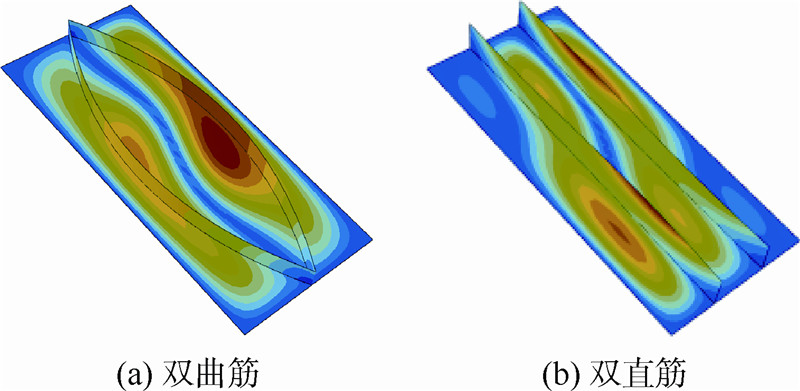图 10 组合载荷下双曲筋和双直筋的一阶模态Fig. 10 First step mode of two curvilinear stiffeners board and two straight stiffeners board for multi-axial load

图选项

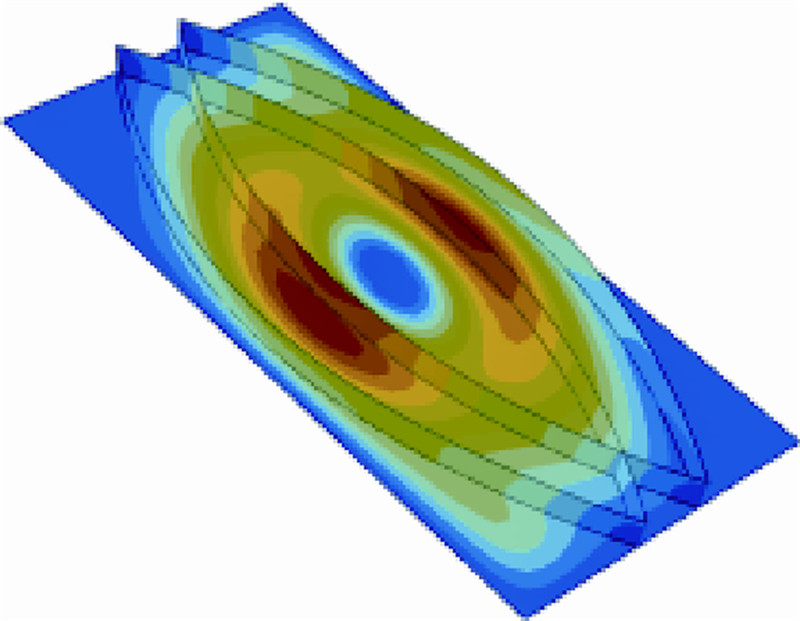图 11 组合载荷下4条曲筋的一阶模态Fig. 11 First step mode of four curvilinear stiffeners board for multi-axial load

图选项

2.2 筋条垂直于板边情况下的曲筋板优化由于片型筋条只能承受面内载荷,为了更方便地施加载荷于筋条上,优化过程约定筋条垂直于板边.设置筋条布局使外载平衡的基础上,研究筋条数目都为2情况下的曲筋加筋板与直筋加筋板的优劣.板大小、外载及边界条件与2.1节的相同.2.2.1 单轴载荷下的优化结果令筋条2个端点可在板的两加载边移动,即对应于图 3中S_1,2={1,1}的布局形式,这里令每条曲筋设1个中间插值点,取筋条高度h_si,筋条厚度t_si,y₁₁,y₁₂为设计变量,其他端点坐标值根据对称性由y₁₁和y₁₂算出.单轴载荷下的优化结果如表 5所示.表 5 单轴载荷下的优化结果Table 5 Optimization results for single-axial load

变量	光板	双直筋	双曲筋
m/kg	1.179 36	1.179 36	1.179 36
σy/N	11 466	62 327	62 899
σvm/kPa	13 900	88 130	92 446
σs/kPa	0	1 478	16 546
n		1 146	1 854
hsi/mm		38.08	38.22
tsi/mm		2.044 8	2.043 1
tp/mm	2.6	2.043 8	2.042 2
f ′1s		0	0
f ′1e		0	0
y11/mm		93.88	94.49
y12/mm		93.88	97.00

表选项


单轴载荷下光板和双直筋的一阶模态如图 12所示,单轴载荷下双曲筋的一阶模态如图 13所示.优化结果表明,曲筋加筋板的优化结果趋近于直筋加筋板,且模态相近,说明在单轴载荷条件下直筋是最优的.

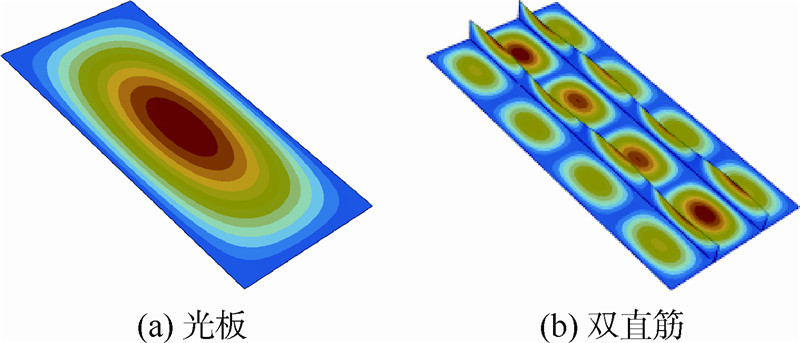图 12 单轴载荷下光板和双直筋的一阶模态Fig. 12 First step mode of bare board and two straight stiffeners board for single-axial load

图选项

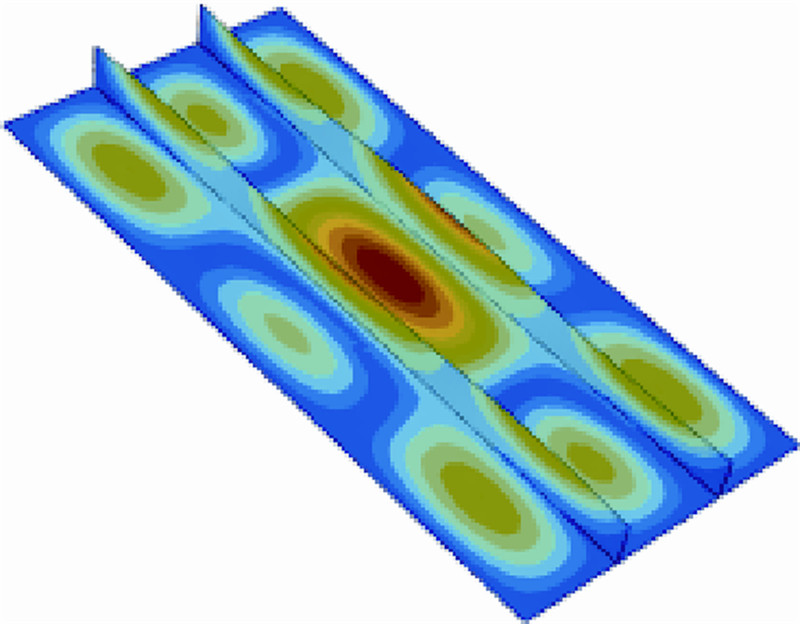图 13 单轴载荷下双曲筋的一阶模态Fig. 13 First step mode of two curvilinear stiffeners board for single-axial load

图选项

2.2.2 组合载荷下的优化结果研究组合载荷即双轴载荷、剪切载荷比值为1∶1的情况.共设计了4种曲筋布局形式,即“S_1,2={1,1}+中间一个插值点”,“S_1,2={3,5}”,“S_1,2={3,2}”,“S_1,2={1,1}+中间无插值点”.其中,后2种曲筋布局由于没有对称性要求,增加设计变量y₂₁.优化结果如表 6所示.表 6 组合载荷下的优化结果Table 6 Optimization results for multi-axial load

变量	光板	双直筋	S1,2={1,1}+中间一个插值点	S1,2={3,5}	S1,2={3,2}	S1,2={1,1}+中间无插值点
m/kg	1.179 36	1.179 36	1.179 36	1.179 36	1.179 36	1.179 36
σy/N	5 021	17 109	19 795	15 211	18 066	16 716
σvm/kPa	13 793	63 069	102 650	65 622	301 447	81 850
σs/kPa	0	5 403	72 738	32 403	313 266	71 830
n		997	2 391	1 467	2 444	1 343
hsi/mm		43.82	20.76	22.71	28.38	35.09
tsi/mm		2.332 1	2.476 0	2.354 2	2.492 7	2.070 5
tp/mm	2.6	1.980 4	2.111 1	2.344 1	2.276 4	2.070 4
f ′1s		0	0			0
f ′1e		0	0			0
y11/mm		43.73	0	134.24	16.40	150
y12/mm			264.89	251.98	142.62	124.17
y21/mm				192.52	67.35

表选项


组合载荷下光板和双直筋的一阶模态如图 14所示,组合载荷下S_1,2={1,1}+中间一个插值点布局和S_1,2={3,5}布局的一阶模态如图 15所示.图 16所示为组合载荷下S_1,2={3,2}布局和S_1,2={1,1}+中间无插值点布局的一阶模态.优化结果表明,S_1,2={1,1}+中间一个插值点,即筋条端点在对边双交叉点布局的临界屈曲载荷比双直筋的高出了15.7%;S_1,2={3,2},即筋条端点在对边和相邻边布局的临界屈曲载荷比双直筋的高出了5.6%,这说明曲筋加筋板相比直筋加筋板拥有更好的提高板稳定性的能力.

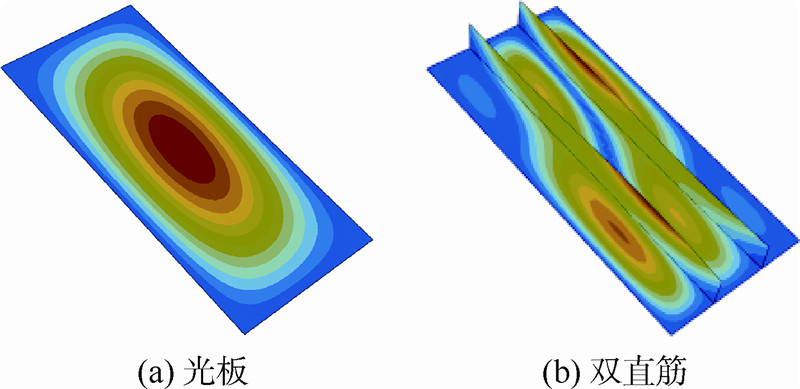图 14 组合载荷下光板和双直筋的一阶模态Fig. 14 First step mode of bare board and two straight stiffeners board for multi-axial load

图选项

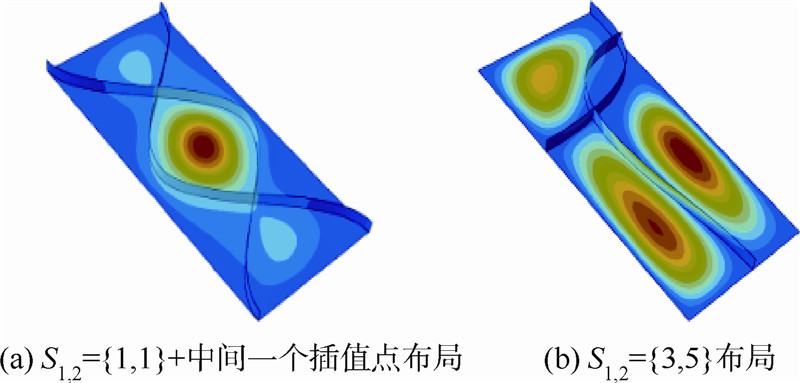图 15 组合载荷下S1,2={1,1}+中间一个插值点布局和S1,2={3,5}布局的一阶模态Fig. 15 First step mode of S1,2={1,1} with one interpolation point and S1,2={3,5} for multi-axial load

图选项

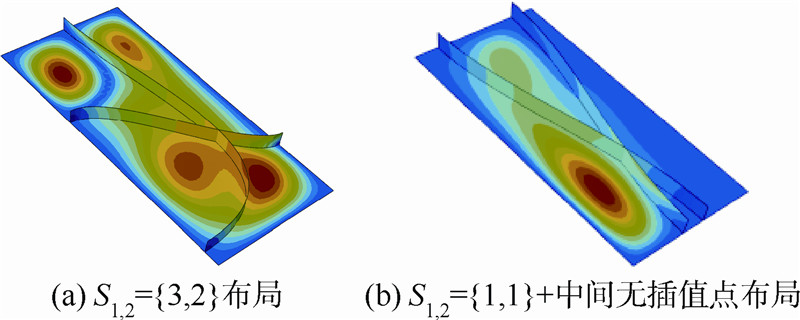图 16 组合载荷下S1,2={3,2}布局和S1,2={1,1}+中间无插值点布局的一阶模态Fig. 16 First step mode of S1,2={3,2} and S1,2={1,1} with no interpolation point for multi-axial load

图选项

3 结 论设计了一种新的曲线片型加筋板优化系统,可以根据需求合理设置设计变量个数,为曲筋加筋板的优化设计提供了广阔的空间.经过对曲筋加筋板的大量优化计算,得出以下结论:1) 在端点闭合的曲筋布局中,证明了2条端点闭合的曲筋比一根直筋更好地提高了板的稳定性,应用这种结构形式,可以将加筋板上的任何一根直筋替换为端点闭合的曲筋.2) 在筋条垂直于板边的布局中,研究了若干种曲筋布局方案,证明了在相同筋条数目情况下,有多种曲筋布局加筋板比直筋加筋板更具优越性.说明了曲线片型加筋板可以获得比传统直筋加筋板更优的稳定性性能,为曲筋加筋板设计的深入研究提供了基础.3) 除稳定性之外,曲筋加筋板的后屈曲特性、疲劳特性、损伤容限和振动特性等性能也需要优化研究.这些特性也同样影响着曲筋加筋板的发展.4) 曲筋加筋板存在很大的发展潜力,但如果将直筋加筋板合理布局,也能获得很好的稳定性性能.由于曲筋加筋板计算量大,加工工艺复杂,所以只有制造工艺和计算机水平发展到一定水平,曲筋加筋板才能体现出它的优势.
参考文献

[1]	张柱国, 姚卫星,刘克龙.基于进化Kriging模型的金属加筋板结构布局优化方法[J].南京航空航天大学学报,2008,40(4): 497-500. Zhang Z G,Yao W X,Liu K L.Configuration optimization method for metallic stiffened panel structure based on updated Kriging model[J].Journal of Nanjing University of Aeronautics and Astronautics,2008,40(4):497-500(in Chinese).
	Cited By in Cnki (22)
[2]	Hao P, Wang B,Li G.Surrogate-based optimum design for stiffened shells with adaptive sampling[J].AIAA Journal,2012,50(11): 2389-2407.
	Click to display the text
[3]	Mulani S B, Slemp W C H,Kapania R K.EBF3PanelOpt:an optimization framework for curvilinear blade-stiffened panels[J].Thin-Walled Structures,2013,63:13-26.
	Click to display the text
[4]	Mulani S B, Havens D,Norris A,et al.Design,optimization, and evaluation of Al-2139 compression panel with integral T-stiffeners[J].Journal of Aircraft,2013,50(4):1275-1286.
	Click to display the text
[5]	Kapania R K, Li J,Kapoor H.Optimal design of unitized panels with curvilinear stiffeners[C]//AIAA 5th ATIO and the AIAA 16th Lighter-than-Air Systems Technology Conference and Balloon Systems Conference,2005,3:1708-1737.
	Click to display the text
[6]	Dang T D, Kapania R K,Slemp W C H,et al.Optimization and postbuckling analysis of curvilinear-stiffened panels under multiple-load cases[J].Journal of Aircraft,2010,47(5):1656-1671.
	Click to display the text
[7]	Mulani S B, Duggirala V,Kapania R K.Curvilinearly T-stiffened panel-optimization framework under multiple load cases using parallel processing[J].Journal of Aircraft,2013,50(5):1540- 1554.
	Click to display the text
[8]	罗煦琼. 一维搜索问题的三次B样条插值法[J].浙江科技学院学报,2008,20(1):1-3. Luo X Q.Cubic B-spline interpolation for one-dimensional search method[J].Journal of Zhejiang University of Science and Technology,2008,20(1):1-3(in Chinese).
	Cited By in Cnki (1)
[9]	Özakça M, Murphy A,van der Veen S.Buckling and post-buckling of sub-stiffened or locally tailored aluminium panels[C]//25th Congress of the International Council of the Aeronautical Sciences 2006.Red Hook,NY:Curran Associates Inc,2006,4:2367-2382.
	Click to display the text