1 试验原理与系统设计1.1 试验原理力约束管材自由胀形试验方法原理如图 1所示,将试验管材的两端完全刚性约束,仅放开其轴向移动的自由度,在管材内部施加均匀液压力p,同时在管材左右两端分别通过伺服侧推油缸施加推力F1,F2,并满足下式:

式中,Fp为内压力p对管材内腔端面Ain的作用力;Ain为试验管材的管端内腔截面积;k1,k2为加载系数;S1,S2为左右两侧伺服油缸上安装的左侧位移传感器和右侧位移传感器的位移反馈值.内压力p均匀上升直至管材破裂过程中保持前述关系不变,同时通过超声测厚仪及探头、胀形高度位移传感器实时监控管材胀形顶点的实时壁厚t和胀形高度h.当k1=k2=1时,侧推力F1,F2正好抵消内压力p对管材内腔端面Ain的作用力Fp,通过获得的胀形过程数据p,t,h即可按照塑性理论推导出试验管材的轴向自由胀形应力应变曲线及材料参数.此种工况下,试验管材仅受到内压力p对管腔内壁的法向作用和管端节点的径向约束,同时保持胀形最高点轴向不窜动,而不受任何他它外力、约束或摩擦的影响.
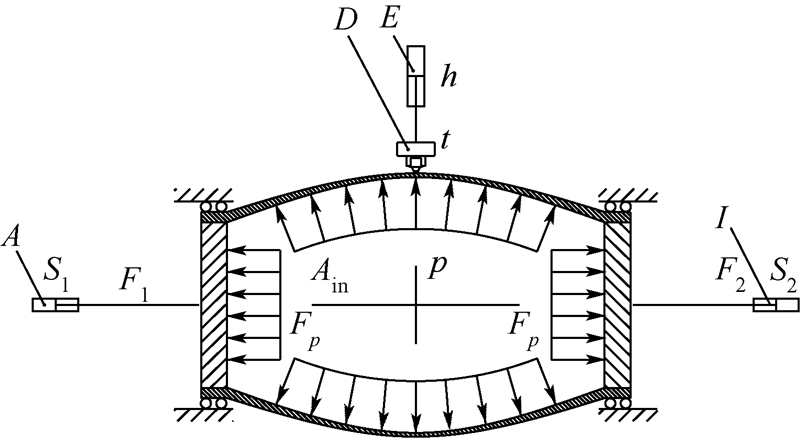 |
| A—左侧位移传感器; D—超声测厚仪及探头; E—胀形高度位移传感器; I—右侧位移传感器.图 1 力约束管材自由胀形试验原理Fig. 1 Principle diagram of TBT system |
| 图选项 |
1.2 试验系统组成如图 2所示,试验系统分为控制系统、液压系统、水系统、增压器和试验工装5部分.液压系统工作介质为液压油,水系统工作介质为乳化液,增压器为液压力转换和放大装置.控制系统同时监测并记录左侧位移传感器、左侧油缸无杆腔压力传感器、左侧油缸有杆腔压力传感器、超声测厚仪及探头、胀形高度位移传感器、超高压压力传感器、右侧油缸有杆腔压力传感器、右侧油缸无杆腔压力传感器、右侧位移传感器9个传感器的实时数据.
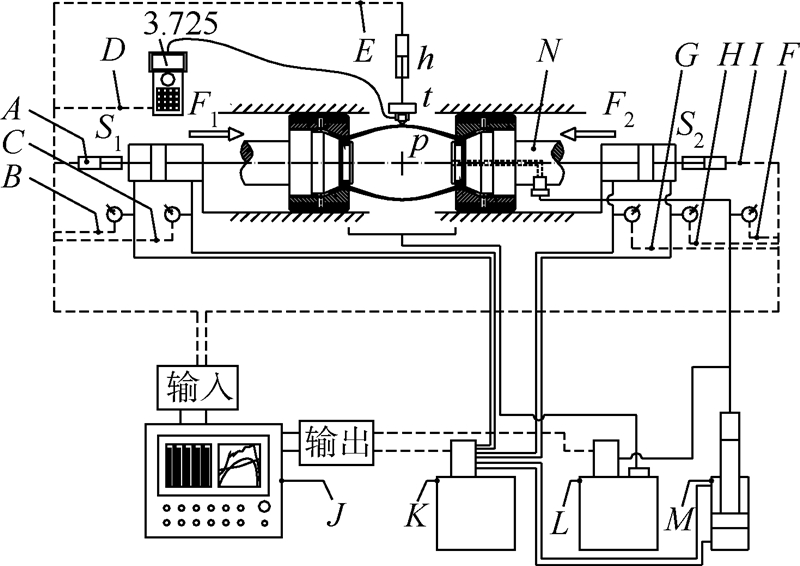 |
| A—左侧位移传感器;B—左侧油缸无杆腔压力传感器; C—左侧油缸有杆腔压力传感器;D—超声测厚仪及探头; E—胀形高度位移传感器;F—超高压压力传感器; G—右侧油缸有杆腔压力传感器; H—右侧油缸无杆腔压力传感器;I—右侧位移传感器; J—控制系统;K—液压系统; L—水系统;M—增压器;N—试验工装.图 2 试验系统组成Fig. 2 Composition of TBT system |
| 图选项 |
2 关键技术实现与验证2.1 管端约束、高压密封与导向结构如图 3所示,试验管材两端的约束和高压密封由左推杆、试验管材、对开螺母卡套部件、右推杆、超高压水管、高压密封圈6部分组成.对开螺母卡套部件包括卡套、内螺纹圆柱销、对开螺母.对开螺母上下瓣和卡套通过内螺纹圆柱销连接为一整体,并可反复拆装.左、右推杆与对开螺母卡套部件采用螺纹连接,并可反复拆卸,试验管材经过扩口的两端被左、右推杆和对开螺母卡套部件夹紧在中间,通过螺纹实现预紧.超高压水管通过螺纹连接在右推杆上,并可通过右推杆上的高压水通道向试验管材内注入高压液体.卡套可以在左右两侧上压半圆形导套和下支撑半圆形导套组成的圆形导向结构内沿轴向自由窜动,配合界面采用大间隙配合,并涂油润滑,左右两侧的下支撑半圆形导套通过螺栓固定在底板上,并通过导向键保证同轴度,从而保证了管材沿轴向的自由移动.
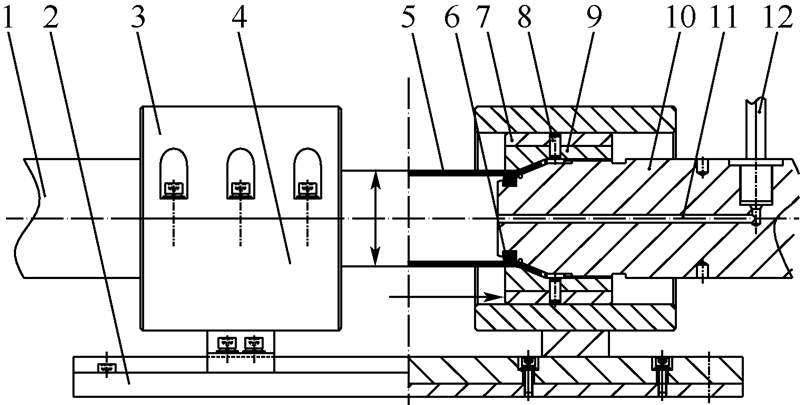 |
| 1—左推杆;2—底板;3—上压半圆形导套;4—下支撑半圆形导套;5—试验管材;6—高压密封圈;7—卡套;8—内螺纹圆柱销;9—对开螺母;10—右推杆;11—高压水通道;12—超高压水管.图 3 试验工装Fig. 3 Tool set |
| 图选项 |
2.2 侧推位移与力的比例伺服控制策略对于比例伺服控制实现式(1)要求的力平衡条件仅需要对两侧伺服油缸进行力控制,当管材收缩时侧推油缸跟随运动.但通过试验发现管材因胀形而收缩过程中两侧伺服油缸的位移是不稳定的,由于系统的不完全对称会导致管材偏移.为了便于超声测厚仪稳定采集实时厚度数据,就需要对侧推油缸的位移进行控制,以确保管材顶点始终处于中间位置.经过反复试验发现,精确控制左侧伺服油缸压力和右侧伺服油缸位移,左侧伺服油缸位移传感器采集的位移数据作为右侧伺服油缸位移控制数据,这种控制策略能够同时保证侧推力和侧推位移的对称,并且侧推油缸的位移量体现的是管材胀形的自由收缩量.如图 4所示,试验采集的数据表明了上述控制策略的有效性,在管材胀形至破裂的过程中,式(1)和式(2)所描述的试验平衡状态始终处于动态稳定中.
 |
| 图 4 轴向力与位移曲线Fig. 4 Force and displacement curve |
| 图选项 |
2.3 关键技术特征根据管端约束条件不同,传统的管材胀形试验方法分为管端固定、管端力加载和管端自由胀形[11].相较于现有试验方法,本文所描述的管材自由胀形试验方法具有如下特征:①在胀形试验之前,管材两端通过翻边模具进行扩口,对开螺母卡套部件将管材的翻边特征完全约束,因而阻滞了管材夹持段的材料向胀形区的流动,保证了管材变形区材料长度的一致性.②由于管材两端的翻边特征完全被对开螺母卡套部件夹持,现有试验方法中管材与夹持模具之间的相对运动边界被转换到了对开螺母卡套部件与导套之间,原有的剧烈摩擦边界被间隙滑动配合所代替,因而在施加大的轴向力之前管材可以在导套内自由滑动.在胀形阶段,夹持段管材的变形很小,对开螺母卡套部件与导套之间的滑动间隙仍旧稳定,滑动摩擦力很小,因而管材可以自由收缩.③除了轴向移动的自由度,管材两端节点的其他自由度被完全约束,加上良好的滑动配合,伺服油缸提供的轴向力加载精确地作用在管材两端.由于翻边特征的特殊固定方式,轴向拉力也可以施加在管材上,这为研究管材在双拉状态下的变形行为提供了非常好的试验条件.
3 试验条件3.1 试验材料试验管材材料为QSTE340 TM高频焊管,长度210 mm(含管材两端夹持段长度各32.5 mm),外径D0=72.5 mm,长径比L0/D0=2.0,变形区长度L0=145 mm,实测原始壁厚t0=3.665 mm.单向拉伸试验测得的屈服强度σs=400 MPa,抗拉强度σb=450 MPa,延伸率≥25%.试验前,在管材表面印上直径2.5 mm的圆形网格,用于测量管材破裂后的面内应变.
3.2 试验设备试验设备为北京航空航天大学飞行器制造工程实验室为完成本试验自主研发的FTBT试验机,如图 5所示.设备最大胀形力250 MPa,压力控制精度0.5 MPa,侧推力0~30 t,位移控制精度0.2 mm.
 |
| 图 5 FTBT管材自由胀形试验机Fig. 5 Free-end tube bulging test machine |
| 图选项 |
4 试验数据采集与分析4.1 数据采集试验采用PD-T1精密型超声波测厚仪测量胀形零件顶点厚度t,Novotechnik TMI系列位移传感器测得胀形高度h,及左右油缸的位移S1,S2,KAVLICO PTE5000系列压力传感器测得胀形压力p.控制系统每秒钟输出2组数据,增压时间20 s,系统输出的顶点壁厚、胀形高度和压力曲线如图 6所示.
 |
| 图 6 试验数据采集曲线Fig. 6 Experimental data |
| 图选项 |
4.2 理论解析模型如图 7所示,力约束管材自由胀形试验中,在式(1)和式(2)满足的情况下,管材仅受到内压力p的作用,轴向推力F1,F2和内压力p对管材内腔端面Ain的作用力Fp相互抵消.
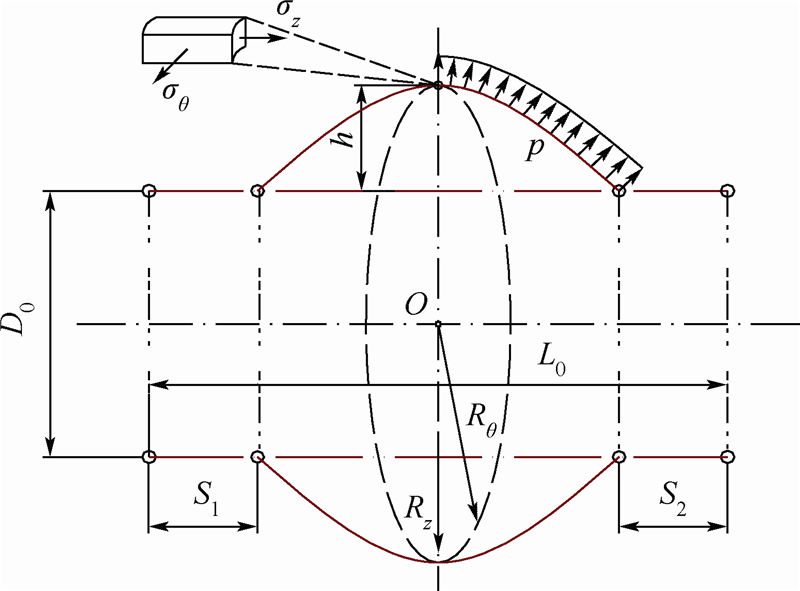 |
| 图 7 力约束管材自由胀形受力平衡示意图Fig. 7 Force equilibrium diagram of free-bulging |
| 图选项 |
根据前述边界条件和几何关系,列出下列平衡方程[12, 13],可以得到胀形管材顶点的应力应变状态.同时需要做出如下假设:1) 薄壁管成形,忽略管材厚向应力,但考虑内压力p的作用;2) 管材胀形过程中,轴向剖面轮廓曲线始终为余弦曲线;3) 塑性变形过程中,材料体积不变;4) 忽略材料各向异性.首先分析管材顶点的应力状态,在塑性变形阶段,管材轴向仅受到内压力p在管材轴向轮廓的投影,轴向应力可以通过下式得出:

式中,R0为管材原始半径,当管材长径比L0/D0=2.0时,端头效应的影响需要考虑在内,根据薄膜理论及静力平衡条件,此时有

式中,σθ为顶点的环向应力分量;σz为顶点的轴向应力分量;Rθ为顶点的环向曲率半径;Rz为顶点的轴向曲率半径;t为顶点的实时壁厚.假设管材轴向剖面轮廓曲线为余弦曲线:
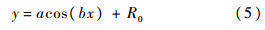
根据几何关系可得:

式中,有a=h,b=π/l,则
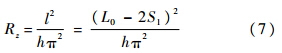
管材两端自由收缩量S1=S2通过图 4(b)可得,将式(3)、式(7)代入式(4)中即可推导出环向应力σθ.管材顶点的真实厚向应变可以通过超声测厚仪采集的实时厚度t得出:

管材环向真实应变为
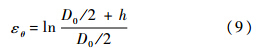
根据体积不变关系可得轴向应变:

平面应力状态下,根据Von Mises屈服准则推导出等效应力:
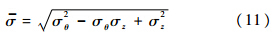
根据下式推导出等效应变:
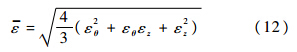
4.3 数据处理与分析将图 4(b)和图 6采集的数据代入前述公式即可获得材料塑性阶段的应力分量(图 8(a))、应变分量(图 8(b)).采用式(13)所述的Swift材料本构拟合材料塑性阶段的等效应力应变曲线如图 8(c)所示.

如图 8(a)所示的应力分量图,环向应力σθ远大于轴向应力σz,受力状态接近于单向拉伸,轴向力的抵消起到了很好的效果,测试结果能够很好地反映管材的环向成形性能.这个结果也是工艺设计所需要的,在实际工程应用中,管材充液成形零件的破裂主要发生在环向.
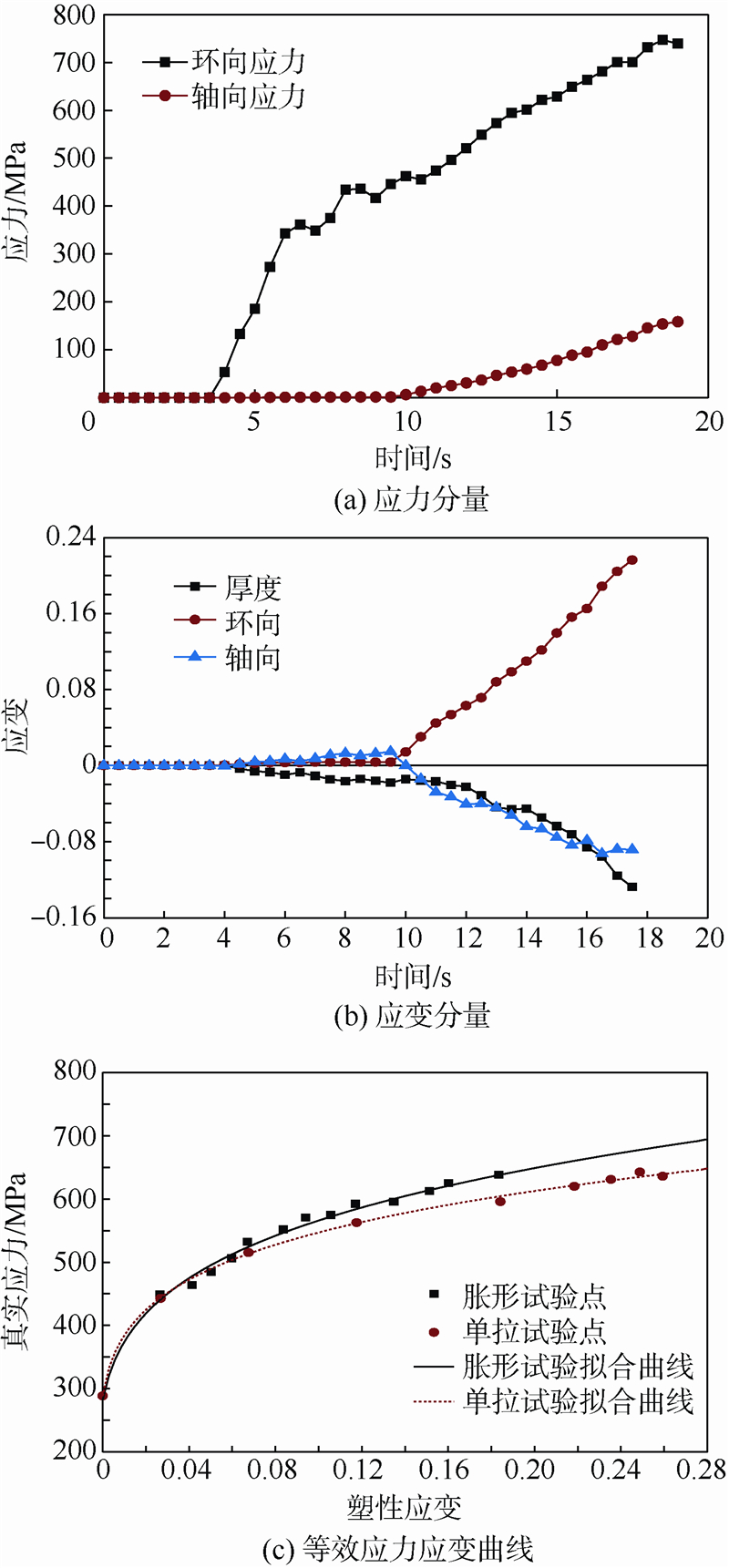 |
| 图 8 应力应变曲线及拟合Fig. 8 Fit of strain stress curve |
| 图选项 |
图 8(b)所示的应变分量图反映了管材胀形过程中厚度逐渐减薄、环向逐渐拉长的过程,对应的轴向应变则经历了先压缩、后拉伸的过程,轴向力的抵消起到了明显的效果[14].在材料发生弹性变形和塑性变形的中前期阶段,胀形高度很低,内压力对管材轴向的作用很小,管材近似于仅受环向主应力的作用,引起明显的轴向和厚向收缩,因而该阶段的轴向应变为负值.该阶段的应力应变状态非常近似于单向拉伸试验,从图 8(b)中也可以看出在该阶段轴向应变与厚向应变近似相等,与单向拉伸试验类似定义该阶段的厚向异性指数r,则r近似为1.0.在胀形后期至破裂,由于胀形高度的增加,内压力对管材轴向的作用逐渐显著,材料应力状态向着双向拉伸快速转变,此时轴向应变趋势出现了明显的扭转上翘趋势,但最终轴向拉应力的作用还是远小于环向拉应力,因而轴向应变始终为负值.进一步根据Swift材料本构拟合材料塑性阶段的等效应力-应变曲线如图 8(c)所示.拟合所得的塑性强度系数K=895.096,硬化指数n=0.202,初始应变ε0=0.003 29.与材料单向拉伸试验获得的数据相比,试验数据结果基本符合材料在高压流体作用下表现出的特性[15, 16].进一步的数据分析、数值模拟和试验工作需要继续完成,以便相互验证,为材料性能测试和工艺设计提供可靠手段和依据.图 9所示的为国产未退火材料和进口退火两种材料进行多次测试的管材胀形高度与内压力关系曲线,图 4和图 6中的数据均由进口退火材料测试获得.通过图 9可以看出试验系统具有较好的重复性,退火材料会有明显的屈服平台,而未退火材料可以获得更高的胀形高度.
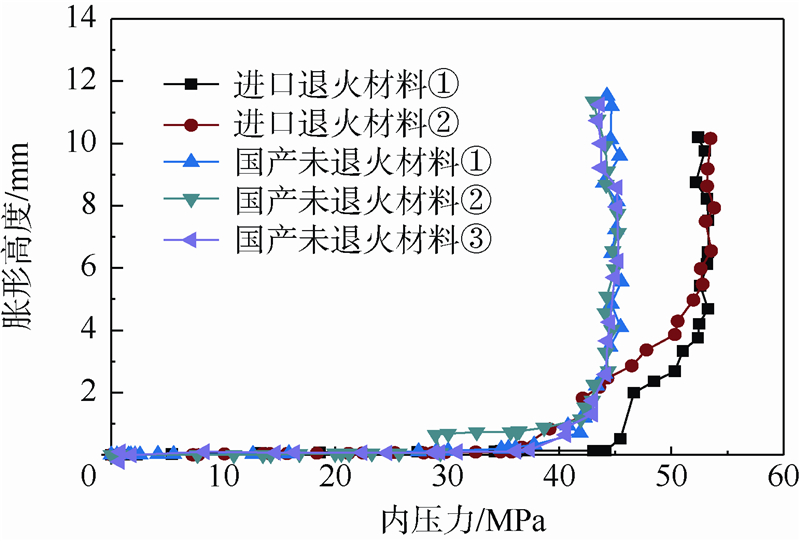 |
| 图 9 胀形高度与内压力关系曲线Fig. 9 Bulging height vs internal pressure curve |
| 图选项 |
5 结 论1) 相对于国际上现有的管材胀形试验机,本文所描述的试验方法和设备解决了3个固有问题:①将实现管端约束的对开螺母卡套部件和密封组件附着在管材两端,从而保证了管材胀形过程中卡套与半圆形导套的滑动间隙,即保证了管端的自由滑动,排除摩擦干扰的同时准确获得了管材胀形时的轴向自由收缩数据;②鉴于翻边特征的良好试验效果,比例伺服油缸可以对管材两端施加精确的推力(或拉力),并能有效阻止管端被夹持材料向变形区的流动;③采用超声测厚仪实时采集管材顶点的厚度变化信息,直接准确测量推导出厚向应变.试验数据的采集具有较好的可重复性精度.2) 在管材胀形过程中,环向应力σθ远大于轴向应力σz,受力状态接近于单向拉伸,轴向力的抵消起到了很好的效果,测试结果能够很好地反映管材的环向成形性能.3) 胀形过程中发生弹性变形和塑性变形的中前期阶段,管材近似于仅受环向主应力的作用,引起明显的轴向和厚向收缩,该阶段的轴向应变为负值,轴向应变与厚向应变近似相等,对应单向拉伸试验可以看出厚向异性指数r近似为1.0.在胀形后期至破裂,材料应力状态向着双向拉伸快速转变,轴向应变趋势出现了明显的扭转上翘趋势,但轴向应变始终为负值.
参考文献
| [1] | Yuan S J, Liu G.3.04-Tube hydroforming (internal high-pressure forming)[J].Comprehensive Materials Processing,2014,3:55-80. |
| Click to display the text | |
| [2] | Ahmetoglu M, Altan T.Tube hydroforming:state-of-the-art and future trends[J].Journal of Materials Processing Technology,2000,98(1):25-33. |
| Click to display the text | |
| [3] | Lang L H, Wang Z R,Kang D C,et al.Hydroforming highlights:sheet hydroforming and tube hydroforming[J].Journal of Materials Processing Technology,2004,151(1):165-177. |
| Click to display the text | |
| [4] | Ouirane A H B, Boudeau N,Velasco R,et al.Error evaluation on experimental stress-strain curve obtained from tube bulging test[J].Thin-Walled Structures,2011,49(10):1217-1224. |
| Click to display the text | |
| [5] | Thiruvarudchelvan S, Seet G L,Ang H E.Computer-monitored hydraulic bulging of tubes[J].Journal of Materials Processing Technology,1996,57(1-2):182-188. |
| Click to display the text | |
| [6] | Yang L F, Guo C.A simple experimental tooling with internal pressure source used for evaluation of material formability in tube hydroforming[J].Journal of Materials Processing Technology,2006,180(1-3):310-317. |
| Click to display the text | |
| [7] | He Z B, Yuan S J,Lin Y L.Analytical model for tube hydro-bulging test,part I:models for stress components and bulging zone profile[J].International Journal of Mechanical Sciences,2014,87:297-306. |
| Click to display the text | |
| [8] | He Z B, Yuan S J,Lin Y L.Analytical model for tube hydro-bulging test,part II:linear model for pole thickness and its application[J].International Journal of Mechanical Sciences,2014,87:307-315. |
| Click to display the text | |
| [9] | Velasco R, Boudeau N.Tube bulging test:theoretical analysis and numerical validation[J].Journal of Materials Processing Technology,2008,205(1-3):51-59. |
| Click to display the text | |
| [10] | Zribi T, Khalfallah A,BelHadjSalah H.Experimental characterization and inverse constitutive parameters identification of tubular materials for tube hydroforming process[J].Materials and Design,2013,49:866-877. |
| Click to display the text | |
| [11] | Imaninejad M, Subhash G,Loukus A.Influence of end-conditions during tube hydroforming of aluminum extrusions[J].International Journal of Mechanical Sciences,2004,46(8):1195-1212. |
| Click to display the text | |
| [12] | Imaninejad M, Subhash G,Loukus A.Experimental and numerical investigation of free-bulge formation during hydroforming of aluminum extrusions[J].Journal of Materials Processing Technology,2004,147(2):247-254. |
| Click to display the text | |
| [13] | Boudeau N, Malecot P.A simplified analytical model for post-processing experimental results from tube bulging test:theory,experimentations,simulations[J].International Journal of Mechanical Sciences,2012,65(1):1-11. |
| Click to display the text | |
| [14] | Varma N S P, Narasimhan R.A numerical study of the effect of loading conditions on tubular hydroforming[J].Journal of Materials Processing Technology,2008,196(1-3):174-183. |
| Click to display the text | |
| [15] | Liu B S, Lang L H,Zeng Y S,et al.Forming characteristic of sheet hydroforming under the influence of through-thickness normal stress[J].Journal of Materials Processing Technology,2012,212(9):1875-1884. |
| Click to display the text | |
| [16] | Strano M, Altan T.An inverse energy approach to determine the flow stress of tubular materials for hydroforming applications[J].Journal of Materials Processing Technology,2004,146(1): 92-96. |
| Click to display the text |
