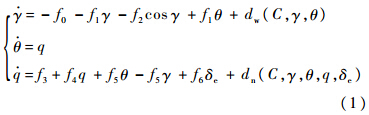
式中,γ,θ,q,δe,C分别表示航迹角、俯仰角、俯仰角速度、升降舵偏度、气动参数;
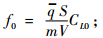
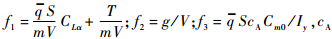为平均气动弦长;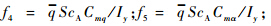
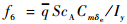，动压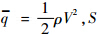
为机翼面积，Iy为绕横轴惯性矩，m为载机与货物总质量，V为空速，T为发动机推力，ρ为空气密度.不确定函数dw(C,γ,θ)和dn(C,γ,θ，q,δe)表示模型不确定性和外界大气干扰的总和,其中模型不确定性主要由超低空地面效应作用引起的气动参数C的变化和飞行状态测量误差等造成的.空投拉平阶段载机高度变化范围是已知的,因此,由地面效应作用引起的气动参数的不确定性是有界的.一般传感器测量误差范围是预先可知的,所以飞行状态测量不确定性是有界的.另外,外界大气扰动也是可以探测的.综上分析,不确定函数dw(C,γ,θ)和dn(C,γ,θ，q,δe)是有界的,即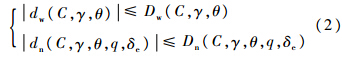
2 混合迭代滑模飞行控制律设计按照时标分离的原则,空投拉平纵向飞控系统包括内环俯仰姿态控制和外环高度跟踪控制.控制目标是通过操纵升降舵δe使航迹角γ沿参考指令快速收敛至0,控制系统结构如图 1所示.
 |
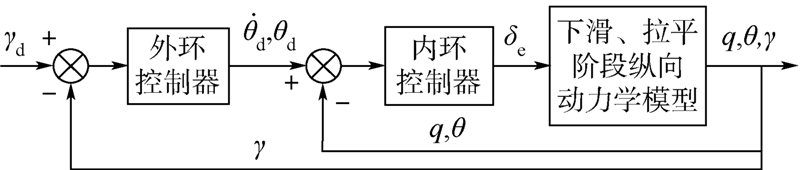| 图 1 空投拉平纵向飞行控制系统结构图Fig. 1 Structure diagram of the airdrop level off longitudinal flight control system |
| 图选项 |
图 1中,外环高度控制器实现对指令信号γd的跟踪,其输出是俯仰角指令信号θd和
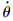d,内环控制器实现对指令信号θd的跟踪.表征系统内环运动的状态方程为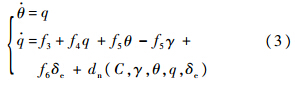
表征系统外环运动的状态方程为
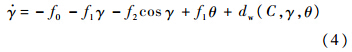
式中,内环输出y=θ,外环输出y=γ,内环俯仰角指令θd,外环航迹角指令γd.空投拉平过程中,载机纵向内、外环运动方程均具有如下非线性不确定系统的形式:
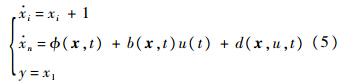
式中,i=1,2,…,n;x=[x1 x2 … xn]T为系统状态;u为控制输入;d(x,u,t)为模型不确定性和外界干扰的总和,满足:
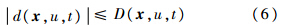
控制目标是使输出y跟踪参考指令yd.所以空投拉平控制问题即转化为对非线性不确定系统(5),设计控制律,使得系统能够跟踪指令信号.对系统(5)设计如下的二级滑模面函数:
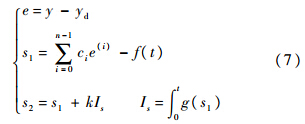
式中,e(i)表示对跟踪误差的阶导数;ci满足使
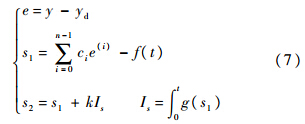为Hurwitz稳定,且cn-1=1;全局动态切换函数f(t)满足: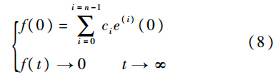
k>0，g(s1)是具有“小变量大增益,大变量小增益”特性的函数,且满足
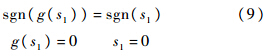
式中a,λ>0为指数趋近常数.设计控制输入,保证第2级滑模切换函数s2收敛,进而迫使系统输出跟踪参考指令yd.设计如下的等效控制加鲁棒切换项的控制律:
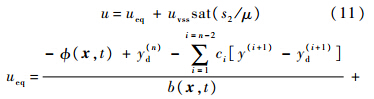
式中,μ>0为边界层厚度;sat(·)为饱和函数.按照式(7)～式(10)的设计方法,针对空投拉平控制系统内、外环设计二级滑模切换函数.对于系统外环,阶次n=1,则二级滑模面函数为
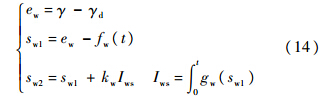
系统外环的等效控制输入为内环俯仰角指令θd,由式(11)～式(13)得系统外环控制律为
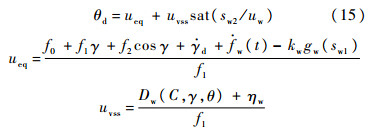
系统内环阶次n=2,则内环二级滑模面函数为
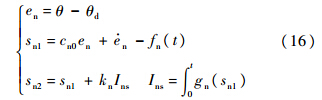
油门杆固持时,系统内环控制为升降舵偏角δe:
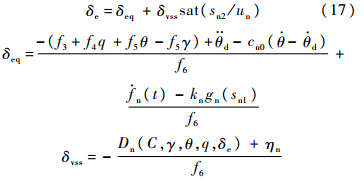
3 鲁棒稳定性证明及跟踪性能分析针对系统(5),设计式(7)所示的滑模面,取式(11)～式(13)所示的控制律,则第2级滑模切换函数s2可以稳定在边界层内,即
证明 若滑模变量s2在边界层外,则式(11)转化为
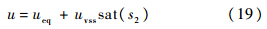
而
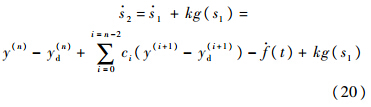
取Lyapunov函数V1=s22/2,则
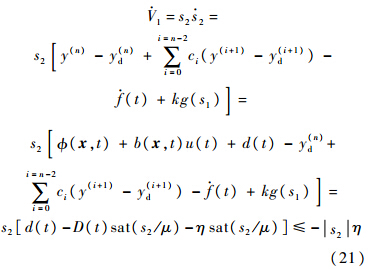
又s2(0)=0<μ,因此s2可以始终收于边界层内.证毕如果s2<μ,则s1≤2μ,并且系统稳态跟踪误差e满足:
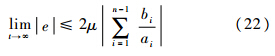
式中,
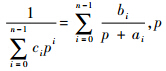为Laplace算子,由于
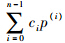为Hurwitz稳定,因此ai>0.证明 定义Lyapunov函数V2=Is2/2,则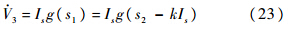
若Is>μ/k,由sgn(g(s1))=sgn(s1),有
又Is(0)=0,则
由式(7)、式(18)、式(25)可知：
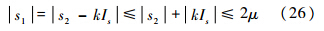
对s1进行Laplace变换：
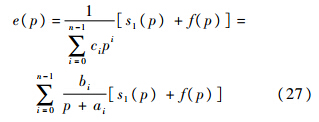
令
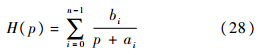
其脉冲响应为
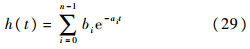
对于输入s1+f,H(p)的零状态响应为
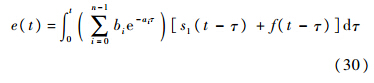
式中τ为指数时间常数.由式(8)、式(26)得
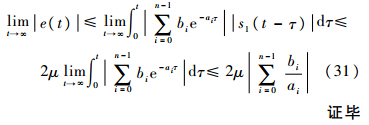
由上述证明可知,如果空投拉平过程存在模型不确定性或外界干扰时,理论上可以通过选取合适参数控制高度跟踪误差任意小.事实上,如果系统的模型不确定性或外界干扰为常值(或最终为常值),即
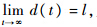,则s1将渐近稳定于0,稳态跟踪误差e也为0.证明 由式(7)、式(11)～式(13),s2在边界层内的运动轨迹为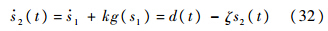
ζ=(D+ζ)/μ,对式(32)取Laplace变换有
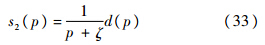
由终值定理,有
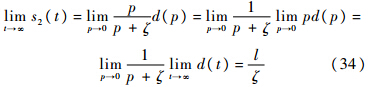
显然
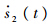一致连续,由Barbalat引理有
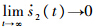,由式(32),有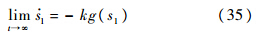
定义Lyapunov函数V3=s12/2,由式(9),当s1≠0时,有
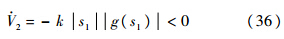
即
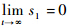,由式(7)、式(8)推出
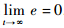证毕4 超低空空投拉平参考轨迹设计当前,空投拉平阶段的参考航迹角指令通常采用如下形式[16]: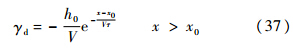
式中，γd为航迹角指令信号；[x0 h0]为初始拉平点位置.在拉平初期,指数参考轨迹存在突变,导致舵面存在较大的偏转速率.针对此问题,本文提出基于余弦曲线的空投拉平参考指令：
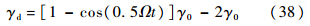
式中
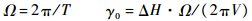
其中,ΔH为拉平起始时刻高度与目标高度之差;T为期望的拉平时间;Ω为拉平时间对应的自然频率.参考航迹角指令对比曲线如图 2所示.
 |
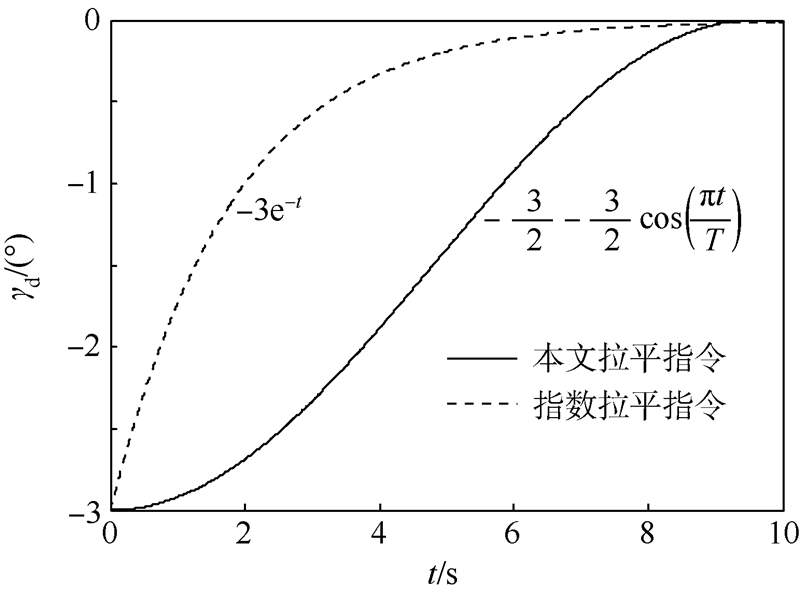| 图 2 本文拉平指令与传统指数拉平指令[16]对比Fig. 2 Contrast of the level off command signal in this paper and the traditional exponential one in reference[16] |
| 图选项 |
由式(38)和图 2可见,本文拉平指令为曲线的半个周期,通过参数设计期望的拉平时间,与传统的指数收敛形式相比,更能满足超低空空投任务对拉平时间的严格要求.而当拉平时间相同时,本文参考航迹初始拉平高度低(曲线积分面积较小),放宽了对运输机拉平能力的要求.此外,余弦的收敛方式在拉平初期是平滑的,从而可避免舵面偏转速率过高的问题.5 仿真验证任务设置:运输机从高度h0=30 m开始进入拉平阶段,空速V=80 m/s,取拉平时间T=9.5 s,拉平结束后要求载机处于预设空投启动高度h=10 m,航迹角归零.仿真首先验证控制律在气动参数摄动和飞行状态测量不确定性均为常值情况下的跟踪性能.假定由地面效应引起的俯仰力矩系数Cm和升力系数CL摄动±10%.外界大气扰动主要对载机气流角产生干扰,因此,它对载机运动特性的影响可等效为一定程度的飞行状态测量不确定性.假定传感器测量误差和大气扰动使得状态γ,θ,q,δe产生±10%的不确定性.则不确定函数为
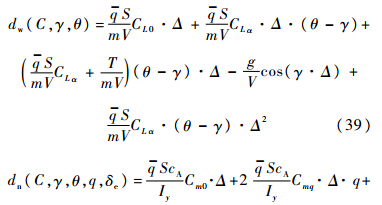
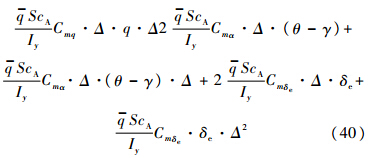
式中Δ=±10%.选取:
控制器参数:
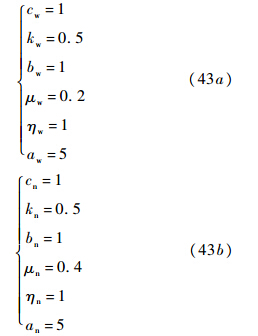
升降舵限幅δe≤25°,仿真结果如图 3所示.由图 3(a)和图 3(b)可知,采用本文控制方法设计的飞控系统可保证空投拉平阶段载机迅速的跟踪到指令值,且在短时间内使跟踪误差趋近于0,控制系统完全抑制了常值的模型摄动,表明控制器具有良好的动态跟踪性能.高度跟踪完全抑制了超调现象,保证了载机平稳地进入空投牵引区域.
 |
| 图 3 气动参数摄动和飞行状态测量误差为常值时的空投拉平仿真Fig. 3 Airdrop level off simulation with constant aerodynamic coefficients perturbation and flight states measurement errors |
| 图选项 |
由图 3(c)可知,升降舵偏转幅值满足系统要求(δe≤25°),但表现出一定程度的振荡现象.升降舵的振荡强度主要取决于边界层厚度的大小,一般μn,μw取值越大,升降舵偏转曲线就越缓和,系统收敛速度会提高,但轨迹跟踪的精度会变差;反之,μn,μw取值越小,升降舵的振荡就越严重,系统收敛速度会降低,但会提高轨迹跟踪的精度.实际空投拉平过程中,由地面效应和传感器测量误差引起的模型摄动以及外界大气扰动是变化的,因此令式(39)、式(40)中的不确定性Δ服从如下的均匀分布:仿真1:
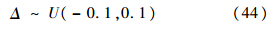
仿真2:
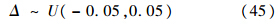
控制器参数同式(43),仿真结果如图 4所示.
 |
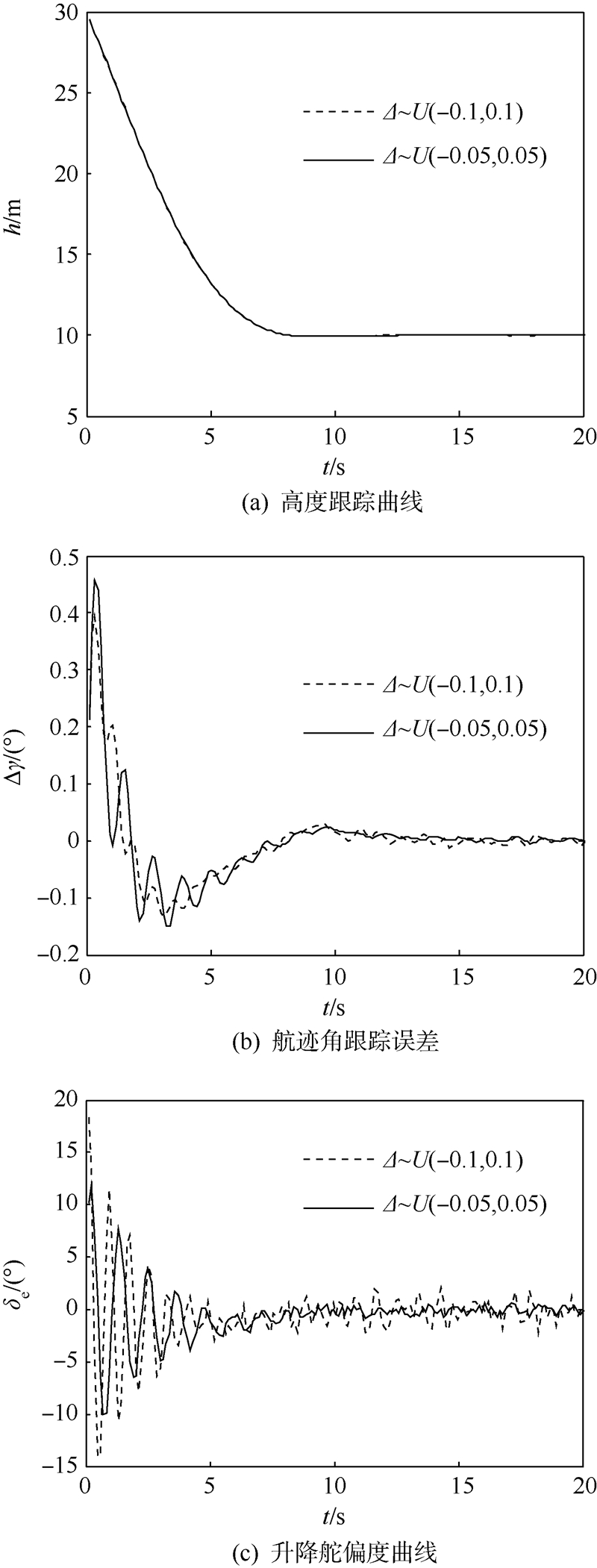| 图 4 气动参数摄动和飞行状态测量误差时变时的空投拉平仿真Fig. 4 Airdrop level off simulation with time-varying aerodynamic coefficients perturbation and flight states measurement errors |
| 图选项 |
由图 4(a)和图 4(b)可见,当气动参数摄动和状态测量误差时变时,航迹角跟踪误差限制在小邻域内,控制系统仍表现出良好的动态跟踪性能,保证载机平稳地进入空投牵引区域.图 4(c)显示升降舵快速切换,这对舵机性能提出了较高要求.仿真验证了设计的飞控系统对动态模型不确定性和扰动的强鲁棒性能.6 结 论1) 本文设计的二级混合迭代滑模变结构空投拉平控制律融合了全局滑模和积分滑模的优点,可保证控制系统在响应全程的鲁棒性,能够完全抑制常值(或最终为常值)的模型不确定性和外界扰动,可以控制动态模型不确定性和外界扰动下稳态跟踪误差的上界.通过常值气动参数摄动、常值飞行状态测量误差和动态气动参数摄动、动态飞行状态测量误差下的仿真实验,验证了控制律的强鲁棒性和良好跟踪性能.2) 基于余弦信号的空投拉平参考轨迹大大放宽了对运输机拉平能力的要求,并可根据任务性能约束灵活设计拉平时间.此外,余弦的收敛方式在拉平初期是平滑的,从而避免了舵面偏转速率过高的问题.3) 本文提出的控制方法和空投拉平参考轨迹可提高运输机在大风、降雨等恶劣气象条件下遂行超低空空投任务的安全性和任务完成性.
参考文献
| [1] | 李广义.国外大型军用运输机发展现状与趋势[J].航空制造技术,2005,12(9):36-43.Li G Y.Status and trends of the large foreign military cargo planes[J].Aeronautic Manufacturing Technology,2005,12(9):36-43(in Chinese). |
| Cited By in Cnki (14) | |
| [2] | Jann T.Coupled simulation of cargo airdrop from a generic military transport aircraft[C]//Proceedings of the 21st AIAA Aerodynamic Decelerator Systems Technology Conference.Reston,VA:AIAA,2011:1-20. |
| Click to display the text | |
| [3] | Dillenburger S P,Cochran J K,Cammarano V R.Minimizing supply airdrop collateral damage risk[J].Socio-Economic Planning Sciences,2013,47(1):9-19. |
| Click to display the text | |
| [4] | Henry M,Lafond K,Noetscher G.Development of a 2,000-10,000 lbs improved container delivery system[C]//Proceedings of the 20th AIAA Aerodynamic Decelerator Systems Technology Conference.Reston,VA:AIAA,2009:1-16. |
| Click to display the text | |
| [5] | Lee C.Low-cost high-altitude low-opening cargo airdrop systems[J].Journal of Aircraft,2012,49(1):349-354. |
| Click to display the text | |
| [6] | Qian J L,Dai C. Unsteady flow structure of an airfoil in ground effect[J].Journal of Shanghai University,2010,14(3):228- 234. |
| Click to display the text | |
| [7] | Molina J,Zhang X,Angland D.On the unsteady motion and stability of a heaving airfoil in ground effect[J].Acta Mechanica Sinica,2011,27(2):164-178. |
| Click to display the text | |
| [8] | Geisbauer S,Schade N,Enk S,et al.Experimental and numerical investigation of the flow topology during airdrop operations[C]//Proceedings of 21st AIAA Aerodynamic Decelerator Systems Technology Conference.Reston,VA:AIAA,2011:1-11. |
| Click to display the text | |
| [9] | 刘日,孙秀霞,董文瀚,等.大气扰动下运输机空投过程建模与仿真分析[J].飞行力学,2013,31(1):24-28.Liu R,Sun X X,Dong W H,et al.Modeling of flight dynamics and analyzing of simulationfor airdrop in atmospheric disturbance[J].Flight Dynamics,2013,31(1):24-28(in Chinese). |
| Cited By in Cnki (2) | |
| [10] | 张晶,申功璋,杨凌宇.基于逆动力学和重心估计的飞行控制系统设计[J].北京航空航天大学学报,2009,35(11):1315-1319.Zhang J,Shen G Z,Yang L Y.Design of flight control system based on inverse dynamics and center of gravity estimation[J].Journal of Beijing University of Aeronautics and Astronautics,2009,35(11):1315-1319(in Chinese). |
| Cited By in Cnki (10) | |
| [11] | 杨晓科,杨凌宇,张晶,等.变重量/重心飞机建模及姿态控制律设计[J].北京航空航天大学学报,2011,37(1):54-57.Yang X K,Yang L Y,Zhang J,et al.Modeling and attitude control of aircraft with variations in mass or center of gravity[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(1):54-57(in Chinese). |
| Cited By in Cnki (11) | |
| [12] | Zhang H Y,Shi Z K.Variable structure control of catastrophic course in airdropping heavy cargo[J].Chinese Journal of Aeronautics,2009,22(2):520-527. |
| Click to display the text | |
| [13] | 李大东,孙秀霞,董文瀚,等.基于线性化反馈的滑模变结构重装空投纵向控制律设计[J].控制理论与应用,2013,30(1):54-57.Li D D,Sun X X,Dong W H,et al.Pitch control for flight in heavy-weight airdrop based on feedback linearization theory and variable structure control[J].Control Theory & Applications,2013,30(1):54-57(in Chinese). |
| Cited By in Cnki (4) | |
| [14] | 申宇,仇原鹰.增益调度积分型切换项滑模控制器设计[J].系统工程与电子技术,2011,33(9):2079-2083.Shen Y,Qiu Y Y.Design of sliding-mode controller with gain-scheduling integral switched term[J].Systems Engineering and Electronics,2011,33(9):2079-2083(in Chinese). |
| Cited By in Cnki (2) | |
| [15] | 李大东,孙秀霞,董文瀚.考虑多种影响因素下的改进重装空投系统建模[J].系统工程与电子技术,2013,35(2):447-451.Li D D,Sun X X,Dong W H.Improved heavy-weight airdrop model considering many influence factors[J].Systems Engineering and Electronics,2013,35(2):447-451(in Chinese). |
| Cited By in Cnki (5) | |
| [16] | Luo Y,Yeh Y H,Ishihara A K. Adaptive backstepping design for a longitudinal UAV model utilizing a fully tuned growing radial basis function network[C]// AIAA Infotech at Aerospace Conference and Exhibit 2011.Reston,VA:American Institute of Aeronautics and Astronautics Inc,2011:1-23 |
| Click to display the text |
