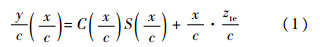
式中:x/c为翼型弦向的无量纲坐标值;C(x/c)和S(x/c)分别称为类别函数和形状函数;zte/c为后缘点的初始位置.C(x/c)一般可表示为
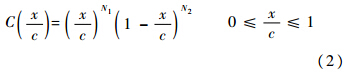
式中:指数N1和N2的取值决定了几何外形的基本特征,对于翼型,取N1=0.5,N2=1.S(x/c)通常由n阶Bernstein多项式加权作为形状函数表达式:
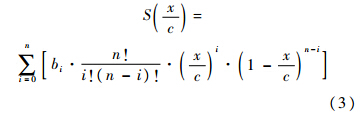
式中:bi为第i阶Bernstein多项式系数.翼型前缘半径和后缘点处切线倾角与形状函数在区间[0,1]端点处的极限值存在以下关系:
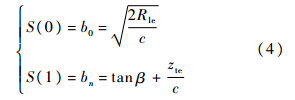
翼型几何控制参数的定义如图 1所示.
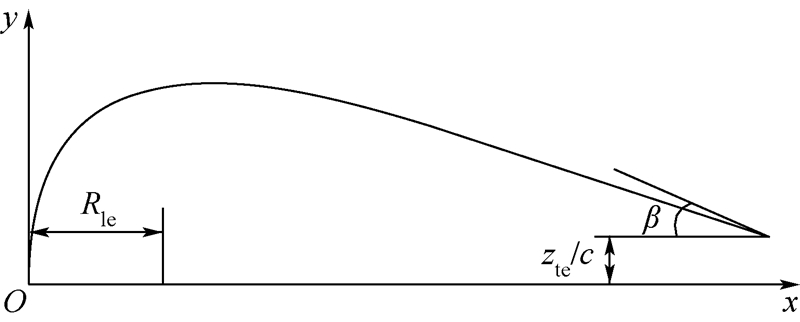 |
| Rle—翼型前缘半径;β—上表面曲线在后缘处切线倾角;zte/c—后缘点的初始位置.图 1 翼型几何控制参数Fig. 1 Parameters for airfoil geometry control |
| 图选项 |
对于优化问题,为减小设计变量数目,Bernstein多项式的阶数应该尽可能低.三阶Bernstein多项式的最大拟合误差在2.5×10-4左右,可以很好地逼近原始翼型[10].因此,本文采用三阶Bernstein多项式对NACA0012翼型进行拟合,拟合结果如图 2所示.
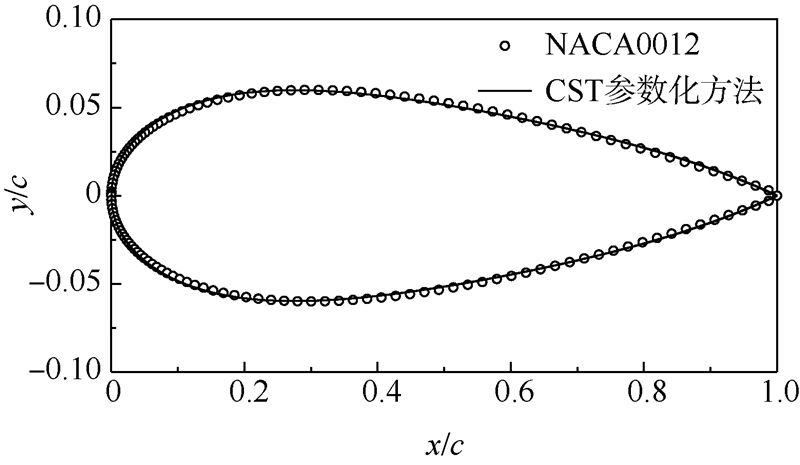 |
| 图 2 NACA0012翼型的拟合结果Fig. 2 Fitting result for NACA0012 airfoil |
| 图选项 |
初始翼型的参数化建模完成后,为实现后缘的连续光滑变形,这里引入变形参数xm/c和Δzte/c.其中,xm/c表征后缘变形的弦向起始位置,Δzte/c表示后缘点的变形距离.图 3所示为可变后缘操纵面简化模型.
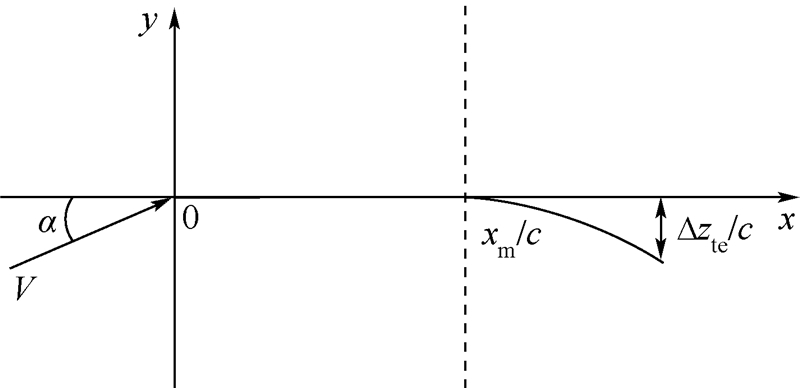 |
| 图 3 可变后缘操纵面简化模型Fig. 3 Simplified model for the control surface of deformable trailing edge |
| 图选项 |
图 3中的曲线作如下定义:
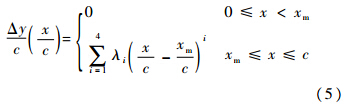
已有研究表明,二阶曲线所表示的变后缘翼型不仅具有良好的气动特性,而且变形时所需的驱动能相对较小[11],故本文选择二阶曲线来表示后缘的几何变形.结合图 3所示的连续光滑变形边界条件,可计算得:
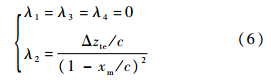
将式(1)中用CST方法得到的初始翼型曲线与式(5)中的变形曲线相结合,得到可变后缘翼型曲线ym/c,定义为
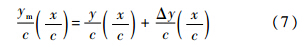
图 4所示为xm/c=0.6及Δzte/c=-0.05时翼型后缘的变形情况.
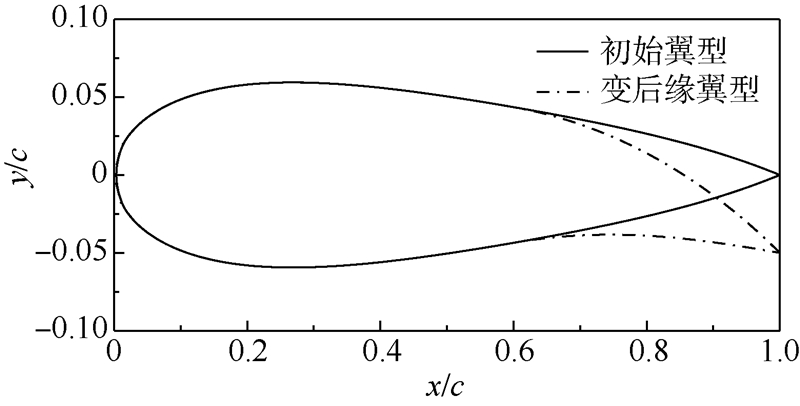 |
| 图 4 可变后缘翼型示意图Fig. 4 Schematic diagram of airfoil with deformable trailing edge |
| 图选项 |
2 网格生成和流场求解 气动系数的计算应用CFD软件FLUENT完成,网格采用如图 5所示的C型结构网格.利用标准k-ε湍流模型和二阶迎风格式进行气动求解.以Ma=0.798,α=3.0243°,Re=6.0×106条件下的NACA0012翼型来检验气动分析的结果.图 6给出了翼型压力系数Cp分布的计算结果和风洞试验结果[12]的对比,可见计算结果与风洞试验结果基本吻合,说明本文的气动分析是准确的.
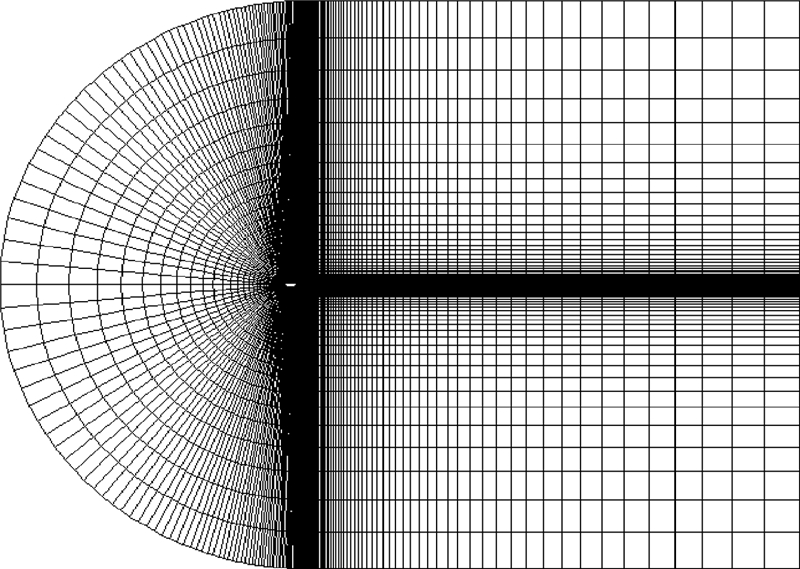 |
| 图 5 C型结构网格Fig. 5 C-type structured grid |
| 图选项 |
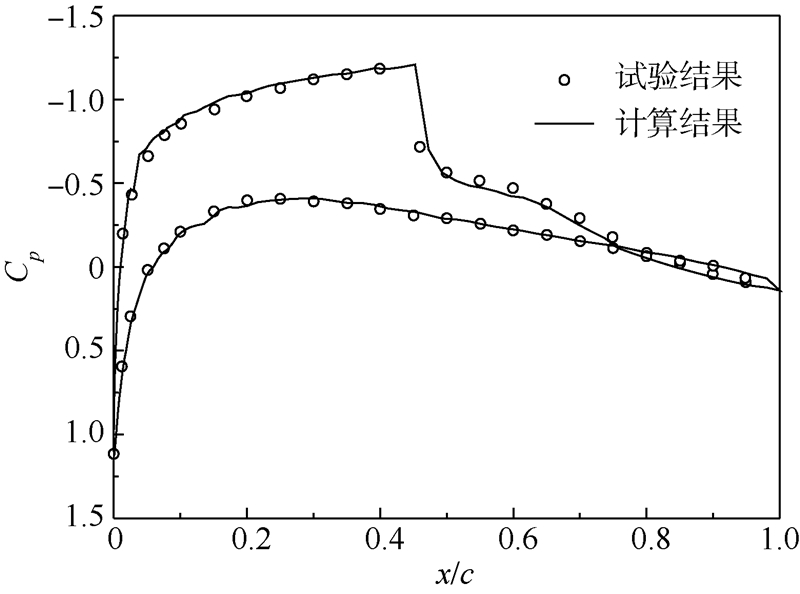 |
| 图 6 压力分布计算结果和试验结果的对比Fig. 6 Comparison of pressure distribution between experiment and CFD |
| 图选项 |
3 优化设计方法 3.1 确定性优化设计方法确定性优化设计方法是在给定的飞行条件下,在设计变量区间内寻找满足约束条件的气动外形最优解.可变后缘翼型由于后缘几何外形的改变,其升力系数CL和阻力系数CD波动明显[13].因此,选取反映综合气动特性的升阻比K作为优化对象,确定性优化目标是在给定马赫数和迎角条件下尽可能提高翼型的升阻比K. 3.2 鲁棒性优化设计方法鲁棒性优化设计方法可以使翼型在一系列的飞行条件下保持足够稳定的气动特性.鲁棒性优化目标是要在给定的马赫数变动区间内,尽可能提高所设计翼型的升阻比,同时尽可能减小升阻比的变动范围.鲁棒性优化模型为

式中:φ为翼型几何形状的设计变量;φ0为设计空间;G(φ)为翼型的几何形状;G0为翼型的几何约束条件;Ma和Ma分别为来流马赫数的下界和上界.翼型气动特性求解过程的非线性程度很高,而且计算量大,要得到式(8)中升阻比均值μ和标准差σ的真实结果非常困难.鉴于此,本文在优化设计过程中采用蒙特卡罗法对马赫数进行随机抽样,再利用样本集的统计预测值来代替均值和标准差的真实值[14].

式中:Ns为试验次数;Mai(Ma≤Mai≤Ma)为第i次抽样试验时所对应的马赫数. 3.3 基于代理模型的遗传算法遗传算法是模拟生物在自然环境中遗传和进化过程而形成的一种自适应全局优化概率搜索算法[15],其优点是不依赖于问题的具体区域,对问题的种类具有很强的鲁棒性.由于遗传算法会产生庞大的计算量,为了提升优化效率,一般可以采用代理模型计算个体的适应度值.文献[16]对多项式响应面模型、径向奇函数模型和Kriging模型的预测情况进行了比较,认为Kriging模型的预测精度最好,并且对于非线性问题能够提供较为精确的逼近效果,适合本文中可变后缘翼型的鲁棒性优化.此外,采用均匀设计方法[17]来选取能够全面代表整体空间的代理模型样本点. 3.4 鲁棒性优化过程综上,可变后缘翼型的鲁棒性优化设计流程如图 7所示.
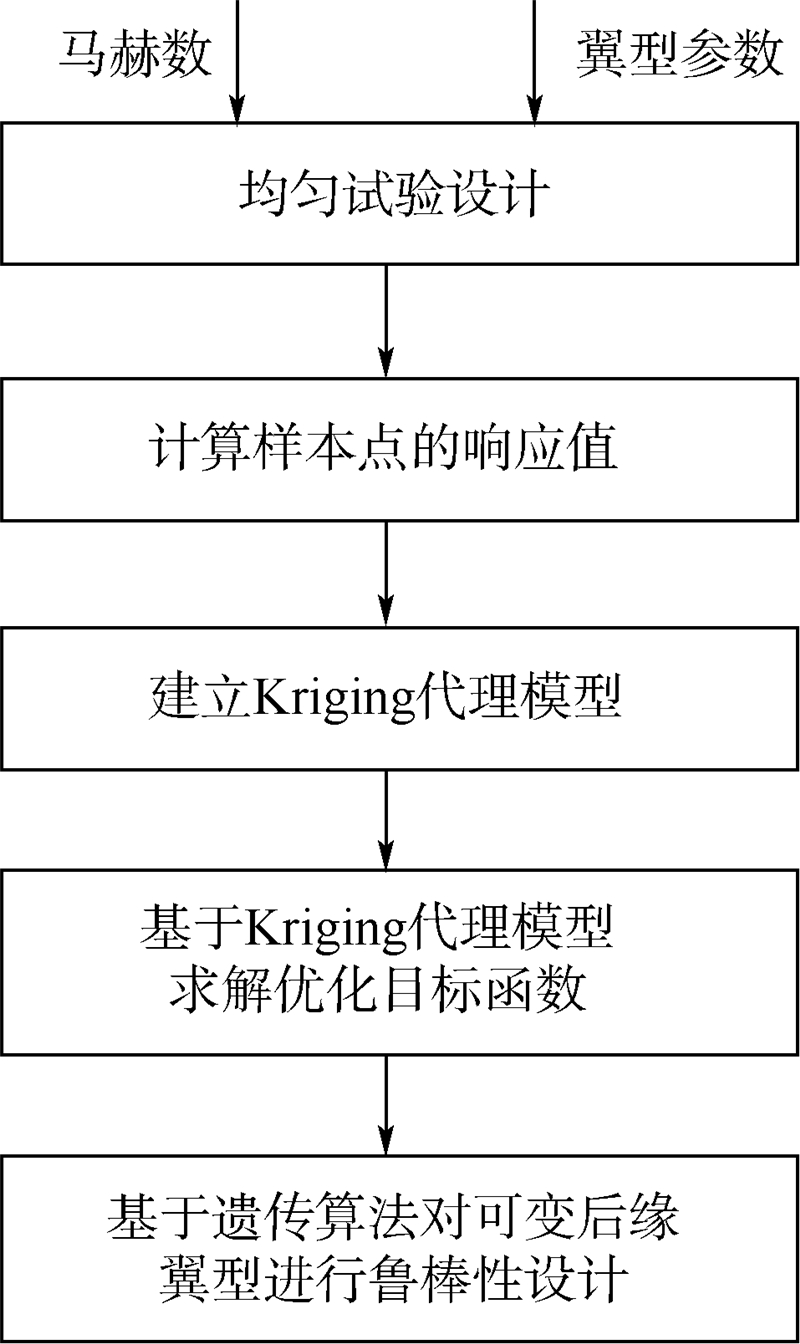 |
| 图 7 翼型鲁棒优化设计流程图Fig. 7 Flow chart of robust airfoil optimization |
| 图选项 |
4 算例及结果分析 4.1 算 例 本文以NACA0012为初始翼型,设计变量为(Rle/c,β1,β2,zte/c,b1,b2,b′1,b′2,xm/c,Δzte/c),其中β1和β2分别表示翼型上下表面曲线的后缘处切线倾角,分别为上下表面曲线的Bernstein多项式系数.为方便表示,这里引入变量φ,令φ=(φ1,φ2,…,φ10)=(Rle/c,β1,…,Δzte/c).变量φ的取值范围如下:

约束条件为翼型最大厚度tmax/c≤0.12.优化过程中将φ1~φ9作为全局变量,φ10则作为局部变量随马赫数变化.由于马赫数对气动特性的影响在跨声速区内表现得最为明显,因此假定马赫数在[0.7,0.8]之间均匀分布[18].遗传算法的控制参数设定为:种群规模(80),交叉概率(0.9),变异概率(0.1),最大进化代数(150).对于确定性优化,将Ma=0.75,α=3°作为设计点;对于鲁棒性优化,由于涉及多个目标,这里引入权重系数w,将多目标优化问题转化为单目标优化问题,如式(12)所示.权重系数w决定了搜索方向,设定不同的权值,可以得到权值变化时的Pareto前沿[19].
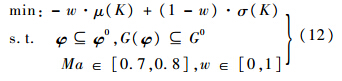
4.2 优化结果分析 图 8所示为确定性优化翼型与初始翼型NACA0012的压力分布和几何外形对比,可以看出优化后翼型具有良好的气动特性.翼型前后缘均产生较大的升力,从而降低了由于后缘变形所引起的附加低头力矩.上表面最大厚度位置向后移动,翼型前半部分变得相对平坦,激波位置后移,强度减弱,这使得优化后翼型具有较高的升阻比.
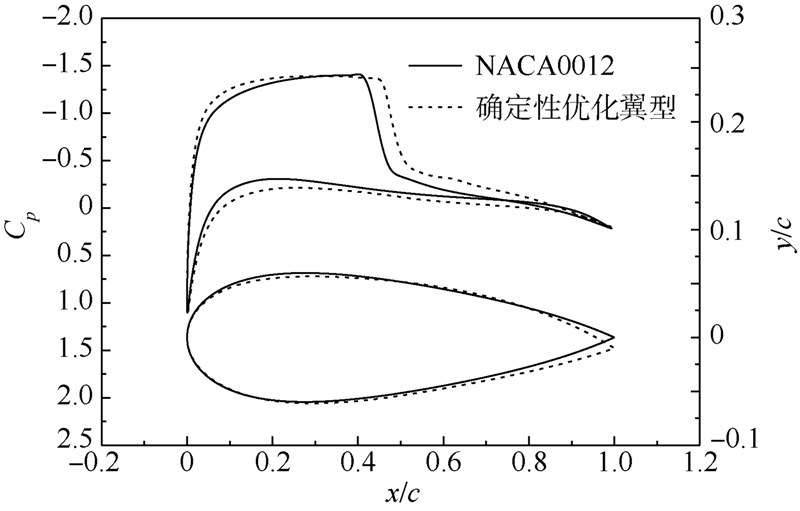 |
| 图 8 翼型外形和压力分布对比Fig. 8 Geometry profile and pressure distribution comparison |
| 图选项 |
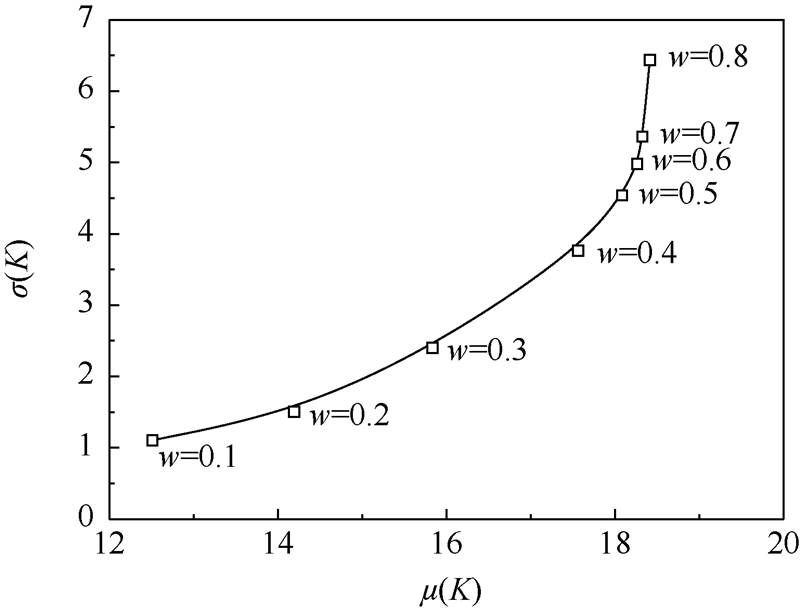
图 9反映了鲁棒性优化结果的Pareto前沿.可以看出当w≤0.3时翼型升阻比的均值较低,气动性能较差;当w≥0.5时翼型升阻比在整个马赫数区间内波动较大,缺乏持续稳定性.相比而言,w=0.4时翼型升阻比的均值保持在17.5左右,远大于w≤0.3时优化结果,且其标准差与w≥0.5时的翼型相比较小,在马赫数持续增大时升阻比的变化较小,能够保持稳定的气动特性,故将其作为本文的鲁棒性优化结果.
 |
| 图 9 权重系数变化时的Pareto前沿Fig. 9 Pareto front varied with weight coefficient |
| 图选项 |
同时,为综合评价可变后缘翼型的设计性能,这里考虑比较后缘连续变形时所需输入的驱动能.从二元可变后缘翼型的气动弹性方程出发,可以推导出驱动能的计算公式[20]为

式中:Δp表示变形前后翼型的表面压力增量;Δy为式(5)所表示的后缘变形曲线.计算翼型后缘连续变形所需驱动能的外界条件为:Ma=0.75,P∞=43765Pa,c=1m.表 1给出了确定性优化翼型、鲁棒性优化翼型(w=0.4)与初始翼型的性能对比.表 1 确定性优化与鲁棒性优化结果比较Table 1 Comparison between deterministic optimization and robust optimization
| 翼型 | μ(K) | σ(K) | xm/c | Δzte | ΔE/J |
| NACA0012 | 14.4129 | 4.3406 | |||
| 确定性翼型 | 17.4048 | 4.9497 | 0.5040 | -0.0113 | 1.3833 |
| 鲁棒性翼型 | 17.5594 | 3.5625 | 0.5370 | -0.0121 | 1.0685 |
表选项
从表 1可以看出,鲁棒性优化翼型升阻比的均值相比于确定性优化翼型有一定程度提升,而标准差有明显的减少,这表明鲁棒设计获得了更稳健的解.从能量角度分析,鲁棒性优化翼型所需的驱动能较小,综合性能更优.因此,不论是考虑气动特性,还是结合能量特性,鲁棒性优化结果均优于确定性优化结果.图 10所示为优化翼型与初始翼型的升阻比随来流马赫数的变化情况.由图 10可知,无论是在设计点还是非设计点上,确定性优化对初始翼型都有很大改善.鲁棒性设计结果对翼型升阻比的改善则表现为当马赫数在一定范围内变化时,升阻比的变化平缓,气动性能更加稳定.虽然鲁棒性优化翼型在设计点附近的性能与确定性结果相比有所下降,但升阻比的变化范围相对较小,而且当马赫数变化时没有出现非设计点性能急剧恶化的情况,实现了可变后缘翼型鲁棒设计目标.
 |
| 图 10 翼型升阻比随马赫数的变化Fig. 10 Lift to drag ratio varied with Mach number |
| 图选项 |
图 11给出了原始翼型与Ma=0.75时各优化翼型的几何形状对比.可见,无论是确定性优化还是鲁棒性优化,翼型后缘均有明显的连续光滑变形,使得后缘产生了更大的升力.相对而言,鲁棒性优化得到的翼型最大厚度位置较确定性优化稍稍前移,导致激波强度较确定性优化稍微偏大,波阻增加,这正是设计点处确定性优化翼型具有较大升阻比的原因.
 |
| 图 11 翼型几何形状对比Fig. 11 Comparison of airfoil geometry shape |
| 图选项 |
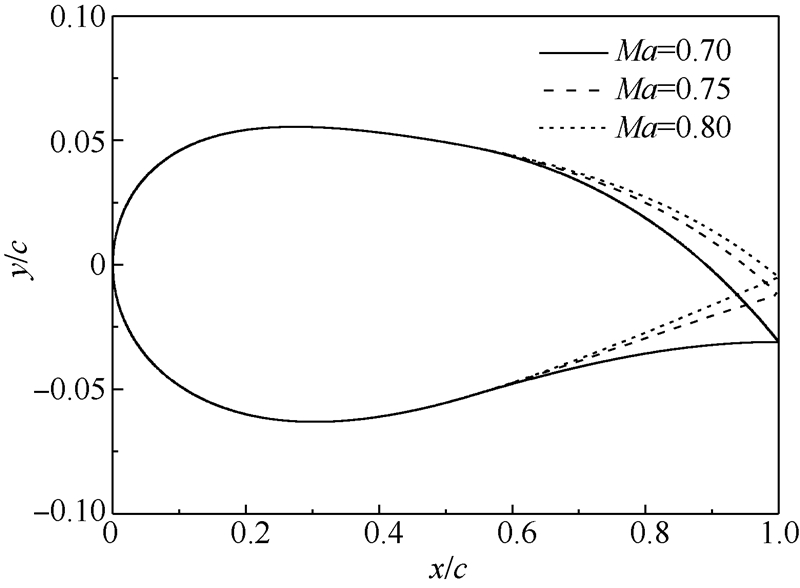
图 12所示为鲁棒性优化翼型几何形状随马赫数的变化情况.可以看出,当马赫数较小时,翼型后缘变形量较大,由后缘所产生的附加升力使翼型升阻比得到改善.但是,随着马赫数的升高,翼型升力增加的同时会使诱导阻力急剧增大,因此翼型后缘变形量将逐渐减少,以保持足够稳定的升阻比.
 |
| 图 12 鲁棒性翼型几何形状随马赫数的变化Fig. 12 Robust airfoil geometry shape varied with Mach number |
| 图选项 |
从图 12中也可以发现鲁棒优化得到的翼型上表面更加平坦,下表面后缘有明显的上凹区域,具有超临界翼型特性,这也是鲁棒性优化翼型在跨声速范围内保持良好气动性能的原因. 5 结 论1) 在CST参数化建模方法基础上引入变形控制参数,可以实现用较少的设计变量表达变后缘翼型的气动外形,使得用遗传算法进行翼型优化设计成为可能.2) 可变后缘翼型的优化结果表明,后缘的连续光滑变形改善了翼型的气动性能,而采用加权法处理多目标鲁棒优化问题,很好地均衡了性能优化和鲁棒性要求,在保持气动性能的基础上又改善了性能的稳定性.3) 与确定性优化翼型相比,鲁棒性优化翼型后缘变形量将随马赫数变化,并且在相同马赫数条件下变形所需的驱动能更低.
参考文献
| [1] | Stanewsky E.Aerodynamic benefits of adaptive wing technology[J].Aerospace Science Technology,2000,4(7):439-452. |
| Click to display the text | |
| [2] | Smith J W,Lock W P,Payne G A.Variable-camber systems integration and operational performance of the AFTI/F-111 mission adaptive wing[M].Edwards:National Aeronautics and Space Administration,Office of Management,Scientific and Technical Information Program,1992:1-3. |
| [3] | De Gaspari A,Ricci S.Combining shape and structural optimization for the design of morphing airfoils[C]//2nd International Conference on Engineering Optimization.Lisbon:ENGOPT,2010:6-9. |
| Click to display the text | |
| [4] | 陈钱,白鹏,尹维龙,等.可连续光滑偏转后缘的变弯度翼型气动特性分析[J].空气动力学学报,2010,28(1):46-53. Chen Q,Bai P,Yin W L,et al.Analysis on the aerodynamic characteristics of variable camber airfoils with continuous smooth morphing trailing edge[J].Acta Aerodynamica Sinica,2010,28(1): 46-53(in Chinese). |
| Cited By in Cnki (20) | |
| [5] | Luckring J M,Hemsch M J,Morrison J H.Uncertainty in computational aerodynamics,AIAA-2003-0409[R].Reston:AIAA,2003. |
| [6] | Huyse L,Padula S L,Lewis R M,et al.Probabilistic approach to free-form airfoil shape optimization under uncertainty[J].AIAA Journal,2002,40(9):1764-1772. |
| Click to display the text | |
| [7] | Padulo M,Campobasso M S,Guenov M D.Novel uncertainty propagation method for robust aerodynamic design[J].AIAA Journal,2011,49(3):530-543. |
| Click to display the text | |
| [8] | Kaul U K,Nguyen N T.Drag optimization study of variable camber continuous trailing edge flap(VCCTEF)using OVERFLOW,AIAA-2014-2444[R].Reston:AIAA,2014. |
| [9] | Kulfan B M,Bussoletti J E.“Fundamental”parametric geometry representations for aircraft component shapes,AIAA-2006-6948[R].Reston:AIAA,2006. |
| [10] | Kulfan B M. Universal parametric geometry representation method[J].Journal of Aircraft,2008,45(1):142-158. |
| Click to display the text | |
| [11] | Forster E,Sanders B.Modeling and sensitivity analysis of a variable geometry trailing edge control surface,AIAA-2003-1807[R].Reston:AIAA,2003. |
| [12] | Ladson C L,Hill A S,Johnson Jr W G.Pressure distributions from high Reynolds number transonic tests of an NACA 0012 airfoil in the Langley 0.3-meter transonic cryogenic tunnel,NASA-TM-100526[R].Washington,D.C.:NASA Langley Research Center,1987. |
| [13] | Andersen P B,Gaunaa M,Bak C,et al.A dynamic stall model for airfoils with deformable trailing edges[J].Wind Energy,2009,12(8):734-751. |
| Click to display the text | |
| [14] | 柳杨,邱志平. 翼型气动性能鲁棒性优化设计[J].北京航空航天大学学报,2011,37(1):41-44. Liu Y,Qiu Z P.Airfoil robust design with uncertainty parameters[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(1):41-44(in Chinese). |
| Cited By in Cnki (3) | |
| [15] | Whitley D. A genetic algorithm tutorial[J].Statistics and Computing,1994,4(2):65-85. |
| [16] | 穆雪峰,姚卫星,余雄庆,等.多学科设计优化中常用代理模型的研究[J].计算力学学报,2005,22(5):608-612. Mu X F,Yao W X,Yu X Q,et al.A survey of surrogate models used in MDO[J].Chinese Journal of Computational Mechanics,2005,22(5):608-612(in Chinese). |
| Cited By in Cnki (190) | |
| [17] | 方开泰. 均匀设计与均匀设计表[M].北京:科学出版社,1994:2-9. Fang K T.Uniform design and uniform design table[M].Beijing:Science Press,1994:2-9(in Chinese). |
| [18] | 丁继锋,李为吉,张勇,等.基于响应面的翼型稳健设计研究[J].空气动力学学报,2007,25(1):19-22. Ding J F,Li W J,Zhang Y,et al.Robust airfoil optimization based on response surface method[J].Acta Aerodynamica Sinica,2007,25(1):19-22(in Chinese). |
| Cited By in Cnki (23) | |
| [19] | Zingg D W,Elias S.Aerodynamic optimization under a range of operating conditions[J].AIAA Journal,2006,44(11):2787-2792. |
| Click to display the text | |
| [20] | Forster E,Sanders B,Eastep F.Synthesis of a variable geometry trailing edge control surface,AIAA-2003-1717[R].Reston:AIAA,2003. |
