可修复件是指故障或损坏后,采用经济可行的技术手段修理,能恢复其原有功能的备件,主要指供修理周转的外场可更换件(Line Replaced Unit,LRU)和内场可更换件(Shop Replaced Unit,SRU).舰载机上可修复件数量较大且占据了绝大部分的备件保障经费,可修复件大多直接关系到舰载机可用度,实践证明,贵重件的修复,不仅可以节约维修资源和费用,而且对提高装备可用性有着重要的作用^{[1, 2]}.可修复件通常具有较长的订货间隔期,储备一定数量的可修复件对于保持舰载机的可用性具有积极的意义^{[3, 4]}.可修复件多级库存的理论基础是Palm于1938年提出的排队论和Sherbrooke以Palm定理为基础提出的Metric模型^[5],以及Slay提出、Sherbrooke完善的Vari-Metric模型^{[6, 7]}.以上模型均基于“无限渠道排队”假设,即:维修能力无限大.但在装备保障实践中,这一假设并不完全符合实际.针对Metric模型假设的不精确性,文献^[8]建立了修理时间服从指数分布的有限服务者模型,将推导出的满足率和短缺数模型与无限维修渠道进行比较,得出了更准确的模型;文献^{[9, 10]}基于M/M/c排队模型研究了多级可修复件的库存配置;文献^[11]综合利用M/M/c和M/G/c模型对有限维修渠道两级库存系统进行了研究;文献^[12]基于有限维修渠道建立了单项可修复件库存整数规划模型;文献^[13]在服务能力约束下,研究了备件订购问题;文献^[14]对维修能力受限的k/N系统备件库存优化模型进行了研究;文献^[15]针对有限维修能力对Vari-Metric进行了适用性修改;文献^[16]在有限维修渠道约束下,对故障件维修周转时间和供应渠道进行了修正;文献^[17]按照三级维修保障策略,建立了有限维修渠道下的备件库存模型.受经费、物理条件等因素限制,舰载机是“有限维修渠道”下的有限能力维修保障,不符合Metric理论所要求的“无限维修渠道”假设.为此,在以上文献研究的基础上,对Metric模型进行适用性扩展,建立舰载机有限维修渠道下的备件库存配置优化模型,以提高舰载机供应保障和持续作战能力.1 问题分析和优化思路1.1 问题分析海军舰载机实行三级维修模式:舰员级、中继级和基地级.舰员级以换件维修为主;中继级主要进行组件级维修;基地级提供全面维修保障.航母编队任务期内,若舰载机发生故障,则拆换故障LRU,送母舰中继级维修,并向供应部门申请LRU.若有库存,则发出一件完好LRU;否则,发生一次备件短缺.中继级部门确定故障LRU是否可修,如果可修,则进行修理,并在修复完成后发到供应部门.供应部门若有短缺,则利用此修复的LRU补充短缺;若无短缺,则储存在供应部门.如果故障件超过中继级维修能力,则发往后方基地,同时向基地申请对该LRU补给.延迟某时间段后,母舰供应部门将收到补给件.设故障LRU仅因一件SRU所致,在母舰中继级维修的故障LRU,如果母舰有该SRU库存,就将其安装到故障LRU上替换故障SRU.若母舰中继级不具备修理此SRU能力,则发往后方基地,同时提出补给申请.如果基地有库存,则补充一件该SRU到母舰;若无库存,则发生补给延误.可修复件的修理和补给延误具有不确定性,假设服从某概率分布.舰载机保障中,舰员级和中继级处于母舰上,共享库存.将舰员级和中继级看作基层站点,则舰载机是两级保障,其备件需求和故障件送修过程如图 1所示.

图 1 备件需求和故障件送修过程Fig. 1 Spare requirement and spares maintenance process

图选项

1.2 优化思路Palm定理假设“无限渠道排队”,舰载机维修是“有限渠道排队”.前者是M/G/∞模型,维修时间相互独立同分布,后者是M/M/c模型,维修时间相互影响.为利用Palm定理,舰载机维修必须符合M/G/∞模型.对比分析两个模型,已知后者中的负指数分布M是前者中一般分布G的特殊形式,问题的关键是将后者中的有限渠道c转换等效于前者中的无限渠道∞.已知M/M/c模型中,在服务强度小于1的情况下,M/M/c模型具有稳定的服务时间,各个故障件逗留时间服从同一均值概率分布,将此逗留时间看作故障件在系统中的平均维修服务时间,相当于具有无限维修渠道,则M/M/c模型可近似于M/G/∞模型.基于排队论,对舰载机有限维修渠道,求取其系统平均排队等待时间W_i,将其与系统平均维修时间T_i加和,得到备件在维修系统中的平均逗留时间T′_i,可将T′_i等效为备件在舰载机维修渠道中的平均服务时间,从而将M/M/c模型等效为M/G/∞模型.即舰载机维修系统转换为:维修时间服从一般分布,维修渠道无限,平均服务时间为T′_i,从而适用Palm定理.1.3 模型假设为简化分析,对模型作如下假设:①任务期间,舰载机任务安排均匀,备件需求服从Poisson分布;②备件是否在某机构修理与库存量或修理工作量无关,由修理机构修理能力决定;③不允许横向供应,上级机构对下级进行补给;④不同部件故障发生、维修相互独立,故障件修复如新;⑤不同故障部件具有相同重要度,缺件均导致舰载机停飞;⑥故障件维修和补给过程采取先到先供应、先到先维修策略;⑦各站点采取连续检查的(s-1,s)库存策略;⑧后方保障基地具备全部维修保障能力,可以对所有备件项进行维修.2 维修渠道维修时间修正舰载机维修一般包括专用渠道和通用渠道,下面分别就专用维修渠道、通用维修渠道和两者结合的混合维修渠道展开分析.2.1 专用维修渠道时间修正专用维修渠道(见图 2)是指由只提供对特定类型故障件维修的若干保障资源(包括维修检测设备、维修保障人员等)结合而成的、具有特定功能的有机整体.

图 2 专用维修渠道Fig. 2 Special repair channel

图选项

这是一个专用型多顾客源多服务台系统,符合M/M/c模型,站点j备件项i平均需求率为m_ij,本地维修率为r_ij;系统有c_ij个相互独立的维修渠道且平均服务率均为μ_ij=1/T_ij.设x为专用维修渠道中的平均故障件数,则整个维修机构的平均服务率为c_ijμ_ij(x≥c_ij),或xμ_ij(x≤c_ij).当m_ijr_ij/(c_ijμ_ij)<1时,维修渠道服务强度为
由M/M/c模型可得专用维修渠道的状态概率:

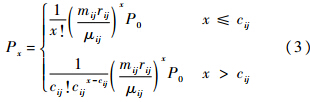
式中:P₀为维修渠道状态为0的概率;P_x为维修渠道状态为x的概率.系统平均队长L_ij和系统中等待队长Q_ij分别为
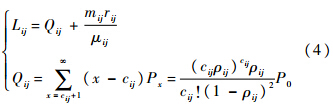
故障件在系统中的平均等待时间W_ij和停留时间T′ij为
2.2 通用维修渠道时间修正通用维修渠道(见图 3)是指由可以提供对多种类型故障件维修的若干保障资源(包括维修检测设备、维修保障人员等)组合而成的、具有特定功能的有机整体.通用维修渠道对结构特征、功能特征和故障类型相似的多项故障件进行维修,这些故障件的维修流程、维修复杂程度、维修所需时间具有相似性;并且,故障件在通用维修渠道中的等待维修时间需要考虑通用维修渠道中的所有类型故障件的修理时间和到达率.因此,通用维修渠道修正思路类似专用维修渠道,在对通用维修渠道故障件到达率和服务率修正的基础上将多项备件转换为单项备件近似处理.

图 3 通用维修渠道Fig. 3 General repair channel

图选项

这是一个通用型多顾客源多服务台系统,系统符合M/M/c模型,可以对k项不同备件提供维修服务,系统中备件项i到达率为m_ijr_ij,系统总的到达率 M_j=∑m_ijr_ij，则备件项i所占比例为
系统有K_j个相互独立的维修渠道,每个维修渠道对备件项i的平均服务时间为T_ij,服务率为μ_ij=1/T_ij,对所有备件项的平均服务时间和平均服务率分别为

则整个维修机构的平均服务率为K_jμ_j(x≥K_j),或xμ_j(x≤K_j),x为通用维修渠道中所有类型故障件总的平均故障件数.当M_j/(K_jμ_j)<1时,维修渠道服务强度为
求得系统整体的到达率和平均服务率后,转换为单项备件排队系统分析,则通用维修渠道的状态概率为


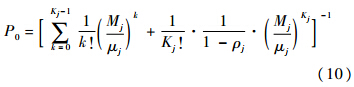
系统平均队长L_j和系统中等待队长Q_j分别为
故障件在系统中的平均等待时间W_j和停留时间T′_j分别为
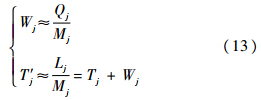
2.3 混合维修渠道时间修正航空母舰一般配置多型舰载机,舰载机科技含量高,结构复杂,航材备件的修复有可能需要专用和通用维修设备设施的共同协作才能完成故障件修复.混合维修渠道是专用维修渠道和通用维修渠道的综合集成,可以看作是一个多阶段维修过程.混合维修渠道模型的修正基于专用和通用维修渠道的修正,在各阶段内部,分布按照各自的修正方法进行;混合维修渠道模型需要特别关注和改变的是故障件到达率的修正,即本阶段故障件到达率是基于前一阶段修复率.下面,主要对到达率进行修正.假设系统为混合维修渠道是两阶段维修系统,第1阶段是专用维修渠道对故障件处理,将初步处理后的需要进一步处理的故障件送入第2阶段的通用维修渠道,直至修复完成,如图 4所示.

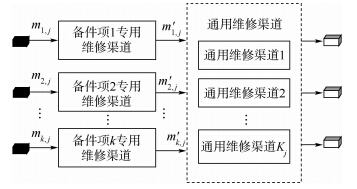图 4 混合维修渠道1Fig. 4 Combined repair channel one

图选项

由专用维修渠道分析,得到备件项i第1阶段修复完成率为
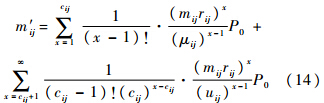
将m′_ij作为备件项i第2阶段维修渠道的到达率,第2阶段k项备件总的到达率 M_j=∑m′_ij. 假设第2阶段有K_j个相互独立的维修渠道,每个维修渠道对备件项i的平均服务时间为T_ij,服务率μ_ij=1/T_ij,对所有备件项的平均服务时间和平均服务率分别为

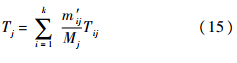
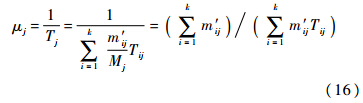
第2阶段通用维修渠道系统的平均服务率为K_jμ_j(x≥K_j),或xμ_j(x≤K_j),x为通用维修渠道中所有类型故障件总的平均故障件数.当M_j/(K_jμ_j)<1时,依据通用维修渠道修正方法,即可得到混合维修渠道的修正结果.混合维修渠道的另一种模式为先进行通用维修渠道处理,在通用维修渠道处理完成后,进入专用维修渠道处理,如图 5所示.根据前述通用维修渠道模型,得到备件项i第1阶段修复完成率为

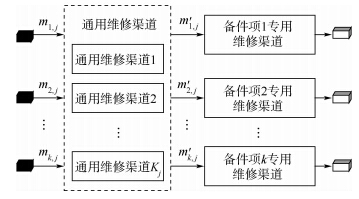图 5 混合维修渠道2Fig. 5 Combined repair channel two

图选项

由得到的m′_ij作为备件项i第2阶段维修渠道的到达率,依据专用维修渠道修正方法,在第2阶段各专用维修渠道服务强度小于1时,得到混合维修渠道的修正结果.对于其他形式的混合维修渠道,可以综合利用以上模型进行分析求解.3 供应渠道备件件数修正维修渠道有限时,舰载机备件供应渠道由以下4部分构成:①供应渠道无短缺时,故障件在修或补给的件数.②因维修渠道有限,排队等待修理的件数.③因上级保障机构库存短缺而造成补给延误的件数.④因本站点缺少维修所需下层级子备件而延误修理的件数.综合以上分析,得出站点j备件项i供应渠道修正后的均值和方差,文中考虑LRU和SRU两层备件,假设SRU下层级备件SSRU供应充足.则LRU供应渠道修正后的均值和方差为

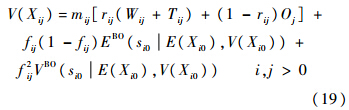
式中:下标0j为站点j的LRU备件项;下标00为站点j的上级保障站点;O_j为站点j申请交付平均时间;f_0j为上级站点LRU短缺造成站点j补给延误的比例;s为库存量;E^BO为备件期望短缺数;V^BO为备件短缺数方差.SRU供应渠道修正后的均值和方差为

式中:下标ij为站点j的SRU_i备件项;下标i0为站点j的上级保障站点;f_ij为SRU短缺造成对站点j补给延误的比例.修正后的备件期望短缺数E^BO和短缺数方差V^BO为


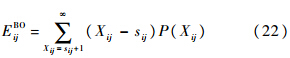
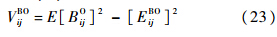
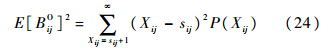
式中:P(X_ij)为备件供应渠道数量的稳态概率分布;B^O为备件短缺数.若供应渠道差均比为1,取泊松分布;若供应渠道差均比大于1,取负二项分布;若供应渠道差均比小于1,取二项分布.4 应用分析在舰载机装备维修中,维修能力有限是普遍存在的,经过对有限维修渠道的修正,使其适用Palm定理.基于上述研究,对舰载机有限维修渠道与无限渠道假设下的备件库存进行对比研究,分析验证有限维修渠道修正模型的应用效果和Palm定理在备件配置中的适用性.设有两个相同的航母战斗群,两者均配备舰载机20架,具有相同的任务安排和维修能力.假设舰载机由备件LRU₁和LRU₂组成,LRU₁由SRU₁₁和SRU₁₂组成,LRU₂由SRU₂₁和SRU₂₂组成.以专用维修渠道为例,对有限维修渠道的修正模型进行应用分析.基本数据见表 1.表 1 备件基本数据Table 1 Basic parameters of spares

备件项	需求率/(件·天-1)		基层级 平均维修 时间/天	隔离率q	维修率r	平均送修时间/天		基地 需求率/ (件·天-1)	基地 平均维修 时间/天	单价/ 万元	安装数/件
	站点1	站点2				站点1	站点2
LRU1	1.500	1.500	0.6		0.8			0.60	0.3	100	2
LRU2	1.200	1.300	0.5		0.7			0.75	0.2	120	1
SRU11	0.600	0.600	3.0	0.5	0.6	15	10	0.78	1.0	50	1
SRU12	0.600	0.600	4.0	0.5	0.5			0.90	2.0	50	2
SRU21	0.504	0.546	4.0	0.6	0.5			0.975	2.0	50	1
SRU22	0.336	0.364	4.0	0.4	0.5			0.65	2.0	70	1

表选项


4.1 维修时间分析由于维修系统中维修渠道数量有限,待修复故障件在维修系统中逗留时间为实际维修时间和等待维修时间之和.根据表 1数据,运用前述有限维修渠道模型修正方法,对维修时间进行修正.表 2给出不同有限维修渠道方案约束下各站点的维修时间修正值,其中维修渠道方案1~3代表各项备件维修渠道维修设备的配置方案.由表 2数据可知,在有限渠道下,维修时间增加,但随着维修渠道数的增加,维修时间递减量趋缓.进一步以备件项LRU₂为例,给出渠道数为1~7时不同备件需求率下的平均维修时间变化,如表 3所示.表 2 备件维修时间Table 2 Repair time of spares

站点	方案	LRU1	LRU2	SRU11	SRU12	SRU21	SRU22
基层站点	无限渠道维修时间/天	0.6	0.5	3.0	4.0	4.0	4.0
	方案1维修渠道数	2	2	2	3	2	2
	站点1时间/天	0.689 3	0.523 1	4.234 9	4.313 7	5.362 0	4.509 1
	站点2时间/天	0.689 3	0.527 3	4.234 9	4.313 7	5.698 9	4.610 9
	方案2维修渠道数	2	1	2	2	2	2
	站点1时间/天	0.689 3	0.862 1	4.234 9	6.250 0	5.362 0	4.509 1
	站点2时间/天	0.689 3	0.917 4	4.234 9	6.250 0	5.698 9	4.610 9
	方案3维修渠道数	3	2	3	4	3	3
	站点1时间/天	0.610 5	0.523 1	3.171 4	4.052 9	4.186 2	4.057 1
	站点2时间/天	0.610 5	0.527 3	3.171 4	4.052 9	4.236 1	4.071 9
后方基地	无限渠道维修时间/天	0.3	0.2	1.0	2.0	2.0	2.0
	维修渠道数	2	2	3	5	5	4
	修正时间/天	0.302 4	0.201 1	1.022 0	2.025 3	2.035 7	2.035 4

表选项


由表 2、表 3和图 6知,维修渠道较少时,维修时间显著增加;随着渠道数量的增加,维修时间逐渐降低,并趋于无限维修渠道下的平均维修时间;维修渠道达到一定数量后,增加渠道带来的效益逐渐趋于0.表 3 不同维修渠道数量下的平均维修时间Table 3 Average repair time with different amount of repair channels

需求率/(件·天-1)	维修渠道数/个
	1	2	3	4	5	6	7
0.9	0.729 9	0.512 7	0.500 8	0.500 0	0.500 0	0.50	0.50
1.2	0.862 1	0.523 1	0.501 8	0.500 1	0.500 0	0.50	0.50
1.5	1.052 6	0.537 0	0.503 5	0.500 3	0.500 0	0.50	0.50
2.0	1.666 7	0.569 8	0.508 0	0.500 9	0.500 1	0.50	0.50

表选项

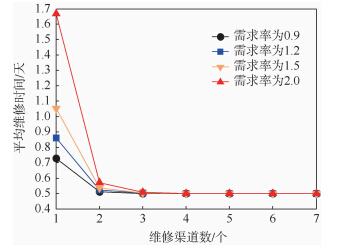图 6 不同维修渠道数和需求率下的平均维修时间Fig. 6 Comparisons of average repair time with different repair channels and demand rates

图选项

维修能力是一个相对量,除了维修系统本身固有能力外,还与备件需求率或故障件到达率密切相关,因此,文中将维修能力看作综合考虑了备件需求率和固有维修能力的相对量.图 7给出当维修渠道数为2~5,需求率从0.5~2.0变化时修正后的平均维修时间变化.

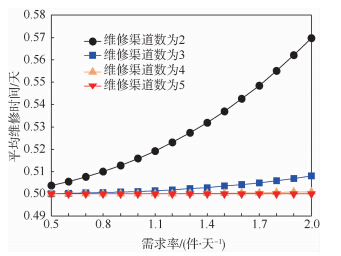图 7 不同需求率下的平均维修时间Fig. 7 Average repair time in different average demand rates

图选项

由图 7可知,随着备件需求率增加,不同维修渠道数量条件下的平均维修时间均增加;维修渠道较少时,平均维修时间增加较快;维修渠道较多时,平均维修时间增加缓慢.4.2 备件库存方案配置效果分析基于表 2中修正时间进行备件配置优化,要求用最少费用使系统可用度达到0.8.运用边际分析法优化求解,得到各方案下的最优备件配置策略,如表 4所示,其中方案1~3代表不同的维修渠道数量配置,参见表 2,方案0代表无限维修渠道.表 4 备件配置方案Table 4 Allocation schemes of spares

方案	LRU1			SRU11			SRU12			LRU2			SRU21			SRU22			可用度/%	费用/万元
	基地	站点1	站点2	基地	站点1	站点2	基地	站点1	站点2	基地	站点1	站点2	基地	站点1	站点2	基地	站点1	站点2
0	0	6	4	0	5	4	0	7	5	0	5	4	0	6	5	0	3	3	80.73	4 100
1	0	6	4	0	6	5	0	7	5	0	5	4	0	6	6	0	3	3	80.19	4 250
2	0	6	4	0	6	5	0	8	6	0	5	4	0	6	6	0	4	3	80.35	4 420
3	0	6	4	0	5	4	0	7	5	0	5	4	0	6	5	0	3	3	80.27	4 100

表选项


由表 4可知,维修渠道越少,需要储备越多的备件,费用也越高;渠道越多,越接近无限维修渠道.将无限维修渠道库存策略代入方案1~3,得到各方案下实际保障效果,如表 5所示.由表 5可知,在维修渠道较少时直接运用多级备件配置模型进行备件配置优化,实际可用度较低,不能满足任务需求.因此,在维修渠道较少时,需要对有限维修能力模型进行修正,使其满足“无限维修渠道”模型的应用条件,以提高备件配置效果.以总费用5 000万元为约束,以最大可用度为目标值,分别基于维修渠道方案0~3配置备件,库存方案如表 6所示.表 5 不同维修渠道数量下实际效果Table 5 Actual effect with different amount of repair channels

度量标准	无限维修渠道	方案1	方案2	方案3
期望短缺数/件	8.172 9	9.421 0	10.550 0	8.380 2
可用度/%	80.73	78.02	75.61	80.27

表选项


由表 6知,在一定费用约束下,随着维修渠道数量的减少,可用度呈下降趋势,但是这种差别并不十分明显;在维修渠道较多时,得出与无限维修渠道条件下较接近的可用度.将无限维修渠道条件下的备件库存方案代入维修渠道方案1~3,得到各维修渠道方案下的实际可用度,如表 7所示.表 6 备件配置策略Table 6 Allocation strategies of spares

方案	LRU1			SRU11			SRU12			LRU2			SRU21			SRU22			可用度/%	费用/万元
	基地	站点1	站点2	基地	站点1	站点2	基地	站点1	站点2	基地	站点1	站点2	基地	站点1	站点2	基地	站点1	站点2
0	0	7	5	0	6	5	0	7	6	0	7	6	0	6	5	0	4	3	91.02	5 000
1	0	7	5	0	6	5	0	7	6	0	7	5	0	7	6	0	4	3	89.16	4 980
2	0	7	5	0	6	5	0	8	7	0	6	5	0	7	6	0	4	3	87.08	4 960
3	0	7	5	0	6	5	0	7	6	0	7	6	0	6	5	0	4	3	90.73	5 000

表选项


由表 7知,将无限维修渠道备件库存策略运用于不同维修渠道方案时,实际可用度与约束模型下求取的库存策略可用度基本一致,说明在一定费用约束、在各备件项维修渠道保持结构相对稳定的情况下,无限维修渠道模型备件库存策略具有较好的适应性.但是,在各备件项维修渠道能力结构变化相对较大、经费较少时,需要重视维修能力有限带来的影响,严格按照有限维修能力模型进行备件库存配置.同时,由于有限维修渠道条件下维修时间的增加,备件库存方案下装备可用度会低于无限维修渠道理论值,这时需要增加费用投入,提高可用度.表 7 不同维修渠道方案下实际效果Table 7 Actual effect with different repair channel plans

度量标准	无限维修渠道	方案1	方案2	方案3
期望短缺数/件	3.693 3	4.457 2	5.356 7	3.818 9
可用度/%	0.910 2	0.892 2	0.875 0	0.907 3

表选项


5 结 论基于排队理论,建立了有限维修渠道下适用Palm定理和Metric理论进行可修复件配置的维修供应渠道修正模型,并进行了应用分析.1) 有限维修条件下,维修能力较低,运用“无限渠道”多级备件配置模型,效果较差,通过对有限维修渠道模型进行适用性修正,提高了备件配置效果,满足任务需求.2) 随着维修能力的增加,故障件维修时间趋于“无限渠道”维修时间,在维修能力较高时,可以近似运用“无限渠道”多级备件配置模型.3) 备件需求率和维修渠道数是影响维修能力的两个重要因素,各备件项维修渠道数保持结构相对稳定和备件购置费用充足时,运用无限渠道模型配置库存能取得较好效果.实际的维修渠道由多种资源构成,需要进一步综合考虑维修渠道内部和维修渠道间的资源竞争等关系,提高维修渠道修正模型的准确性.致谢 感谢审稿专家认真审阅稿件,并提出宝贵的修改意见.感谢韩维主任对论文研究的帮助.
参考文献

[1]	何亚群, 谭学峰, 金福禄.基于可用度的飞机可修件需求分析[J].系统工程与电子技术, 2004, 26(6):848-849. He Y Q, Tan X F, Jin F L.Demand analysis of aircraft repairable spares based on availability[J].Systems Engineering and Electronics, 2004, 26(6):848-849(in Chinese).
	Cited By in Cnki (20)
[2]	罗祎, 阮旻智, 袁志勇.多级维修供应下可修复备件库存建模与优化[J].系统工程理论与实践, 2013, 33(10):2623-2630. Luo Y, Ruan M Z, Yuan Z Y.Modeling and optimization of repairable spare parts under the multi-echelon maintenance supply[J].Systems Engineering-Theory & Practice, 2013, 33(10):2623-2630(in Chinese).
	Cited By in Cnki (3)
[3]	Sherbrooke C C.Optimal inventory modeling of systems multi-echelon techniques[M].2nd ed.Boston:Kluwer Academic Publishers, 2004:4-6, 25-32, 111-112.
[4]	刘喜春, 王磊, 许永平, 等.战时可修复备件供应保障优化模型[J].系统工程与电子技术, 2010, 32(12):2595-2598. Liu X C, Wang L, Xu Y P, et al.Research on ABMS based wartime spares support adaptation decision[J].Systems Engineering and Electronics, 2010, 32(12):2595-2598(in Chinese).
	Cited By in Cnki (6)
[5]	Sherbrooke C C.METRIC:A multi-echelon technique for recoverable item control[J].Operational Research, 1968, 16(1):122-141.
	Click to display the text
[6]	Slay F M.Vari-Metric:An approach to modeling multi-echelon resupply when the demand process is Poisson with a gamma prior, Report AF301-3[R].Santa Monica, CA:RAND, 1984.
[7]	Sherbrooke C C.Vari-Metric:Improved approach approximations for multi-indenture, multi-echelon availability models[J].Operations Research, 1986, 34(2):311-319.
	Click to display the text
[8]	Gross D.On the ample service assumptions of Palm's theorem in inventory modeling[J].Management Science, 1982, 28(9):1065-1079.
	Click to display the text
[9]	Kim J S, Shin K C, Yu H K.Optimal algorithm to determine the spare inventory level for a repairable-item inventory system[J].Computers & Operations Research, 1996, 23(3):289-297.
	Click to display the text
[10]	Kim J S, Shin K C, Park S K.An optimal algorithm of repairable-item inventory systems with depot spares[J].Journal of the Operational Research Society, 2000, 51(3):350-357.
	Click to display the text
[11]	Díaz A, Fu M C.Models for multi-echelon repairable item inventory systems with limited repair capacity[J].European Journal of Operational Research, 1997, 97(3):480-492.
	Click to display the text
[12]	Rappold J A, Van Roo B D.Designing multi-echelon service parts networks with finite repair capacity[J].European Journal of Operational Research, 2009, 199(3):781-792.
	Click to display the text
[13]	Bijvank M, Koole G, Vis I F A.Optimising a general repair kit problem with a service constraint[J].European Journal of Operational Research, 2010, 204(1):76-85.
	Click to display the text
[14]	Ruiz-Castro J E, Li Q L.Algorithm for a general discrete k-out-of-n:G system subject to several type of failure with an indefinite number of repairpersons[J].European Journal of Operational Research, 2011, 211(1):97-111.
	Click to display the text
[15]	Sleptchenko A, Van der Heijden M C, Van Harten A.Effects of finite repair capacity in multi-echelon, multi-indenture service part supply systems[J].International Journal of Production Economics, 2002, 79(3):209-230.
	Click to display the text
[16]	阮旻智, 李庆民, 黄傲林, 等.有限维修渠道约束下多级维修供应系统库存控制[J].航空学报, 2012, 33(11):2018-2027. Ruan M Z, Li Q M, Huang A L, et al.Inventory control of multi-echelon maintenance supply system under limited repair channel constraint[J].Acta Aeronautica et Astronautica Sinica, 2012, 33(11):2018-2027(in Chinese).
	Cited By in Cnki (9)
[17]	夏国清, 陈红召.面向使用可用度的舰载机可修备件库存模型[J].哈尔滨工程大学学报, 2013, 34(1):98-103. Xia G Q, Chen H Z.Operational availability oriented inventory model for repairable spare parts of embarked air-wings[J].Journal of Harbin Engineering University, 2013, 34(1):98-103(in Chinese).
	Cited By in Cnki (4)