
式中:|P|为边P的初始长度,||表示的是进行距离计算;K弹性常量.弹性常量K通过决定集束的强度被用来控制网络中集束数量,由于网络中的边的初始长度一般都不同,因此将其划分为折线段之后,通过上述公式计算,则任意一条边都具有不同的局部弹性系数kp.根据物理模型,分割片段上的插值点均为相互吸引的带电小球,引力Fe被施加在相互影响的两条边上对应的插值点对之间,如图 1所示,引力存在于p0和q0、p1和q1、p2和q2以及p3和q3之间.引力大小反映插值点之间影响程度,由于逆平方模型相对逆线性模型能够产生更强以及更加局部化的集束,采用逆平方模型计算两插值点之间引力,使得引力和两个插值点的距离成反相关,即两插值点之间越接近,距离越短,则引力越大,距离越远,则引力越小.
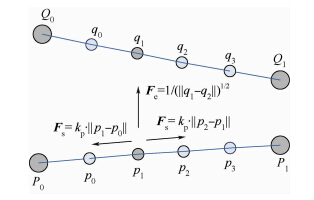 |
| 图 1 分段FDA物理模型Fig. 1 Segmental FDA physical model |
| 图选项 |
每一步迭代过程中,位于边P上的插值点pi,需要计算邻接插值点pi-1和pi+1施加的弹力Fs以及其他所有边上对应插值点施加的引力Fe,最终插值点pi收到的合力Fpi为两者矢量相加之和,即Fpi=Fs+Fe,其中
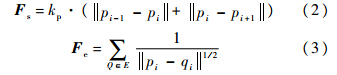
式中:kp为插值点所在边P的局部弹性系数;E为除了插值点所在边P的所有边集合;表示的是进行矢量计算,结果为矢量.1.1.2 基于模拟退火算法的迭代策略分段FDA模型包括物理模型以及迭代过程两部分,其中物理模型给出节点之间相互作用力模型,迭代过程则依据物理模型迭代运算节点之间的作用力,计算节点在力的作用下移动距离,更新节点位置,直到达到终止条件.从退火算法中得到启发,进行N轮迭代,随着迭代次数的增加,逐次减少迭代步长,判断是否符合迭代终止条件,如果不符合则进行下一轮迭代,否则将终止迭代运算.每一轮迭代过程中,边的插值点数量P逐次增加,迭代次数I以及迭代步长λ逐次减少,其中,第i轮迭代过程:
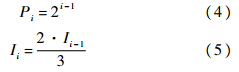
每步迭代过程,插值点的位置都将在所受合力的作用下朝合力的方向前进一定距离,步长为λ,第i轮迭代的步长为λi.1.1.3样条曲线集束模型 根据分段FDA模型将网络中的边分割划分,计算其相互之间作用力,经过一定次数迭代之后,系统达到稳定状态,终止迭代,即认为找到插值点的理想位置,然后将连线的起始点以及插值点作为B样条曲线生成的控制点,生成集束曲线.随着曲线阶数的增大,高阶样条曲线受控制点影响过度,曲线和B样条特征多边形体现出高相似度,弯曲程度变得“僵硬”,难以看到曲线的明显变化,并且由于阶次的影响,高阶样条曲线可能会产生多余的摆,因此本文生成二次B样条曲线.图 2(a)为国内航空网络节点连接子图,对单个节点的细节展示更加清晰,图 2(b)是应用分段FDA集束简化后,网络图的绘制能够实现边的汇聚,更有利于展现网络整体连接模式,生成的曲线降低了追踪连线的难度,从而减少视觉杂乱.因此在网络相对稀疏的情况下,节点连接图能够发挥直线指向性强的特点,易于表现连线的方向以及两点之间的连接关系;而集束后的曲线方法则易于展现聚类的群组以及揭示网络的整体结构特点.集束后的网络图仍然存在部分连线过度弯曲变形的问题,如图 2(c)、图 2(d)所示,分别为图 2(a)、图 2(b)右上角的局部细节展示.部分节点周围曲线出现了过度弯曲,导致变形现象.汇聚的曲线都由控制点控制生成,而控制点则由分段FDA算法迭代运算中的插值点生成,因此连线对应插值点之间的引力是造成集束曲线弯曲变形的主要原因,需要对模型进一步修改.
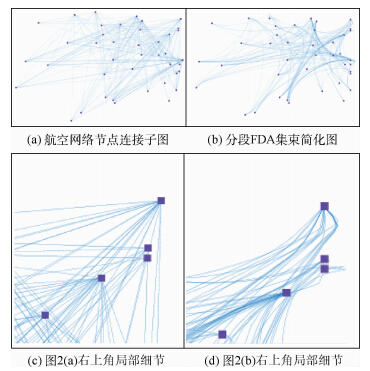 |
| 图 2 分段FDA集束简化图Fig. 2 Segmental FDA bundling simplification |
| 图选项 |
1.2 群组边相容集束模型近年来,研究人员通过对城市道路交通网络拓扑结构[18]、机场航线网络[19, 20]、人口迁移网络流[21]等复杂网络进行研究分析,发现了网络一般都具有一个共同性质——群组结构,即网络是由若干个“群组”或“类别”组成,群组内部节点之间的相互连接紧密,而群组和群组之间的连接则相对稀疏[22].因此,考虑改进分段FDA集束模型,首先将网络中的节点通过群组发现算法进行聚类,以群组内节点关系强连接和群组间节点关系弱连接为约束条件,挖掘网络中的群组结构.针对群组内节点连接密度高的特点,对组内连线引入边相容原则,计算连线之间的匹配系数,利用匹配系数衡量边与边之间相似度,通过相似度度量边之间集束程度,进而调整网络中边与边之间的相互作用,最后修改FDA物理模型.1.2.1 CNM群组划分目前使用最多的群组发现算法是基于模块度(Q)的算法,基本思路是把群组发现问题转化为网络优化问题,将搜索网络中最优群组结构作为目标约束条件.CNM算法[23]由Clauset、Newman和Moore等于2004年提出,它以Newman快速算法[24]为基础,由于采用基于堆的数据结构计算和更新网络模块度的方法,算法复杂度从O(n3)降低到O((m+n)·n),实现算法效率的大幅提高;另一方面,CNM算法在迭代过程中合并多对群组以防止网络过早地收缩到少数较大的群组,能使网络群组均匀分布,因此采用CNM算法对网络中的节点进行聚类.CNM算法基于模块度增量矩阵,基本思路是将网络看成点集,每个节点各自单独构成群组,再合并相互间具有强连接关系的节点对,使其成为一个较大的群组,然后重复搜索并合并具有强连接性的群组.整个流程形成了一个自下而上的树状图,如图 3所示,不同合并层次就对应着一种群组划分结构,不同颜色代表不同的群组划分.
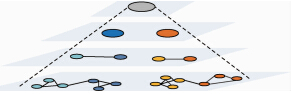 |
| 图 3 CNM算法流程Fig. 3 CNM algorithm flow |
| 图选项 |
1.2.2 群组边相容原则群组内部节点密度高,相互连线密集,位于同一个组内的节点之间构成强连接关系,在分段FDA集束模型中,不考虑任意两条边之间关系直接计算其相互作用,造成插值点偏移抖动,影响以插值点作为控制点生成的样条曲线,导致部分连线过度弯曲.因此,考虑引入一定的匹配参数,度量组内边的相似程度,从而决定其在何种程度进行集束.针对群组内节点连接密度高的特点,对组内连线应用边相容原则,通过相容性滤除相关性较低的边.计算连线之间的匹配系数,利用匹配系数衡量边与边的相似度,通过相似度度量边之间的集束程度,进而调整网络中边与边之间的相互作用,最后对FDA模型进行修改.为度量任意两条边的相容性,根据Holten提出的匹配原则从角度、尺度、位置、视觉这4个方面考虑[11](见图 4).
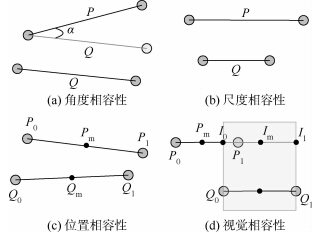 |
| 图 4 边相容原则Fig. 4 Edge consistent principle |
| 图选项 |
1) 角度相容性原则.从边的延伸方向考虑度量两条边之间的相似性,计算他们之间的夹角,认为夹角越小,越能够体现出他们在网络中朝着相同方向延伸发展,有相似的趋势,汇聚在一起的程度越高.几乎垂直的两条边在网络中具有截然不同的延伸方向,不应该通过集束汇聚在一起,因此,引入角度相容性系数Ca(P,Q)∈[0, 1]来度量,其中
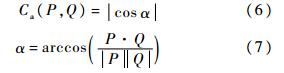
如图 4(a)角度相容性示意图,边P与Q之间的角度相差越大,则其相容系数Ca(P,Q)越小,当Ca(P,Q)为0时,P与Q垂直,当Ca(P,Q)为1时,P与Q相互平行,此时角度相容性系数最大,从延伸方向的角度考虑,边P与Q应具有较高的集束程度.2) 尺度相容性原则.从尺寸考虑边的相似性,计算两者之间的尺寸差异,这一原则主要为避免长度较小的边为适应和长度较大的边进行集束而发生过度弯曲,因此尺寸大小越相似,其汇聚程度越高.图 5为边扭曲变形示意图,主要由尺寸差异造成,其中两条边的原始线段以及受力弯曲后的曲线段分别用黑色和蓝色表示,两者之间存在的静电引力用橙色表示.
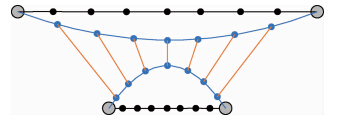 |
| 图 5 集束中边扭曲变形Fig. 5 Curve distortion by bundling |
| 图选项 |
引入尺度相容性系数Cs(P,Q)∈[0, 1],其中

式中:lavg为边P与Q长度之和的一半,即
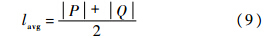
如图 4(b)所示,当P与Q长度相等时,尺度相容系数Cs(P,Q)为1,两者汇聚程度最高;当较长的边和较短的边长度之比趋向无穷大时,尺度相容系数Cs(P,Q)趋向于0,两者具有较低的汇聚程度.3) 位置相容性原则.位置相容性从边所在位置考虑,尽量避免网络中相聚过远的边集束,减少其影响程度.以两条边中心的距离衡量两条边的距离,进而度量两者之间的位置相容性,相容性系数Cp(P,Q)∈[0, 1]计算公式如下:
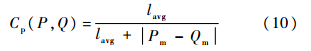
式中:Pm和Qm分别为边P与Q的中心点.如图 4(c)所示,如果Pm和Qm重合,则Cp(P,Q)等于1,如果Pm和Qm趋向于无穷大,则Cp(P,Q)趋近于0.4) 视觉相容性原则.从视觉的角度度量两条边之间的匹配性,即使两条边同时满足以上3个原则,它们也可能具有较低的集束相容性.图 4(d)所示中将一条边竖直平移,则构成的相互平行的两条边,其节点起始位置差异较大,故应具有较小的相容性,视觉相容性Cv(P,Q)∈[0, 1]计算公式如下:
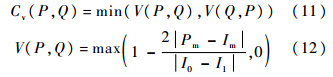
式中:Im为I0与I1中点.图 4(d)为P至Q的视觉相容性系数示意图,C(P,Q)决定于由边Q延伸出的长度与边P的交叉部分,计算在边P上交叉点I0与I1.当Pm与交叉部分中点Im相重合(理想情况下),视觉相容性系数等于1;当两条边的平行延伸没有重合部分时,视觉相容性系数等于0.根据边相容原则进行调整之后,对FDA模型进行适度修正,综合以上4种相容性系数,定义任意两条边P与Q的相容性系数Ce(P,Q)∈[0, 1]为

边P与Q的整体相容性系数Ce(P,Q)由4种相容性系数相乘求得,任意一个相容性系数较低都将对整体相容性系数造成较大影响.对应到网络图中即为,任意两条具有较高汇合程度的边必须对以上4条原则同时具有较高的切合度,结合上文推导的任意一点所受合力重新定义为
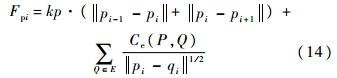
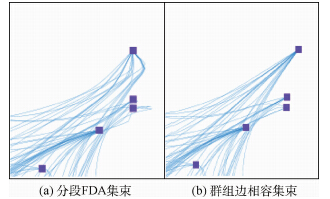
即当P与Q两条边相容性系数为0时,它们之间作用力也为0,即不考虑P与Q相互之间作用.1.3 群组边相容集束简化 应用CNM聚类,建立网络的群组结构,对组内节点之间的连线,应用边相容原则,计算连线之间的相容性系数,利用相容性系数修改算法模型,迭代更新插值点作为样条曲线控制点,生成样条曲线,完成网络的绘制.图 6中从节点发出的连线两两之间角度差异细微,连线的延伸方向相似度高,认为它们应该具有较高的集束显著性,图 6(a)应用分段FDA集束模型,图 6(b)为应用群组边相容进行改进.对比两者,曲线汇聚的集束都能够表现网络中显著的连接脉络,而图 6(b)中的曲线过渡更加平滑,在节点周围以及边密集区域发生的抖动现象较少,应用群组边相容后能够改善集束产生的连线扭曲变形,达到优化网络图绘制的目的.
 |
| 图 6 群组边相容后集束对比Fig. 6 Bundling comparison by group edge consistent |
| 图选项 |
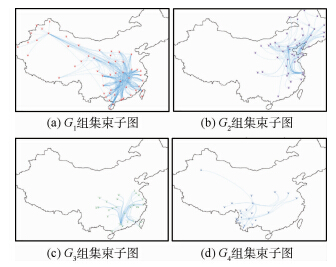
2 典型实例验证分析全球航班数据,采集世界各地机场间往来航班,由于航班具有往返特性,航线构成的网络图具有无向性.为能清晰显示网络布局效果,便于对比分析算法效果,实验中过滤后保留国内航班数据对集束简化模型进行实验验证分析,节点数目为152,航班次数为1167,网络直径为4,平均网络距离为2.15,网络密度为0.102. 2.1 群组结构分析基于CNM算法将网络进行聚类,将航空网络划分为4个群组,群组内集束连接示例图 7(a)~图 7(d)分别对应于群组划分的G1~G4组,由图可知各分组内节点能基本保持地理相近,G1和G2组节点连接关系相对密集,G3和G4组则相对薄弱.群组内网络半径为3~4,即网络中任意两点最多需要经过3个中间点即可相互到达,划分的4个群组内平均网络距离都接近2,即对每个节点平均需要经过1个中间点到达另外一个节点.
 |
| 图 7 群组内集束连接Fig. 7 Bundling within group |
| 图选项 |
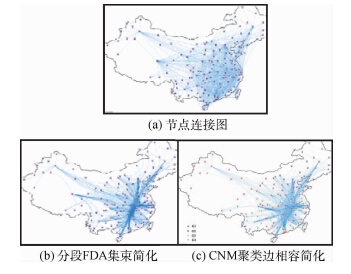
2.2 视觉凌乱度分析基于边集束的网络图绘制共有的一个特征是使用曲线绘制网络中的边,Holten在层次边集束技术中使用了三次B样条曲线[6],通过调整曲线的控制点,样条曲线能够生成清晰明了、条理清楚的集束.Zhou在基于能量的网络图层次聚类中则使用了Bezier曲线和Catmull-Rom样条曲线[25].Holten等在基于力导引的边集束[11]以及Cui等在基于几何的网络图边聚类中都使用平滑多边形的方式[12],根据多边形生成平滑曲线.直线图于节点连线之间的指向性更加清晰准确,易于表现连线的方向以及两点之间的连接关系;而曲线则易于展现聚类的簇,以及揭示网络整体结构.曲线的表现形式能够使其更加利于追踪,同时带来视觉上的良好体验,实验中采用二次样条曲线绘制,图 8中对比节点连接图和集束简化图,可以看出集束后的网络图整体结构更加清晰,视觉凌乱现象得到减少.比较图 8(b)和图 8(c),分段FDA集束简化图的集束汇聚程度过高,导致网络边集中在少数几个条带中,导致边在局部区域过度集中,为曲线追踪造成困难.考虑分组和边相容原则后,应用CNM聚类边相容集束模型后,网络中集束相对宽松,汇聚的条带空间利用率更高.同时整体呈现出十字型交叉脉络,边汇聚形成的东西方向集束构成十字型横边,南北方向集束构成十字型竖边,由集束后的网络图能够挖掘出网络脉络和连接模式.
 |
| 图 8 集束简化模型对比Fig. 8 Bundling simplification model comparison |
| 图选项 |
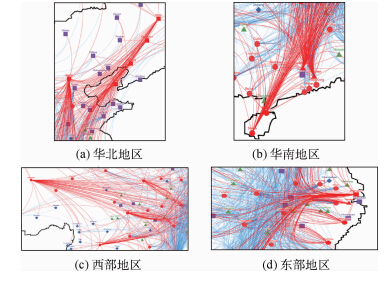
2.3 连接模式分析 对国内航空网络,按照节点地理位置所处群组,分别从群组中各自挑选出度数较高的5个节点,重点关注群组中关注点在网络中的连接情况,并将其高亮显示,获得了网络中节点的连接模式,示例图如图 9所示.
 |
| 图 9 连接模式分析Fig. 9 Connection mode analysis |
| 图选项 |
图 9为航空网络中高度数节点的分布和连接,具有两大特点:行政性和地理性.行政性,节点大多属于省会城市,政治、经济资源集中;地理性,处于沿海或交通便利的内陆.表明资源的集中和地理位置的便利使其与网络中的其他节点交流频繁,对网络有较强影响力.分析节点连接,发现其呈现一定连接模式.图 9(a)、图 9(b)节点实际位置对应于华北地区和华南地区,对比两图可以观察到南北连线形成强烈的汇聚,集束结果表明南北跨地域间交流呈枢纽型发展.图 9(c)、图 9(d)对应于西部地区和东部地区,对比两图观察到东西部之间连线汇聚性表现不明显,表明东西跨地域间交流呈发散性发展.这种连接模式从总体上体现了国家航空网络建设的发展趋势,南北经济发达地区资源集中,交通便利,在网络中起到枢纽作用,相互交流密集,东西部地区经济相对薄弱、资源匮乏,与其他区域交流更加广泛.3 结 论 本文针对网络中的视觉凌乱,以国内航线数据为实验对象绘制航空网络,提出了两种集束简化的改进方法,经实验验证表明:1) 算法具有一定准确性和有效性,分析结果表明本文的简化模型能够在一定程度上减少视觉凌乱,使网络的拓扑结构和连接特点更加清晰可见.2) 算法对网络进行信息挖掘,发现了航空网络的群组结构和整体上呈现十字脉络连接模式,东西和南北走向的航线分别汇聚集结成束,表明交流的密集性.3) 集束简化模型适用性广,绘制的网络图具有良好的视觉效果和可读性.本文重点关注挖掘网络的整体连接模式,针对复杂网络分析仍需提供关于节点底层细节信息,有待进一步研究.
参考文献
| [1] | Eades P. A heuristic for graph drawing[J].Congressus Numerantium,1984,42(1):149-160. |
| Click to display the text | |
| [2] | Kamada T,Kawai S.An algorithm for drawing general undirected graphs[J].Information Processing Letters,1989,31(1):7-15. |
| Click to display the text | |
| [3] | Davidson R,Harel D.Drawing graphs nicely using simulated annealing[J].ACM Transactions on Graphics,1996,15(4):301-331. |
| Click to display the text | |
| [4] | Fruchterman T M J,Reingold E M.Graph drawing by force-directed placement[J].Software:Practice and Experience,1991,21(11):1129-1164. |
| Click to display the text | |
| [5] | Ellis G,Dix A.A taxonomy of clutter reduction for information visualization[J].IEEE Transactions on Visualization and Computer Graphics,2007,13(6):1216-1223. |
| Click to display the text | |
| [6] | Holten D. Hierarchical edge bundles:visualization of adjacency relations in hierarchical data[J].IEEE Transactions on Visualization and Computer Graphics,2006,12(5):805-812. |
| Click to display the text | |
| [7] | Chung P J,Deek J,Feinstein H E,et al.A structure-function study of map Tau:analyzing distinct map Tau domains in mediating microtubule assembly and bundling using synchrotron SAXS[J].Biophysical Journal,2012,102(3):700a. |
| Click to display the text | |
| [8] | Gansner E R,Koren Y.Improved circular layouts[C]//Graph Drawing,14th International Symposium,GD 2006.Berlin:Springer-Verlag,2006:386-398. |
| Click to display the text | |
| [9] | Gansner E R,Hu Y F,North S,et al.Multilevel agglomerative edge bundling for visualizing large graphs[C]//Proceedings of the 2011 IEEE Pacific Visualization Symposium.Piscataway,NJ:IEEE Press,2011:187-194. |
| Click to display the text | |
| [10] | Phan D,Xiao L,Yeh R,et al.Flow map layout[C]//Proceedings of IEEE Information Visualization Symposium.Piscataway,NJ:IEEE Press,2005:219-224. |
| Click to display the text | |
| [11] | Holten D,Van J J W. Force-directed edge bundling for graph visualization[J].Computer Graphics Forum,2009,28(3): 983-990. |
| Click to display the text | |
| [12] | Cui W,Zhou H,Qu H,et al.Geometry based edge clustering for graph visualization[J].IEEE Transactions on Visualization and Computer Graphics,2008,14(6):1277-1284. |
| Click to display the text | |
| [13] | Lambert A,Bourqui R,Auber D.Winding roads:routing edges into bundles[J].Computer Graphics Forum,2010,29(3):853-862. |
| Click to display the text | |
| [14] | Ozan E,Christophe H,Fernando P,et al.Graph edge bundling by medial axes[J].Visualization and Computer Graphics,2011,17(12):2364-2383. |
| Click to display the text | |
| [15] | Wong N,Carpendale S.Using edge plucking for interactive graph exploration[C]//IEEE Information Visualization Symposium,Poster Compendium.Piscataway,NJ:IEEE Press,2005:51-52. |
| Click to display the text | |
| [16] | Wong N,Carpendale S,Greenberg S.EdgeLens:an interactive method for managing edge congestion in graphs[C]//IEEE Information Visualization Symposiu.Piscataway,NJ:IEEE Press,2003:51-58. |
| Click to display the text | |
| [17] | Zhou H,Xu P P,Yuan X R,et al.Edge bundling in information visualization[J].Tsinghua Science and Technology,2013,18(2): 145-156. |
| Click to display the text | |
| [18] | 李树彬,吴建军,高自友,等.基于复杂网络的交通拥堵与传播动力学分析[J].物理学报,2011,60(5):1-9. Li S B,Wu J J,Gao Z Y,et al.The analysis of traffic congestion and dynamic propagation properties based on complex network[J].Acta Physica Sinica,2011,60(5):1-9(in Chinese). |
| Cited By in Cnki (35) | Click to display the text | |
| [19] | Bagler G. Analysis of the airport network of India as a complex weighted network[J].Elsevier,2008,387(12):2972-2980. |
| Click to display the text | |
| [20] | Li W,Cai X. Statistical analysis of airport network of China[J].Physical Review E,2004,69(2):1-6. |
| Click to display the text | |
| [21] | Guo D. Flow mapping and multivariate visualization of large spatial interaction data[J].IEEE,2009,15(6):1041-1048. |
| Click to display the text | |
| [22] | 汪小帆,李翔,陈关荣.复杂网络理论及其应用[M].北京:清华大学出版社,2006:162-163. Wang X F,Li X,Chen G R.Complex network theory and application[M].Beijing:Tsinghua University Press,2006:162-163(in Chinese). |
| Click to display the text | |
| [23] | Clauset A,Newman M E J,Moore C.Finding community structure in very large networks[J].Physical Review E,2004,70(6): 66111. |
| Click to display the text | |
| [24] | Newman M E J. Fast algorithm for detecting community structure in networks[J].Physical Review E-Statistical,Nonlinear,and Soft Matter Physics,2004,69(6):066133-1-5. |
| Click to display the text | |
| [25] | Zhou H,Yuan X R,Cui W W,et al.Energy-based hierarchical edge clustering of graphs[C]//IEEE Pacific Visualisation Symposium 2008.Piscataway,NJ:IEEE Press,2008:55-62. |
| Click to display the text |
