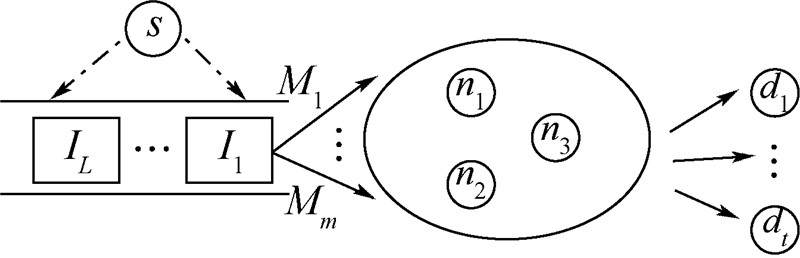
 |
| 图 1 网络模型图Fig. 1 Network model |
| 图选项 |
然后将每条原始消息向量用长度为m的单位向量进行扩展生成扩展向量[14]Mi':
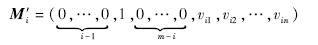
对m个扩展向量进行随机网络编码,编码后向量为
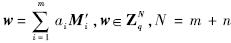,N=m+n,其中ai是从有限域中随机选取的.将代标识符I随着消息一起传输,则编码后消息格式如图 2所示. |
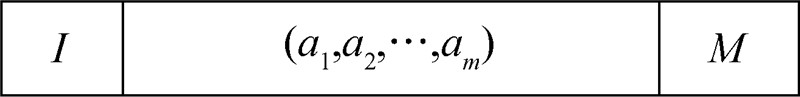| 图 2 编码后的消息格式Fig. 2 Message format after network coding |
| 图选项 |
2) 中继节点收到k个消息向量w1,w2,…,wk,将它们进行线性组合,得新的编码向量W=
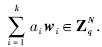.3) 目的节点收到m个线性无关的消息向量后,可得到一个m行m+n列的矩阵,将其前m列构成的矩阵记为C,后n列构成的矩阵记为P,则可由式(1)恢复得到原消息.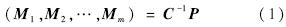 
1.2 网络编码代间污染攻击代标识符的主要作用就是区分不同的编码向量所张成的消息子空间,如果不同消息子空间的消息发生了串扰就产生了代间污染.造成代间污染有两种攻击方式[15],具体代间污染攻击模型如图 3所示.在模型中,n1和n2是普通节点,n3和n4是恶意节点,n5是污染节点.
 |
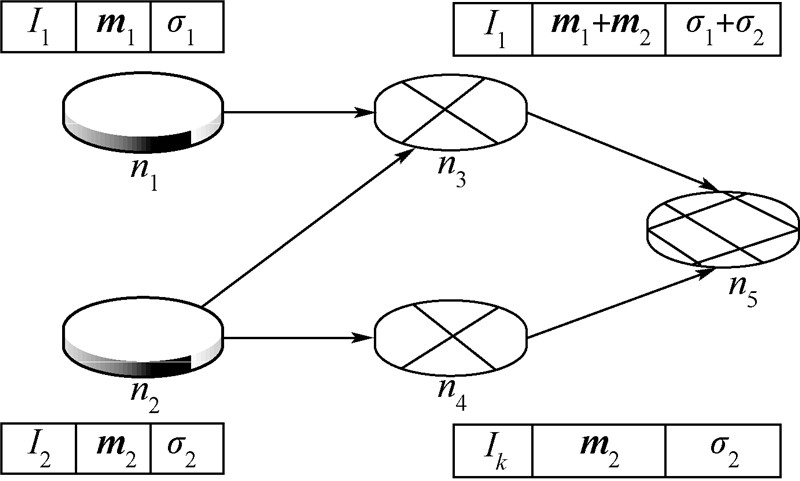| 图 3 代间污染攻击模型Fig. 3 Model of inter-generation pollution attack |
| 图选项 |
一种攻击方式是对消息的攻击.节点n1输出代I1的消息,节点n2输出代I2的消息.当恶意节点n3收到来自代I1的消息m1和代I2的消息m2时,将其编码得到消息组合m′=m1+m2,通过同态签名,可得到消息m′的合法签名σ′=σ1+σ2.但是由于新产生的消息组合m′既不属于代I1也不属于代I2,所以该消息属于污染消息,当其参与目的节点解码时将导致解码错误.另一种攻击方式是对代标识符的攻击.恶意节点n4转发代I2消息m2到节点n5的过程中,随意伪造或篡改I信息,消息将指向错误的消息子空间,则节点n5也会受到污染.上述两种攻击方式均会导致线性子空间的消息发生串扰,使目的节点无法正确解码.1.3 双线性对相对于有限域乘法群上的离散对数问题,椭圆曲线加法群上离散对数问题的求解更难,它可用更小的密钥保证更高级别的安全性.所以在Boneh等[16]借助椭圆曲线上的双线性对给出了基于身份的加密体制后,双线性对被用来构造各种密码协议.令G1是阶为大素数q的加法循环群,生成元为P.令G2是阶为q的乘法循环群.假设G1,G2上的离散对数问题都是困难的.若映射e:G1×G1→G2满足如下性质则为双线性对.1) 双线性性:对于任意的P,Q∈G1,a,b∈Zq*,都有e(aP,bQ)=e(P,Q)ab.2) 非退化性:存在P,Q∈G1使得e(P,Q)≠1.3) 可计算性:对于任意的P,Q∈G1,存在多项式时间算法能够计算e(P,Q).对双线性映射e的性质1)进行推导可得如式(2)的等式:
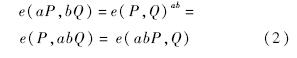
2 签名方案2.1 定 义网络编码同态签名方案由下列四元组概率多项式时间算法构成.1) 系统参数建立(Setup).输入安全参数1τ,输出素数q、源节点公钥以及私钥.2) 签名(Sign).输入私钥,一个随机选取的代标识符I∈{0,1}*,一个消息向量w,输出消息的签名σ.3) 消息组合(Combine).输入一个代标识符,k个消息向量Zi,k个随机编码系数ai∈Zq,输出消息组合W及其签名σ.
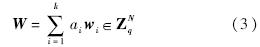
4) 批验证(Batch Verify).输入一组待验证的消息向量wi,公钥和当前传输的代标识符I∈{0,1}*,经验证算法输出有效或者无效.2.2 具体构造对于四元组算法的具体构造如下.1) 系统参数建立(Setup):给定系统参数1τ,系统选取参数G1,G2,P,q,e,HG,其中HG是一个单向抗碰撞hash函数HG:{0,1}*→G1.然后系统选取随机数α∈Zq*和ri∈Zq*(i=1,2,…,N)作为系统私钥.计算Di=αri·P(i=1,2,…,N)作为系统公钥.假设源节点要发送l个代的消息,那么给每个代随机选取一个代标识符I,计算Gpk=HG(I).源节点公开公共参数{G1,G2,e,q,P,{Di}Ni=1,Gpk,HG}.2) 签名(Sign):给定代I的一组扩展后的消息向量M′=(M′1,M′2,…,M′m),其中M′i=(v1,v2,…,vN).计算Gsk=α·Gpk.计算签名为
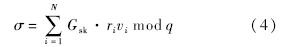
式中,Gsk可看成代对应的私钥,Gsk·ri可看成消息对应的私钥.所以同一代的消息对应着相同的代私钥和消息私钥.3) 消息组合(Combine):当接收到k个属于代I的消息向量后,节点对其进行随机线性网络编码操作得到新的消息向量为
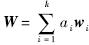,并利用签名的同态性质,由k条消息组合中的签名直接生成新消息对应的签名sign(W).性质1 方案具有同态性质.证明 设wi=(vi1,vi2,…,viN)(i=1,2,…,k)是长度为N的向量,则由式(4) 可得: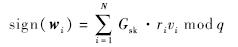 
那么中间节点收到k个消息向量后,进行随机线性网络编码得到向量
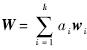.对其进行签名计算有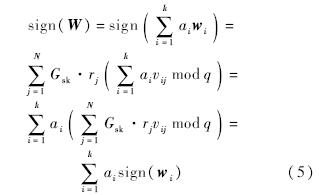 
因此证明了方案具有同态性质.从而得到新消息向量的签名计算式为
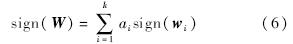
4) 批验证(Batch Verify):在对代I的消息进行批验证时,借鉴文献[7]中对分代网络编码的缓冲模式,假设节点对一个代消息的缓冲时间为t,则节点在缓冲时间结束前对所有代标识符为I的消息进行验证.设节点在代I缓冲时间结束前收到了k个代I的数据包,其形式分别为(I,w1,σ1),(I,w2,σ2),…,(I,wk,σk),其中,wi=(v′1,v′2,…,v′N).那么首先计算HG(I),验证HG(I)=Gpk是否成立,然后验证式(7)是否成立:
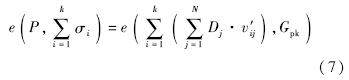
若式(7)成立则所有消息都属于代I的消息,不存在代间污染攻击.否则再对每一个消息向量进行单独验证确定哪一个是污染消息向量,验证方式与式(7)类似:
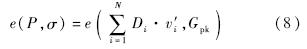
3 方案分析3.1 正确性分析对方案中的两个验证公式进行正确性的分析.1) 节点验证单个签名的情况.
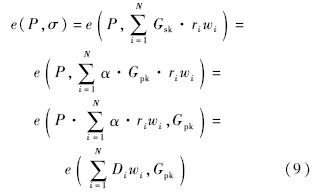
2) 节点批验证的情况.
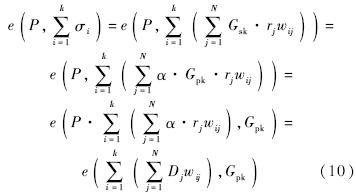
由以上两个推导过程可证明方案的正确性.3.2 安全性分析1) 安全定义.定义1 在随机预言模型下,如果一个概率多项式时间的攻击者在以下的安全游戏中的优势是可忽略的,则网络编码同态签名方案是安全的.① 初始化:挑战者运行Setup算法生成公开参数和系统私钥,并把系统公开参数发送给攻击者,保存私钥.② 询问:攻击者指定一系列的消息子空间Vi∈ZqN.对于每一个i,挑战者从{0,1}*任意选择一个代标识符Ii与之对应,通过签名算法Sign生成代Ii中每个消息向量的签名σi,并将签名σi和代标识符Ii发送给攻击者.③ 伪造:攻击者输出I*∈{0,1}*,非零消息向量m*(m*不属于代Ii),以及签名σ*.若I*=Ii,或者I*≠Ii时验证Verify(I*,m*,σ*)合法,则说攻击者赢得了本次游戏.2) 安全性证明.① 在I*=Ii但m*不属于代Ii的消息的情况下证明方式与文献[15]类似.在询问阶段,攻击者选择由向量(M1,M2,…,Mm)张成的消息子空间V并向挑战者询问该消息子空间中各消息向量的签名.挑战者收到询问请求后通过随机预言机进行应答.挑战者首先选取I作为V的代标识符,然后通过签名算法生成各向量Mi的签名σi,并将签名σi和代标识符I发送给攻击者.由此攻击者可获得式(11)的方程组:
式中
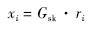攻击者输出伪造消息向量(I,m*,σ*),m*V.如果此伪造消息量能够通过验证,那么以下方程组成立: 
假设式(11)的系数矩阵与增广矩阵的秩为λ,则其解的个数为qn－λ,式(12)的秩为λ+1,解为qn－λ－1,同时也可知式(11)中将有q个解满足式(12).当q足够大时,攻击者赢得游戏的概率1q可忽略不计.② I*≠Ii时,在随机预言模型下,哈希函数HG被看成是一个随机预言机,而攻击者没有能力在多项式时间内找到I*≠Ii使得HG(I*)=HG(Ii),所以Gpk*≠Gpk,验证时不能通过.3.3 开销分析将本方案与Boneh方案的验证开销进行比较分析.两个方案开销的比较分析分为对验证计算开销的比较以及验证时对数据包等待时间的比较.1) 验证计算开销的比较.在比较验证计算开销时,不考虑数据包等待带来的开销.Boneh方案中,其签名形式为
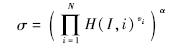
验证形式为
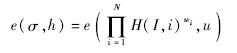
式中,α为系统私钥;u=hα为系统公钥.本方案和Boneh方案中均采用了双线性对来构造网络编码签名方案.由于在两个方案验证过程中的模加、模乘以及哈希操作的开销远小于双线性对操作的开销,所以以下的验证计算开销分析中只考虑双线性对操作的开销比较.对两个方案的验证计算开销进行比较之前先假设中间节点收到同代的消息条数平均为λ.令Ce为执行双线性对操作所需时间.① 不存在代间污染攻击的情况下,Boneh方案对每条消息进行验证时需进行两次双线性对操作,其所需时间为(2×λ)Ce.由于不存在代间污染攻击,所以本方案下只需要进行一次批验证即可,由验证式(7)可知本方案进行批验证只需两次双线性对操作,所需时间为2×Ce.② 当存在代间污染攻击的情况下,Boneh方案所需时间与不存在代间污染攻击下所需时间一样为(2×λ)Ce.使用本方案先进行批验证,确定存在代间污染攻击后,还需对每条消息进行逐一验证确定哪一个是污染消息,所以需要时间为批验证时间加上所有单个验证的时间,其总耗时为(2×λ+2)Ce.此种情况下两方案所需时间之比为
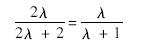
综合两种情况考虑,假设节点受到污染攻击的概率为p.则采用本方案验证所需的平均时间为p(2λ+2)Ce+(1－p)2Ce=2Ce(pλ+1)，此时两方案验证时间之比为
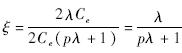.当λ≥2，即至少有两条同代的消息到达验证节点,且节点受到代间污染攻击概率p<1/2时,ξ始终大于1,即本方案的验证开销更小.由以上分析可知,本方案和Boneh方案相比,节点在有多条同代消息到达且发生代间污染概率p<1/2情况下的计算开销更小.2) 数据包等待时间比较.在比较数据包等待时间带来的开销时,不考虑验证计算开销.图 4和图 5分别为单验证模型和批验证模型.单验证时,节点收到数据包立刻开始验证,数据包不需要等待;批验证时,数据包等待直到缓冲时间结束前,节点进行批验证.由图 4和图 5可见,在相同的时间内,因为数据包到达速率一样,所以二者缓冲数据包数量相同,数据包等待时间不影响批验证开销. |
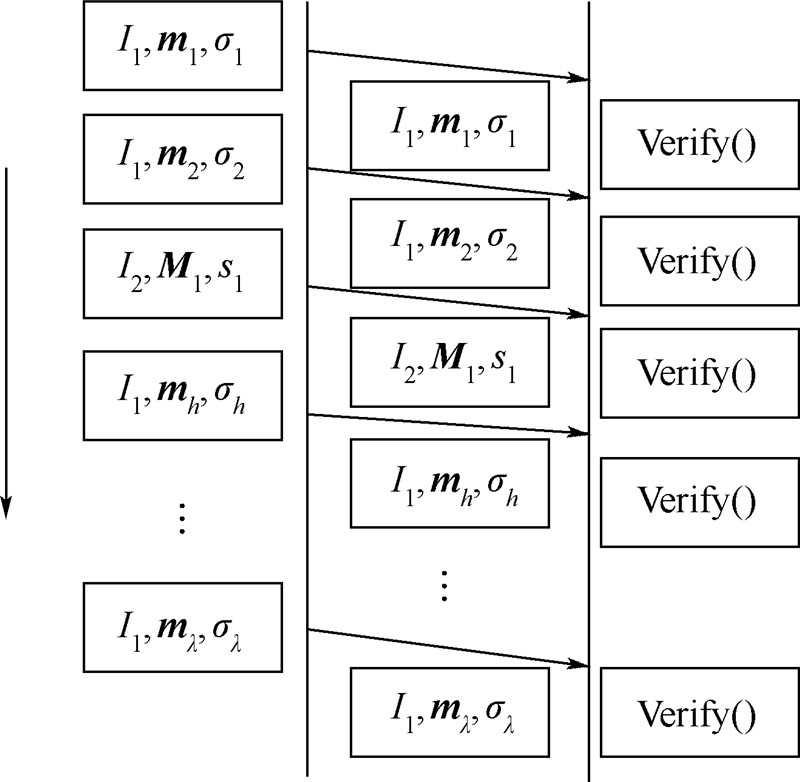| 图 4 单验证模型Fig. 4 Individual verification model |
| 图选项 |
 |
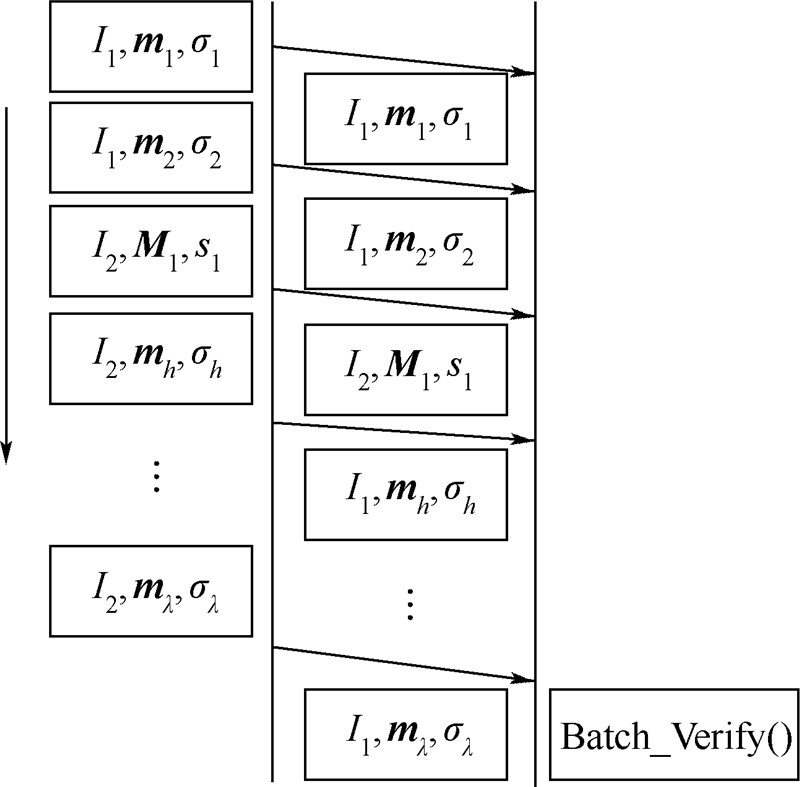| 图 5 批验证模型Fig. 5 Batch verification model |
| 图选项 |
综上考虑,结合批验证的方案与普通的单验证方案相比能够有效地节省验证开销,提高系统效率.4 结 论1) 提出一种具有同态性质的网络编码签名方案,解决网络编码中存在的因代间污染攻击造成的消息串扰问题.2) 在节点有多条同代消息到达且发生代间污染攻击概率p<1/2情况下,本方案与Boneh方案相比,验证效率更高.
参考文献
| [1] | Ahlswede R, Cai N,Li S.Network information flow[J].IEEE Transactions on Information Theory,2000,46(4):1204-1216. |
| Click to display the text | |
| [2] | He M,Chen L, Wang H,et al.Survey on secure transmission of network coding in wireless networks[C]//International Conference on Computer Science and Service System.Washington,D.C.:IEEE,2012:1216-1219. |
| Click to display the text | |
| [3] | 曹张华,唐元生. 安全网络编码综述[J].计算机应用,2010,30(2):499-505. Cao Z H,Tang Y S.Survey on secure network coding[J].Journal of Computer Applications,2010,30(2):499-505(in Chinese). |
| Cited By in Cnki (13) | Click to display the text | |
| [4] | Yu Z,Wei Y, Ramkumar B,et al.An efficient signature-based scheme for securing network coding against pollution attacks[C]//Proceedings of International Conference on Computer Communications(INFOCOM).Washington,D.C.:IEEE,2008:1409- 1417. |
| Click to display the text | |
| [5] | 裴恒利,尚涛, 刘建伟.融合时间戳和同态签名的安全网络编码方法[J].通信学报,2013,34(4):28-35. Pei H L,Shang T,Liu J W.Secure network coding method merged with timestamp and homomorphic signature[J].Journal on Communication,2013,34(4):28-35(in Chinese). |
| Cited By in Cnki (3) | Click to display the text | |
| [6] | Shang T, Pei H L,Liu J W.Secure network coding based on lattice signature[J].China Communication,2014(1):138-151. |
| Click to display the text | |
| [7] | Chou P A, Wu Y,Jain K.Practical network coding[C]//Proceedings of the Annual Allerton Conference on Communication Control and Computing,2003. |
| Click to display the text | |
| [8] | Zhao F, Kaller T,Medard M,et al.Signatures for content distribution with network coding[C]//IEEE International Symposium on Information Theory.Washington,D.C.:IEEE,2007:556-560. |
| Click to display the text | |
| [9] | Kehdi E, Li B.Null keys:limiting malicious attacks via null space properties of network coding[C]//Proceedings of International Conference on Computer Communication(INFOCOM).Washington,D.C.:IEEE,2009:1224-1232. |
| Click to display the text | |
| [10] | Boneh D, Freeman D,Katz J,et al.Signing a linear subspace:signature schemes for network coding[C]//12th International Conference on Practice and Theory in Public Key Cryptography.Berlin:Springer,2009:68-87. |
| Click to display the text | |
| [11] | Tseng Y M, Wu T Y,Wu J D.Towards efficient ID-based signature schemes with batch verifications from bilinear pairing[C]//International Conference on Availability,Reliability and Security.Washington,D.C.:IEEE,2009:935-940. |
| Click to display the text | |
| [12] | Camenisch J, Hohenberger S,Pedersent M Q.Batch verification of short signatures[C]//Advances in Cryptology-Eurocrypt 2007.Berlin:Springer,2007:246-263. |
| Click to display the text | |
| [13] | 黄佳庆,李宗鹏. 网络编码原理[M].北京:国防工业出版社,2012:31. Hang J Q,Li Z P.Network coding principles[M].Beijing:National Defense Industry Press,2012:31(in Chinese). |
| [14] | Lee S H, Gerla M,Krawczyk H,et al.Performance evaluation of secure network coding using homomorphic signature[C]//International Symposium on Network Coding(NetCod).Piscataway,NJ:IEEE,2011:1-6. |
| Click to display the text | |
| [15] | Liu G J, Wang B.Secure network coding against intra/inter-generation pollution attacks[J].Communications,China,2013,10(8):100-110. |
| Click to display the text | |
| [16] | Boneh D, Franklin M.Identity-based encryption from the Weil pairing[C]//Advances in Cryptology-CRYPTO 2001.Berlin:Springer,2001:213-229. |
| Click to display the text |
