水下航行体在垂直发射过程中,由于受到牵连速度影响形成不对称空泡,会造成一个弯矩,弯矩过大将严重影响垂直发射航行体的弹道和载荷.了解水下航行体这种特殊的受力情况对水下发射动力学分析有很大意义.通过多相流动控制方式可以稳定空泡并控制空泡形态,受多相流动控制的航行体周围会产生空气、水、水蒸气三相混合介质,航行体周围的流体动力特性更加复杂.国内外****对空化问题做了大量的试验研究与数值计算.Reichardt^[1]于1945年首次提出通过人工通气的方法生成超空泡,后来的通气空泡研究均基于这一思想；Silberman和Song^[2]通过试验研究了通气空泡的振荡规律,得到了通气量与空泡形态和泡内压力之间的关系.Lindau等^[3]建立了一套高雷诺数下的超空泡航行体多相流计算程序.闵景新等^[4]通过数值模拟研究了垂直发射过程中局部空泡对流体动力的影响以及不同头型对空泡的抑制作用.Kawakami和Arndt^[5]通过水洞试验分析了通气空泡形态及空泡闭合处现象,并得到了水洞阻塞效应作用下的最小空化数.Matveev和Miller^[6]通过水洞试验研究了空泡在不同空化数下的稳定长度,并分析了空泡在没有泄气和有泄气情况下空泡的长度变化.Ramesh等^[7]通过边界元法研究了不同通气孔直径和不同空化器形状条件下所产生的空泡波动问题.黄彪等^[8]通过试验研究了轴对称体空化水动力脉动特性.王一伟等^[9]通过数值模拟研究了航行体出水载荷问题,提出了出水溃灭压力物理模型.目前为止,流动控制方法主要分为主动控制法和被动控制法.微涡流发生器(MVG，Micro-Vortex Generator)被视为现阶段亚声速、超声速及高超声速进气道中最具有应用前景的被动流动控制装置,并成为近几年边界层分离控制研究的热点.研究人员利用涡流发生器延缓边界层流体分离，从而进一步增加机翼的升力并减小阻力^{[10, 11]}.Wendt和Hingst^[12]模拟了二维翼型尾流发生器作用下尾涡的脱落过程,建立了尾涡的峰值涡量、涡流发生器尺寸以及来流条件之间的关系.Lu等^{[13, 14]}通过实验和数值模拟研究了涡流发生器周围的漩涡特征和流场结构.于彦泽等^[15]进行了大型飞机流动控制的减阻机理研究.季路成和林峰^[16]通过数值仿真研究了绕凸包主动流动控制.虽然流动控制已经成为流体工程领域的研究热点,但水下运动体多相流动控制相关的文献仍然较少.本文针对潜射航行体水下运动过程多相流场及流体动力特点,基于流动控制思想,通过改变通气口在航行体上的轴向位置和周向位置实现对航行体多相流空泡形态及表面压力特性等的控制,进而改善潜射航行体的载荷和弹道.
1 数学模型1.1 流体动力学控制方程由于数值计算时通气质量对应的气体流速较低,所以不考虑计算过程中气体可压缩性带来的影响,假设流体介质是不可压缩的.连续性方程为
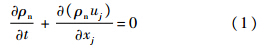
式中,ρ_n=(1－α₂－α₃)ρ₁+α₂ρ₂+α₃ρ₃为混合物的密度,ρ₁,ρ₂和ρ₃为空气、水和水蒸气的密度,α₁,α₂和α₃为空气、水和水蒸气的体积分数,α₁+α₂+α₃=1；t为时间；u_j为速度分量;x_j为坐标值.动量守恒方程为
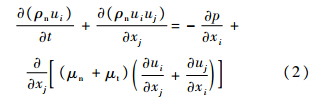
式中,μ_n=(1－α₂－α₃)μ₁+α₂μ₂+α₃μ₃为混合物的动力黏性系数,μ₁,μ₂和μ₃分别为空气、水和水蒸气的黏性系数；μ_t为湍流黏性系数；p为气泡周围流场压强.
1.2 湍流模型湍流是流场结构中的一种强非线性流体状态,是空化流场的主要特征之一.在空泡的发展尤其是尾部闭合阶段均存在着湍流现象.基于Baseline k-ω(湍动能-湍动耗散率)的剪切压力输运(SST，Shear Stress Transport)湍流模型解决了湍流剪切应力的输运问题,综合了近壁面k-ε(耗散率)模型的稳定性及边界层外部k-ω模型的独立性,不仅可以准确地预测各种来流,还可以在不同压力梯度情况下精确模拟分离现象.基于Baseline k-ω的SST湍流模型控制方程^[17]为
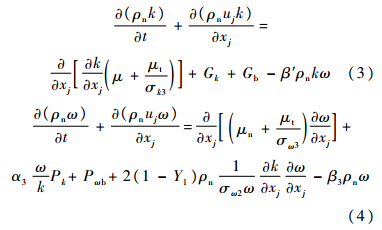
式中,σ_k3，σ_ω2，σ_ω3和β₃为模型经验常数；μ为流体的黏性系数；G_k为黏性力产生的湍动能生成项；G_b为浮力产生的湍动能生成项；β′为系数,β′=0.09；P_k为湍动能项；P_ωb为ω的产生项；Y₁为混合函数.SST湍流模型中的涡黏度限制方程为
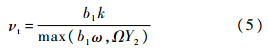
式中,b₁为系数,b₁=0.31；ν_t=μ_t/ρ，为采用的k-ω模型中的表达形式，其中，ρ为液体密度；Ω为应变率的不变测度；Y₂为混合函数.
1.3 空化模型当流场中发生空化现象时,水蒸气和水两相之间的质量转换输运方程为
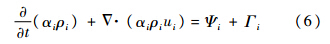
式中,Δ为Nabla算子；Ψ_i为广义源；Г_i为进入第i相的单位体积质量源.空化模型采用基于Rayleigh-Plesset方程的简化形式：
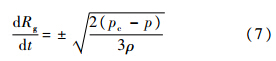
式中,R_g为气泡半径；p_c为饱和蒸气压.若单位体积内气泡数量为N_g,则气体体积分数为
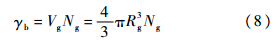
式中,V_g和R_g分别为单个气泡的体积和半径.气泡生长和凝结的质量m·转换表达式为
式中,ρ_g和ρl分别为气体和液体密度；p_∞为相对压力；C为经验常数.在一般的空化问题中,水蒸汽凝结速率远小于空化速率.因此,在空化状态和凝结状态下的经验常数不同，在CFX中分别为C_vap=50,C_cond=0.01.
2 数值计算模型2.1 计算模型设置及网格划分计算模型为半球头回转体,其直径为D,总长度为L；计算流域为长度为13L,径向为10D的三维圆柱流域,入口与回转体头部顶点的距离为2L,出口与回转体底部的距离为10L.计算流域入口设置为速度入口,出口边界条件为压力出口,为减小壁面带来的阻塞效应,将流域壁面边界条件设置为速度入口,航行体表面通气口边界设置为质量流量入口,航行体剩余的表面均设置为不可滑移壁面,计算模型及流域边界条件如图 1所示.表 1为通气口位置分布.通气口长度为1/4弹体柱段周长,宽度为1/80弹体柱段周长,按照通气口在迎流面轴向位置的不同，依次将试验方案命名为方案1、方案2和方案3.方案4和方案5的通气口轴向位置与方案2的相同,通气口分别处于背流面和侧流面.

图 1 计算模型及流域边界条件Fig. 1 Computational model and boundary conditions of flow

图选项

表 1 通气口位置Table 1 Positions of ventilation holes

通气口	方案1	方案2	方案3	方案4	方案5
轴向位置	(3/10)L	(11/20)L	(4/5)L	(11/20)L	(11/20)L
周向位置	迎流面	迎流面	迎流面	背流面	侧流面

表选项


计算网格划分如图 2所示.将航行体头部、通气口处以及航行体尾部区域等压力梯度变化较大的流场区域网格进行加密,航行体近壁面网格第1层厚度为2×10^-4 m,远场网格进行稀疏化处理,综合考虑计算效率和计算精度,选取计算网格数量为60万.

图 2 计算网格划分Fig. 2 Mesh of model

图选项

2.2 通气角度的选择文献^[18]分析了通气角度对空泡长度和半径的影响.文献^[19]研究了通气角度对黏性阻力及压差阻力的影响,并发现不同通气角度时的阻力系数基本相同.根据上述文献的研究结论,为了在保证通气方向尽量与流速方向相近的同时使气体从通气口顺利流出,计算过程中选取的通气角度为20°.
3 数值计算方法验证与计算结果分析3.1 数值计算方法验证为验证计算方法的有效性,对图 1中的半球头回转体在无重力条件下的空化问题进行数值计算,自然空化数选择为0.3.图 3为水相体积分数为α时的等值云图,将数值计算得到的航行体表面压力分布曲线与文献^[20]中试验测得的表面压力进行对比,数值计算结果与试验结果^[20]对比如图 4所示.从表面压力系数分布曲线中可以看出,数值计算结果与试验结果吻合较好,证实了计算方法的有效性.

图 3 水相体积分数为α时的等值云图Fig. 3 Contour at liquid volume fraction α

图选项

图 4 数值计算结果与试验结果[20]对比Fig. 4 Comparison of numerical results and test results[20]

图选项

3.2 通气空泡形态分析在上述计算模型的基础上,开展轴向位置和周向位置水下垂直发射航行体空泡形态及流体动力问题的数值模拟研究.水下航行体所在的笛卡尔坐标系如图 1所示,计算时航行体垂直于水面,因此重力方向为x轴正方向,设在航行体头部x=0处的绝对压力值为p₀,则x轴方向上航行体某一位置受到的绝对压力为p₀+ρgx,g为重力加速度；数值计算过程中的饱和蒸汽压为3 510 Pa,参考压力为101 325 Pa.图 5为不同通气口轴向位置的航行体空泡形态.从图 5(a)中可以看出,在有横流无通气口的情况下,航行体的迎流面和背流面空泡出现明显的不对称现象.在迎流面加上通气口后,迎流面和背流面的泡长差明显减小.由于图 5(b)中通气口比较靠前,在航行体尾部仍存在泡长差；图 5(c)中没有泡长差,形成一个包裹航行体的完整空泡；图 5(d)中通气口在迎流面空泡末端以下,所以对通气口上部分无空泡区域没有起到补充作用.图 6为不同通气口轴向位置的航行体气相体积分数,对比3种方案可知,方案2与另外2种方案相比,空泡可以更好地包裹航行体.

图 5 不同通气口轴向位置的航行体空泡形态Fig. 5 Cavity shapes of vechicles with different ventilation hole axial positions

图选项

图 6 不同通气口轴向位置的航行体气相体积分数Fig. 6 Air volume fraction of vehicles with different ventilation hole axial positions

图选项

3.3 航行体阻力变化分析3.3.1 轴向位置的影响在计算过程中改变通气口在航行体上的轴向位置,对比分析航行体的阻力系数.计算结果表明,在航行体迎流面不同位置的通气口能够起到不同程度的减阻效果.不同通气口轴向位置的航行体阻力系数对比如图 7所示.在相同通气率情况下,方案1由于通气口位置比较靠前,阻力系数较大,随着通气口位置的后移,减阻效果越来越明显.在不同通气率情况下,随着通气率的增大,方案1的压差阻力系数呈现先增大后减小的趋势,黏性阻力系数单调减小,由于总阻力系数中压差阻力系数占主要地位,因此其总阻力系数也呈现先增大后减小的趋势；方案2的压差阻力系数和黏性阻力系数呈单调减小趋势,且黏性阻力系数在相同通气率情况下比另外2个方案的小；方案3的黏性阻力系数在通气率较小时比方案1的小,随着通气率的增大逐渐大于方案1.这是由于经过方案1的流动控制后,迎流面的空泡长度增大,而方案3中通气孔的位置比较靠后,对迎流面空泡长度的影响较小.综合来看,方案2和方案3均起到了减阻的效果,方案2的减阻效率更高.

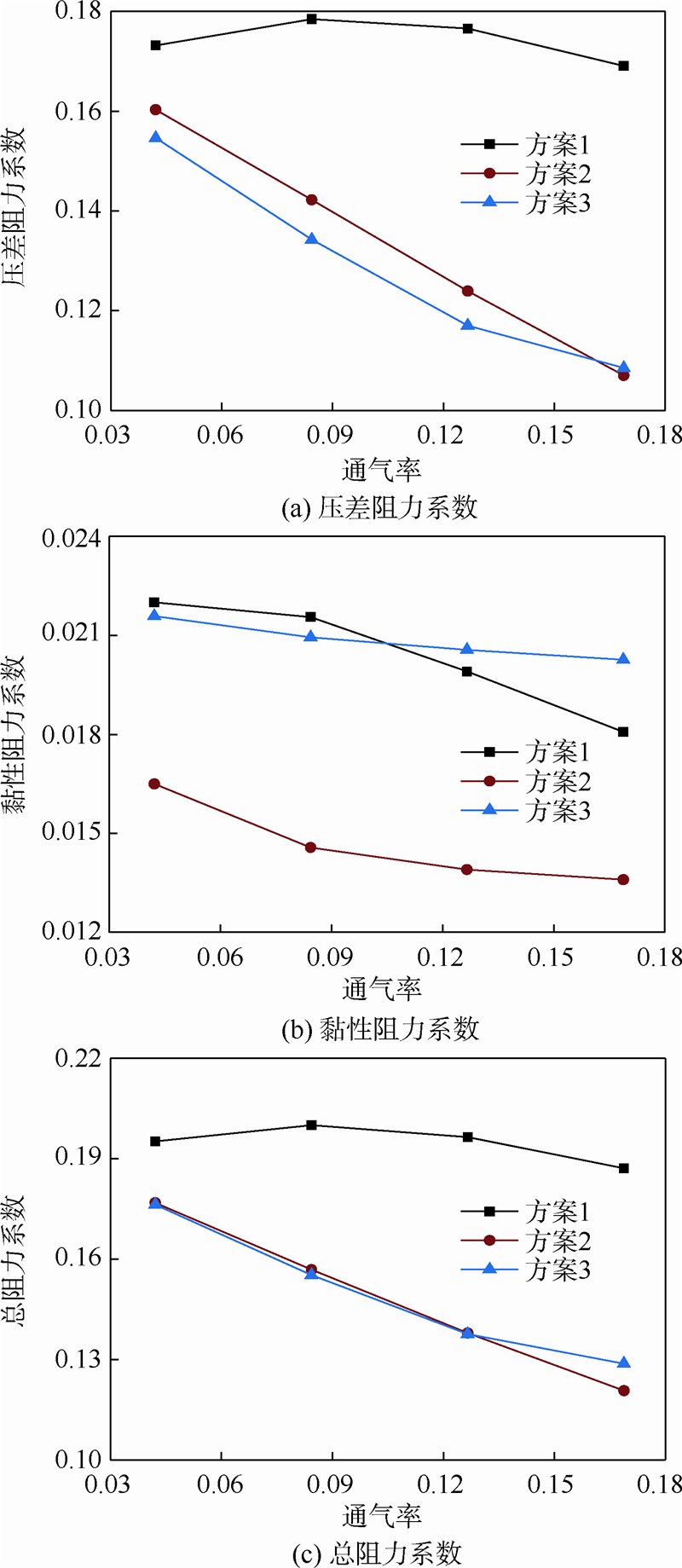图 7 不同通气口轴向位置的航行体阻力系数对比Fig. 7 Comparison of drag coefficients of vehicles with different ventilation hole axial positions

图选项

3.3.2 周向位置的影响通过对不同通气口周向位置航行体的分析可知,周向位置同样会对减阻控制效果产生影响,方案2流动控制效果较好,因此选择方案2中通气口所在的轴向位置对比分析不同通气口周向位置的减阻效果,方案2、方案4和方案5中通气口分别处于迎流面、背流面和侧流面.方案4和方案5中通气口的位置如图 8所示,不同通气口周向位置的航行体阻力系数对比如图 9所示.可以看出,随着通气率的增加,方案2的压差阻力系数和黏性阻力系数与另两个方案相比最小,方案4的压差阻力系数随着通气率的增加先降低后升高.综合以上分析可知,方案2的总阻力系数变化稳定,并且当通气率最大时达到最小值.

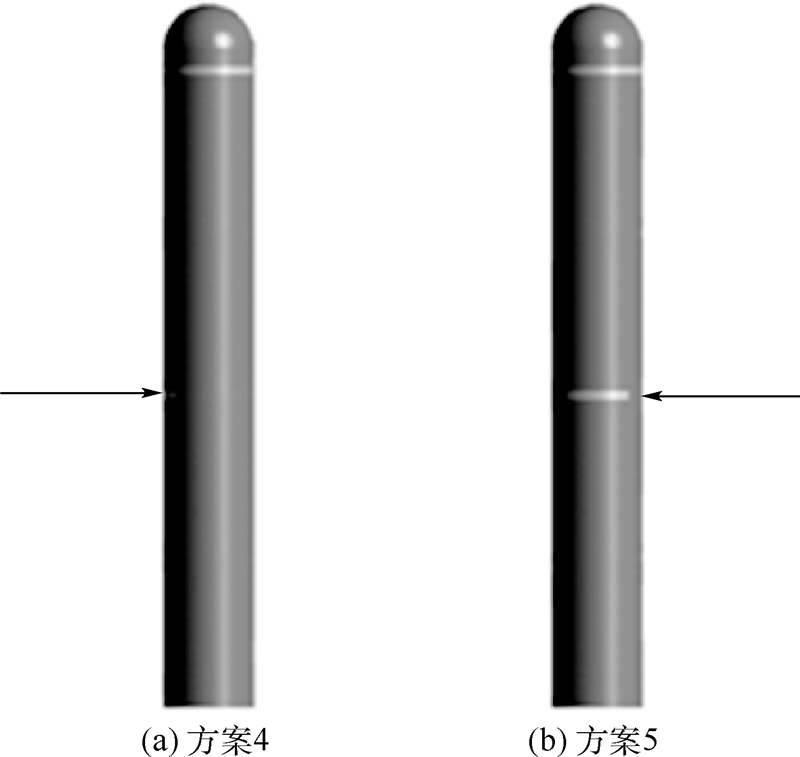图 8 方案4和方案5中通气口的位置Fig. 8 Positions of ventilation holes in Scheme 4 and Scheme 5

图选项

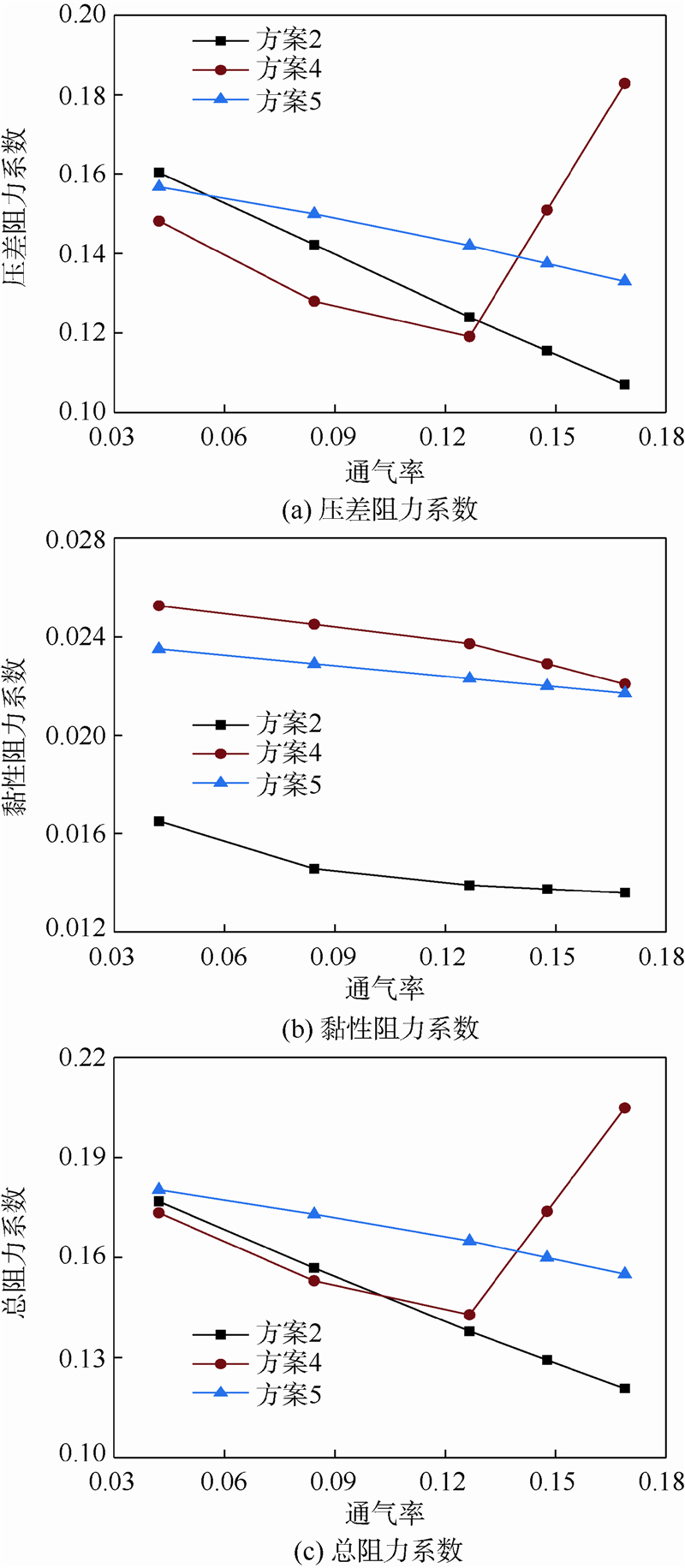图 9 不同通气口周向位置的航行体阻力系数对比Fig. 9 Comparison of drag coefficients of vehicles with different ventilation holecircumferential positions

图选项

3.3.3 航行体表面压力分析对比分析采用方案2控制后和无控制情况下的表面压力分布,提取航行体轴向(9/10)L处周向表面压力系数,航行体表面压力分布对比如图 10所示,其中z轴负方向为迎流面,正方向为背流面.可以看出,控制后航行体的迎流面和背流面最大表面压力系数均减小；压力系数曲线均存在波动现象,但控制后的曲线波动减小,这主要是因为控制后空泡分布对于压力分布产生了影响；控制后航行体表面压力系数经过侧流面低压区后,沿z轴正方向增大的幅度逐渐减小,且在背流面区域压力分布更加均匀.可见,水下航行体多相流体控制不仅可以有效降低作用在航行体表面的压力,同时又有利于航行体表面压力的均匀分布.

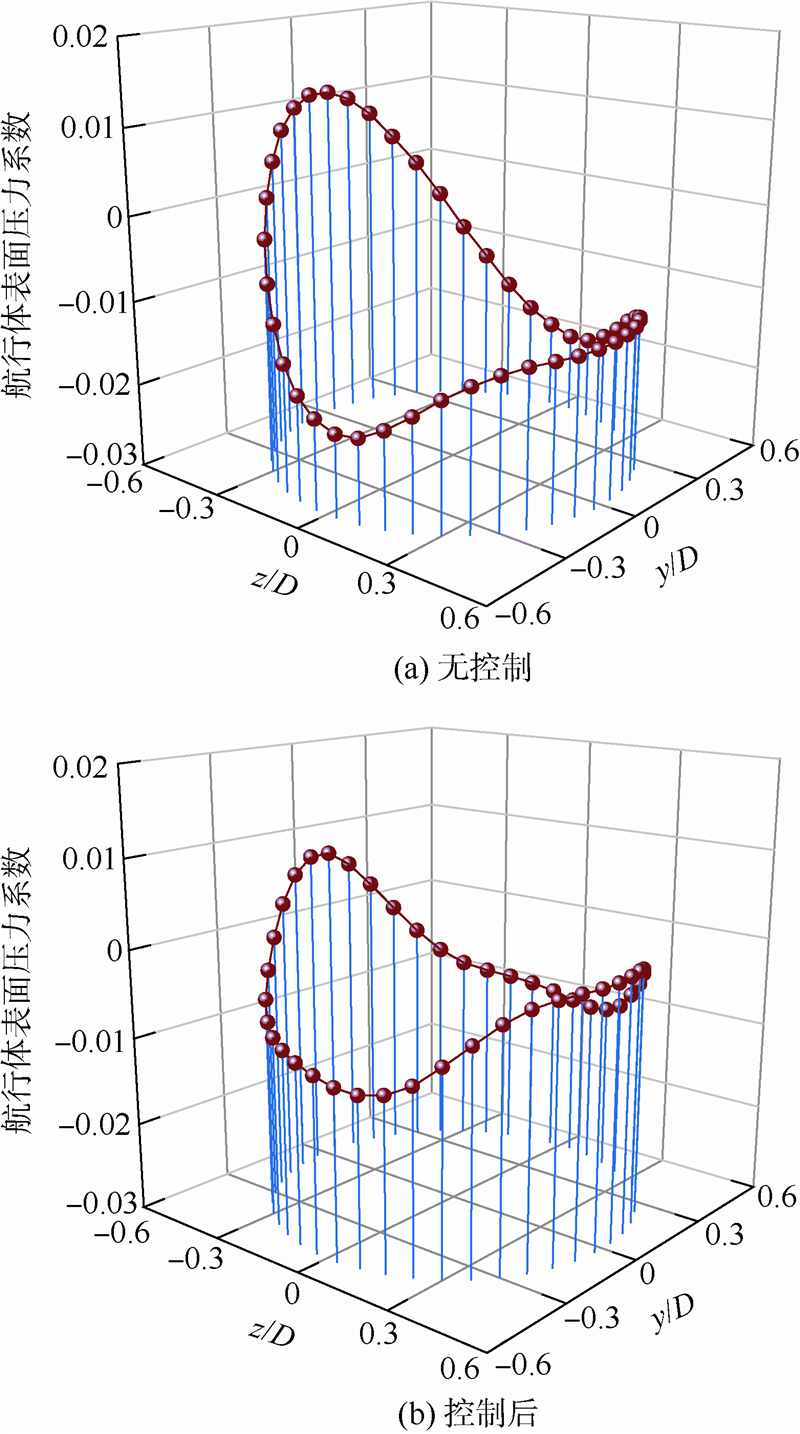图 10 航行体表面压力分布对比Fig. 10 Comparison of pressure distribution of vechicles

图选项

4 结 论采用三维数值模拟方法对比分析了水下航行体在不同流动控制方案下的通气空泡形态特征、阻力系数和表面压力分布变化特性，结果显示：1) 通过流动控制可有效减小在有横流作用下垂直发射航行体空泡的不对称性.2) 对于不同的通气口轴向位置,通气口在前部时,航行体尾部仍有较大面积的沾湿区,因此黏性阻力较大；通气口在中部时,可控制空泡完全覆盖航行体,黏性阻力最小.前部通气口产生的压差阻力最大,中部和后部通气口的基本相同.可见,中部通气口可以有效减小黏性阻力系数和压差阻力系数.3) 控制水下垂直发射航行体迎水面位置的通气口不仅可以减小水下航行体的表面压力,而且可以减小迎流面到背流面压力曲线的波动,从而有利于表面压力均匀分布.本文仅对不同控制方法的水下航行体流体动力问题作了初步研究,但在通过流动控制方法控制水下航行体载荷和弹道这一问题上,仍需要进一步的探索.
参考文献

[1]	Reichardt H. The laws of cavitation bubbles at axially symmetrical bodies in a flow[M].Gottingen:Kaiser Wilhelm Institute für Stromungsforschung,1945:322-326.
[2]	Sliberman E, Song C S.Instability of ventilated cavities[J].Journal of Ship Research,1959,5(1):13-33.
	Click to display the text
[3]	Lindau J W, Kunz R F,Mulherin J M,et al.Fully coupled,6-DOF to URANS,modeling of cavitating flows around a supercavitating vehicle[C]//Fifth International Symposium on Cavitation.Osaka:[s.n.],2003:124.
	Click to display the text
[4]	闵景新,魏英杰, 王聪,等.潜射导弹垂直发射过程流体动力特性数值模拟[J].兵工学报,2010,31(10):1303-1309. Min J X,Wei Y J,Wang C,et al.Numerical simulation on hydrodynamic characteristics of submarine missile in the vertical launch process[J].Acta Armamentarii,2010,31(10):1303-1309(in Chinese).
	Cited By in Cnki (380)
[5]	Kawakami E, Arndt R E.Investigation of the behavior of ventilated supercavities[J].Journal of Fluids Engineering,2011,133(9): 091305.
	Click to display the text
[6]	Matveev K, Miller M.Air cavity with variable length under a model hull[J].Proceedings of the Institution of Mechanical Engineers,Part M:Journal of Engineering for the Maritime Environment,2011,225(2):161-169.
	Click to display the text
[7]	Ramesh S S, Lim K,Khoo B.An axisymmetric hypersingular boundary integral formulation for simulating acoustic wave propagation in supercavitating flows[J].Journal of Sound and Vibration,2012,331(19):4313-4342.
	Click to display the text
[8]	黄彪,王国玉, 权晓波,等.轴对称体空化水动力脉动特性的实验研究[J].工程力学,2012,29(2):239-244. Huang B,Wang G Y,Quan X B,et al.Experimental study on fluctuating hydrodynamics around axisymmetric bodies[J].Engineering Mechanics,2012,29(2):239-244(in Chinese).
	Cited By in Cnki (161)
[9]	王一伟,黄晨光, 杜特专,等.航行体垂直出水载荷与空泡溃灭机理分析[J].力学学报,2012,44(1):39-48. Wang Y W,Huang C G,Du T Z,et al.Mechanism analysis about cavitation collapse load of undervater vehicles in a vertical launching process[J].Chinese Journal of Theoretical and Applied Mechanics,2012,44(1):39-48(in Chinese).
	Cited By in Cnki (331)
[10]	Bragg M, Gregorek G.Experimental study of airfoil performance with vortex generators[J].Journal of Aircraft,1987,24(5):305-309.
	Click to display the text
[11]	Calarese W, Crisler W.Afterbody drag reduction by vortex generators,AIM-85-0354[R].Nevada:AIAA,1985.
	Click to display the text
[12]	Wendt B, Hingst W.Flow structure in the wake of a wishbone vortex generator[J].AIAA Journal,1994,32(11):2234-2240.
	Click to display the text
[13]	Lu F K, Pierce A J,Shih Y,et al.Experimental and numerical study of flow topology past micro vortex generators[C]//40th Fluid Dynamics Conference and Exhibit.Chicago:[s.n.],2010:4463.
	Click to display the text
[14]	Lu F K, Li Q,Liu C.Microvortex generators in high-speed flow[J].Progress in Aerospace Sciences,2012,53:30-45.
	Click to display the text
[15]	于彦泽,刘景飞, 蒋增龑,等.大型飞机后体流动控制及减阻机理研究[J].空气动力学学报,2011,29(5):640-644. Yu Y Z,Liu J F,Jiang Z Y,et al.The investigation of flow control and drag reduction mechanism for transport airplane aft-body[J].Acta Aerodynamica Sinica,2011,29(5):640-644(in Chinese).
	Cited By in Cnki (241)
[16]	季路成,林峰. 绕凸包主动流动控制的初步数值研究[J].工程热物理学报,2007,27(1):45-47. Ji L C,Lin F.Numerical studies about active flow control over a hump flow[J].Journal of Engineering Thermophysics,2007,27(1): 45-47(in Chinese).
	Cited By in Cnki (155)
[17]	Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications[J].AIAA Journal,1994,32(8):1598-1605.
	Click to display the text
[18]	黄海龙,黄文虎, 王聪,等.数值模拟通气角度对超空泡形态特性影响分析[J].工程力学,2007,24(12):195-208. Hung H L,Huang W H,Wang C,et al.Numerical analysis of the influence of angle of ventilation on the shapes of supercavity[J].Engineering Mechanics,2007,24(12):195-208(in Chinese).
	Cited By in Cnki (133)
[19]	孙铁志,魏英杰, 王聪,等.孔状通气条件下潜射航行体流体动力特性研究[J].兵工学报,2013,34(11):1424-1430. Sun T Z,Wei Y J,Wang C,et al.Research on hydrodynamic characteristics of submarine launched vehicle with ventilation holes[J].Acta Armamentarii,2013,34(11):1424-1430(in Chinese).
	Cited By in Cnki (24)
[20]	Acosta A. The effect of a longitudinal gravitational field on the supercavitating flow over a wedge[J].Journal of Applied Mechanics,1961,28(2):188-192.
	Click to display the text