1 FLL-PLL载波跟踪算法1.1 FLL和PLL鉴别器的设计根据信号的体制(DS_BPSK)确定所需要的鉴别器,同时需要抑制载波,采用二象限反正切鉴别器,可以在高低信噪比下都能接近最佳,I(Ips(k))、Q(Qps(k))两路信号在进入鉴别器前需要对积分结果作叉积(PCross)和点积(PDot),得到鉴频器和鉴相器的结构图如图 1所示.
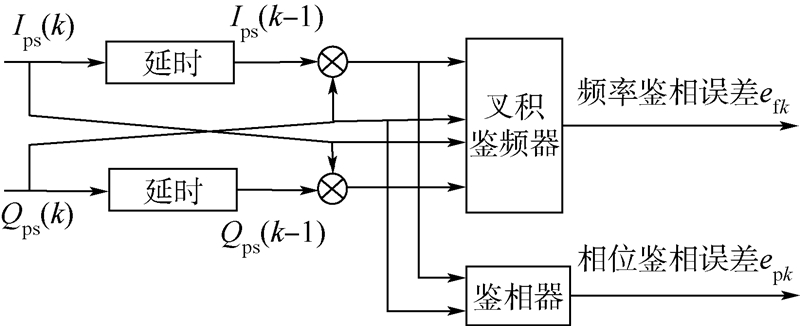 |
| 图 1 鉴频器和鉴相器的结构Fig. 1 Structure of frequency discriminator and phase discriminator |
| 图选项 |
鉴相过程中得出的叉积(PCross)和点积(PDot)误差分别为
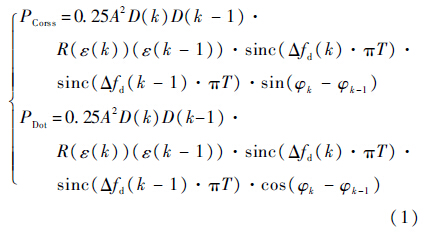
式中:A为正余弦信号幅度;D(k)为调制数据;ε(k)为伪码相位估计偏差;R为伪随机码相关函数;Δfd(k)为多普勒频移估计残差;T为积分时间;φk为相位.
采用二象限反正切误差鉴别器对叉积和点积结果鉴别得到输出的频率误差为
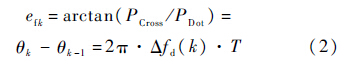
式中:θk为输出相位误差.
可见,误差量与单位时间内的频率变化成正比,可以控制载波NCO达到频率跟踪的目的.斜率与信号幅度无关,频率鉴别范围为[-1/4T,1/4T].
对于鉴相器,由于其不受数据跳变的影响,因此可采用四象限反正切鉴相算法,得到输出的相位误差为

式中:Ips为同相支路;Qps为正交支路.
在输入误差为±π范围内保持为线性.在高和低信噪比下均为最佳,斜率与信号幅度无关.
1.2 环路滤波器的设计高动态的信号一般包括加速度和加加速度分量,为了克服这两项动态应力误差,需要对环路的阶数进行确定.
对于二阶锁频环,其传递函数[9]为

式中:b21=Δωn/2,Δωn为自然角频率的阶跃量;b1=42/3Bn≈1.886 Bn,Bn为环路带宽.
加速度的数学模型为频率的一次斜升信号,据此二阶锁频环FLL的稳态相位误差为
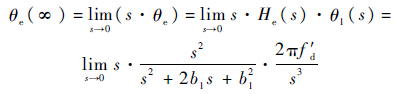
又:
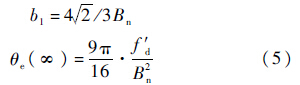
可见,二阶锁频环跟踪频率斜升信号时,存在频率稳态相差,其大小与环路带宽平方成反比,与频率变化率成正比.
对于三阶锁相环,环路滤波器的闭环传递函数[10]:

当输入信号存在加速度分量,三阶锁相环PLL的稳态误差为0.
当输入信号存在加加速度分量,其数学模型为频率的二次斜升信号,假设信号的二次变化率为fd,输入信号的相位的变化为:θ2(t)=

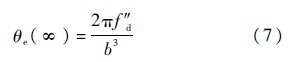
又:b=1.2Bn所以稳态相位误差:

因此,三阶锁相环可以很好地克服加速度的动态应力误差,对于加加速度误差会有一个稳定的相位误差,因此在环路的跟踪锁定过程中,FLL单独工作时需要将跟踪误差调整至接近稳态误差,就认为锁定加速度信号分量,在PLL单独工作、接近稳态误差时,认为锁定加加速度分量.根据以上锁频环和锁相环的设计过程的推导,可以确定二阶FLL与三阶PLL组合的方式,FLL的输出为频率分量,需要在环路滤波器的接入点提前一个积分环节,以便使频率积分为相位,添加至环路迭代中,环路滤波器的结构如图 2所示.
 |
| 图 2 二阶FLL辅助三阶PLL环路的滤波器结构Fig. 2 Loop filter structure of second-order FLL auxiliary third-order PLL |
| 图选项 |
参数定义如下:
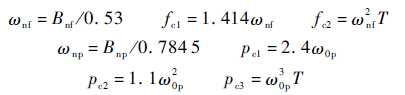
式中:Bnp为相位噪声带宽;Bnf为频率噪声带宽.
2 FLL-PLL组合算法的优化FLL-PLL的载波跟踪算法,既要保证锁定速度,又要提高环路的跟踪精度,FLL-PLL的载波跟踪方案的优化主要从组合环路的状态确定和状态转变的门限值确定进行.FLL-FPLL-PLL组合算法具有较优性能的环路闭合过程是:以FLL的形式牵引至频率锁定,然后过渡到FLL辅助PLL的方式,至相位锁定,之后再转换为PLL单独工作的精确跟踪模式,直到相位锁定丢失.FLL-FPLL-PLL组合环路状态之间的状态转换门限值是根据蒙特卡罗仿真实验以及借鉴工程实现的经验值确定的,根据门限值进行状态转换可以增加跟踪环路转换连续性和跟踪精确度,减少环路失锁的概率.
2.1 组合环路的状态分析针对目前的FLL-PLL组合跟踪算法,对环路跟踪曲线进行对比验证其合理性.
FLL-PLL的跟踪方案,即为FLL先牵引至锁定状态,然后PLL单独工作的方式.由于FLL是在PLL的前一个积分环节进入环路,从FLL的跟踪直接切换至PLL跟踪状态,显然环路状态的过渡不连续,会影响环路跟踪性能,甚至出现环路失锁的问题.
FLL-FPLL跟踪方案,FLL牵引而后转换为FLL和PLL同时工作的组合方式FPLL.由于二阶FLL的相位跟踪精度低于三阶PLL,并且在环路滤波器的工作过程中,是将FLL输出的频率误差和PLL输出的相位误差进行融合处理,会引入较大的环路误差,因此FLL和PLL同时工作的方式会使环路的误差增大.FLL-FPLL跟踪方案切换至FPLL状态后,在低信噪比的信道环境下融入噪声过大易使环路失锁.FLL-FPLL-PLL的跟踪过程中,当环路处于PLL单独精确跟踪阶段,相比前一阶段的FPLL环路误差会明显减小.
2.2 状态转换门限的确定为了保证3种状态能够较优的切换,切换时机的判决门限尤为重要.如果FLL断开较早,跟踪环路无法锁定;如果FLL断开较晚,使环路的鉴相误差的抖动范围变大,影响跟踪精确度.
对于FLL牵引状态转换至FLL辅助PLL的锁定状态的门限值可以设为FLL的动态应力误差极限值,当考虑存在加速度分量时,根据式(5)的推导过程可知FLL剩余一个固定频差:
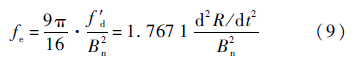
式中:R为发射机与接收机之间的视线距离.fe存在一个极限值,当接近极限值时,可以增加PLL进入环路,环路进入FLL辅助PLL的锁定状态,图 2中的pc1、pc2、pc3误差值添加到环路中,可以有较宽的跟踪范围,保证环路锁定速度.
对于FPLL状态转换至PLL的精确跟踪状态的检测门限设为锁相环的快捕带宽.锁相环的快捕带宽是环路不经过周期跳变而直接快速锁定输入信号范围[11].工程应用中,设计信号的快捕方案时,要求快捕得到的信号相位估计值与输入信号的实际相位差处于锁相环的快捕带宽内,才能保证锁相环快速进入跟踪状态.锁相环的快捕带宽与环路的带宽相关,经过多次蒙特卡罗仿真实验,以及借鉴工程实现的经验值,考虑小于锁相环的单边最小带宽的2.5倍,检测门限值为

当达到门限值,图 2中的fc1和fc2设为0,将FLL断开.环路进入PLL精确跟踪状态,实时地调整环路带宽,提高跟踪精度.单边最小带宽定义为[10]

式中:ωn为自然震荡角频率;ξ为环路的阻尼系数,取值为0.707.
3 FLL-FPLL-PLL跟踪环路的优化跟踪环路的优化主要是对环路带宽的实时调整,分为状态转换时刻的带宽调整和PLL单独工作时的带宽调整两方面.
为了在环路状态转变后环路的过渡更加连续,同时尽量提高跟踪精度,状态转换时刻的带宽选择至关重要,根据前面的分析,可按照以下规则进行:
1) FLL在牵引跟踪状态,带宽要尽量设置得宽,提高锁定速度.
2) 当转换至FPLL状态,FLL环的环路带宽减少,PLL带宽在调整范围内选择最大值.
环路状态切换至PLL单独工作的精确调整状态时,环路已经进入锁定状态,可以根据环路误差的来源,优化环路带宽,使环路误差达到最小值.锁相环的相位测量误差源包括相位抖动误差和动态应力误差,这两者存在矛盾,当带宽变大,相位抖动误差增大,而动态应力误差减少.而造成相位抖动的误差源又主要分为热噪声、振荡器引起的振荡器颤动以及阿伦偏差引起的振荡器颤动3种[12].
PLL的总误差函数关系式为
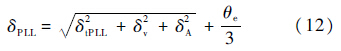
式中:δtPLL为热噪声误差;δv为由振荡器引起的振荡器颤动;δA为由阿伦偏差引起的振荡器颤动.
由PLL振动源引起误差可以忽略,PLL误差只考虑热噪声误差和动态应力误差两方面[12].将其代入式(12)得
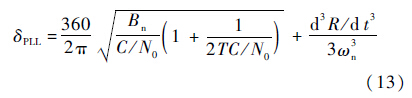
式中:C为输入环路的信号功率;N0为单边噪声功率谱密度;ωn=Bn/0.784 5;d3R/dt3为视线上加加速度,设其动态值为30 g/s,载波频率为1.6 GHz.
根据二象限反正切鉴别器,PLL的跟踪门限[12]

根据式(12)可知:

跟踪环路带宽一定要选得尽可能小以提供足够的环路信噪比ρ,一般需要保证在15~20 dB范围之内[13]:
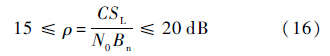
式中:SL为环路的平方损耗,一般取-3 dB左右[13].
由载噪比C/N0和信噪比Eb/N0之间的关系公式可知[14, 15]:
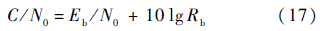
式中:Rb为符号速率,取1 kb/s;Eb/N0取3~5 dB的动态范围(微弱信号的Eb/N0一般小于5 dB),由此根据式(16)和式(17)可知:
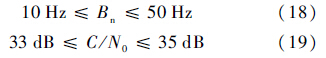
因此带宽优化问题变成了有约束的二元非线性优化问题:
Minimize:
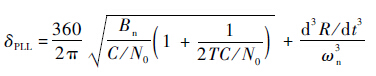
Subject to:

采用active-set法求多变量函数的最小值点,其计算过程如表 1所示.
表 1 有效集算法的优化过程Table 1 Optimization process of active-set algorithm
| 迭代次数 | 函数值 | 最大约束 | 方向导数 | 一阶最优值 |
| 0 | 7.134 86 | 0 | ||
| 1 | 6.482 74 | -4.844 | -0.854 | 0.505 |
| 2 | 5.136 31 | 0 | -0.687 | 0.204 |
| 3 | 5.063 08 | 0 | -0.204 | 0.185 |
| 4 | 4.882 76 | 0 | -0.166 | 0.054 3 |
| 5 | 4.851 94 | 0 | -0.054 3 | 0.020 8 |
| 6 | 4.845 46 | 0 | -0.020 8 | 0.004 3 |
| 7 | 4.845 12 | 0 | -0.004 43 | 0.000 479 |
| 8 | 4.845 11 | 0 | -0.000 479 | 1.27×10-5 |
表选项
计算结果如下:
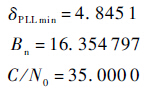
根据优化结果可以得出如下结论:
1) 目标函数的最小误差为4.845 1,远小于PLL的失锁极限值15°,表明信号存在加加速度分量的情况下,二阶FLL辅助三阶PLL的工作方式可以稳定的工作.
2) 带宽为16 Hz、载噪比为35 dB时误差取得最小值,验证了载噪比越高PLL的跟踪精度越高的结论.
3) 在带宽调整优化的过程中,由于相位抖动误差和动态应力误差存在矛盾性,并不是带宽值越小相位误差越少,而是存在最优值.因此在高动态的航天测控通信环境下,可以根据其实际情况计算带宽最优值.
当进入PLL单独工作的PLL精确跟踪状态时,已经进入锁定状态,不需考虑锁定速度,为了提高环路的跟踪精度,按照带宽最优值调整带宽.如果立即调整带宽至最优值,容易出现环路失锁的问题;并且由于环路的存在瞬时误差值过大的情况,会造成带宽误调整,因此需要增加环路调整的约束条件,根据实际测试过程中提出了试探调整的办法.
试探法是指在一段时间内取环路滤波器的相位误差的平均值,当其均值稳定,可以试探减少带宽,在带宽减少后仍然观测相差的变化情况,如果相差变大就将带宽还原为调整前的值,如果相差变小,就将带宽保持为调整后的值.
鉴于环路会出现瞬时噪声过大的情况,通过取多次相差均值的方式,降低错误调整的机率.其数学模型为
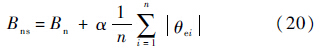
式中:Bns为环路动态调整带宽;α为带宽调整系数,取值范围为[0, 1].
根据以上的试探法的要求可以通过调整系数α的值,调整带宽,使带宽逐步地达到最优值.
4 仿真验证为了验证本文提出的载波跟踪优化算法的性能,对信号的跟踪过程进行仿真.
仿真1 为了验证FLL-FPLL-PLL载波跟踪优化算法的可靠性,与FLL-PLL和FLL-FPLL两种算法进行对比,在Eb/N0=3 dB,捕获结束后的剩余频偏|frem|=200 Hz、加速度|arem|=50 Hz/s相同的条件下进行仿真,并且跟踪过程中未进行带宽调整,容易出现环路失锁问题.图 3是FLL-PLL算法仿真结果,开始阶段FLL环已经锁定频率,但是在转变为PLL跟踪状态时,由于直接跳转至PLL跟踪阶段,出现过渡不连续的情况造成环路失锁;图 4中环路进入FPLL状态后,并未断开FLL[7, 16].由于FLL的调整误差较大,环路中引入噪声过大,使环路调整不稳定,在锁定一段时间后失锁.对比发现,在只有加速度的情况会出现失锁问题,当存在加加速度的动态环境下,环路失锁问题变得更频繁,因此在高动态低信噪比的环境下,FLL-FPLL-PLL组合方案优势会更明显.
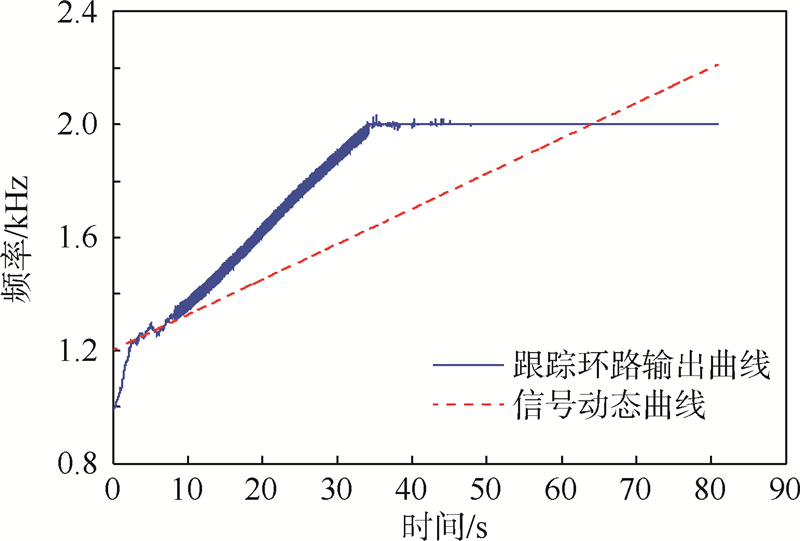 |
| 图 3 FLL-PLL不连续环路滤波器输出Fig. 3 Output of discontinuity FLL-PLL loop filter |
| 图选项 |
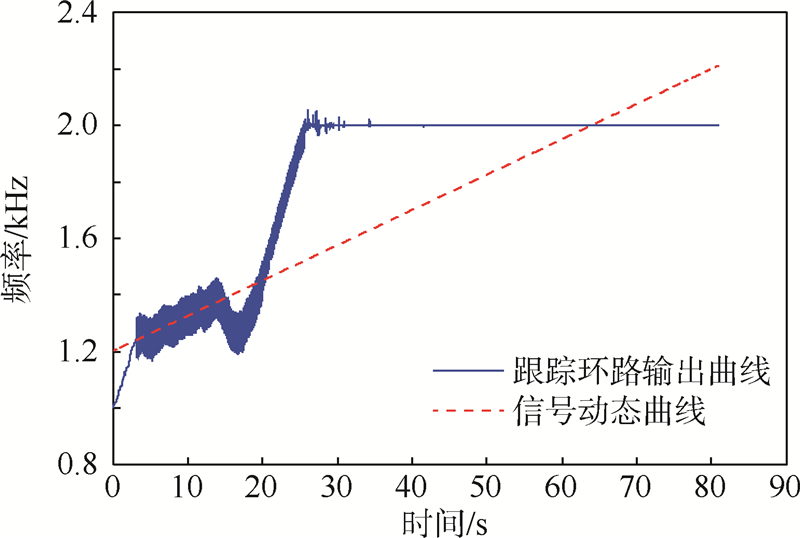 |
| 图 4 FLL-FPLL的环路滤波器输出Fig. 4 Output of FLL-FPLL loop filter |
| 图选项 |
FLL-FPLL-PLL载波跟踪优化算法的环路滤波器频率输出如图 5所示,可以看出环路的状态转变和带宽调整过程:FLL牵引状态可以快速地消除捕获阶段剩余的多普勒频移,快速达到锁定状态,转换至FLL辅助PLL状态,误差减少至快捕带宽,转变至PLL精确跟踪状态,进而根据提出的环路优化调整策略对带宽进行了调整,将带宽调整至最优值,可以看出环路滤波器的输出误差值不断减少.
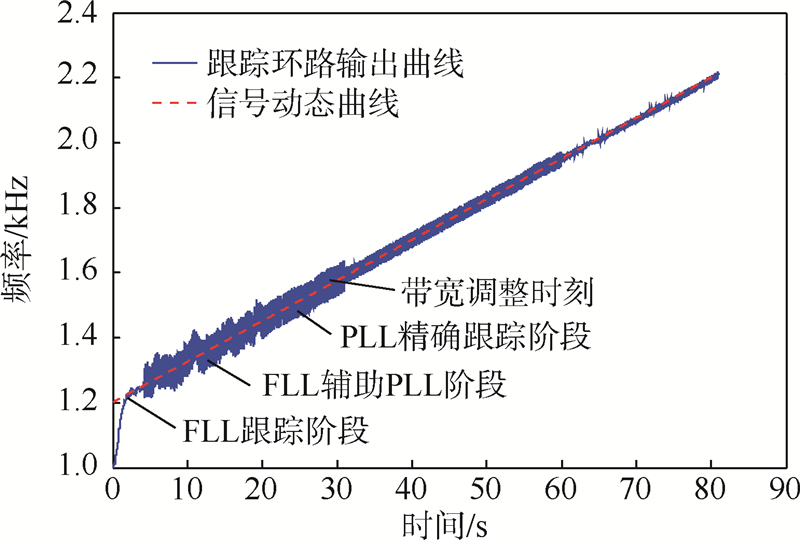 |
| 图 5 FLL-FPLL-PLL环路输出Fig. 5 Output of FLL-FPLL-PLL loop filter |
| 图选项 |
仿真2 为了验证最优带宽的存在性,以及有效集算法解算的带宽最优值的可靠性,在载噪比分别为33~35 dB的情况下,仿真带宽与总的噪声误差之间的关系如图 6所示.
 |
| 图 6 不同C/N0带宽与噪声误差的关系Fig. 6 Relationship between bandwidth and noise error under different C/N0 |
| 图选项 |
仿真3 为了验证跟踪更高动态信号的可靠性,以及FLL-FPLL-PLL算法和带宽调整策略的可靠性.以火星探测器进入阶段的接收信号为例,从变化多普勒频偏为-300~300 kHz,变化率a为-800~800 Hz/s,经过载波粗捕获后达到frem≤200 Hz,arem≤50 Hz/s,加加速度|arem|=5 Hz/s2,中频中心频点为70 MHz的情况下,进行了蒙特卡罗仿真.图 7给出了带宽优化算法跟踪误差仿真结果:环路进入PLL精确调整状态后,需要根据实际的跟踪环境,调整带宽使之达到最优值,在此过程中,会出现带宽调整的误操作,试探法调整带宽的策略就会调整至原带宽值,减少误调整的机率.图 8给出跟踪过程中,环路的误差仿真曲线,可以看出环路误差在带宽的调整过程中不断地减少,相比传统的跟踪环路提高了环路跟踪精度.经过多次蒙特卡罗仿真验证锁相环的锁定时间大约为700 ms,与普通的锁相环的锁定时间相当.
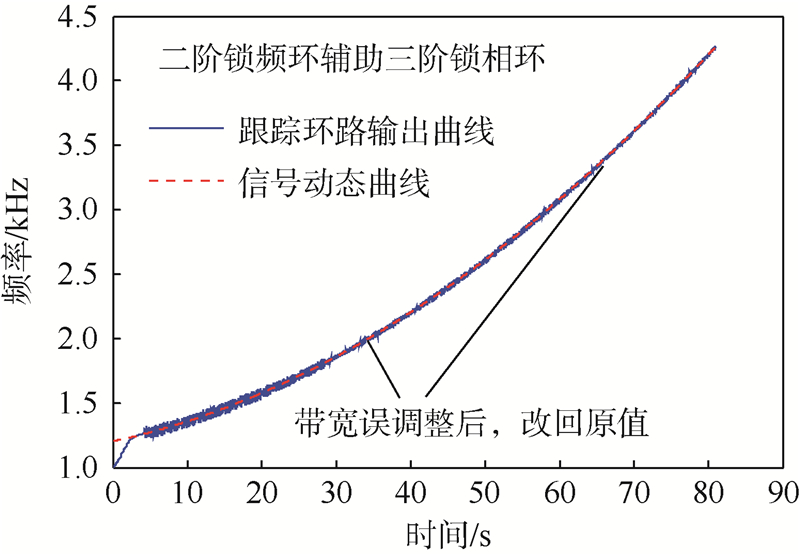 |
| 图 7 带宽试探调整算法的验证Fig. 7 Testing of tentative fitting bandwidth algorithm |
| 图选项 |
 |
| 图 8 跟踪环路误差曲线Fig. 8 Loop tracking error curve |
| 图选项 |
5 结 论1) FLL和PLL的组合方式具有最佳组合方式,并分析确定了状态之间的转换时机,使状态转换更为连续.
2) 提出了试探法调整带宽和优化环路的方法,在高动态低信噪比的情况下,环路调整误差低至3 Hz,提高了跟踪精度,实现了高动态微弱信号精确跟踪.
参考文献
| [1] | Fountain G H,Kusnierkiewicz D Y,Hersman C B,et al.The new horizons spacecraft[M].New York:Springer,2009:23-47. |
| [2] | 唐友喜,邵士海.改进的基于二维扩频WCDMA非Rake接收机[J].通信学报,2005,36(11):93-99.Tang Y X,Shao S H.Improved non-Rake receiver based on two dimensional spread spectrum for WCDMA systems[J].Journal on Communications,2005,36(11):93-99(in Chinese). |
| Cited By in Cnki | |
| [3] | Li Y,Fu H,Kam P Y.Improved,approximate, time-domain ML estimators of chirp signal parameters and their performance analysis[J].IEEE Transactions on Signal Processing,2009,57(4):1260-1272. |
| Click to display the text | |
| [4] | Li W,Liu S,Zhou C,et al.High dynamic carrier tracking using Kalman filter aided phase-lock loop[C]∥Wireless Communications,Networking and Mobile Computing.Piscataway,NJ:IEEE Press,2007:673-676. |
| Click to display the text | |
| [5] | Miao J F,Sun Y R,Liu J Y,et al.A Kalman filter based tracking loop in weak GPS signal processing[C]∥International Conference on Fuzzy Systems and Knowledge Discovery.Piscataway,NJ:IEEE Press,2009:438-442. |
| Click to display the text | |
| [6] | 卢辉斌,王伟伟,谷青川.低信噪比高动态条件下的载波同步技术[J].信息与控制,2010,39(4):451-454.Lu H B,Wang W W,Gu Q C.Carrier synchronization technique for low SNR and high dynamic condition[J].Information and Control,2010,39(4):451-454(in Chinese). |
| Cited By in Cnki (4) | |
| [7] | 王俊,李加琪,吴嗣亮.锁频环辅助下锁相环的跟踪误差分析[J].北京理工大学学报,2011,31(7):838-843.Wang J, Li J Q,Wu S L.Tracking error analysis of FLL-assisted-PLL[J].Transactions of Beijing Institute of Technology,2011,31(7):838-843(in Chinese). |
| Cited By in Cnki (16) | |
| [8] | 程乃平,任宇飞,吕金飞.高动态扩频信号的载波跟踪技术研究[J].电子学报,2003,12A(31):2147-2150.Cheng N P,Ren Y F,Lu J F.Study of carrier tracking for high-dynamic spread spectrum signals[J].Acta Electronica Sinica,2003,12A(31):2147-2150(in Chinese). |
| Cited By in Cnki (112) | |
| [9] | 占巍,张晓林,常啸鸣.跳频对DS/FH接收机载波跟踪精度影响分析[J].北京航空航天大学学报,2012,38(10):1358-1361.Zhan W,Zhang X L,Chang X M.Impact analysis on frequency hopping to carrier tracking precision in DS/FH hybrid spread spectrum receiver[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(10):1358-1361(in Chinese). |
| Cited By in Cnki | |
| [10] | 张厥盛,郑继禹,万心平.锁相技术[M].西安:西安电子科技大学出版社,2004:38-39.Zhang J S,Zheng J Y,Wan X P.Phase-locked technology[M].Xi'an:Xidian University Press,2004:38-39(in Chinese). |
| [11] | 卢满宏,周三文,谌明,等.深空测控通信技术专题研究[J].遥测遥控,2007,28(增刊):11-16.Lu M H,Zhou S W,Chen M,et al.Research on deep space TT&C and communication[J].Journal of Telemetry,Tracking and Command,2007,28(Sup.):11-16(in Chinese). |
| Cited By in Cnki (13) | |
| [12] | 寇艳红.GPS原理与应用[M].2版.北京:电子工业出版社,2007:131-141.Kou Y H.Understanding GPS principles and applications[M].2nd ed.Beijing:Publishing House of Electronics Industry,2007:131-141(in Chinese) |
| [13] | 闫春生.用于深空的自主软件无线电接收机[M].北京:清华大学出版社,2010:180.Yan C S.Autonomous software-defined radio receiver for deep space applications[M].Beijing:Tsinghua University Press,2010:180(in Chinese). |
| [14] | Vilnrotter V A,Hinedi S,Kumar R.Frequency estimation techniques for high dynamic trajectories[J].IEEE Transactions on Aerospace and Electronic Systems,1989,25(4):559-577. |
| Click to display the text | |
| [15] | Satorius E,Estabrook P,Wilsonetal J.Direct-to-earth communications and signal processing for mars exploration rover entry,descent,and landing,IPN Progress Report 42-153[R].Washington,D.C.:NASA,2003:1-35. |
| Click to display the text | |
| [16] | 匡鸿博,茅旭初,王永凯.一种用于高动态环境的GPS信号跟踪方法[J].上海交通大学学报,2012,46(6):854-858.Kuang H B,Mao X C,Wang Y K.A tracking method for GPS signal under high dynamic condition[J].Journal of Shanghai Jiao Tong University,2012,46(6):854-858(in Chinese). |
| Cited By in Cnki (6) |
