目前国际和国内航天界普遍采用NASA编制的质子模型AP8和电子模型AE8来计算辐射带质子和电子的通量,并以此为基础评估辐射带对航天器的影响[3, 5, 6].目前我国可获得的AP8/AE8模型的最新版本分别完成于1976年和1983年,这两个版本使用的都是20世纪70年代以前的数据[7, 8],观测资料比较陈旧,模型计算值与实际观测值经常存在较大偏差[4, 6, 9, 10, 11, 12],使得这两个版本的模型应用到当前航天任务中存在时效局限性.NASA在后期对AP8/AE8模型进行了多次修订和补充,形成了多种修正版本,并且于2006年联合美国多家单位开始开发用于替代AP8/AE8的辐射带质子和电子的新模型:AP9/AE9[6],但由于技术封锁,我国目前还无法获得AP8/AE8的修正版本和AP9/AE9.因此,我国自主研发辐射带模型对于我国航天工程的可持续发展具有现实和战略的意义.地面高度为300~1 000 km的轨道空间即低地球轨道(Low-Earth Orbit,LEO)空间是大量应用卫星运行的区域[13].因此,这一区域是辐射带建模中最重要的区域之一.
1 我国辐射带监测数据情况我国从20世纪80年代开始对空间环境展开了大规模探测,其中LEO空间辐射带高能粒子分布是探测的重点[14].截至到目前为止,已发射卫星中搭载有高能粒子探测器的卫星共有50余颗,其中LEO卫星超过30颗.部分高能粒子探测仪器的卫星轨道、观测对象、能量范围、通道数和观测时段如表 1所示.这些仪器的设计原理相同,都为半导体型探测器.
表 1 高能粒子探测仪器参数Table 1 High energy charged particle detector parameters
| 卫星名称 | 轨道 | 观测对象 | 能量范围/MeV | 通道数 | 观测时段 |
| 神舟四号、神舟五号 | 近圆轨道,高度340 km,倾角42° | 质子能谱 | 2.9~300 | 10 | 2002-12—2004-05 |
| 电子能谱 | 0.2~5.0 | 9 | |||
| 天宫一号 | 近圆轨道,高度380 km,倾角43° | 质子能谱 | >1.5 | 8 | 2011-10至今 |
| 电子能谱 | >0.2 | 8 | |||
| 风云三号A星、B星、C星 | 近圆轨道,高度830 km,倾角98° | 质子能谱 | 3~300 | 6 | 2008-05至今 |
| 电子能谱 | 0.15~5.7 | 5 | |||
| 风云一号C星、D星 | 近圆轨道,高度860 km,倾角98° | 质子能谱 | 2.9~300 | 5 | 1995-05—2010-06 |
| 电子通量 | >1.6 | 1 | |||
| 实践五号 | 近圆轨道,高度860 km,倾角98° | 质子能谱 | 2.9~300 | 5 | 1999-05—2000-02 |
| 电子能谱 | 0.15~5.7 | 5 | |||
| 实践四号 | 大椭圆轨道,近地点200 km,远地点36 000 km,倾角28.5° | 质子能谱 | 4~300 | 1994-02—1994-08 | |
| 电子能谱 | 0.5~4 | 5 | |||
| 风云二号A星、B星 | 静止轨道 | 质子能谱 | 2.9~300 | 3 | 1997-06—1998-04 2000-06—2001-02 |
| 质子通量 | >1.1 | 1 | |||
| 电子通量 | >1.4 | 1 | |||
| 风云二号C星、D星、E星 | 静止轨道 | 质子能谱 | 10~300 | 3 | 2004-10至今 |
| 电子通量 | >0.35 >2 | 2 | |||
| 风云二号F星 | 静止轨道 | 质子能谱 | >4 | 6 | 2012-01至今 |
| 电子能谱 | >0.2 | 11 |
表选项
不同仪器获得的探测数据在联合使用前,必须经过交叉定标[15].因此在建模过程中,研究人员对表 1所列数据进行了同化处理,并以此为基础建立了LEO、中地球轨道(Medium-Earth Orbit,MEO)和同步轨道(Geosynchronous Orbit,GEO)辐射环境数据库,数据库包含了超过一个完整太阳活动周(11 a)的LEO空间辐射带数据,可以用于LEO空间辐射带建模.
2 辐射带建模的方法本文利用我国辐射带高能粒子的探测数据建立的自主辐射带模型和NASA的AP8/AE8均为经验模型,即模型的基础是具有特定组织结构的数据,文中将这种具有特定组织结构的数据定义为表单.在辐射带模型中,表单指的是能描述辐射环境某一给定时刻、给定空间环境状态下在所有空间维度上分布特征的粒子通量数据列表.AP8/AE8仅含有一组代表太阳活动高年和低年时对应高能粒子通量平均分布的表单,不能给出辐射带随地磁场长期变化而引起的缓变,也不能反映太阳活动周内的各种周期性变化和各种突发性扰动变化[16],因此称其为静态模型;代替它的AP9/AE9只能通过输出结果中的概率间接地反映各种变化对辐射带的影响[17],说明AP9/AE9也不是真正意义上的动态模型.
本文试图建立的自主辐射带模型的建模主要步骤如图 1所示.从图 1中可以看出,模型输出结果是通过对模型数据中的4组表单进行查询、计算并将结果进行叠加后得到的,因此这4组表单是模型的核心内容.这4组表单分别给出辐射带的宁静状态、长期缓变状态、周期变化状态和扰动变化状态,因此自主辐射带模型属于动态模型,这也是该模型相比于AP8/AE8的最大改进之处.表单的建立流程如图 2所示.同化后的数据在空间中离散分布,必须先经过空间网格化处理,使数据在空间中均匀分布后,再进行分类处理,生成各类数据库.因此,空间网格化是建模中的重要步骤.3种轨道空间中,LEO空间卫星最多,且LEO空间包含了多个不同高度的轨道,而MEO(特指高度为22 000 km、倾角为55°的卫星轨道)空间和GEO空间均仅包含单一轨道的若干颗卫星.因此,LEO空间的数据网格化成为建模中的重点.
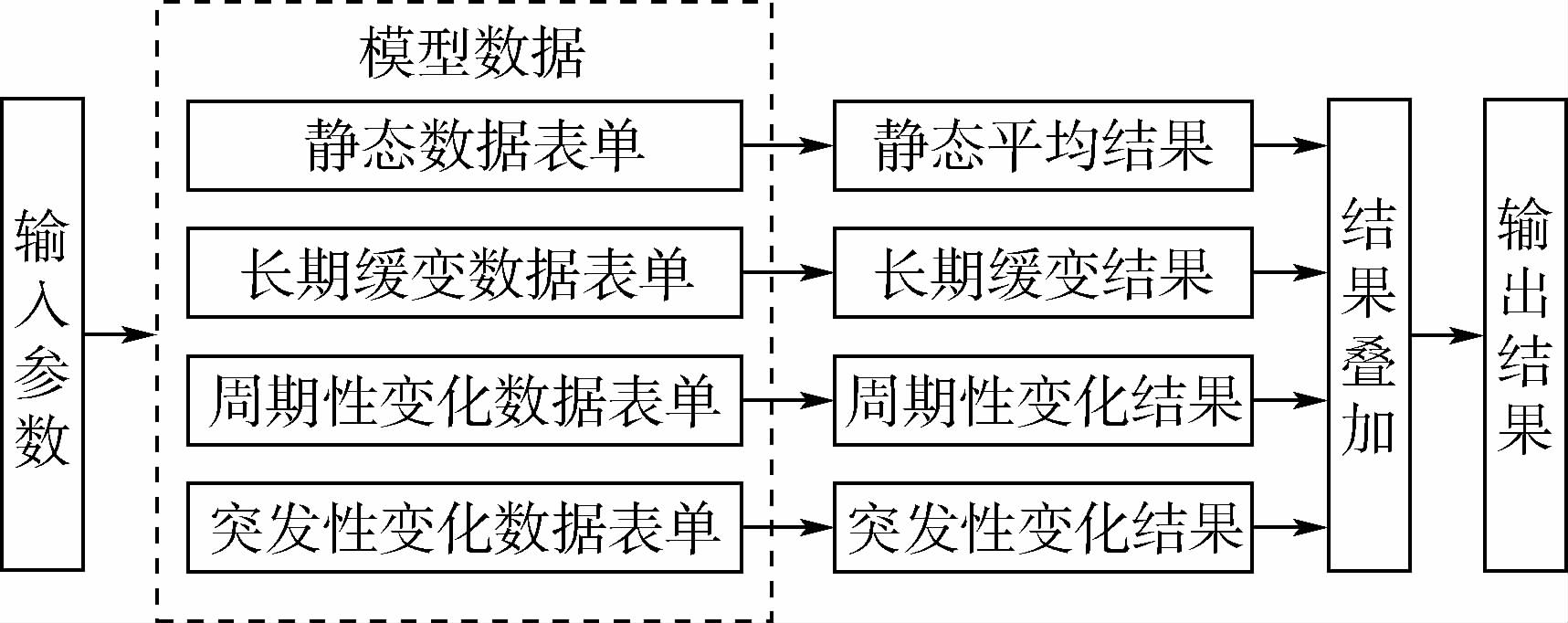 |
| 图 1 自主辐射带模型框架 Fig. 1 Framework of own radiation belts model |
| 图选项 |
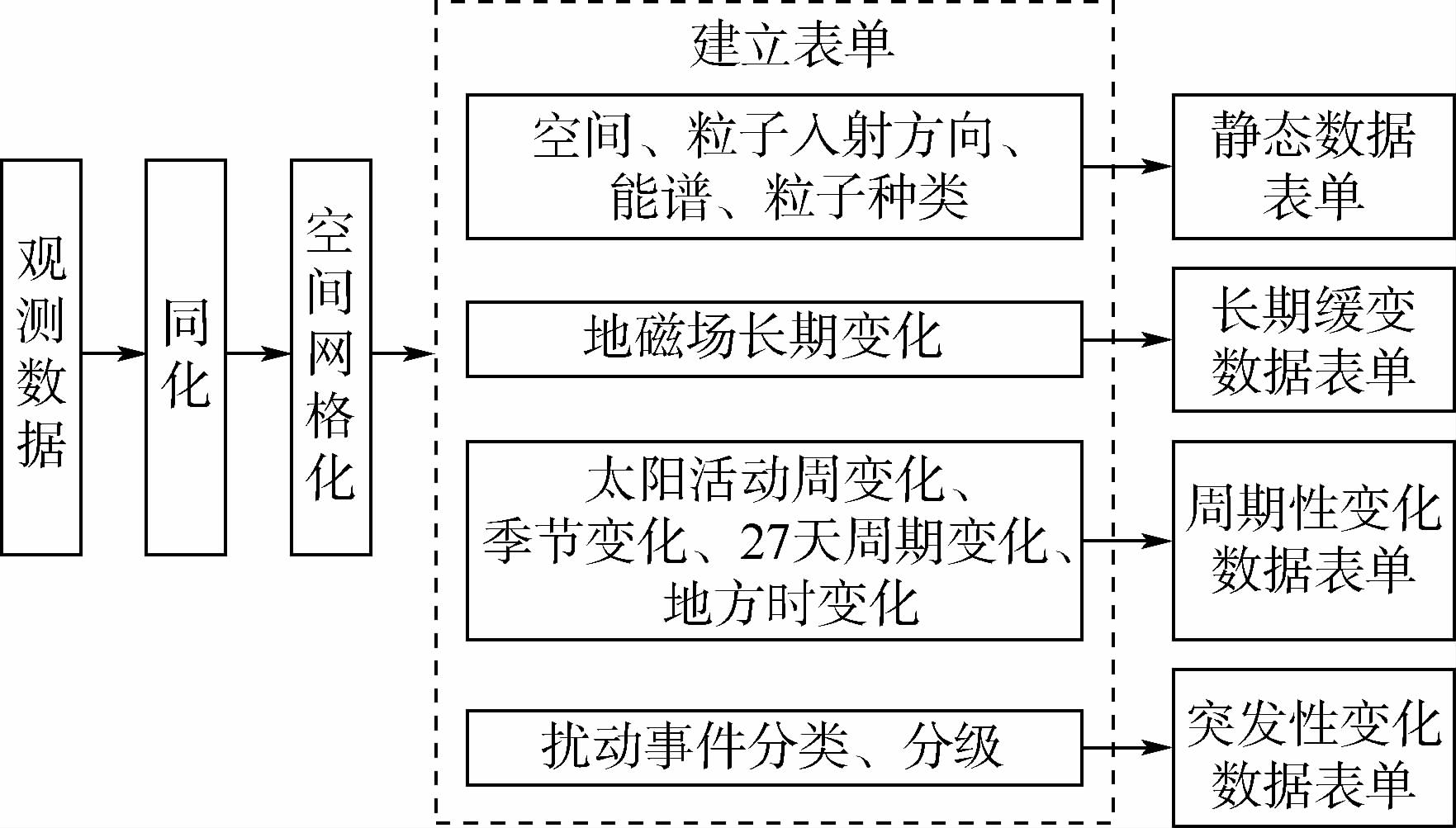 |
| 图 2 自主辐射带模型表单建立流程 Fig. 2 Procedure of creating data table in own radiation belts model |
| 图选项 |
3 LEO空间数据网格化3.1 空间数据网格鉴于LEO空间观测数据的分布特点,为了得到如图 3所示的空间数据网格,本文采取了以下处理方法进行数据网格化:
1) 利用11个轨道高度上的卫星观测资料,完成对应11个空间球面上的数据网格化.对于同系列卫星观测数据的使用原则是,利用其中部分卫星的观测资料完成插值,剩余卫星的观测资料用于对插值结果进行验证.
2) 11个空间球面以外的空间,利用11个空间球面的数据网格,结合大椭圆轨道卫星的观测资料通过插值获得;11个空间球面之间的区域采用内插,高度范围为300~340 km、860~1 000 km的区域采用外插.
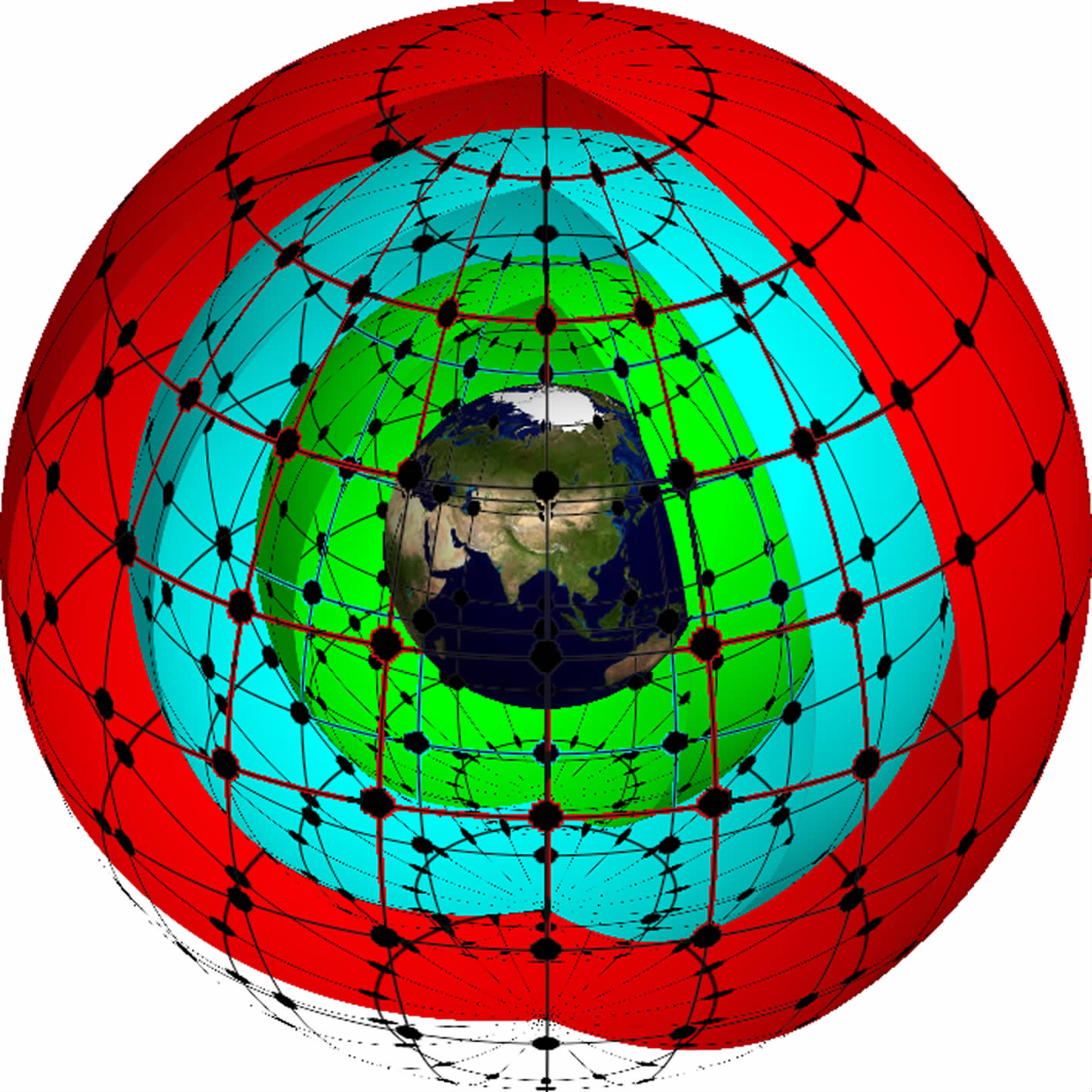 |
| 图 3 LEO空间数据网格 Fig. 3 Data grid of LEO space |
| 图选项 |
3.2 可选用的插值方法空间网格点上的粒子通量大小是通过对观测数据插值获得的,而插值中最关键的步骤是利用同一空间球面上观测数据进行插值得到该球面上的网格点通量.常用的插值方法包括反距离加权法(Inverse Distance Weighting,IDW)[18]、克里格法(Kriging)[19]、自然邻点法(natural neighbor)[20]、最近邻点法(nearest neighbor)[21]、多元回归法(polynomial regression)[22]、最小曲率法(minimum curvature)[23, 24]、C1连续5次双变量插值法(quintic)[25, 26]、改进谢别德法(modified Shepard’s)[27, 28, 29]径向基函数法(Radial Basis Function,RBF)[30, 31]、三角形剖分法(triangulation)[32, 33, 34]等.这些方法在基本原理、数学模型、计算效率等方面各不相同,但在使用中一般都需要输入辅助参数,例如:克里格法需要输入所采用的变异函数的类型、变程、块金值、基台值[35];改进谢别德法需要输入节函数的两个影响半径[36];径向基函数法需要确定插值使用的径向基函数[37].
在应用插值方法时,由于网格点和观测数据分布在球面上,因此插值形式应为球面插值;同时由于辐射带内的粒子通量分布服从幂律谱[38],因此计算中应采用对数插值.
使用空间球面上的网格点通量可以反演出该球面上任意位置的通量.通过对反演结果的误差分析可以确定网格点通量的精度,进而确定选取的插值方法是否合适.对反演结果的误差分析主要是对反演值(P)和观测值(O)之差(D=P-Q)进行分析.误差分析包括两部分:计算各类误差成分在总误差中的比例和计算误差大小[39].本文采用均方误差(Mean Square Error,MSE)来描述误差比例.MSE包括系统均方误差(systematic MSE)MSEs和非系统均方误差(unsystematic MSE)MSEu,其中MSEs由3部分组成,包括MSE中的偏移成分(additive MSE)MSEa、缩放成分(proportional MSE)MSEp和MSEa、MSEp互相依赖成分(interdependence MSE)MSEi.以上误差的计算方法由式(1)~式(6)给出:
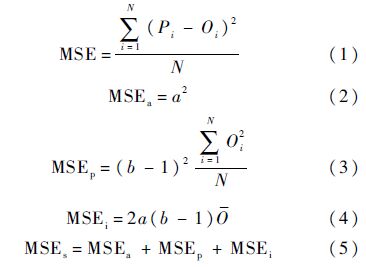
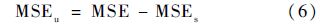
式中:N为观测点数;Pi和Oi分别为第i点的计算值和观测值;O为观测值的平均值;a和b分别为以O为自变量、以P为因变量采用最小二乘法拟合出的直线的截距和斜率.
本文采用RMSE、RMSEs、RMSEu、RMSEa、RMSEp、RMSEi来描述误差大小,这6个参数值的量纲与粒子通量相同,大小分别等于MSE、MSEs、MSEu、MSEa、MSEp、MSEi的平方根,符号与MSE、MSEs、MSEu、MSEa、MSEp、MSEi相同.同时,还采用了一致性系数d来描述P和O的一致程度,d的计算方法为
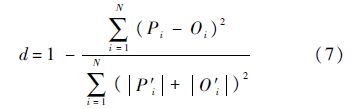
式中:P′i和O′i分别由式(8)和式(9)给出:
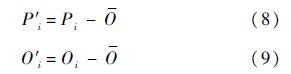
d的取值范围在0.0~1.0之间,d越接近1.0表示计算值和观测值的一致性越高.
3.3 插值方法的应用本文通过对轨道高度为630 km的两颗卫星的观测数据的处理来说明空间球面上的数据网格化方法及精度评估标准.这两颗卫星为同系列卫星,各自搭载了一台由中国科学院空间中心空间环境探测研究室研制的高能粒子探测器,两台探测器的工作原理、制造工艺和技术指标完全相同.该探测器可以对6个能道的高能质子通量和1个能道的高能电子通量同时进行观测.选定的观测数据为2010年8月29日至10月10日期间能量范围为3~5 MeV的质子通量,该时间段内空间环境始终保持宁静,得到的观测数据中不包含突发性空间环境扰动引起的质子通量变化.
数据处理的具体步骤如下:
1) 利用其中一颗卫星的数据,选取一种插值方法,给定该方法所需的各项参数值,得到卫星所处空间球面上的网格点通量,网格划分以经度、纬度为单位,每1°作为一个网格.
2) 使用网格点通量反演另一颗卫星各观测位置的通量,反演采用趋势面插值法,即在网格点中选取3个点,此3个点形成的三角形是可以包围采样位置的最小三角形,将网格点的经度、纬度作为x、y坐标,通量作为z坐标,拟合出一个趋势面方程,利用该方程计算出观测位置的通量.
3) 将反演值与观测值进行比对,得到所选定插值方法在采用选定参数时的误差分析结果.
在第3.2节给出的各种插值方法中,反距离加权法、自然邻点法、最近邻点法、克里格法和径向基函数法支持球面插值,克里格法和径向基函数法在使用中需要较多的人工干预才能得到精度较高的结果,不适于工程应用.因此,在实际建模中本文选择了反距离加权法、自然邻点法和最近邻点法进行对比.表 2给出了这3种插值方法处理结果的误差分析对比,改变反距离加权法的输入参数会得到不同的处理结果,表 2给出的是其误差分析最优的结果.从表 2给出的结果可以看出,反距离加权法在最优状态下得到的处理结果的精度高于自然邻点法和最近邻点法,原因在于其输入参数优化处理能够大幅减小系统偏差(RMSEs)中的缩放成分(RMSEp),自然邻点法和最近邻点法没有可调整的输入参数,反距离加权法有两个输入参数可以调整,其计算原理为
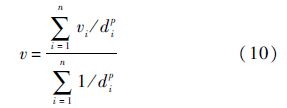
式中:v^为待插值点的属性值,即网格点通量;vi为参与插值的离散点属性,即观测位置的通量;di为观测位置和网格点的距离,因此,可以通过调整距离的阶数p和观测数据的范围n获得不同的插值结果,而在实际应用中一般是通过改变搜索半径r来控制参与插值的观测数据的范围.
表 2 采用反距离加权法、自然邻点法和最近邻点法处理结果的误差分析对比Table 2 Error analysis comparison of processing results of IDW,natural neighbor and nearest neighbor
| 方法 | a | b | RMSE/ (cm-2·sr-1·s-1) | RMSEu/ (cm-2·sr-1·s-1) | RMSEs/ (cm-2·sr-1·s-1) |
| 自然邻点法 | -0.695 11 | 1.251 67 | 71.685 75 | 46.598 82 | 54.473 82 |
| 最近邻点法 | -0.487 22 | 1.251 92 | 73.888 11 | 49.802 22 | 54.581 97 |
| 反距离加权法 | -2.196 72 | 1.017 09 | 48.647 80 | 48.483 42 | 3.995 68 |
| 方法 | RMSEa/ (cm-2·sr-1·s-1) | RMSEp/ (cm-2·sr-1·s-1) | RMSEi/ (cm-2·sr-1·s-1) | MSEu/MSE | MSEs/MSE |
| 自然邻点法 | 0.695 11 | 54.580 76 | -3.485 11 | 0.422 56 | 0.577 44 |
| 最近邻点法 | 0.487 22 | 54.657 84 | -2.919 82 | 0.454 31 | 0.545 69 |
| 反距离加权法 | 2.196 72 | 3.707 74 | -1.614 77 | 0.993 25 | 0.006 75 |
| 方法 | MSEa/MSE | MSEp/MSE | MSEi/MSE | d | |
| 自然邻点法 | 0.000 09 | 0.579 71 | -0.002 36 | 0.978 11 | |
| 最近邻点法 | 0.000 04 | 0.547 21 | -0.001 56 | 0.976 78 | |
| 反距离加权法 | 0.002 04 | 0.005 81 | -0.001 10 | 0.987 48 |
表选项
在计算中,将r的范围确定为1~22 013.14 km,其中1 km为观测点至网格点距离的最小值,22 013.14 km为卫星轨道球面上大圆的半周长.在此范围下,本文获得了p从1~10的处理结果.图 4和图 5所示分别为不同p取值下的d和RMSE的对比.从图 4可以看出,当r<1 000 km时,不同p取值下的结果基本相同;当r>1 000 km时,在p=1和p=2的情况下d会随着r的增加迅速减小,在p≥3的情况下d基本保持不变,仍然维持较高水平.图 5所示的RMSE的变化规律与d类似,在p=1、2和3的情况下最小RMSE值均小于p≥4,但获得最小RMSE的r各不相同.图 4和图 5的结果说明,在p≥4的情况下,当r>65 km时,不同p值下d和RMSE的变化规律几乎完全相同,说明此种情况下单纯增大r不能影响插值结果的精度,这是由反距离加权法的原理决定的.从式(10)中可知,p增大会增加距离网格点较近的实测点在插值结果中的权重.因此,当r取值使得搜索范围包含全部对插值结果有主要作用的实测点后,增大r基本不会改变插值结果的精度.
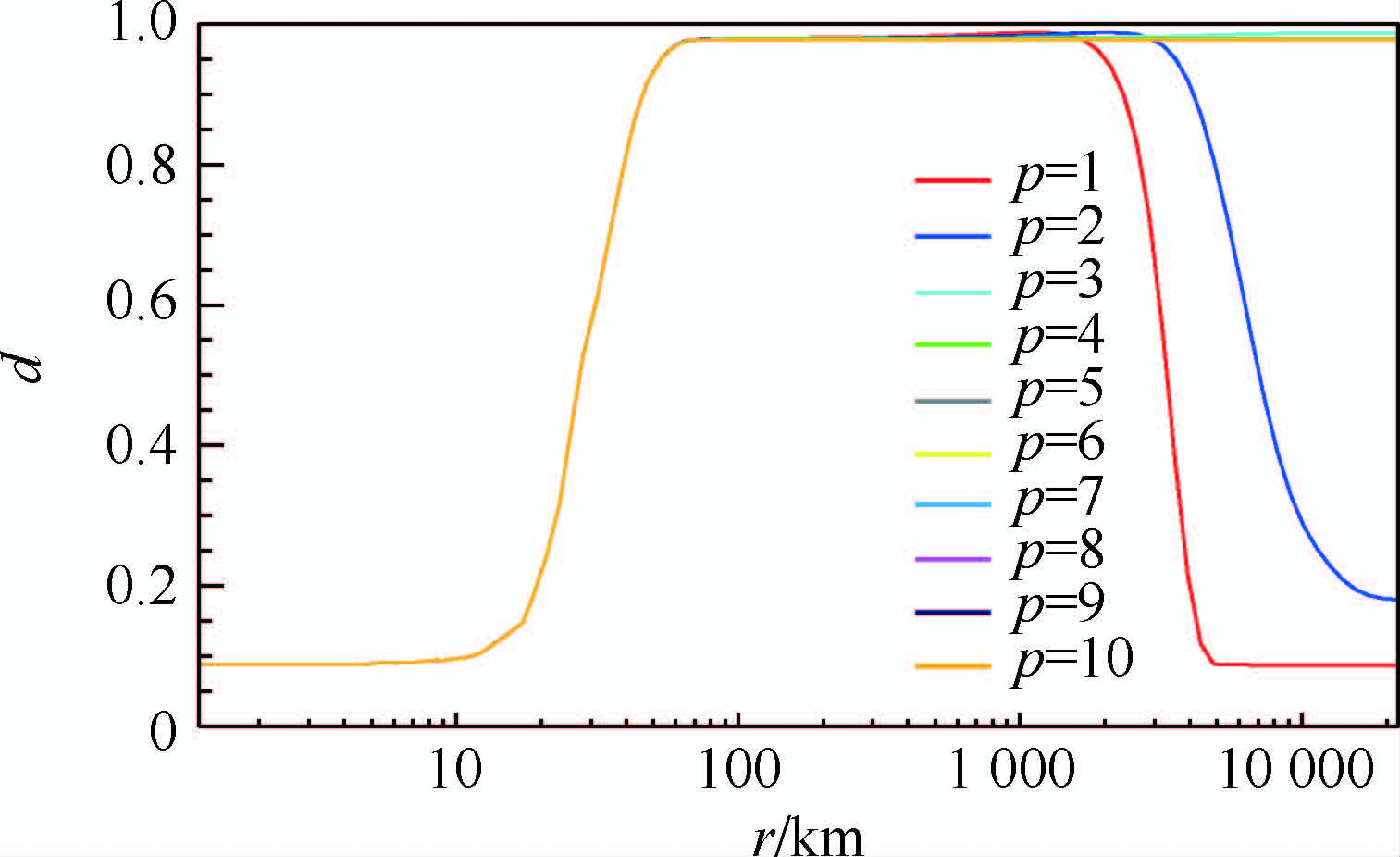 |
| 图 4 反距离加权法取不同p时处理结果的d对比 Fig. 4 Comparison of processing results of d with different p in IDW |
| 图选项 |
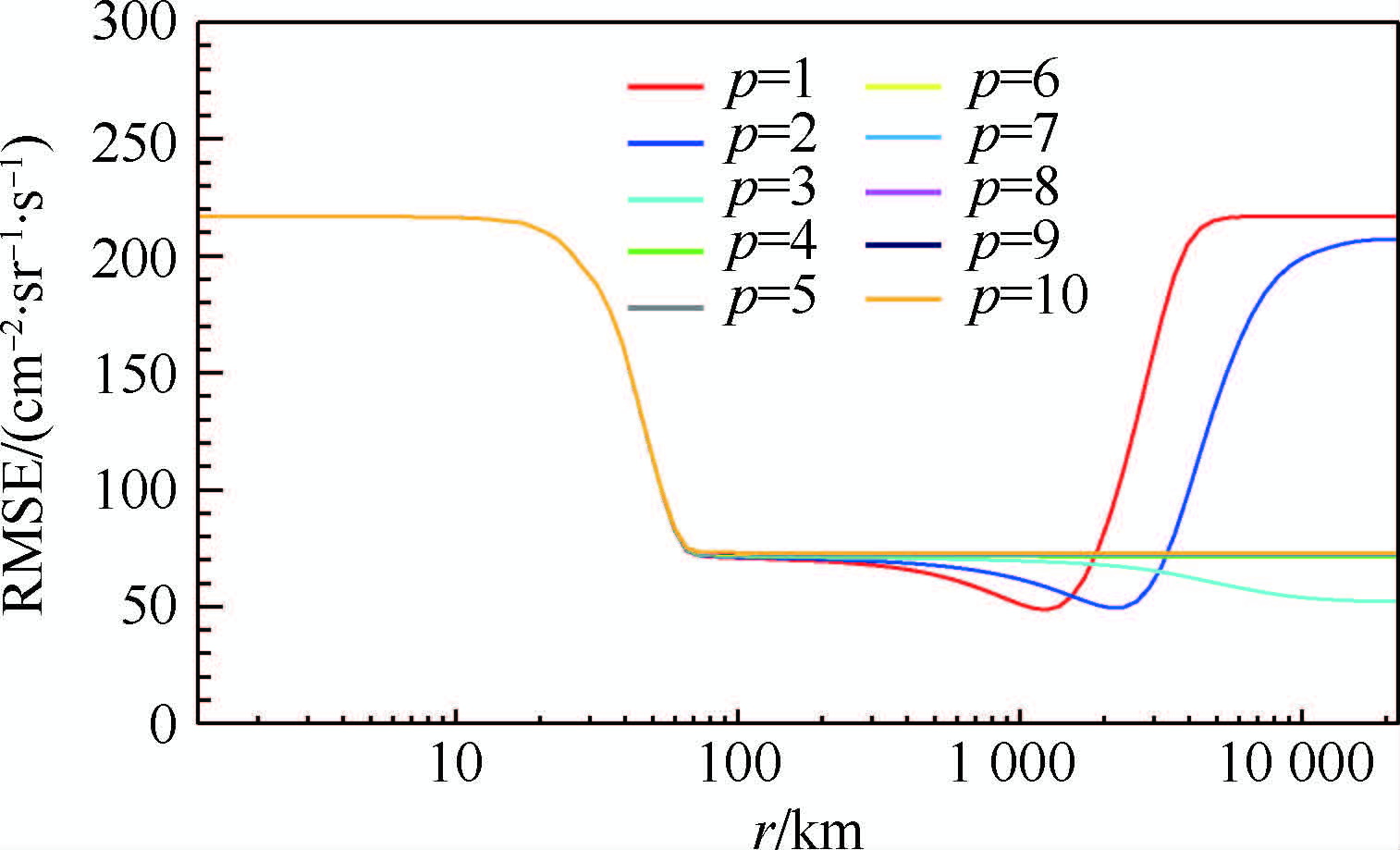 |
| 图 5 反距离加权法取不同p时处理结果的RMSE对比 Fig. 5 Comparison of processing results of RMSE with different p in IDW |
| 图选项 |
图 6给出了反演结果和观测结果的对比,反演结果采用反距离加权法处理获得,p从1取到10,选定的r使当前p下反演结果的RMSE最小.
 |
| 图 6 质子通量观测结果和网格数据反演结果对比 Fig. 6 Proton flux comparison of observation and inversion result by data grid |
| 图选项 |
从图 6可以发现观测结果具有以下缺陷:
1) 本底较高,基本维持在大于10/(cm2·sr·s)的水平,这是由探测器几何因子较小决定的.
2) 通量范围在10~100/(cm2·sr·s)的区间内,观测结果抖动比较严重,这是受仪器本底噪声和观测数据采用遥测分层值方式采集的共同影响造成的.
理想的网格数据给出的反演结果,应该可以对观测数据中出现的以上缺陷予以修正.对比图 6给出的各阶反演结果,可以发现它们具有以下特点:
1) 通量大于100/(cm2·sr·s)时,各阶反演结果与观测结果一致性均较高.
2) 通量小于100/(cm2·sr·s)时,低阶(p=1,p=2)反演结果具有较好的消除抖动的效果,对于本底以下的通量具有较好的外推效果.
因此,使用反距离加权法进行处理,当距离阶数p选定为1或2时,得到的反演结果合理程度更高;同时,根据图 4和图 5给出的误差分析结果,选择合适的搜索半径r,可以使反演结果精度最高.
4 结 论本文说明了自主辐射带模型属于动态模型的原因,指出了自主模型相比于AP8/AE8的改进之处,即可以给出各种辐射带周期性变化和扰动变化;讨论了辐射带自主建模的目标和思路,针对LEO空间数据网格化问题,根据目前我国自主探测数据的实际情况,使用了空间分层的方式对每一个卫星所处空间球面上的数据分别进行处理;在生成数据网格的插值计算中,根据各常用插值方法的特点,选择反距离加权法、自然邻点法和最近邻点法作为考察的插值方法,通过对网格数据反演结果的误差分析和与观测结果的比对,确定反距离加权法具有更高的精度,且反距离加权法在采用低阶距离的情况下生成的数据网格得到的反演结果具有更高的合理性,并可以对实测数据中的一些缺陷进行弥补.
本文讨论的LEO空间数据网格化方法的评价标准建立在误差分析的基础上,是一种数值分析的方法.实际上,辐射带的形成有着复杂的物理机制,其内部高能带电粒子的分布也服从相应的物理规律,因此辐射带建模不能脱离物理理论的指导.在后续工作中需要重点改进的地方是将物理理论与数值分析方法相结合,利用物理理论对数值分析方法进行完善.
参考文献
| [1] | Bothmer V,Daglis I A.Space weather:Physics and effects[M].New York:Springer,2007:154-159. |
| [2] | 徐文耀.地球电磁现象物理学[M].合肥:中国科学技术大学出版社,2009:388-389. Xu W Y.Physics of electromagnetic phenomena of the earth[M].Heifei:University of Science and Technology of China Press,2009:388-389(in Chinese). |
| [3] | 沈自才.空间辐射环境工程[M].北京:中国宇航出版社,2013:4-29. Shen Z C.Space radiation environmental engineering[M].Beijing:China Astronautic Publishing House,2013:4-29(in Chinese). |
| [4] | 姜景山,王文魁,都亨,等.空间科学与应用[M].北京:科学出版社,2000:649-652. Jiang J S,Wang W K,Du H,et al.Space science and applications[M].Beijing:Science Press,2000:649-652(in Chinese). |
| [5] | 褚桂柏.空间飞行器设计[M].北京:航空工业出版社,1996:49-54. Chu G B.Space vehicle design[M].Beijing:Aviation Industry Press,1996:49-54(in Chinese). |
| [6] | Ginet G P,O'Brien T P.Trapped radiation and plasma models requirements specification,AE-9/AP-9[R].Washington,D.C.:NASA,2009. |
| [7] | Vette J I.The AE-8 trapped electron model environment,NASA STI/Recon Technical Report N,1991,92:24228[R].Washington,D.C.:NSSDC/WDC-A-R&S,1991. |
| [8] | Sawyer D M,Vette J I.AP-8 trapped proton environment for solar maximum and solar minimum,NASA STI/Recon Technical Report N,1976,77:18983[R].Washington,D.C.:NSSDC/WDC-A-R&S,1976. |
| [9] | 王世金,叶宗海.实践四号卫星高能质子重离子探测器探测数据初步分析[J].航天器工程,1995,4(3):1-7. Wang S J,Ye Z H.Initial data analysis from the energetic proton and heavy ion detector on-board SJ-4 satellite[J].Spacecraft Engineering,1995,4(3):1-7(in Chinese). |
| Cited By in Cnki (3) | |
| [10] | 师立勤,王世金,叶宗海,等.实践五号高能粒子环境探测结果[C]//实践五号卫星空间探测与试验成果学术会议论文集.北京:中国空间科学学会空间探测专业委员会,2002:51-61. Shi L Q,Wang S J,Ye Z H.et al.Energetic particle environment detection results by SJ-5 satellite[C]//Symposium of the Scholar Meeting on Space Exploration and Test Results by SJ-5 Satellite.Beijing:Space Exploration Committee of Chinese Society of Space Research,2002:51-61(in Chinese). |
| [11] | 王世金,朱光武,梁金宝,等.FY-1C卫星空间粒子成分监测器及其探测结果[J].上海航天,2001,18(2):24-28. Wang S J,Zhu G W,Liang J B,et al.FY-1C space particle composition monitor and the results detected[J].Aerospace Shanghai,2001,18(2):24-28(in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [12] | Leonov A,Cyamukungu M,Cabrera J,et al.Pitch angle distribution of trapped energetic protons and helium isotope nuclei measured along the Resurs-01 No.4 LEO satellite[J].Annales Geophysicae,2005,23(9):2983-2987. |
| Click browse the original | |
| [13] | 王鹏,徐青,李建胜,等.空间环境建模与可视化仿真技术[M].北京:国防工业出版社,2012:92-95. Wang P,Xu Q,Li J S,et al. Space environment modeling and visual simulation techniques[M].Beijing:National Defence Industry Press,2012:92-95(in Chinese). |
| [14] | 王世金,朱光武,梁金宝.我国空间环境天基监测网建设[C]//中国空间科学学会空间探测专业委员会第十六次学术会议论文集(上).北京:中国空间科学学会空间探测专业委员会,2003:65-68. Wang S J,Zhu G W,Liang J B.Space-based space weather monitoring network building in China[C]//Symposium of the 16th Scholar Meeting Held by Space Exploration Committee of Space Science Society in China(I).Beijing:Space Exploration Committee Chinese Society of Space Research,2003:65-68(in Chinese). |
| [15] | Friedel R H W,Bourdarie S,Cayton T E.Intercalibration of magnetospheric energetic electron data[J].Space Weather,2005,3(9):2561-2570. |
| Click browse the original | |
| [16] | 庄洪春.宇航空间环境手册[M].北京:中国科学技术出版社,2000:140-148. Zhuang H C.Aerospace environmental handbook[M].Beijing:China Science and Technology Press,2000:140-148(in Chinese). |
| [17] | O'Brien T P.A framework for next-generation radiation belt models[J].Space Weather,2005,3(7):1891-1904. |
| Click browse the original | |
| [18] | Serón F J,Badal J I,Sabadell F J.Spatial prediction procedures for regionalization and 3-D imaging of Earth structures[J].Physics of the Earth and Planetary Interiors,2001,123(2):149-168. |
| Click browse the original | |
| [19] | Isaaks E H,Srivastava R M.Applied geostatistics[M].New York:Oxford University Press,1989:279-322. |
| [20] | Watson D F.Contouring:A guide to the analysis and display of spatial data[J].Computer Methods in the Geosciences,1993,19(10):1571-1572. |
| Click browse the original | |
| [21] | Aurenhammer F.Voronoi diagrams:A survey of a fundamental geometric data structure[J].ACM Computing Surveys(CSUR),1991,23(3):345-405. |
| Click browse the original | |
| [22] | PIZOR P J.Principles of geographical information systems for land resources assessment[J].Soil Science,1987,144(4):306. |
| Click browse the original | |
| [23] | Barrodale I,Skea D,Berkley M,et al.Warping digital images using thin plate splines[J].Pattern Recognition,1993,26(2):375-376. |
| Click browse the original | |
| [24] | Powell M J D.Tabulation of thin plate splines on a very fine two-dimensional grid,DAMTP 1992/NA2[R].Cambridge:University of Cambridge,1992. |
| [25] | Akima H.Algorithm 761:Scattered-data surface fitting that has the accuracy of a cubic polynomial[J].ACM Transactions on Mathematical Software(TOMS),1996,22(3):362-371. |
| Click browse the original | |
| [26] | Renka R J,Cline A K.A triangle-based C1 interpolation method[J].Rocky Mountain Journal,1984,14(1):223-238. |
| Click browse the original | |
| [27] | Franke R,Nielson G.Smooth interpolation of large sets of scattered data[J].International Journal for Numerical Methods in Engineering,1980,15(11):1691-1704. |
| Click browse the original | |
| [28] | Renka R J.Algorithm 790:CSHEP2D:Cubic shepard method for bivariate interpolation of scattered data[J].ACM Transactions on Mathematical Software (TOMS),1999,25(1):70-73. |
| Click browse the original | |
| [29] | Shepard D.A two-dimensional interpolation function for irregularly-spaced data[C]//Proceedings of the 1968 23rd ACM National Conference.New York:ACM,1968:517-524. |
| [30] | Franke R.A critical comparison of some methods for interpolation of scattered data,NPS-53-79-003[R].Monterey,CA:Naval Postgraduate School,1979. |
| [31] | Hardy R L.Theory and applications of the multiquadric-biharmonic method 20 years of discovery 1968-1988[J].Computers & Mathematics with Applications,1990,19(8-9):163-208. |
| Click browse the original | |
| [32] | Peucker T K,Fowler R J,Little J J,et al.The triangulated irregular network[C]//International Symposium on Cartography and Computing:Applications in Health and Environment.Gaithersburg,Maryland:AmericanCongress on Surveying and Mapping,1978:516-532. |
| [33] | Krajewski S A,Gibbs B L.Understanding contouring:A practical guide to spatial estimation and contouring using a computer and basics of using variograms[M].Boulder,CO:Gibbs Associates,2001:20-25. |
| [34] | Lee D T,Schachter B J.Two algorithms for constructing a Delaunay triangulation[J].International Journal of Computer & Information Sciences,1980,9(3):219-242. |
| Click browse the original | |
| [35] | 侯景儒,尹镇南,李维明,等.实用地质统计学[M].北京:地质出版社,1998:45-50. Hou J R,Yin Z N,Li W M,et al.Practical geology statistics[M].Beijing:Geological Publishing House,1998:45-50(in Chinese). |
| [36] | 张维娜,吕云霄,吴美平.改进谢别德插值方法在地磁图构建中的应用[J].导航与控制,2011,10(1):28-32. Zhang W N,Lv Y X,Wu M P.Application of modified shepard interpolation in geomagnetic map[J].Navigation and Control,2011,10(1):28-32(in Chinese). |
| [37] | 魏义坤,杨威,刘静.关于径向基函数插值方法及其应用[J].沈阳大学学报,2008,20(1):7-9. Wei Y K,Yang W,Liu J.Interpolation method of radial basis function and its application[J].Journal of Shenyang University,2008,20(1):7-9(in Chinese). |
| Cited By in Cnki (27) | Click to display the text | |
| [38] | 涂传诒.日地空间物理学:行星际与磁层.下册[M].北京:科学出版社,1988:118-127. Tu C Y.Sun-earth space physics:Interplanetary and magnetosphere (II)[M].Beijing:Science Press,1988:118-127(in Chinese). |
| [39] | Willmott C J.On the validation of models[J].Physical Geography,1981,2(2):184-194. |
| Click browse the original |
