随着分数阶微分方程理论研究的不断完善,分数阶偏微分方程数值方法的研究引起了****们越来越多的重视.最近几年,出现了许多分数阶偏微分方程数值方法的成果.Liu等[4]提出了一种直线法,把空间分数阶Fokker-Planck方程转化为一阶微分系统进而求其数值解.Meerschaert等[2, 3]和Tadjeran等[5, 6]分别提出了空间分数阶偏微分方程的显示Euler方法、隐式Euler方法和分数阶Crank-Nicolson(C-N)方法,进行了稳定性和收敛性分析.Liu等[7]讨论了Levy-Feller对流弥散过程的随机步和有限差分逼近.Zhuang等[8]考虑了一类变阶的分数阶对流扩散方程的显式和隐式Euler格式,进行了收敛分析.更多分数阶偏微分方程数值方法的文献,可参考文献[4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18].
注意到很多分数阶微分方程差分方法的文献处理的都是一维问题空间分数阶导数或者时间分数阶导数,对高维问题以及空间时间分数阶导数很少有人涉及[3, 9].受到以上研究工作的启发,本文研究二维空间时间分数阶色散方程的有限差分格式.由于分数阶问题的隐式差分格式在每一时间步都需要处理非稀疏线性系统,于是隐式差分格式是计算密集型的.通过把偏微分方程差分方法中经常用到的交替方向隐式差分格式推广到分数阶偏微分方程,从而克服了这一问题.
1 问题描述考虑二维空间时间分数阶色散方程:
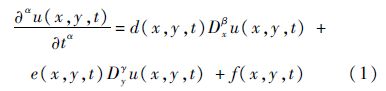
式中:0<t≤T;0<x<Lx;0<y

式中:u为溶质的浓度;d(x,y,t)和e(x,y,t)分别为x和y方向的扩散系数;时间分数阶导数$\frac{{{\partial }^{\alpha }}u\left( x,y,t \right)}{\partial {{t}^{\alpha }}}$为α(0<α≤1)阶Caputo分数阶导数,其定义为[10]
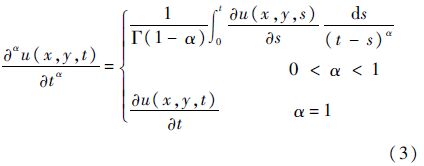
其中:Γ(·)为伽马函数;Dxβu(x,y,t)和Dyγu(x,y,t)分别为β(1<β≤2)和γ(1<γ≤2)阶的Riemann-Liouville分数阶导数,其分别定义为

从物理意义方面考虑,要求0<α≤1、1<β、γ≤2,并且u(0,y,t)=u(x,0,t)=0.这意味着在下边界没有示踪剂泄漏.函数f(x,y,t)可用来表示源和汇.当α=1、β=γ=2时,方程式(1)还原为经典的二维色散方程.以下假设d(x,y,t)≥0并且e(x,y,t)≥0,即流体是从下边界到上边界.在上述条件下方程式(1)存在唯一的光滑解[11].
2 隐式差分格式令tn=nτ,n=0,1,…,N;xi=ihx,i=0,1,…,Nx;yj=jhy,j=0,1,…,Ny,其中$\tau =\frac{T}{N}$为时间步长,hx=$\frac{{{L}_{x}}}{{{N}_{x}}}$和hy=$\frac{{{L}_{y}}}{{{N}_{y}}}$为空间步长.令ui,jn为差分方法的数值解.引入记号Δtu(xi,yj,tn)=u(xi,yj,tn+1)-u(xi,yj,tn),按如下方式对时间分数阶导数进行离散:
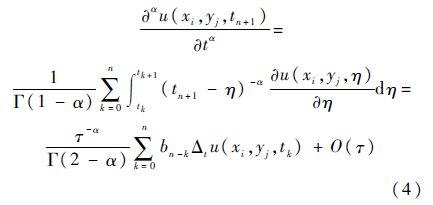
式中:bk=(k+1)1-α-k1-α,k=0,1,…,N.
对于空间分数阶导数Dxβu(xi,yj,tn+1)和Dyγu(xi,yj,tn+1),采用转移Grünwald公式[2]:

式中:
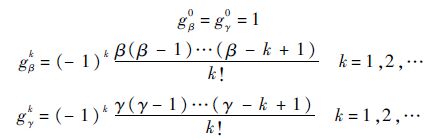
分别令
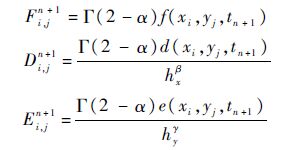
由式(4)~式(6),可以得到如下的隐式差分格式:

式中:0≤n≤N-1;1≤i≤Nx-1;1≤j≤Ny-1.式(7)又可表示为

初边值条件分别离散为
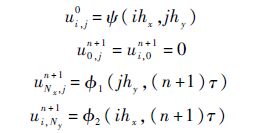
式中:0≤n≤N-1;0≤i≤Nx;0≤j≤Ny.
引理1[2] 系数bk、gβk、gγk(k=0,1,…)满足bk>0,bk>bk+1(k=0,1,…)并且
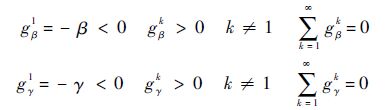
从式(4)~式(6)知,二维隐式差分格式式(8)与分数阶初边值问题式(1)、式(2)是相容的,并且有局部截断误差O(Δt)+O(Δx)+O(Δy).下面证明差分格式式(8)是稳定的,从而由Lax等价定理[12]在分数阶方程中的应用[2],式(8)是收敛的.分别令
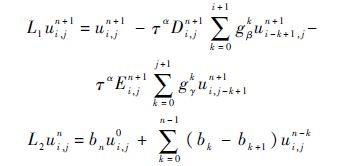
则式(8)可表示为
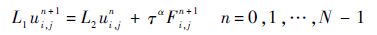
假定vi,jn(0≤i≤Nx,0≤j≤Ny,0≤n≤N)为式(8)的逼近解,则误差εi,jn=vi,jn-ui,jn满足L1εi,jn+1=L2εi,jn
式中:1≤i≤Nx-1;1≤j≤Ny-1;n=0,1,….令En=[ε1,1n,ε2,1n,…,εNx-1,1n,ε1,2n,ε2,2n,…,εNx-1,Ny-1n]T
引理2 ||En||∞≤||E0||∞,n=0,1,….
证明 当n=0时,令
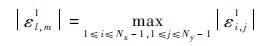
根据引理1,有$\sum\limits_{k=0}^{l+1}{g_{\beta }^{k}}<0,\sum\limits_{k=0}^{m+1}{g_{\gamma }^{k}}<0$于是

因此||E1||∞≤||E0||∞.
假定||Ek||∞≤||E0||∞,k=1,2,…,n,令n+1层上的误差|εl,mn+1|=$\underset{1\le i\le {{N}_{x}}-1,1\le j\le {{N}_{y}}-1}{\mathop{\max }}\,$|εi,jn+1|.由引理1:

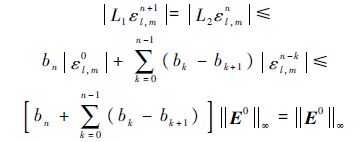
即||En+1||∞≤||E0||∞.
证毕
以上分析表明分数阶隐式差分格式式(8)是相容的并且无条件收敛的,因此由Lax等价定理,有以下结论.
定理1 分数阶隐式差分格式式(8)是以O(Δt)+O(Δx)+O(Δy)无条件收敛的.
3 交替方向隐式差分格式二维隐式差分格式式(8)是收敛的并且有局部误差O(Δt)+O(Δx)+O(Δy).然而在每一时间步,需要处理(Nx-1)×(Ny-1)个未知量的非稀疏线性系统,于是隐式差分格式是计算密集型的.随着网格的加细和空间维数的提高,计算复杂度变得非常庞大.为了解决这个问题,下面把偏微分方程差分方法中常用的交替方向隐式差分格式推广到分数阶偏微分方程,即在每一时间步只求解一个方向.
定义分数阶偏差分算子:
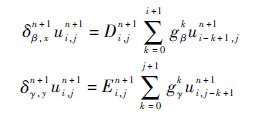
则隐式差分格式式(8)可表示为
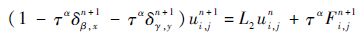
对于交替方向隐式差分格式,上述算子形式相应变为方向分离乘积的形式:

这产生了一个额外的误差扰动
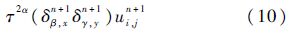
在计算上,上述形式的交替方向隐式差分格式可表示为如下的迭代形式.在时间层tn+1:
1) 首先对每个固定的yj求解x方向,产生中间解ui,j*,n+1:
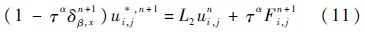
2) 对每个固定的xi求解y方向:

数值解ui,jn+1和ui,jn的初边值由给定的初边值条件给出.在进行第1步求解式(11)之前,中间解ui,j*,n+1的边界条件应由式(12)给出(采用ui,jn+1在边界的值),否则,格式收敛速度将会受到相反的影响.例如对右边界条件,可以通过
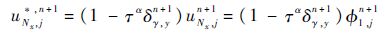
计算ui,j*,n+1的边界值,用于建立和求解方程式(11).
下面证明隐式差分格式的交替方向方法式(11)、式(12)是相容的和稳定的,因此由Lax等价定理,也是收敛的.交替方向隐式差分格式的额外扰动误差式(10)的阶为O(Δt2α),因此由式(11)、式(12)定义的交替方向隐式差分格式是相容的,并且有局部截断误差O(Δtα)+O(Δx)+O(Δy).
假定vi,jn(0≤i≤Nx,0≤j≤Ny,0≤n≤N)是式(11)和式(12)的逼近解,则误差εi,jn=vi,jn-ui,jn满足:
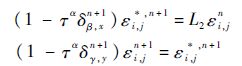
这里的εi,j*,n+1定义为vi,j*,n+1-ui,j*,n+1,其中上下标范围:1≤i≤Nx-1;1≤j≤Ny-1;n=0,1,….分别令

引理3 ||En+1||∞≤||E0||∞,n=0,1,….
证明 当n=0时,令
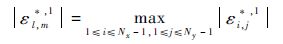
根据引理1和式(11),有

因此||E*,1||∞≤||E0||∞.
令|εr,s1|=$\underset{1\le i\le {{N}_{x}}-1,1\le j\le {{N}_{y}}-1}{\mathop{\max }}\,$|εi,j1|,根据引理1和式(12),有
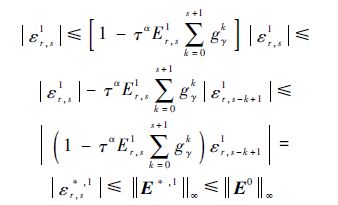
因此||E∞1||≤||E0||∞.
假定||Ek||∞≤||E0||∞,k=1,2,…,n,令|εl,m*,n+1|=$\underset{1\le i\le {{N}_{x}}-1,1\le j\le {{N}_{y}}-1}{\mathop{\max }}\,$|εi,j*,n+1|,根据引理1,得

令|εr,sn+1|=$\underset{1\le i\le {{N}_{x}}-1,1\le j\le {{N}_{y}}-1}{\mathop{\max }}\,$|εi,jn+1|,再次根据引理1和式(12),得

因此||En+1||∞≤||E0||∞.
证毕
通过以上分析,由式(11)、式(12)定义的分数阶交替方向隐式差分方法是相容的和无条件稳定的,因此由Lax等价定理在分数阶方程中的应用[2],有如下结论.
定理2 分数阶交替方向隐式差分式(11)、式(12)是以O(Δtα)+O(Δx)+O(Δy)无条件收敛的.
注意到交替方向隐式差分格式是以阶O(Δtα)+O(Δx)+O(Δy)无条件收敛的,隐式差分格式(8)是以O(Δt)+O(Δx)+O(Δy)无条件收敛的,而0<α≤1,所以为了减少计算复杂度,牺牲了一些收敛精度.
4 数值实验考虑二维分数阶色散方程:

式中:(x,y)∈(0,1)2;0≤t≤T;初值u(x,y,0)=x2y2,Dirichlet边值u(x,0,t)=u(0,y,t)=0
u(1,y,t)=(t2+1)y2
u(x,1,t)=(t2+1)x2
验证可知,方程式(13)的精确解为u(x,y,t)=(t2+1)x2y2
表 1是交替方向隐式差分格式计算结果与精确解之间的最大误差.最后一列误差率表示上一行最大绝对误差与本行最大绝对误差的比率,即数值方法的收敛速度.可以看到最大绝对误差是以速度2几乎线性下降的,这与理论分析结果是一致的.
表 1 交替方向隐式差分格式最大误差与误差率Table 1 Maximum error and error rate of alternating directions implicit scheme
| 时间步长 | 空间步长 | 最大误差 | 误差率 |
| 0.100 000 0 | 0.100 000 0 | 0.014 269 5 | |
| 0.025 000 0 | 0.050 000 0 | 0.008 392 7 | 1.700 227 6 |
| 0.006 250 0 | 0.025 000 0 | 0.004 567 3 | 1.837 562 7 |
| 0.001 562 5 | 0.012 500 0 | 0.002 380 1 | 1.918 953 0 |
表选项
5 结 论通过对空间分数阶导数的转移Grünwald差分近似,分别构造了有界区域上二维空间时间分数阶色散方程的隐式差分格式和交替方向隐式差分格式,应用数学归纳法证明了两种格式的稳定性和收敛性:
1) 隐式差分格式是以O(Δt)+O(Δx)+O(Δy)无条件收敛的.
2) 交替方向隐式差分格式的收敛阶为O(Δtα)+O(Δx)+O(Δy).
3) 虽然交替方向隐式差分格式在时间方向上的收敛精度低于隐式差分格式,但在计算复杂度上考虑,交替方向隐式差分格式优于隐式差分格式.
4) 数值模拟结果与理论分析是一致的.
对于更广泛的分数阶偏微分方程数值逼近问题,比如无界区域上分数阶偏微分方程的数值方法、分数阶偏微分方程的高阶近似差分格式等问题,将在后续的工作中进行研究.
参考文献
| [1] | Arrarás A,Portero L,Jorge J C.Convergence of fractional step mimetic finite difference discretizations for semilinear parabolic problems[J].Applied Numerical Mathematics,2010,60(4):473-485. |
| Click to display the text | |
| [2] | Meerschaert M,Tadjeran C.Finite difference approximations for fractional advection-dispersion flow equations[J].Journal of Computational and Applied Mathematics,2004,172(1):65-77. |
| Click to display the text | |
| [3] | Meerschaert M,Scheffler H,Tadjeran C.Finite difference methods for two-dimensional fractional dispersion equation[J].Journal of Computational Physics,2006,211(2):249-261. |
| Click to display the text | |
| [4] | Liu F,Anh V,Turner I.Numerical solution of the space fractional Fokker-Planck equation[J].Journal of Computational and Applied Mathematics,2004,166(1):209-219. |
| Click to display the text | |
| [5] | Tadjeran C,Meerschaert M,Scheffler H.A second-order accurate numerical approximation for the fractional diffusion equation[J].Journal of Computational Physics,2006,213(2):205-213. |
| Click to display the text | |
| [6] | Tadjeran C,Meerschaert M.A second-order accurate numerical method for the two-dimensional fractional diffusion equation[J].Journal of Computational Physics,2007,220(2):813-823. |
| Click to display the text | |
| [7] | Liu Q,Liu F,Turner I,et al.Approximation for the Levy-Feller advection-dispersion process by random walk and finite difference method[J].Journal of Computational Physics,2007,222(1):57-70. |
| Click to display the text | |
| [8] | Zhuang P,Liu F,Anh V,et al.Numerical methods for the variable-order fractional advection-diffusion equation with a nonlinear source term[J].SIAM Journal of Numerical Analysis,2009,47(3):1760-1781. |
| Click to display the text | |
| [9] | Liu F,Zhuang P,Anh V,et al.Stability and convergence of the difference methods for the space-time fractional advection- diffusion equation[J].Applied Mathematics and Computation,2007,191(1):12-20. |
| Click to display the text | |
| [10] | Podlubny I.Fractional differential equations[M].New York:Academic Press,1999:51-87. |
| [11] | Ervin J S,Roop J P.Variational solution of fractional advection dispersion equations on bounded domains in R d [J].Numerical Mathematics-Theory Methods and Applications,2007,23(2):256-281. |
| Click to display the text | |
| [12] | Richtmyer R D,Morton K W.Difference methods for initial-value problems[M].New York:Krieger Publishing Co.,1994:133-200. |
| [13] | Ghazizadeh H R,Maerefat M,Azimi A.Explicit and implicit finite difference schemes for fractional Cattaneo equation[J].Journal of Computational Physics,2010,229(19):7042-7057. |
| Click to display the text | |
| [14] | Gao G,Sun Z.A compact finite difference scheme for the fractional sub-diffusion equations[J].Journal of Computational Physics,2011,230(3):586-595. |
| Click to display the text | |
| [15] | Sousa E.Finite difference approximations for a fractional advection diffusion problem[J].Journal of Computational Physics,2009,228(11):4038-4054. |
| Click to display the text | |
| [16] | Li C,Zeng F.The finite difference methods for fractional ordinary differential equations[J].Numerical Functional Analysis and Optimization,2014,34(2):149-179. |
| Click to display the text | |
| [17] | Zhang Y,Liao Z,Lin H.Finite difference methods for the time fractional diffusion equation on non-uniform meshes[J].Journal of Computational Physics,2014,265(1):195-210. |
| Click to display the text | |
| [18] | Brunner H,Han H,Yin D.Artificial boundary conditions and finite difference approximations for a time-fractional diffusion wave equation on a two-dimensional unbounded spatial domain[J].Journal of Computational Physics,2014,276(3):541-562. |
| Click to display the text |
