然而专家系统在空战机动决策上的应用也有它自身不可避免的缺陷,由于专家系统知识库中存储的知识都是固化的数据,空战时一旦出现系统知识库未存储的空战态势,专家系统就失效了[6, 7].为了防止空战时出现系统失效的情况,本文在已有的专家系统中引入滚动时域法[8],当系统出现失效时,系统采用滚动时域代替专家系统进行空战机动决策.
1 专家系统机动决策最优控制模型的构建1.1 空战机动决策专家系统基本结构空战机动决策专家系统主要由3个部分组成,即知识库、机动库和推理机.当专家系统无人战机进入备战状态时,机载传感器获得当前敌我双方态势信息,由专家系统推理机将态势信息与知识库中各个规则的条件进行匹配,直到找到与态势信息相符的规则,根据该规则所对应的结论,调用机动库中相应的飞行机动,并予以执行.当无人战机执行完机动后,专家系统会按设定的时间间隔再次调用机载传感器获取下一时刻的态势信息,然后再次进行决策,直至空战结束.由此可知,可以将整个无人战机的空战过程分割成一个个离散的时间域,每个时间域里,无人战机通过机动的选择与调用,来完成该时域内的决策和无人战机的飞行,这些机动的叠加就是无人战机的最终飞行轨迹.
1.2 最优控制模型的构建通过以上对空战专家系统的分析,将整个空战过程离散化,专家系统机动决策最优控制问题可描述成方程组(式(1)~式(3))中最优控制序列u(t)∈Ω,t=t0,t1,…,tn-1的求解,使得性能指标J(xtk,utk)最大[9].其中,Ω为控制量u(t)的控制约束,时间t0,t1,…,tn-1分别为专家系统进行决策的每一时刻.
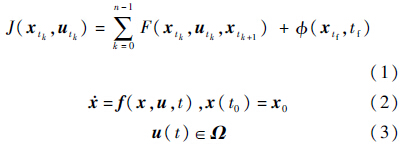
式中:$\sum\limits_{k = 0}^{n - 1} {F\left( {{x_{{t_k}}},{u_{{t_k}}},{x_{{t_{k + 1}}}}} \right)} $为积分指标;$\phi $(xtf,tf)为终端指标;$\dot x = f\left( {x,u,t} \right),x({t_0}) = {x_0}$为系统状态方程;t0和xt0分别为初始时间和初始状态;tf和xtf分别为终端时刻和终端状态;k=0,1,…,n-1.
1.2.1 系统状态方程描述为了描述载机和目标机的相对运动,空战中双方态势分别用状态向量Xr、Xb来表示,下标r和b分别代表我方(红方)和敌方(蓝方).
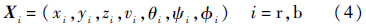
式中:xi、yi和zi为地坐标系下战机的位置坐标;vi为战机的速度;θi、ψi和$\phi $i分别为在地坐标系中战机的航迹倾斜角、航迹方位角和航迹滚转角.
忽略侧滑角的影响,且假设发动机推力沿着飞行速度方向,则飞机在航迹坐标系上的质点动力学方程为

式中:V为飞行速度大小;$\dot V$为速度变化率;θ为航迹倾斜角;nx沿着飞行速度方向,通常称为切向过载或轴向过载;ny和nz均垂直于飞行速度矢量,法向过载${n_n} = \sqrt {n_y^2 + n_z^2} $;ωy和ωz分别为航迹坐标系相对于地轴坐标系的转动角速度在航迹坐标系OYk轴和OZk轴上的分量;g为重力加速度.此模型中,控制向量为过载nx、ny、nz.
再通过地坐标系和航迹坐标系的转换矩阵Lkg,由ωy和ωz可求得战机在地坐标系下的航迹倾斜角角速度$\dot \theta $、航迹方位角角速度$\dot \psi $和航迹滚转角角速度$\dot \phi $.
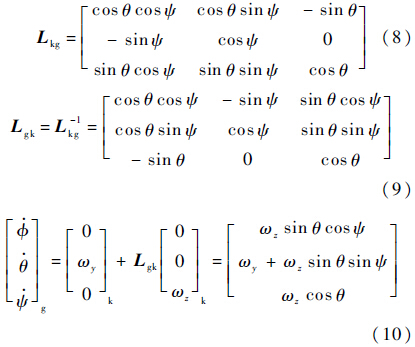
将战机质心的速度矢量投射到地面坐标轴系后,可得到相应的运动学方程组:
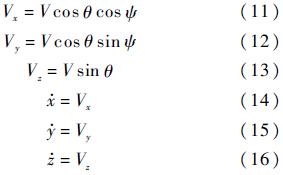
式中:Vx、Vy和Vz分别为速度V在地坐标系OZg轴、OXg轴和OYg轴上的分量.
则根据动力学方程组(式(5)~式(7))和运动学方程组(式(11)~式(16))可知,只要给定了战机的任意时刻的初始状态和该时刻的控制量过载nx、ny和nz即可通过求解上述动力学方程组来得到战机下一时刻的状态.
1.2.2 控制约束设计机动动作库包含供决策选用的动作集,是建立空战机动决策模型的基础.现阶段,在决策系统设计中,普遍采用美国国家航空航天局(NASA)****提出的7种基本操纵动作[10]:最大加速、最大减速、最大过载爬升、最大过载俯冲、最大过载左转、最大过载右转和稳定飞行.基本上,所有的机动都可以分解为这7种操纵动作的一种或者几种的叠加.本文机动动作库在构建了7种基本操纵动作的基础上,又以经典空战战术飞行动作为依据,建立的一些空战中常用的战术动作,包括盘旋机动、半斤斗机动和蛇形机动等.
对于7个基本操纵动作的设计,本文战机系统状态方程选取过载nx、ny和nz作为控制变量,所以可以通过设计这些参数的变化规律来控制战机完成机动动作.对于战术动作库的设计,可以将战术机动分解为这7种基本操纵动作中一种或几种的叠加.在飞行过程中,战机根据空战态势、武器发射条件等,为满足特定的战术要求,在特定的态势和时间,切换7种基本动作,从而完成特定的战术动作设计.
通过以上机动库设计原理和系统状态方程的分析,由于机动库中过载nx、ny和nz这些参数的变化规律都已经设计好,空战专家系统是通过机动的选择和调用来实现对飞机状态Xi的控制,所以这里的控制约束Ω指的是专家系统机动库,控制量u(t)为机动库中的各个机动.
1.2.3 空战机动决策指标函数的建立以我机位置为原点R(O),在地坐标系下对两机空战态势关系进行分析,如图 1所示.
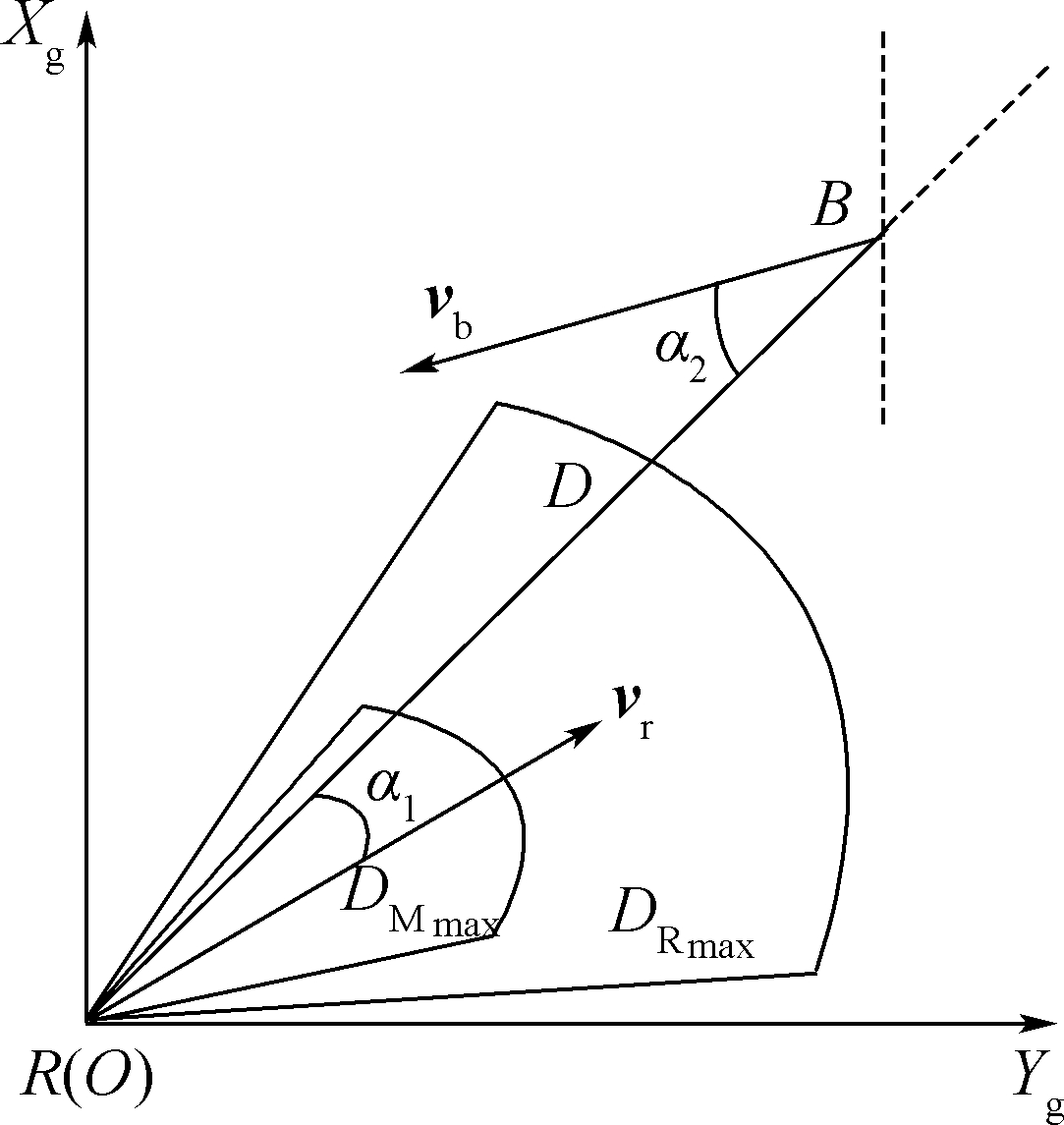 |
| α1,α2—目标方位角和目标进入角; vr,vb—我机速度矢量和敌机速度矢量; B—敌机位置;R(O)—我机位置;D—目标距离; DRmax—我机雷达最大探测距离; DMmax—我机导弹最大不可逃逸距离.图 1 双机空战态势关系Fig. 1 Relation of situation of two sides in air combat |
| 图选项 |
空战目的都是发现、跟踪、击毁空中目标,使其失去对我方形成威胁的能力.机载雷达和空空导弹已成为了现代空战的主要探测和攻击武器,空战态势优势函数的建立,应该从空战态势对战机雷达跟踪区和导弹攻击区的影响这两方面进行定量分析[11, 12, 13, 14].所以本文在建立态势优势函数时,主要考虑角度优势函数、距离优势函数和能量优势函数.
1) 角度优势函数.
角度优势函数关系到我机对目标的有效跟踪.当我机的目标方位角小时,我机导弹发射的离轴角也越小,有利于提高导弹命中率,使我机对敌机的威胁达到最大,实现我机对敌机的有效跟踪.本文选取空空导弹不可逃逸离轴角ψMmax为60°,雷达探测最大角度ψRmax为85°,将目标方位角分为雷达搜索区、导弹攻击不可逃逸区和雷达搜索区以外3个区域,并构造角度优势函数:
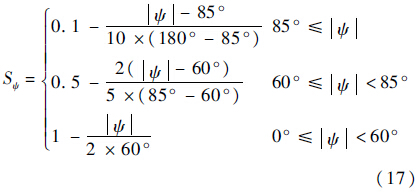
2) 距离优势函数.
距离优势函数主要体现为敌机是否在我机导弹的射程范围内.当目标线长度D远大于我机导弹的最大不可逃逸距离DMmax时,可以认为我机的距离优势很小,随着空战双方相对距离的减小,敌机进入我机的导弹的射程范围内,我机的距离优势逐渐增大,可以认为当$D = \frac{{{D_{\rm Mmin }} + {D_{\rm Mmax }}}}{2}$时距离优势达到最大值,随着双距离的进一步减小,甚至当目标线长度D小于我机导弹的最小不可逃逸距离DMmin时,我机的距离优势开始逐渐减小并趋于0.根据以上分析,距离优势函数为

式中:

如果当D=DMmin或D=DMmax时,均有SD=0.95,则有正态分布标准差为
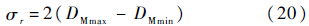
3) 能量优势函数.
战机能量优势函数主要与战机速度和高度有关.战机的能量越大,则战机机动能力越强,使战机在超视距空战中能尽快机动到对目标机实施打击的最佳空战位置,而且在较大能量时,空空导弹使用速度更大,对目标机实施攻击的成功率更高.本文将能量看作战机动能与势能的和,定义战机单位能量为

式中:H为战机当前高度.战机能量优势函数为
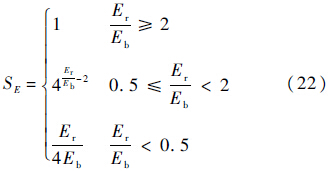
式中:Er为我方(红方)战机单位能量;Eb为敌方(蓝方)战机单位能量.
综合考虑角度和距离之间的相关关系,在此,以乘积表示角度与距离的综合优势.最终可以得出空战态势优势函数的计算公式为

式中:K1和K2为加权系数,且有K1+K2=1(0<K1,K2<1).
结合以上所建立的空战态势优势函数,以任意时刻我机态势优势值与敌机态势优势值的差值作为我机进行机动决策的指标:
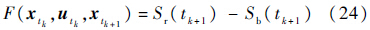
式中:Sr(tk+1)和Sb(tk+1)分别为我机和敌机在tk+1时刻的态势优势值;最优控制模型的积分指标$\sum\limits_{k = 0}^{n - 1} {F\left( {{x_{{t_k}}},{u_{{t_k}}},{x_{{t_{k + 1}}}}} \right)} $体现整个空战过程中我机相对于敌机的态势优势的累积.
2 基于滚动时域控制的专家系统决策控制方法与仿真验证2.1 基于滚动时域控制的专家系统控制方法滚动时域控制(Receding Horizon Control,RHC)是20世纪70年代由工业界首先构思出来的一种控制方法,其核心是在线滚动优化,将广义控制全局问题的求解转化为在线滚动进行的一系列局部优化问题,使得计算复杂性和计算资源消耗都大幅降低.滚动优化把整个RHC任务过程分为一个个相互重叠(单步预测时是不重叠的)但不断向前推进的优化区间,称为滚动时域.在某一滚动时域的开始,用系统的当前状态作为初始条件,在线求解该有限时域开环最优控制问题,得到最优控制序列.并在该时刻,仅取最优控制序中的第1个控制信号实际作用到系统中.在下一滚动时域,重复以上过程.随着动态过程的延续,控制算法推进预测时域向前滚动,从而形成滚动优化.对于含状态约束以及输入约束等限制条件的系统,在不知道目标未来运动信息的条件下,滚动时域控制是一种有效的控制方法[15, 16].滚动时域控制原理如图 2所示.
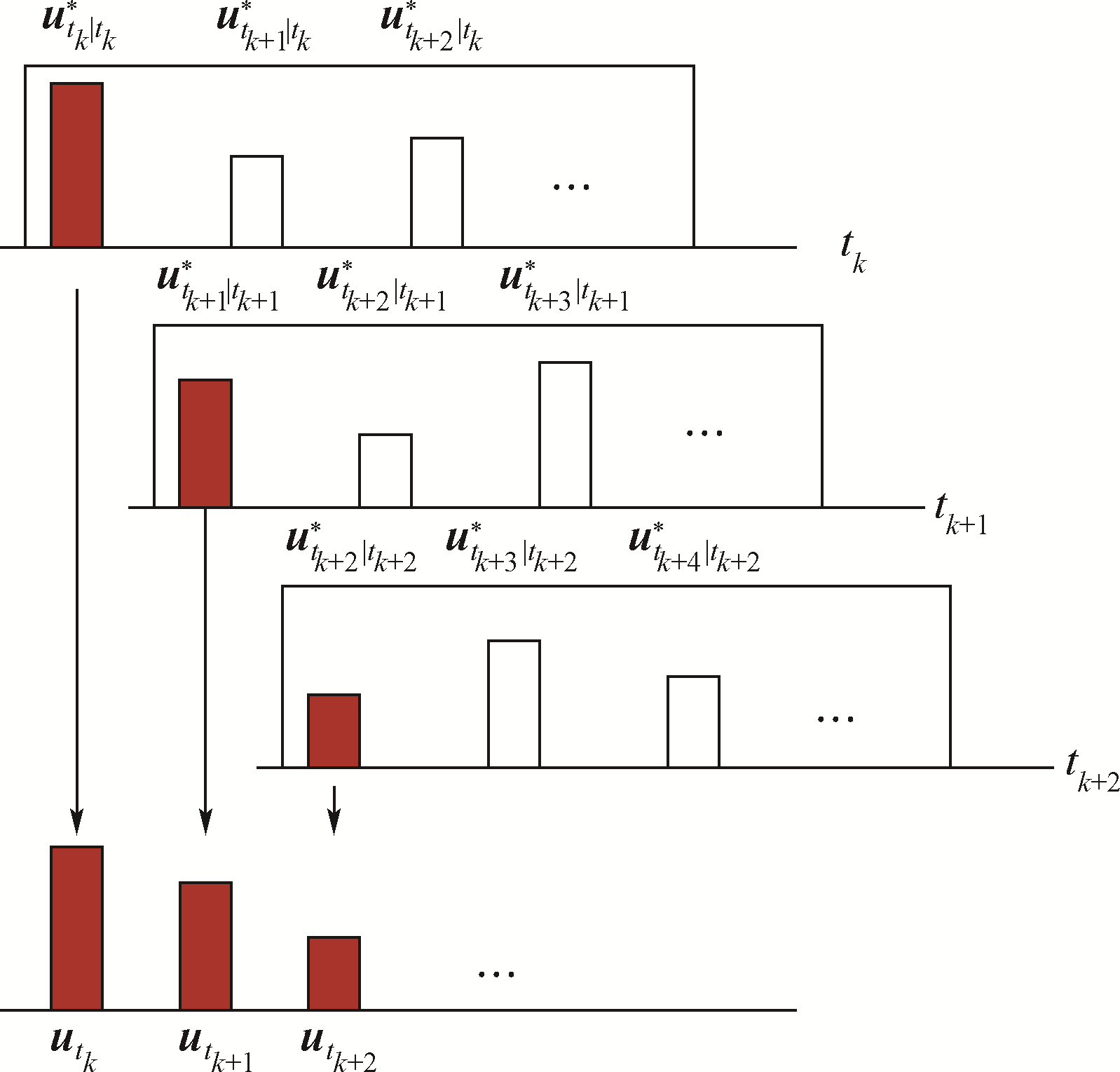 |
| 图 2 滚动时域控制原理图Fig. 2 RHC schematic |
| 图选项 |
通过以上分析,假设每一次决策之间的时间间隔是固定的,定义任意起始时刻tk的滚动时域为[tk,tk+nΔt],n为滚动时域步长,Δt为决策时间间隔,则图中$\left[{u_{{t_k}|{t_k}}^ * ,u_{{t_{k + 1}}|{t_k}}^ * ,\ldots ,u_{{t_{k + n}}|{t_k}}^ * } \right]$可表示为$\left[{{u_{{t_k}|{t_k}}},{u_{{t_k} + \Delta t|{t_k}}},\ldots ,{u_{{t_k} + n\Delta t|{t_k}}}} \right]$.根据第2节所建立的专家系统空战机动决策最优控制模型,则求解滚动时域内最优控制序列$\left[{{u_{{t_k}|{t_k}}},{u_{{t_k} + \Delta t|{t_k}}},\ldots ,{u_{{t_k} + n\Delta t|{t_k}}}} \right]$的指标函数为
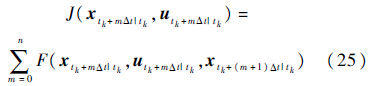
2.2 仿真验证设定空战初始条件为原专家系统中未定义的空战态势,即原专家系统失效,通过原专家系统和改进后专家系统的仿真对比,验证改进后的专家系统具有更强的适应性.仿真初始条件如表 1所示.
表 1 真初始条件Table 1 Initial conditions for simulation
| 战机 | x/m | y/m | z/m | v/(m·s-1) | θ/(°) | ψ/(°) |
| 我机 | 10000 | 10000 | 10000 | 150 | 0 | 60 |
| 敌机 | 10000 | 0 | 10000 | 150 | 0 | 0 |
表选项
图 3和图 4分别为原专家系统空战仿真结果和滚动时域法改进后的专家系统仿真结果.
 |
| 图 3 原专家系统机动决策Fig. 3 Expert system maneuver decision |
| 图选项 |
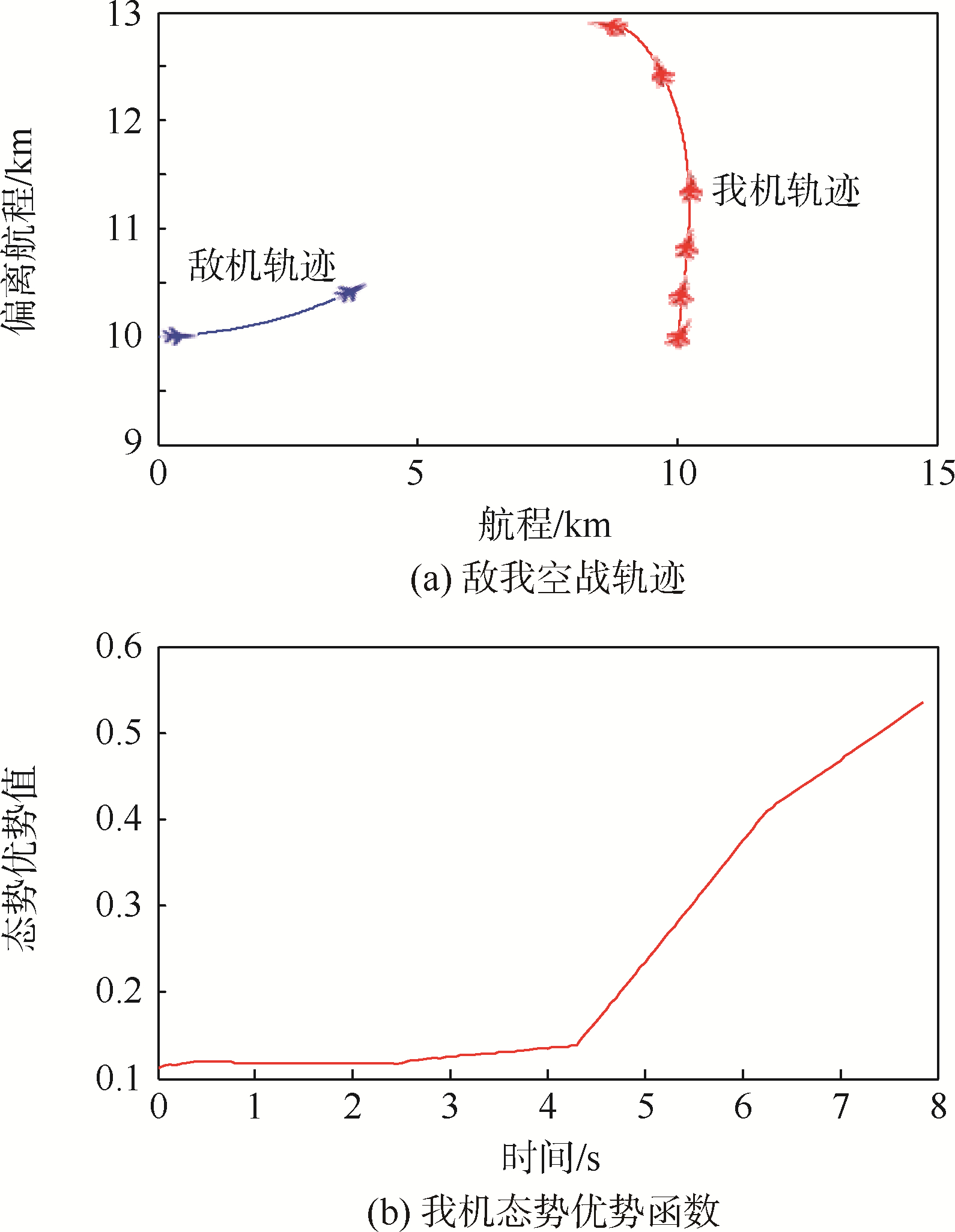 |
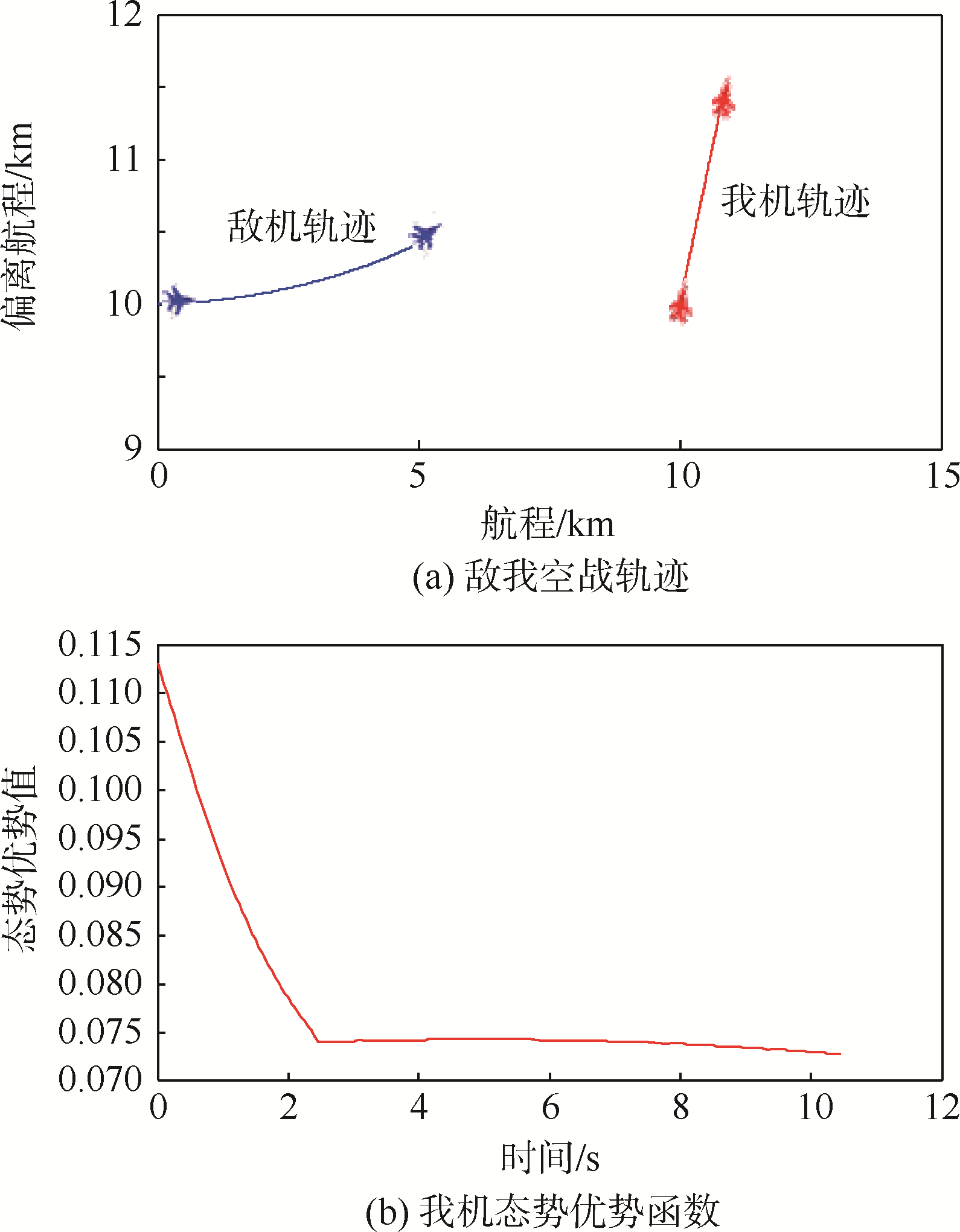
| 图 4 改进专家系统机动决策Fig. 4 Improved expert system maneuver decision |
| 图选项 |
由图 3可以看出空战开始,原专家系统就出现失效状况,我机维持起始飞行状态,作匀速直线运动,我机态势优势值也呈现递减的趋势,最终被敌机击落.
图 4为引进滚动时域法后的专家系统,在专家系统决策出现失效的情况下,系统采用滚动时域控制代替专家系统进行空战机动决策.如图 4所示,敌我空战开始时刻,专家系统出现失效,滚动时域法求解最优控制机动.第1阶段,我机作偏航纯跟踪机动,向敌机偏转同时保持一定的增速;第2阶段,我机通过最大加速直飞行机动与敌机拉开距离;第3阶段,当我机和敌机拉开一定的距离,我机作最大过载左转弯机动,快速向敌机偏转;第4阶段,当我机角度向敌机偏转到一定角度时,我机对敌机形成侧向攻击态势,由专家系统进行决策,我机继续采用最大过载左转弯机动;第5阶段,通过前两个阶段的最大过载左转弯机动,我机与敌机形成迎头攻击态势,继续由专家系统进行决策,我机采用偏航纯跟踪机动,实现对敌的跟踪.由图 4可知,引进滚动时域法后的专家系统,在专家系统法失效的情况下,仍能做出有效的机动,实现敌我态势的逆转,我机态势优势值呈递增的趋势.
3 结 论本文建立了一套基于滚动时域的无人战机空战决策专家系统.通过与原专家系统的仿真对比,验证了改进后的系统在专家系统法失效的情况下,能快速地进行自主决策,使我机有效地规避目标威胁并达成攻击条件.基于滚动时域的无人战机空战决策专家系统不仅保留了专家系统机动决策法的优点,而且克服了专家系统法适应性差的缺陷.综合分析可得基于滚动时域的无人战机空战决策专家系统的特点为:
1) 系统能充分发挥专家的经验优势,决策过程不需复杂的算法计算,有利于提高机动决策的实时性.
2) 系统具有良好的可维护性和扩展性.对于不同的机型,系统可以根据需要对知识库中的知识进行增删、修改、扩充等操作.
3) 系统具有更强的灵活性和适应性.系统综合使用专家系统法和滚动时域法进行决策,在任何的空战态势下,都能做出有效的机动决策.
除了实现对专家系统的改进,本文建立的专家系统机动决策最优空战模型,对以后专家系统的研究以及智能算法的引入都具有一定的借鉴意义.
参考文献
| [1] | Galati D G.Game theoretic target assignment strategies in competitive multi-team systems[D].Pittsburgh:University of Pittsburgh, 2004. |
| Click to display the text | |
| [2] | Imado F, Kuroda T.A method to solve missile-aircraft pursuit-evasion differential games[C]//Proceedings of the 16th IFAC World Congress.Laxenburg:IFAC, 2005, 16:176-181. |
| [3] | Virtanen K, Raivio T.Modeling pilot's sequential maneuvering decisions by a multistage influence diagram[J].Journal of Guidance, Control, and Dynamics, 2004, 27(4):665-677. |
| Click to display the text | |
| [4] | 董彦非,郭基联,张恒喜.空战机动决策方法研究[J].火力与指挥控制, 2002, 27(2):75-78. Dong Y F, Guo J L, Zhang H X.The methods of air combat maneuvering decision[J].Fire Control & Command Control, 2002, 27(2):75-78(in Chinese). |
| Cited By in Cnki (37) | |
| [5] | 赵威.基于专家系统的双机协同攻击决策技术研究[D].西安:西北工业大学, 2007. Zhao W.Based on expert system coordination air fight decision research[D].Xi'an:Northwestern Polytechnical University, 2007(in Chinese). |
| Cited By in Cnki (10) | |
| [6] | Platts J T, Howell S E, Peeling E C, et al.Increasing UAV intelligence through learning[C]//AIAA 3rd "Unmanned Unlimited" Technical Conference, Workshop and Exhibit.Reston:AIAA, 2004, 1:270-282. |
| Click to display the text | |
| [7] | Xiao L, Sun D, Liu Y, et al.A combined method based on expert system and BP neural network for UAV systems fault diagnosis[C]//2010 International Conference on Artificial Intelligence and Computational Intelligence.Piscataway, NJ:IEEE Press, 2010, 3:3-6. |
| Click to display the text | |
| [8] | Xu B, Kurdila A, Stilwell D J.A hybrid receding horizon control method for path planning in uncertain environments[C]//The 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway, NJ:IEEE Press, 2009:4887-4892. |
| Click to display the text | |
| [9] | McGrew J S, How J P, Williams B, et al.Air-combat strategy using approximate dynamic programming[J].Journal of Guidance, Control, and Dynamics, 2010, 33(5):1641-1654. |
| Click to display the text | |
| [10] | Fred A, Giro C, Michael F.Automated maneuvering decisions for air to air combat[R].Reston:AIAA, 1987. |
| Click to display the text | |
| [11] | James S M.Real-time maneuvering decisions for autonomous air combat[D].Massachusetts:Massachusetts Institute of Technology, 2008. |
| Click to display the text | |
| [12] | 马伟江,姚佩阳,周翔翔.改进的超视距空战态势评估方法[J].计算机工程与设计, 2011, 32(6):2096-2099. Ma W J, Yao P Y, Zhou X X.Improved method of situation assessment in BVR air combat[J].Computer Engineering and Design, 2011, 32(6):2096-2099(in Chinese). |
| Cited By in Cnki (2) | |
| [13] | 吴文海,周思羽,高丽.基于导弹攻击区的超视距空战态势评估改进[J].系统工程与电子技术, 2011, 33(12):2679-2685. Wu W H, Zhou S Y, Gao L.Improvements of situation assessment for beyond-visual-range air combat based on missile launching envelope analysis[J].Journal of Systems Engineering and Electronics, 2011, 33(12):2679-2685(in Chinese). |
| Cited By in Cnki (13) | |
| [14] | 张洪波,李国英,丁全心.超视距空战下的态势评估技术研究[J].电光与控制, 2010, 17(4):9-13. Zhang H B, Li G Y, Ding Q X.Research on situation assessment in BVR air combat[J].Electronics Optics & Control, 2010, 17(4):9-13(in Chinese). |
| Cited By in Cnki (14) | |
| [15] | 付昭旺,李战武,强晓明.基于滚动时域控制的战斗机空战机动决策[J].电光与控制, 2013, 20(3):20-29. Fu Z W, Li Z W, Diang X M.Tactical decision-making method based on receding horizon control for air combat[J].Electronics Optics & Control, 2013, 20(3):20-29(in Chinese). |
| Cited By in Cnki (2) | |
| [16] | Bellingham J, Richards A, How J P.Receding horizon control of autonomous aerial vehicles[C]//Proceedings of the American Control Conference, 2002.Piscataway, NJ:IEEE Press, 2002, 5:3741-3746. |
| Click to display the text |
