文献[1, 2]使用非线性动态逆方法设计了解耦控制器,但是无法保证在模型不能精确已知情况下系统的鲁棒性.文献[3, 4]基于滑模控制理论设计了MIMO系统控制器,并分别应用到直升机控制和机器人控制问题上,但是滑模控制带来的抖振问题会对控制系统产生不利影响.文献[5]提出了利用神经网络在线整定比例-积分-微分(Proportion-Integration-Differentiation,PID)参数的解耦控制方法,但是应用到非线性程度和耦合程度较强的MIMO系统上会导致控制精度无法满足.文献[6, 7, 8, 9, 10]分别将模糊理论和神经网络等智能方法与自适应控制和鲁棒控制相结合,提出了MIMO系统的智能控制方法,但只是针对输出量直接为状态量的情况,未考虑更一般的情况.
意大利****Tornambe和Valigi[11, 12]提出了一种不确定MIMO系统的分散控制方法,使用观测器方法得到通道耦合项和不确定性项的估计值,然后补偿到解耦控制律中.本文在此方法基础上,利用模糊系统的非线性泛逼近能力和神经网络的自学习能力,针对不确定的MIMO非线性系统提出了一种基于模糊神经网络的自适应解耦控制方法,并给出了理论证明及仿真验证.与已有的MIMO系统控制方法相比,本文的区别和贡献在于把模糊神经网络观测器方法与Tornambe分散控制思想进行了结合,并考虑了输出方程形式更为一般的情况.
1 问题描述对于多输入多输出仿射非线性系统,有

式中:x∈Rn为系统状态;u∈Rm为系统输入;y∈Rm为系统输出;f′(x)、G′(x)和h(x)为光滑非线性函数,即
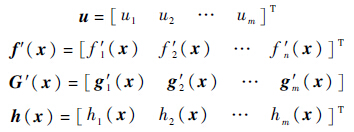
由于系统参数不确定性的影响,f′(x)和G′(x)的值无法准确获知.控制目标是设计控制律u∈Rm实现系统镇定.
假设 1 系统式(1)具有相对阶[r1 r2 … rm]T,其中,ri(i=1,2,…,m)为第i个输出的相对阶.
假设 2 系统的内动态是稳定的.
对系统式(1)进行输入输出线性化[13]可得
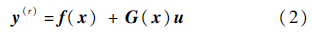
式中:
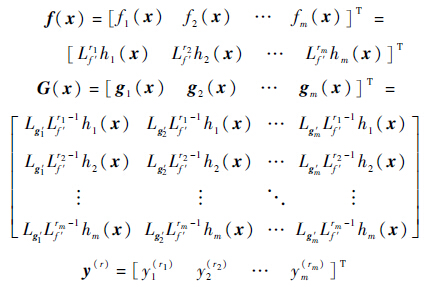
其中:L代表求解李导数.
2 主要结果2.1 解耦控制对于式(2)中的第i个输出,有
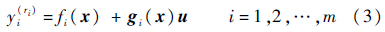
表示成输入项和系统扰动项之和的形式为
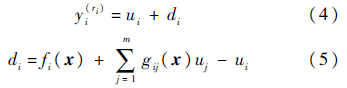
通过把系统其他输入和状态的影响归结为系统扰动项di,实现输入与输出的一一对应,使多输入多输出系统变为了多个带有扰动项的单输入单输出系统.该扰动项既包含了通道耦合项,也包含了系统不确定性项.
第i个输出变量设计系统的期望动态为
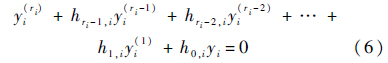
式中:hri-1,i,hri-2,i,…,h1,i,h0,i使得多项式sri+hri-1,isri-1+…+h1,is+h0,i是Hurwitz多项式.
若扰动项di已知,可以得到控制律为
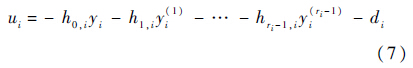
记Yi=[yi yi(1) … yi(ri-1)]T,把控制律式(7)代入式(4)可得

式中:

2.2 模糊神经网络由于不确定性的影响,系统扰动项di的值无法准确获得,可以利用观测器方法得到系统扰动项的近似值.本文结合了模糊系统的非线性泛逼近能力和神经网络的自学习能力,采用模糊神经网络构造观测器来得到系统扰动项的估计值.
设计如下模糊规则:
规则j:IF x1 is A1j,and … and xn is Anj,THEN di is dij
其中:Aij为输入变量的模糊子集.
则模糊系统的输出为
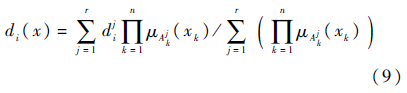
式中:μ(xk)为隶属度函数;r为模糊规则数.
定义
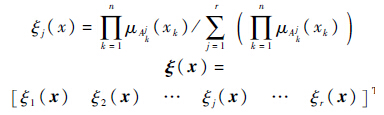
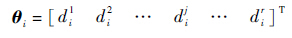
可得

引理 1[14, 15] 对于非线性函数di(x)∈R,对于任意精度εm>0,存在最优权值向量θi,使得
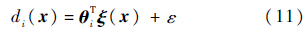
式中:ε为逼近误差,满足|ε|≤εm.
2.3 基于模糊神经网络的自适应解耦控制对于第i个输出yi,模糊神经网络观测器为
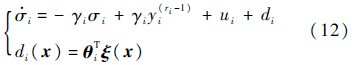
式中:σi为扰动观测器的状态变量;常数γi>0为观测器的参数;di(x)为扰动项di的估计值;θi为最优权值向量的估计值.
定义观测误差为
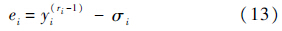
定义权值向量估计误差为

所设计的控制律为
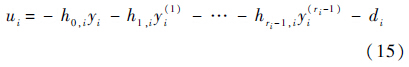
代入系统方程式(4)中可得
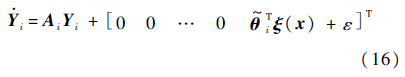
由于矩阵Ai是Hurwitz的,所以存在正定对称矩阵Pi,使得AiTPi+PiAi<0.
结合系统动态方程式(4)和观测器方程式(12),第i个观测误差的动态方程为
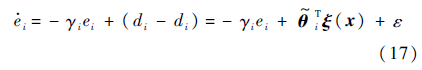
记pi为Pi的最后一列,另定义
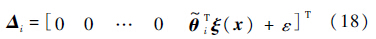
定理 1 对于动态系统式(1),如果采用模糊神经网络观测器式(12),控制律式(15)以及如下权值向量自适应律:
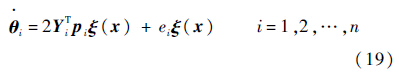
当对于所有的i=1,2,…,n都满足
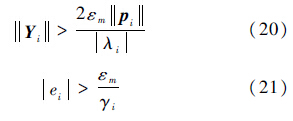
则系统输出Yi、观测误差ei以及权值向量逼近误差
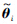 是一致最终收敛的.
是一致最终收敛的.证明 定义李雅普诺夫函数:
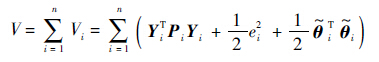
代入输出动态式(16)和误差动态式(17)可得
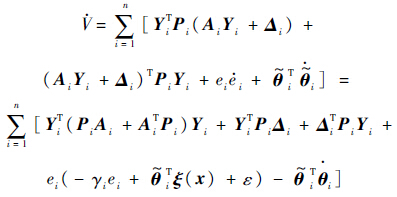
由于pi为Pi的最后一列,则
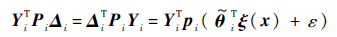
由于AiTPi+PiAi为负定矩阵,则AiTPi+PiAi特征值实部都小于0,记λi为其模值最小的特征值,可得
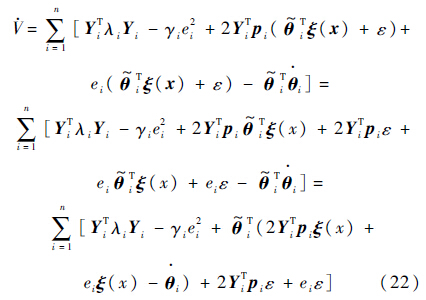
把权值自适应规律式(19)代入式(22)可得
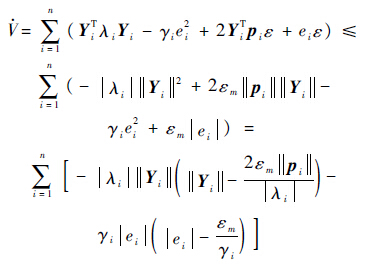
当对于所有的i=1,2,…,n都满足||Yi||>
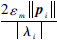 并且
并且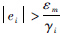 时,
时,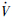 <0.
<0.根据Lyapunov稳定性原理,系统输出Yi、观测误差ei以及权值向量逼近误差
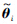 是一致最终收敛的.
是一致最终收敛的.证毕
闭环系统结构如图 1所示.可见模糊神经网络观测器利用系统输入和输出信息逼近得到系统扰动项的估计值,然后作为补偿信号加入解耦控制器,用以消除通道耦合和不确定性对系统带来的影响.
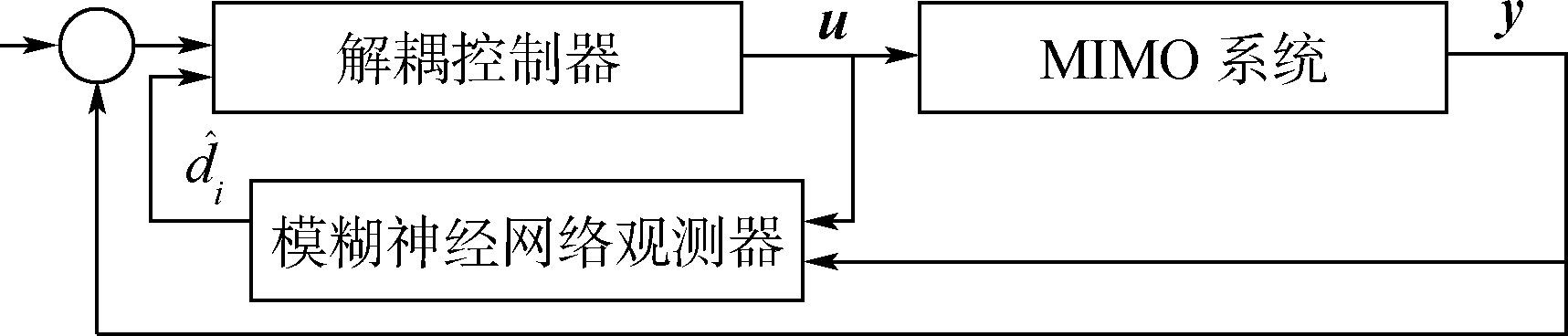 |
| 图 1 闭环系统结构Fig. 1 Closed-loop system structure |
| 图选项 |
3 仿真结果考虑如下非线性MIMO对象:
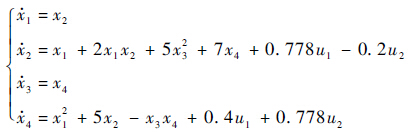
输出方程为
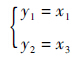
式中:x1、x2、x3和x4为状态变量;u1和u2为输入变量;y1和y2为输出变量.根据状态方程的具体形式和控制系数的大小,把系统划分为两个通道,即{x1,x2,u1}和{x3,x4,u2},然后分别设计模糊神经网络观测器和自适应解耦控制律.
控制器和观测器相应的参数选择如下:
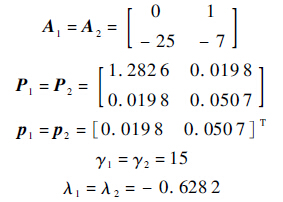
则
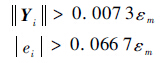
由于εm为任意小的正常数,所以系统输出Yi、观测误差ei以及权值向量逼近误差
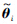 是一致最终收敛的.
是一致最终收敛的.为了验证本文方法的鲁棒性,仿真中在状态方程中引入加性和乘性的正弦摄动,即
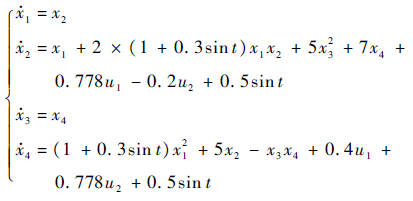
除了本文的控制方法之外,对传统的分通道输出反馈控制方法进行了仿真,即在控制律式(15)中去除扰动项估计值的补偿,两种方法对比结果如图 2~图 4所示.
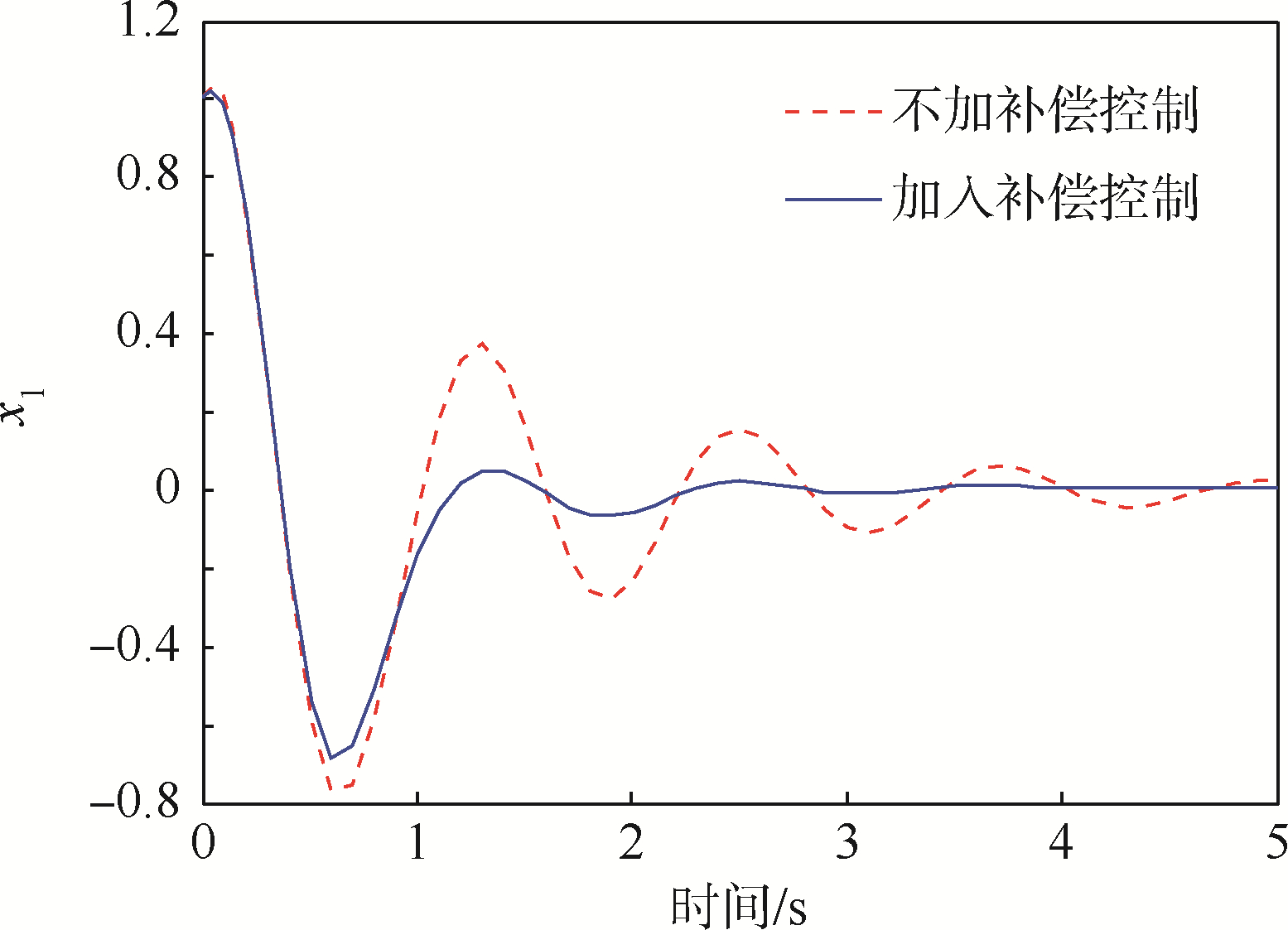 |
| 图 2 x1控制效果Fig. 2 Control performance of x1 |
| 图选项 |
 |
| 图 3 x3控制效果Fig. 3 Control performance of x3 |
| 图选项 |
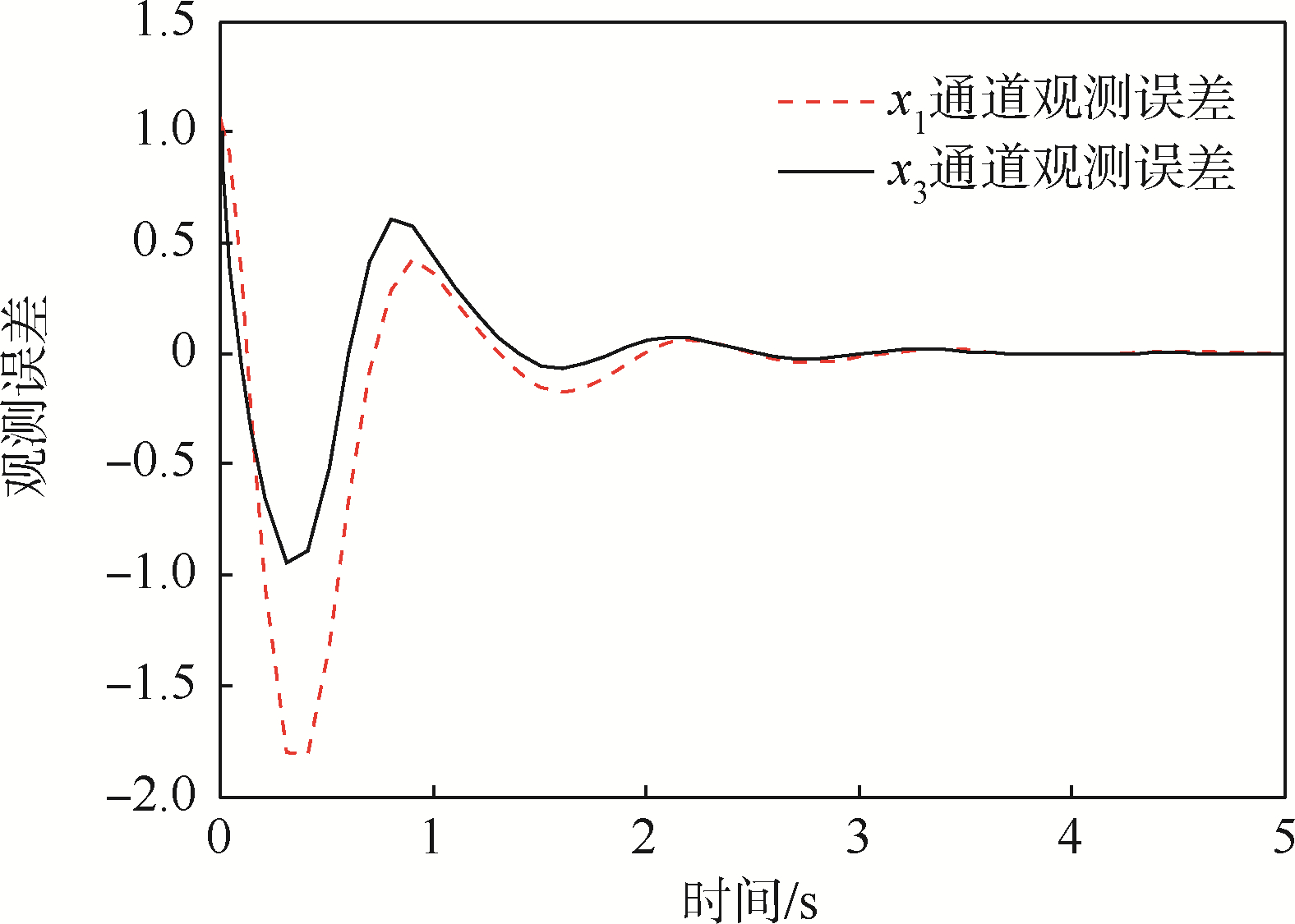 |
| 图 4 模糊神经网络观测误差Fig. 4 Fuzzy neural networks observer errors |
| 图选项 |
由图 2和图 3可见,本文所设计控制器快速精确地稳定了x1和x3,而传统的输出反馈会导致震荡,难以保证较好的控制效果,这表明了控制律中加入的补偿项很好地消除了通道耦合和不确定性对系统带来的影响.由图 4可见,模糊神经网络观测器的观测误差快速收敛.以上结果验证了本文所设计控制方法的稳定性和有效性.
4 结 论1) 基于Tornambe分散控制思想,结合反馈线性化方法,给出了输出方程形式更为一般情况下,MIMO非线性系统的分通道解耦控制律.
2) 结合模糊系统的非线性泛逼近能力和神经网络的自学习能力,通过观测器方法给出了通道耦合和不确定性的估计值,并作为补偿信号加入到解耦控制律中,消除了其对系统的影响.
参考文献
| [1] | 曾宪法,张磊,申功璋.基于动态逆和分散控制的导弹控制系统设计[J].北京航空航天大学学报, 2007, 33(11):1303-1307. Zeng X F, Zhang L, Shen G Z.Design of control systems for missiles based on dynamic inversion and decentralized control[J].Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(11):1303-1307(in Chinese). |
| Cited By in Cnki (11) | |
| [2] | Siwakosit W, Snell S A, Hess R A.Robust flight control design with handling qualities constraints using scheduled linear dynamic inversion and loop-shaping[J].IEEE Transcations on Control Systems Technology, 2000, 8(3):483-494. |
| Click to display the text | |
| [3] | McGeoch D J, McGookin E W, Houston S S.MIMO sliding mode attitude command flight control system for a helicopter[C]//Proceedings of AIAA Guidance, Navigation, and Control Conference and Exhibit.Reston:AIAA, 2005:1-15. |
| Click to display the text | |
| [4] | Yang Y L, Shi Z H.Sliding control for a class of MIMO uncertain nonlinear system based on neural networks[C]//Proceedings of International Conference on Electronics, Communications and Control.Piscataway, NJ:IEEE Press, 2011:479-484. |
| Click to display the text | |
| [5] | 张杰,邹继刚,李文秀.多输入多输出系统的神经网络PID解耦控制器[J].哈尔滨工程大学学报, 2000, 21(5):6-9. Zhang J, Zou J G, Li W X.PID neural network for decoupling control of multi-input and multi-output system[J].Journal of Harbin Engineering University, 2000, 21(5):6-9(in Chinese). |
| Cited By in Cnki (42) | |
| [6] | Hao W J, Liu G L, Wang S Y, et al.Observer-based fuzzy adaptive control for a class of MIMO nonlinear systems[C]//Proceedings of IMACS Conference on Computational Engineering in Systems Applications.Piscataway, NJ:IEEE Press, 2006:239-244. |
| Click to display the text | |
| [7] | Li Y, Tong S C, Li Y M.Observer-based adaptive fuzzy back-stepping control of MIMO stochastic nonlinear strict-feedback systems[J].Nonlinear Dynamics, 2012, 67(2):1579-1593. |
| Click to display the text | |
| [8] | Li Y M, Ren C E, Tong S C.Adaptive fuzzy backstepping output feedback control for a class of MIMO time-delay nonlinear systems based on high-gain observer[J].Nonlinear Dynamics, 2012, 67(2):1175-1191. |
| Click to display the text | |
| [9] | Chen M, Zhou Y L, Guo W W.Robust tracking control for uncertain MIMO nonlinear systems with input saturation using RWNNDO[J].Neurocomputing, 2014, 144:436-447. |
| Click to display the text | |
| [10] | Grinits E V, Bottura P C.Adaptive neural-based backstepping control of uncertain MIMO nonlinear systems[C]//Proceedings of International Joint Conference on Neural Networks.Piscataway, NJ:IEEE Press, 2006:4468-4475. |
| Click to display the text | |
| [11] | Tornambe A, Valigi P.A decentralized controller for the robust stabilization of a class of MIMO linear systems[J].Systems and Control Letters, 1992, 18(5):383-390. |
| Click to display the text | |
| [12] | Tornambe A, Valigi P.A decentralized controller for the robust stabilization of a class of MIMO dynamical systems[J].Journal of Dynamic Systems, Measurement, and Control, 1994, 116(2):293-304. |
| Click to display the text | |
| [13] | 曲鑫.临近空间高超声速飞行器关联协调控制技术研究[D].北京:北京航空航天大学, 2013. Qu X.Research on coupling coordinated control technology for near space hypersonic vehicle[D].Beijing:Beihang University, 2013(in Chinese). |
| [14] | Kim E.A discrete-time fuzzy disturbance observer and its application to control[J].IEEE Transactions on Fuzzy Systems, 2003, 11(3):399-410. |
| Click to display the text | |
| [15] | Kim E.A fuzzy disturbance observer and its application to control[J].IEEE Transactions on Fuzzy Systems, 2002, 10(1):77-84. |
| Click to display the text |
