对于电中小尺寸的天线-天线罩系统,全波数值法可以精确高效地得到仿真结果.但是,工作于微波尤其是毫米波段的天线罩通常具有很大的电尺寸,随着系统规模的增加,待求未知量也急剧增多,现有的全波数值分析方法对这种结构电磁特性的分析往往需要消耗大量的内存和计算时间,即便使用加速算法如多层快速多极子(Mutilevel Fast Multipole Algorithm,MLFMA)[2]等方法降低了计算复杂度,但计算效率仍然不高.而且,已有文献大多研究发射模式下天线罩对天线特性的影响,而极少有文献讨论接收模式下电大尺寸天线-天线罩系统的电性能分析,而后者在工程中应用极多,如带罩相控阵的校准测量一般都是在接收模式下进行.因此,接收模式下带罩天线系统电磁特性的有效分析是计算电磁学领域一个颇具挑战性的研究课题.
针对这一问题,本文结合全波快速分析法与高频射线算法各自的优势,提出了一种基于多层快速多极子加速的IE/MSI(Integral Equation/ Modified Surface Integration)+MLFMA混合算法,在保证计算精度满足工程需要的情况下,消除了传统方法求解此类问题时存在的计算时间长、效率低下的弊端.本文详细地论述了该方法的基本理论和技术细节,给出的数值算例证明了其高效性与精确性.
1 理论基础被动接收模式下的天线-天线罩系统模型如图 1所示,模型可等效为入射平面波照射下N层介质天线罩加载的天线阵列中等效电流分布的求解.如引言所述,本文提出了一种新的全波分析与高频近似方法相结合的混合算法.整个算法可分为2个步骤:①由基于MSI的高频方法得到天线罩内的场分布E和H;②再将此场分布作为天线阵列的激励场,利用基于体-面混合积分方程(Volume Surface Integral Equation,VSIE)和MLFMA的快速全波分析方法精确计算天线阵列的电流分布,便可得到所有感兴趣的电磁参数.本文称此算法为IE/MSI方法[3].与纯粹的全波数值法不同,在此方法中只有天线阵列部分采用全波求解,而天线罩部分则只用高频射线法计算,因此该方法极大地减少了内存用量.
 |
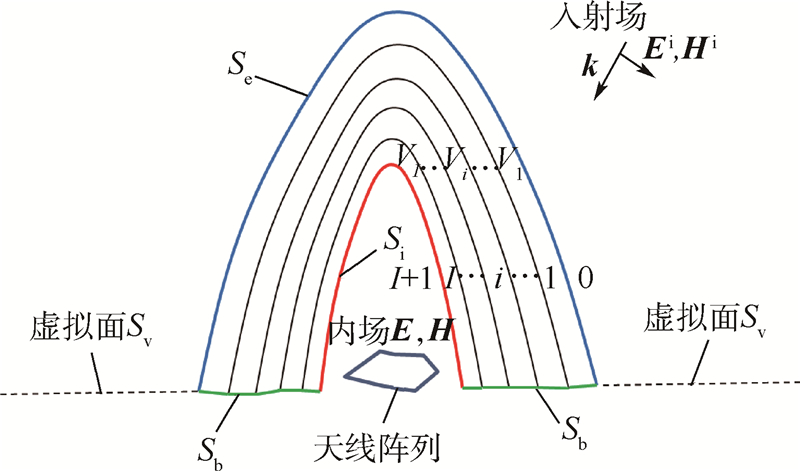| Ei,Hi—入射电磁场;Se—天线罩外表面;k—波矢量;i=0,1,…,I+1—介质天线罩的层数;Vi=V1,V2,…,VI—各层天线罩实体.图 1 天线-天线罩系统模型Fig. 1 Model of antenna-radome system structure |
| 图选项 |
上述过程中的第②步可以按照已有的全波方法精确计算出阵列中的电流分布,问题在于第①步中天线罩内场分布E、H的计算.传统的口径积分-表面积分法(Aperture-Integration Surface-Integration,AI-SI)[4],只能得到处于发射工作模式下天线加罩后的辐射方向图等信息,但由于等效原理的失效,这种方法不能计算天线工作于接收状态下的场分布.为此,本文将天线罩的底面Sb向外做任意无限延伸,形成一个带有空洞结构的无限大虚拟面Sv(图 1中虚线部分).此虚拟面Sv和天线罩的内表面Si、天线罩的底面Sb一起形成了一个完整的无限大曲面,此曲面将整个三维空间分成了2个无限大半空间,将其中的下半空间视为天线罩内场区域.那么,根据面等效原理,天线罩内场区域的电磁场E和H可以由3个不同曲面上的等效电磁流作表面积分得到.同时,假定由非实际结构虚拟面Sv上的等效电磁流产生的部分场,不随天线罩实际结构的改变而发生变化.这样,2次使用高频近似方法SI就可得到实际天线罩结构下,天线罩内场区域中的电磁场分布E和H.然后,再以此场分布作为天线阵列的激励源,计算出阵列中等效电流分布.
在天线阵列中,设S为其中任意形状的理想导体表面,V为任意形状且介电常数为ε的非磁性介质体,那么若入射电场为Ei,则电场在天线阵列的导体表面上和介质体中应分别满足积分方程:
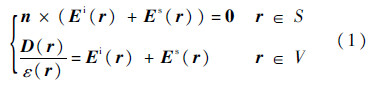
式中:Es为散射电场;D为介质体内的电位移矢量;r为坐标矢量;n为表面单位法向矢量.式(1)两式联立,即构成了基于电场的VSIE.其中,Es由导体表面的等效面电流与介质体内的等效体电流所产生的部分场叠加而成:
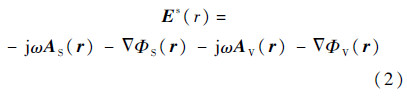
式中:AS和ΦS分别为面电流产生的磁矢位和电标位;AV和ΦV分别为体电流产生的相应位函数;
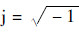;ω为角频率.利用MLFMA,可将式(2)的VSIE计算模型的计算复杂度降至O(NlogN)量级,其中N为未知量个数.但是同时也注意到,MSI计算天线罩内区域透射场过程的计算复杂度为O(MN)量级,其中M和N分别为天线罩内壁三角形和天线罩内场区域采样点的个数.这就意味着MSI将消耗混合算法的大部分时间,尤其是在电大尺寸罩复杂天线阵列的情况下,罩内场计算将占据整个算法90%以上的计算时间.这就导致在某些情况下,IE/MSI的计算时间甚至比全波算法的计算时间更长.
为了加速MSI的计算,进一步提高计算效率,将整个天线-天线罩系统用2套MLFMA树形结构覆盖,如图 2所示.其中,树形结构1覆盖整个带罩天线系统,首先用于MSI的MLFMA加速计算[5].第2套树形结构2仅覆盖天线阵列及附属结构(如反射地板),用于天线阵列所对应的VSIE模型的MLFMA快速求解.本文称此改进后的方法为IE/MSI+MLFMA法.可以看出,改进型算法中MSI部分的计算复杂度也降到了O(NlogN)量级,这就使得该算法不仅占用内存少,而且计算时间也大为缩短,从而实现了对电大尺寸带罩天线系统快速高效仿真的目标.
 |
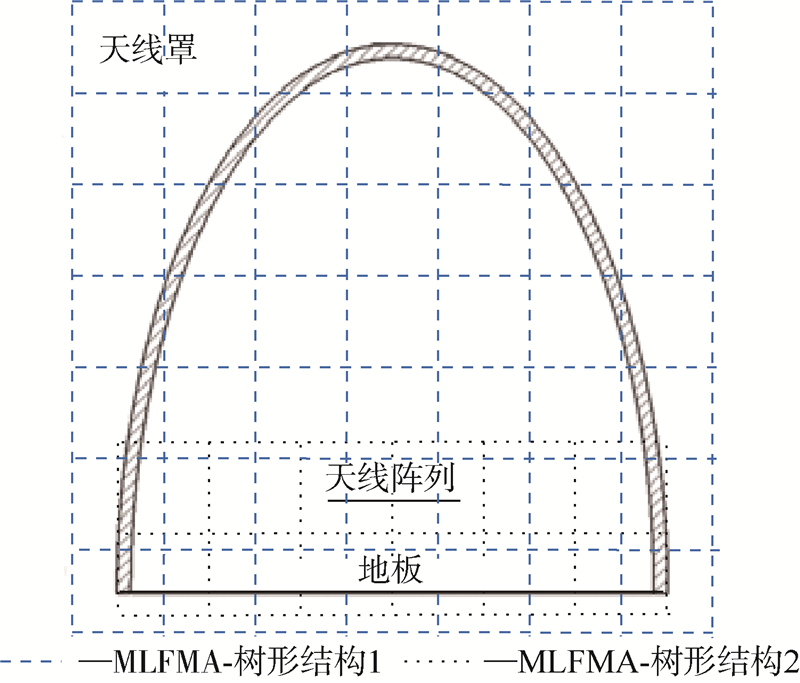| 图 2 IE/MSI+MLFMA方法中的MLFMA树形结构Fig. 2 MLFMA-tree structure applied for MSI+MLFMA method |
| 图选项 |
2 相关数值计算技术2.1 基于改进型球谐函数展开的MLFMA技术求解VSIE在传统MLFMA求解积分方程的过程中,远区盒子之间的相互作用是通过单位球面上平面波的积分来实现的.为了提高计算效率,基函数在Ewald球面上的过采样信息,即基函数的方向图,需要事先计算并存储下来.采样率由底层对角转移矩阵的带宽决定,但过采样将浪费大量的核心内存.为解决这一问题,国外****针对面积分方程提出了一种基于球谐函数展开的多层快速多极子方法(Spherical harmonics Expansion-MLFMA,SE-MLFMA)[6, 7],这种方法不再直接存储方向图信息,而是转化为对方向图球谐函数展开系数的存储,由于展开系数的个数远小于球面上的过采样点数,因此SE-MLFMA方法可将传统MLFMA的内存用量由2N(L+1)2c1c2B降至(3N/2)(P+1)(P+2)c1c2B.其中,L为底层多极子模式数,P为球谐函数的截断参数,一般取P=L/2-1,N为未知量个数，c1和c2为两个常数：c1与积分方程类型有关:电场积分方程对应c1=1,而混合场积分方程对应c1=2；c2是与数值计算精度相关的常数,单精度时c2=8,双精度时c2=16.而且,底层平面波发散过程的计算可以利用球谐函数的正交性质来加速,这就使得在保证精度与减少内存用量的前提下能够提高计算速度.
与SIE不同,在VSIE的MLFMA求解中,由于体基函数在底层盒子中密集存在而导致方向图的存储需要大量内存,传统的SE-MLFMA方法在内存用量和计算效率方面仍存在不足.为此,本文传统方法做了两方面的改进[8]:①有别于传统MLFMA中积分方程的并矢形式,将VSIE写成了混合位形式;②不同于传统MLFMA中RWG与SWG基函数[9, 10]基于公共边/公共面的分组方式,采用了基于三角形/四面体的分组形式.改进后的算法与传统方法相比,计算性能上有3点提高:
1) 方向图存储量进一步下降至2Nt(P+1)(P+2)c2B.此时,方向图的内存消耗仅与三角形与四面体的总数Nt成正比,而与公共边和公共面的总数N无关.而对于通常的网格剖分,Nt的值要远小于N,因此方向图的内存用量大为降低.
2) 方向图存储量不再与SIE类型有关.对于传统的SE-MLFMA,混合场积分方程中方向图存储量需求是电场积分方程的2倍,而对改进型算法而言,以上两种不同类型积分方程的方向图内存用量完全相同.
3) 更快的计算速度.为了避免Gibbs现象以及获得更小的P值,传统并矢形式的SE-MLFMA算法的聚集、转移及发散过程在极坐标系下进行,而底层方向图的聚合与发散需要在直角坐标系下完成.因此,传统算法中方向图函数需要在直角坐标系与极坐标系下进行反复转换;而对于改进算法,MLFMA的所有过程均可在直角坐标系下完成,因此省去了坐标系间多次转换步骤,提高了计算速度.
2.2 预处理技术天线阵列的VSIE模型经MLFMA离散化后通常得到形如ZI=V的大型线性方程组,其中，Z为非奇异广义阻抗矩阵,V为激励矢量,I为待求的展开系数矢量.MLFMA中采用迭代法求解该线性方程组,其收敛速度由矩阵Z的条件数所决定.通常VSIE对应的Z矩阵条件数较差,导致迭代求解的收敛速度一般较慢,甚至可能出现不收敛的情况.因此,采用预处理技术改善问题的数值性态是提高计算效率的有效途径之一.
预处理技术构造出新的矩阵方程
或
式中:M为预条件矩阵;y为预条件中间向量.新线性系统的条件数由MZ或ZM来决定.显然,若M为Z-1的一个很好的近似,则新系统的数值性态将得到大大改善.但是,对于MLFMA而言,由于仅有近区场矩阵Znear被显式存储,因此常用Znear来构造M.
在对VSIE的求解中,本文采用了2种不同的预处理技术构造矩阵M,即不完全LU分解(Incomplete Low-Up,ILU)方法和稀疏近似逆(Sparse Approximate Inverse,SAI)方法.
2.2.1 ILU预处理技术ILU预处理将近场作用矩阵Znear做不完全LU分解,然后将预条件矩阵M表示为
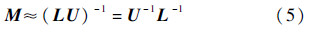
式中:L和U分别为下三角和上三角矩阵.由于L-1与U-1并不显式存储,因此ILU实质上是隐式预处理.为了降低内存用量、加快分解速度,在进行ILU分解时必须要舍弃一些元素.根据舍弃策略的不同,常用的ILU预处理方式有无填充不完全分解预处理ILU(0)、多层填充不完全分解预处理ILU(k)(k为填充度)、双门槛不完全分解预处理ILUT(Threshold ILU)、带选主元形式的ILUTP(ILUT with Pivot)等.其中,由于ILUT与ILUTP具有鲁棒性好、精度可调节和内存用量可控的优势,本文选择了这2种预处理技术加速VSIE的MLFMA求解.大量的计算结果表明,对于中等规模的天线阵列电磁仿真问题,ILUT及ILUTP可以取得良好的预条件效果[11, 12].
然而,ILU预条件也有自身的缺陷.由于其自身结构所限,ILU预条件的分解及迭代求解过程均难以并行.近年来,虽有****对可并行化的多水平不完全LU分解法(ILUM)进行了探讨,但未见深入研究.这限制了计算程序的可扩展性,使得在求解大规模电磁散射问题时,ILU预处理成为了技术瓶颈.
2.2.2 SAI预处理技术SAI预处理[13]的基本思想是通过求解稀疏矩阵Z的Frobenius范数最小化问题构造预条件矩阵M,以期所得的M与稀疏矩阵Z的乘积能尽可能近似等于单位矩阵I.由于矩阵M为显式存储形式,因此SAI为显式预处理技术.MLFMA中一般用Znear来构造M矩阵,其Frobenius范数最小化问题可以分解为该矩阵单独的各列向量的最小二乘问题：
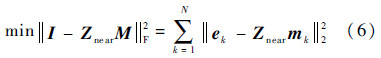
式中:ek和mk分别为单位矩阵I与预条件矩阵M的第k列元素组成的列向量.显然,相互独立的mk可以被单独求解,因此SAI预条件具有天然并行性.实际操作过程中,对于特定的第k个最小二乘问题,常采用Znear的缩减矩阵Zk并通过QR分解来计算.如设Jk为矩阵Znear的第k行非零元素的列号组成的集合：
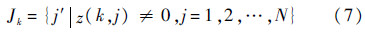
式中：j′为列编号.同样用Ik表示Jk所对应的各列非零元素的行号的集合：
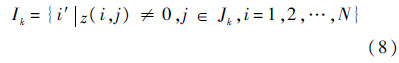
式中:i′为行编号.这样对于任意的mk,Znear可被缩减为相应的子矩阵Zk=Z(Ik,Jk).显然,当Znear足够稀疏时,对Zk进行QR分解的计算量为O(1)量级.
然而,通过式(6)可知,构造M时需要进行N次最小二乘计算,这导致了即使用缩减矩阵来构造M的耗时依然很“漫长”.因此,本文的改进方法是将SAI与MLFMA的分组方式结合起来.从MLFMA的特点可知,未知量之间的相互作用不再是一一对应,而是通过包含未知量的盒子来进行近、远相互作用.这时,每个特定盒子所包含的所有未知量相对应的近场元素排列方式(即非零元素的位置)是一致的.例如,假设G为某一底层非空盒子所包含的所有未知数编号的集合,则对于所有k∈G,Znear的缩减矩阵Zk均相同.因此,对于所有k∈G,仅需进行一次QR分解即可求得所有mk.这使得构造M时所需求解的最小二乘问题降为Ngroup(Ngroup为底层非空盒子数,个).由于Ngroup<<N,因此M的构造时间得以成倍下降,效率大幅提升.
需要指出的是,SAI对于矩阵的稀疏程度非常敏感.对于某些包含复杂精细结构的仿真目标,其网格剖分往往过于密集,这就导致了Znear的稀疏程度较低.此时,即使采用了与MLFMA相结合的SAI来构造预条件矩阵M,其耗时也将难以忍受.若采用同ILUT预条件类似的舍弃策略,则预处理效果往往大打折扣.另外,随着仿真目标电尺寸的增大,近场矩阵Znear对全局矩阵Z的近似性将变得越来越差,这是所有预条件技术都会遇到的问题,这需要通过人为地扩大用于构造M的矩阵规模来缓解.
2.3 并行计算技术VSIE的求解过程中,数值仿真时间将随着目标电尺寸的增加而成平方量级增长,对于电尺寸较大的问题,这样的计算速度显然是不可接受的.现代并行计算技术是提高仿真速度的重要手段之一,在计算电磁学领域,这一技术已经得到国内外****的广泛研究[14, 15, 16, 17, 18].针对大型带罩天线阵列的电磁仿真问题和现有的多核计算平台,本文提出了一种新的结合单程序多数据以及单指令多数据并行计算模型的混合并行计算模式,很好地结合了基于共享内存式架构的OpenMP并行模型与基于矢量逻辑运算单元(Vector Arithmetic Logic Unit,VALU)的硬件矢量加速技术两者的优点.与基于GPU(Graphic Processing Unit)的加速技术[14]相比,VALU加速技术[15]具有2个明显优势:①由于VALU仅是CPU的一个基本单元,因此不需要添加任何其他硬件设备而仅需做程序上的改动;②应用了VALU加速技术的程序其计算速度一定比不使用该技术时快,而同样的结论并不适用于GPU加速.
以下将着重讨论在共享内存式的计算机架构下,应用该混合并行技术加速VSIE的MLFMA求解的几个关键技术[17, 18].
2.3.1 OpenMP并行程序设计中的关键问题MLFMA算法的实现中,最耗时的两个部分为近场矩阵填充与矩阵向量相乘(Matrix-Vector Product,MVP).前一部分的OpenMP并行实现十分简单,直接将使用了Guided策略的OpenMP命令应用到程序的最外重循环即可获得良好的并行效果;而MVP部分包含两个过程:近场相互作用(Near-Field Interaction,NFI)与远场相互作用(Far-Field Interaction,FFI).
其中,FFI通过3个步骤实现:聚集、转移和发散.聚集和发散过程的程序代码主要包含三重循环:父盒子循环(Father Box,FB)、子盒子循环(Son Box,SB)以及平面波循环(Plane Wave,PW).传统串行程序中,按照FB-SB-PW循环顺序设计的代码将会获得最高的执行效率,然而并行程序中若将OpenMP的指令直接应用到最外重的FB循环上,随着聚集过程的进行,父盒子数目迅速下降,甚至有可能出现父盒子数目少于线程数的情况,导致各线程间的负载越来越难以达到平衡.因此,为了取得更高的并行效率,需要调整程序的循环次序.数值实验结果表明,在高层循环中,虽然PW循环作为最外重循环可以获得最高的并行效率,但计算时间会明显增加.同时,由于每一层中子盒子数目都要多于父盒子数目,故而在不增加计算时间的前提下,将子盒子循环设置为最外重循环更易于实现负载平衡.因此,对于聚集与发散过程的并行设计而言,最佳的循环结构应为SB-FB-PW.转移过程的算法同样包含三重循环:盒子循环、每个盒子的次相邻盒子循环以及平面波循环.同样,从低层到高层每层包含非空盒子的数目迅速下降,在高层若直接将OpenMP指令应用到盒子循环将不能获得良好的并行效率.不仅如此,由于盒子与其次相邻盒子都处于同一层中,应用到聚集和发散过程中的循环策略也不适用于转移过程.因此,需要重新考虑循环策略.实验数据表明,在高层中,平面波循环作为最外重循环可以获得更高的并行效率以及更短的并行时间,而在低层将盒子循环作为最外重循环更为合适.因此必然存在一个过渡层,过渡层的两侧应采用不同的循环策略以获得最优的并行效率.然而,过渡层的选择取决于总层数以及高层盒子内的平面波数量,若选择不当则并行效率将会大打折扣.大量的实验数据表明,当在某一层分配到每个线程中的循环数大于60时,选择这一层作为过渡层是较为合适的.
近场相互作用NFI的实质是一个CSR格式存储的稀疏矩阵与一个向量相乘,简单的代码结构造成了内存数据的存取速率滞后于CPU的计算速率.OpenMP中,随着参与NFI计算的线程数增加,这一滞后现象将变得越来越严重,最终使得NFI的并行计算会遭遇“内存墙”问题.这一问题导致NFI的计算时间不会再随参与计算的线程数的增加而减少,严重影响了程序的并行效率与可扩展性.为了解决这一问题,本文的策略是将NFI的代码与聚集过程中底层盒子方向图聚合的代码合并.由于NFI的计算与底层方向图的聚合都是针对基函数的操作,因此可以使这两部分的计算共享同一内存寻址时间,从而将NFI“隐藏”到方向图的聚合过程中.这时,由于方向图的聚合过程较为复杂,与内存的寻址时间相比,CPU的计算时间将起主导作用,这样就减弱了“内存墙”现象带来的影响.实验数据表明,采用合并策略以后,并行效率大幅提升.
2.3.2 VALU硬件加速技术的关键问题VALU为CPU的一个基本单元,与浮点运算单元(FPU)每次只能对一个数据进行操作不同,VALU可以对4个数据同时进行操作.其运算规则依赖于SSE指令集,而就Windows系统而言,Win98之后的所有系统均支持此指令集,并且从SSE2起,VALU开始支持双精度的浮点数运算.因此,理论上应用了VALU加速的程序比普通程序最多可以快4倍.然而,应用了VALU加速技术的代码,并非仅是对原有程序进行简单调整,而是要从算法结构上做出根本改变[17, 18].同OpenMP相比,VALU加速技术粒度更细,对程序细节的要求也更高.一般而言,只有纯粹的赋值语句与多重循环的最内重循环才可利用此项技术.不仅如此,应用VALU的程序代码还需满足以下3个条件:①循环体内的每一个语句能够独立执行;②除编译器的标准内部函数外,循环体内不能调用任何自定义函数;③对于需要退出条件的循环,只能有一个出入口.
影响VALU加速性能的一个重要因素是数据对齐.由于只有当CPU每次从缓存中读取的数据个数为4时才可应用VALU进行加速,因此,若参与计算的数组第一维度较小并且不是4的整数倍时,VALU的加速性能将会大受影响.这就需要在进行代码的编写工作时,仔细考虑算法流程,尽量将能够应用VALU加速技术进行计算的数组的第一维度存储成4的整数倍.
另外,VALU单元只能针对整数与实数进行运算,而对于MLFMA运算中最常用的复数类型是不适用的.因此,首先需要将代码中所有的复数运算全部转化为实数形式.实际操作过程中,4个同种类型的数据(实数或整数)被收集成数据流的形式同时输入到VALU中;经过同一个计算周期后,4个计算结果又以数据流的形式同时输出.需要指出的是,这4个数据必须进行的是同类型的运算才可应用VALU进行加速.
3 数值算例本节采用两个数值算例来验证上述算法的正确性与计算效率.其中,计算代码基于Intel Visual FORTRAN平台编写,并且采用普通PC机进行计算,其配置水平如表 1所示.
表 1 计算平台配置水平 Table 1 Configuration level of computing platform
| CPU类型 | 核心数 | 内存大小 | 操作系统 |
| Intel CoreTM i5-4570 @3.2GHz | 4 | DDR3 16GB | Windows7 Ultimate x64 |
表选项
另外,为分析程序的并行效率,定义并行加速比为
式中:T为串行程序(serial)执行时间;Tv为并行程序(OpenMP)执行时间.所有数值算例均采用重启型GMRES求解器进行求解,其中重启次数为100,收敛精度为0.001.
3.1 微带天线阵列带A夹层罩的微带天线阵列系统工作频率为10.3GHz,模型如图 3(a)所示.A夹层天线罩关于yOz面对称,表 2中给出了天线罩各层的具体参数.天线阵列由4个如图 3(b)所示的方形切角微带贴片单元组成,4个贴片单元分别放在坐标系x轴和y轴上并距离坐标原点50mm，基板介电常数为2.55.阵列剖分所得的三角形个数为23300,四面体个数为20656,总的未知量为82352;天线罩剖分所得三角形个数为45824.
 |
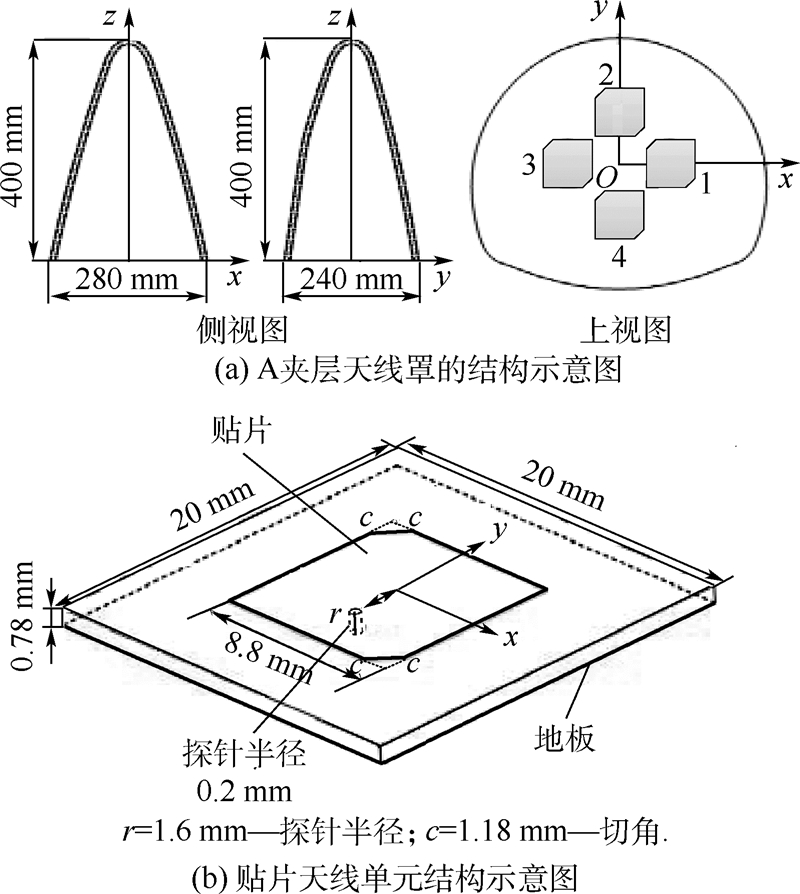| 图 3 带罩微带天线阵列Fig. 3 Radome-enclosed microstrip patch antenna array |
| 图选项 |
表 2 A夹层天线罩的参数 Table 2 Parameters of A-type sandwiched radome
| 层数 | 相对介电常数 | 损耗角正切 | 厚度/mm |
| 蒙皮1 | 4.0 | 0.02 | 0.6 |
| 夹芯2 | 1.07 | 0.002 | 8.8 |
| 蒙皮3 | 4.0 | 0.02 | 0.6 |
表选项
图 4给出了分别应用传统MLFMA(conv.)与SE-MLFMA(se)算法并结合ILU预处理技术得到的不同入射角度下端口1的接收电压值,入射角度分辨率为2°.其中,对于SE-MLFMA,P的取值为2.从图 4中可以看出,SE-MLFMA与传统MLFMA相比精度虽稍有下降,但完全可以满足工程需求.为了对比,图 4中也给出了当P=3时SE-MLFMA的仿真结果,可以看出,此时SE-MLFMA与传统MLFMA的仿真结果高度吻合.总的计算时间、加速比与方向图的内存需求如表 3中ex1所示,其中se2和se3分别对应P=2和P=3.
 |
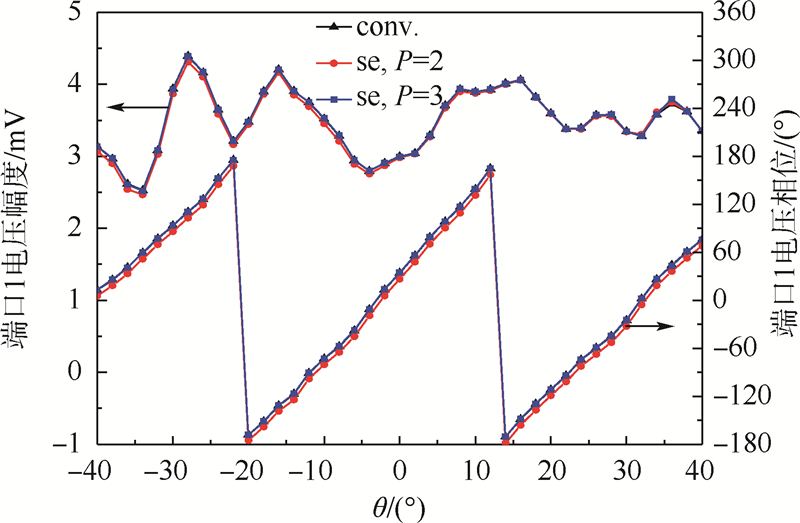| 图 4 不同入射角度下端口1的接收电压变化Fig. 4 Variation of receiving voltage at port 1 changing with different incidence angles |
| 图选项 |
表 3 仿真所耗的总时间、并行加速比及方向图内存用量 Table 3 Total solving time, parallel ratio and pattern memory cost of simulations
| 算例 | 类型 | 总时间/s | 加速比 | 方向图内存/MB | 峰值内存/MB |
| ex1 | Serial&conv. | 2995 | 1.72 | 21.55 | 6049 |
| OpenMP&conv. | 1743 | ||||
| Serial&se2 | 2860 | 1.71 | 8.07 | 6036 | |
| OpenMP&se2 | 1672 | ||||
| Serial&se3 | 2951 | 1.71 | 13.40 | 6041 | |
| OpenMP&se3 | 1724 | ||||
| ex21 | Serial&se | 66647 | 3.62 | 60.61 | 4978 |
| OpenMP&se | 18389 | ||||
| ex22 | Serial&se | 81968 | 3.59 | ||
| OpenMP&se | 22860 |
表选项
从表 3中可以看出,SE-MLFMA的方向图内存用量仅为传统MLFMA的37.4%,而总的计算时间大体持平.这就使得SE-MLFMA在保证精度与计算速度的前提下,大幅降低了仿真时的核心内存用量.另外,此例中程序的并行加速比仅为1.7,这是由ILU预处理不可并行所导致.由此可见,ILU预处理技术对并行程序的可扩展性有较大限制.
3.2 带罩天线阵的接收方向图1604个半波阵子单元组成天线阵,工作频率为16.5GHz.天线罩为半波长壁罩,带罩天线阵列的模型如图 5所示.
 |
| 图 5 1604个单元的带罩天线阵列模型结构Fig. 5 Structure of a radome enclosed antenna array model with 1604 elements |
| 图选项 |
图 5中阵列俯仰间距为9.375mm,方位间距为21.25mm,反射板为直径750mm的理想导体圆盘.阵列剖分所得的三角形个数为330383,总的未知量个数为483724;天线罩剖分所得三角形个数为803556.其中,超球体方程天线罩外形为
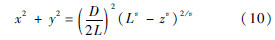
式中:超球体的直径D与高度L均为750mm,系数v=1.8;x、y和z分别为3个方向的尺度.
应用SE-MLFMA并结合SAI预条件分别对不加罩的孤立阵与加罩后的天线阵进行仿真,得到的接收方向图如图 6所示,其中分辨率为0.25°.从图 6中可以看出,孤立阵与加罩阵的接收方向图相差不大,表明所设计的天线罩具有较好的电磁特性.仿真的计算时间、加速比与方向图的内存需求分别如表 3中的ex21(孤立阵)、ex22(加罩阵)所示.从表 3可以看出,加罩前后天线阵列的总体仿真时间差距并不大,这说明IE/MSI+MLFMA算法极大降低了天线罩对天线阵列仿真效率的影响.此外,由于采用了可并行的SAI预处理技术,与第3.1节中的算例相比并行程序的加速比有了大幅提升,达到了3.6.这说明SAI预处理技术具有良好的并行特性,尤其适用于电大尺寸目标的仿真计算.
 |
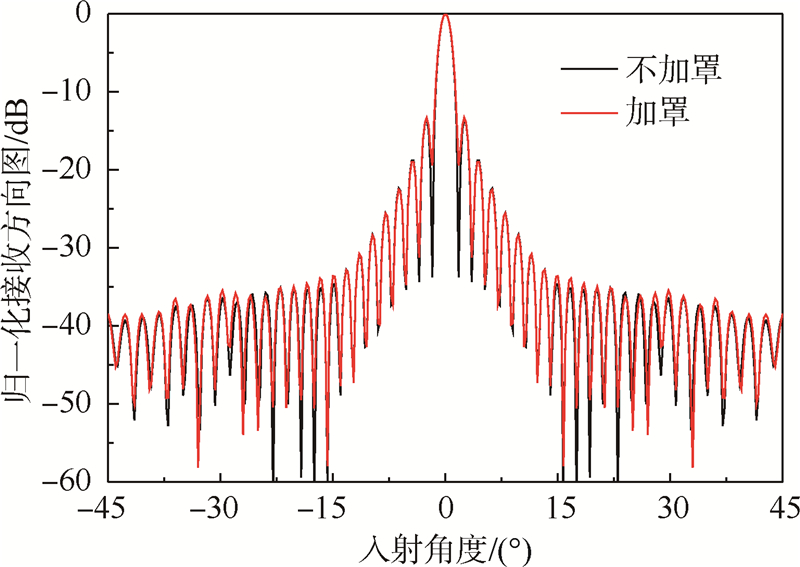| 图 6 偶极子阵列接收方向图Fig. 6 Receiving pattern of dipole array |
| 图选项 |
4 结 论本文针对接收模式下的天线-天线罩系统,提出了一种全波法结合高频法的混合算法,结合仿真结果,得到:
1) 将IE/MSI+MLFMA混合算法成功应用于加罩天线阵系统的电磁仿真计算.在具体的算法实现过程中,球谐函数展开、ILU与SAI预处理技术、OpenMP+VALU的混合并行等技术的应用使得该算法得到了相当大的改进.
2) 通过具体算例可知,加罩前后天线阵列的总体仿真时间差距并不大,这说明IE/MSI+MLFMA算法极大降低了天线罩对天线阵列仿真效率的影响,实现了对电大尺寸天线-天线罩系统的快速、高效仿真,并且具有良好的可扩展性.
3) 具体的程序细节方面,对于SE-MLFMA的应用,当P=2时已经完全可以满足工程需求;相较于ILU,SAI预处理技术具有良好的并行特性,尤其适用于电大尺寸目标的仿真计算,使得并行程序的加速比得到大幅提升.
参考文献
| [1] | Kozakoff D J.Analysis of radome-enclosed antennas[M].Norwood,MA:Artech House,2010:5-8. |
| [2] | Chew W C,Jin J M,Michielssen E,et al.Fast and efficient algorithms in computational electromagnetics[M].London:Artech House,2001:77-85. |
| [3] | Wang B B,He M,Liu J B,et al.An efficient integral equation/modified surface integration method for analysis of antenna-radome structures in receiving mode[J].IEEE Transactions on Antennas and Propagation,2014,62(9):4884-4889. |
| Click to display the text | |
| [4] | Paris D T.Computer-aided radome analysis[J].IEEE Transactions on Antennas and Propagation,1970,18(1):7-15. |
| Click to display the text | |
| [5] | Wang B B,He M,Liu J B,et al.Efficient method for analysis of radome in receiving mode[C]∥Proceedings of Asia-Pacific Microwave Conference.Piscataway, NJ:IEEE Press,2014:1408-1410. |
| Click to display the text | |
| [6] | Eibert T F.A diagonalized multilevel fast multipole method with spherical harmonics expansion of the k-space integrals[J].IEEE Transactions on Antennas and Propagation,2005,53(2):814-817. |
| Click to display the text | |
| [7] | Ismatullah I,Eibert T F.Surface integral equation solutions by hierarchical vector basis functions and spherical harmonics based multilevel fast multipole method[J].IEEE Transactions on Antennas and Propagation,2009,57(7):2084-2093. |
| Click to display the text | |
| [8] | He M,Liu J B,Zhang K.Improving the spherical harmonics expansion based multilevel fast multipole algorithm[J].IEEE Antennas and Wireless Propagation letters,2013,12:551-554. |
| Click to display the text | |
| [9] | Rao S M,Wilton D R,Glisson A W.Electromagnetic scattering by surfaces of arbitrary shape[J].IEEE Transactions on Antennas and Propagation,1982,30(3):409-418. |
| Click to display the text | |
| [10] | Schaubert D H,Wilton D R,Glisson A W.A tetrahedral modeling method for electromagnetic scattering by arbitrarily shaped inhomogeneous dielectric bodies[J].IEEE Transactions on Antennas and Propagation,1984,32(1):77-85. |
| Click to display the text | |
| [11] | Sertel K,Volakis J L.Incomplete LU preconditioner for FMM implementation[J].Microwave and Optical Technology Letters,2000,26(4):255-257. |
| Click to display the text | |
| [12] | Lee J,Zhang J,Lu C C.Incomplete LU preconditioning for large scale dense complex linear systems from electromagnetic wave scattering problems[J].Journal of Computational Physics,2003,185:158-175. |
| Click to display the text | |
| [13] | Malas T,Gurel L.Accelerating the multilevel fast multipole algorithm with the sparse-approximate-inverse preconditioning[J].Society for Industrial and Applied Mathematics,2009,31(3):1968-1984. |
| Click to display the text | |
| [14] | Peng S X,Nie Z P.Acceleration of the method of moments calculations by using graphics processing units[J].IEEE Transactions on Antennas and Propagation,2008,56(7):2130-2133. |
| Click to display the text | |
| [15] | 余文华,李文兴.高等时域有限差分法[M].哈尔滨:哈尔滨工程大学出版社,2011:23-39.Yu W H,Li W X.The advanced FDTD method[M].Harbin:Harbin Engineering University Press,2011:23-39(in Chinese). |
| [16] | Velamparambil S,Chew W C.Analysis and performance of a distributed memory multilevel fast multipole algorithm[J].IEEE Antennas and Propagation Magazine,2005,53(8):2719-2727. |
| Click to display the text | |
| [17] | Liu J B,He M,Zhang K,et al.Parallelization of the multilevel fast multipole algorithm by combined use of OpenMP and VALU hardware acceleration[J].IEEE Transactions on Antennas and Propagation,2014,62(7):3884-3889. |
| Click to display the text | |
| [18] | 刘金波,何芒,基于OpenMP与VALU硬件加速的表面积分方程矩量法混合并行求解技术[J].北京理工大学学报,2014,34(1):50-55.Liu J B,He M.A hybrid parallelization technique based on OpenMP and VALU acceleration for the method of moments solution of the surface integral equations[J].Journal of Beijing Institute of Technology,2014,34(1):50-55(in Chinese). |
| Cited By in Cnki |
