运用时变系数建模分析处理非平稳信号时,时变系统的参数能否准确辨识直接关系到信号的瞬时特征提取结果.目前,时变系统的参数辨识方法主要有两种:①自适应算法,如经典的递推最小二乘法、最小均方算法及卡尔曼滤波法[4].如果时变系统参数变化较慢,或信号具有弱平稳特性时,自适应算法可以对时变系统参数进行准确辨识.如果时变系统参数变化太快,由于自适应算法的收敛性缺陷,导致时变系统参数的结果估计产生延迟[5].②基函数展开式方法,即将时变系统参数表示为一组已知基函数的线性加权组合[6],将时变系统建模问题转化为关于基函数的时不变参数辨识问题,通过对时不变参数的辨识进而得到时变系数.当信号具有较强非平稳特性时,基函数展开式方法可以对时变系数进行有效估计[2].目前,可供选择的基函数包括傅里叶基、勒让德多项式、小波基等[3, 4, 6, 7, 8, 9].每种基函数都有自己的逼近性能,如傅里叶基函数和勒让德基函数可以有效辨识变化缓慢且平滑的时变系数,小波基函数可以有效辨识变化剧烈或有突变的时变系数[5].目前,基函数的选择没有一个确定的方法[7, 8].
近年来,B样条小波基函数常常被引入到时变系统辨识当中[4, 7, 9, 10],对时变系统的参数利用区间B样条小波进行线性表示.B样条小波作为分段多项式,具有很好的局部特性,由Chui和Wang[9]首次引入作为多分辨率小波和多尺度函数.对于在每一个尺度空间和小波空间里,在有限的区间上,小波维数是有限的,即:任意一个函数都可以被有限维数的小波函数进行逼近,这一特性使得区间B样条小波作为基函数,对时变系统的时变系数进行展开[4, 7, 9, 10].Chon等[8]根据勒让德多项式和Walsh函数具有灵活的逼近性能,对时变系数进行展开,取得了较好的跟踪效果.总之,选择具有多种尺度或多种逼近性能的基函数对时变系统的参数进行展开,从而使时变系统的瞬时特征能够被快速、准确地提取与识别.
径向基函数因具有多尺度和多分辨率特性已被成功用于信号处理和系统辨识中,所以可将时变系统的系数用一组多尺度径向基函数(Multi-Scale Radial Basis Function,MRBF)来展开,对时变系统参数进行识别.径向基函数(Radial Basis Function,RBF)是一种距离函数,具有中心对称性,且具有很好的局部特性.由于RBF具有良好的局部特性且尺度可以调整,采用粒子群优化算法(Particle Swarm Optimization,PSO)自动地选择最优的RBF尺度[11],从而使参数辨识结果更加准确,对时变系统参数的局部特征有效辨识[12].
综上所述,本文运用MRBF对线性时变系统在白噪声激励下的时变系统参数进行展开,并用PSO算法选择最优的RBF尺度,对时变系数进行准确辨识的方法.首先介绍了时变自回归模型及基函数展开式方法的参数辨识过程;然后介绍了高斯径向基函数及其中心、个数、尺度的选择方法;最后以时变系数包含多种波形的二阶随时间变化的线性模型为例,通过算例仿真辨识,将该法与递推最小二乘法、勒让德多项式展开式方法进行了实验对比研究,实验结果证明了本文方法的可行性及有效性.
1 时变自回归参数建模法1.1 时变自回归模型p阶时变自回归参数模型输出为
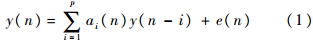
式中:ai(n)为时变系数,i为模型阶次序号(i=1,2,…,p,n=1,2,…,N);N为采样数据长度;e(n)为均值为0、方差为σf的高斯白噪声.
1.2 时变系数辨识对第1.1节时变自回归模型中的时变系数进行辨识的方法主要有两种:第1种是自适应算法,如递归最小二乘算法、卡尔曼滤波算法等[4];第2种方法是引入基函数展开式方法,将时变模型的系数表示为一组基函数的线性组合,将时变问题转变为关于基函数的线性时不变问题.根据前言的讨论,本文主要研究采用第2种方法.基函数展开式方法对时变系统进行辨识,将时变系数ai(n)表示为一组基函数的线性组合:
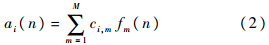
式中:ci,m为展开式的时不变系数;fm(n)为基函数;M为基函数的维数.将式(2)代入式(1)可得
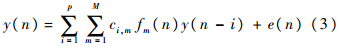
式(3)为时不变参数模型.
引入基函数对时变系数进行展开后,时变自回归模型由式(1)变为式(3),从而把式(1)的时变系数估计求解转化为对式(3)的时不变模型求解.估计 ci,m 后,再将其代入式(2),即可得到时变系数ai(n)的估计值.
将式(3)改写成矩阵形式表示:

式中:Y=[y(1) y(2) … y(N)]T为观测时间序列;上标T为矩阵转置;C为待求的时不变参数构成的未知列向量;e为e(n)的向量表示方法;H为回归矩阵:
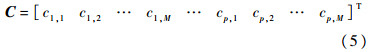

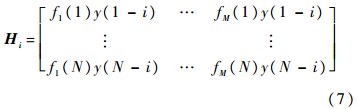
由以上推导可以得出,时变回归模型利用基函数展开式可以将时变模型式(1)中原来p个时变系数的识别问题转化为p×M个定常参数的识别,即将原来非平稳过程的参数识别转化为一个线性时不变系统的辨识[6].模型表示为矩阵形式后,由最小二乘法解出时不变参数C的估计值Ĉ:
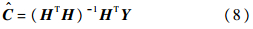
求出时不变参数C的估计值Ĉ后,直接代入式(2)即可求出时变系数ai(n)的估计值âi(n).
2 径向基函数2.1 高斯径向基函数如第1.2节所述,时变自回归模型的时变系数由一组基函数的线性组合表示,将时变系统建模问题转化为关于已知基函数展开式的时不变系数估计问题.目前可供选择的基函数有多种,如傅里叶基、勒让德多项式、小波基及径向基函数等[6, 7, 8, 9, 10, 11],每种基函数都有自己的逼近性能.
径向基函数是取值取决于距离的实值函数,距离是输入点与中心点之间的距离.距离函数为欧式距离或其他距离函数.径向基函数有多种,如高斯分布函数、薄板样条函数、Multiquadric函数等[13].对于时变系数的逼近属于多元函数的逼近,由于高斯径向基函数满足局部分布、中心径向对称、非负衰减的特性,具有逼近性能强、效果好,学习速度快等优点[5].同时,具有较好的平滑特性,受信号特征的影响较小,而大部分信号的特性也呈现高斯分布,因此本文采用高斯径向基函数作为时变模型参数辨识的基函数展开式.高斯径向基函数公式[14]为
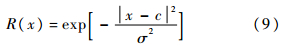
式中:c为径向基函数的中心;σ2为基函数的尺度,决定了基函数围绕中心点的距离;x为输入样本.在RBF作为基函数时,x=1,2,…,N为离散采样时间序列.
选择最优尺度的径向基函数是准确估计时变模型参数的关键步骤,其主要任务是确定最优RBF的维数、中心和尺度.
2.2 RBF维数选择为使时变系统参数估计结果更加准确,从而有效地提取非平稳信号的瞬时特征,RBF的最优维数选择以模型的拟合效果为依据.模型拟合效果由相关指数来衡量,其公式[15]为
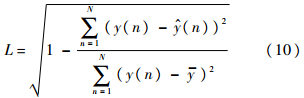
式中:L为相关指数;N为采样数据长度;ŷ(n)为模型真实输出y(n)的模型预测输出;y为y(n)的均值.相关指数越大说明模型拟合效果越好.为了找到最优的RBF维数,通过计算RBF维数与相关指数之间的关系来确定.如果RBF维数选取太低,会导致时变系数的估计误差较大,模型拟合效果较差.如果RBF维数太高,计算复杂度增大,出现冗余,最终也会导致参数误差增大.因此,可以通过计算相关指数与RBF维数的关系曲线来确定RBF的最优维数.
2.3 RBF中心的选择RBF的中心决定了RBF在整个时变系数估计的位置.为了使RBF分布到整个时变系数中,以确保RBF对时变系数的所有局部进行准确估计,本文将RBF的中心均匀分布到时变系数中,设第k个RBF公式及RBF的中心分别表示为
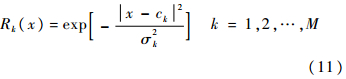

式中:ck为第k个RBF的中心;σ2k为第k个RBF的尺度,决定了该基函数围绕中心点的距离.
2.4 RBF尺度的选择传统的基于RBF展开式的时变系数估计方法采用同一固定的尺度,优点是时变系数展开式模型建立较为简单,但泛化能力较差[16].由于高斯径向基函数尺度越大,对样本输入的覆盖范围越大,敏感性越差(输入值x远离中心ck时,高斯径向基函数输入值变化不明显,且趋近于0),大尺度的径向基函数只能刻画信号的全局性特征;高斯径向基函数尺度越小,对样本输入的覆盖范围越小,敏感性越好,小尺度的径向基函数对信号局部特性刻画较好,但总的参数估计准确率低.基于这种考虑,为了同时兼顾局部和全局特性,本文同时采用大尺度和小尺度的径向基函数对时变系数进行展开.
RBF的候选尺度为

式中:sk为需要进行调节的任意整数.PSO智能算法,能够根据不同的参数分布特点,自适应地选取多尺度径向基函数的最优尺度.选择RBF最优尺度目的是能够更加准确估计时变系数,进一步能够准确地提取非平稳信号的瞬时特征.
RBF-PSO算法主要步骤包含:
1) 初始化:包括初始化粒子、粒子个数、适应度值、局部最优粒子、全局最优粒子、粒子最大值和最小值、速度最大值、迭代次数等.取随机整数为粒子赋初始值,多种尺度的选取可根据参数变化来确定.初始适应度值设为0,粒子数和迭代次数可根据参数变化特征来调整.
2) 计算每个粒子的适应度值.即将粒子代入式(13),得到RBF的候选尺度,再代入RBF公式(11),得到多尺度RBF,将MRBF展开式方法对时变模型进行参数估计,得到测量数据y的模型预测值?,最后根据式(10)计算相关指数,得到适应度值.
3) 更新局部最优粒子和全局最优粒子:找到适应度最大的粒子,该粒子作为局部最优粒子,若其适应度值比全局最优粒子大则赋值给全局最优粒子.
4) 更新速度和粒子:根据局部最优粒子和全局最优粒子更新速度和粒子.速度更新公式和粒子更新公式[16]分别为


式中:u为粒子;v为粒子速度;Cbest为局部最优粒子;gbest为全局最优粒子;uj(n)为第n次循环的第j个粒子;uj(n+1)为uj(n)更新后的粒子;vj(n)为第n次循环的第j个粒子的速度;vj(n+1)为vj(n)更新后的速度;Cbest(n)为第n次循环的局部最优粒子;gbest(n)为第n次循环后当前全局最优粒子;θ为0~1之间的随机数;c1和c2为加速系数,其作用是防止粒子陷入局部最优[17]:
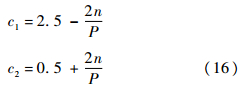
式中:P为最大循环次数,n=1,2,…,P.
5) 返回步骤2),重复执行步骤2)~步骤4)直到达到最大迭代次数.最后得到的全局最优粒子即为最终选择的粒子,代入式(13)得到径向基函数的最优尺度.
3 仿真实验3.1 时变自回归模型为了验证提出的基于MRBF展开式方法对时变系数估计方法的有效性,以时变系数包含多种波形的二阶时变自回归模型为例做仿真实验,分别用递推最小二乘法、勒让德多项式展开法和MRBF展开法对该模型的时变系数进行辨识,比较3种不同方法的时变系数辨识结果,并对其性能进行评估.
二阶时变自回归模型为

式中:a1(n)和a2(n)为式(17)的时变系数;e(n)为均值为0,方差为0.04的高斯白噪声,其信噪比约为21 dB.时变系数为
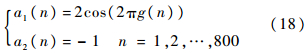
其中:g(n)定义为
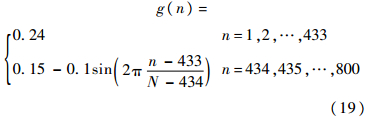
为了验证提出的MRBF展开式方法在强噪声环境下对时变系数具有多种波形的时变系统的辨识效果,模型式(17)的时变系数由3种不同波形构成:常值、突变和正弦波.
3.2 实验结果分析及性能评估采用本文提出的MRBF展开式方法对模型式(17)的时变系数进行辨识,其中RBF的最优维数可由式(10)求得,图 1为基于MRBF展开法估计二阶模型式(17)得到的相关指数随RBF维数变化如图 1所示.由图 1可以得知,相关指数开始随着RBF的维数增加而增大,然后趋于平稳,最后又递减.即维数小于40时,相关指数呈上升趋势,维数大于40时,相关指数有下降趋势,因此选择RBF的最优维数为40.
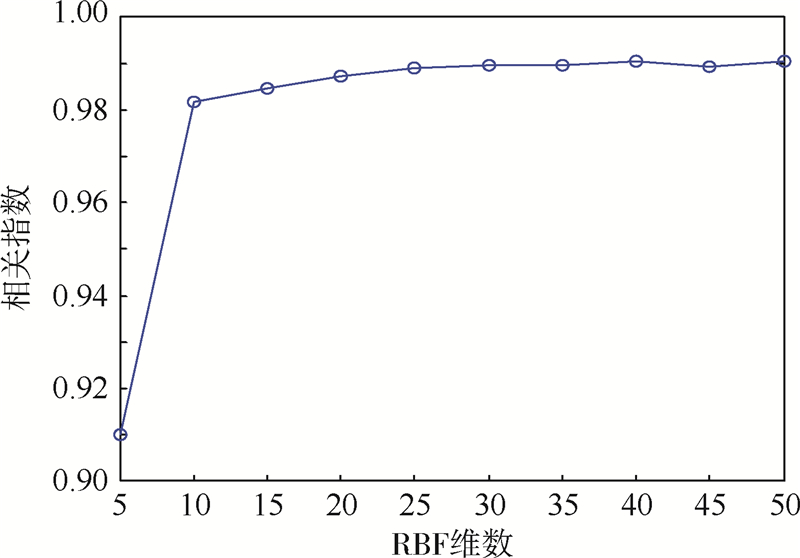 |
| 图 1 相关指数随RBF维数变化Fig. 1 Correlation index changing with RBF dimension |
| 图选项 |
由第2.3节可知,RBF的中心均匀分布到时变系数辨识中,RBF的最优尺度由PSO算法选择确定.图 2为MRBF展开式算法中选取的最优RBF,其尺度由PSO算法选择,用于估计模型式(17)的时变系数.
 |
| 图 2 MRBF展开式方法中选取的最优RBFFig. 2 Selected optimal RBF in MRBF expansion method |
| 图选项 |
利用递推最小二乘算法,勒让德多项式展开式方法及提出的MRBF展开式方法,分别对时变系统式(17)的时变系数进行辨识,可以得到3种时变系数瞬时变化的辨识结果,并与理论值进行比较,基于不同方法的时变系数辨识结果如图 3所示.3种方法的结果分别如图 3(a)~图 3(c)所示.时变系数辨识的常用方法如递推最小二乘法的参数估计结果波动较大,原因在于带遗忘因子的递推最小二乘算法的辨识方法跟踪能力不够,不能准确抓住信号的突变.勒让德多项式展开式方法因仅具有全局特性而对于平滑和缓慢变化的时变系数估计,识别效果比较理想.而提出的MRBF展开式方法由于其较强的局部分析能力,能很好地跟踪突变信号,其估计的时变系数结果比较平滑,特别在参数突变部分对时变系数跟踪结果明显优于传统的递推最小二乘算法及勒让德多项式展开式方法,实验结果说明本文方法在强噪声环境干扰下对具有多种波形的时变系数仍具有良好的跟踪能力,证实了提出方法的有效性.
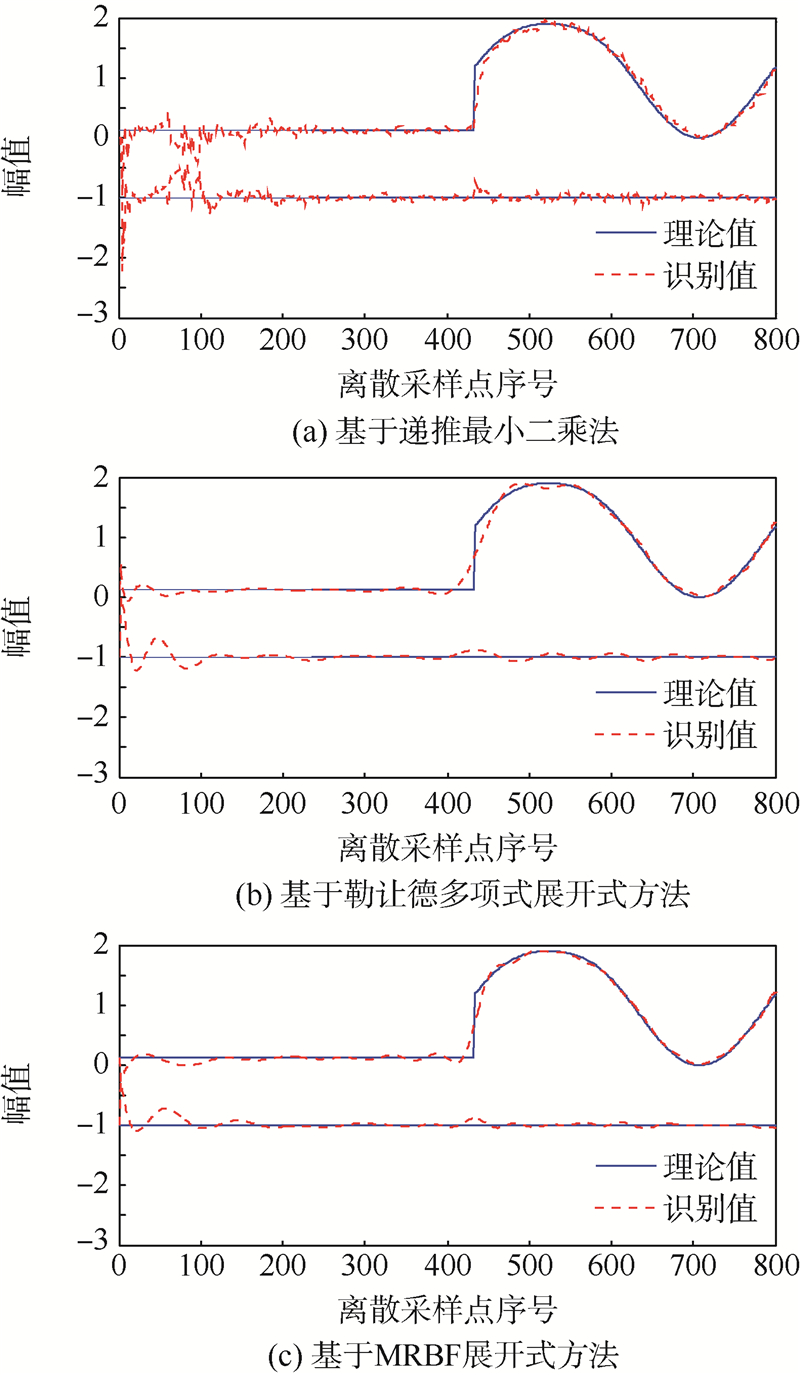 |
| 图 3 基于不同方法的时变系数辨识结果Fig. 3 Identification results of time-varying parameters using different methods |
| 图选项 |
为了定量评估提出方法对时变系统参数辨识的识别精度,引入平均绝对误差(Mean Absolute Error,MAE)及标准根均方差(Normalized Root Mean Squared Error,NRMSE)评价时变系统参数的准确估计能力[7],参数估计值与理论值的MAE和NRMSE越小,表明误差越小,时变系统参数的估计性能越好.
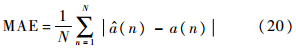
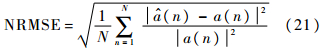
表 1为3种方法的参数估计值与真实值的MAE和RMSE对比结果.由表 1可知,3种时变系数辨识方法中,递推最小二乘法及勒让德多项式展开式方法的MAE和NRMSE值明显比MRBF展开式方法的MAE和NRMSE值大,该实验结果表明,基于MRBF展开式方法对具有3种波形:常值、突变和正弦波的时变系数能够准确辨识,该结果进一步证实了提出方法的有效性.表 1中:a1和a2为例子给出的时变自回归模型中两个真实的时变系数.
表 1 3种参数估计方法的MAE和NRMSE对比 Table1 Comparison of MAE and NRMSE using three parameter estimation approaches
| 参数辨识方法 | MAE | NRMSE | ||
| a1 | a2 | a1 | a2 | |
| 递推最小二乘 | 0.0689 | 0.0635 | 0.4929 | 0.4580 |
| 勒让德展开法 | 0.0488 | 0.0541 | 0.3676 | 0.3844 |
| 本文方法 | 0.0419 | 0.0410 | 0.3043 | 0.2969 |
表选项
4 结 论1) 针对时变系数包含多种波形的时变系统,本文提出了一种新型的基于MRBF-PSO算法的时变系统辨识方法.该算法兼顾了多尺度径向基函数的局部分析能力及粒子群优化算法的最优估计等优点,可以准确、迅速地识别时变系统的参数,有效提高时变系统的动态跟踪能力.
2) 仿真实验结果表明,与常用的时变系数辨识算法如递推最小二乘算法、勒让德基函数展开法相比,对于在强噪声干扰下的时变系统,该新型的时变系数估计方法仍能取得良好的参数辨识效果,为时变系统建模方法的时变系数估计提供了一种新的思路.
3) 时变系统的参数辨识问题是学术界研究的难点,该算法可以有效识别包含多种波形的时变系统参数,具有普遍适用性,因而可以用于大多数时变系统的动力学问题分析.为了进一步验证提出方法的性能及工程实用性,除了仿真实验验证该算法具有良好的识别精度之外,在接下来的研究工作中,继续研究该算法对实际工程系统如高速飞行器、高速列车以及大型的柔性航天结构等动力学问题的应用前景及工程实用价值.
参考文献
| [1] | Boashash B,Azemi G,Toole J M.Time-frequency processing of nonstationary signals:Advanced TFD design to aid diagnosis with highlights from medical applications[J].IEEE Signal Processing Magazine,2013,30(6):108-119. |
| Click to display the text | |
| [2] | 续秀忠,张志谊,华宏星,等.应用时变系数建模方法辨识时变模态参数[J].航空学报,2003,24(3):230-233.Xu X Z,Zhang Z Y,Hua H X,et al.Identification of time-variant modal parameters by a time-varying parametric approach[J].Acta Aeronautica et Astronautica Sinica,2003,24(3):230-233(in Chinese). |
| Cited By in Cnki (17) | |
| [3] | Niedzwiecki M.Identification of time-varying process[M].New York:John Wiley & Sons,2000:83-94. |
| [4] | 顾海雷,史治宇,许鑫.基于B样条小波基函数时变多变量AR模型的时变结构参数识别[J].振动与冲击,2013,32(19):86-92.Gu H L,Shi Z Y,Xu X.Parameter identification for a time-varying structure using a multi-variable AR model based on interval B-spline wavelet base functions[J].Journal of Vibration and Shock,2013,32(19):86-92(in Chinese). |
| Cited By in Cnki (1) | |
| [5] | 于开平,庞世伟,赵婕.时变线性/非线性结构参数识别及系统辨识方法研究进展[J].科学通报,2009,54(20):3147-3156.Yu K P,Pang S W,Zhao J.Advances in method of time-varying linear/nonlinear structural system identification and parameter estimate[J].Chinese Science Bulletin,2009,54(20):3147-3156(in Chinese). |
| Cited By in Cnki (25) | |
| [6] | 陈宇,陈怀海,李赞澄,等.基于时变AR模型和小波变换的时变系数识别[J].国外电子测量技术,2011,30(7):20-23.Chen Y,Chen H H,Li Z C,et al.Identification of time-varying parameters base on time-varying AR model and wavelet transform[J].Foreign Electronic Measurement Technology,2011,30(7):20-23(in Chinese). |
| Cited By in Cnki (11) | |
| [7] | Li Y,Wei H L,Billings S A,et al.Time-varying model identification for time-frequency feature extraction from EEG data[J].Journal of Neuroscience Methods,2011,196:151-158. |
| Click to display the text | |
| [8] | Chon K H,Zhao H,Zou R,et al.Multiple time-varying dynamics analysis usingmultiple sets of basis functions[J].IEEE Transactions on Biomedical Engineering,2005,52(5):956-960. |
| Click to display the text | |
| [9] | Chui C K,Wang J H.On compactly supported spline wavelets and a duality principle[J].Transactions of American Mathematical Society,1992,330:903-915. |
| Click to display the text | |
| [10] | Li Y,Wei H L,Billings S A.Identification of time-varying systems using multi-wavelet basis functions[J].IEEE Transactions on Control Systems Technology,2011,19(3):656-663. |
| Click to display the text | |
| [11] | Billings S A,Wei H L,Balikhin M A.Generalized multiscale radial basis function networks[J].Neural Networks,2007,20(10):1081-1094. |
| Click to display the text | |
| [12] | 李秀英,韩志刚.一种基于粒子群优化的非线性系统辨识方法[J].控制与决策,2011,26(11):1627-1631.Li X Y,Han Z G.Identification approach for nonlinear systems based on particle swarm optimization[J].Control and Decision,2011,26(11):1627-1631(in Chinese). |
| Cited By in Cnki (10) | |
| [13] | 秦玉灵,孔宪仁,罗文波.基于径向基函数响应面的机翼有限元模型修正[J].北京航空航天大学学报,2011,37(11):1465-1470.Qin Y L,Kong X R,Luo W B.Finite element model updating of airplane wing based on Gaussian radial basis function response surface[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(11):1465-1470(in Chinese). |
| Cited By in Cnki (5) | |
| [14] | Chang L C,Chang F J,Wang Y P.Auto-configuring radial basis function networks for chaotic time series and flood forecasting[J].Hydrological Process,2009,23(17):2450-2459. |
| Click to display the text | |
| [15] | 孙健,吴森堂.基于改进粒子群优化算法的巡航导弹航路规划[J].北京航空航天大学学报,2011,37(10):1228-1232.Sun J,Wu S T.Route planning of cruise missile based on improved particle swarm algorithm[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(10):1228-1232(in Chinese). |
| Cited By in Cnki (4) | |
| [16] | Chen S,Hong X,Bing L L,et al.Non-linear system identification using particle swarm optimization tuned radial basis function models[J].International Journal of Bio-Inspired Computation,2009,1(4):246-258. |
| Click to display the text | |
| [17] | Pinkey C,Kusum D,Millie P.Novel inertia weight strategies for particle swarm optimization[J].Memetic Computing,2013,5(3):229-251. |
| Click to display the text |
