空间绳系结构研究涵盖的学科领域十分广泛,包括动力学、控制、电学、空间环境和材料结构等多个学科的交叉.仅就动力学领域而言,空间系绳摆动和高阶振动的解析模型是一组非线性、非自治、耦合的常微分和偏微分方程组[12],无法进行求解,现有的研究常常基于一定的简化,例如忽略系绳的弹性、忽略系绳的质量[13]等.对于系绳复杂空间运动的数值模拟常常采用离散质量的系绳模型,例如朱仁璋和Banerjee等[14, 15]将系绳视为无质量弹簧连接的钢珠,Biswell等[16]研究绳系系统在气动刹车中的应用时将系绳视为弹簧阻尼铰接的刚性杆;Grassi和Lorenzini等[17, 18]也在研究中将系绳处理为由弹簧-阻尼连接的集中质量单元.离散模型的问题之一是其计算效率受到单元数目和系绳刚度的限制很难提高.
本文提出了一种半解析离散质量系绳模型,作为精确解析模型和简单离散数值模型的折中.系绳视为由球铰连接的弹性杆,假定弹性杆做一维振动,得到纵向振动的解析表达,并通过球铰的运动模拟系绳的弯曲和扭转.这样,所提出的模型可以用更少的单元包含系绳的高阶模态,更精确地模拟系绳的空间运动,同时避免解析求解的困难.另外,本文利用递推算法[19]推导所提出模型的运动方程.递推算法适合编程实现,且无需构建高维的系统质量和刚度矩阵,不涉及系统质量阵的求逆运算,其计算量仅和离散数量呈线性关系,从而有效提高了数值仿真的运算速度.
1 基本假设和坐标系定义所研究的绳系卫星系统由主星、子星和连接两者的柔性系绳组成,系绳长度远小于轨道半长轴.绳端卫星视为刚体,系绳的纵向变形和横向摆振通过离散质量模型进行近似:将系绳离散为n根由球铰连接的一维均质柔性杆,假定各段柔性杆只发生纵向的弹性形变,不同杆之间弹性变形是互相独立的,且只承拉不承压.系绳的弯曲和扭转通过球铰运动模拟.
对于离散后由n+2个体组成的刚柔混合链式系统,从子星开始按照远离子星的顺序依次将各体编号,称为体ℜj;定义体ℜj连接编号较小个体(内接体)的点为内接点,连接编号较大个体(外接体)的点为外接点,分别用Ij和Oj表示;内接点Ij连接着铰hj,主星的外接点和子星的内接点分别为各自的质心,子星通过一个六自由度的虚铰与惯性系连接,如图 1所示.
 |
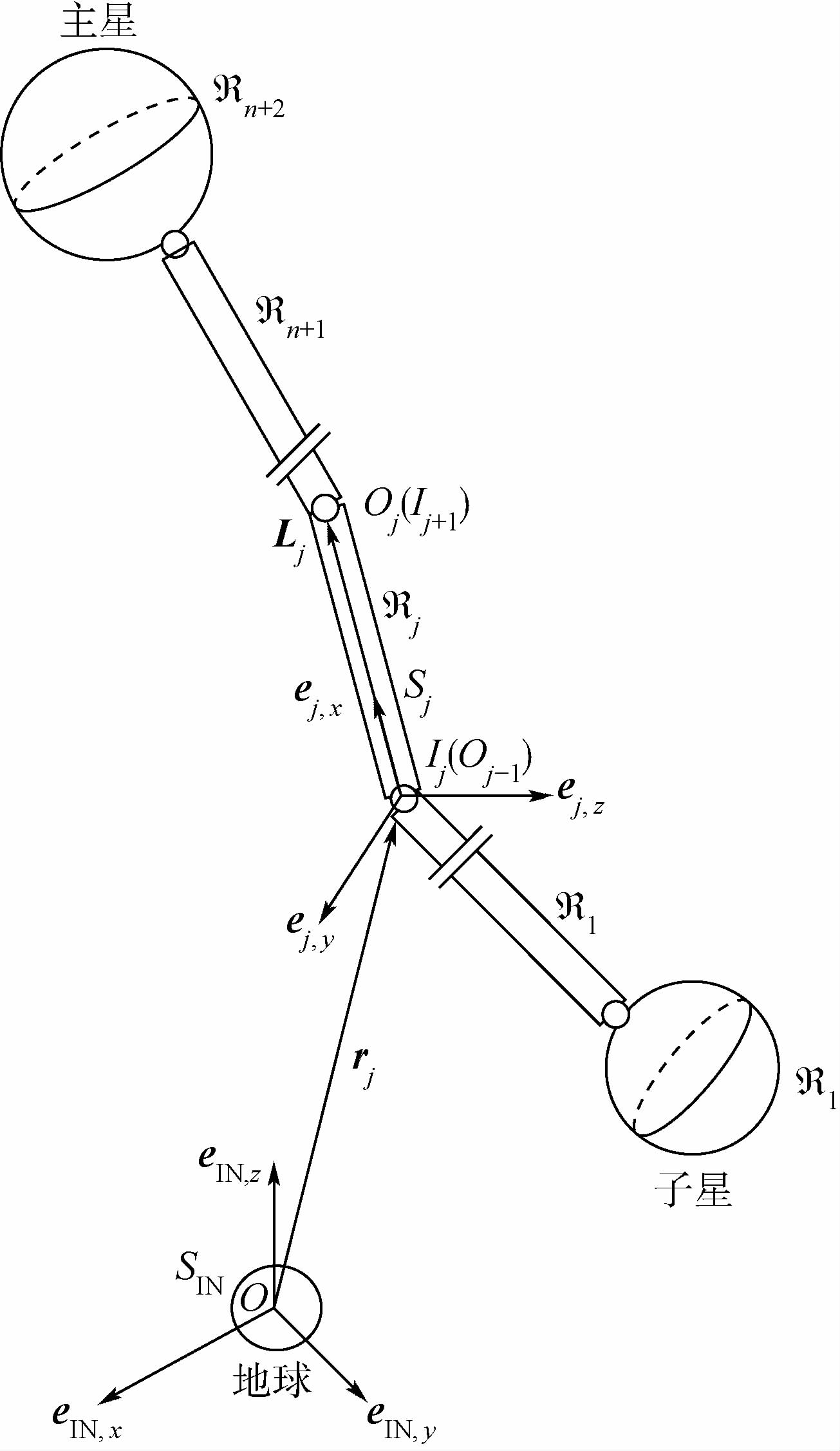| Lj—j点到Oj点的矢量；ej,x、ej,y、ej,z—坐标系Sj的x、y、z轴单位向量；rj—地心到Ij点的矢量；SIN—地心惯性坐标系；eIN,x、eIN,y、eIN,z—坐标系SIN的x、y、z轴单位矢量.图 1 铰接柔性杆绳系模型示意图Fig. 1 Sketch map of hinged-flexible-rods tether model |
| 图选项 |
为研究系统的动力学,建立坐标系如下:
1) 地心惯性坐标系SIN:坐标系原点位于地心,x轴指向春分点,z轴指向天球北极,与y轴构成右手坐标系.
2) 轨道坐标系So:坐标系原点位于地心,x轴指向绳系系统的质心;坐标系So与SIN的关系为
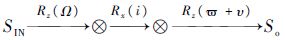,其中Rz(Ω)为绕着z轴转过Ω角度，Rx(i)为绕着x轴转过i角度，Rz(
+υ)为绕着z轴转过+υ角度，Ω、i、和υ分别为轨道的升焦点赤经、轨道倾角、近地点幅角和真近点角.3) 各体的本体坐标系S1~Sn+2:本体系Sj固连于体ℜj,原点位于Ij,当系绳处于当地铅垂方向时,各本体系与轨道系方向一致.
2 刚柔混合模型的递推算法递推算法的总体思路分为3个阶段:第1步由根体(子星)向端体(主星)进行运动学传递,得到每个体的速度和加速度非线性项;第2步从端体向根体进行动力学传递,将系统动力学方程组中的单体个数逐渐减少,最终得到不含其余体信息的根体动力学,求解根体运动;第3步由根体向端体进行运动学传递,得到每个体的加速度.
2.1 单体动力学方程采用模态坐标法描述体ℜj上某处(s=ξ,s为杆上的局部坐标)的弹性变形为
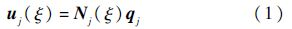
式中:qj为体ℜj的模态坐标.只考虑柔性杆沿着纵向的一维振动,并取一端固定,一端自由的边界条件,则第k阶固有圆频率和无量纲模态振型分别为[20]
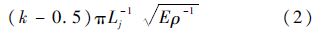
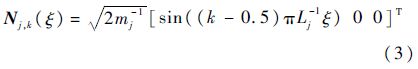
式中:E和ρ分别为绳的弹性模量和密度;Lj和mj分别为体ℜj的杆长和质量.
利用Kane法建立单体的动力学方程,经过推导最终可以得到单体ℜj的动力学方程为
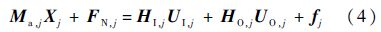
式中:UI,j=[FI,jT TI,jT]T;UO,j=[FO,jT TO,jT]T;FI,j、TI,j、FO,j、TO,j分别为作用于内接点和外接点的外力和外力矩;fj为分布力(例如重力、电磁力等)的广义力,式中其余变量含义如下.
对于柔性杆(j=2,3,…,n+1),广义速度包含速度、角速度和弹性变形,即
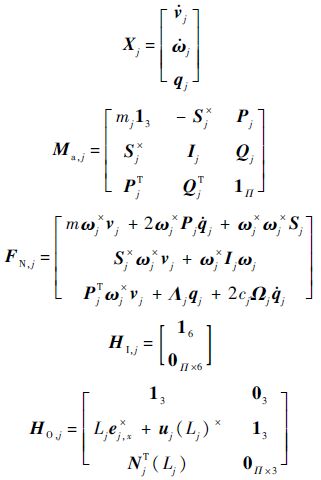
式中:vj和ωj为坐标系Sj的绝对速度和角速度在Sj的投影列阵;ej,x为Sj坐标系x轴的单位向量;Λj为以体ℜj固有圆频率(见式(2))平方为主元的对角方阵;Ωj为以体ℜj固有圆频率为主元的对角方阵;cj为阻尼系数;1和0分别为单位阵和零矩阵;Π为选取的模态阶数;Sj和Ij分别为体ℜj的静矩和惯量,为避免旋转柔性体的刚化问题,采用线性化假设,即忽略静矩和惯量中的弹性变形相关项;右上标“×”代表向量的叉乘矩阵;平动和转动耦合系数阵Pj和Qj的表达式分别为
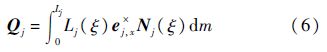
对于刚性绳端星(j=1或j=n+2),其动力学方程不含弹性变形相关项,即
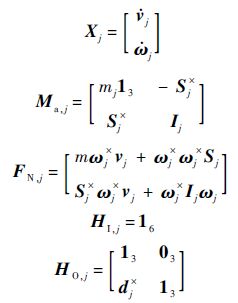
式中:dj为绳端星外接点相对于其内接点的矢量.
2.2 运动学递推关系内接体为柔性杆时(j=3,4,…,n+2),坐标系Sj与Sj－1的速度和角速度关系分别为
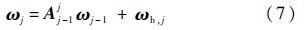
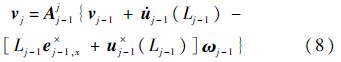
式中:ωh,j为铰hj转角速度在Sj的投影阵;Aj－1j为Sj－1至Sj的坐标转化矩阵.对式(7)和式(8)进行求导得到加速度的递推关系式：
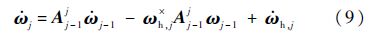
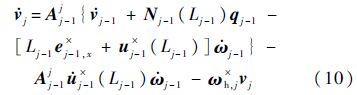
内接体为刚体时的运动学递推关系更为简单,只需将式(8)和式(10)中的弹性变形项删除即可:
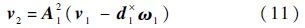
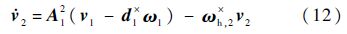
为方便给出广义加速度递推关系,将体ℜj的广义加速度Xj分为与广义速率的一阶导数相关部分XL,j(线性部分),以及与广义速率一阶导数无关的部分XN,j(非线性部分),再将XL,j分为与内接体相关部分
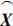L,j,以及和铰hj运动相关部分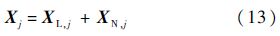
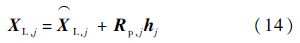
式中:hj为铰hj的广义加速率,而Rp,j为对应的偏速度,指出铰hj运动的一个广义方向,在其上只有做功的广义力.各体之间存在递推关系如下:
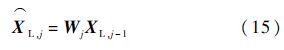
下面按照刚柔连接的不同,给出式(14)~式(16)中各项的具体表达式.
1) 主星(j=n+2).
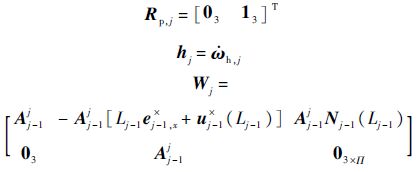
2) 柔性杆(j=3,4,…,n+1).
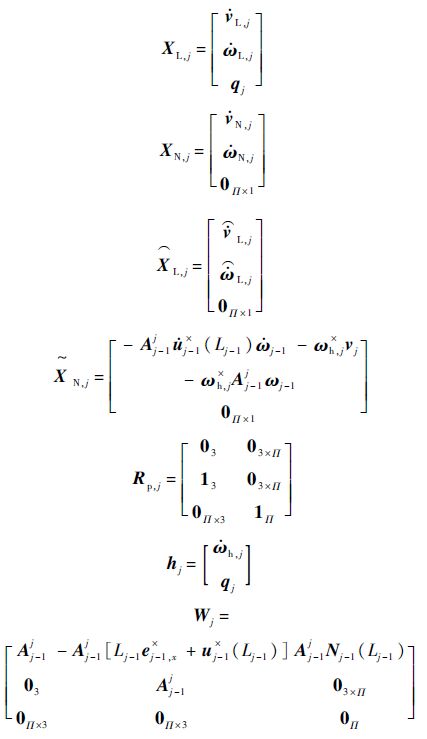
3) 柔性杆(j=2,内接刚体).
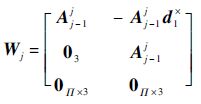
其余项表达式同2).
4) 子星(j=1).
其余项表达式同1).
2.3 动力学递推关系端体ℜn+2外接点的力和力矩FO,j、TO,j已知,即作用于主星的主动控制,将式(14)代入式(4)可得端体动力学方程为
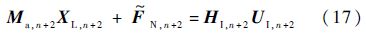
式中:
式中:uI,n+2为铰hn+2处做功的广义力.本文只考虑铰hn+2的摩擦力矩和沿着杆纵向的回复力矩(即系绳的抗扭力矩,忽略系绳抗弯力矩),即有
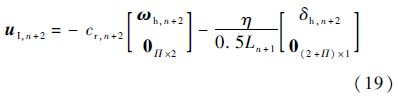
式中:cr,j为铰hj的摩擦系数；δh,j为铰hj在Sj坐标系x轴方向的转动角度；η为系绳的抗扭刚度,本文将第j段系绳发生的扭动均分到两端球铰,即对于非连接绳端星的铰hj而言,式(19)中第2项的分母应为Lj.
利用式(14),进一步整理式(18)可解得
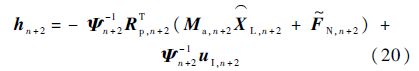
式中:
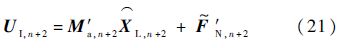
式中:
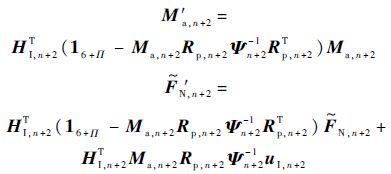
此时,内接体广义力UI,n+2完全由内接体的运动变量描述.注意到体ℜn+2受到的内接体作用力与体ℜn+1受到的外接体作用力是一对反作用力,即
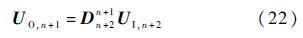
式中:
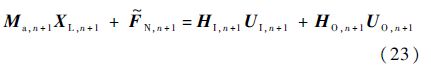
式中:
将式(21)和式(22)代入式(23),得到
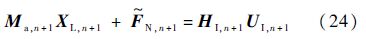
相比式(23),式(24)的质量阵和非线性项做了如下更新以涵盖外接体的影响.
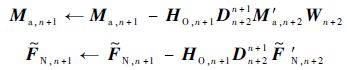
可见,经过更新后体n+1和体n+2的方程式(17)形式完全形同,即上述如式(20)求解球铰广义加速率hj的过程可以一直进行直至根体,得到
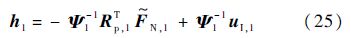
至此,式(25)不再包含内接体信息,可以直接求解.然后利用2.2节得到的运动学关系求解每个体的运动.
2.4 算法修正若柔性杆ℜj变形uj(Lj)为负,根据系绳不可受压的物理特性,认为此时弹性杆内的实际张力为零,分以下两种情况对2.1~2.3节建立的算法进行修正.
1) |uj(Lj)|≤δ,δ是一个较小的正参数.即此段系绳虽然松弛但变形不大,可以认为体ℜj的惯量和质量参数不发生较大变化,即无需改变前文建立的单链式递推算法,只需要将体ℜj的弹性模量E设为0即可.
2) |uj(Lj)|>δ.此时该段系绳发生较大的变形,无法用杆近似,惯量参数也有较大的变化,可以认为系绳断为两截,应分段采用前文建立的单链式递推算法,体ℜj－1成为链ℜ1~ℜj－1的端体,ℜj+1则成为链ℜj+1~ℜn+2的根体.另外时时计算uj(Lj)的值,若减小至δ以下,则切换回单链递推算法.uj(Lj)可由以下公式计算:
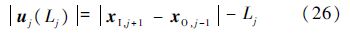
式中:xI,j+1和xO,j－1分别为ℜj+1内接点的位置矢量和ℜj－1外接点的位置矢量.
3 数值仿真对本文提出的基于递推算法的刚柔混合绳系模型进行数值仿真,分析模型的有效性.采用凯芙拉纤维材料的均质系绳,主(子)星为质量均匀的正方体,绳系点位于其底(顶)面中心,仿真所用参数汇总如表 1所示.另外,为简化起见,假定TSS运行于轨道高度为1 000 km的赤道圆轨道,仅考虑球形引力场重力梯度力矩的影响.仿真软件采用MATLAB Simulink平台搭建,运算主机处理器为Inter Core i7-3770,主频3.4 GHz.
表 1 绳系卫星系统仿真参数Table 1 Simulation parameters of TSS
| 参量名 | 数值 | 参量名 | 数值 |
| 主星质量/kg | 1 000 | 系绳密度/(g·cm-3) | 1.44 |
| 主星尺寸/m | 1×1×1 | 系绳弹性模量/GPa | 131 |
| 子星质量/kg | 100 | 系绳剪切模量/GPa | 1.8 |
| 子星尺寸/m | 0.4×0.4×0.4 | 纵向振动阻尼 | 0.005 |
| 系绳长度/km | 5 | 弯曲扭转阻尼 | 0.005 |
| 系绳直径/mm | 2 | 计算步长/s | 0.01 |
表选项
首先给出面内扰动下的模型仿真结果:系绳离散单元数为5,初始面内摆角为5°,仿真时间2个轨道周期.图 2给出主星姿态角变化情况,图 3和图 4给出4个球铰的运动情况(未给出方向转角为0),仿真中姿态运动学均采用3-1-2转序.可以看出绳端星随系绳摆动,摆动频率近似为1.7倍轨道频率,这与已有理论分析[21]结果吻合;从球铰运动反映出系绳的横向振动的存在,在阻尼作用下,临近子星的系绳段高阶振动很快消失,但是临近惯量更大的主星的系绳段振动仍然存在.图 5给出杆单元1和2的外接点纵向弹性变形,两者变化情况非常相似,由于初始扰动带来的纵向振动趋于稳定,其余未给出的杆单元变化也几乎和两者相同.图 6为最后时刻各杆单元的弹性变形,由于本文采用了一端固接、一端自由的振动模态,杆在外接点纵向变形达到最大,系绳的变形不满足连续性,但是通过比较可以发现靠近主星的两段杆(4,5)变形最大且几乎相同,而仅考虑重力影响时,系绳张力最大处正位于系统重心(杆5上),因此若单元数足够,铰接杆模拟的纵向变形总体而言是可信的.
 |
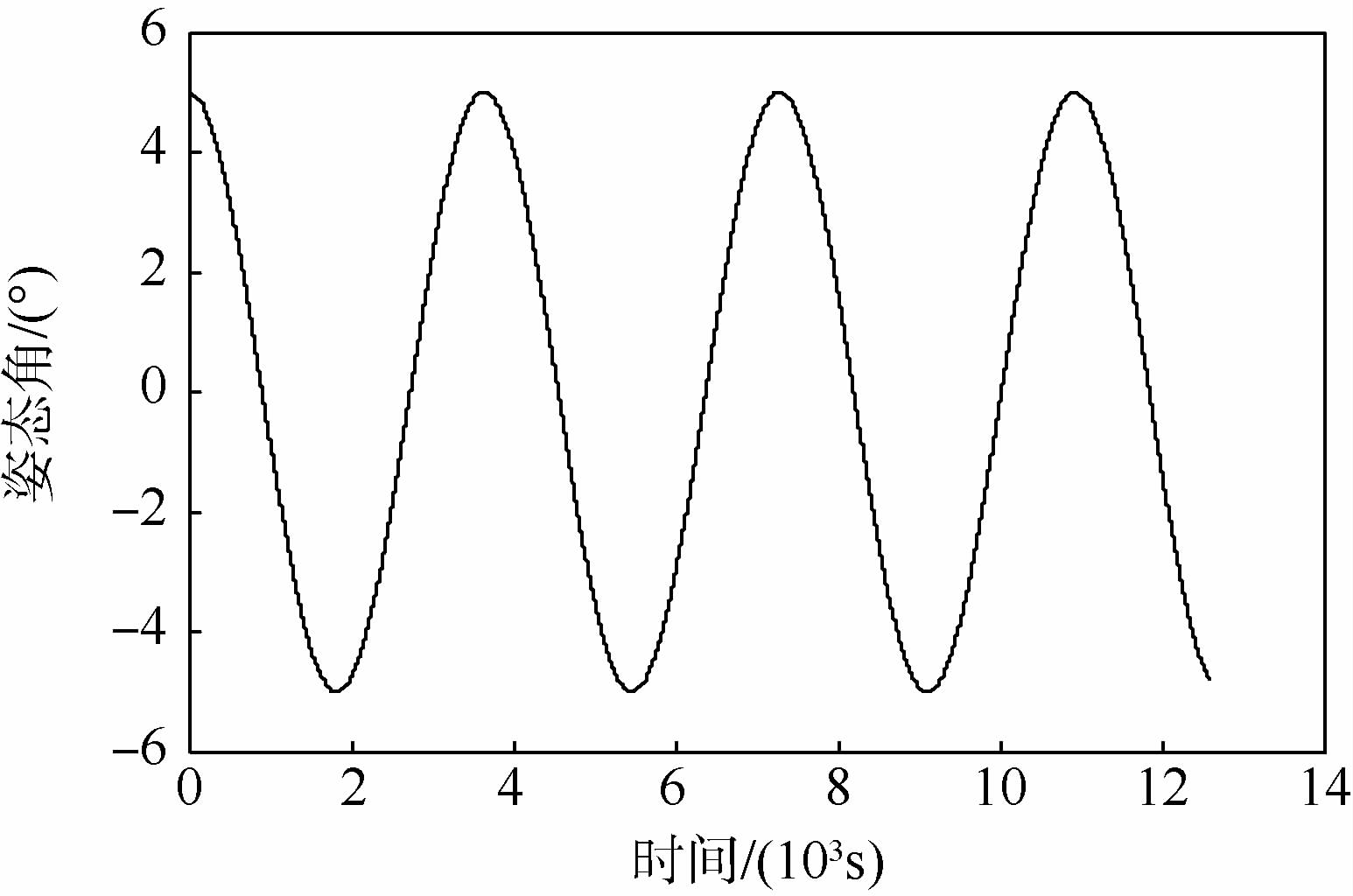| 图 2 主星姿态角变化(z轴)Fig. 2 Attitude angle of main satellite (z axis) |
| 图选项 |
 |
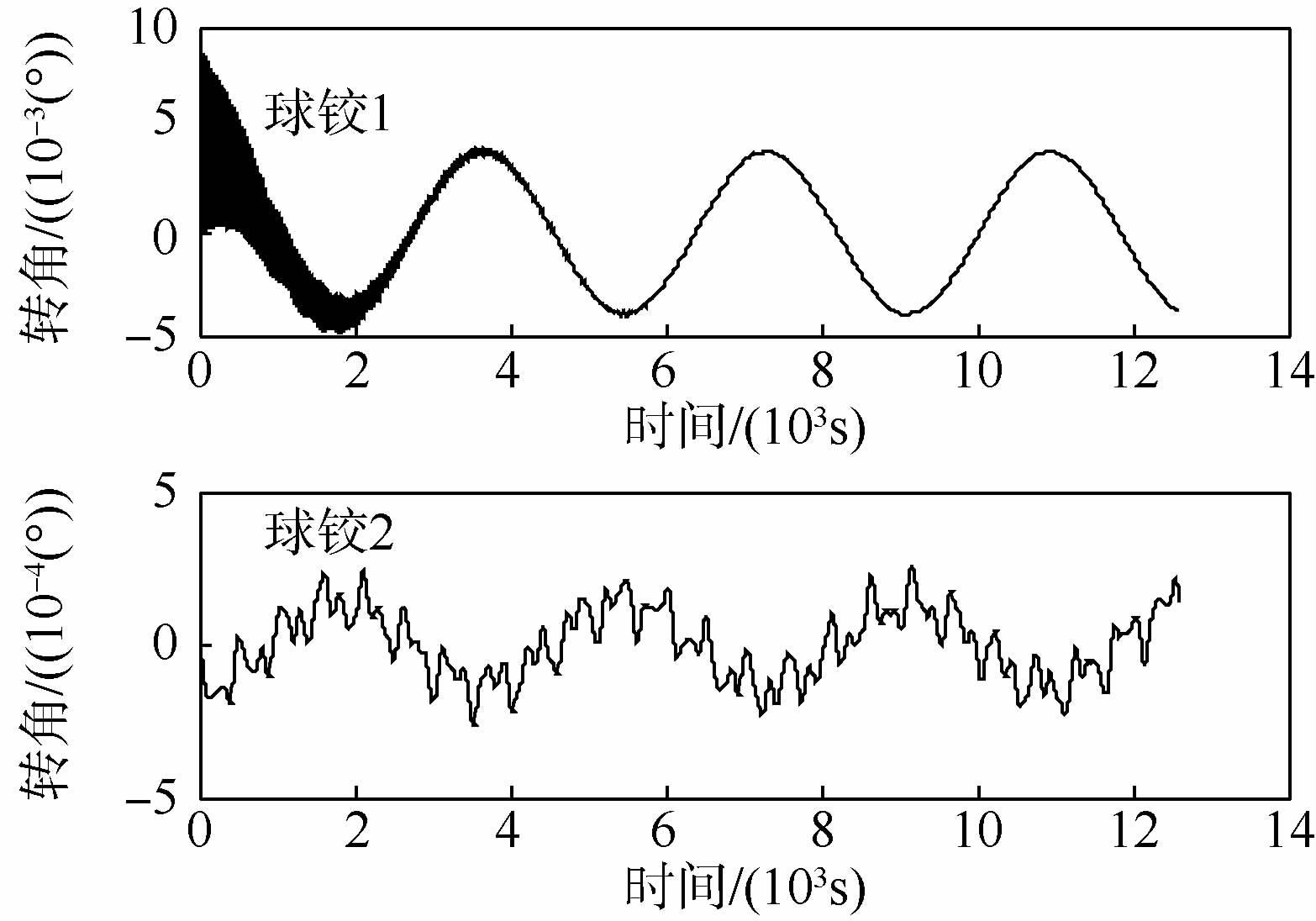| 图 3 球铰1和2转角(z轴)Fig. 3 Rotation angles of spherical hinges 1 and 2 (z axis) |
| 图选项 |
 |
| 图 4 球铰5和6转角(z轴)Fig. 4 Rotation angles of spherical hinges 5 and 6 (z axis) |
| 图选项 |
 |
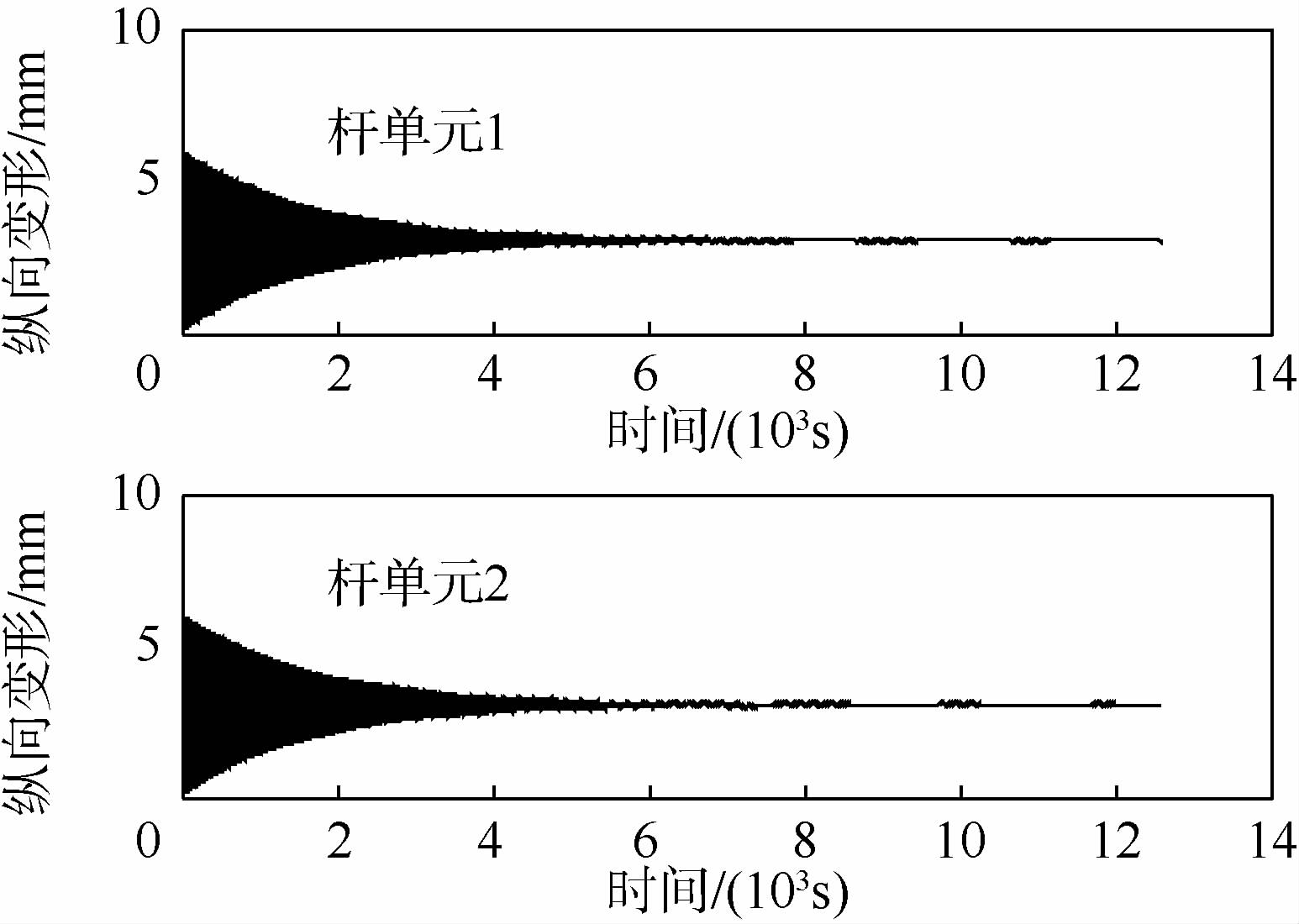| 图 5 杆单元1和2外接点的纵向变形(x轴)Fig. 5 Longitude deformations at outer-point of elements 1 and 2 (x axis) |
| 图选项 |
 |
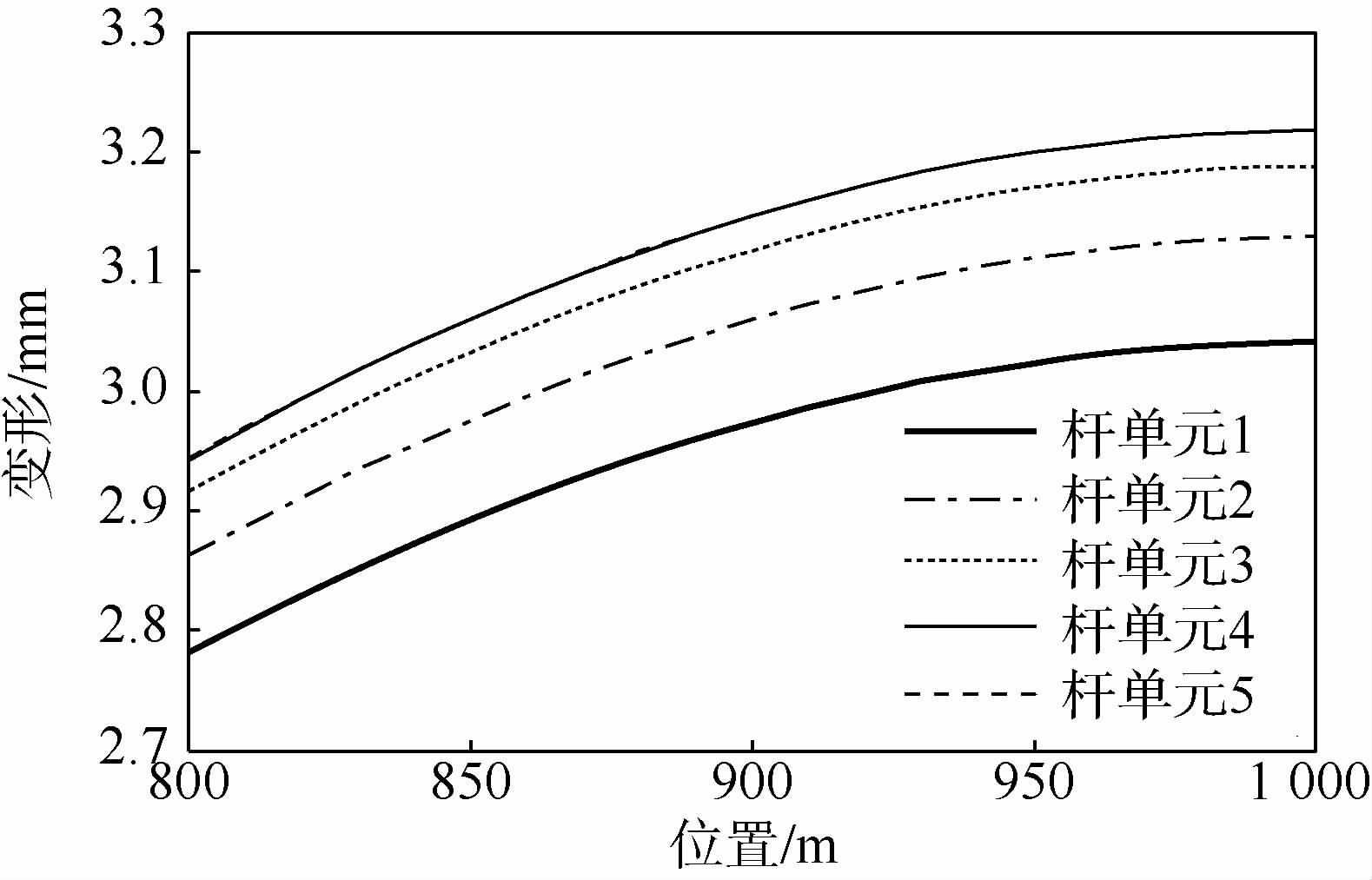| 图 6 最后时刻各杆单元的纵向变形(x轴)Fig. 6 Longitude deformations of elements at final moment (x axis) |
| 图选项 |
面外扰动下的仿真结果与面内情形类似,这里仅给出主星的姿态变化(见图 7,初始面外角5°)和部分铰的运动情况(见图 8),易见面外摆动频率满足两倍轨道频率的理论结果[21].
 |
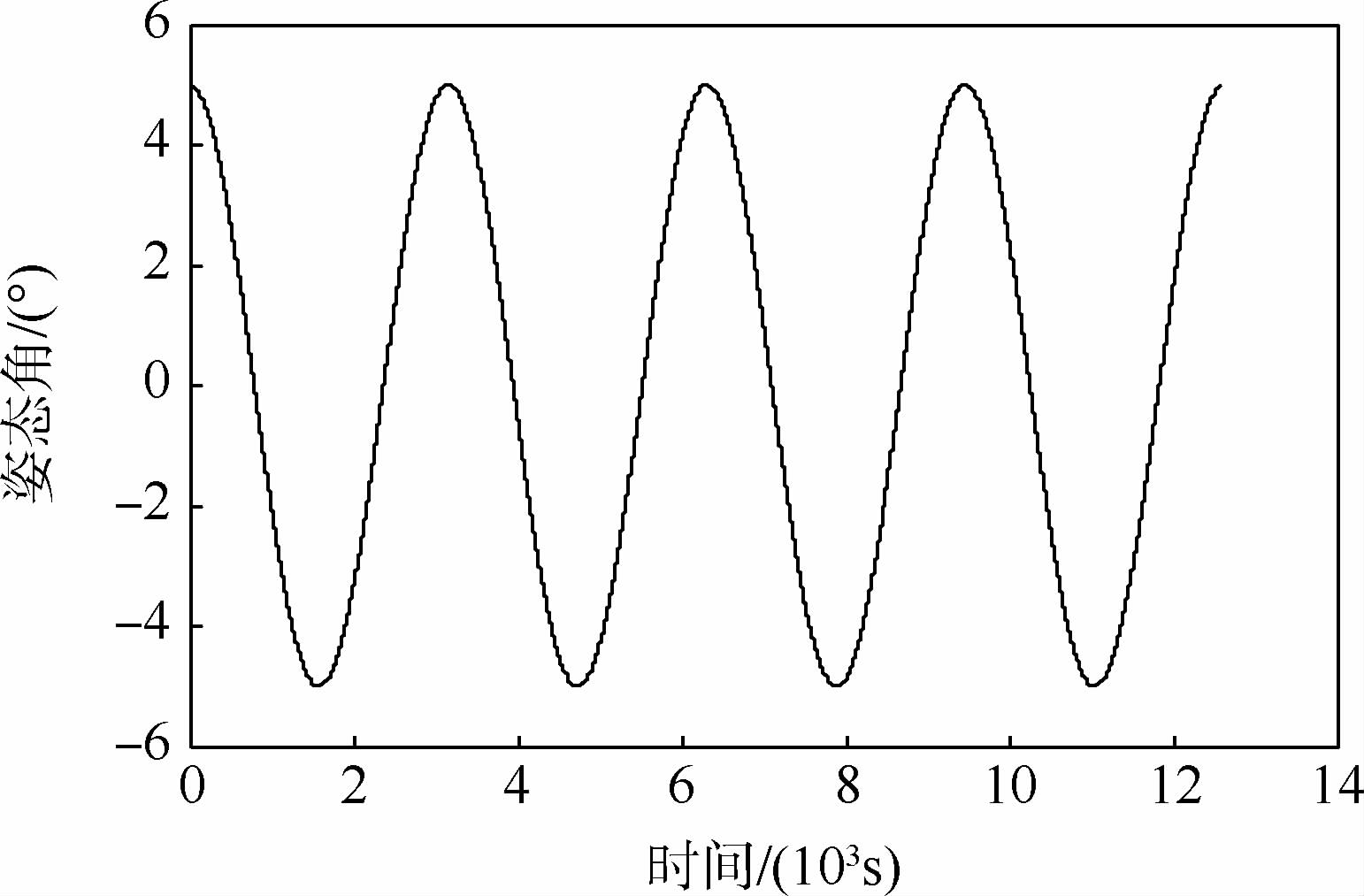| 图 7 主星姿态角变化(y轴)Fig. 7 Attitude angle of main satellite (y axis) |
| 图选项 |
 |
| 图 8 球铰1和2转角(y轴)Fig. 8 Rotation angles of spherical hinges 1 and 2 (y axis) |
| 图选项 |
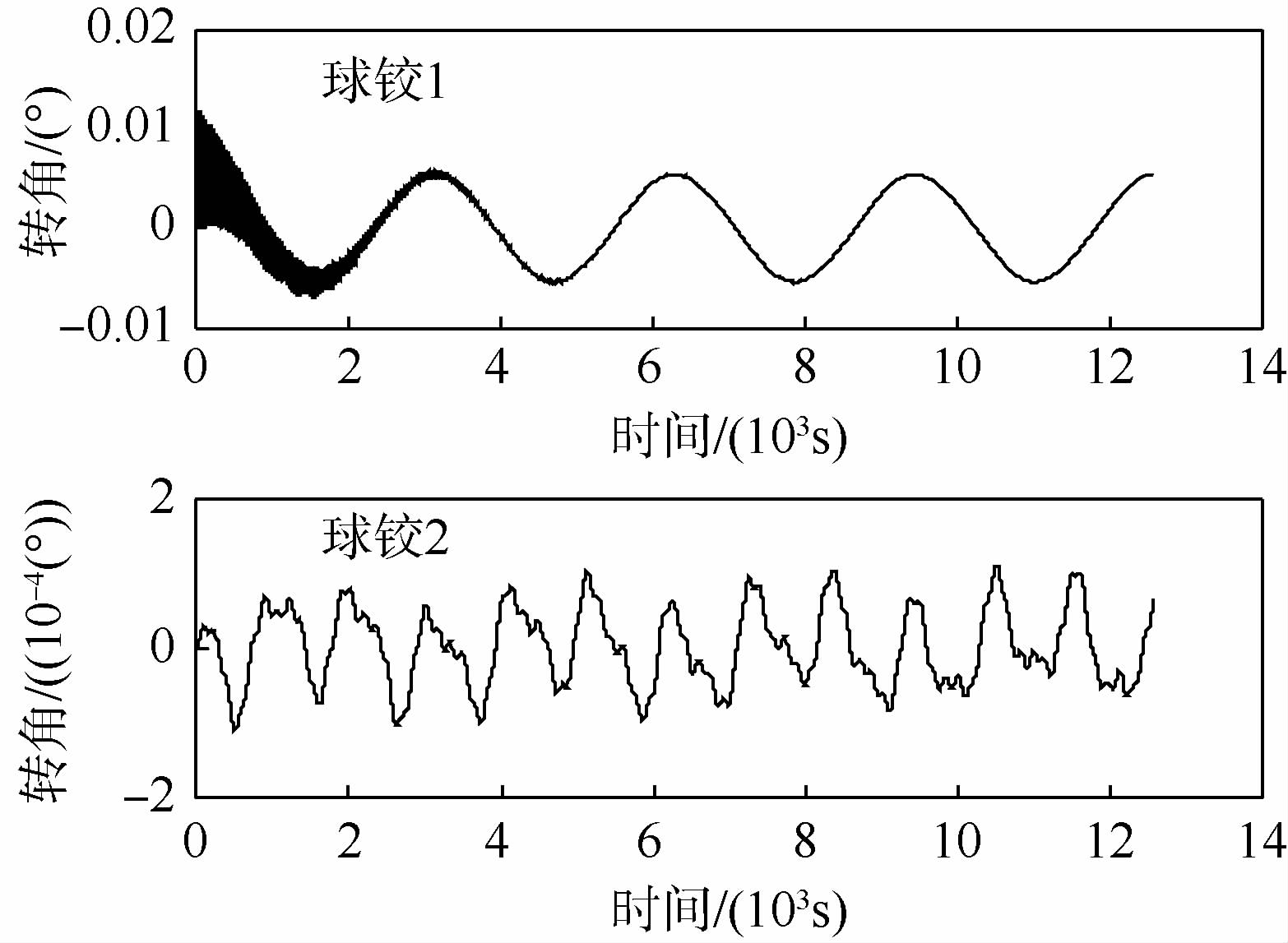
接着给出系绳同时存在面内外初始摆角和扭转变形的仿真算例:初始的面内外角度分别为5°和2°,系绳初始时刻相较主星有1°的扭转角度,仿真时间为1个轨道周期.图 9和图 10分别给出主星和子星姿态角的影响,可见两星的姿态逐渐趋于一致.从球铰的运动状况可以看出系绳扭转和弯曲的耦合,如图 11表明铰2在x方向的转动激励了其余两方向的转动,图 12给出的铰5运动放大图验证了这一点.如果选取更大的初始扰动,耦合效应将更为明显.
 |
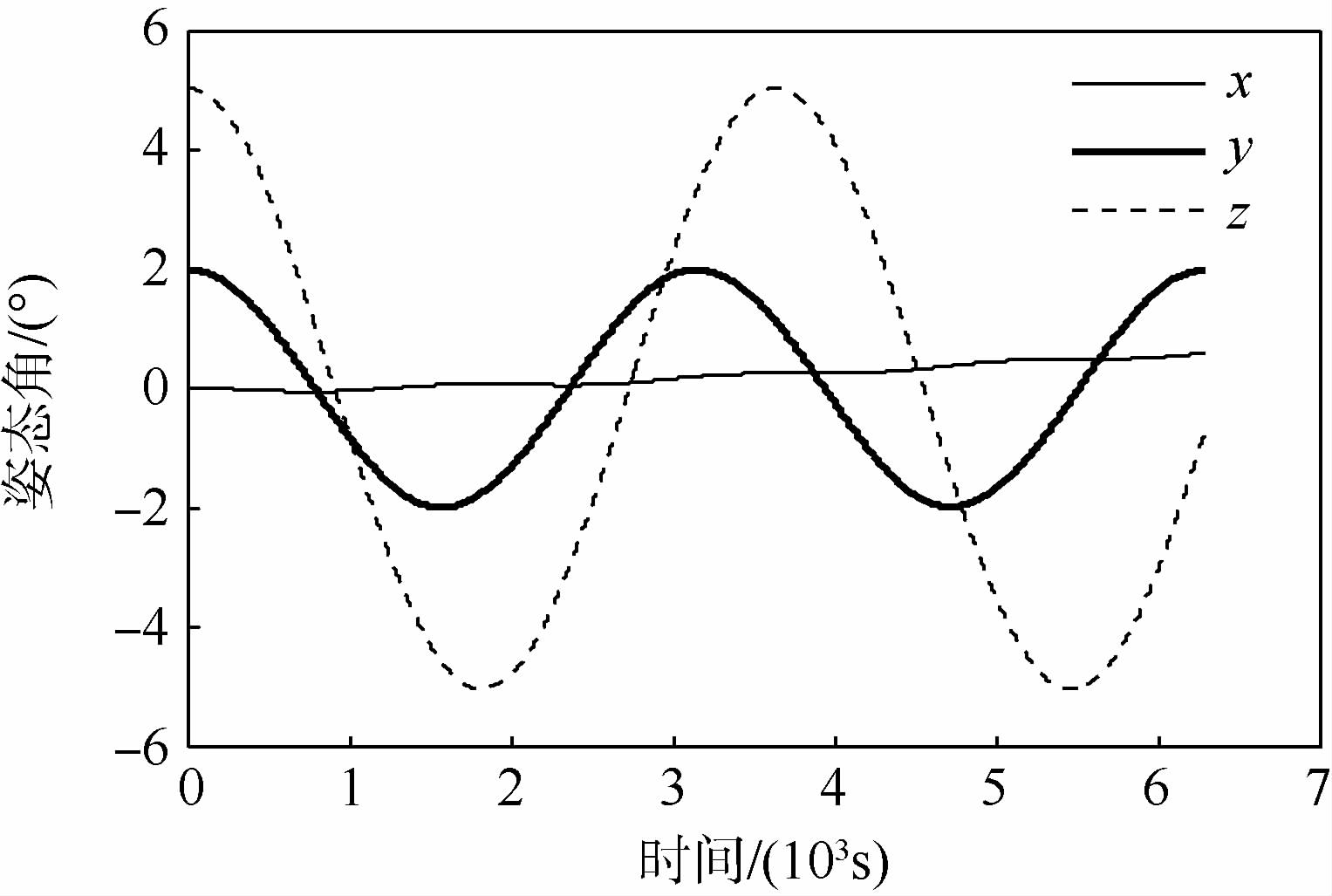| 图 9 主星姿态角变化Fig. 9 Attitude angle of main satellite |
| 图选项 |
 |
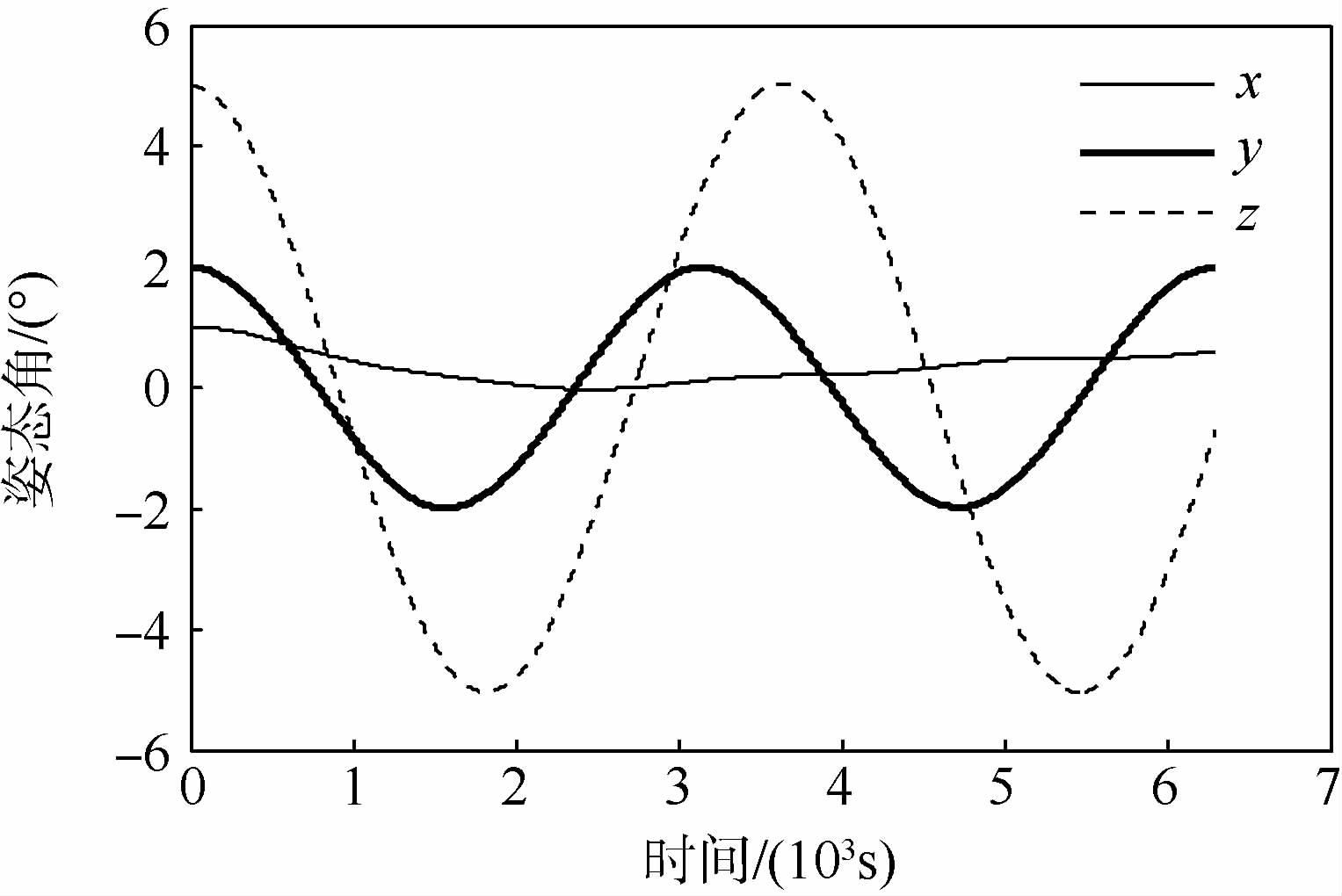| 图 10 子星姿态角变化Fig. 10 Attitude angle of sub satellite |
| 图选项 |
 |
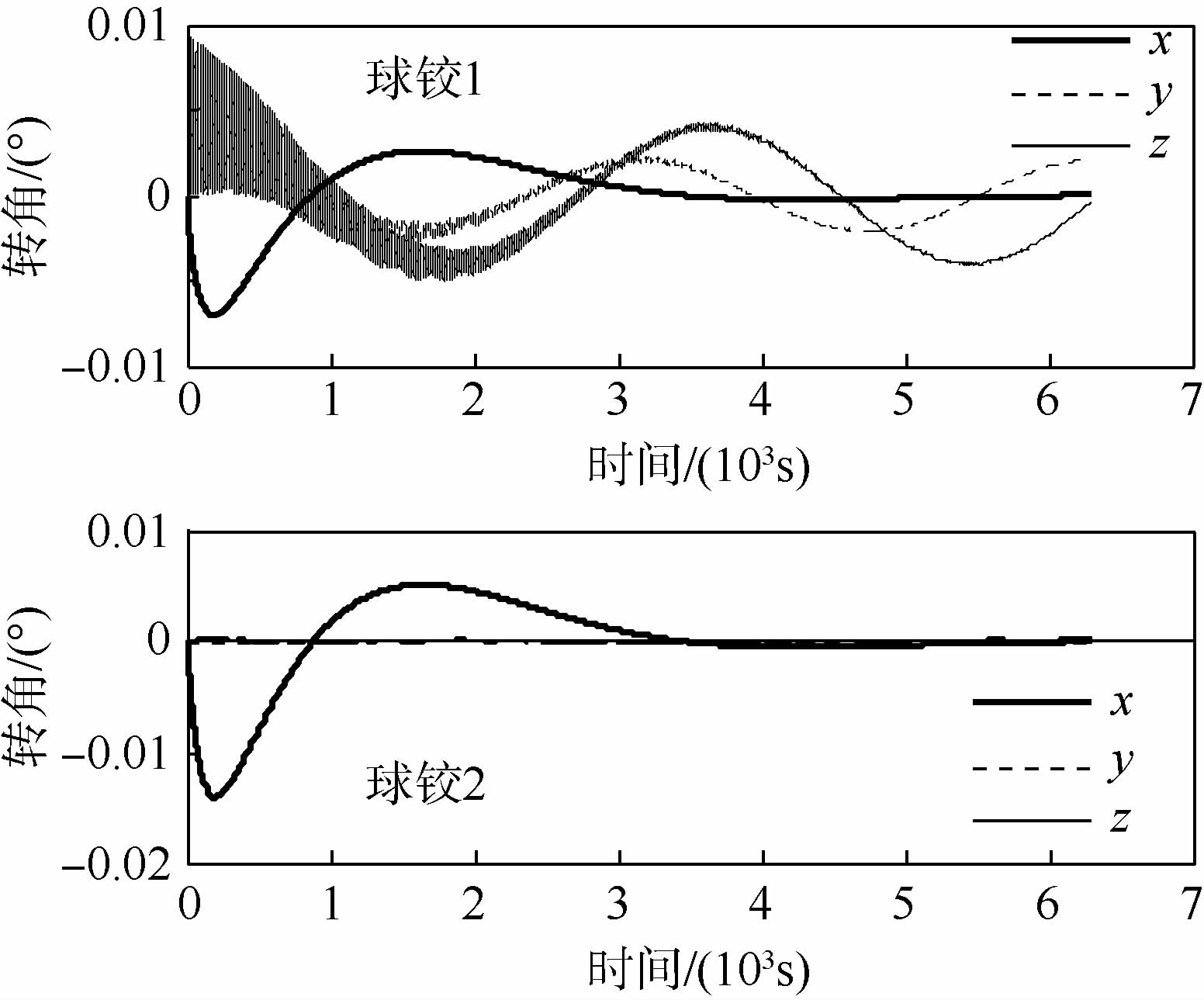| 图 11 球铰1和2转角Fig. 11 Rotation angles of spherical hinges 1 and 2 |
| 图选项 |
 |
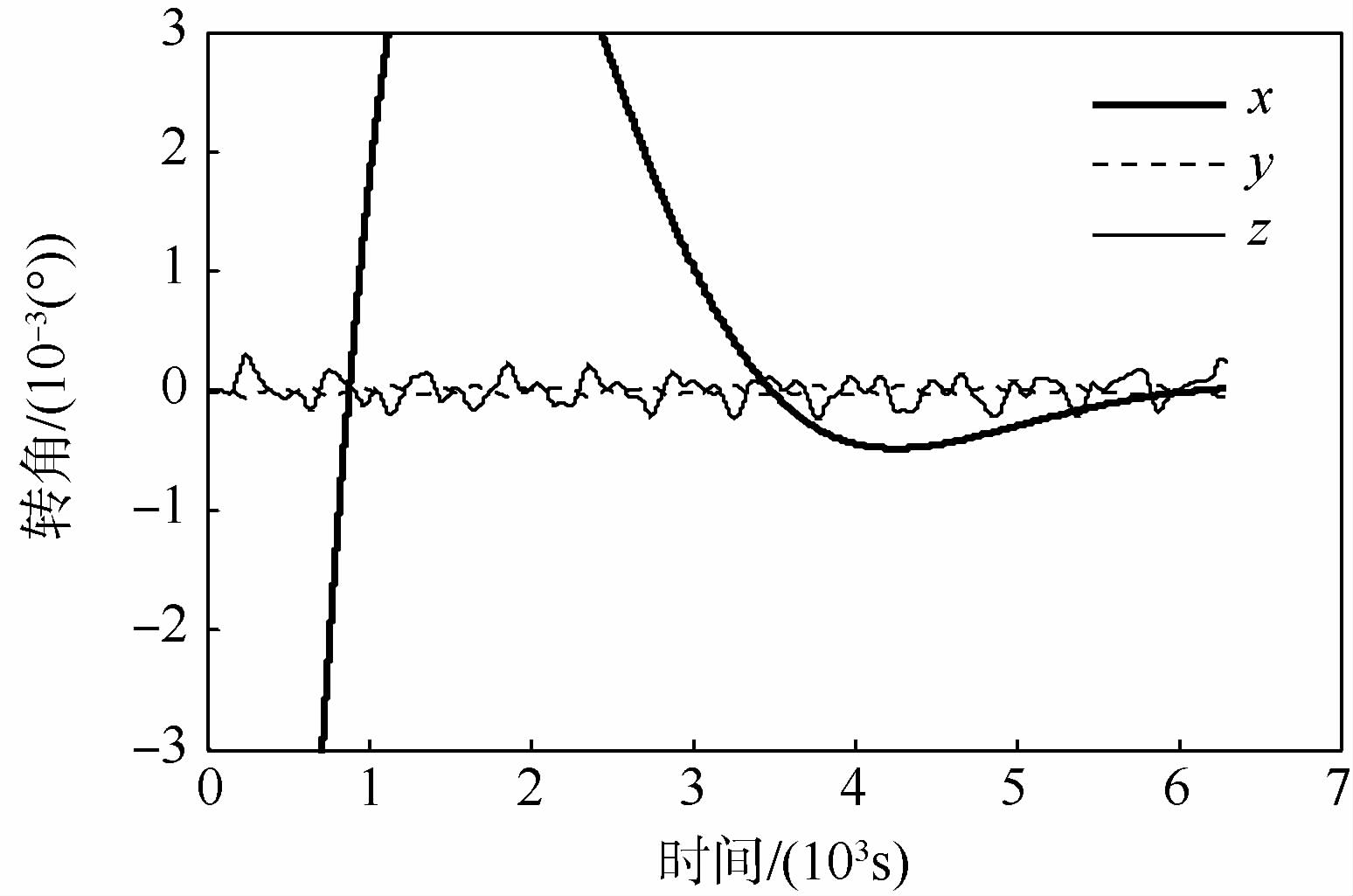| 图 12 球铰5转角Fig. 12 Rotation angles of spherical hinge 5 |
| 图选项 |
最后对模型的计算效率进行了测试,采用同样的参数对5°初始扰动的面外扰动算例进行仿真,当离散单元为1、5和10时仿真一个轨道周期花费的时间分别为2 895、7 554和12 653 s,时间随单元数近似呈线性变化.
4 结 论本文针对空间绳系卫星系统提出了一种基于递推算法的铰接柔性杆模型,研究过程揭示的主要结论如下:
1) 所提出离散模型能够用较少的单元数模拟空间系绳的纵向不均匀变形,同时模拟系绳的弯曲和扭转,适用范围较广.
2) 系绳阻尼作用下接近大惯量绳端星的柔绳段横向振动较靠近小惯量绳端星的柔绳段减小更快.
3) 采用递推算法易于编程实现,且计算量随离散单元数量线性增长,在同等精度下运算效率高.本文数值仿真中未考虑重力梯度外的空间干扰力,模型不能直接用于仿真系绳的释放和回收,系绳纵向模态的选取仍需考察,这些都是今后的研究要点.
参考文献
| [1] | Cartmell M P, McKenzie D J.A review of space tether research[J].Progress in Aerospace Sciences, 2008, 44(1): 1-21. |
| Click to display the text | |
| [2] | Hoyt R, Slostad J, Mazzoleni A P.The multi-application survivable tether (MAST) experiment, AIAA-2003-5219[R].Reston: AIAA, 2003. |
| Click to display the text | |
| [3] | Nishid S I, Kawamoto S, Okawa Y, et al.Space debris removal system using a small satellite[J].Acta Astronautica, 2009, 65(1-2): 95-102. |
| Click to display the text | |
| [4] | Wen H, Jin D P, Hu H Y.Advances in dynamics and control of tethered satellite systems[J].Acta Mechanica Sinica, 2008, 24(3): 229-241. |
| Click to display the text | |
| [5] | National Research Council.NASA space technology roadmaps and priorities: Restoring NASA's technological edge and paving the way for a new era in space[M].Washington, D.C.: The National Academies Press, 2012: 129-130. |
| [6] | Kawamoto S, Makida T, Sasaki F, et al.Precise numerical simulations of electrodynamic tethers for an active debris removal system[J].Acta Astronautica, 2006, 59(1-5): 139-148. |
| Click to display the text | |
| [7] | Covello F. Application of electrical propulsion for an active debris removal system: A system engineering approach[J].Advances in Space Research, 2012, 50(7): 918-931. |
| Click to display the text | |
| [8] | Grossi M. Future of tethers in space[C]//Proceedings of 4th International Conference on Tethers in Space.Hampton, VA: Science and Technology, 1995: 11-23. |
| [9] | Kumar K D. Review of dynamics and control of nonelectrodynamic tethered satellite systems[J].Journal of Spacecraft and Rockets, 2006, 43(4): 705-720. |
| Click to display the text | |
| [10] | Sasaki S, Tanaka K, Higuchi K, et al.A new concept of solar power satellite: Tethered-SPS[J].Acta Astronautica, 2007, 60(3): 153-165. |
| Click to display the text | |
| [11] | Quinn D A, Folta D C.A tethered formation flying concept for the SPECS mission, AAS-00-015 [R].San Diegos Califormia: AAS, 2000. |
| Click to display the text | |
| [12] | Krupa M, Poth W, Schagerl M, et al.Modeling, dynamics and control of tethered satellite systems[J].Nonlinear Dynamics, 2006, 43(1-2): 73-96. |
| Click to display the text | |
| [13] | 彭建华, 刘延柱.绳系卫星的混沌运动[J].上海交通大学学报, 1996, 30(11): 32-35. Peng J H, Liu Y Z.Chaos in the tethered satellite system[J].Journal of Shanghai Jiao Tong University, 1996, 30(11): 32-35(in Chinese). |
| Cited By in Cnki (11) | |
| [14] | 朱仁璋, 雷达, 林华宝.绳系卫星系统复杂模型研究[J].宇航学报, 1999, 20(3): 7-12. Zhu R Z, Lei D, Lin H B.A sophisticated dynamical model of tethered satellite systems[J].Journal of Astronautics, 1999, 20(3): 7-12(in Chinese). |
| Cited By in Cnki (28) | |
| [15] | Banerjee A K. Dynamics of tethered payloads with deployment rate control[J].Journal of Guidance, Control, and Dynamics, 1990, 13(4): 759-762. |
| Click to display the text | |
| [16] | Biswell B L, Puig-Suari J, Longuski J M, et al.Three-dimensional hinged-rod model for elastic aerobraking tethers[J].Journal of Guidance, Control, and Dynamics, 1998, 21(2): 286-295. |
| Click to display the text | |
| [17] | Grassi M, Cosmo M L.Attitude dynamics of the small expendable-tether deployment system[J].Acta Astronautica, 1995, 36(3): 141-148. |
| Click to display the text | |
| [18] | Lorenzini E C, Cosmo M, Vetrella S, et al.Dynamics and control of the tether elevator/crawler system[J].Journal of Guidance, Control, and Dynamics, 1989, 12(3): 404-411. |
| Click to display the text | |
| [19] | Hu Q, Jia Y H, Xu S J.Recursive dynamics algorithm for multibody systems with variable-speed control moment gyroscopes[J].Journal of Guidance, Control, and Dynamics, 2013, 36(5): 1388-1398. |
| Click to display the text | |
| [20] | 凯利S G. 机械振动[M].贾启芬, 等译.北京: 科学出版社, 2002: 151-152. Kelly S G.Mechanical vibration[M].Translated by Jia Q F, et al.Beijing: Science Press, 2002: 151-152(in Chinese). |
| [21] | Cosmo M L, Lorenzini E C.Tethers in space handbook[M].3rd ed.Washington D.C.: NASA, 1997: 119-126. |
