Hunter和Nosratinia在2006年[4]率先提出了编码协作机制,并系统地研究了基于Turbo码的编码协作系统的性能.与Turbo码相比,LDPC码具有能够接近香农限的译码性能[5],具有可实现并行的迭代译码的优点,而得到广泛的关注.文献[6]提出以一种基于软信息的译码转发策略,中继转发的不是译码的硬判决信息而是软信息的对数似然比,其仿真证明该策略可以取得比放大转发和传统译码转发更好的分集增益.文献[7]研究了半双工中继信道下软信息译码转发机制,将中继译码后的所有软信息进行归一化处理后,再进行LDPC软信息编码,进一步提高了系统的分集增益.文献[8, 9]研究了适用于LDPC码的中继协作系统及其联合迭代译码(JID)算法,但当中继译码不成功时,中继都停止转发,这样就不能发挥分集增益的优势了.
由于采用的LDPC码是系统码,中继经过迭代译码尝试后,即使没有完全译码成功,利用LDPC码元内部的固有特性,中继也会纠正一定的错误信息.为了充分利用中继迭代译码输出的软信息,更好地解决中继译码不成功而无法实现分集的问题,本文提出了基于QC-LDPC码联合分层译码(JLD)的混合转发协作系统.当中继译码成功时,采用理想编码协作策略,目的节点对接收来自源节点和中继节点的不同冗余信息,采用JLD算法进行联合译码,若中继译码错误,则采用译码软信息转发策略,目的节点对接收到来自源节点和中继节点的相同位置的冗余信息进行信息合并后,代入译码器进行传统分层译码(LD)[10].
1 中继混合转发协作系统1.1 中继混合转发协作系统模型为了充分利用中继带来的分集增益的优势,本文提出了基于QC-LDPC码联合分层译码的混合转发协作系统如图 1所示.
 |
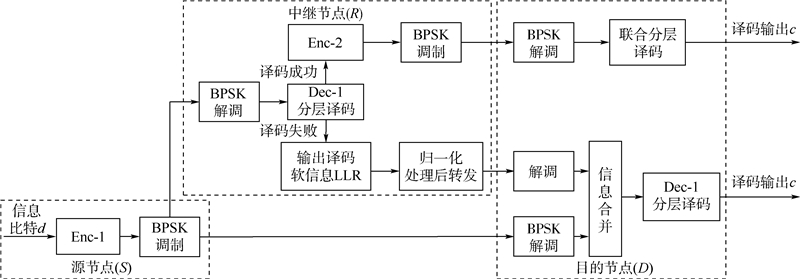| 图 1 中继混合转发协作系统模型Fig. 1 Relay hybrid-and-forward cooperative system model |
| 图选项 |
在中继理想编码协作模式下,第1阶段,源节点S将待发送的信息比特d经过第1个QC-LDPC编码器Enc-1编码和BPSK调制后,向目的节点D和中继节点R广播编码调制后的信号.在瑞利衰落信道下,中继节点和目的节点在此阶段接收到的信号分别为
式中:xS(i)为源节点的发送信息;nSR(i)和nSD(i)为零均值方差为N0的复加性高斯白噪声;αSR和αSD为常规Rayleigh衰落因子,其E[α2]=1,且概率密度函数为p(α)=2αe－α2.
第2阶段,中继节点R对接收到的信号代入译码器Dec-1进行分层译码,若译码成功,则再用第2个QC-LDPC编码器Enc-2编码,并将其进行BPSK调制后发送给目的节点,此时目的节点接收到的信号为
目的节点接收到两路不同的冗余信息后,根据一定的译码策略进行联合迭代译码,这样可以充分利用两路信号的非相关特性和码元内部的固有特性,从而更好地发挥纠错性能.
当信道条件恶劣时,中继译码不成功时,本文称之为中继非理想编码协作,此时中继就切换到译码软信息转发模式,将译码后的软信息对数似然比(LLR)值进行归一化处理后,调制发送给目的节点,而不是像传统译码转发方式转发的是硬判决的信息,从而充分发挥中继带来的编码增益的优势.目的节点对接收到相同位置的冗余信息进行信息合并后,再代入译码器Dec-1进行分层译码.
1.2 中继理想编码协作中的QC-LDPC系统码文献[11]提出了具有完全线性编码复杂度的QC-LDPC码的构造方法,更适于采用收敛性更快的LD算法.根据文献[11]的算法,本文设计了用于本文协作系统中源节点和中继节点编码的QC-LDPC系统码.
首先定义信息位和校验位长度分别为N-M1和M1,从而得到码长为N的码字c1,然后将编码器Enc-1的校验矩阵H1分为信息部分AM1×(N－M1)和校验部分BM1×M1,因此H1可写成
其中：AM1×(N－M1)可以根据度序列确定基矩阵非零元素的位置,再由置换矩阵进行置换扩展.而校验部分的结构为
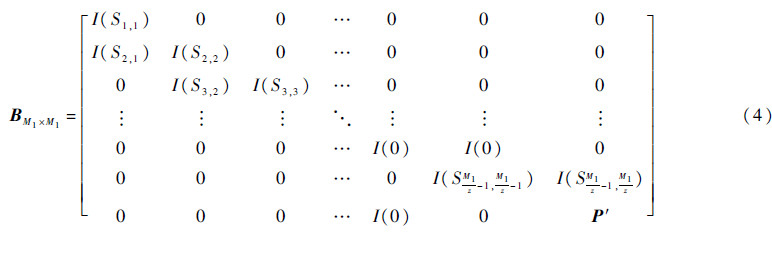
式中:I(Si,j)为单位矩阵循环移位Si,j次后得到的循环置换矩阵,0≤Si,j≤z-1;z为QC-LDPC码循环置换矩阵的维数,且N、M1均为z的整数倍,当Si,j=0时,I(Si,j)为单位矩阵.式(4)中主对角线和次对角线的I(Si,j)都是由非零置换矩阵置换,其余“0”的位置为全零矩阵置换.其中P子块的结构为
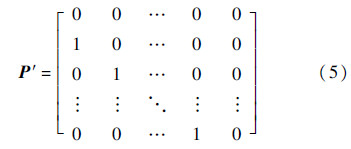
根据如式(4)的结构,源节点S可以由N－M1的信息比特直接线性递推求出所有M1个校验位[11],生成码长为N的码字c1,而不需要校验矩阵进行高斯消去或列变换处理,从而实现正比于码长的编码复杂度.当中继节点R对接收的来自S的码字进行译码,且译码成功时,则R再将译出的码字经过校验矩阵为H2的编码器Enc-2进行第2次编码,增加M2位校验位,生成码字c2.
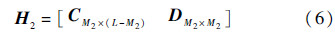
式中:DM2×M2的结构跟式(4)相同.若L=N,则构造的系统码为非正规QC-LDPC系统码,若L－M2=N,则构造的系统码为正规QC-LDPC系统码[9].由于c1和c2有相同的信息位,为了取得系统性能和传输速率的折中,故中继仅转发码字c2的校验位给目的节点.
由H·cT=0T可得,对于整个协作系统的目的接收机而言,整个系统的等效校验矩阵为
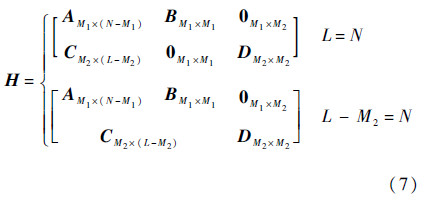
为了更好地提高联合译码的性能,与文献[8]的构造方法相比,在构造QC-LDPC系统码,本文还充分考虑了H1和H2两个校验方程组成的等效校验矩阵H的环路特性[12],保证等效校验矩阵H不存在4环,从而保证联合译码的性能;与文献[8]的构造方法相比,在保证可以实现正比于码长的线性编码复杂度的同时,本文根据文献[11]还可以保证所选择的度序列对具有更好的码容量[13].具体QC-LDPC码优化构造算法可参考文献[11].
2 中继混合转发协作系统JLD算法2.1 目的节点接收码字的双层Tanner图结构第1.1节提出的中继混合转发协作系统若采用非正规QC-LDPC系统码,则对目的节点而言,整个编码系统等效校验矩阵的双层Tanner图结构如图 2所示.
 |
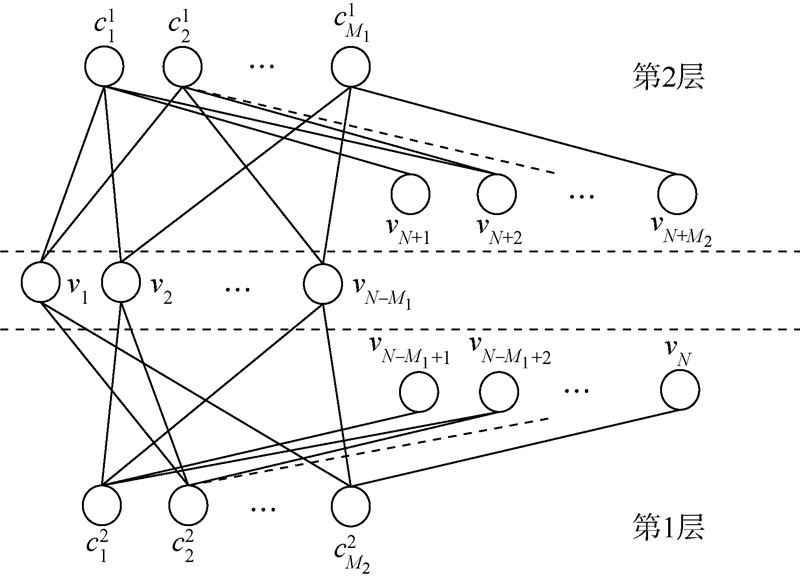| 图 2 非正规QC-LDPC系统码的双层Tanner图Fig. 2 Bilayer Tanner graph of irregular QC-LDPC systematic codes |
| 图选项 |
如图 2所示的非正规QC-LDPC系统码的双层Tanner图,vn(n=1,2,…,N－M1)同时参与了H1和H2两个校验方程,vn(n=N－M1+1,N－M1+2,…,N)仅参与了H1一个校验方程,而vn(n=N,N+1，…,N+M2)则仅参与了H2一个校验方程.
2.2 基于双层Tanner图的QC-LDPC码JLD算法为了充分发挥系统的编码增益,文献[8]提出了联合迭代译码算法,其主要思想是：目的节点根据接收到信号求得每个变量节点的初始信息,然后水平处理更新每层每个校验节点传递给变量节点的消息.在垂直处理过程中,每层每个变量节点的变量消息除了来自本层其他校验节点的校验消息外,还来自另一层与之相邻的所有校验节点的校验消息,从而实现了译码过程中两层间软信息的交换.
文献[10]中证明,在相同迭代次数下,LD算法具有更好的译码性能.因为在每次迭代过程中,变量消息可得到多次更新,从而提高整个系统的译码性能.由于本文构造的非正规LDPC系统码为QC-LDPC码,可以满足LD过程中同一层校验矩阵的列重必须不大于1的要求.
在上述双层Tanner图中,vn为所有变量节点集合,c(t)mt(t=1,2)为第i层校验矩阵的所有校验节点组成的集合,mt为第i层校验矩阵的列数,即m1∈M1,m2∈M2,Ntc(i)代表与校验节点c(t)i相连的所有变量节点组成的集合,0≤i≤mt.
本文JLD算法的具体步骤如下.
步骤1 译码初始化.
1) 根据Tanner图将校验节点按层划分为Kt层,其中
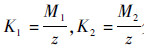分别记作LK1和LK2,则有∪k=1K1Lk=H1,∪k=1K2Lk=H2.2) 目的节点根据接收到的软信息yj(j=1,2,…,N+M2),求得瑞利衰落信道下,变量节点的初始信息为
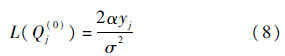
式中:σ2为噪声方差.
3) 将各层校验节点的校验消息L(Ri,j(l,ξt))初始化为0,其中,l为迭代次数,0≤ξt≤Kt,ξt为译码运行到的层数.
4) 迭代次数初始化为l=1,层数初始化为ξ1=1,ξ2=0.
步骤2 第1层校验消息及变量消息更新.
对于每个校验节点ci(1)∈Lξ1,其传递给与之相连的变量节点的校验消息为
变量节点传递给与之相连的校验节点的变量消息为
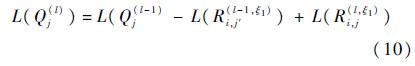
步骤3 硬判决及校验.
对迭代后的变量消息进行判决,判决准则为
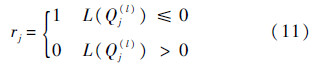
得到判决后的码字rn=(r1,r2,…rn),如果H·rTn=0T则停止迭代输出rn为译出码字,否则进入下一层迭代,即ξ1=ξ1+1,返回执行步骤2,直到ξ1=K1.若ξ1=K1且H·rTn≠0T,证明第1层分层译码结束,将译码更新得到的变量消息作为初始消息,代入第2层校验矩阵,ξ2=ξ2+1,执行步骤4.
步骤4 第2层校验消息及变量消息更新.
对于每个校验节点ci(2)∈Lξ2,其传递给与之相连的变量节点的校验消息为
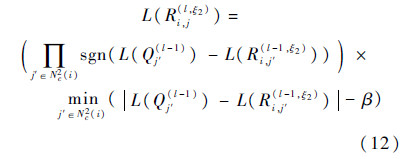
变量节点传递给与之相连的校验节点的变量消息为
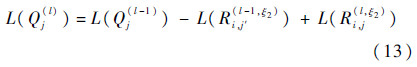
步骤5 硬判决及校验.
判决准则为
得到判决后的码字rn,如果H·rTn=0T则停止迭代输出rn为译出码字,否则进入下一层迭代,即ξ2=ξ2+1,返回执行步骤4,直到ξ2=K2.若ξ2=K2,证明第2层分层译码结束,即一次完整的JLD迭代结束.若H·rTn≠0T,返回执行步骤2,l=l+1,层数初始化为ξ1=1,ξ2=0,直到译码成功或者达到最大迭代次数,跳出循环.本文提出的JLD算法,通过逐层更新变量消息,加快了的交互信息在两层Tanner图中的传递,可以提高了译码的性能.
3 非理想编码协作时的转发策略当信道条件恶劣时,中继译码不成功时,中继就有编码协作切换到译码软信息转发模式,将迭代译码后的软信息LLR值进行归一化处理后,再进行调制后发送给目的节点,充分发挥迭代译码的置信度传播优势.与传统译码转发方式转发的是硬判决的信息的策略相比,译码软信息转发策略可以充分发挥中继带来的分集增益的优势.目的节点对接收到相同位置的冗余信息进行初始信息合并后,再带入译码器进行传统分层译码.
在译码软信息转发模式下,经归一化处理后,中继转发的信号为
式中:LpSR(i)为中继第p次译码迭代后第i个变量节点的LLR值;
为该组码字的LpSR(i)的平均功率:
对于上述的译码软信息转发策略,可以用高斯近似来分析.对于一个无限长或非常长的基于信息传播的译码器来说,若输入译码器的信道LLR值是服从独立、同一高斯分布,那么译码后输出的LLR值也将近似服从高斯分布[14, 15].这里的译码器包括本文QC-LDPC码所采用的分层译码器,以及卷积码的BCJR(Bahl-Cocke-Jelinek-Raviv)译码器等.
假设源节点到中继节点所采用的码长N足够长时,则译码迭代输出的LLR值服从高斯分布,当xS(i)=+1时,设μR(μR>0)为译码迭代输出的LLR值的均值,σ2R为输出的LLR值的方差.根据文献[7],μR和σ2R可以预先通过统计求得,在实时传输时,中继节点不需要发送给目的节点.
中继转发的信号可以等效为一个均值为μ^xS(i)的信号,加上方差为σ^2R的高斯噪声影响的结果,则式(15)表示为
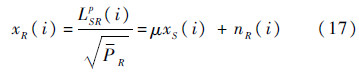
式中:
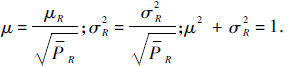
因此,源节点到中继节点的等效信噪比(SNR)为
则目的节点接收到来自中继节点的信号为
根据式(18)和式(19)可得,目的节点接收到来自中继节点的信号的似然比为
根据式(8)和式(20)可得,非理想编码协作目的节点合并后的LLR值为
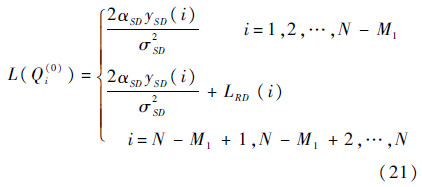
将式(21)作为变量节点的初始消息代入译码器Dec-1进行传统分层译码即可.
4 仿真分析本节对本文提出的基于QC-LDPC码JLD的混合转发协作系统进行了仿真,比较了非正规QC-LDPC系统码在非协作传输、中继理想编码协作传输,以及中继混合转发协作传输中的性能,并且与文献[8]提出的JID算法进行了比较分析.
假设本文协作通信系统中的信道是相互独立且均为平坦瑞利衰落信道,设中继节点到目的节点的接收信噪比与源节点到目的节点的接收信噪比相等.源节点和中继节点均选择码长为2304,码率为1/2的QC-LDPC码(QC-LDPC-1,QC-LDPC-2),其围长均为8,度序列分布均为
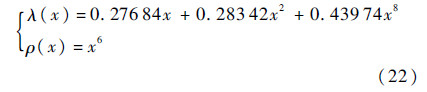
则对整个目的节点接收机而言,整个非正规QC-LDPC码协作系统的码长为3456,码率为1/3,围长为6.
图 3给出了采用本文JLD算法与文献[8]提出的JID算法,非正规QC-LDPC系统码的中继理想编码协作和非协作系统的性能比较,译码迭代次数均设为4次.本文的中继非协作系统目的节点采用传统LD算法,而文献中继非协作系统目的节点采用传统LLR译码算法[16].仿真结果显示,在相同仿真条件下,中继理想编码协作系统的性能都要明显优于非协作系统;在误码率(BER)为10-5时,本文的JLD算法较JID译码算法有约1.9dB的增益,这主要归功于在JLD算法过程中
 |
| 图 3 不同译码算法下中继理想编码协作和非协作系统的性能比较Fig. 3 Performance comparison of different decoding algorithms between relay perfect cooperative system and non-perfect cooperative system |
| 图选项 |
变量消息在两层Tanner图中得到多次更新,加快了整个系统的译码性能.在误帧率(FER)为10-2时,本文JLD算法较JID算法也有约2.4dB的增益,这将大大提高了中继在协作过程中的分集作用.
为了更直观地体现本文提出的译码软信息转发可以带来很好的编码和分集增益,图 4给出了非理想协作时中继采用JID算法时不同协作策略的性能比较,迭代次数设为4次,HF(Hybrid-and-Forward)代表本文提出的混合转发策略.如图 3所示,中继采用LLR译码算法,当源节点到中继节点的信噪比为6dB时,中继才开始有正确译码的分组出现,因此仿真中源节点到中继节点的信噪比分别取6、7和8dB.如图 4所示,本文提出的HF策略明显优于文献[8]提出的编码协作策略,当源节点到中继节点的信噪比为8dB时,本文的HF策略与理想编码协作的性能很接近,当误码率为10-5时,与文献[8]提出的编码协作策略相比,可以获得约2.2dB的增益,这充分说明本文采用的HF策略可以充分发挥中继节点带来的分集增益的优势.
 |
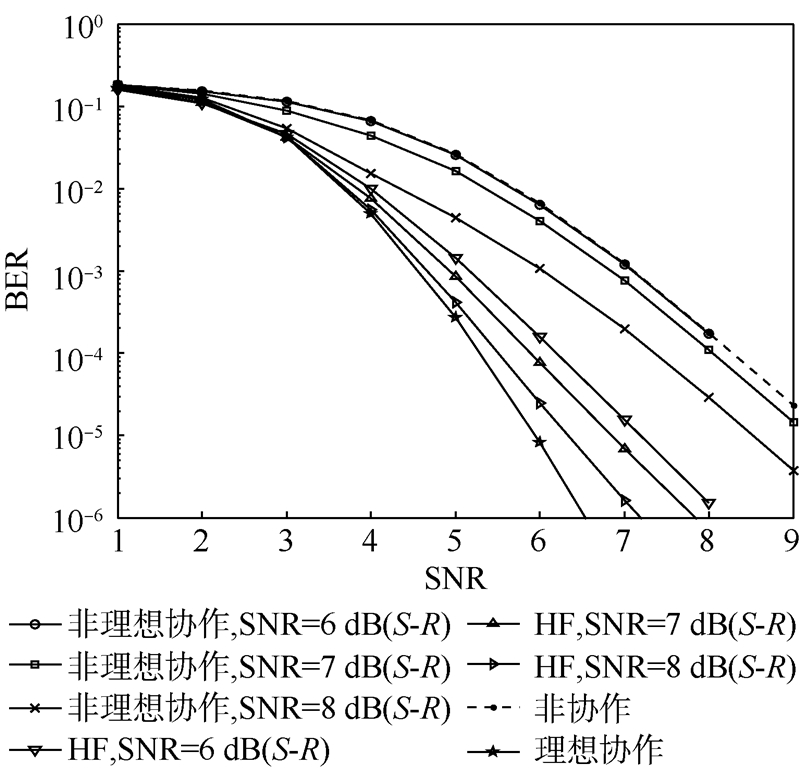| 图 4 非理想编码协作系统中,不同协作策略的性能比较Fig. 4 Performance comparison of different cooperative strategies in non-perfect cooperative system |
| 图选项 |
图 5给出了非理想协作系统中,中继采用本文提出的HF协作策略的不同联合迭代算法的性能比较,迭代次数设为4次.由图 3和图 5可得,当源节点到中继节点的信噪比为4dB时,无论采用哪种协作策略,中继节点都不能正确译码,这充分说明采用译码软信息转发,可以解决传统编码协作中继译码不正确时中继不能提供分集增益的问题.如图 5所示,当源节点到中继节点的信噪比为6dB时,本文提出的HF协作策略与理想编码协作的性能很接近;并且采用本文提出的JLD算法可以明显提高整个协作系统的译码性能,当源节点到中继节点的信噪比为5dB且误码率达到10-5时,本文提出的JLD算法与JID算法相比,可以获得约2.1dB的编码增益.
 |
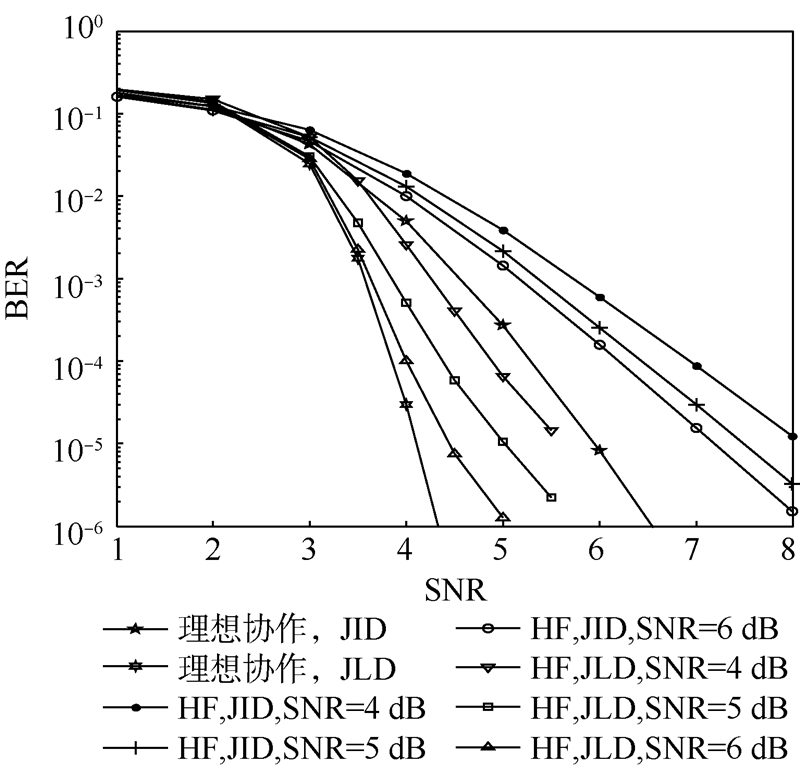| 图 5 非理想编码协作系统中,不同联合译码算法的性能比较Fig. 5 Performance comparison of different joint decoding algorithms in non-perfect cooperative system |
| 图选项 |
5 结 论本文在综合分析了编码协作机制的基础上提出了基于QC-LDPC码的JLD算法并构造了完全线性编码且适合于中继协作系统的QC-LDPC码,经实验仿真表明:
1) 提出的基于QC-LDPC码的JLD算法,可以有效地提高协作系统的译码性能.在相同仿真条件下,中继理想编码协作系统的性能都要明显优于非协作系统;在误码率为10-5时,本文的JLD算法较JID译码算法有约1.9dB的增益.
2) 提出的HF策略,充分发挥了中继带来的编码和分集优势.当源节点到中继节点的信噪比为8dB时,本文的HF策略与理想编码协作的性能很接近,当误码率为10-5时,与文献[8]提出的编码协作策略相比,可以获得约2.2dB的增益.
此外,本文提出的协作系统还可以进一步应用于多中继协作系统以及多跳协作路由系统中.
参考文献
| [1] | Ding Y,Zhang K,Wong K M.Ergodic channel capacities for amplify-and-forward half-duplex cooperative systems[J].IEEE Transactions on Information Theory,2009,55(2):713-730. |
| Click to display the text | |
| [2] | Razaghi P,Yu W.Bilayer LDPC codes for decode-and-forward in relay channel[J].IEEE Transactions on Information Theory,2007,53(10):3723-3739. |
| Click to display the text | |
| [3] | Li C X,Yue G S,Khojastepour M A,et al.LDPC-coded cooperative relay system:Performance analysis and code design[J].IEEE Transactions on Communications,2008,56(3):485-488. |
| Click to display the text | |
| [4] | Hunter T E,Nosratinia A.Diversity through coded cooperation[J].IEEE Transactions on Wireless Communications,2006,5(2):283-289. |
| Click to display the text | |
| [5] | 赵明,张晓琳.改进的基于剩余度置信度传播的LDPC解码算法[J].北京航空航天大学学报,2014,40(3):350-354.Zhao M,Zhang X L.Decoding for LDPC codes with enhanced residual belief-propagation[J].Journal of Beijing University of Aeronautics and Astronautics,2014,40(3):350-354(in Chinese). |
| Cited By in Cnki | |
| [6] | Bao X K,Jing L.Efficient message relay for wireless user cooperation:Decode-amplify-forward (DAF) and hybrid DAF and coded-cooperation[J].IEEE Transactions on Wireless Communications,2007,6(11):3975-3984. |
| Click to display the text | |
| [7] | Azmi M H,Li J,Yuan J H,et al.LDPC codes for soft decode-and-forward in half-duplex relay channels[J].IEEE Journal on Selected Areas in Communicaions,2013,31(8):1-12. |
| Click to display the text | |
| [8] | 陈静文,仰枫帆.基于非正规LDPC码的中继协作通信及其联合迭代译码的性能研究[J].电子学报,2010,38(7):1535-1540.Chen J W,Yang F F.Study on the irregular-LDPC-based relay cooperation and performance of joint iterative decoding[J].Acta Electronica Sinica,2010,38(7):1535-1540(in Chinese). |
| Cited By in Cnki (5) | |
| [9] | 张顺外,仰枫帆,宗鹏.基于联合迭代译码的LDPC编码协作系统[J].西南交通大学学报,2011,46(3):469-475.Zhang S W,Yang F F,Zong P.LDPC-coded cooperative system based on joint iterative decoding[J].Journal of Southwest Jiaotong University,2011,46(3):469-475(in Chinese). |
| Cited By in Cnki (4) | |
| [10] | Mansour M M.A turbo-decoding message-passing algorithm for sparse parity-check matrix codes[J].IEEE Transactions on Signal Processing,2006,54(11):4376-4392. |
| Click to display the text | |
| [11] | 张嵩,马林华,唐红,等,完全线性编码复杂度的QC-LDPC码的构造方法及短环优化算法[J].吉林大学学报:工学版,2013,43(6):824-829.Zhang S,Ma L H,Tang H,et al.Construction of QC-LDPC codes with total linear encoding complexity and eliminating short cycles[J].Journal of Jilin University:Engineering and Technology Edition,2013,43(6):824-829(in Chinese). |
| Cited By in Cnki | |
| [12] | Li C,Yue X,Wang X,et al.LDPC code design for half-duplex cooperative relay[J].IEEE Transactions on Wireless Communications,2008,7(11):4558-4567. |
| Click to display the text | |
| [13] | Hou J L,SiegelP H,MilsteinL B.Performance analysis and code optimization of low-density parity-check codes on Rayleigh fading channels[J].IEEE Journal on Selected Areas in Communicaions,2001,19(5):924-934. |
| Click to display the text | |
| [14] | Xie K,Li J.On accuracy of Gaussian assumption in iterative analysis for LDPC codes[C]//IEEE International Symposium on Information Theory.Piscataway,NJ:IEEE Press,2006:2398-2402. |
| Click to display the text | |
| [15] | Chung S Y,Richardson T J,Urbanke R L.Analysis of sum-product decoding of low-density parity-check codes using a Gaussian approximation[J].IEEE Transactions on Information Theory,2001,47(2):657-670. |
| Click to display the text | |
| [16] | Fossorier M,Mihaljevlc M,Imai H.Reduced complexity iterative decoding of low-density parity-check codes based on belief propagation[J].IEEE Transactions on Communications,1999,47(5):673-680. |
| Click to display the text |
