随着数据采集成本不断降低及应用需求的增长,现代民机采集的状态参数越来越多,近年来国内外对于飞行数据进行了一些研究.文献[2]研究了QAR超限事件飞行操作风险诊断方法;文献[3, 4, 5]研究了利用QAR数据建立燃油流量回归模型监控飞机性能,这些研究仅考虑多自变量和单一因变量的回归模型,也没有研究故障检测方法;文献[6, 7, 8, 9, 10, 11, 12, 13]针对飞行数据用信号处理、聚类、特征提取和符号动力学方法等进行异常监测,这些方法主要是对单变量信号进行研究,没有考虑多变量的情况;文献[14]研究了人工神经网络模型在B737飞机引气系统重要阀门的故障预测并进行验证;文献[15]研究了基于无迹卡尔曼滤波方法检测和隔离飞机引气温度控制系统的传感器和阀门作动器故障;文献[16]通过有限元仿真分析预测飞机引气系统管道裂纹增长故障,这些研究只是利用故障历史数据和仿真方法对引气系统部分部件故障进行了研究,而没有充分利用QAR记录的引气系统状态监控数据来进行系统故障诊断.相关的一些使用飞行数据来构建模型进行故障研究包括美国宇航局的感应监测系统[17]和美国阿尔贡国家实验室的多元状态估计技术[18],但由于技术保密看不到详细细节.文献[19]研究了同型号飞机相同系统的基于飞行数据的多元回归模型,但模型的参数估计算法用于单飞行循环数据,没有考虑多飞行循环数据的参数估计.本文研究了多飞行循环数据的民机引气系统多元回归模型和故障诊断方法,设计了适合多飞行循环飞行数据的模型参数最大后验估计算法,通过仿真数据验证了方法有效性,然后利用真实的引气系统飞行状态监控数据进行了引气系统故障诊断,验证了方法的可行性.该研究可为我国运输类飞机、通用飞机运营支持技术的关键技术飞机状态监控和健康管理提供技术参考.
1 多元线性回归模型及故障诊断多元线性回归分析是一种有效的数据处理方法,在工业、农业、医学、社会调查、生物信息处理等领域被广泛应用.应用民机飞行数据建立回归模型和参数估计时,考虑研究对象和民机飞行数据特点才能建立有效故障诊断应用模型.下文将研究民机多飞行循环数据的引气系统多元线性回归模型和基于该模型的故障诊断.
设民机引气系统状态监控飞行数据为
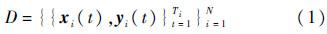
式中:i=1,2,…,N为飞行循环序号;xi(t)为t时刻影响系统输出的k个监测参数数据点,xi(t)∈Rk;yi(t)为t时刻系统输出m个监测参数数据点,yi(t)∈Rm;t=1,2,…,Ti,Ti为第i个飞行循环采集到数据样本数.设x1,x2,…,xk为k个自变量,y1,y2,…,ym为m个因变量,在同工况时因变量和自变量建立多元线性回归模型:
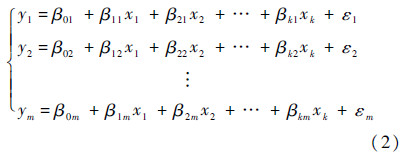
式中:βkm为自变量k对应变量m的回归系数;εm为误差.
式(2)可简化为矩阵形式:
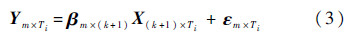
式中:
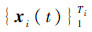 为X向量第i飞行循环子集;
为X向量第i飞行循环子集;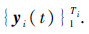 .为Y向量第i飞行循环子集式(3)可看作多飞行循环民机引气系统多元线性回归模型,式(3)可等价为
.为Y向量第i飞行循环子集式(3)可看作多飞行循环民机引气系统多元线性回归模型,式(3)可等价为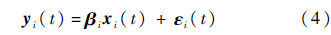
式中:假设ε(t)为独立同分布Νm(0,Σ),ε(t)~Νm(0,Σ),Σ∈Sm,Sm为m×m的正定阵,为估计系统真值.对于性能正常的民机引气系统所有的飞行循环都应有类似的βi∈Rm×(k+1),即βi相似βj对所有j≠i;εi(t)∈Rm为第i飞行循环时模型残差,其协方差矩阵Σi与Σj相似(j≠i),这符合多飞行循环实际,而传统的多元回归并不考虑协方差矩阵Σi与Σj相似性.
利用式(4)对应的模型进行系统故障诊断,主要采用扩展的标准多元统计过程控制(Multivariate Statistical Process Control,MSPC)方法[20].对于诊断某一飞行循环系统故障要计算βi的Hotelling T2统计值:
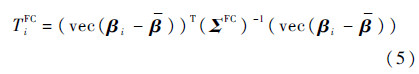
式中:

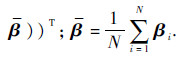
检测阈值LFC用指定置信水平λ的F分布对应值
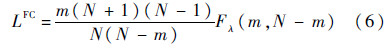
如果TiFC>LFC就认为引气系统在第i个飞行循环发生故障.
在第i个飞行循环内检测发生故障的时刻t则要计算残差εi(t)的Hotelling T2统计值:
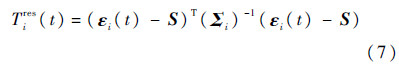
故障检测阈值Lres的确定用λ置信水平、参数m和Nt-m的F分布:
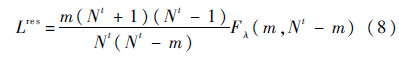
式中:
 ,如果Tires(t)>Lres就认为引气系统在第i个飞行循环t时刻发生故障.
,如果Tires(t)>Lres就认为引气系统在第i个飞行循环t时刻发生故障.式(4)模型用于民机系统故障诊断需估计所有飞行循环i的回归系数βi、残差εi(t)的协方差Σi和超参数S.
2 模型的参数估计传统的多元回归模型估计参数是模型系数βi,常用的方法是最大似然估计[21]和近来发展的智能化算法[22],这些方法对单个飞行循环飞行数据的多元回归模型的参数估计研究较多,参数估计时没有考虑多飞行循环间的残差的协方差矩阵服从的分布.为利用式(4)的回归模型进行民机系统故障诊断,本文设计了回归模型的多个飞行循环的协方差矩阵服从同分布的最大后验参数估计方法来估计βi、残差εi(t)的协方差Σi和总体协方差S.使用最大后验概率方法来估计想要的参数,首先要研究多元回归模型的Σi和εi(t)随机变量的密度函数.
对回归模型,由于ε(t)是独立同分布,则yi(t)~Νm(βixi(t),Σi),yi(t)的联合密度分布为
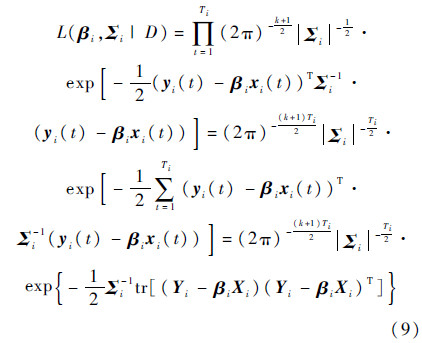
式(9)就是一个飞行循环监测数据样本的似然函数,对式(9)求对数,忽略附加常量得βi,Σi对数似然:
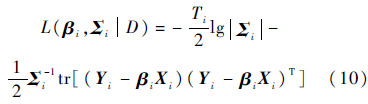
式(10)中参数矩阵βi无先验值,对多个飞行循环协方差Σi假定符合威沙特先验分布:
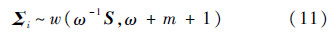
式中:ω为先验超参数,表示估计不同飞行循环的Σi之间的相似度.对Σi的密度函数求对数,得对数先验为
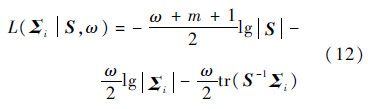
根据逆威沙特矩阵是多变量正态分布的共轭先验分布,S~w-1(αΩ,α-m-1),则S的密度函数求对数,得对数先验为
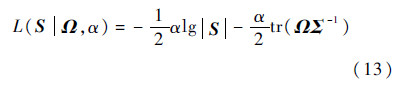
式中:超参数α为S与Ω的相似度;Ω为式(4)对应模型的所有飞行循环的总体先验协方差.
多个飞行循环的引气系统回归模型(式(4))全概率密度函数为
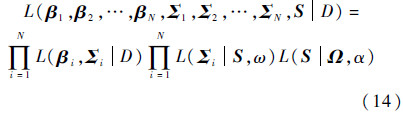
对式(14)两边取对数,忽略常量,得对数后验:
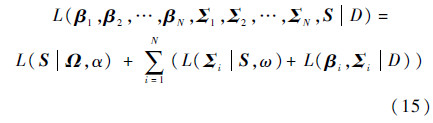
将式(9)、式(10)和式(12)代入式(15)的最大后验估计就是就求L(β1,β2,…,βN,Σ1,Σ2,…,ΣN,S|D)的最大值:
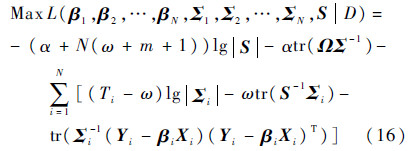
式中:βi、Σi(i=1,2,…,N)和S为待估参数;超参数α、ω和Ω用来调节待估参数性能的给定值.为求解式(16),令Σi-1=Οi,Σ-1iβi=Ηi,S-1=ΖTΖ,则式(16)可变形为

若式(17)被证明是凸形[23],则有最优解.
对式(17)中的O、H和Z分别求导并变回原来参数则可以得出式(18)~式(20):
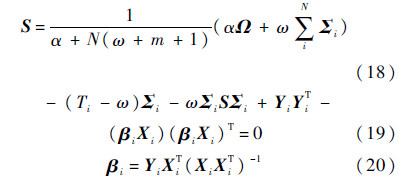
式(18)中的S的估计是先验引气系统协方差矩阵Ω和每个飞行循环引气系统协方差矩阵的加权和,当超参数α=0和N很大时,S就是每个飞行循环协方差矩阵和的均值.式(20)回归参数βi的估计值和和每一个飞行循环的回归最小二乘法估计相同.式(19)超参数ω=0即不考虑各飞行循环引气系统多元回归协方差服从同分布,并用式(20)替换βi得
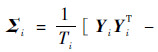
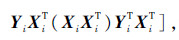 ,结果和单个飞行循环的多元回归最大后验估计相同,这说明单飞行循环是多飞行循环回归模型的一个特例,多飞行循环的回归模型鲁棒性更好.
,结果和单个飞行循环的多元回归最大后验估计相同,这说明单飞行循环是多飞行循环回归模型的一个特例,多飞行循环的回归模型鲁棒性更好.3 求解算法求解式(17)的最优问题采用块坐标下降(Block Coordinate Descent,BCD)法进行矩阵Σi和S的更新,该算法能够保证收敛和提高收敛速度[24, 25],适用于观测数据量大和多批次数据,算法流程如图 1所示.
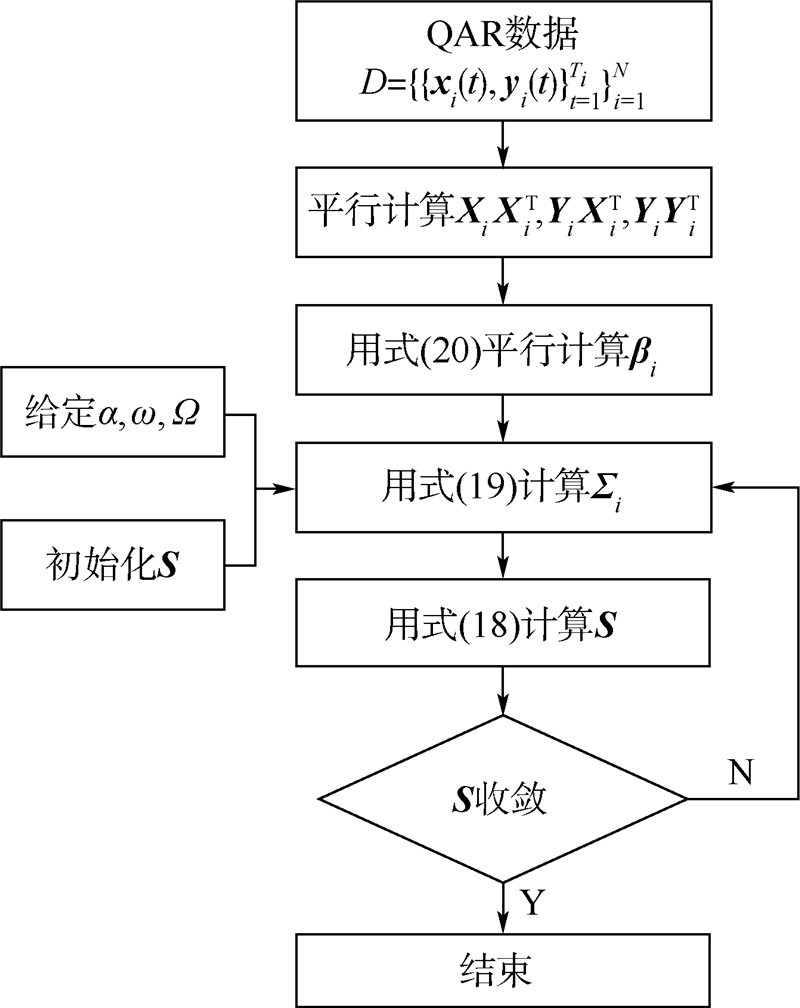 |
| 图 1 引气系统线性多元回归参数估计算法流程图Fig. 1 Parameter estimation algorithm flowchart of bleed air system linear regression |
| 图选项 |
根据多个飞行循环的引气系统飞行数据估计引气系统线性模型参数βi、Σi和S步骤如下:
1) 根据每个飞行循环引气系统飞行数据计算矩阵XiXiT,YiXiT,YiYiT.
2) 利用式(20)计算每个飞行循环引气系统模型的βi.
3) 初始化S.
4) 对给定S利用式(19)求解每个飞行循环引气系统模型的Σi.
5) 用第4)步解出的Σi代入式(18)计算S.
6) 判断S是否收敛,如果收敛停止计算,否则回到第4)步.
超参数α、ω和Ω一般根据经验来给定,α>0、ω>0,当已知S近似Ω则α给定一个较大的值,当每个飞行循环Σi近似S时ω给定一个较大的值,当Ω缺少先验信息时令Ω=μI(I为单位矩阵,μ为比例系数).
4 例 子4.1 仿真数据对参数估计和故障诊断验证飞行循环i生成的m=2、Ω=0、βi~Ν((1.25,0.78,0.91,-0.218),3Ι)、α=0、Σi~w(ω-1S,ω+m+1)、xi(t)~Ν(0,3Ι)、yi(t)~N(βixi(t),Σi)、
 和I为单位矩阵的某系统输入和输出仿真数据.
和I为单位矩阵的某系统输入和输出仿真数据.对仿真数据采用传统的不考虑每个飞行循环的协方差矩阵服从同分布的最大后验估计方法(mean1)来估计每个飞行循环的多元回归模型的协方差矩阵(Σi)和系数βi.另外就是采用本文考虑每个飞行循环的协方差矩阵服从同分布的最大后验估计方法(mean2)估计每个飞行循环的多元回归模型的协方差矩阵(Σi)和系数βi.对于βi值估计精度两种方法相同,对于Σi估计效果采用Frobenius范数
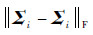 来衡量.系统的故障诊断准确率和Σi-1估计准确度有关,Σi-1越接近Σi-1故障诊断准确率越高,采用Frobenius范数
来衡量.系统的故障诊断准确率和Σi-1估计准确度有关,Σi-1越接近Σi-1故障诊断准确率越高,采用Frobenius范数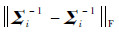 评估.当ω=5时分别固定飞行循环数N和飞行循环内样本数Ti,对应改变Ti和N仿真运行500次,计算平均的
评估.当ω=5时分别固定飞行循环数N和飞行循环内样本数Ti,对应改变Ti和N仿真运行500次,计算平均的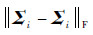 和
和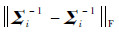 ,仿真数据结果见表 1.作N=10时Ti与
,仿真数据结果见表 1.作N=10时Ti与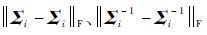 的关系见图 2,作Ti=10时N与
的关系见图 2,作Ti=10时N与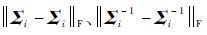 的关系见图 3.
的关系见图 3.表 1 两种方法的
 和
和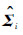 协方差矩阵估计结果Table 1 Estimating result of covariance matrix
协方差矩阵估计结果Table 1 Estimating result of covariance matrix  and
and 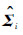 by two methods
by two methods| 评估 | 方法 | Ti=100,N=10 | Ti=100,N=20 | Ti=100,N=40 | Ti=100,N=80 | Ti=100,N=160 | Ti=100,N=320 |
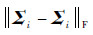 | mean2 | 0.2086388 | 0.2389166 | 0.2500243 | 0.2334119 | 0.2283133 | 0.2326539 |
| mean1 | 0.21316 | 0.2545369 | 0.2659922 | 0.240786 | 0.2334272 | 0.2332565 |
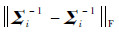 | mean2 | 0.5852457 | 0.5545882 | 0.5621796 | 0.5359386 | 0.6200657 | 0.6235864 |
| mean1 | 0.6536554 | 0.6188554 | 0.6225665 | 0.5916896 | 0.6836775 | 0.68848 |
| 评估 | 方法 | Ti=50,N=10 | Ti=100,N=10 | Ti=150,N=10 | Ti=200,N=10 | Ti=250,N=10 | Ti=300,N=10 |
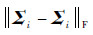 | mean2 | 0.2853868 | 0.2086388 | 0.1665929 | 0.1434759 | 0.1316231 | 0.1210948 |
| mean1 | 0.2983763 | 0.21316 | 0.169149 | 0.1452664 | 0.1332216 | 0.1220289 |
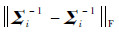 | mean2 | 0.8991059 | 0.5852457 | 0.470849 | 0.42069 | 0.3604597 | 0.3249798 |
| mean1 | 1.08632 | 0.6536554 | 0.5047816 | 0.4420486 | 0.3793956 | 0.3366573 |
表选项
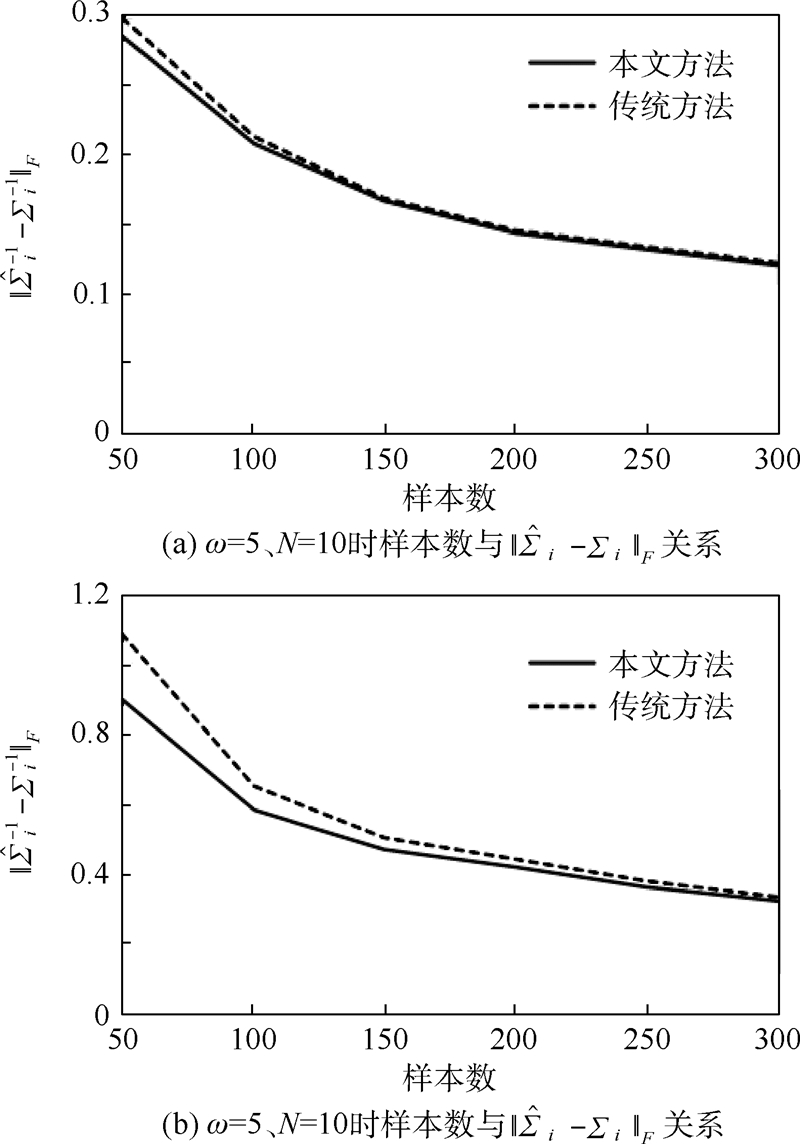 |
图 2 不同样本数时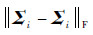 与 与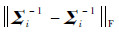 的估值(ω=5,N=10)Fig. 2 Estimating value of 的估值(ω=5,N=10)Fig. 2 Estimating value of 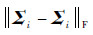 and and 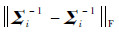 in different sample numbers (ω=5,N=10) in different sample numbers (ω=5,N=10) |
| 图选项 |
 |
图 3 不同飞行循环数时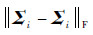 与 与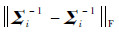 的估值(ω=5,Ti=100)Fig. 3 Estimating value of 的估值(ω=5,Ti=100)Fig. 3 Estimating value of 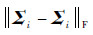 and and 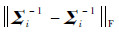 in different flight cycle numbers (ω=5,Ti=100) in different flight cycle numbers (ω=5,Ti=100) |
| 图选项 |
图 2可以看出在ω=5飞行循环数固定时本文方法在估计Σi和Σi-1时精度均好于不考虑每个飞行循环多元回归模型的协方差间的相似时的最大后验估计;并且在估计飞行循环中飞行数据是小样本的系统模型Σi时,本文方法效果明显好于传统方法,但随着样本数增加两种方法效果趋同.图 3中固定飞行循环中观测样本Ti=100,改变飞行循环数估计Σi和Σi-1时,本文方法优于传统方法,特别是对Σi-1估计本文方法有较好的效果,但是随着飞行循环数的增加,两种方法对参数Σi和Σi-1估计精度并没有明显的变化趋势.
取100个飞行循环,每个飞行循环按上文参数仿真生成100个样本,在上述仿真数据第30个和第80个飞行循环中分别注入突变故障.当λ=0.99时,用式(5)和式(7)分别进行故障诊断,结果如图 4所示.
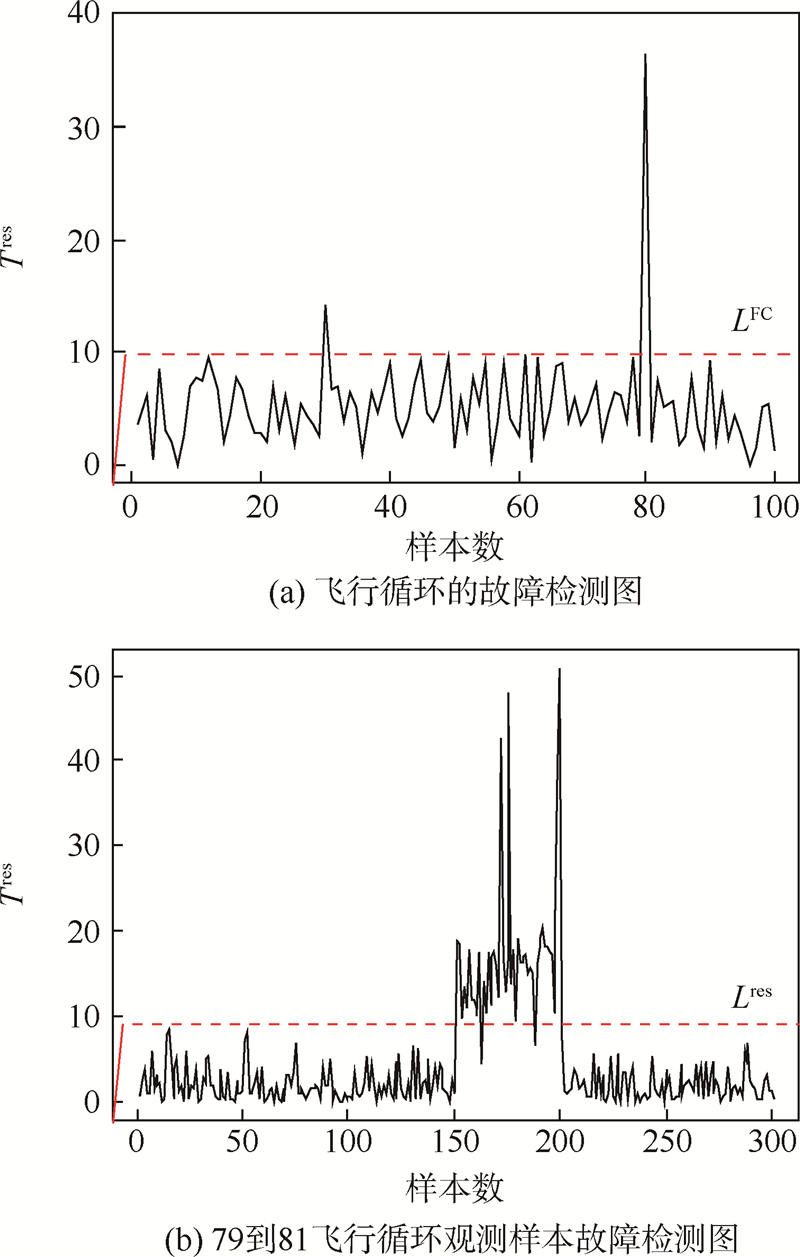 |
| 图 4 Tres飞行循环和观测样本的故障检测图Fig. 4 Fault detection of flight cycles and observed sample by Tres |
| 图选项 |
故障诊断性能评估主要采用准确率(Accuracy,A)、虚警率(False Alarm Rate,FAR)和漏警率(Missing Alarm Rate,MAR)的指标.以飞行循环为样本进行故障诊断时A=100%、FAR=0、MAR=0;以飞行循环中观测样本值进行故障诊断时A=99.81%、FAR=0.057%、MAR=0.1%.
从图 4可以看出本文方法能够从飞行循环和观测样本的Tres有效检测系统故障.
4.2 民机引气系统故障诊断实例使用某航空公司民机引气系统有温度调控故障的200个飞行循环的真实状态监测数据,其中含有故障记录前50个飞行循环和维修后150个飞行循环的QAR数据.根据飞机飞行剖面和监控状态参数地/空、机翼防冰、左发整流罩防冰、右发整流罩防冰、左空调组件、右空调组件监测值,选用飞机在巡航状态并且机翼防冰、左发整流罩防冰、右发整流罩防冰关闭,左空调组件、右空调组件开启时的QAR数据来验证本文方法.引气系统建模参数如表 2所示.
表 2 引气系统建模参数Table 2 Bleed air system modeling parameters
| 变量 | 监测参数 | 参数单位 |
| 自变量 |
|
| 因变量 |
|
表选项
可通过式(5)、式(6)计算TFCi和LFC;根据维修后引气系统正常时的150个飞行循环巡航数据估计出
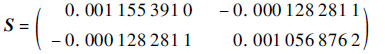
然后根据式(7)、式(8)计算故障维修前50个飞行循环的Tires(t)和Lres,为了便于绘图观察,把Tires(t)转化成
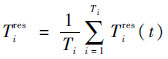 ,当λ=0.99分别进行故障诊断,结果如图 5所示.
,当λ=0.99分别进行故障诊断,结果如图 5所示.从图 5可以看出,本文方法根据飞行状态监控数据建立多元回归统计模型可以有效诊断引气系统是否发生故障,图 5(a)用飞行循环中的模型系数进行引气系统故障诊断,异常发生在第42个飞行循环,提前8个飞行循环诊断出故障;图 5(b)用飞行循环样本残差进行引气系统故障诊断,在第39飞行循环检测到异常,提前11个飞行循环诊断出故障,用飞行循环样本残差进行引气系统故障诊断效果较好.但是用飞行循环样本残差故障检测,由于采集数据噪声的影响会产生虚警,如图 5(b)第42个飞行循环被检测为正常.
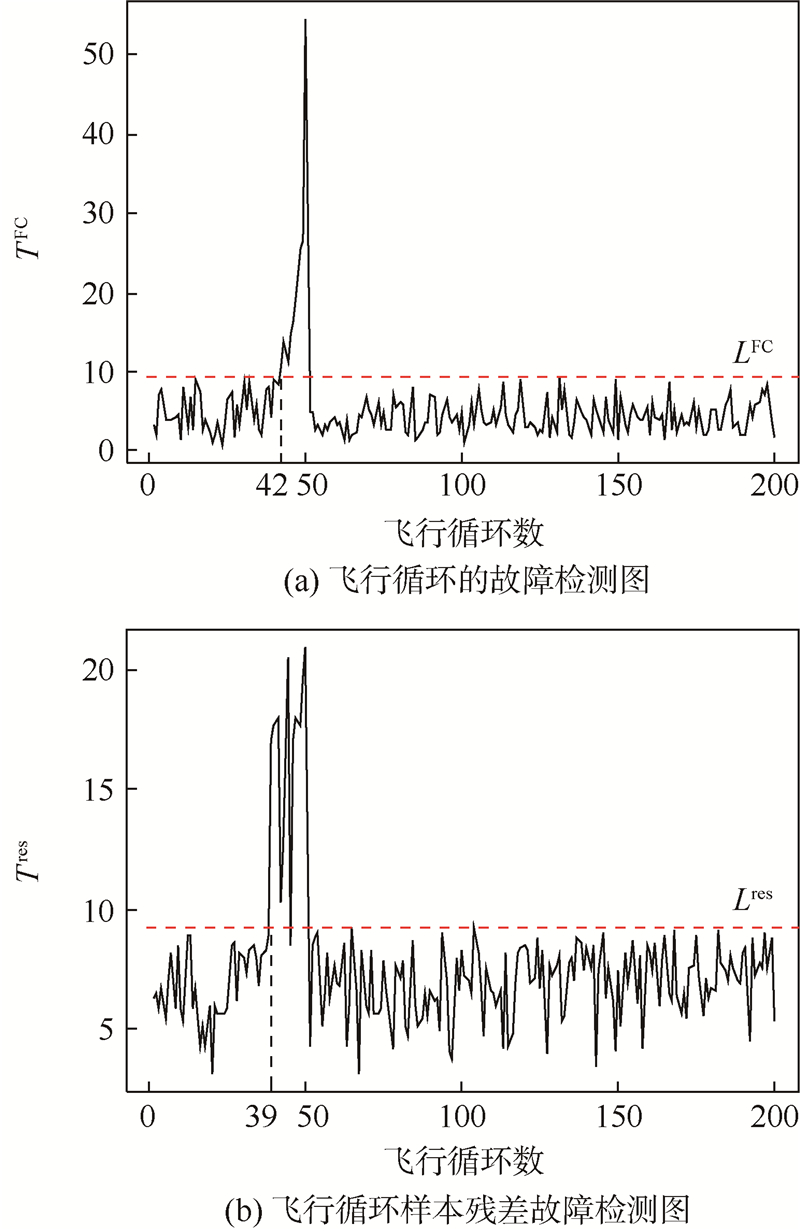 |
| 图 5 Hotelling T2引气系统故障检测图Fig. 5 Fault detection of bleed air system by Hotelling T2 |
| 图选项 |
5 结 论本文研究了一种适合多飞行循环QAR数据的民机引气系统多元线性回归的故障诊断方法,通过对仿真数据和实际含故障的飞行循环数据分析得出:
1) 飞行循环和飞行循环内故障检测方法均可有效检测引气系统故障,且飞行循环内故障检测能提前故障发现时机.
2) 基于历史飞行数据的民机引气系统性能的多元线性模型使用本文方法估计模型参数在小样本时有较好的效果.
3) 本文方法适用于QAR数据建模,为分析QAR数据中蕴含的规律提供了工具.该方法可提前检测引气系统故障,实现“风险关口前移”,对保障飞机的运行安全性和准点率、提前安排维修计划有重要意义.
下一步将结合实际飞行数据在工程应用中进一步验证改进本文所提方法,同时推广应用到民机其他复杂系统的故障诊断.
参考文献
| [1] | 周新颖,谭朝阳,刘倩.挖潜“大数据”时代QAR如何改变飞行运营?[N].中国民航报,2013-10-25(04).Zhou X Y,Tan Z Y,Liu Q,In tapping the potential of “big data” era how exploit QAR to change the flight operations?[N].CCAC Journal,2013-10-25(04)(in Chinese). |
| [2] | 祁明亮,邵雪焱,池宏.QAR超限事件飞行操作风险诊断方法[J].北京航空航天大学学报,2011,37(10):1207-1210.Qi M L,Shao X Y,Chi H.Flight operations risk diagnosis method on quick-access-record exceedance[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(10):1207-1210(in Chinese). |
| Cited By in Cnki (5) | |
| [3] | 孔成安,李文华,尹湛.利用QAR数据实施飞机性能监控[J].中国民用航空,2008,94(10):54-56.Kong C A,Li W H,Yin Z.Monitoring aircraft performance with QAR data[J].China Civil Aviation,2008,94(10):54-56(in Chinese). |
| Cited By in Cnki (17) | |
| [4] | 耿宏,揭俊.基于QAR数据的飞机巡航段燃油流量回归模型[J].航空发动机,2008,34(4):46-50. Geng H,Jie J.Fuel flow regression model of aircraft cruise based on QAR data[J].Aeroengine,2008,34(4):46-50(in Chinese). |
| Cited By in Cnki (19) | |
| [5] | 曹惠玲,贾超.基于QAR的飞机爬升阶段燃油流量回归模型研究[J].中国民航大学学报,2013,31(3):31-35.Cao H L,Jia C.Research of fuel flow regression model of aircraft climb phase based on QAR[J].Journal of Civil Aviation University of China,2013,31(3):31-35(in Chinese). |
| Cited By in Cnki (3) | |
| [6] | 王帮峰,林剑祥,芦吉云.基于EEMD—HT的飞行数据小突变信号检测[J].振动、测试与诊断,2013,33(3):388-392.Wang B F,Lin J X,Lu J Y.Small mutation signal detection for flight data based on empirical mode decomposition and Hilbert transform[J].Journal of Vibration,Measurement & Diagnosis,2013,33(3):388-392(in Chinese). |
| Cited By in Cnki | |
| [7] | 韩旻,赵清洲.一种基于阴性选择算法的飞行数据异常值检测方法[J]航空计算技术,2010,40(4):53-55.Han M,Zhao Q Z.A detection method of abnormal flight data based on negative selection[J]Aeronautical Computing Technique,2010,40(4):53-55(in Chinese). |
| Cited By in Cnki (2) | |
| [8] | 吕永乐,郎荣玲.基于奇异值分解的飞行数据降噪方法[J].计算机工程,2010,38(3):260-262.Lyu Y L,Lang R L.Noise reduction method for flight data based on singular value decomposition[J].Computer Engineering,2010,38(3):260-262(in Chinese). |
| Cited By in Cnki (10) | |
| [9] | Dimogianopoulos D G,Hios J D,Fassois S.Fault detection and isolation in aircraft systems using stochastic nonlinear modelling of flight data dependencies[C]//Proceedings of 14th Mediterranean Conference on Control and Automation.Piscataway,NJ:IEEE Press,2006:1-6. |
| Click to display the text | |
| [10] | Das S,Sarkar S,Ray A,et al.Anomaly detection in flight recorder data:A dynamic data-driven approach[C]//Proceedings of American Control Conference(ACC).Piscataway,NJ:IEEE Press,2013:2668-2673. |
| Click to display the text | |
| [11] | Chu E,Gorinevsky D,Boyd S.Detecting aircraft performance anomalies from cruise flight data[C]//AIAA Infotech Aerospace Conference.Reston:AIAA,2010:2010-0337. |
| Click to display the text | |
| [12] | Gorinevsky D,Matthews B,Martin R.Aircraft anomaly detection using performance models trained on fleet data[C]//Proceedings of Conference on Intelligent Data Understanding (CIDU).Piscataway,NJ:IEEE Press,2012:17-23. |
| Click to display the text | |
| [13] | Chu E,Gorinevsky D,Boyd S P.Scalable statistical monitoring of fleet data[C]//World Congress of the International Federation of Automatic Control (IFAC).Laxenburg:IFAC,2011,18(1):13227-13232. |
| Click to display the text | |
| [14] | Abdelrahman W G,Al-Garni A Z,Al-Wadiee W.Application of back propagation neural network algorithms on modeling failure of B-737 bleed air system valves in desert conditions[J].Applied Mechanics and Materials,2012,225:505-510. |
| Click to display the text | |
| [15] | Shang L,Liu G.Sensor and actuator fault detection and isolation for a high performance aircraft engine bleed air temperature control system[J].IEEE Transactions on Control Systems Technology,2011,19(5):1260-1268. |
| Click to display the text | |
| [16] | Lakkundi A B.Prediction of crack growth in aircraft engine bleed air ducts using finite element and crack growth analysis[D].Wichita:Wichita State University,2006. |
| Click to display the text | |
| [17] | Iverson D L.Inductive system health monitoring[C]//Proceedings of International Conference on Artificial Intelligence (IC-AI).Athens,Georgia:CSREA Press,2004:605-611. |
| Click to display the text | |
| [18] | Gross K C,Singer R M,Wegerich S W,et al.Application of a model-based fault detection system to nuclear plant signals,ANL/RA/CP-92110[R].1997. |
| Click to display the text | |
| [19] | Gorinevsky D.Bayesian fault isolation in multivariate statistical process monitoring dimitry gorinevsky[C]//Proceedings of American Control Conference (ACC).Piscataway,NJ:IEEE Press,2011:1963-1968. |
| Click to display the text | |
| [20] | Wang H,Chai T Y,Ding J L,et al.Data driven fault diagnosis and fault tolerant control:Some advances and possible new directions[J].Acta Automatica Sinica,2009,35(6):739-747. |
| Click to display the text | |
| [21] | Lee S Y,Tsang S Y.Constrained maximum likelihood estimation of two-level covariance structure model via EM-type algorithms[J].Psychometrika,1999,36(4):435-450. |
| Click to display the text | |
| [22] | 刘锦萍,郁金祥.基于改进的粒子群算法的多元线性回归模型参数估计[J].计算机工程与科学,2010,(4):101-105.Liu J P,Yu J X.Parameter estimation of multiple linear regression models based on the improved particle swarm optimization algorithm[J].Computer Science & Engineering,2010,(4):101-105(in Chinese). |
| Cited By in Cnki (20) | |
| [23] | Boyd S P,Vandenberghe L.Convex optimization[M].Cambridge:Cambridge University Press,2004:82-93. |
| Cited By in Cnki | Click to display the text | |
| [24] | Nesterov Y.Efficiency of coordinate descent methods on huge-scale optimization problems[J].SIAM Journal on Optimization,2012,22(2):341-362. |
| Click to display the text | |
| [25] | Richtárik P,Takáč M.Iteration complexity of randomized block-coordinate descent methods for minimizing a composite function[J].Mathematical Programming,2012,144(1-2):1-38. |
| Click to display the text |
