根据所使用信息量的不同,这里将多位置对准分为两类:多位置解析对准和多位置精对准.多位置解析对准[8, 9]方法只使用停止状态下的惯性传感器输出数据,转动过程中的数据不使用,通过精密转动机构绕天向轴转过一个或多个特定角度(如90°或180°),然后根据各静止位置间的解析关系补偿掉惯性传感器的偏置误差;多位置精对准[10, 11, 12]方法使用整个停止和转动过程中的惯性传感器输出数据,进行捷联惯导解算,同时采用卡尔曼滤波等算法,估计出惯性测量单元(IMU)的偏置和姿态.
传统的多位置解析对准方法一般要求SINS绕天向轴旋转90°或180°,这就需要将SINS安装在一个伺服平台上,以实现90°或180°的转动,这对工程带来不便,且伺服平台的精度会影响多位置解析对准的精度.本文对多位置解析对准所需最小条件进行了讨论,指出理论上任意两位置即可解算出IMU的偏置,给出了解析计算方法,通过仿真实例加以说明和验证,它可以作为一种简易初始对准或现场标定方法;另外通过解析方法指出在特殊姿态下,某单一轴向的加速度计常值偏置或陀螺常值漂移可以直接被较好地估计出来,这为改进多位置初始对准方法提供理论支持.
1 任意两位置解析对准1.1 理论分析IMU是捷联惯导系统的主要组成部分.它由互相重合的三轴陀螺和三轴加速度计组成,记三轴陀螺的输出为w=[wx,wy,wz]T,三轴加速度计的输出为f=[fx,fy,fz]T.若基座完全静止,IMU受且仅受地球自转和重力作用.地球自转角速度大小为wie,重力加速度值为g,IMU所在地球纬度为L.设三轴陀螺的输出误差∇w=[∇wx,∇wy,∇wz]T,三轴加速度计的输出误差为∇f=[∇fx,∇fy,∇fz]T.将当地东北天地理坐标系作为导航坐标系(简记为n系),IMU载体坐标系简记为b系,n系到b系的坐标变换矩阵记为Cnb,则有下式成立[6, 13]:
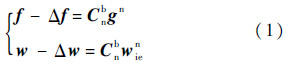
式中：gn=[0,0,g]T；wien=[0,wiecos L,wiesin L]T,由式(1)可得
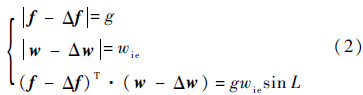
式中：|·|为取模运算符.对于多位置对准,由于对准过程在短时间内完成,可认为IMU的偏置在这段时间内保持不变.偏置误差是IMU误差的主要组成部分,这里只考虑IMU的常值偏置误差.记三轴陀螺的常值漂移为ε=[εx,εy,εz],三轴加速度计的常值偏置为∇=[∇x,∇y,∇z]T,IMU通过旋转得到任意两位置进行多位置初始对准,在第1个位置处的IMU输出为w1和f1,在第2个位置处的IMU输出为w2和f2.通过以上分析,有
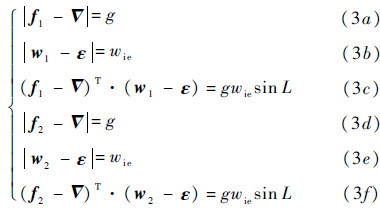
式中:有∇x、∇y、∇z、εx、εy、εz共6个未知数.除了上述方程组所表达的已知信息外,还有一个先验信息,即IMU偏置只会在一个较小的数值范围,这对求解过程有帮助.式(3)的解析解难以求得,这里介绍一种几何方法.
由式(3a)得到的∇的解的集合构成一个球面,由式(3d)得到的∇的解的集合也构成一个球面,两个球面相交构成圆周,从而由(3a)和式(3d)得到的∇的解的集合在这个相交而成的圆周上.该圆周可准确求得,引入转角变量α,其范围为0≤α < 2π,∇可由α唯一确定.同理,由式(3b)和式(3e)得到的ε的解的集合在对应的相交圆周上,引入转角变量β,其范围为0≤β < 2π,ε可由β唯一确定.
由式(3a)和式(3d),两球面相交成圆周,图 1为两球面的横截面图,记所在坐标系的坐标原点为O,图 1中,A=(fx1,fy1,fz1),A点为球A球心,B=(fx2,fy2,fz2),B点为球B球心,
=g,两球面相交所构成的圆周的圆心为C,半径为
,易得
,CD=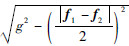
,记相交圆周半径为Rf. |
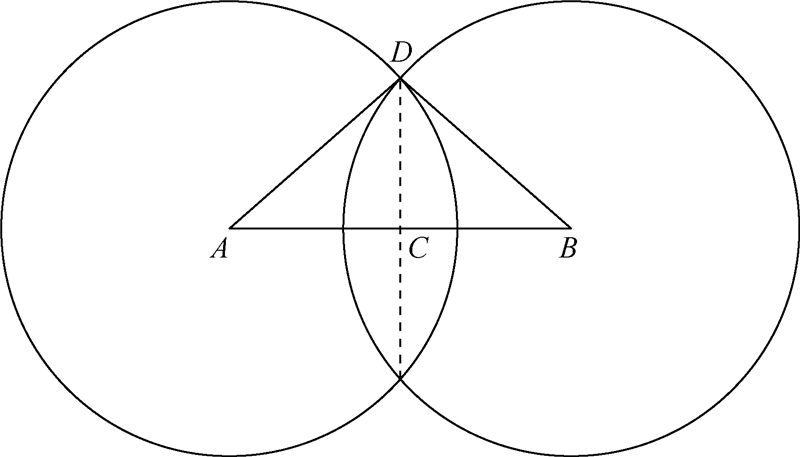| 图 1 两球面相交成圆周的截面图Fig. 1 Cross-section of a circumference formed by two intersected spherical surfaces |
| 图选项 |
同理可得式(3b)和式(3e)对应球面相交构成圆周的圆心为
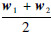,半径Rw为
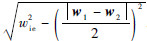.已知圆周,那么给定圆周上某点绕其圆心相对初始位置的旋转角度就可以确定该点坐标.点(Rf cos α,Rf sin α,0),0≤α< 2π的集合构成一个圆周,记为圆周K.图 1所示的相交圆周可以看成是圆周K通过翻转和平移得到.
如图 2所示,
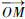是垂直于圆周K的其中一个单位向量[0,0,1]T,
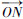是垂直于图 1所示相交圆周的一个单位向量,满足
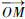,旋转到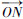可以看成是坐标系Oxyz通过旋转常规姿态角而得到,即先绕z轴转动航向角ψ,再绕x轴转动俯仰角θ,如图 2所示,得到的姿态变换矩阵为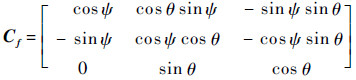
这里ψ和θ易根据向量
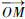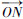和求得. |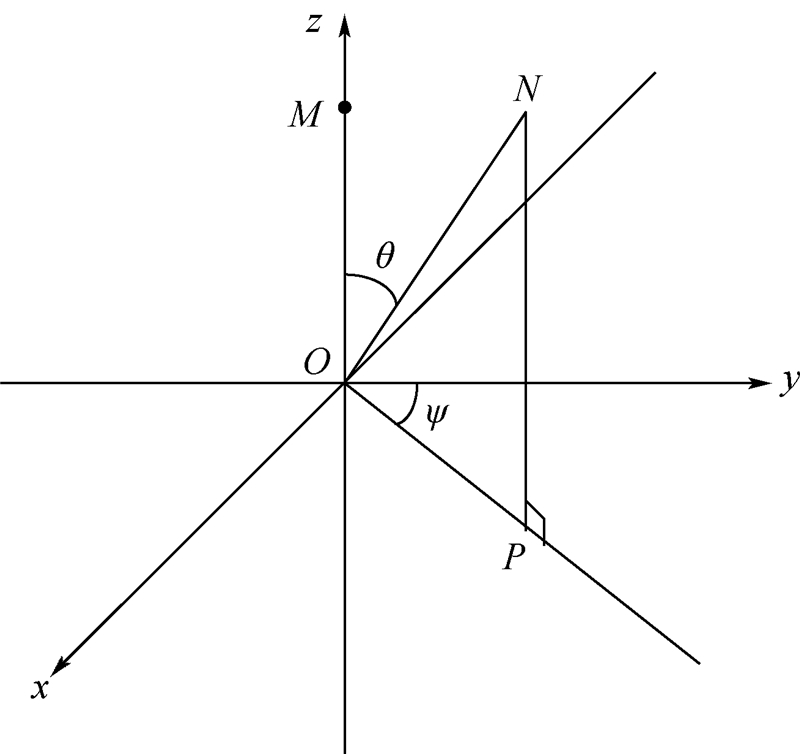
| 图 2 圆周的平移和翻转Fig. 2 Translational and rotational motion of circumference |
| 图选项 |
图 1所示相交圆周上的点的坐标可以用向量表示为Cf[Rf cosα,Rfsin α,0]T+
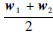,即由式(3a)和式(3d)可得三轴加速度计常值偏置∇满足: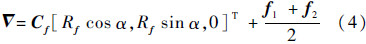
同理,式(3b)和式(3e)对应球面相交构成圆周上的点的坐标可以用向量表示为Cw[Rwcos β,Rwsin β,0]T+
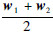,这里Cw为对应的姿态变换矩阵.即由式(3b)和式(3e)可得三轴陀螺常值漂移ε满足:
通过取不同的α和β值,可以得到相应的∇和ε,它们即是各自相交圆周上的点,将之代入式(3c)和式(3f),等号成立即为正解.这里难以得到解析解,采用数值计算方法求解,通过搜索J1和J2趋于零时得到对应的α和β值,从而根据式(4)和式(5)计算出∇和ε.
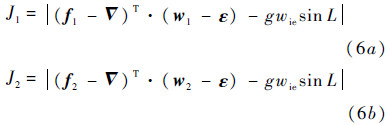
求得加速度计常值偏置和陀螺常值漂移,可以根据静基座解析粗对准方法[13, 14]获得载体姿态,惯性传感器偏置误差得到补偿后求得的姿态精度将会得到提高.
1.2 实例仿真这里举一仿真实例描述和验证上述任意两位置初始对准过程,相关仿真参数设计如下:
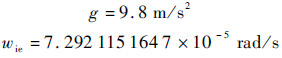
式中：σ∇i和σεi(i=x,y,z)分别为加速度计和陀螺测量白噪声；γn、θn和ψn(n=1,2)分别为第n个位置处的横滚角、俯仰角和航向角.
在第一个位置处采集1 min数据取平均,在第二个位置处采集1 min数据取平均,分别模拟出两个位置处的IMU平均输出数据如下:
则可由式(4)和式(5)计算出加速度计常值偏置和陀螺常值漂移的可能理论取值,结果如图 3、图 4所示.
 |
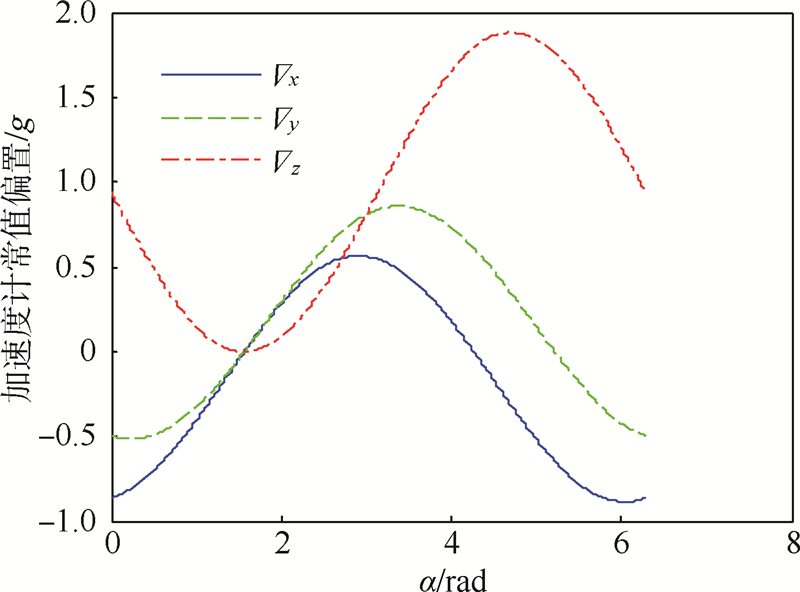| 图 3 三轴加速度计常值偏置取值范围Fig. 3 Value range of constant biases of three-axis accelerometers |
| 图选项 |
 |
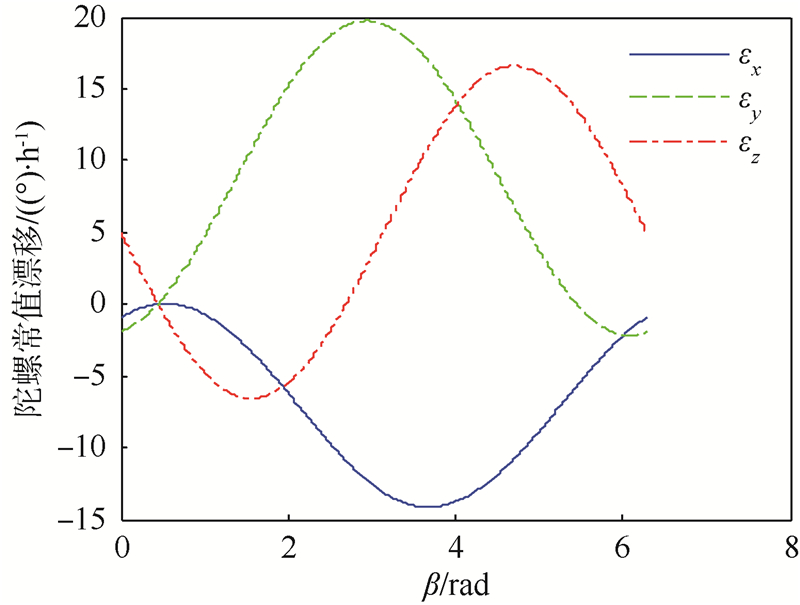| 图 4 三轴陀螺常值漂移取值范围Fig. 4 Value range of constant drifts of the three-axis gyroscopes |
| 图选项 |
惯性级陀螺仪的随机漂移率为0.015(°)/h(相当于地球自转角速率的0.1%),惯性级加速度计的随机零位偏值应优于10-4g.显然偏置为小值,不可能达到图 3和图 4中出现的那么大的值,根据所使用的IMU的性能级别,可知待测IMU的偏置范围.若使用的是1‰级别的IMU,可设定∇i < 10-2g,εi < 0.1(°)/h(i=x,y,z).根据该先验知识,得到对应的α和β取值范围,可以大大减小搜索范围.根据不同的α和β取值,可以分别解算出式(6a)和式(6b)所示J1和J2的值,计算结果如图 5、图 6所示.
 |
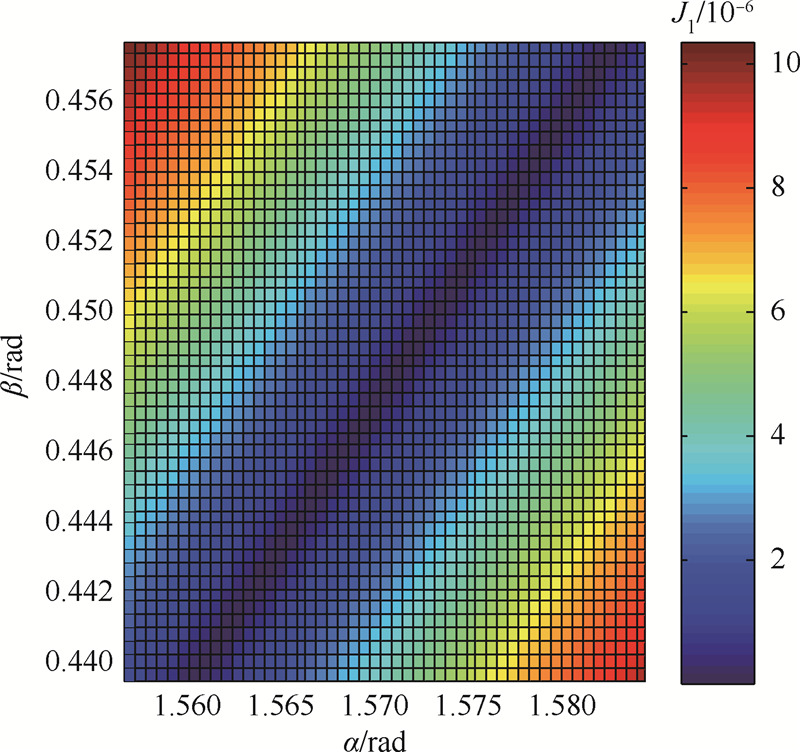| 图 5 取不同α和β的值时对应的J1值Fig. 5 J1 value given different values of α and β |
| 图选项 |
 |
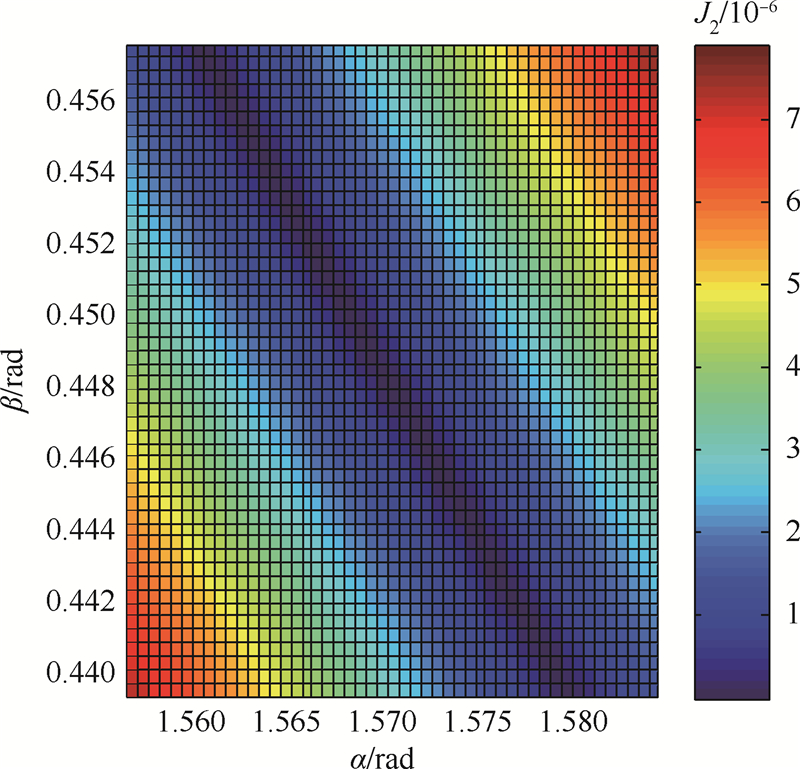| 图 6 取不同α和β的值时对应的J2值Fig. 6 J2 value given different values of α and β |
| 图选项 |
J1和J2都趋于零的点在图 5和图 6所示的中间区域,进一步缩小搜索范围并减小搜索步长进行二次搜索,直到搜索得到满足所需求解精度的唯一解,计算出的加速度计常值偏置和陀螺常值漂移和题设一致.
2 特殊姿态下的偏置估计大部分情况下的初始对准过程中,IMU处于水平或近似水平状态,近似水平位置处,fx,fy趋于零,fz趋于重力值g,有下述推导过程成立:
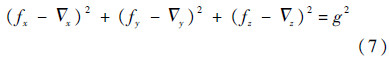
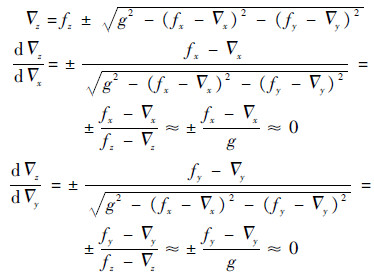
即∇z受∇x及∇y影响极小,根据先验知识,设各轴的偏置在[-2×10-4g,2×10-4g]范围内.在取值范围内分别取∇x及∇y不同的偏置值,根据式(7)解算出对应的∇z,可得图 7所示结果.
 |
| 图 7 Δz随∇x及∇y的变化对应的取值范围Fig. 7 Value range of ∇z changing with different values of Δx and ∇y |
| 图选项 |
由图 7可知,当∇x及∇y在[-2×10-4g,2×10-4g]范围内变化时,∇z的变化范围约为[1.94×10-4g,2.06×10-4g],可见,∇z的变化范围很小.这样可估计出∇z,估计误差约为6×10-6g,这和静基座卡尔曼初始精对准过程时天向加速度计偏置可以被很好估计的效果一致[15].同样原理,当IMU某轴向和地球自转轴向接近时,该轴向的陀螺常值漂移可以被很好估计,基于此原理,根据IMU输出反馈可将IMU相应轴置于接近天向或地球自转轴向的位置,以便估计出相应轴向的加速度计常值偏置或陀螺常值漂移.
3 结论本文对最简多位置解析对准进行了研究,指出任意两位置理论上可以解析计算出IMU常值偏置,并通过仿真实例加以说明和验证,为后续研究多位置初始对准提供了理论依据;同时这也是一种简易的无需机械转动机构的多位置对准方法,它还可以作为测量IMU偏置的简便方法,测试过程不需要精密转台或分度头、对夹具和测试基准无特殊要求,适合于装机后的现场标定.另外,从解析方法的角度指出在水平位置下,天向加速度计常值偏置可以被很好估计,这和卡尔曼精对准过程天向的加速度计常值偏置观测度高的结论一致;同样原理,当IMU某轴向和地球自转轴向接近时,该轴向的陀螺常值漂移可以被很好估计,基于此原理,根据IMU输出反馈将IMU相应轴置于接近天向或地球自转轴向的位置,可较好地估计出相应轴向的加速度计常值偏置或陀螺常值漂移.
参考文献
| [1] | Paul G S.Blazing gyros:The evolution of strapdown inertial navigation technology for aircraft[J].Journal of Guidance, Control, and Dynamics, 2013, 36(3):637-655. |
| Click to display the text | |
| [2] | Liu X X, Xu X S, Wang L H, et al.A fast compass alignment method for SINS based on saved data and repeated navigation solution[J].Measurement, 2013, 46(10):3836-3846. |
| Click to display the text | |
| [3] | Titterton D, Weston J L.Strapdown inertial navigation technology[M].2nd ed.London:Institution of Engineering and Technology, 2004:277-308. |
| Click to display the text | |
| [4] | Cho S Y, Lee H K, Lee H K.Observability and estimation error analysis of the initial fine alignment filter for nonleveling strapdown inertial navigation system[J].Journal of Dynamic Systems, Measurement and Control, 2012, 135(2):44-45. |
| Click to display the text | |
| [5] | Wang X.Fast alignment and calibration algorithms for inertial navigation system[J].Aerospace Science and Technology, 2009, 13(4-5):204-209. |
| Click to display the text | |
| [6] | Wu Y X, Zhang H L, Wu M P, et al.Observability of strapdown INS alignment:A global perspective[J].IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1):78-102. |
| Click to display the text | |
| [7] | Xiong J, Guo H, Yang Z H.A two-position SINS initial alignment method based on gyro information[J].Advances in Space Research, 2014, 53(11):1657-1663. |
| Click to display the text | |
| [8] | 王巍.光纤陀螺惯性系统[M].北京:中国宇航出版社, 2013:449-464.Wang W.Inertial navigation system of the fiber optic gyroscope[M].Beijing:China Astronautic Publishing House, 2013:449-464(in Chinese). |
| Cited By in Cnki | |
| [9] | 邓志红, 付梦印, 张继伟, 等.惯性器件与惯性导航系统[M].北京:科学出版社, 2012:261-265.Deng Z H, Fu M Y, Zhang J W, et al.Inertial device and inertial navigation system[M].Beijing:Science Press, 2012:261-265(in Chinese). |
| Cited By in Cnki | |
| [10] | Lee J G, Park C G, Park H W.Multiposition alignment of strapdown inertial navigation system[J].IEEE Transactions on Aerospace and Electronic Systems, 1993, 29(4):1323-1328. |
| Click to display the text | |
| [11] | Chung D, Lee J G, Park C G, et al.Strapdown INS error model for multiposition alignment[J].IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(4):1362-1366. |
| Click to display the text | |
| [12] | 赵长山, 秦永元, 周琪.参数辨识双位置对准改进算法[J].中国惯性技术学报, 2009, 17(6):631-635.Zhao C S, Qin Y Y, Zhou Q.Modified two-position parameter identification alignment method[J].Journal of Chinese Inertial Technology, 2009, 17(6):631-635(in Chinese). |
| Cited By in Cnki (2) | |
| [13] | 秦永元.惯性导航[M].北京:科学出版社, 2006:361-363.Qin Y Y.Inertial navigation[M].Beijing:Science Press, 2006:361-363(in Chinese). |
| Click to display the text | |
| [14] | Zhao H, Shang H, Wang Z, et al.Comparison of initial alignment methods for SINS[C]//World Congress on Intelligent Control and Automation (WCICA).Piscataway, NJ:IEEE Press, 2011:42-47. |
| Click to display the text | |
| [15] | Song L, Zhang C, Lu J.Self-alignment of full skewed RSINS:Observability analysis and full-observable Kalman filter[J].Journal of Systems Engineering and Electronics, 2014, 25(1):104-114. |
| Click to display the text |
