相比于普通的异步电机,对于无轴承异步电机的控制更加困难,其定子上多加的一套径向力悬浮绕组更是加强了其多变量、非线性和强耦合性特征,并且电磁转矩和径向悬浮力之间还存在耦合.因此,如何实现其解耦控制,获得较优良的控制性能是急需解决的问题,当前比较流行、性能稳定可靠的方法是采用磁场定向控制[9, 10, 11].而在此方法中,转子位置信息的反馈是不可避免的,传统的方法是采用机械式位置传感器来获取反馈的位置信号.然而,这一类传感器的存在,不仅增加了系统成本,而且使无轴承异步电机轴向尺寸变大,同时在无轴承异步电机控制系统中必须增加相应的位移信号检测、差分和滤波电路,给系统带来了安装、连线复杂以及由此产生的可靠性问题等.因而,阻碍了无轴承异步电机系统应用的低成本和实用化.故研究转子位置参数的在线自辨识,将无位置传感器运行理论引入到无轴承异步电机控制系统,具有重要的理论意义与应用价值.
当前国内外****对无轴承电机无位置传感器的研究主要采用高频注入法[12, 13],但此类方法都需要设计高频激励源,不利于降低控制系统成本,因此有必要探寻一种既能满足电机无位置传感器运行需求,又能节约系统成本的控制策略.为此,本文研究了无轴承异步电机磁链变化与转子径向位置之间的关系,首先获取径向悬浮力绕组的磁链,再根据建立的磁链-位移方程,设计了无轴承异步电机转子径向位置估计器,以此来实现电机转子位置的自检测.此方法的关键在于对径向悬浮力绕组磁链的准确辨识,根据现有的磁链辨识方法,可归纳为3大类: U - I 法、 I - ω 法和 U - ω 法,其中: U 为电压; I 为电流; ω 为电机角速度. U - I 法根据绕组反电动势求解磁链值,具有算法简单、抗扰动性能强等优点,但基于此类磁链辨识方法因为有纯积分运算环节的存在,初始化误差问题难以得到解决; I - ω 法相比于 U - I 法,提高了磁场辨识精确度,但在算法中引入了转子参数,使得此类算法的抗扰动性能降低;将 U - I 法和 I - ω 法结合在一起便构成了 U - ω 法,此类算法同时兼有抗扰动性能强和精确度高等优点,但算法复杂,对硬件设计要求较高,因此适用性能较差[14].
本文以无轴承异步电机为研究对象,为解决反电动势法(Back Electromotive Force,BEMF)在转子位置辨识中由于纯积分环节带来的初始化偏差问题,提出一种基于改进反电动势法的无转子径向位置传感器矢量控制策略,以此来提高无轴承异步电机转子径向位置辨识的准确性与精确度.MATLAB/Simulink工具箱中的仿真结果表明:此种无径向位移传感器控制策略能够有效跟踪转子位置,且电机同时具有优良转速和转矩响应.进一步的实验结果同样表明:所提控制方法的转子自检测位置与转子实测位置偏差极小,最大不超过10μm,实现了电机无径向位置传感器方式下的稳定悬浮运行.验证了本文所提基于改进反电动势法的无轴承异步电机无径向位置传感器控制策略的正确性与有效性.
1 电机径向位置自检测基本原理 1.1 无轴承异步电机结构及运行机理在普通异步电机的定子绕组中再嵌入一套径向悬浮力绕组,便构成了无轴承异步电机.通过定子中两套不同极对数绕组磁场的相互作用,破坏传统电机气隙磁场的对称性,产生电磁转矩和径向力,能同时实现转子悬浮和旋转功能[15, 16, 17]. 为了清楚地说明无轴承异步电机的结构和运行机理,给出了如图 1所示的3D模型结构图.两套三相绕组共同叠绕在一个定子槽内,外圈为转矩绕组,其极对数和电角频率分别为p1和 ω 1;内圈为径向悬浮力绕组,其极对数和电角频率分别为p2和 ω 2.
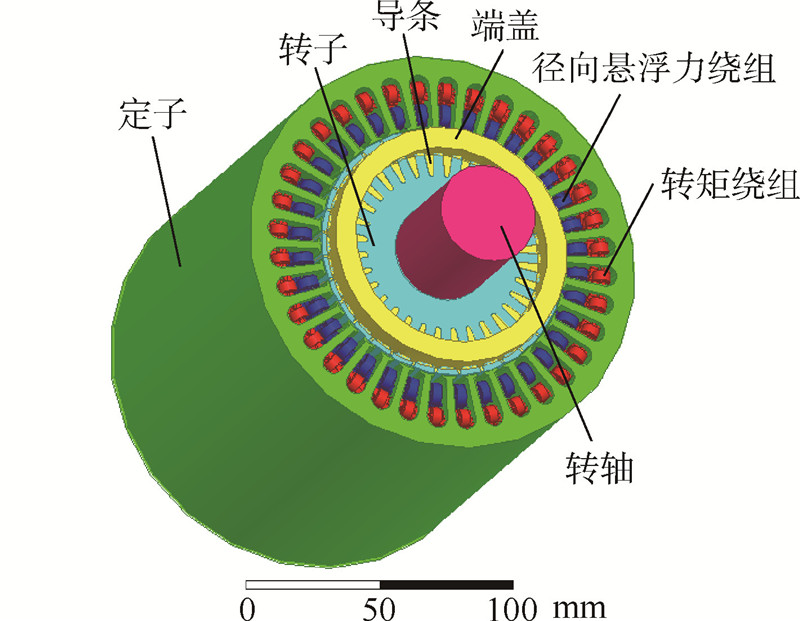 |
| 图 1 BIM的3D模型Fig. 1 3D model for a BIM |
| 图选项 |
如果电机中两套绕组的关系满足:极对数p1=p2±1,电角频率 ω1=ω 2,便可产生可控的径向悬浮力.图 2所示为径向悬浮力产生原理图,其中p1=1,p2=2.当单独在转矩绕组通入电流 I 1时,则产生对称分布的两极磁链 Ψ 2;同样,当单独在悬浮力绕组中通入电流 I 2时则产生对称分布的四极磁链 Ψ 4.但是,当同时通入如图 2所示方向的电流 I 1和 I 2时,产生的两磁场叠加后,由于气隙上侧 Ψ 2和 Ψ 4同向,造成此处气隙磁密增加;而气隙下侧 Ψ 2和 Ψ 4反向,造成此处气隙磁密减少,不平衡的气隙磁密便产生了沿y轴正方向的径向悬浮力 F y. 如若要产生沿y轴负方向的径向悬浮力,则只需要在悬浮力绕组中通入与 I 2反方向的电流.同理,若要获得沿x轴方向的径向悬 浮力,则只需在悬浮力绕组中通入与 I 2垂直的电流.无轴承异步电机电磁转矩产生机理同普通异步电机一样,都是来源于洛仑兹力.
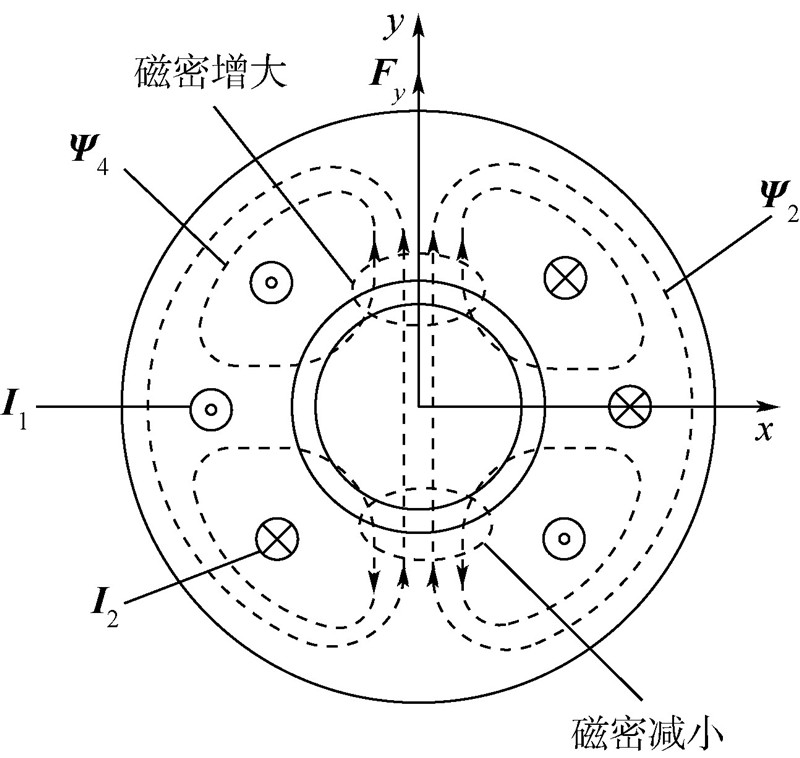 |
| 图 2 径向悬浮力产生机理图Fig. 2 Principle diagram of radial suspension forcegeneration for BIM |
| 图选项 |
1.2 基于改进反电动势法的径向悬浮力绕组磁链观测在两相静止坐标系下,无轴承异步电机径向悬浮力绕组的磁链观测模型可表示为
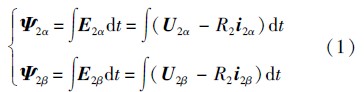
将式(1)进行拉普拉斯变换可得
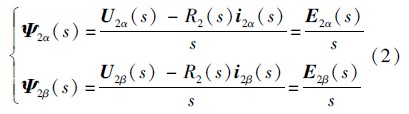
式中:s为拉普拉斯算子; E 2α、 E 2β,U 2α、 U 2β,i 2α、 i 2β 分别为径向悬浮力绕组反电动势、电压及电流在α、β轴上的分量;R2为径向悬浮力绕组等效电阻.
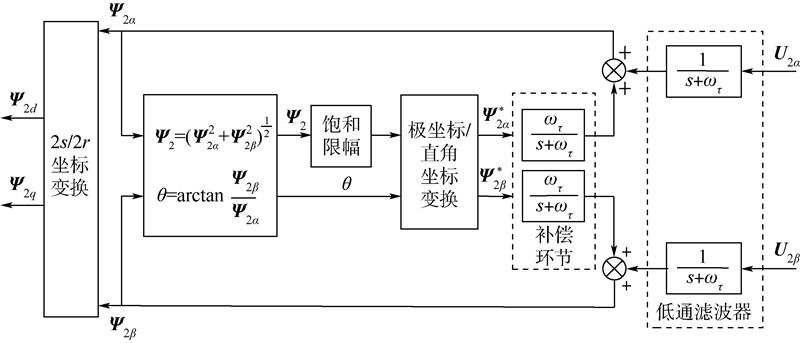
由分析可知,径向悬浮力绕组磁链观测模型为纯积分运算,如若被积分变量的初始相位值并非±π/2时,就会给计算带来初始化误差,为此,引入一个截止频率为 ωτ的低通滤波器作为输入信号代替纯积分环节以消除偏差,ωτ 取为k倍的电机同步旋转频率,本文中k取0.2.但是,低通滤波器的加入会引起相位滞后与幅值偏差,为此,还需添加径向悬浮力绕组磁链的参考值 Ψ *2α、 Ψ *2β 进行幅值和相位补偿.由此便可获得改进后的径向悬浮力绕组观测模型,如图 3所示,而精确的径向悬浮力绕组磁链表达式为
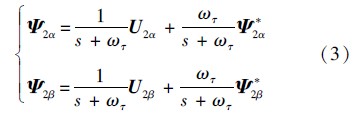
 |
| 图 3 改进反电动势法模型Fig. 3 Model of the improved BEMF method |
| 图选项 |
整个模型的工作过程如下:首先由径向悬浮力绕组磁链 Ψ 2α、 Ψ 2β获得磁链的幅值 Ψ 2与角度θ;然后对 Ψ 2进行饱和限幅后进入极/直坐标变换,并且将磁链限幅值设定为参考值,此时便得到磁链参考值 Ψ *2α、 Ψ *2β. 将输出的 Ψ 2α、 Ψ 2β 经两相静止坐标到两相旋转坐标的坐标变换后得到d-q旋转坐标下的径向悬浮力绕组磁链 Ψ 2d、 Ψ 2q.
1.3 径向位置自检测模型根据文献[18],无轴承异步电机绕组的电感矩阵可表示为
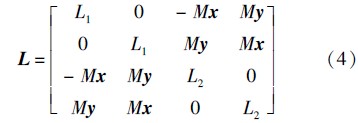
将式(4)代入无轴承异步电机磁链方程可得
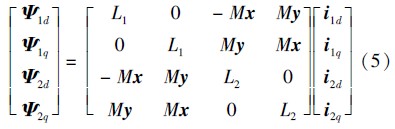
式中: Ψ 1d、 Ψ 1q和 i 1d、 i 1q 分别为转矩绕组磁链及电流在d、q轴上的分量; Ψ 2d、 Ψ 2q和 i 2d、 i 2q 分别为径向悬浮力绕组磁链和电流在d、q轴上的分量; x 和 y 为转子的径向位置偏移;L1、L2和M分别为转矩绕组和径向悬浮力绕组的自感及它们之间的互感系数.
当转子未偏心时,则 x = y = 0 ,由式(5)得
式中: Ψ 2d0和 Ψ 2q0 分别为转子未偏心时的径向悬浮力绕组磁链在d和q轴上的分量.
相同情况下,当转子有偏心位移时,由式(5)得到的径向悬浮力绕组磁链表示为
定义由转子偏心引起的径向悬浮力绕组磁链偏差为Δ Ψ 2d和Δ Ψ 2q,则
根据式(6)~式(8)可求得
此时可得转子位置自检测框图如图 4所示.
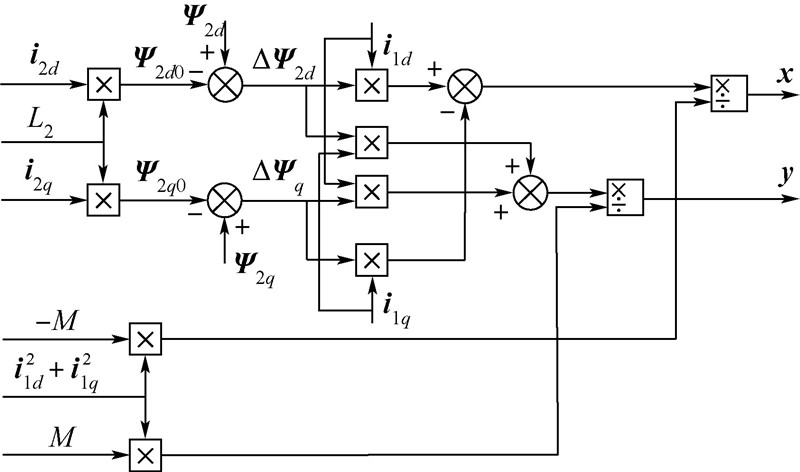 |
| 图 4 径向位置自检测模型Fig. 4 Self-detecting model of radial position |
| 图选项 |
2 控制系统的仿真与实验分析 2.1 控制系统的组成本文采用基于转矩绕组气隙磁场定向的矢量控制技术,来实现对无轴承异步电机的控制.此时有

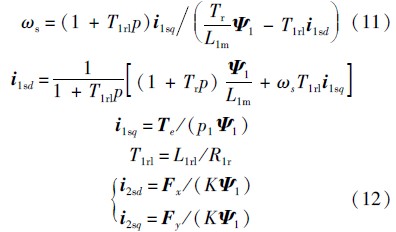
式中: ω s为转差角频率,ω s= ω 1- ω r,ω r为转子角频率,ω 1为电机同步角频率;Tr=L1r/R1r为转子时间常数,R1r和L1rl分别为转矩绕组转子电阻与漏感; i 1sd和 i 1sq 分别为转矩绕组定子电流在d、q轴上的分量;L1r和L1m分别为转矩绕组转子自感和转矩绕组互感;p为微分算子;K=πp1p2L2m/(12lrμ0W1W2),L2m为径向悬浮力绕组互感,l、r和μ0分别为转子的有效长度、转子外径、真空磁导率,W1和W2分别为转矩绕组和悬浮绕组的有效匝数; T e 为转矩.
如图 5所示整个电机控制系统中主要包含了悬浮和旋转两个部分.其中,悬浮部分,输入的电压、电流经过坐标变换得到 i 1d、 i 1q、 i 2d、 i 2q、 U 2d、 U 2q分量,将 U 2d、 U 2q和截止角频率 ωτ 代入式(3)后得到转子磁链 Ψ 2d和 Ψ 2q,而 i 2d、 i 2q经过式(6)的变换后将得 到 Ψ 2d0和 Ψ 2q0,然后 Ψ 2d、 Ψ 2q、 Ψ 2d0、 Ψ 2q0经过式(8)的减法运算后获得了Δ Ψ 2d和Δ Ψ 2q,最后 i 1d、 i 1q、Δ Ψ 2d和Δ Ψ 2q 经过位移公式(9)辨识出径向位移 x 和 y ;转矩部分,将给定气隙磁链 Ψ *1和转矩 T *e 经过气隙磁场定向控制、坐标变换、电流反馈型脉宽调制(Current Regulated Pulse Width Modulation,CRPWM)逆变后最终得到转矩绕组三相电流.
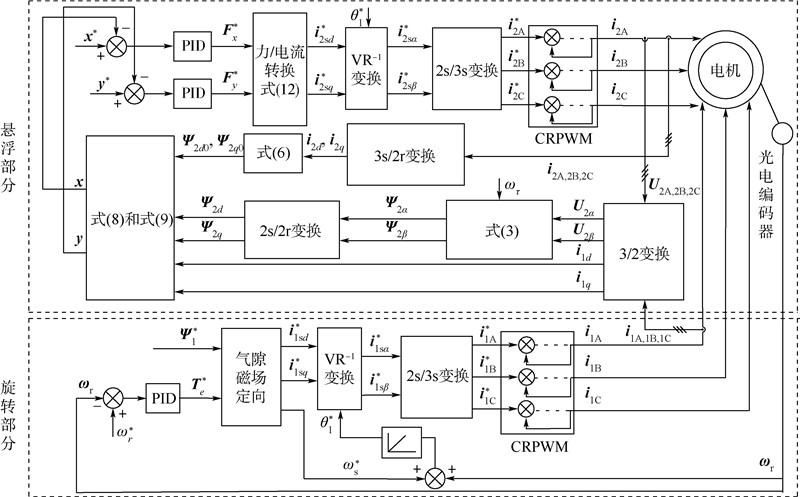 |
| ω *s—给定转差角速度; ω *r—给定转子角速度; θ *1—给定转子位置角; x *,y *—给定径向位置偏移值; F *x,F *y —给定径向悬浮力; i 1A,1B,1C—转矩绕组三相电流值,i 1A,i 1B,i 1C的简写; i *1A,i *1B,i *1C—给定转矩绕组三相电流值; i *1sα,i *1sβ —转矩绕组定子电流在α,β轴上的分量; i *2sα,i *2sβ —给定转矩绕组定子电流在α,β轴上的分量; i *1sd,i *1sq —给定转矩绕组定子电流在d,q轴上的分量; i *2A,i *2B,i *2C—给定径向悬浮力绕组三相电流值; i 2A,2B,2C—径向悬浮力绕组三相电流值; U 2A,2B,2C—径向悬浮力绕组三相电压值; U 2α,U 2β —径向悬浮力绕组电压在α,β轴上的分量; Ψ 2α,Ψ 2β —径向悬浮力绕组磁链在α,β轴上的分量.图 5 无径向位移传感器控制系统框图Fig. 5 Block diagram of radial displacement-sensorless control system |
| 图选项 |
2.2 系统仿真结果及分析为验证利用所提方法构造的无轴承异步电机无位置传感器控制策略的准确性与可行性,基于图 5控制系统结构,在MATLAB/Simulink工具箱中对搭建了整个控制系统的仿真模型.电机参数设置如下:转子外径r=97.6mm,转子质量m=2.85kg,铁芯长度l=105mm,转动惯量J=7.69g·m2;悬浮绕组:极对数p2=2,额定功率Q2=500W,额定电流 I 2=2.86A,转子漏感L2rl=5.42mH,转子电阻R2r=0.075Ω,定、转子互感L2m=9.32mH,定子漏感L2sl=2.67mH;转矩绕组:极对数p1=1,额定功率Q1=1kW,额定电流 I 1=2.86A,转子电阻Rlr=11.48Ω,转子漏感Llrl=9.22mH,转子互感Llm=158.56mH,定子漏感Llsl=4.54mH.给定气隙磁链 Ψ *1=0.6Wb,给定转速为6000r/min.
图 6所示为在空载情况下,无轴承异步电机给定转速为6000r/min时转子径向位移自检测情况下的仿真波形图.图 6(a)为转子的转速响应与局部放大效果图,可以看出,电机在0.38s内就达到了给定转速,响应较快,转速超调量极小,最终转速稳定在6000r/min左右.图 6(b)为转矩响应,起动转矩较大,响应较快,稳定误差很小.为了清晰地观察转子径向位置偏移情况,图 6(c)和图 6(d)给出了在t=0~0.5s时间内电机径向位移自检测系统所检测出的转子位置与实际转子位置的对比波形图.比较可得,自检测系统能够较好地跟踪转子的实际径向位置偏移,最大误差不超过10μm,0.38s之后自检测径向位置基本和实际转子径向位置重合.仿真结果表明无轴承异步电机实现了稳定悬浮,同时也证明了该无径向位移传感器自检测策略的有效性.
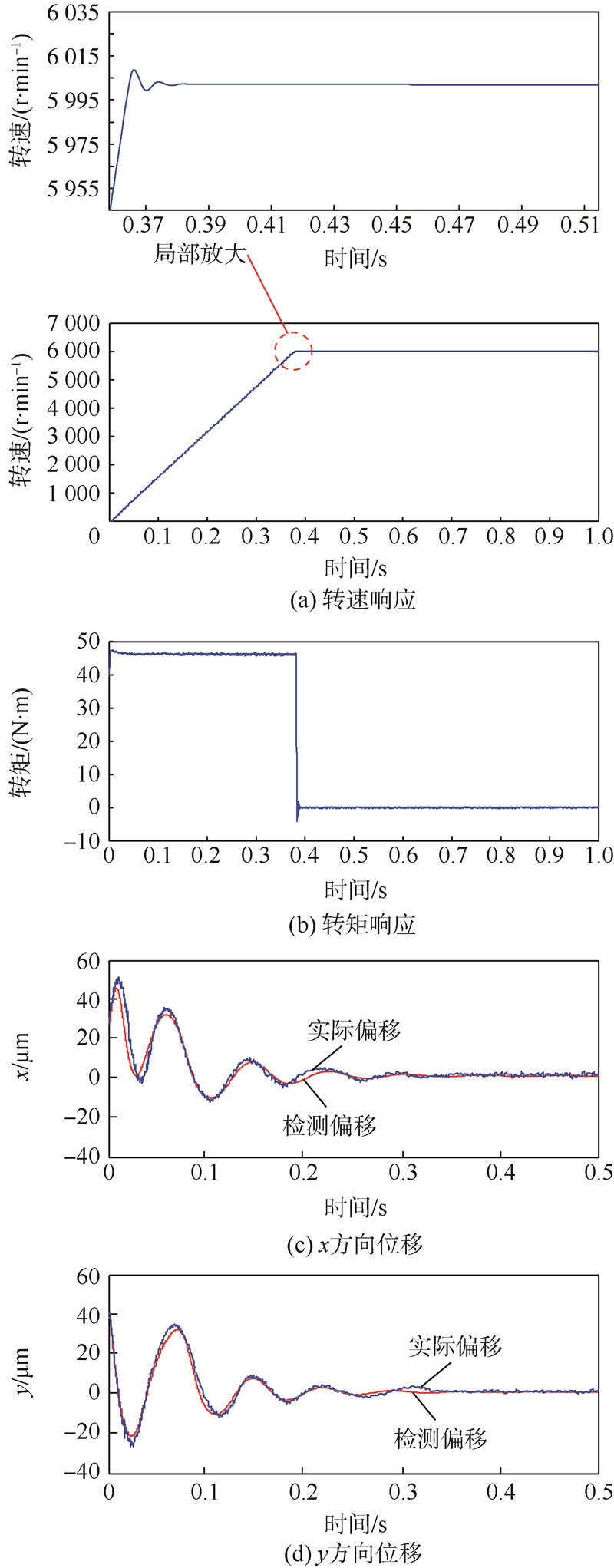 |
| 图 6 控制系统仿真结果Fig. 6 Simulation results for control system |
| 图选项 |
2.3 实验及结果分析为进一步验证基于改进反电动势法的无径向位置控制策略的有效性,利用如图 7所示的一台无轴承异步电机样机构建了整个控制系统的实验平台.实验中的控制芯片采用TMS320F2812,样机参数与仿真参数一致,转速设置为2000r/min.为更准确对比自检测径向位置与实际径向位置的误差,在样机上配备了电涡流位移传感器.无轴承异步电机无径向位置传感器控制系统实验框图如图 8所示.位移实验结果如图 9所示.
 |
| 图 7 实验样机实物图Fig. 7 Prototype physical diagram |
| 图选项 |
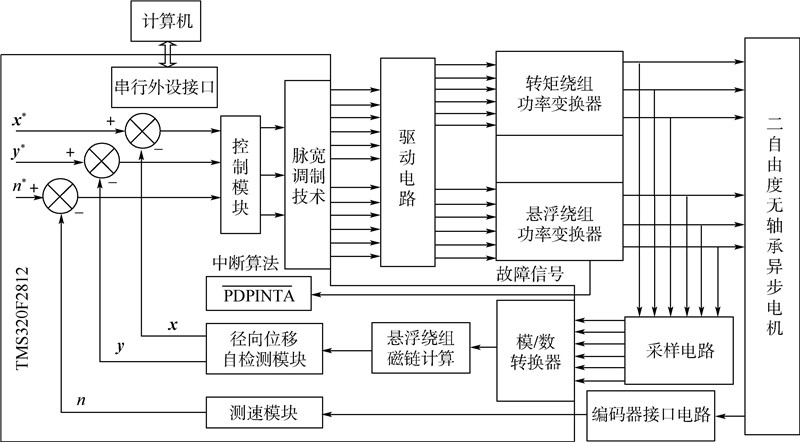 |
| x ,y —x轴和y轴方向上自检测识别的转子径向位移; x *,y *—x轴和y轴方向给定的转子径向位移;n—定测转速;n* —电机给定转速. 图 8 控制系统实验框图Fig. 8 Experimental block diagram of control system |
| 图选项 |
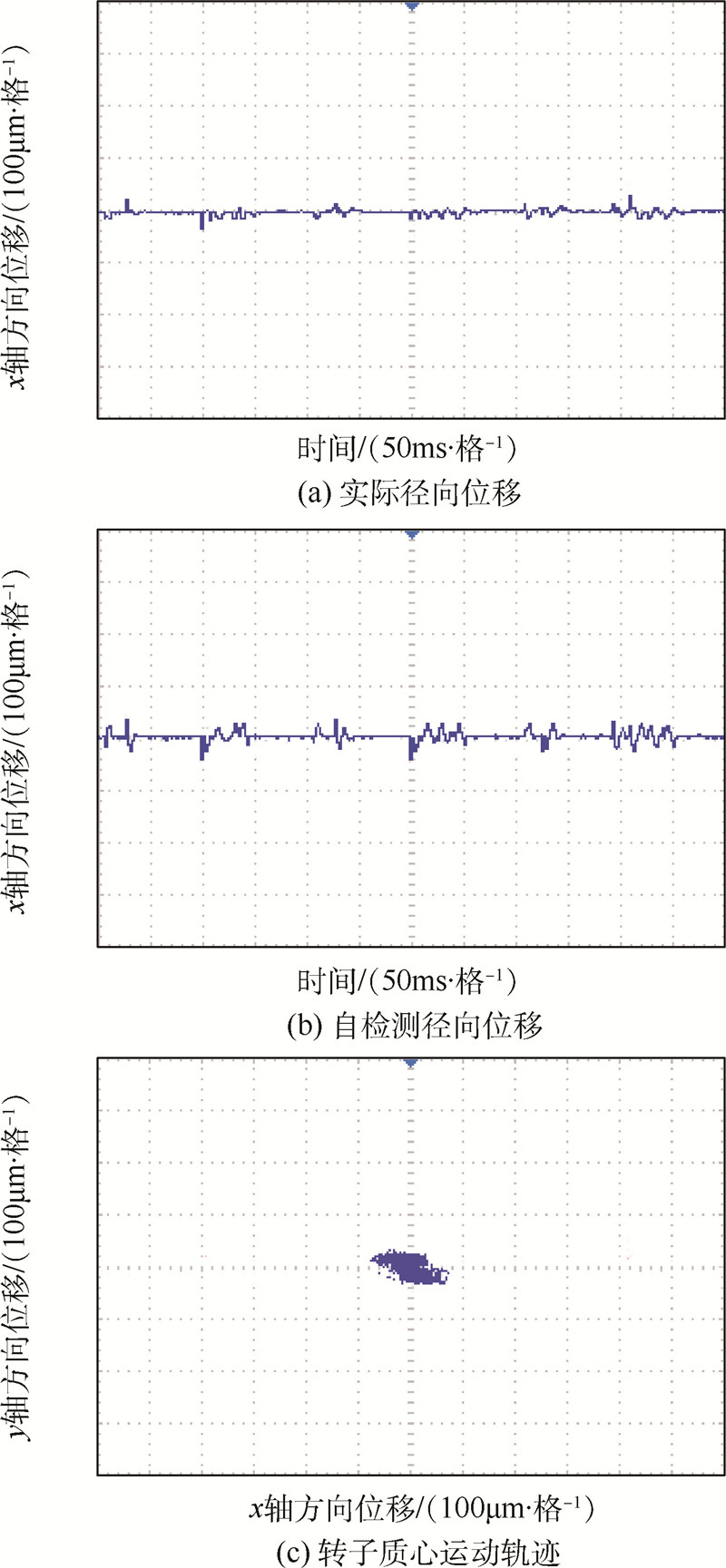 |
| 图 9 位移实验结果Fig. 9 Experimental results of displacements |
| 图选项 |
图 9(a)是电涡流位移传感器存在时,电机转子实际径向位置在x轴方向上的波形图,图 9(b)为电涡流位移传感器不存在时,采用所提方法得到的x轴方向上转子径向位置波形图.对比图 9(a)和(b)可以发现,所设计的无位置传感器控制系统能够有效跟踪转子位置,只是电机在无位置传感器状态运行时,转子径向位置的峰-峰值略大,但两种状态下的转子位置误差小于10μm,同仿真结果一致,验证了基于改进反电动势法的无轴承异步无位置传感器控制方法的正确性与有效性.
图 9(c)为转速为2000r/min时,无径向位置传感器状态下,转子质心运动轨迹波形图.如图 9(c)所示,电机转子质心在x轴方向的径向位移最大偏移值为80μm,在y轴方向的最大偏移值为50μm,都远小于电机的气隙值0.4mm,从而证明了使用所提控制检测方法能够实现无轴承异步电机无位置传感器方式下的稳定悬浮运行.
3 结 论为消除机械式位置传感器带来的不利影响,提高无轴承异步电机结构紧凑性,促进无轴承异步电机向低成本和实用化方向发展,采用一种改进反电动势法的无径向位置传感器矢量控制.通过仿真和实验结果可以得出:
1) 基于此种改进反电动势法的位移自检测方法构造的矢量控制系统,不仅能实现悬浮力绕组磁链的准确辨识,有效观测转子径向位移,还具有优良的转速和转矩特性.
2) 利用改进反电动势法的转子位置跟踪方法,具有良好的位置在线自检测能力,转子位置辨识响应快,能实现低成本的无轴承异步电机无位置传感器方式下的稳定悬浮运行.
参考文献
| [1] | de Almeida A T, Ferreira F J T E,Quintino D A.Technical and economical considerations on super high-efficiency three-phase motors[J].IEEE Transactions on Industry Applications,2014,50(2):1274-1285. |
| Click to display the text | |
| [2] | 代颖,张千帆, 宋立伟,等.抑制车用异步电机电磁噪声的槽配合[J].中国电机工程学报,2010,30(27):32-35. Dai Y,Zhang Q F,Song L W,et al.Slot combination for electromagnetic noise suppression of EV driving induction motor modeling and control of induction machines with pole-phase modulation[J].Proceedings of the CSEE,2010,30(27):32-35(in Chinese). |
| Cited By in Cnki (13) | |
| [3] | 裴文卉,符晓玲, 张承慧.电动汽车用感应电机动态平衡点的反馈耗散Hamilton控制[J].控制理论与应用,2013,30(9):1138-1144. Pei W H,Fu X L,Zhang C H.Feedback passive Hamilton control for dynamic equilibrium points of induction motors for electric vehicles[J].Control Theory & Applications,2013,30(9):1138-1144(in Chinese). |
| Cited By in Cnki (2) | |
| [4] | 杨泽斌,汪明涛, 孙晓东.基于自适应模糊神经网络的无轴承异步电机控制[J].农业工程学报2014,30(2):78-86. Yang Z B,Wang M T,Sun X D.Control system of bearingless induction motors based on ANFIS[J].Transactions of the Chinese Society of Agricultural Engineering,2014,30(2):78-86(in Chinese). |
| Cited By in Cnki (2) | |
| [5] | Schuhmann T, Hofmann W,Werner R.Improving operational performance of active magnetic bearings using Kalman filter and state feedback control[J].IEEE Transactions on Industrial Electronics,2012,59(2):821-829. |
| Click to display the text | |
| [6] | 赵旭升,邓智泉, 汪波.一种磁悬浮开关磁阻电机用轴向径向磁轴承[J].北京航空航天大学学报,2011,37(8):973-978. Zhao X S,Deng Z Q,Wang B.Axial radial magnetic bearing in magnetic suspending switched reluctance motor application[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(8):973-978(in Chinese). |
| Cited By in Cnki (8) | |
| [7] | Chiba A, Deido T,Fukao T,et al.An analysis of bearingless AC motors[J].IEEE Transactions on Energy Conversion,1994,9(1):61-68. |
| Click to display the text | |
| [8] | Sun X D, Chen L,Yang Z B,et al.Speed-sensorless vector control of a bearingless induction motor with artificial neural network inverse speed observer[J].IEEE/ASME Transactions on Magnetics,2013,18(4):1357-1366. |
| Click to display the text | |
| [9] | Suzuki T, Chiba A,Rahman A,et al.An air-gap-flux-oriented vector controller for stable operation of bearingless induction motors[J].IEEE Transactions on Industry Applications,2000,36(4):1069-1076. |
| Click to display the text | |
| [10] | 朱熀秋,沈玉祥, 张腾超,等.无轴承异步电机数学模型与解耦控制[J].电机与控制学报,2007,11(4):321-325. Zhu H Q,Shen Y X,Zhang T C,et al.Mathematics model and decoupling control for self-bearing induction motors[J].Electric Machines and Control,2007,11(4):321-325(in Chinese). |
| Cited By in Cnki (33) | |
| [11] | Hua W, Cheng M,Lu W,et al.A new stator-flux orientation strategy for flux-switching permanent magnet motor based on current-hysteresis control[J].Journal of Applied Physics,2009,105(7):07F112-07F112-3. |
| Click to display the text | |
| [12] | Tera T, Yamauchi Y,Chiba A,et al.Performances of bearingless and sensorless induction motor drive based on mutual inductances and rotor displacements estimation[J].IEEE Transactions on Industrial Electronics,2005,53(1):187-194. |
| Click to display the text | |
| [13] | 年珩,贺益康, 黄雷.内插式永磁无轴承电机转子位置/位移综合自检测[J].中国电机工程学报,2007,27(9):52-58. Nian H,He Y K,Huang L.Integrated self-sensing of rotor position and displacement for inset PM type bearingless motor[J].Proceedings of the CSEE,2007,27(9):52-58(in Chinese). |
| Cited By in Cnki (26) | |
| [14] | 蔡国洋,黄守道. 无轴承异步电机气隙磁场辨识方法与应用[J].电机与控制学报,2007,11(2):116-119. Cai G Y,Huang S D.The air-gap field identification methods and application of bearingless induction motors[J].Electric Machines and Control,2007,11(2):116-119(in Chinese). |
| Cited By in Cnki (11) | |
| [15] | Chiba A, Power D T,Rahman M A.Characteristics of a bearingless induction motor[J].IEEE Transactions on Magnetics,1991,27(6):5199-5201. |
| Click to display the text | |
| [16] | 卜文绍,万山明, 黄声华,等.无轴承电机的通用可控磁悬浮力解析模型[J].中国电机工程学报,2009,29(30):84-89. Bu W S,Wan S M,Huang S H,et al.General analytical model about controllable magnetic suspension force of bearingless motor[J].Proceedings of the CSEE,2009,29(30):84-89(in Chinese). |
| Cited By in Cnki (15) | |
| [17] | 汪明涛. 无轴承异步电机径向悬浮力研究及无传感技术实现[D].镇江:江苏大学,2014. Wang M T.Research on radial suspension force and sensorless technology for bearingless induction motors[D].Zhenjiang:Jiangsu University,2014(in Chinese). |
| Cited By in Cnki | |
| [18] | Chiba A,Power D T,Rahman M A.Analysis of no-load characteristics of a bearingless induction motor[J].IEEE Transactions on Industry Applications,1995,31(1):77-83. |
| Click to display the text |
