在传感器的动态校准方面,国际已取得了一定的成果.文献[2]提出了一种激波管校准条件下用于小量程压力传感器的模块化校准方法[2];该方法同时采取了数字温度补偿技术用以减小激波气体升温对校准结果的影响.文献[7]提出一种0-A-0动态激励加载方法,实现了对被校准压力传感器校准结果的重复测量[7].Haboussa等[8]将激波管引入到光纤压力传感器的动态校准中,使得压力传感器的最大测量误差被控制在被测压力的10%以下.文献[9]在选用激波管对压力传感器进行校准时,为了减小激波管特征输出中的干扰强度,建立了一个动态纠正模型[9].总的来说,该方面的研究丰富了动态校准的内容;然而,采用激波管进行动态校准依然存在不足,其中最典型的问题是——被校准压力传感器输出数据中存在较强干扰;目前大部分方法无法在该条件下获取传感器的动态性能指标,即使部分方法存在抗干扰措施或补偿,但是无法给出这些措施的有效程度,进而也无法给出所得结果可靠性的指标.究其原因是由于无法从干扰数据中挖掘表征传感器特征输出数据以及表征校准可靠性的成分.信息挖掘被认为是解决这一问题的最有效方式[1, 10].
信息挖掘是一种从干扰数据中挖掘有效信息的重要途径[10, 12].在信息挖掘处理中,当前使用的主流方法有自助法(Bootstrap Method,BM)和GM(1,1)(Grey Model)等[10, 13, 14].因此,BM法与GM(1,1)可以被看作是当前能剔除被校准传感器输出数据干扰的仅有的有效方式.在前人研究的基础上,孟浩等将GM(1,1)用于数据序列的动态滤波,所得效果显著优于通用的高斯滤波法[14];葛乐矣和王中宇等将灰色预测应用于预报测量序列动态测量误差[15, 16];在GM(1,1)基础上,Preston提出了动态测量效果的灰假设评价方法[17].然而,这两种方法在使用中也存在一些突出的问题：GM(1,1)会产生额外的灰色生成不确定度,导致所得结果包含异常信息[13, 18];BM法在数据量较少的情况下,难以模拟原始数据的分布信息[12, 19].基于BM和GM(1,1)的特点,本文提出一种结合这两种方法的数据处理操作,将其作为本文所提估计方法的重要组成部分,用于激波管条件下被校准压力传感器输出数据的预处理;处理后所得的数据序列包含传感器的本征数据以及校准实验可靠性的信息,这是准确获得被校准压力传感器的动态性能指标及其可靠性的重要基础.
被校准传感器的动态性能指标是表征其动态特征的最直接方式,这些指标对其测量应用场合的选取具有重要的指导意义.本文提出一种用于激波管校准条件下压力传感器动态参数估计的新方法.首先,使用信息挖掘的预处理操作对被校准压力传感器的输出数据进行处理,得到最优估计序列、上界序列和下界序列;其次,构建白化滤波器和差分模型用于处理已得到的3个数据序列,进而得到最优估计模型、上界模型和下界模型;最后,求解最优估计模型,得到被校准压力传感器动态性能指标的最优估计,解上界模型和下界模型,得到所得动态性能指标的估计区间.
1 参数估计法1.1 估计原理压力传感器在激波管校准条件下,其动态参数指标的估计包含信息挖掘、滤波和建模及指标求解等关键步骤.其中信息挖掘是一种基于GM(1,1)与BM的信息预处理操作,用于从被校准压力传感器的输出序列中分离表征传感器动态特征的数据,以及表征校准可靠性的信息;滤波和建模用于获取被校准压力传感器的特征模型;求解相应模型,得到被校准压力传感器的动态性能指标及其估计区间.参数估计的原理如图 1所示.
 |
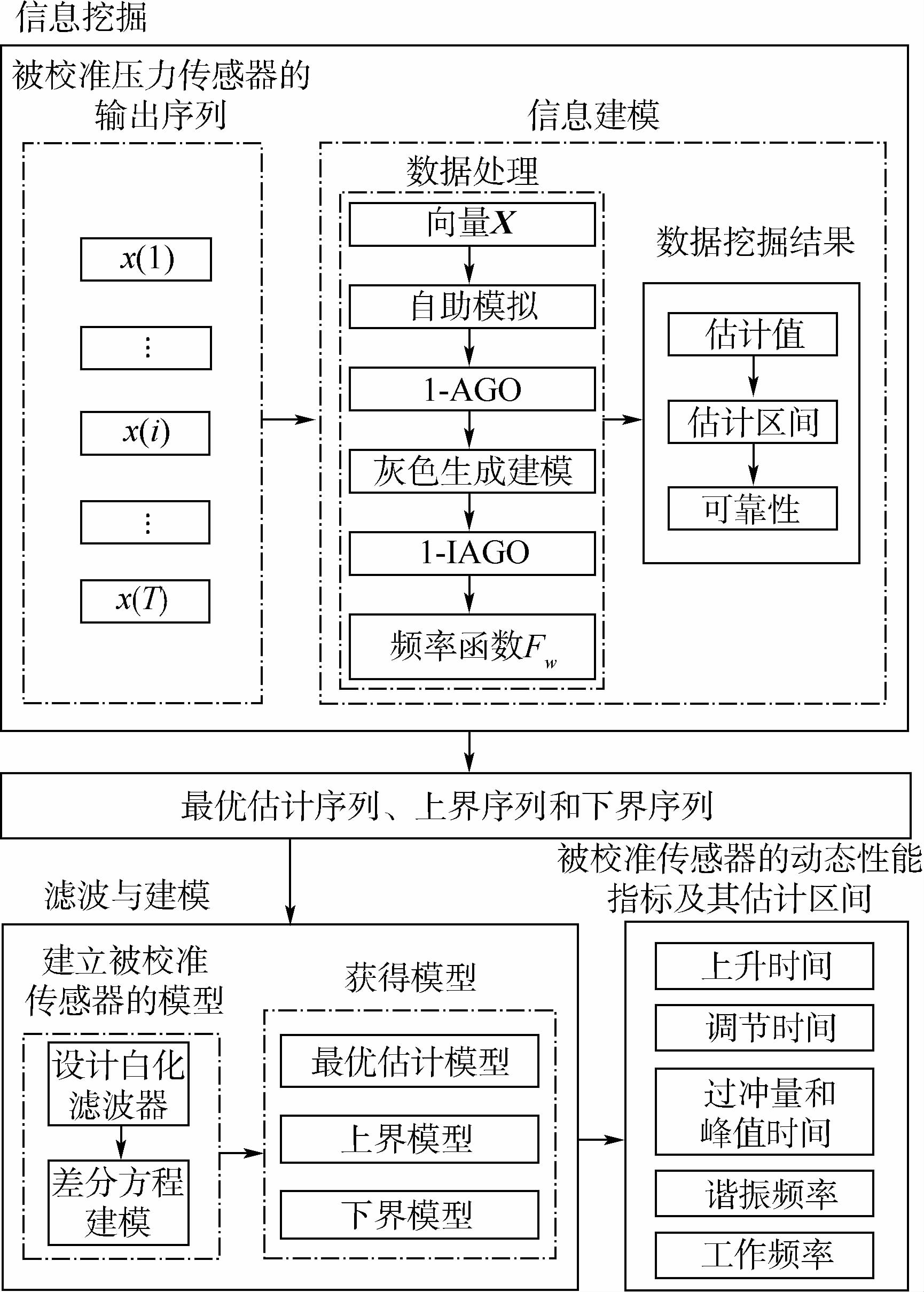| 图 1 参数估计的原理图Fig. 1 Principle diagram of parameter estimation |
| 图选项 |
1.2 信息挖掘假设在激波管的阶跃压力激励下,被校准压力传感器的输出为
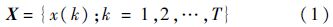
式中:T为最大采样时间点,其小于激波管校准平台的稳定作用时间.
从序列X中提取与时间点k紧邻的前m个数据,构成子序列向量Xm:
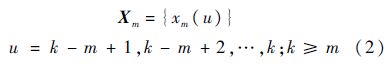
从Xm中等概率、可放回地随机抽取1个数据,抽取m次,得到一个自助样本Yb,它有m个抽样数据;连续重复B次,得到B个自助抽样样本,用Y矩阵表示为
式中:Yb为第b个自助抽样样本,其表示为
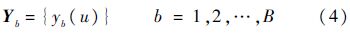
式中:yb(u)为在Yb中的第u次采样.
对Yb序列进行一次累加生成(one Accumulated Generating Operation,1-AGO)[13, 14, 15, 16]处理,得到累加序列Xb:
对得到的累加序列作紧邻均值生成:
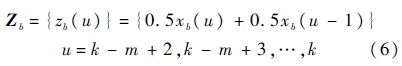
在初始条件xb(k-m+1)=yb(k-m+1)下的最小二乘解为
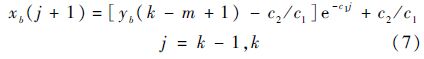
其中,c1与c2为
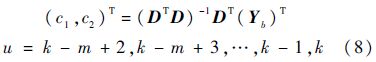
式中:D=(-Zb,I)T;I=(1,1,…,1).
对得到的解进行一次累减生成(one Inverse Accumulated Generating Operation,1-IAGO)[13, 14, 15, 16],得到在时刻w=k+1的最优估计输出
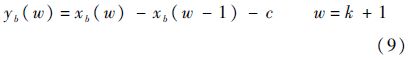
对Y中的B个自助抽样样本分别进行上述处理,这样在w=k+1时刻就得到B个数据.这些数据构成如下序列:
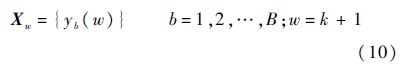
由于B很大,可以用式(10)结果建立关于属性xm的频率函数:
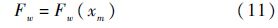
被校准压力传感器在w=k+1时刻的无偏估计可使用加权平均表示为
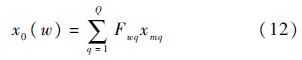
式中:Q为对Xw的分组数;xmq为第q组的中值;Fwq为在xmq的估计自助频率.
置信水平为
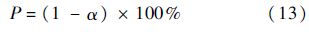
式中:α为校准实验干扰的显著水平且,α∈[0,1],α的设置与实验条件(主要为实验平台及实验参数两个方面)相关,其值由式(14)给出:
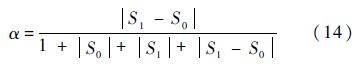
式(14)中,实验条件具体包含:校准平台稳定持续时间、阶跃压力的幅值不确定度和平台波形的不均匀性等;S0为压力传感器在激波管校准下的最优实验条件,其可以定量化表示为:S0=(S0(1),S0(2),…,S0(i),…,S0(g));S1为实际校准实验条件,表示为:S1=(S1(1),S1(2),…,S1(i),…,S1(g)).式(14)中:
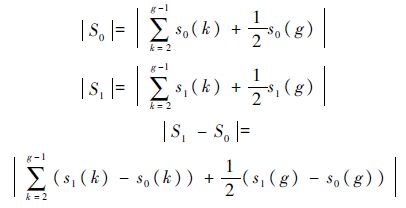
在置信水平P下的估计区间为
式中:XL为xm对应概率为α/2时的参数值,它是估计区间的下界值;XU为xm对应概率为1-α/2时的参数值,它是估计区间的上界值.
所有的上界值组成上界;类似地,所有下界值组成下界.如果某估计值落在其对应的估计区间之外,说明其包含较强的干扰分量,那么该估计值是不合理的.因此,当h个估计值落于估计区间之外时的信息生成可靠性为
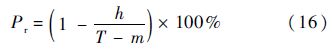
定义k时刻的估计相对误差为式(17),用以评价信息挖掘效果.
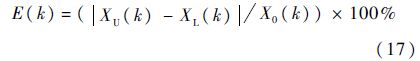
式中:XU(k)为上界在时刻k的值;XL(k)为下界在时刻k的值;X0(k)为被校准压力传感器的时刻k的值.
基于式(17),定义校准时间范围内的最大估计相对误差为
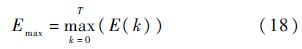
同理,定义如式(19)所示的最小估计相对误差为
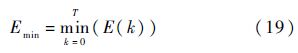
1.3 滤波与建模在压力传感器的动态校准中,最终的步骤是建立数学模型,用以全面描述被校传感器的动态性能[1].在有测量噪声的情况下,该数学模型用差分方程可以表示为
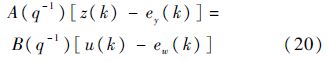
式中:u(k)为被校准压力传感器的输入观测量;z(k)为被校准压力传感器的输出观测量;ey(k)为输入观测中的随机误差;ew(k)为输出观测中的随机误差;q-1为移位运算符,且有A(q-1)=1+a1q-1+a2q-2+…+anq-n和B(q-1)=b0+b1q-1+b2q-2+…+bnq-n.
设ε(k)=A(q-1)ey(k)-B(q-1)ew(k),则式(20)可以改写为
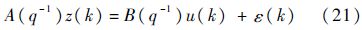
在工程的数据处理中,如果输入观测量足够好的话,那么ew(k)项比较小以至可以忽略;在该情况下可以得到
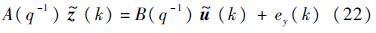
式中:
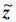(k)=z(k)/A(q－1);
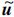(k)=u(k)/A(q－1),其中1/A(q-1)为白化滤波器.参数ai和bi(i=1,2,…,n,a0=1)可以通过最小二乘法(Least Square Method,LSM)求出,最小二乘法的限定条件为
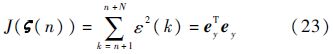
式中:ζ(n)=(bn,an,…,b2,a2,b1,a1,b0)T.
给定常量V,N0为被校准压力传感器输出数据的总数,且有N=N0-V与0＜n≤V.
在求出ai和bi(i=1,2,…,n,a0=1)之前,
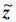(k)与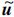(k)也是未知,因而式(22)未知.本文使用迭代法来计算它们,ε(k)为收敛指标,L为最大迭代次数,相应的步骤如下:1) 基于u(k)与z(k),使用最小二乘法求出ai和bi(i=1,2,…,n,a0=1)的最小二乘估计值,并将它们作为迭代的初值.
2) 假设第l次迭代得到如下结果:
之后便可算得
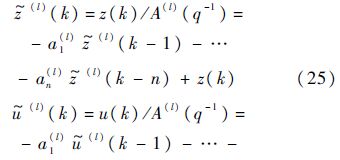
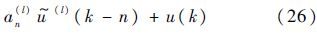
且当k＜0时,
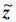(l)(k)=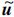(l)(k)=0.3) 基于{
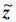(l)(k),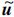(l)(k),k=0,1,…,N0},对式(27)作最小二乘估计,求得参数a(l+1)与b(l+1).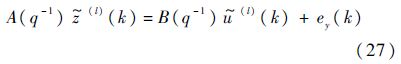
4) 设l=l+1,返回步骤2)继续迭代计算,直至达到收敛要求或是达到最大迭代次数L.
使用1.3节的处理步骤对最优估计序列、上界序列和下界序列分别进行处理,得到最优估计模型、上界模型和下界模型.
求解最优估计模型,得到被校准压力传感器的时域指标(如上升时间、峰值时间、调节时间和超调量等)和频域指标(如工作频率和谐振频率等).
2 实例分析为验证本文所得估计方法的可靠性,选用恩德福克200系列压阻传感器在北京长城计量测试技术研究所进行了激波管条件下的校准实验,现场如图 2所示.
 |
| 图 2 校准实验Fig. 2 Calibration test |
| 图选项 |
实验平台包含激波管、被校准压力传感器、高压气体源、控制系统和瞬态数据采集器.瞬态数据采集器是控制系统的重要组成部分,它高速地从被校准传感器采集输出数据并将其传输至控制系统存储.使用本文所提估计方法对存储在控制系统且包含被校准压力传感器激发模态信息的数据进行处理,得到被校准压力传感器的模型及关键的动态特征指标.
实验平台技术指标及关键实验参数见表 1,所列项涉及到干扰显著性水平值的设置.例如,当表 1第3列中为“满足”时,对应该行的指标为最优,其不会对传感器的校准产生不可忽略的影响,因此在设置条件数列时,将该值定量化为“1”;若为“不满足”,则在设置条件数列定量化为“0”.基于上述分析,可得此次实验最优条件数列为S0=(1,1,1,0.04,1,1,1,21.8,0.24),本次实验条件数列为S1=(1,1,1,0.02,1,1,1,23,0.27);基于干扰显著性水平计算式(14),得到α=0.029.
表 1 激波管实验平台与校准实验的技术参数Table 1 Technical parameters of shock tube platform and calibration test
| 指标 | 最佳实验要求 | 取值 |
| 阶跃压力的上升时间 | ＜10 ns | 满足 |
| 平台压力的持续时间 | >4 ms | 满足 |
| 平台压力波形的不均匀性 | 优于±2% | 优于±1% |
| 阶跃压力的幅值不确定度 | ＜4% | ＜2% |
| 入射激波 | 1 MPa | 满足 |
| 反射激波 | 1 MPa | 满足 |
| 采样频率 | 大于5 MHz | 满足 |
| 环境温度 | 21.8℃ | 23℃ |
| 相对湿度 | 24% | 27% |
表选项
图 3为激波管动态校准实验中记录的压力传感器输出波形.使用本文所提预处理操作对图 3数据进行处理,得到最优估计值、上界和下界曲线,如图 4所示.图 4中的估计值是在原始信息基础上,对部分已知信息优化生成的结果;该结果突出了传感器的本征输出成分,描述了在阶跃压力激励下,被校准压力传感器所激发出的真实模态信息.图 4中的上界和下界数据表征该校准数据的可靠程度,通过图中曲线直观判断,此次实验所得上下界数据基本上实现了对被校准传感器输出模态信息的包络.
 |
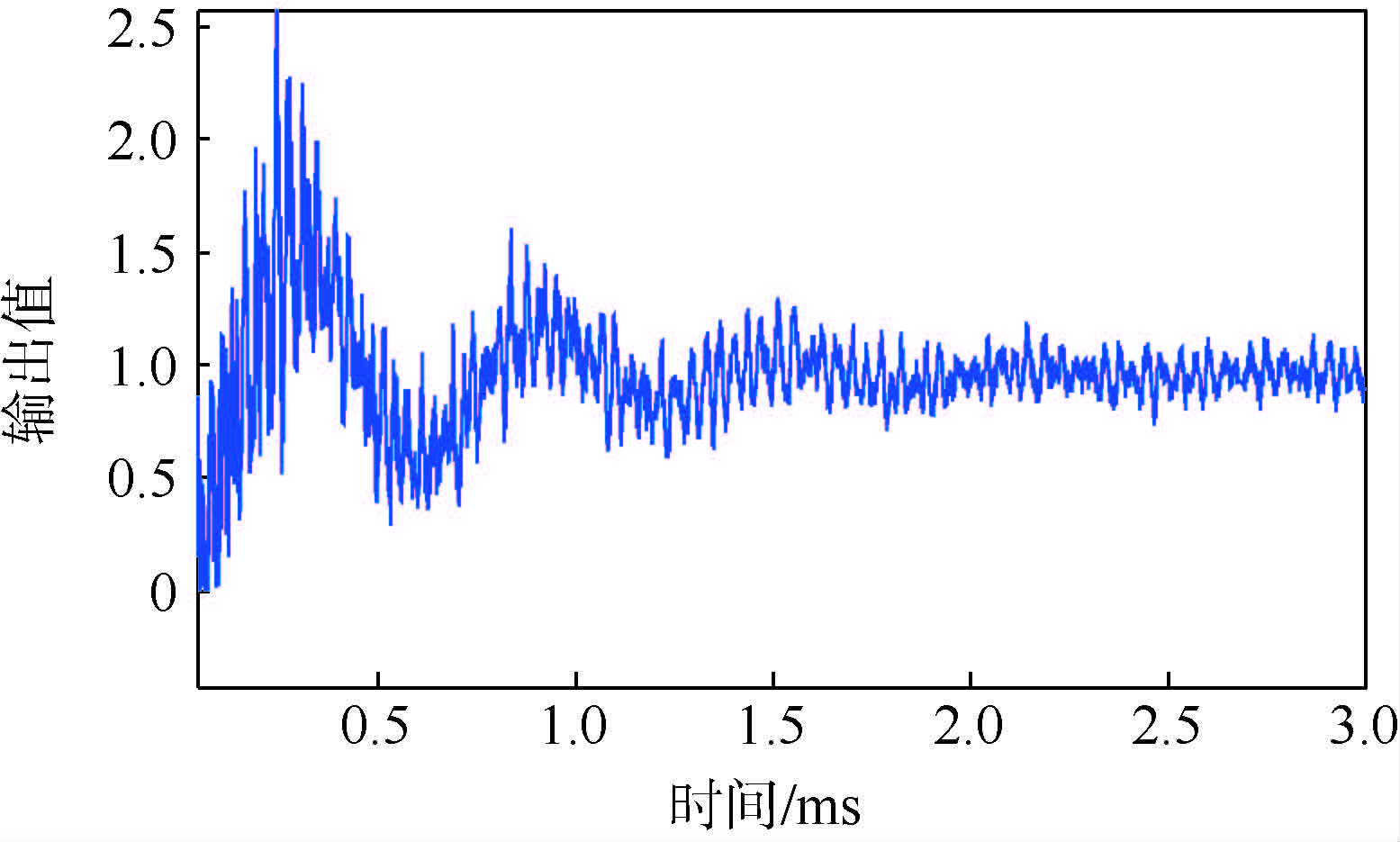| 图 3 压力传感器在激波管校准条件下的特征响应信号Fig. 3 Characteristic response signal of pressure transducer calibrated by shock tube |
| 图选项 |
 |
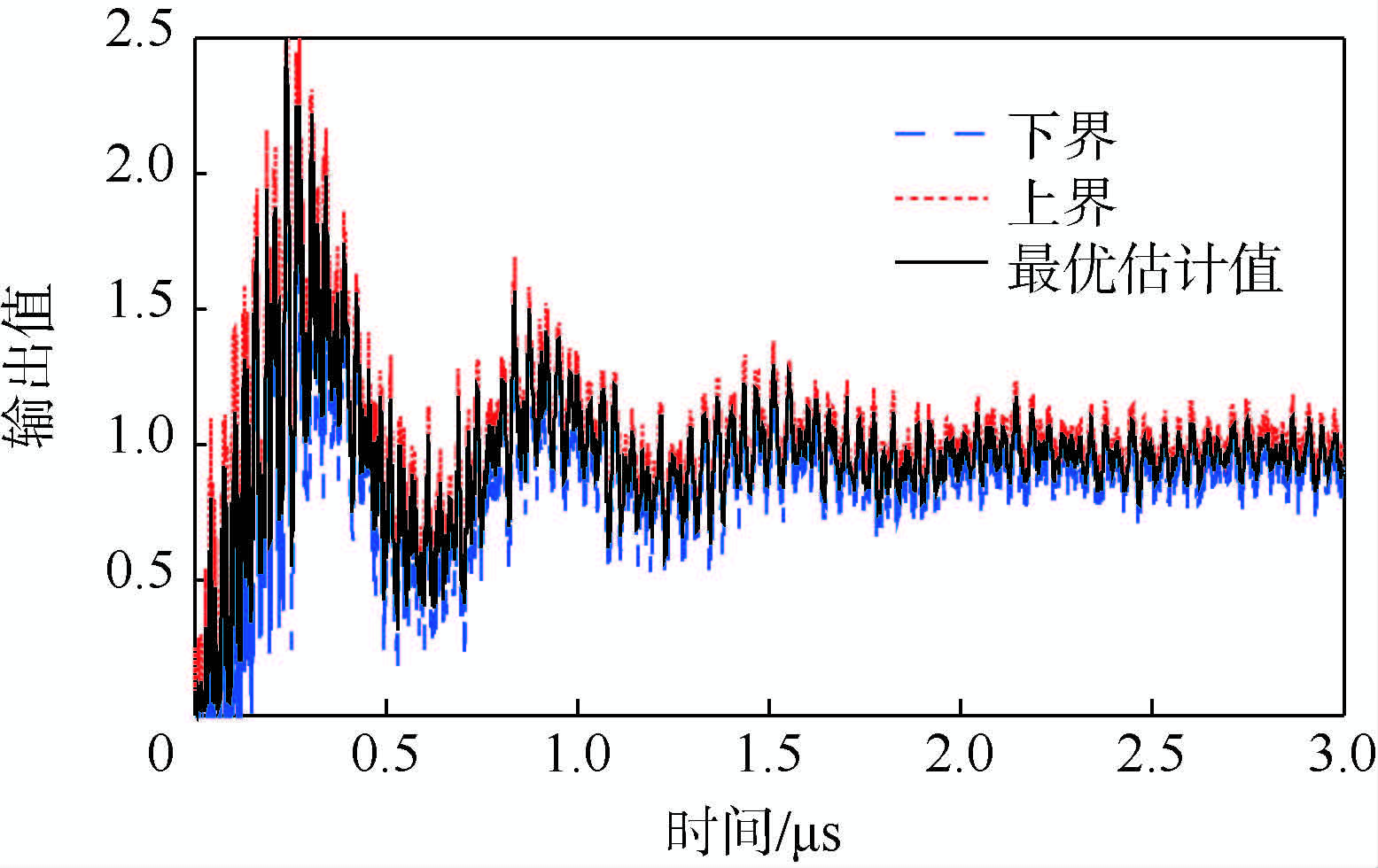| 图 4 被校准传感器响应信号的生成信息Fig. 4 Generating information of characteristic response signal |
| 图选项 |
良好的上下界是合理评价最终模型的关键,当所得可靠性越高,表明所得上、下界能最大程度包络原始数据信息,同时估计值中的干扰信息控制到了最小.在此使用文中所提的可靠性指标来评价预处理操作所得数据的可靠性.为了直观地评价所得数据的可靠性,这里将本文方法所得结果与目前常用方法有BM法和GM(1,1)法所得结果相比较.
表 2为3种方法所得结果在Emax、Emin和可靠性Pr这3个指标方面的对比数据.
表 2 不同方法计算所得可靠性的对比Table 2 Comparison of reliability calculated by different methods
| 方法 | Emax/% | Emin/% | NU | NL | Pr/% |
| 本文方法 | 5.67 | 0.34 | 150 | 215 | 97.57 |
| BM | 12.56 | 4.41 | 835 | 730 | 89.56 |
| GM(1,1) | 11.30 | 5.73 | 1 305 | 1 565 | 80.86 |
表选项
从表 2数据可以看出,在15 000个输出数据中,本文预处理方法所得结果超出上、下界的数据个数为365个,得出可靠性为97.57%,这在3种方法中是最高的.另外,本文方法所得Emax=5.67%,Emin=0.34%,这2个指标数据都明显小于另外2种常用方法所得对应结果.综上所述,本文处理方法所得上、下界数据能够包络原始数据信息.对图 4中所得估计数据分别进行滤波、差分建模处理,得到如下差分模型:y(k)-1.606 5y(k-1)+0.847 6y(k-2)=-7.099×10-4u(k)+0.182 8u(k-1)+4.888×10-2u(k-2)
进一步处理得到描述被校准压力传感器动态性能的离散传递函数:
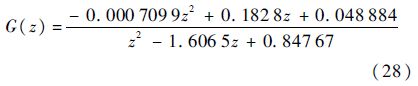
使用输出响应不变法对式(28)作进一步处理,最后得到表征被校准压力传感器的最优估计模型:
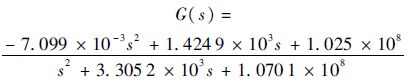
同样地,对上、下界数据进行上述操作,分别得到连续传递函数的上界模型
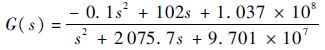
和下界模型
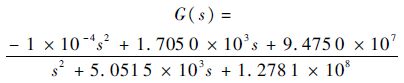
对得到的3个模型分别作波特图,所得数据如图 5所示.
 |
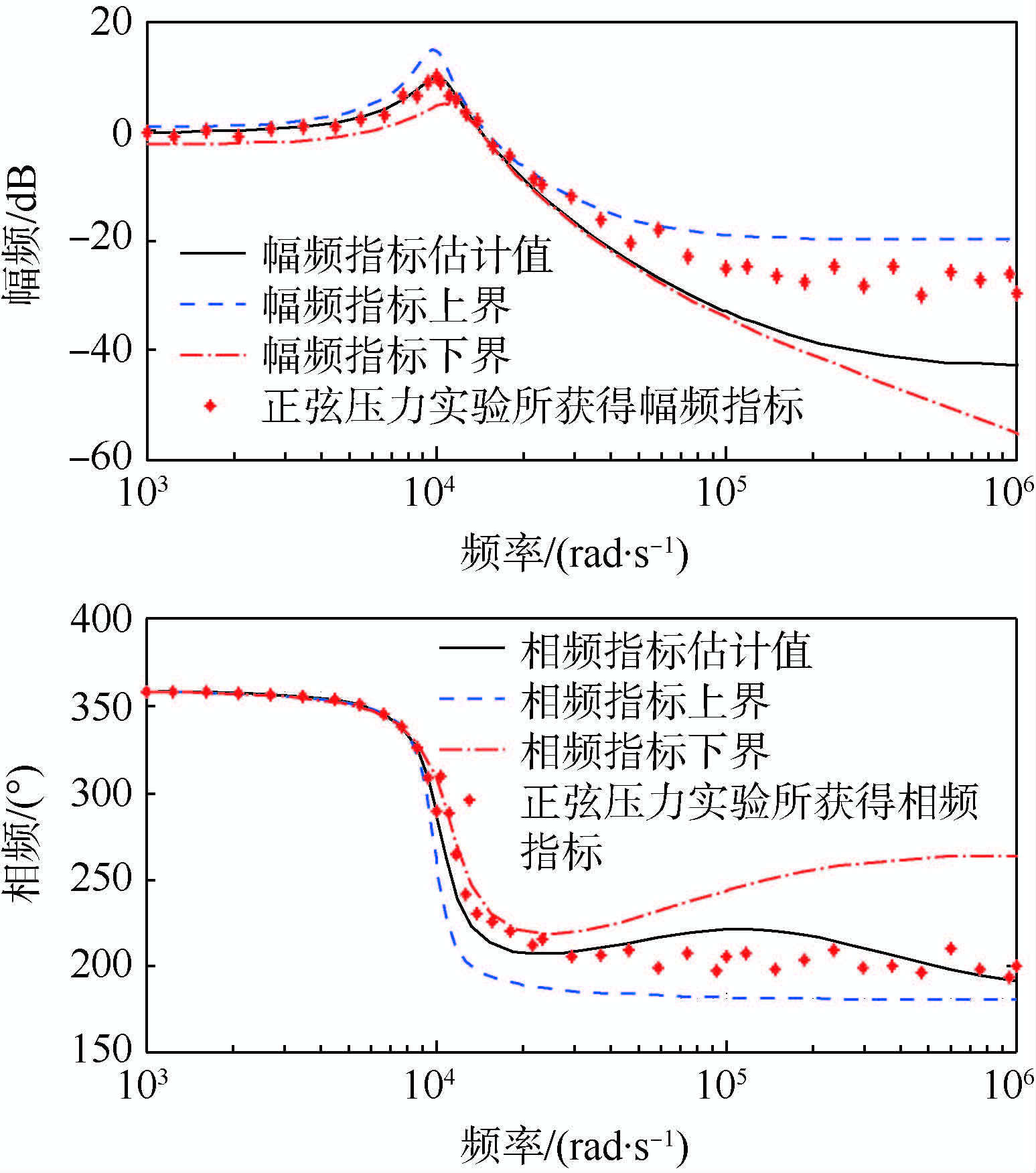| 图 5 被校准传感器的幅频和相频特性Fig. 5 Amplitude and phase-frequency characteristic of calibrated pressure transducer |
| 图选项 |
从图 5中可以看出,由最优估计模型得到的幅频曲线完全包络由上界模型与下界模型对应的幅频曲线中,而且相频曲线也存在类似结果.从图 5中还可以看出,当频率小于104 rad/s时,3条幅频曲线较为接近、3条相频曲线也较接近;当频率逐渐增大,曲线间的差异性逐渐增强.以上分析说明,在低频段的区间包络效果较好;在高频段,压力传感器的幅值误差和相移较大.需要说明的是,在实际工程中,人们通常关注的正是如图 5中所示的低频段特性.
为了验证所得最优估计模型的准确性,使用正弦压力发生器对被校准压力传感器进行频域实验.所用正弦压力发生器及比对校准的标准传感器的关键指标如表 3所示.图 5中正弦压力实验所获得相频指标曲线所示信息为被校准压力传感器在离散频率点的频域特征.对比正弦压力实验所得离散频率点的频域数据与最优估计模型所得幅频、相频曲线可以发现,在低频段,不同方法所得结果具有较好的一致性.为更直观地对比所得数据之间的关系,下面将对上述的一致性进行定量化分析.
表 3 正弦压力发生器和标准传感器的关键数据Table 3 Key parameters of sine pressure generator and standard transducer
| 关键技术指标 | 正弦压力发生器 | 标准压力传感器 | ||||
| 校准压力范围/MPa | 工作频率范围/kHz | 波形畸变度/% | 振幅灵敏度误差/% | 相角误差/(°) | 静态精度水平[20] | |
| 参数 | 0~2 | 0.1~20 | ≤0.5 | ≤1 | ±1.5 | 0.01级 |
表选项
图 6中所示的两条曲线分别为正选压力实验所得幅频数据与最优估计模型所得幅频特性曲线在对应离散频率点的幅值差值,以及压力实验所得相频数据与最优估计模型所得相频特性曲线在对应离散频率点的相移差值.从相移差值数据可以看出,当频率值大约小于9×103 rad/s时,最优估计模型所得相移特征数据与实验所得值的差异性远小于0.5°;当频率逐渐增加,差异性有逐渐增大的趋势,但是在测试频率范围内该差值依然小于5.5°,该差值依然位于国家校准规程[21]规定的可接受范围内.
 |
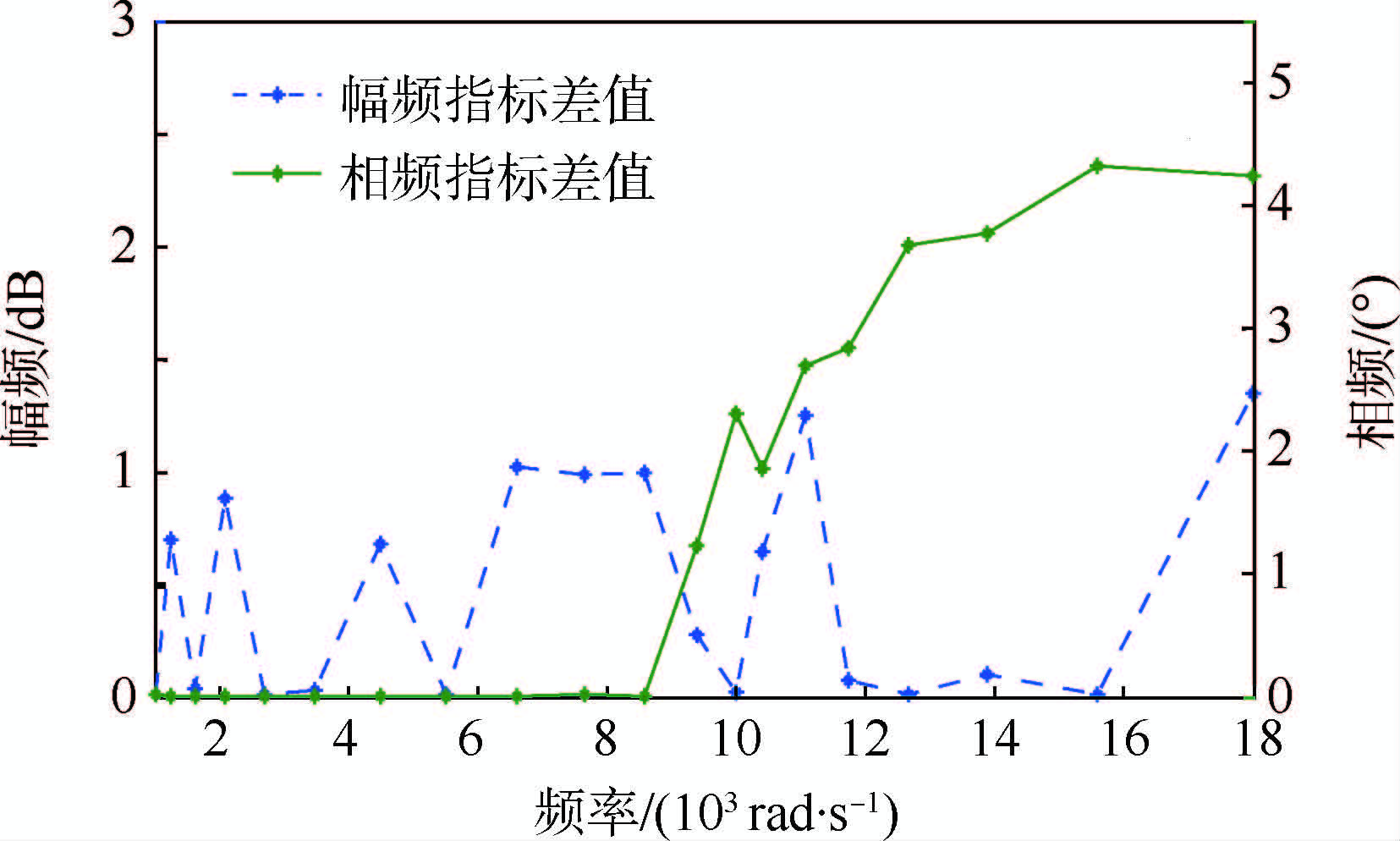| 图 6 不同方法得到的幅频和相频指标的差值Fig. 6 Difference between amplitude-frequency and phase-frequency using different methods |
| 图选项 |
另外,从幅值差值数据可以看出,随着频率增大,该差值呈现波动性;当频率小于9×103 rad/s时,波动值大体小于1 dB;当频率继续增大,波动值只呈现出微弱的增长,但该值仍不超过1.5 dB.需要指出的是,在验证频率范围内,幅值精度依然处于国家校准规程允许范围[21].
综上,频域特性角度的验证结果表明所得到的最优估计模型是合理的.
求解经过频率特征验证的最优估计模型、上界模型和下界模型;其中最优估计模型得出被校准压力传感器的时域与频域指标的估计值;上界模型和下界模型相应值组成对应指标的估计区间(见上界值和下界值),上界值和下界值依据其大小,构成估计区间的上限值和下限值.表 4中的名义值为厂商提供的恩德福克200系列压阻传感器动态性能指标近似数据，从表 4数据可以看出,动态性能指标的估计值均位于对应的估计区间内,另外名义值也位于该区间;本文方法所得估计区间表明在当前实验条件下,求出的被校准压力传感器动态性能指标位于该区间的概率为97.3%;上升时间Tr、峰值时间Tp、超调量σ与调节时间Ts等关键指标的估计值与名义值的相对误差分别为4%,4.15%,3.37%和8.17%,工作频率的相对误差为9.15%,谐振频率的相对误差仅为1.74%;表 4数据表明本文方法所得结果与名义值具有较好的一致性.由表 4数据可知,本文所提的估计方法能有效估计激波管校准条件下压力传感器输出的特征数据,并得出可靠的动态性能指标.
表 4 被校准压力传感器动态性能指标Table 4 Dynamic performance indicators of calibrated pressure transducer
| 动态指标 | Tr/μs | Tp/μs | σ/% | Ts/μs | 工作频率/(rad·s-1) | 谐振频率/(rad·s-1) |
| 估计值 | 0.174 8 | 0.291 3 | 61.199 0 | 2.214 4 | 4 501.5 | 10 070 |
| 上界值 | 0.183 4 | 0.326 1 | 78.169 9 | 3.852 4 | 1 606.6 | 9 739 |
| 下界值 | 0.159 8 | 0.266 3 | 50.008 0 | 1.473 7 | 7 405.4 | 10 735 |
| 名义值 | 0.167 8 | 0.303 4 | 59.134 0 | 2.395 4 | 4 913.4 | 10 245 |
表选项
最后需要指出的是,在实际应用中常将被校准压力传感器近似为低级系统;另外,在压力传感器进行动态测量时,人们通常依据其主要动态性能指标的大体值来判断其是否满足测量要求.因此,在进行压力传感器动态校准时,这种给出传感器的主要动态性能指标并附上表征该估计值可靠性的估计区间的处理方法是具有工程意义的.
3 结 论本文提出一种挖掘数据信息的参数估计方法,用以解决压力传感器激波管校准条件下的动态参数估计问题.选取了恩德福克200系列压力传感器进行了校准实验,并采用本文所提方法对压力的传感器输出数据进行了处理,得出了表征压力传感器动态性能的最优估计模型及包含校准可靠性信息的上界模型及下界模型;进行了正弦压力实验从频率特性角度对所建立模型的可靠性进行了验证;基于最优估计模型得出了被校准压力传感器的时域和频域动态性能指标,基于上、下界模型得出了动态性能指标的估计区间.
1) 正弦压力实验的结果表明：在低频段,最优估计模型所得相频数据与正弦实验所得结果的绝对差值小于0.5°,对应幅频数据的绝对差值小于1.3 dB;并且最优估计模型与正弦实验所得频率特性数据完全包络于由上、下界模型所得频率特性曲线内.
2) 最优估计模型所得的动态性能指标数据与传感器厂商所给数据相比,频域指标的相对误差均不大于9.15%,时域指标均小于8.17%;所有最优估计模型所得性能指标数据均位于估计区间内.
参考文献
| [1] | 黄俊钦.测试系统动力学及其应用[M].北京:国防工业出版社,2013:5-6. Huang J Q.Measurement system dynamics and its application[M].Beijing:National Defense Industry Press,2013:5-6(in Chinese). |
| [2] | Mozek M,Vrtacnik D,Resnik D,et al.Calibration system for smart pressure sensors[J].Informacije Midem-Journal of Microe Lectronics Electronic Components and Materials,2006,36(3):161-165. |
| [3] | Wisniewiski D.Second generation shock tube calibration system[J].International Journal of Acoustics and Vibration,2012,17(3):133-138. |
| [4] | Persico G,Gaetani P,Guardone A.Dynamic calibration of fast-response probes in low-pressure shock tubes[J].Measurement Science & Technology,2005,16(9):1751-1759. |
| Click to display the text | |
| [5] | Revel G M,Pandarese G,Cavuto A.The development of a shock-tube based characterization technique for air-coupled ultrasonic probes[J].Ultrasonics,2014,54(6):1545-1552. |
| Click to display the text | |
| [6] | Kajikawa H,Kobata T.Reproducibility of calibration results by 0-A-0 pressurization procedures for hydraulic pressure transducers[J].Measurement Science and Technology,2014,25(1):015008. |
| Click to display the text | |
| [7] | Sharifian S A,Buttsworth D R.Evaluation of glued-diaphragm fibre optic pressure sensors in a shock tube[J].Shock Waves,2007,16(3):189-197. |
| Click to display the text | |
| [8] | Haboussa G,Ortiz R,Deletombe E,et al.A measurement study of a pressure transducer subjected to water drop impact[J].International Journal of Crashworthiness,2008,13(1):49-66. |
| Click to display the text | |
| [9] | Medici E F,Allen J S,Waite G P.Modeling shock waves generated by explosive volcanic eruptions[J].Geophysical Research Letters,2014,41(2):414-421. |
| Click to display the text | |
| [10] | 王中宇,刘智敏,夏新涛.测量误差与不确定度评估[M].北京:科学出版社,2008:11-12. Wang Z Y,Liu Z M,Xia X T,et al.Measurement error and uncertainty evaluation[M].Beijing:Science Press,2008:11-12(in Chinese). |
| [11] | Yatracos Y.Assessing the quality of bootstrap samples and of the bootstrap estimates obtained with finite resampling[J].Statistics & Probability Letters,2002,59(3):281-292. |
| Click to display the text | |
| [12] | Davidson R,Mackinnon J G.Bootstrap confidence sets with weak instruments[J].Econometric Reviews,2014,33(5-6):651-675. |
| Click to display the text | |
| [13] | Yin M S.Fifteen years of grey system theory research:A historical review and bibliometric analysis[J].Expert Systems with Applications,2013,40(7):2767-2775. |
| Click to display the text | |
| [14] | Wang Z Y,Meng H,Fu J H.Novel method for evaluating surface roughness by grey dynamic filtering[J].Measurement,2010,43(1):78-82. |
| Click to display the text | |
| [15] | Ge L Y,Wei Z,Huang S L.Novel error prediction method of dynamic measurement lacking information[J].Journal of Testing and Evaluation,2012,40(1):37-42. |
| Click to display the text | |
| [16] | Ge L Y,Wang Z Y.Novel uncertainty-evaluation method of virtual instrument small sample size[J].Journal of Testing and Evaluation,2008,36(3):273-279. |
| Click to display the text | |
| [17] | Preston S P,Wood A T A.Two-sample bootstrap hypothesis tests for three-dimensional labeled landmark data[J].Scandinavian Journal of Statistics,2010,37(4):568-587. |
| Click to display the text | |
| [18] | Tien T L.A research on the prediction of machining accuracy by the deterministic grey dynamic model DGDM(1,1,1)[J].Applied Mathematics and Computation,2005,161(3):923-945. |
| Click to display the text | |
| [19] | Kajikawa H,Kobata T.Effects of pressurization procedures on calibration results for precise pressure transducers[J].Measurement Science and Technology,2010,21(6):065104. |
| Click to display the text | |
| [20] | JJG860—94 压力传感器检定规程(静态)[S].北京:国家质量技术监督局,1994:1-3. JJG860—94 Verification regulation of pressure transducer(static)[S].Beijing:China State Bureau of Technical Supervision,1994:1-3(in Chinese). |
| [21] | JJG 624—2005 压力传感器动态检定规程[S].北京:国家质量技术监督局,2005:1-4. JJG 624—2005 Verification regulation of dynamic pressure transducers[S].Beijing:China State Bureau of Technical Supervision,2005:1-4(in Chinese). |
