
式中:t为时间量;ξ、η、ζ分别为3个曲线坐标;Q为守恒量;F、G、H为对流项;FV、GV、HV为黏性项.式(1)中各量均根据所研究对象的特征长度、来流密度和速度进行了无量纲化.采用有限体积法进行计算,空间离散方法采用Roe格式,时间推进采用LU-SGS(Lower-Upper Symmetric Gauss-Seidel)隐式方法,湍流模型采用Menter的剪切应力输运(SST)两方程模型.2 模型与网格2.1 计算模型模型为一旋成体,由尖拱和圆柱两部分组成,模型示意图如图 1所示.
 |
| 图 1 模型示意图Fig. 1 Schematic diagram of model |
| 图选项 |
尖拱长度为200mm,圆柱段长度为215mm,直径D为50mm.喷口直径为8mm,标准模型的喷口位置距顶端225mm,另外2个模型喷口位置距顶端分别为325mm和375mm.依照喷口与尖拱顶端的水平距离,将模型命名为J225、J325和J375.喷管出口马赫数为1,总压为55atm(latm=101.325kPa),流量为0.54kg/s.来流马赫数为3.3,静温为84.2K,基于圆柱直径D的来流雷诺数为4.13×106.2.2 网格生成在网格生成时,除了保证网格之间的过渡和壁面法向网格加密之外,还根据喷流特点,对喷口位置处的网格采用“O”型拓扑,并对附近网格进行加密,保证对喷口周围流动结构的准确捕捉.3 基本流场3.1 流场结构横向喷流干扰流场具有复杂的波系结构和涡系结构,且具有很强的非定常效应[9, 10].为便于后面的分析,以下主要针对流场中的波系结构进行介绍,并着重关注弹体表面的压力分布规律.图 2为横向喷流干扰流场结构,显示了计算得到的标准模型在0攻角下的对称面流场和壁面压力分布.可以看到,在喷口上方,由于喷流干扰作用,导致来流流动受到阻碍,在喷口前方形成了弓形激波;弓形激波与边界层相互作用,产生逆压梯度,导致喷口上游出现了流动分离和分离激波.同时,在分离激波和喷口之间存在着强度很大的高压区;在喷口位置,喷流迅速膨胀至超低压状态,然后与周围压力相对较高的气体作用,产生马赫盘、桶状激波以及滑移线等流动结构.此外,喷口下游产生了大范围的低压区.在弹体下游远离喷口的位置,由于流动再附,产生了小范围的压力恢复区.两股来自喷口上游的高压气体随马蹄涡来到弹体下表面,并与自由来流汇聚,从而产生了高压干扰区.
 |
| 图 2 横向喷流干扰流场结构Fig. 2 Flow structure of cross jet interaction |
| 图选项 |
根据空间流场结构和壁面压力分布规律,可以将弹体表面划分为5个区域:喷流未扰区、高压分离区、低压尾迹区、压力恢复区及弹体下表面的高压干扰区,如图 3所示.
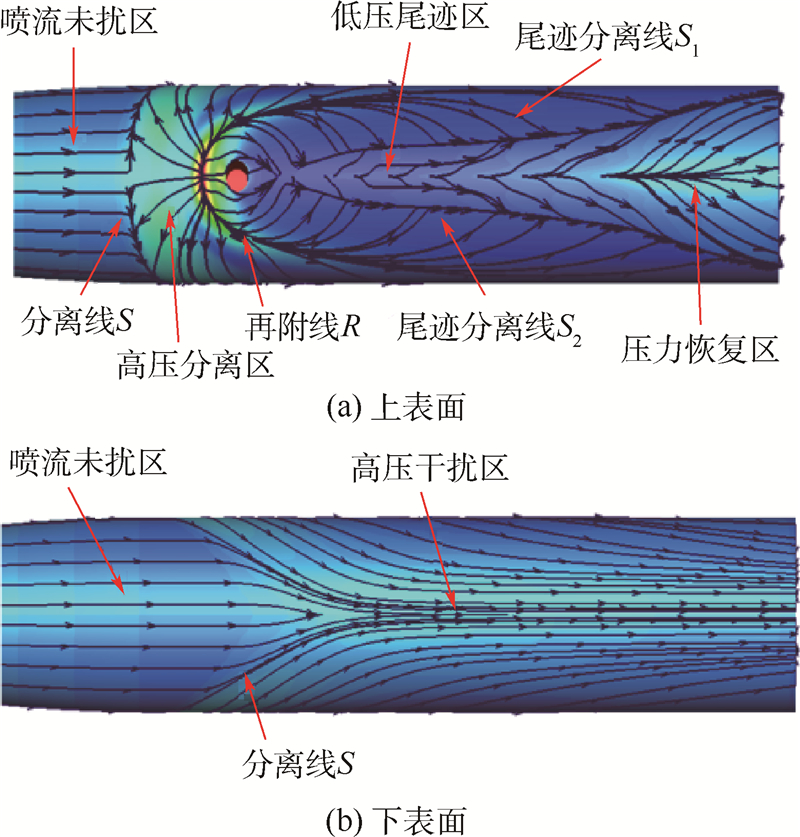 |
| 图 3 壁面压力分布与极限流线Fig. 3 Wall pressure distribution and limiting streamlines |
| 图选项 |
3.2 压力分布为了更好地研究喷流干扰下的流场,同时也为了对数值模拟结果进行验证,给出在喷流干扰和无喷干扰条件下的弹体表面压力系数Cp分布并与实验测量数据[11]进行对比.图 4(a)是经过喷流中心的上表面对称线沿程压力分布,可以看到喷流作用时弹体上表面从前向后呈现出4段规律迥异的压力系数分布,它们分别对应弹体4个不同的压力特征区域.图 4(b)为弹体下表面对称线上的沿程压力系数分布,可以看到喷流作用时弹体下表面呈现出大范围的高压区.图 5(a)和图 5(b)分别给出了喷口上游和下游不同站位的周向压力系数分布.
 |
| 图 4 沿程压力系数分布Fig. 4 Longitudinal pressure coefficient distribution |
| 图选项 |
 |
| 图 5 喷口上、下游不同站位的周向压力系数分布Fig. 5 Circumferential pressure coefficient distribution in upstream and downstream positions of jet location |
| 图选项 |
通过与实验数据的对比看出:数值模拟的计算结果准确反映了真实的压力分布情况,充分说明本文的数值方法能够很好地模拟喷流干扰流场.3.3 侧向控制力实际作用效果弹体在横向喷流干扰流场中受到的侧向气动力可分为3个部分:无喷流干扰下的气动力Fjoff、喷流直接产生的气动力Fj、喷流与主流相互作用形成的干扰气动力Fji和干扰力矩Mji.其中Fjoff可以通过计算没有喷流干扰下的流场得到,Fj可由喷流推力计算公式[12]得到:

式中:γ为空气的比热比;Pj和Aj分别为喷口处的静压和喷口截面积;Mj为设计喷流力作用力矩.而Fji则需要首先计算得到喷流干扰下的气动力Fjon和无喷流干扰下的气动力Fjoff,然后利用式(3)得到:
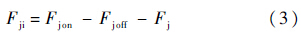
喷流干扰力矩Mji以喷流中心为计算原点,以抬头力矩为正.其计算公式为
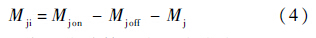
式中:Mj以喷流中心为计算原点的大小为0;Mjon和Mjoff分别为有喷流和无喷流干扰下的侧向力矩.为了更好地反映不同条件下的喷流干扰效果,更有效地表达干扰流场中的喷流干扰力和力矩,通常定义参数喷流力放大因子Kf和喷流力作用位置xeff:

Kf>1,表示喷流干扰力与喷流推力同向,起到增强喷流侧向控制的效果,反之起到减弱作用;xeff为负值时,表示喷流干扰效果产生绕喷流中心的低头力矩,反之为抬头力矩;xeff绝对值越小,表示侧向控制力实际作用点离喷流中心越近,反之越远.表 1给出了标准模型在0 攻角下的喷流力放大因子的计算值和实验值的对比.表 1 Kf计算值与实验值对比Table 1 Comparison of Kf between numerical and experimental results
| 计算结果 | Fji/N | Fj/N | Kf |
| 实验值 | -31.2 | 355.2 | 0.912 1 |
| 计算值 | -32.1 | 355.2 | 0.909 6 |
表选项
3.4 喷流干扰力/力矩沿程增长系数为分析弹体不同位置的干扰压力分布对侧向控制力的贡献,定义干扰力和力矩沿程增长系数[14, 15]:
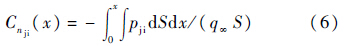
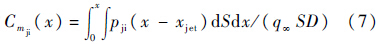
式中:S和D分别为参考截面积和参考长度;q∞为来流动压;pji为壁面干扰压力,为喷流干扰下的壁面压力与无喷干扰下的壁面压力之差;xjet为喷流中心位置.图 6为标准模型在0 攻角下的Cnji和Cmji沿程分布曲线.可以看出,Cnji和Cmji的分布在2个区域变化较大:x=180~230mm和x=230~375mm.区域1对应高压分离区,干扰压力积分得到的合力与喷流推力同向,起到增强侧向控制力的作用,同时产生绕喷口中心的低头力矩;区域2对应弹体上表面的低压尾迹区和下表面的高压干扰区,此区域的干扰压力与喷流推力反向,削弱了喷流侧向控制力效果,同时产生较大的低头力矩.压力恢复区和喷流未扰区对喷流干扰力、力矩几乎没有贡献.
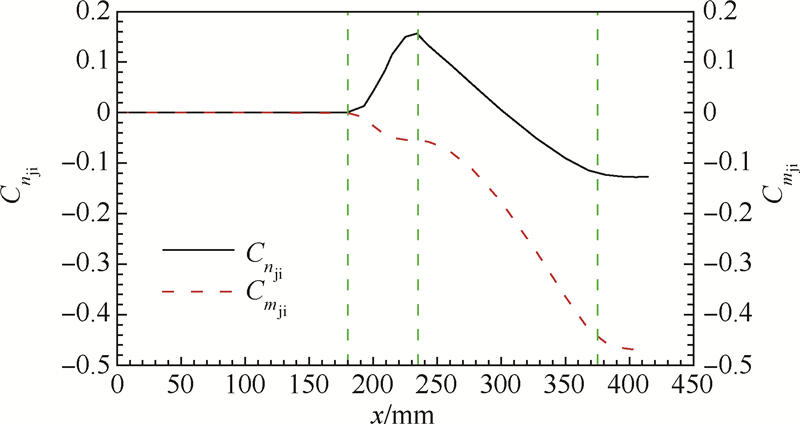 |
| 图 6 Cnji和Cmji沿程分布曲线Fig. 6 Longitudinal distribution curves of Cnji and Cmji |
| 图选项 |
为了将高压干扰区与低压尾迹区的作用效果相区别,分别对喷口下游弹体上、下表面的壁面干扰压力做沿程积分,结果如图 7所示.可以看出,弹体上下表面的干扰压力均起到削弱侧向控制力的作用,并且上表面(低压尾迹区)对侧向控制力的影响要大于下表面(高压干扰区).
 |
| 图 7 弹体上下表面的Cnji分布 Fig. 7 Cnji distribution on upper and lower surface of the body |
| 图选项 |
4 攻角对侧向控制力的影响计算选取0、±5、±10、±15、±20 9个攻角来研究不同攻角下的喷流干扰效果.图 8展示了模型J225的Kf和xeff随攻角α的变化规律.
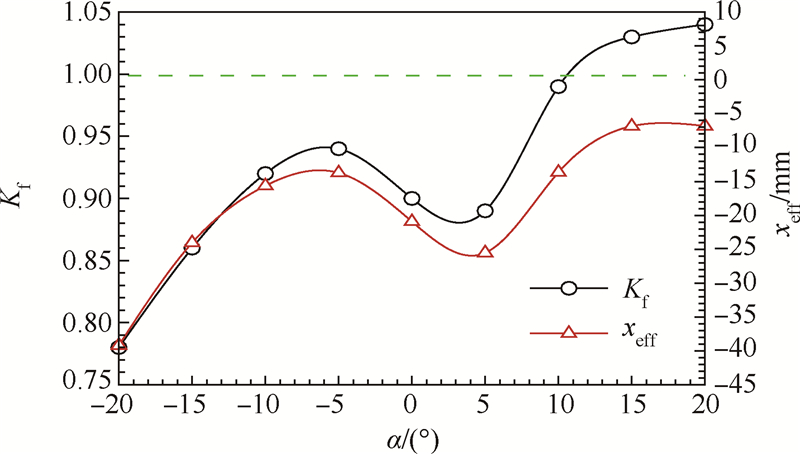 |
| 图 8 Kf和xeff随攻角的变化曲线Fig. 8 Curves of Kf and xeff changing with angle of attack |
| 图选项 |
Kf和xeff随攻角的变化趋势表现出很强的一致性,在-20 ~-5 以及5 ~20 两个区间内都随攻角的增大而增大,但在-5 ~5 区间会随攻角的增大而减小.下面就Kf和xeff的这一规律从流场结构和壁面干扰压力分布的变化做进一步阐述.图 9展示了3个典型攻角下的流场结构.可以看出,随着攻角的增大,喷流干扰强度降低,弓形激波强度衰弱;喷流前的高压分离区范围扩大,但壁面压强下降;喷流膨胀效应增强,喷流后的低压范围沿流向扩张、周向收缩;高压干扰区从弹体下部逐渐向上移动,压力恢复区不断向后移动,直至脱离弹体.
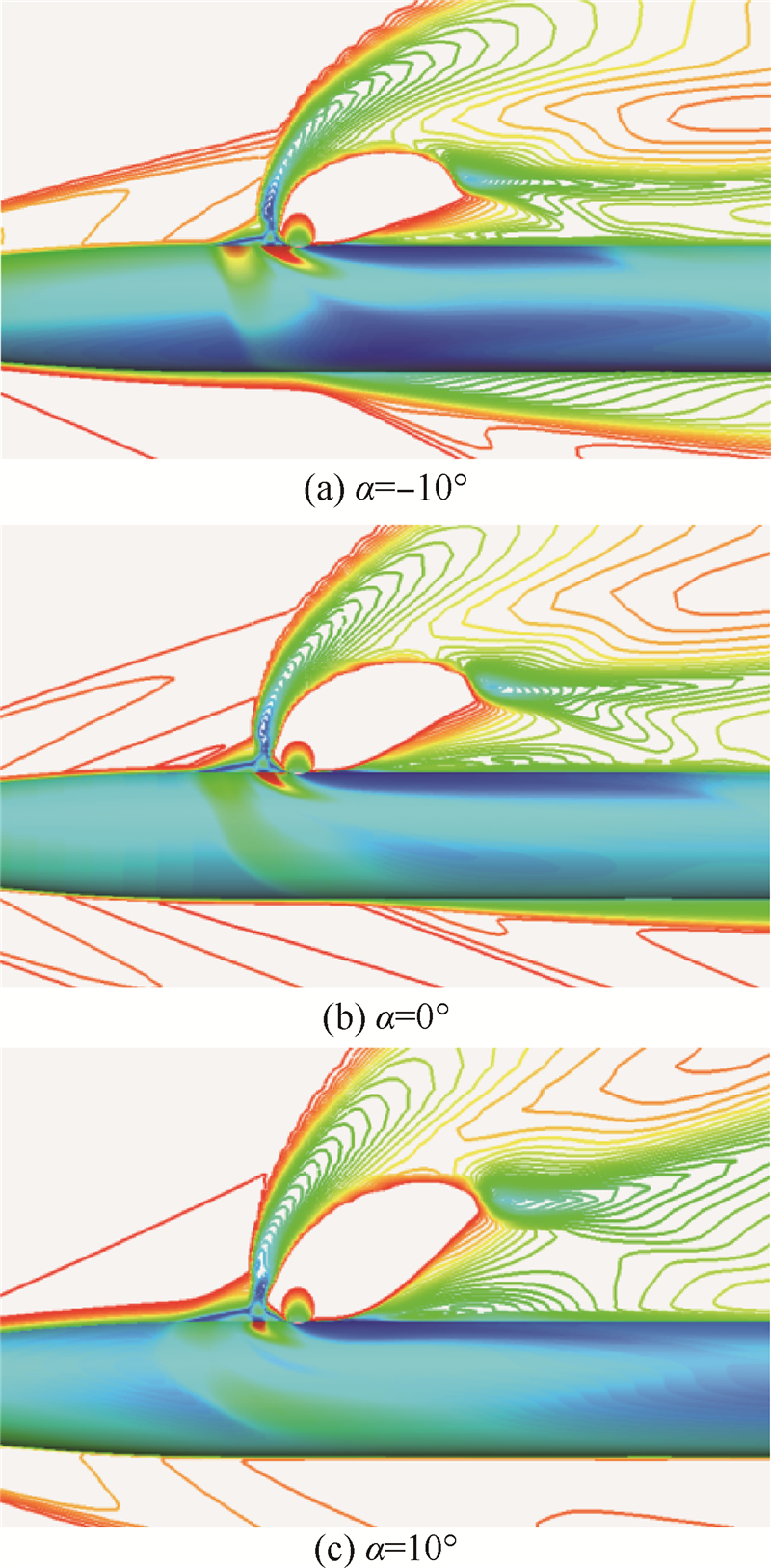 |
| 图 9 不同攻角下的流场结构Fig. 3 Flow structure at different angles of attack |
| 图选项 |
为定量分析弹体壁面干扰压力分布在不同攻角下的变化规律以及对侧向控制力的影响情况,需要借助喷流干扰力沿程增长系数进行研究.图 10分别给出了Cnji在负攻角、小攻角和正攻角下的沿程分布情况.可以看出:喷口上游的高压分离区产生的喷流干扰力几乎不随攻角发生变化,而喷口下游的低压尾迹区和高压干扰区产生的喷流干扰力随攻角变化较大.随着攻角的增大,喷流干扰力在喷口下游的沿程下降速率变缓,尤其在攻角-20 ~-10 和5 ~15 之间表现明显.攻角大于10 以后,作用于喷口下游弹体表面的喷流干扰力由负转正,最终起到增强侧向控制力的效果.在-5 ~5 之间,喷流干扰力在喷口下游的沿程下降速率几乎没有发生变化,而下降区间却在扩大,这导致喷流干扰力朝着减弱侧向控制力的方向变化.
 |
| 图 10 不同攻角下的Cnji分布Fig. 10 Cnji distribution at different angles of attack |
| 图选项 |
5 喷流位置对侧向控制力的影响为研究喷流位置对侧向控制力的影响,选择模型J225、J325和J375在9个攻角下分别予以计算,得到不同喷流位置下Kf和xeff随攻角的变化曲线,如图 11所示.
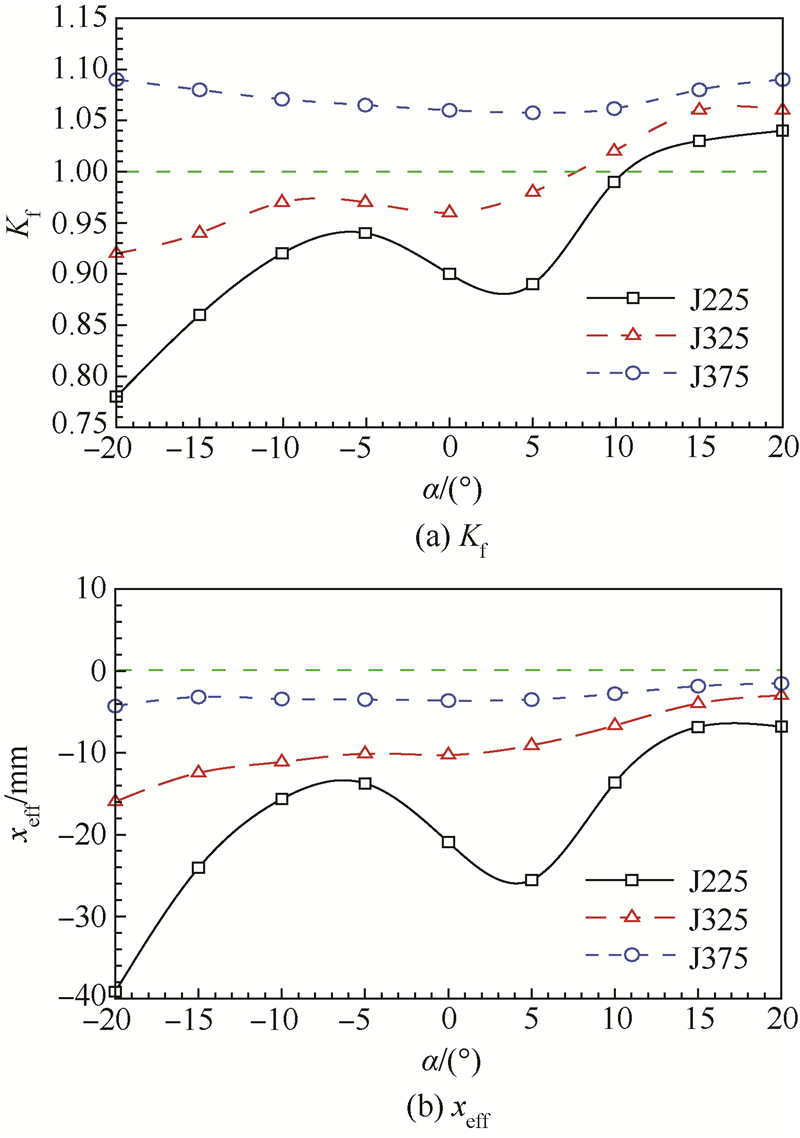 |
| 图 11 不同喷流位置下Kf和xeff随攻角的变化曲线Fig. 11 Curves of Kf and xeff changing with angle of attack at different jet locations |
| 图选项 |
可以看出:①不同喷流位置下,Kf和xeff随攻角的变化表现出很强的相似性和一致性;②在相同攻角下,喷流位置越靠后,Kf和xeff越大;③喷流位置越靠后,Kf和xeff随攻角变化的波动幅度也越小;④无论喷流位置如何后移,喷流干扰力作用位置始终表现为负值.图 12给出了不同喷流位置下Cnij的沿程分布.
 |
| 图 12 不同喷流位置下的Cnij沿程分布Fig. 12 Cnij distribution at different jet locations along longitudinal direction |
| 图选项 |
可以看出,喷流位置的后移造成了整个喷流干扰区域的后移,这将直接导致低压尾迹区和高压干扰区作用范围的缩小,从而减弱喷流干扰力造成的不利影响,改善了侧向控制力实际作用效果:侧向控制力增强,作用位置向喷口中心移动,随攻角变化的波动幅度也在衰减.6 结 论通过数值模拟方法得到了超声速横向喷流干扰流场,并研究了攻角和喷流位置对喷流侧向控制力的影响规律.1)根据弹体表面压力分布特征,将喷流干扰区域分为4个区域:高压分离区、低压尾迹区、高压干扰区和压力恢复区.前3个区域的干扰压力分布决定了喷流侧向控制效果,而低压尾迹区是影响侧向力实际作用效果的决定因素.2)攻角增大时,低压尾迹区周向干扰范围和干扰压力强度下降,高压干扰区由弹体下表面向上表面移动,喷流干扰力逐渐由负转正,侧向控制力增强.但在攻角为-5 ~5 时,低压尾迹区流向干扰范围迅速扩大,喷流侧向控制力减弱.3)喷流位置的改变会影响到低压尾迹区和高压干扰区的作用范围.喷流位置越靠后,低压尾迹区作用范围越小,喷流造成的不利干扰效果减弱,横向喷流的侧向控制效果越好.
参考文献
| [1] | 李素循.激波与边界层主导的复杂流动[M].北京:科学出版社, 2007:167-170. Li S X.Complicated flow governed by shock and boundary layer[M].Beijing:Science Press, 2007:167-170(in Chinese). |
| [2] | Srivastava B.Computational analysis and validation for lateral jetcontrolled missiles[J].Journal of Spacecraft and Rockets, 1997, 34(5):584-592. |
| Click to display the text | |
| [3] | DeSpirito J.Factors affecting reaction jet interaction effects on projectiles, AIAA-2011-3031[R].Reston:AIAA, 2011. |
| Click to display the text | |
| [4] | Zhang J M, Cai J S, Cui Y D.Effect of nozzle shapes on lateral jets in supersonic cross flows, AIAA-2009-1477[R].Reston:AIAA, 2009. |
| Click to display the text | |
| [5] | Ibrahim I M, Murugappan S, Gutmark E J.Penetration, mixing andturbulent structures of circular and non-circular jets incross flow, AIAA-2005-0300[R].Reston:AIAA, 2005. |
| Click to display the text | |
| [6] | Li Z, Murugappan S, Gutmark E, et al.Numerical simulation and experiments of jets in cross flow, AIAA-2006-0307[R].Reston:AIAA, 2006. |
| Click to display the text | |
| [7] | Srivastava B.Lateral jet control of a supersonic missile:Compu-tational and experimental comparisons[J].Journal of Spacecraft and Rockets, 1998, 35(2):140-146. |
| Click to display the text | |
| [8] | 阎超.计算流体力学方法与应用[M].北京:北京航空航天大学出版社, 2006:18-25. Yan C.Methods and application of computational fluid dynamics[M].Beijing:Beihang University Press, 2006:18-25(in Chinese). |
| [9] | 闫宝琴, 李素循, 许能喜.横向喷流引起的三维复杂干扰流场结构研究[J].流体力学实验与测量, 2004, 18(3):59-63. Yan B Q, Li S X, Xu N X.Study of a 3D complex interference flow field structure induced by transverse jet[J].Experiments and Measurements in Fluid Mechanics, 2004, 18(3):59-63(in Chinese). |
| Click to display the text | |
| [10] | Liu T, Woodiga S. Experimental examination of skin friction topology in separated flows, AIAA-2010-0045[R].Reston:AIAA, 2010. |
| Click to display the text | |
| [11] | Graham M, Weinacht P, Brandeis J.Numerical investigation of supersonic jet interaction for finned bodies[J].Journal of Spacecraft and Rockets, 2002, 39(3):376-383. |
| Click to display the text | |
| [12] | 耿云飞.高超声速飞行器减阻防热新方法数值模拟研究[D].北京:北京航空航天大学, 2011. Geng Y F.Numerical simulation of the new methods of drag reduction and thermal protection in the hypersonic vehicle design[D].Beijing:Beijing University of Aeronautics and Astronautics, 2011(in Chinese). |
| [13] | Graham M, Weinacht P.Numerical investigation of supersonic jetinteraction for axisymmetric bodies[J].Journal of Spacecraft and Rockets, 2000, 37(5):675-683. |
| Click to display the text | |
| [14] | Gruber M R, Nejad A S, Chen T H, et al.Transverse injection from circular and elliptic nozzles into a supersonic cross flow[J].Journal of Propulsion and Power, 2000, 16(3):449-457. |
| Click to display the text | |
| [15] | Julius B, Jacob G.Experimental investigation of super- and hypersonicjet interaction on missile configurations[J].Journal of Spacecraft and Rockets, 1998, 35(3):296-302. |
| Click to display the text |
