目前,利用激光清除空间碎片成为国际公认可行的主动清除空间碎片的手段之一.通过高能激光辐射到碎片表面产生的喷射冲量效应[5],使碎片获得速度增量,在合适的位置处可以实现对空间碎片减速降轨的目的.
近年来,欧美国家均开展了地基激光清除空间碎片的相关研究,其中最著名的是美国的ORION计划[6, 7, 8, 9, 10].但是,目前国外在该方面的研究尚处于激光对空间碎片的作用机理和大功率激光器的研制阶段,对于激光作用空间碎片产生速度增量后的清除策略研究很少.国内洪延姬、金星、徐浩东等对激光清除空间碎片的基本概念、基本技术和基本问题进行了介绍,并对碎片清除方法作了一定研究[11, 12, 13, 14, 15].徐浩东等分析了速度增量的作用位置对降轨的影响,并以此建立了空间碎片的降轨模型[13].但是他们只分析了速度增量在轨道近地点和远地点两个特殊位置的影响,降轨模型也仅限于共面变轨的理想情况.金星等提出了针对椭圆轨道空间碎片的单脉冲和多脉冲变轨的计算方法,并对激光站布站区域和空间碎片变轨范围作了一定分析[14].他们也只讨论了共面情况下速度增量对变轨的影响.但是由于地基激光站固定在地面,采用共面变轨清除碎片在实际情况下很难实现.
本文在分析激光辐照产生的速度增量对空间碎片减速降轨的普遍原理的基础上,研究地基激光清除空间碎片的策略.首先推导了不同速度分量的变化对碎片新轨道近地点高度的影响模式,即不仅考虑共面变轨的影响,还考虑异面变轨的影响;然后以此为基础,提出了确定有效变轨区域的约束条件和计算方法,并据此制定清除碎片的策略方案;最后通过仿真实验,验证了该策略方案的有效性.
1 改变不同速度分量的降轨效果由于在椭圆轨道上碎片的飞行速度v处处不同,且激光辐照在碎片上产生的速度增量Δv与飞行速度v的夹角也不同,那么变轨后的新轨道也会因此不同.为了更有效地降低碎片轨道的近地点高度hP,在此研究不同速度分量变化对轨道近地点高度hP的影响模式.
1.1 空间碎片轨道速度分解如图 1所示,在椭圆轨道上,真近点角为f的空间碎片S,其速度v在轨道面内,并与轨迹线相切.速度v在两个不同直角坐标系中分解为
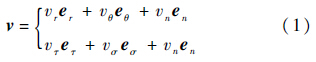
式中:vr、vθ、vτ、vσ和vn分别为v的径向、横向、切向、法向和侧向分量;er、eθ、eτ、eσ和en分别为径向、横向、切向、法向和侧向单位向量.在开普勒轨道中,碎片的速度分量vσ和vn都是0,故用虚线表示.
 |
| A-远地点;P-近地点;r-失径图 1 轨道速度分解示意图Fig. 1 Orbital velocity decomposition diagram |
| 图选项 |
在这些速度分量中,vτ沿着轨迹的切线方向,vn垂直轨道平面,因此下面研究v在(eτ,eσ,en)坐标系下的速度分量对新轨道近地点高度hP的影响.
1.2 脉冲变轨由于激光的脉宽都在ns量级,跟轨道周期相比是非常短暂的.因此用地基激光清除空间碎片时,其轨道变化可视为脉冲变轨方式,即速度有突变增量,但不引起空间碎片位置的变化.
如图 2所示,已知空间碎片在t0时刻的位置r0和速度v0,在该时刻激光束辐照在该碎片上,产生了Δv的速度增量,碎片进入新轨道中,其速度为v1.
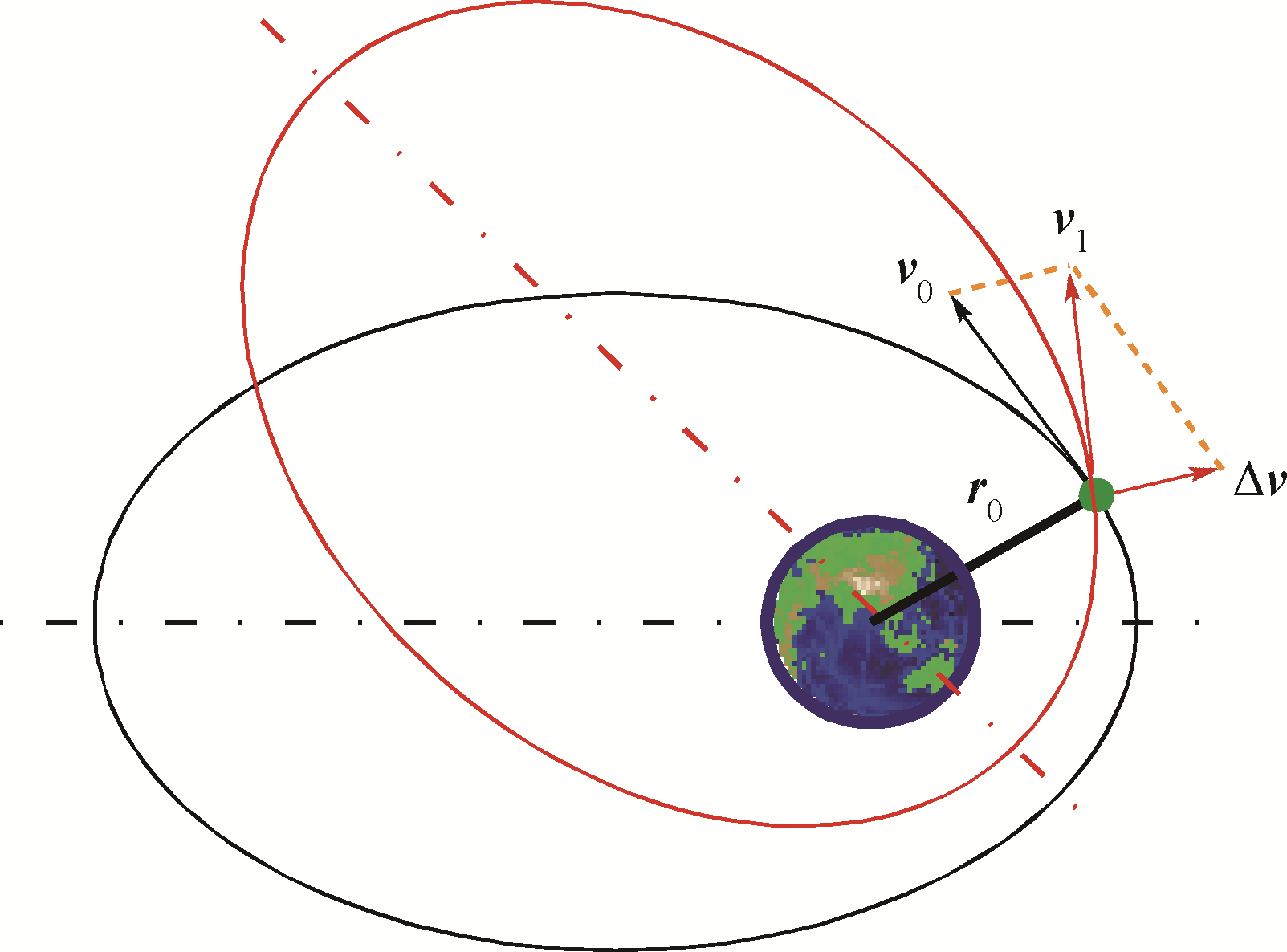 |
| 图 2 脉冲变轨示意图Fig. 2 Impulse orbit transfer diagram |
| 图选项 |
新、旧轨道的参数满足:
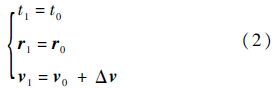
式中:下标1为新轨道参数;下标0为旧轨道参数.
对于开普勒轨道,一组(r,v)唯一确定了一个轨道.下面推导轨道的近地点高度hP与(r,v)的关系式.根据运动方程能量积分和动量矩积分可得
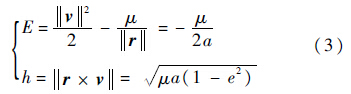
式中:μ为地心引力常数;a为轨道的半长轴长;e为轨道的偏心率.根据式(3)可知,已知一组(r,v),可以唯一确定a和e.因此得到轨道的近地点高度hP的关系式为
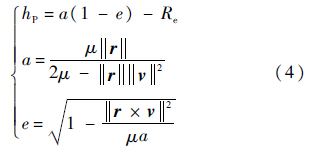
式中:Re为地球半径.
1.3 不同速度分量的影响结果分析不考虑摄动影响,把空间碎片与地球视为二体系统.碎片初始轨道给定,在真近点角f处,其位置和速度(r,v)唯一确定.在此处沿着某一速度分量方向进行一次脉冲变轨,即产生大小为Δv的速度增量,例如eσ方向,则此时此处的位置和速度变成(r,v+Δveσ),利用式(4)求解出新轨道的hP.然后在原轨道不同的真近点角f处,改变该速度分量,计算新轨道的hP,得到hP随f的变化曲线.最后按照此方案,分别改变不同的速度分量,以确定不同速度分量变化对新轨道近地点高度hP的影响模式.
选定的初始轨道信息为近地点高度hP=800 km,远地点高度hA=1 200 km,单脉冲速度增量大小Δv=0.01 km/s.计算结果如图 3所示.
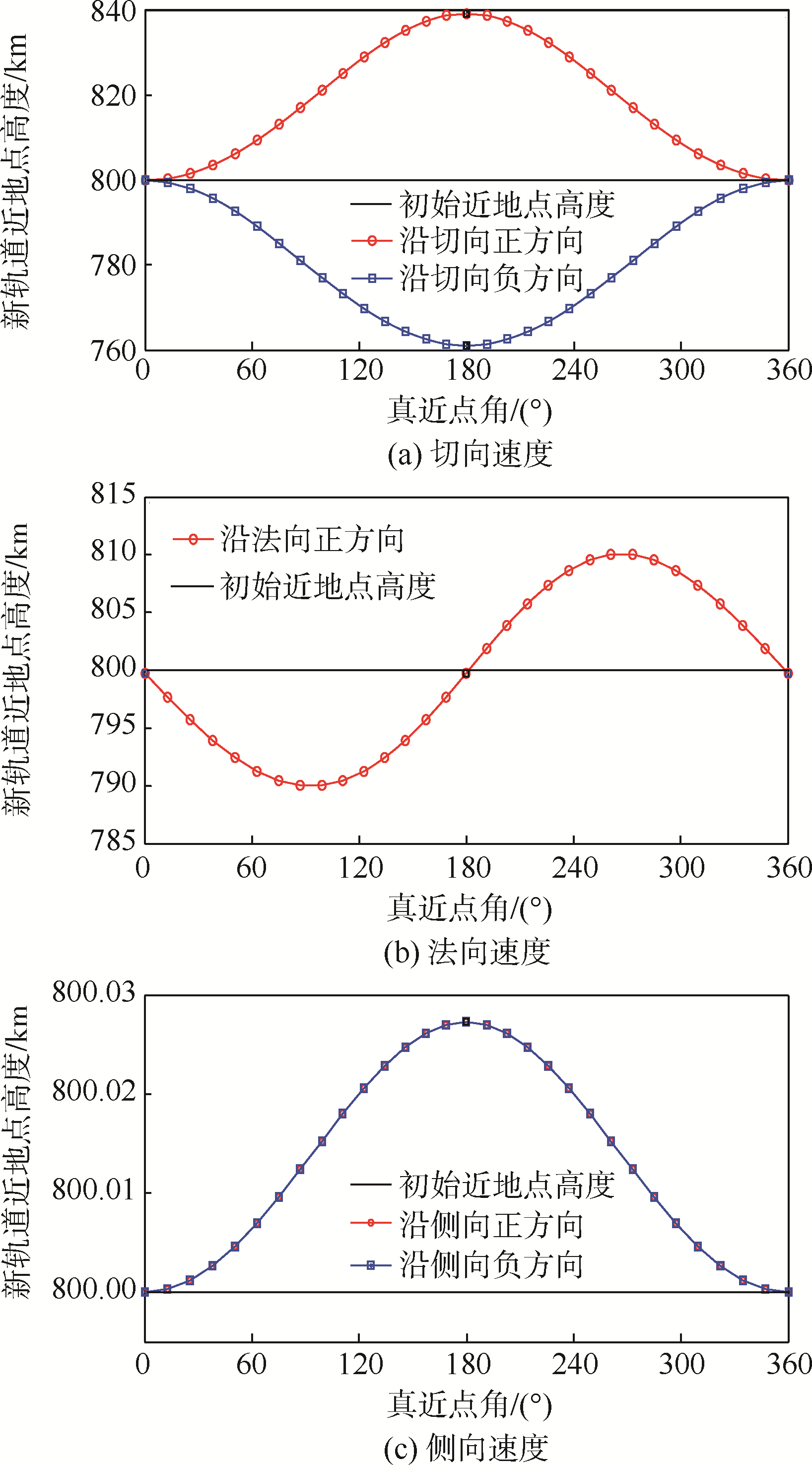 |
| 图 3 改变不同速度分量的降轨效果图Fig. 3 Diagram of effect that changing different velocity components has on orbit transfer |
| 图选项 |
1) 改变切向速度.
沿着切向正负方向施加一次脉冲冲量,其速度v变为v±Δveτ,在不同真近点角处变轨后的新轨道近地点高度如图 3(a)所示.只要在非近地点处减小vr,就会降低新轨道的hP;只要在非近地点处增大vτ,就会升高新轨道的hP;并且在远地点附近改变vτ,会更有效地改变近地点高度hP.
2) 改变法向速度.
由于地基激光只能沿着法向速度正方向改变其速度,施加一次脉冲冲量后,其速度v变为v+Δveσ,在不同真近点角处变轨后的新轨道近地点高度如图 3(b)所示.只要在非近地点处改变vn,就会升高新轨道的hP,而且沿着侧向速度正负方向的效果相同;与vτ作用类似,在远地点附近改变vn,升高新轨道的hP作用明显.
3) 改变侧向速度.
沿着侧向正负方向施加一次脉冲冲量,其速度v变为v±Δven,在不同真近点角处变轨后的新轨道近地点高度如图 3(c)所示.在不同位置增大vσ,新轨道的近地点高度可能降低,也可能升高;在真近点角f∈(0°,180°)内增大vσ,一定能够降低新轨道的近地点高度.
为了更加直观地看出在大小相同的速度增量Δv的作用下,不同速度分量变化对新轨道近地点高度的影响程度,将沿切向速度负方向、法向速度正方向和侧向速度正方向增加相同速度增量的曲线绘制在同一坐标系下,如图 4所示.
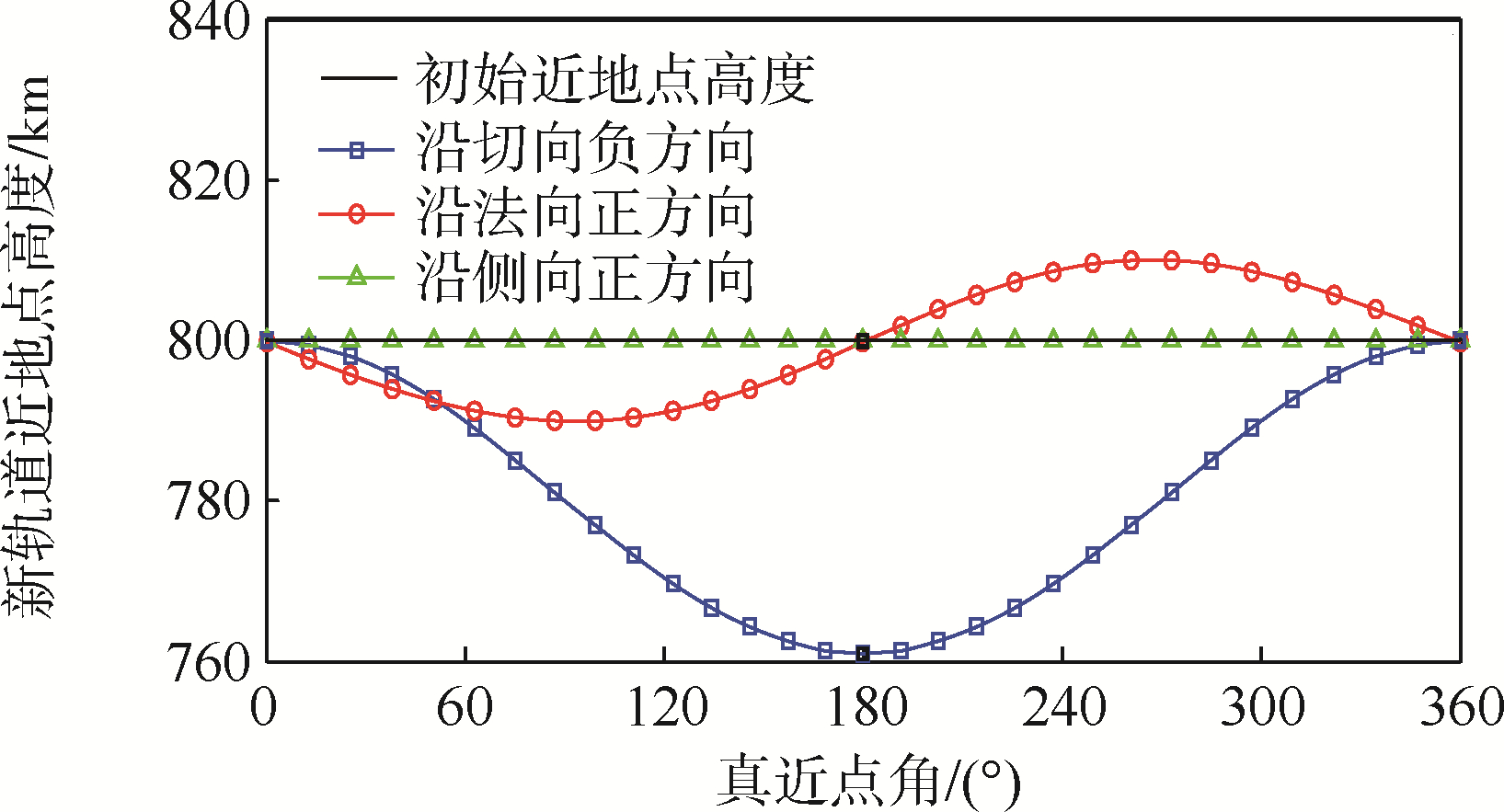 |
| 图 4 3个速度分量变化的影响程度对比Fig. 4 Comparison of influence degree of changing three different velocity components |
| 图选项 |
图 4表明,在切向、法向和侧向3个速度分量影响下,改变切向速度对新轨道的hP影响程度(相同速度增量下,hP的绝对变化量)最为显著,法向速度影响程度次之,侧向速度影响最弱.
2 变轨区域和速度增量的确定2.1 确定变轨区域根据第1节中的结论,就地基激光站而言,法向速度vσ只能增加,因此在f∈(0°,180°)轨道阶段变轨有利于降低新轨道的hP;选取合适的激光站位置,切向速度可以减小,在真近点角为(0°,180°)和(180°,360°)轨道阶段都可以降低新轨道的hP;因此,在相同速度增量的前提下,为了有效降低新轨道的hP,应该选择真近点角f∈(0°,180°)的范围内实施变轨.
由于切向速度vτ的变化对新轨道的hP影响显著,且侧向速度vn一旦出现就会升高新轨道的hP,因此脉冲速度增量Δv应该与碎片的速度v成钝角,且尽量减小其与轨道平面的夹角φ,即尽可能地减小侧向速度增量的产生.
此外,由于地基激光站布置在地面,受到地球的影响,激光器的作用范围只能在地平面以上的空间区域内,而且激光束也受到有效作用距离hef的限制.
为了实现地基激光清除空间碎片的目的,需要确定对碎片实施变轨的有效区域.考虑以上因素后,确定变轨区域的示意图如图 5所示:激光站L位于初始轨道平面内(激光站可以不在轨道平面内,该假设是为了方便说明),其相应的真近点角为f0.O为地心,rL为激光站的矢径,rLS为从激光站L指向碎片S的激光束,在利用激光产生脉冲速度增量Δv时,假定Δv与rLS同向.
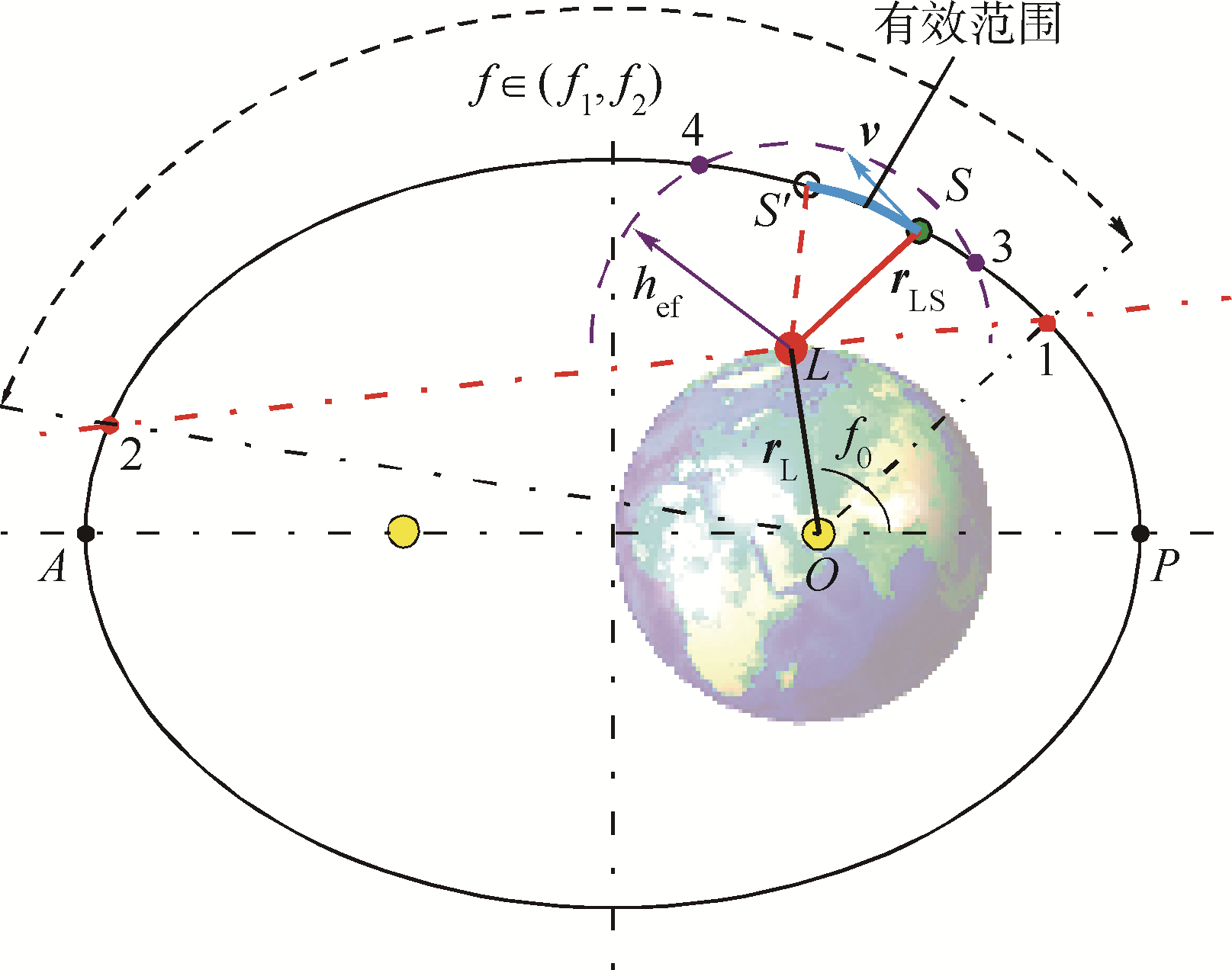 |
| 图 5 确定变轨区域示意图Fig. 5 Diagram of determining orbit transfer area |
| 图选项 |
确定变轨区域有效范围约束条件和基本算法如下.
1) 水平视场范围[f1,f2].
过L作垂直rL的直线交椭圆轨道与1、2两点,交点对应的真近点角分别为f1和f2,则[f1,f2]称为激光站的水平视场范围.在数学上,可用rL·rLS≥0表示该物理含义.
2) 激光束有效作用距离hef.
以L为圆心,hef为半径作圆,交椭圆轨道于3、4两点,则3、4之间的轨道部分处于激光束的有效作用距离以内.在数学上为:rLS≤hef.
3) 激光束与速度v夹角.
为了减小切向速度增量,脉冲速度增量Δv与速度v的夹角应该大于90°,即激光束与速度v的夹角是钝角,如图 7中S与S′之间的轨道部分,在数学上表达为rLS·v<0.
4) 激光束与轨道平面夹角.
碎片轨道平面的法向量可用角动量h=r×v表示,因此激光束与轨道平面夹角φ可以表示为φ=|π/2-arccos(eh·erLS),其中:eh和erLS分别为h和rLS的单位向量.为了尽可能减小侧向速度分量,可以对φ进行限制,即φ<φ0,φ0为设定的小角度.
2.2 确定速度增量由于激光器的单次脉冲总能量恒定,对不同轨道高度的碎片产生的冲量是不同的,即脉冲速度增量的大小也是随轨道高度的改变而变化的.假定在激光束有效作用距离内,激光器可以精确聚焦到碎片上.根据文献[15],碎片所获得的速度增量大小Δv与其轨道高度(也即激光器焦距z)的关系推导如下.
远场激光束光斑直径ds与发射镜直径Db的关系为

式中:ag为光束常数;N为衍射极限倍数;λ为波长;下标s和b分别表示远场和近场;z为激光器焦距.
近场功率密度Ib与脉宽为τb的激光单脉冲能量Eb的关系为

远场功率密度Is与近场功率密度Ib的关系为
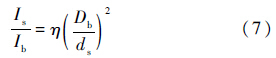
式中:η为大气能量传输效率.
注入靶材表面的能量密度Fs为

单脉冲获得速度增量的大小Δv为

式中:Cm为冲量耦合系数;AS为碎片面积;m为碎片质量.
联立式(5)~式(9),得到Δv与z的关系为
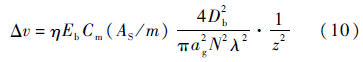
式(10)表明,当激光单脉冲能量Eb和其他常数不变,且把空间碎片视为无质量变化和姿态变化的系统时,即空间碎片的面质比(AS/m)保持不变,激光脉冲冲量完全转化为沿着激光束方向的速度增量,碎片获得的Δv与z的平方成反比.
若激光器在激光束有效作用距离hef处产生的速度增量为Δv0,则在有效作用距离以内的任意位置,激光器产生的速度增量大小为
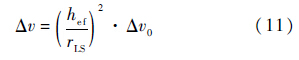
3 仿真实验及结果分析由于激光能量有限,一次脉冲产生的速度增量不足以使碎片新轨道的hP降低到能在大气层中迅速烧毁的高度.因此,为了达到清除碎片的目的,需要对其进行连续脉冲变轨.
3.1 仿真实验方案为了方便进行仿真计算,对该问题进行模型简化:
1) 考虑地球自转和非球形(J2摄动)的影响,不考虑其他摄动力,此时碎片的运动满足摄动方程式(12).
2) 地基激光站固定在地球表面,并且给定经纬度.
3) 激光器可以自主变焦寻得,即只要满足变轨条件,激光器总能准确聚焦在碎片上.
4) 激光辐照在碎片表面产生的速度增量沿着激光束的方向.
5) 碎片面质比保持不变.
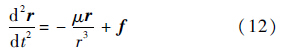
式中:f为摄动力;r为失径r的长度.
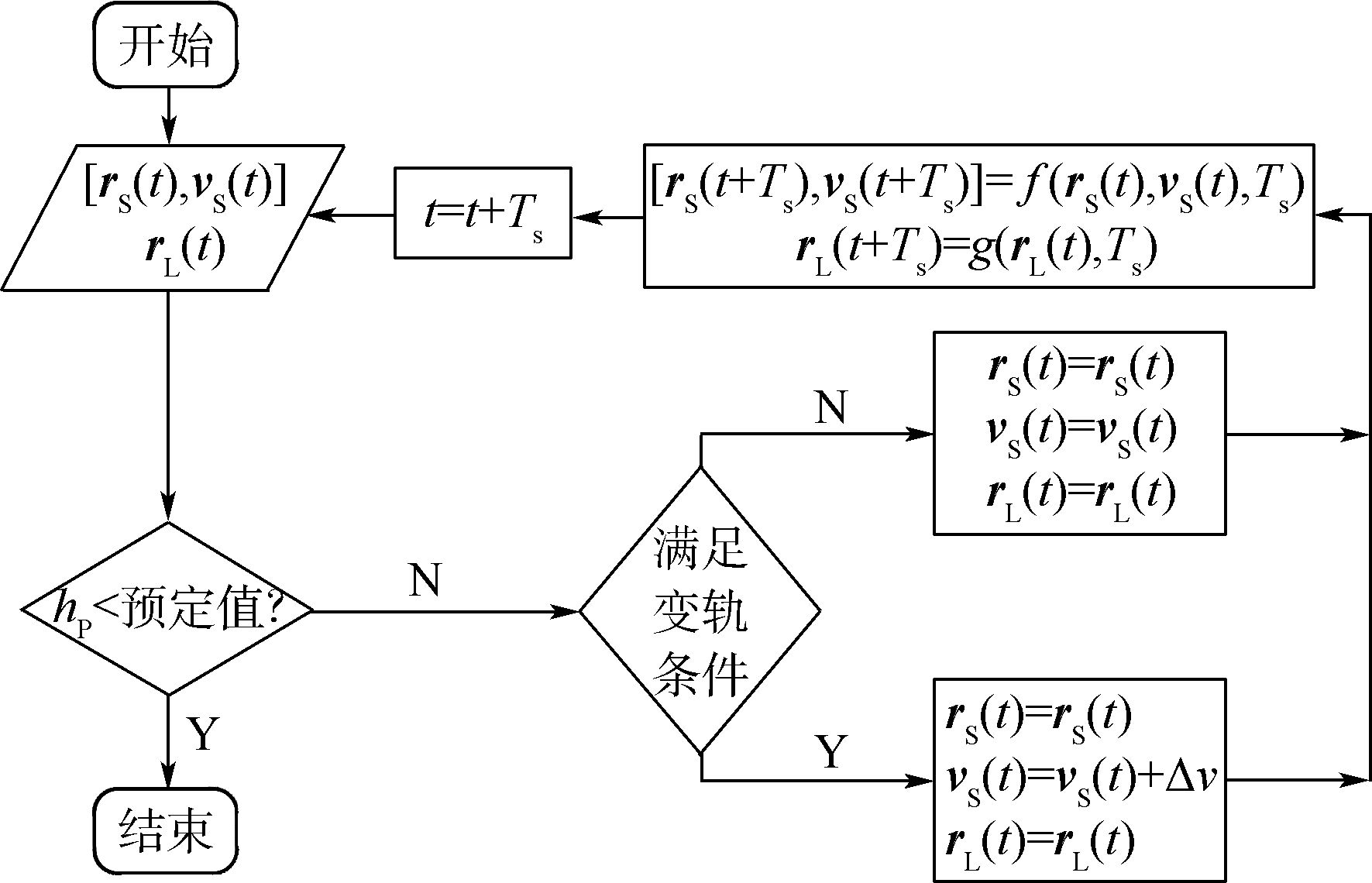
在该简化模型的基础上,连续脉冲变轨仿真计算的流程如图 6所示.
 |
| 图 6 连续脉冲变轨仿真计算流程图Fig. 6 Simulating calculation flow diagram of orbit transfer by continuous impluse |
| 图选项 |
1) 根据给定空间碎片的初始轨道参数和地基激光站的经纬度,将其转换成地球赤道惯性坐标系下的空间碎片位置rS(t)、速度vS(t)以及激光站的位置rL(t).
2) 根据空间碎片位置rS(t)和速度vS(t),计算此时轨道的hP.若hP比预定值小,空间碎片在大气阻力的作用下会很快烧毁,结束计算;否则,进入下一步骤.
3) 根据空间碎片位置rS(t)和速度vS(t)以及激光站的位置rL(t),判断此时是否满足变轨条件.若满足变轨条件,保持rS(t)和rL(t)不变,令vS(t)变成vS(t)+Δv;否则,rS(t)、rL(t)和vS(t)都保持不变.
4) 利用摄动方程进行数值积分,求解一个积分步长Ts后空间碎片位置rS(t+Ts)和速度vS(t+Ts);并根据地球自转,计算Ts时间后激光站的位置rL(t+Ts).(注:如果满足变轨条件,积分步长Ts应该不大于激光器的脉冲周期TL;否则,积分步长Ts可以适当取较大的值,本文取为脉冲周期TL的整数倍.)
5) 把更新后的空间碎片位置rS(t+Ts)、速度vS(t+Ts)以及激光站的位置rL(t+Ts)返回步骤2),继续计算,直至循环结束.
3.2 仿真结果分析为了验证仿真计算方案的有效性,下面举例进行验证,所需实验参数如表 1所示.
表 1 实验参数列表Table 1 Experiment parameters list
| 类别 | 参数名称 | 数值 |
| 初始轨道 | 近地点高度hP/km | 800 |
| 远地点高度hA/km | 1 200 | |
| 轨道倾角i/(°) | 30 | |
| 升交点赤经Ω/(°) | 80 | |
| 近地点辐角ω/(°) | 0 | |
| 过近地点时间τ/s | 0 | |
| 轨道周期Tg/s | 6 306.9 | |
| 地基激光站 | 激光站经纬度/(°) | E120°,N30° |
| 激光器频率fL/Hz | 10 | |
| 有效作用距离hef/km | 1 500 | |
| hef处激光单脉冲速度增量大小Δv0/(km·s-1) | 1.078×10-5 | |
| 地球 | 地心引力常数μ/(km3·s-2) | 3.986 004 36×105 |
| 地球平均半径Re/km | 6 378.14 | |
| 自转周期Te/s | 86 164 | |
| 仿真程序 | 近地点高度预定值h0/km | 150 |
| 仿真步长Ts/s | 0.1 | |
表选项
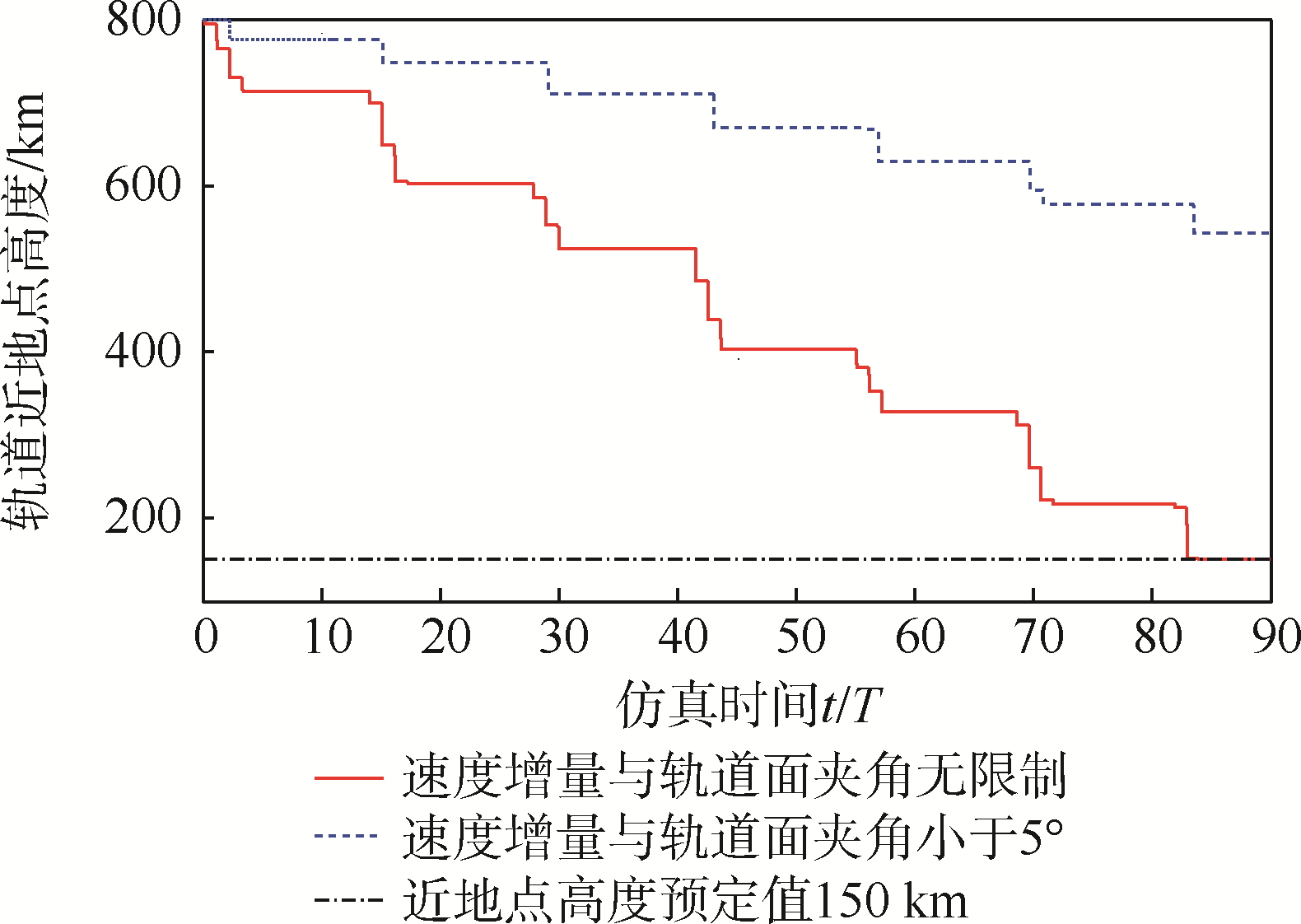
经过仿真计算,在考虑速度增量与轨道面夹角的限制与否的两种工况下,轨道近地点高度随时间的变化趋势如图 7所示.
 |
| 图 7 轨道近地点高度随时间变化曲线Fig. 7 Orbital perigee height curves over time |
| 图选项 |
如图 7所示,一座地基激光站在φ无限制的工况下,经过连续的脉冲作用,成功地将碎片的近地点高度从800 km降到150 km.即在该简化的模型下,可以成功实现地基激光清除空间碎片的目的.
仿真计算总时间为90个初始轨道周期,共计157.678 1 h,两种工况下碎片的清除效果如表 2所示.
表 2 两种工况下碎片清除效果比较Table 2 Comparison of debris removal effect under two different operating conditions
| 工况 | 脉冲总数/个 | 速度增量总和/(km·s-1) | 激光有效作用时长/s | hP减少量/km |
| φ无限制 | 24 238 | 0.468 6 | 2 423.8 | 650.0 |
| φ<5° | 8 051 | 0.168 8 | 805.1 | 255.4 |
表选项
此外图 7也表明,地基激光站在两种工况下的有效作用时段大致相同,但是在φ<5°工况下变轨区域的有效范围更加狭窄,该工况下的有效作用时长明显小于φ不受限制工况下的有效作用时长,因而在相同的90个初始轨道周期内,地基激光站在φ<5°工况下不能把碎片的近地点高度从800 km降到150 km.因此,在实际情况下地基激光站采用共面变轨方式(即φ=0°的情况)清除空间碎片是难以实现的.这也验证了本文提出空间碎片清除策略更加有效.
4 结 论本文主要讨论了利用地基激光清除空间碎片的策略:
1) 不同速度分量的变化对新轨道近地点高度的影响是不同的.其中,切向速度分量变化的影响最为显著,法向速度分量次之,侧向速度分量影响最小.
2) 对于不同位置、不同视角的空间碎片,需要根据地基激光站的特性来确定实施变轨的有效区域.
3) 仿真结果表明连续脉冲变轨降低轨道近地点高度的策略方案更加有效,可行性更高.
本文忽略了大气阻力、空间碎片面质比变化以及激光器实际工作条件等因素的影响,仿真模型相对简单,有待于日后进一步完善.
参考文献
| [1] | Kaplan M H.Survey of space debris reduction methods[C]//AIAA SPACE 2009 Conference and Exposition.Reston:AIAA, 2009:1-11. |
| Click to display the text | |
| [2] | Phipps C R, Baker K L, Libby S B, et al.Removing orbital debris with lasers[J].Advances in Space Research, 2012, 49(9):1283-1300. |
| Click to display the text | |
| [3] | Campbell J W, Taylor C R.Ground-based laser propulsion for orbital debris removal[C]//Space Technology and Applications International Forum-1998.Meville, New York:AIP Publishing, 1998, 420(1):1212-1218. |
| Click to display the text | |
| [4] | Smith E S, Sedwick R J, Merk J F, et al.Assessing the potential of a laser-ablationpropelled tug to remove large space debris[J].Journal of Spacecraft and Rockets, 2013, 50(6):1268-1276. |
| Click to display the text | |
| [5] | 李清源.强激光对飞行器的毁伤效应[M].北京:中国宇航出版社, 2012:192-193. Li Q Y.Damage effects of vehicles irradiated by intense lasers[M].Beijing:China Astronautic Publishing House, 2012:192-193(in Chinese). |
| [6] | Campbell J W.Project ORION:Orbital debris removal using ground-based sensors and lasers, NASA-TM-108522[R].Hampton, VA:NASA Technical Memorandum, 1996. |
| Click to display the text | |
| [7] | Phipps C R, Albrecht G, Friedman H, et al.ORION:Clearing near-earth space debris using a 20 kW, 530 nm, earth-based, repetitively pulsed laser[J].Laser and Particle Beams, 1996, 14(1):1-44. |
| Click to display the text | |
| [8] | Phipps C R.ORION:Challenges and benefits[C]//Proceedings of SPIE, the International Society for Optical Engineering.Bellingham, WA:SPIE, 1998, 3343:575-582. |
| Click to display the text | |
| [9] | Early J T, Bibeau C, Phipps C.Space debris de-orbiting by vaporization impulse using short pulse laser[C]//Proceedings of SPIE, the International Society for Optical Engineering.Bellingham, WA:SPIE, 2004, 5448(1):441-452. |
| Click to display the text | |
| [10] | Rubenchik A M, Barty C P J, Beach R J, et al.Laser systems for orbital debris removal[C]//AIP Conference Proceedings.Meville, New York:AIP Publishing, 2010, 1278(1):347-353. |
| Click to display the text | |
| [11] | 金星,洪延姬,李修乾.cm级空间碎片的激光清除过程分析[J].强激光与粒子束, 2012, 24(2):281-283. Jin X, Hong Y J, Li X Q.Removal processes analysis of centimeter-scale space debris using laser irradiation[J].High Power Laser and Particle Beams, 2012, 24(2):281-283(in Chinese). |
| Cited By in Cnki (1) | |
| [12] | 常浩,金星,洪延姬,等.地基激光清除空间碎片过程建模与仿真[J].航空学报, 2012, 33(6):994-1001. Chang H, Jin X, Hong Y J, et al.Modeling and simulation on ground-based lasers cleaning space debris[J].Acta Aeronautica et Astronautica Sinica, 2012, 33(6):994-1001(in Chinese). |
| Cited By in Cnki (8) | |
| [13] | 徐浩东,李小将,张东来.地基激光辐照空间碎片降轨模型研究[J].现代防御技术, 2012, 40(3):18-23. Xu H D, Li X J, Zhang D L.Deorbit and capture model of ground-based laser irradiating space debris[J].Modern Defence Technology, 2012, 40(3):18-23(in Chinese). |
| Cited By in Cnki | |
| [14] | 金星,洪延姬,常浩.地基激光清除椭圆轨道空间碎片特性的计算分析[J].航空学报, 2013, 34(9):2064-2073. Jin X, Hong Y J, Chang H.Simulation analysis of removal of elliptic orbit space debris using ground-based laser[J].Acta Aeronautica et Astronautica Sinica, 2013, 34(9):2064-2073(in Chinese). |
| Cited By in Cnki (1) | |
| [15] | 洪延姬,金星,王广宇,等.激光清除空间碎片方法[M].北京:国防工业出版社, 2013:51-52. Hong Y J, Jin X, Wang G Y, et al.Methods of space debris removal by laser[M].Beijing:National Defense Industry Press, 2013:51-52(in Chinese). |
