有关无动力飞行器着陆轨迹设计的研究,吸引了国内外****的广泛关注.文献[3]针对X-34通过解决两点边界值问题,采用轨迹推演计算方法设计了进场着陆轨迹.文献[6, 7]针对RLV通过轨迹几何参数迭代并采用轨迹拓展的方法设计了能量管理段和进场着陆段的轨迹.文献[8]针对某RLV应用能量分析法对能量消耗进行分析,设计了包括S型转弯段、航向校正圆柱过渡段和下滑拉平着陆段的投放轨迹.文献[9]采用hp自适应伪谱法对无动力飞行器的着陆轨迹进行了设计.然而现有的文献在设计着陆轨迹的过程中,通常不考虑气动舵面对着陆轨迹的影响,不考虑RLV在着陆全程是否有足够的舵面调节余量,也不考虑飞行器的构型变化引起的气动特性变化对着陆性能的影响,甚至忽略了RLV沿设计的轨迹飞行是否有足够的时间放下起落架(包括正常放下和故障情况下应急放下)等重要因素.但飞行器的气动舵面偏转可操纵范围、构型变化及起落架放下过程却对于飞行器能否安全着陆具有较大影响[10, 11, 12],因此设计着陆轨迹时不可忽略.
常规飞机着陆轨迹通常采用下滑/指数拉平形式,而对于航天飞机、X-34、X-37B等具有小升阻比、无动力特性的高超声速飞行器的进场着陆轨迹常采用深下滑/圆弧拉起/指数拉起/浅下滑形式[13].本文针对变构型多操纵面RLV,考虑气动舵面调节余量和构型变化对飞行器着陆性能的影响,在对起落架放下时间、拉平法向过载及接地动压进行约束限制的情况下,基于质点动力学方程优化设计深下滑着陆轨迹和由圆弧拉起/指数拉起/浅下滑轨迹组成的拉平着陆轨迹.
1 进场着陆轨迹RLV进场着陆轨迹由深下滑段着陆轨迹和拉平段着陆轨迹组成,其中深下滑段着陆轨迹是一条斜直线,拉平段着陆轨迹是由3条平滑连接的曲线组成,分别为圆弧拉起轨迹、指数拉起轨迹和浅下滑轨迹,着陆轨迹如图 1所示.在深下滑段RLV以固定的轨迹倾角保持恒定的动压,拟平衡下滑飞行.为了使RLV接地升降速度较小,RLV接地时需有较小的轨迹倾角.圆弧拉起段的作用是逐渐减小轨迹倾角,使深下滑段较大的轨迹倾角过渡到浅下滑段较小的轨迹倾角.为避免圆弧拉起段过渡到浅下滑段时引起法向加速度突跳,引入指数拉起段,以使法向加速度平稳过渡到浅下滑段[3].
 |
| 图 1 RLV进场着陆轨迹Fig. 1 RLV approach and landing trajectory |
| 图选项 |
图 1中,在地面坐标系Odxdydzd中建立RLV进场着陆轨迹,原点Od为理论接地点,Odxd沿跑道中心线与着陆方向同向,Odyd在含跑道中心线的铅垂面内指向上方,Odzd由右手螺旋法则确定.A点为深下滑起始点;E点为浅下滑轨迹的结束点,在轴Odyd上;B点、C点、D点分别为相邻两条轨迹的交点;O点为圆弧圆心；r为圆弧半径;点A、B、C、D、E、O的坐标分别为(R0,H0)、(R1,H1)、(R2,H2)、(R3,H3)、(R4,H4)、(a,b);点B、C、E处的轨迹倾角分别为θ1、θ2、θ3.
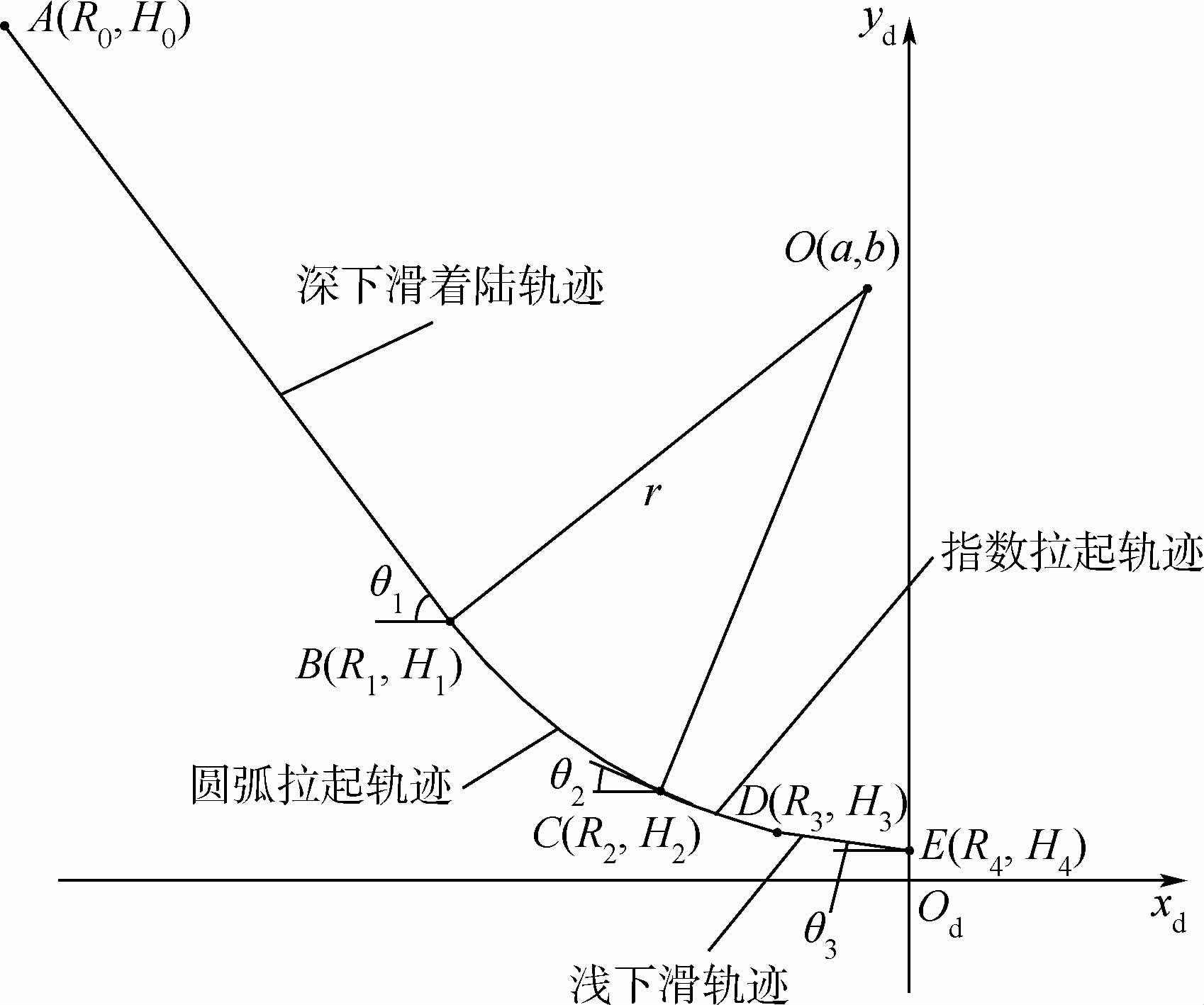
着陆轨迹的相邻轨迹平滑连接,其数学表达式是高度对距理想接地点距离的分段连续函数.
深下滑着陆轨迹:
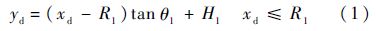
圆弧拉起轨迹:
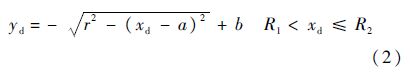
指数拉起轨迹:
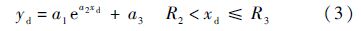
浅下滑轨迹:
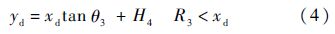
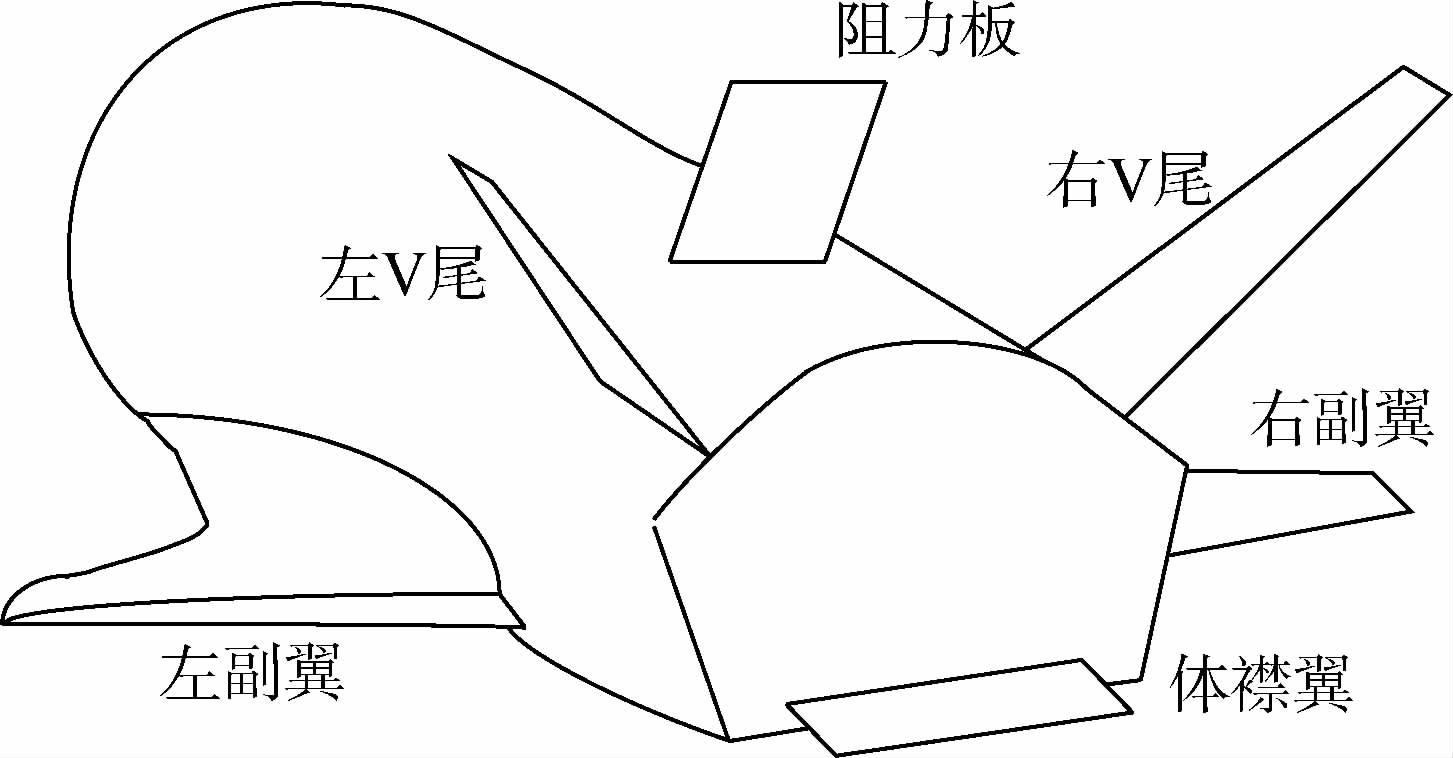
2 RLV多操纵面配置与控制RLV进场着陆,无动力为其特点,通过操纵相关舵面实现着陆飞行.RLV一般具有多操纵面,包括左右V尾、左右副翼、阻力板和体襟翼,如图 2所示.
 |
| 图 2 RLV气动外形Fig. 2 RLV aerodynamic configuration |
| 图选项 |
图 2中,左右V尾异向偏转实现升降舵(δe)操纵功能,同向偏转实现方向舵(δr)操纵功能;左右副翼同向偏转实现襟翼(δea)操纵功能,异向偏转实现副翼(δa)操纵功能；体襟翼(δbf)置于适当的位置,起增升和配平作用.
RLV进场着陆过程中,通过控制升降舵偏转,改变迎角,从而改变升力,实现高度跟踪控制;通过阻力板(δsb)偏转来改变飞行器阻力,实现速度控制.
在深下滑段,升降舵和阻力板偏角应尽量靠近中立位置,以便在飞行器具有气动参数误差及风干扰情况下,飞行器仍具有足够的控制操纵能力.因此在设计深下滑着陆轨迹时,应考虑相应舵面的偏转位置.
在拉平段,为增升需要,襟翼将逐渐增加偏角,起落架在满足飞行状态条件后开始释放,应保证在接地前起落架释放到位.襟翼偏角变化和起落架释放称为构型变化.构型变化对飞行器的气动有较大的影响,因此在着陆轨迹设计时应考虑构型变化.
3 深下滑着陆轨迹
3.1 深下滑拟平衡方程由于RLV的升阻比较小,其下滑倾角通常较大[14, 15].在深下滑段,RLV以较大的下滑角固定的动压直线下滑,纵向所受的力包括升力Y、阻力X和自身重力mg,受力分析如图 3所示.图 3中，xt为机体轴系的x轴，沿机身轴线或机翼平均气动弦线指向前方；xq为气流轴系的x轴,沿飞行速度矢量V指向前方.
 |
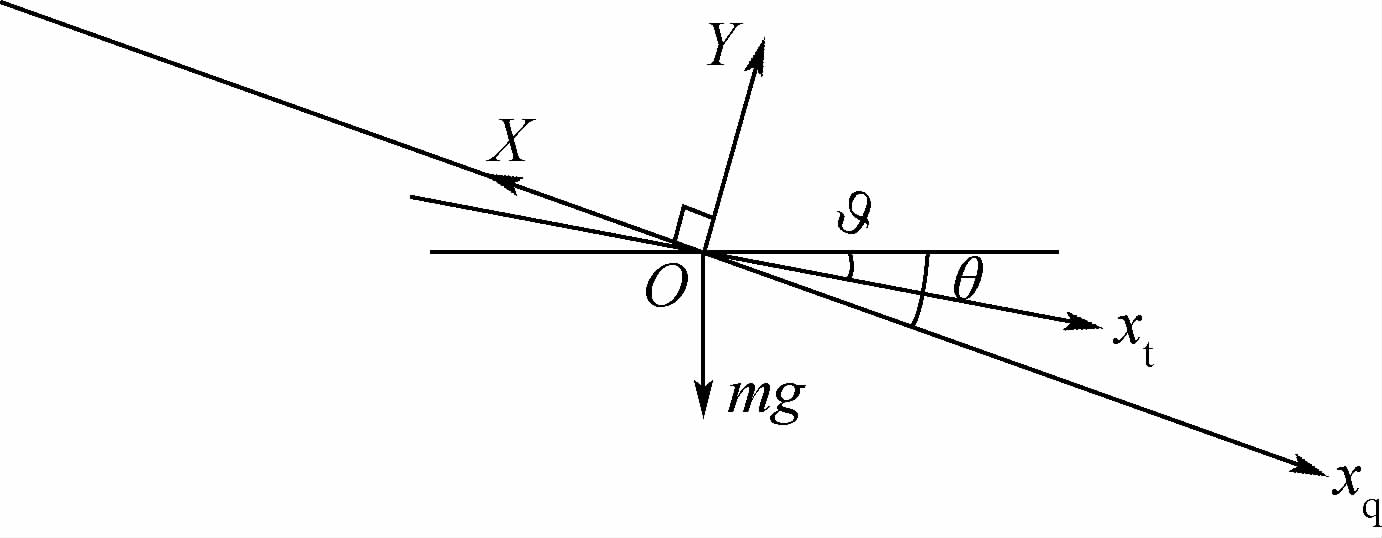| 图 3 深下滑段RLV受力分析Fig. 3 Force analysis for RLV in steep-glide phase |
| 图选项 |
根据理论力学刚体质心动力学和运动学理论,在气流坐标系中建立质心动力学方程:
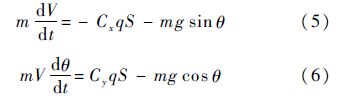
式中:动压q=ρV2/2,ρ为空气密度,V为速度;m、g、S和θ分别为质量、重力加速度、机翼面积、下滑轨迹倾角;Cx和Cy分别为阻力系数和升力系数.
根据刚体转动动力学定理,在机体坐标系中建立绕质心转动的动力学方程:
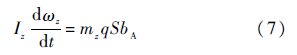
式中:ωz为俯仰角速度;bA为机翼的平均气动弦长;Iz和mz分别为飞行器绕机体轴Ozt的转动惯量和俯仰力矩系数.
将动压q对时间t求导得
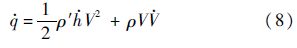
式中:ρ′为空气密度ρ对高度h的导数.
将式(8)代入式(5),整理得
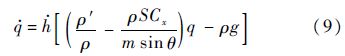
RLV以固定的动压q直线下滑,则RLV满足以下关系:
RLV在下滑过程中纵向合力矩为0,则
式(10)～式(12)构成深下滑拟平衡条件.
系数Cx、Cy、mz与飞行器起落架状态、迎角及各气动舵面偏角相关.
3.2 深下滑着陆轨迹优化设计在设计深下滑着陆轨迹时,RLV横侧向状态量和舵面偏角均为0.设计深下滑轨迹的过程即寻找合适的参数q、θ、α、δe、δea、δbf、δsb使得深下滑拟平衡条件成立,同时各气动舵面配平偏角尽量靠近中立位置.
为使各气动舵面有充足的偏转空间,分别将升降舵俯仰力矩中值位δe*、阻力板阻力中值位δsb*、襟翼的中立位置、体襟翼的中立位置作为基准值.将各气动舵面偏离基准值的程度作为待优化的性能指标,因此优化目标函数为
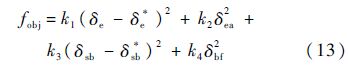
式中：k1、k2、k3、k4分别为加权系数.
参数q、θ、α、δe、δea、δbf、δsb的取值范围如下:
其中:*min和*max分别代表相应参数可能的最小值和最大值.
采用遗传算法在取值范围内进行寻优,在满足约束条件式(10)~式(12)的情况下,使得目标函数最小.
深下滑着陆轨迹参数H1和R1与拉平轨迹相关,在拉平着陆轨迹的优化设计过程中确定.
4 拉平着陆轨迹4.1 拉平着陆轨迹生成对于进场着陆轨迹,相邻两段的着陆轨迹平滑连接,即连接点处轨迹倾角、高度和距原点的距离均相同.根据几何关系建立以下方程:
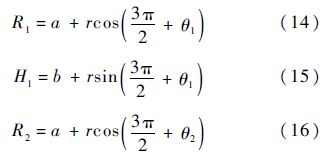
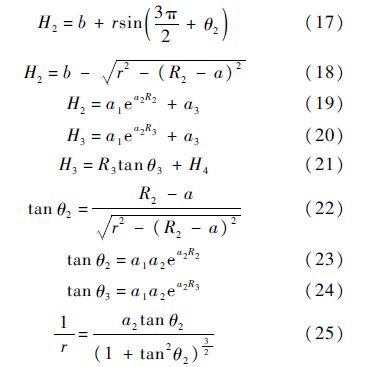
式中:H4为RLV接地时重心高度;圆弧半径r由RLV进入圆弧拉起点的飞行速度Vkcirc及法向加速度aycirc确定,即
其中:
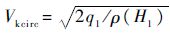为拉平起始点动压.对于浅下滑轨迹倾角θ3,θ3和飞行器接地地速Vdt及升降速度Vyt存在以下关系:
根据接地性能要求,综合考虑飞行器允许最大接地地速Vdtmax、允许最大接地升降速度Vytmax,确定参数θ3的值.
由方程式(14)~式(26)推导出未知参数H1、H3、θ2、aycirc、r、a、b、a1、a2、a3、R1、R2、R3之间的关系式:
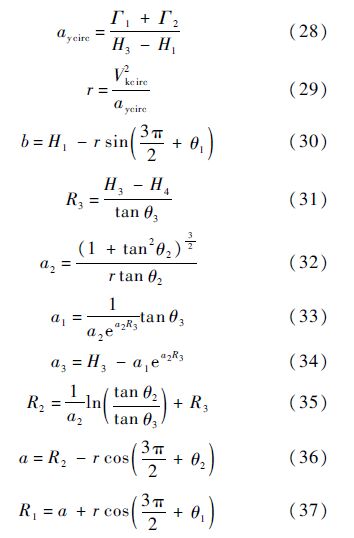
式中：
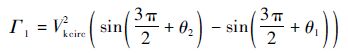
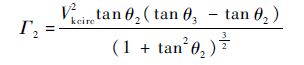
由上述关系式可知,确定参数H1、H3、θ2,即可求出aycirc、r、a、b、a1、a2、a3、R1、R2、R3的值,进而可以生成一条拉平着陆轨迹.
4.2 拉平着陆轨迹推演第4.1节给出了拉平着陆轨迹相关参数之间的关系式,只要确定参数H1、H3、θ2后,即可生成一条拉平着陆轨迹.RLV沿该轨迹飞行是否满足着陆要求,需基于质点动力学方程通过轨迹推演的方法来判断.对于任意一条拉平着陆轨迹,可把高度划分为若干等份,对于每等份高度点,仅存在唯一的动压及迎角使飞行器达到瞬时平衡.对每条着陆轨迹,飞行器接地动压唯一.
以下将RLV在速度轴系中的质点动力学方程由基于时间的质点动力学方程转换成基于高度的质点动力学方程,整理式(6)和式(9)得
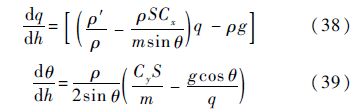
整理式(39)得
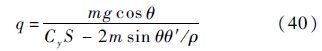
式中：θ′=dθ/dh为轨迹倾角对高度的导数,θ与θ′的表达式分别为
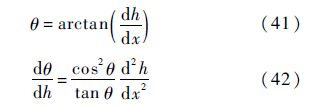
那么对于圆弧拉起轨迹、指数拉起轨迹和浅下滑轨迹关于轨迹倾角θ和轨迹倾角对高度的导数θ′的数学表达式分别为
圆弧拉起轨迹:
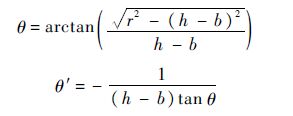
指数拉起轨迹:
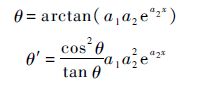
由于
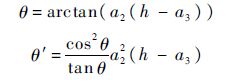
浅下滑轨迹:
θ=θ3
θ′=0
可见动压q及动压对高度的导数q′仅与高度h和力系数Cx、Cy相关,其中Cx、Cy与飞行器起落架状态、迎角α及各气动舵面偏角相关.
将拉平段的高度等分为n份,每等份的高度增量为Δh,第k等份对应的高度为
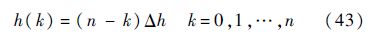
高度h(k)处动压q(k)的求法有两种方式,分别为基于式(38)和式(40),其中基于式(38)计算的动压为
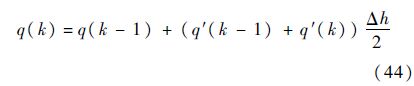
式中:q(k－1)、q′(k－1)分别为前一个高度的动压和动压对高度的导数；q(k)、q′(k)分别为当前高度的动压和动压对高度的导数.
高度h(k)处地速为
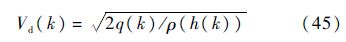
已知高度h(k)处的轨迹倾角θ(k),则升降速度为
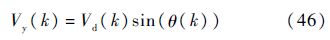
则RLV高度降低Δh的时间为
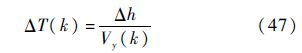
RLV沿拉平着陆轨迹的飞行时间为
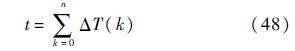
在进行轨迹推演时,随着陆进程的推进,各气动舵面偏角和起落架角度将发生变化,变化过程如下:
当RLV进入拉平段时,升降舵、襟翼、体襟翼和阻力板的偏角将由当前时刻对应的值经过规定的时间线性地偏至规定值,之后保持不变,各舵面偏角的变化过程为
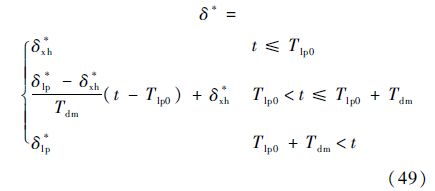
式中:Tlp0为飞行器进入拉平段的时刻;Tdm为舵面偏角变化时间;δxh*为飞行器进入下滑段时刻各舵面对应的偏角;δlp*为飞行器进入拉平段后各气动舵面的规定值.
考虑到RLV在拉平段的升阻比相比深下滑段变得更小,为减缓飞行器动压降低过快,致使迎角过大,则阻力板偏角将变小,以减小飞行器阻力;襟翼和体襟翼偏角将下偏至某个角度,以增加飞行器升力.
在拉平段,当RLV动压小于允许放下起落架最大动压qg时,起落架开始放下,起落架状态由收起状态匀速放下,起落架角度变化过程为
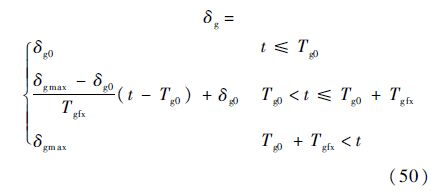
式中:Tg0为起落架满足放下条件的时刻;Tgfx为起落架放下时间;δg0为起落架收起状态角度;δgmax为起落架放下状态角度.
可见各气动舵面偏角及起落架角度与时间t相关,而时间t又与高度h相关,因此各气动舵面偏角及起落架角度与高度h相关.
对于第k个高度点,高度h(k)可求,时间t可求,则该高度点的轨迹倾角、轨迹倾角对高度的导数、各舵面偏角及起落架角度均可求.此时该高度点的力系数Cx(k)、Cy(k)变为仅关于迎角α(k)的函数,基于式(40)计算的动压qfx(k)和基于式(44)计算的动压qqx(k)也变为仅关于迎角α(k)的函数.由于
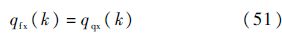
则式(51)是自变量为α(k)的一元非线性方程.采用MATLAB中函数fsolve()解非线性方程.求得迎角α(k),即可得到动压q(k),进而可得到法向过载为
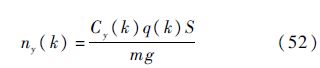
假设RLV在高度h(i)处动压q(i)≤qg,满足起落架放下条件,起落架开始释放,记起落架开始放至RLV接地的时间为Tg,即
式中:Tt为飞行器接地时刻.
从拉平起始点开始逐个高度点依次推演,直到接地.在轨迹推演过程中,保存每个高度点对应的法向过载ny,推演结束后,采用MATLAB中函数max()得到拉平最大法向过载nymax.记录最大法向过载nymax、接地动压qt、起落架开始放至RLV接地的时间Tg,为下一步拉平着陆轨迹优化设计做准备.
拉平着陆轨迹推演过程如图 4所示.
 |
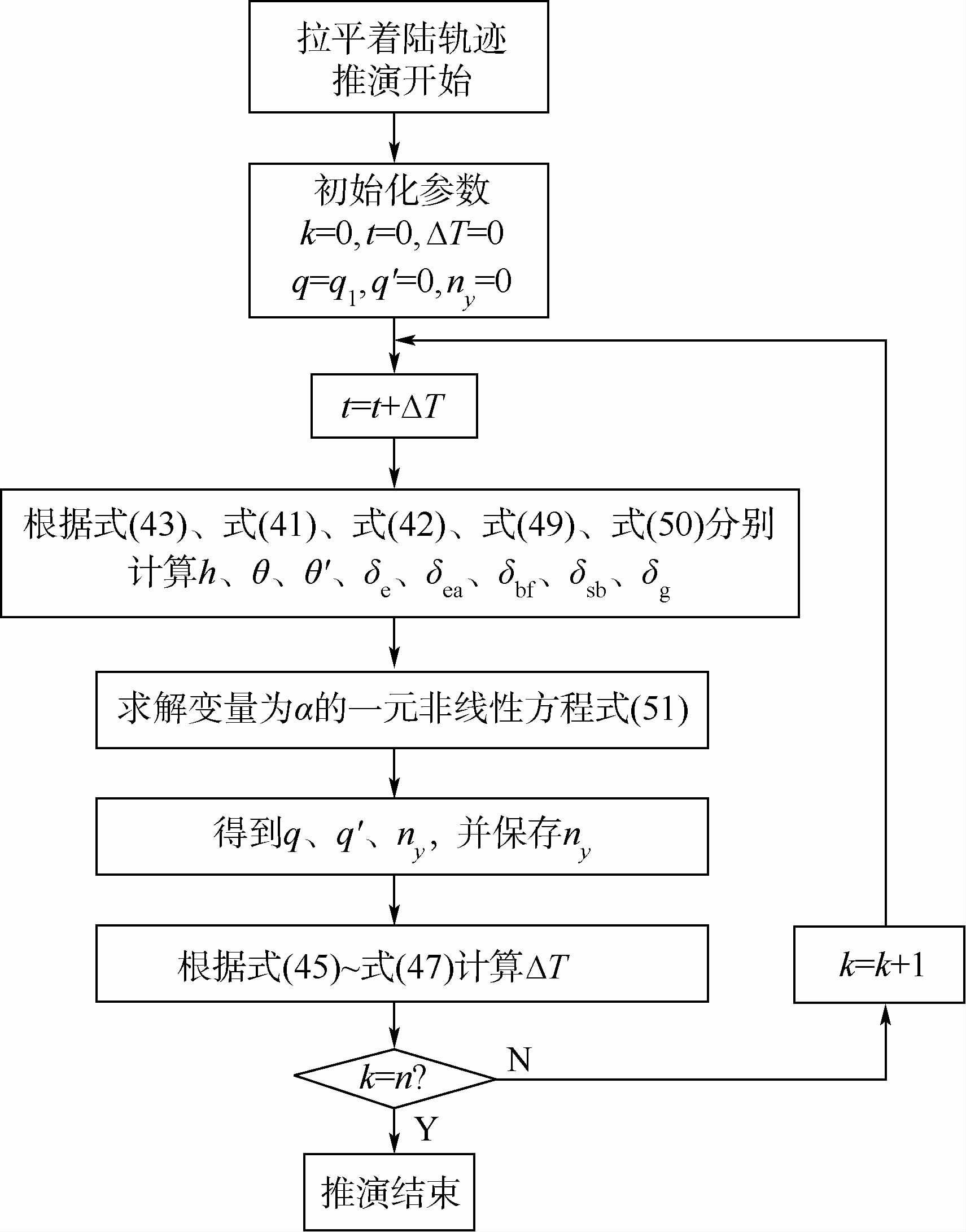| 图 4 拉平着陆轨迹推演过程Fig. 4 Process of flare landing trajectory propagation |
| 图选项 |
4.3 拉平着陆轨迹优化设计设计最优拉平着陆轨迹的过程即为选取合适的参数H1、H3、θ2,根据式(28)~式(37)求得着陆轨迹相关参数,并结合着陆轨迹方程式(1)~式(4)生成着陆轨迹,RLV沿该轨迹着陆,需保证RLV在接地前有足够的时间放下起落架,从起落架开始放下至RLV接地的时间Tg不小于规定时间TgLx,并且与其他轨迹相比,沿该轨迹飞行的最大法向过载nymax最小,同时沿该轨迹飞行的接地动压qt为理想接地动压qd.因此,可将设计最优拉平着陆轨迹的过程转换为多参数多约束优化设计问题.
优化目标函数为
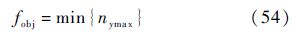
多约束条件为
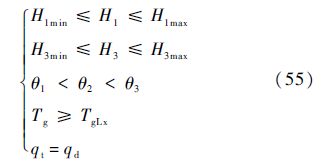
式中:H1min、H1max分别为拉平起始点高度可能的最小值和最大值；H3min、H3max分别为浅下滑轨迹起始点高度可能的最小值和最大值,这些值在优化前根据具体情况设定.
采用遗传算法在取值范围内进行寻优,在满足多约束条件(式(55))的情况下,使得优化目标函数(式(54))最小.
理想接地动压qd由理想接地状态得到.RLV在接地时刻理想情况下其法向达到瞬时平衡,即法向加速度近似为0 m/s2,则
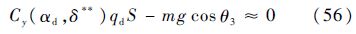
那么
式中:αd为理想接地迎角；δ**为接地时刻各舵面偏角及起落架角度.
根据迎角、俯仰角和轨迹倾角之间的关系,可知理想接地迎角：
式中:
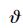d为理想接地俯仰角.理想接地俯仰角
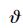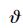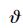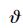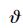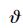d的值可根据RLV接地要求来确定.一般规定接地俯仰角t应处于[min,max]范围内,可取d=(min+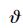max)/2,则理想接地迎角αd可确定,进而理想接地动压qd也可确定.5 算 例某多操纵面RLV深下滑起始高度为3 000 m,接地时重心高度为1.3 m.
按照第3节中方法设计深下滑着陆轨迹.
参数q、θ1、α、δe、δea、δbf、δsb的取值范围分别为：q∈[9 kPa,12 kPa]，θ1∈[-25°,-13°]，α∈[0°,18°]，δe∈[-30°,30°]，δea∈[-30°,30°]，δbf∈[-20°,20°]，δsb∈[0°,80°].
升降舵俯仰力矩中值位δe*、阻力板阻力中值位δsb*分别为-2.6°、38°,则优化目标函数为fobj=k1(δe－(－2.6))2+k2δea2+k3(δsb－38)2+k4δbf2式中:k1、k2、k3、k4的值均为1.
采用遗传算法进行寻优,在满足约束条件的情况下,使目标函数最小.优化结果为：q=10 536 Pa,θ1=-18.3°,α=4.8°,δe=-2.3°,δea=0.5°,δbf=0.2°,δsb=38.3°.
按照第4节中方法优化设计拉平着陆轨迹.
根据RLV接地性能要求,取轨迹倾角θ3为-1°,接地俯仰角为7°,则接地迎角、接地动压、接地地速、接地升降速度分别为8°、3 469 Pa、81.5 m/s、1.4 m/s.允许起落架放下最大动压qg为8 kPa,要求起落架开始放至RLV接地时间不小于21 s.拉平段阻力板偏角δsblp、襟翼偏角δealp、体襟翼偏角δbflp分别为22°、10°、13°,舵面偏角变化时间Tdm为3 s.起落架角度δg0、δgmax分别为0°、90°,起落架放下时间Tgfx为10 s.参数H1、H3、θ2的取值范围为：H1∈[300 m,500 m]，H3∈[3 m,5 m]，θ2∈(-18.3°,-1°).
采用遗传算法进寻优,轨迹参数优化结果为：H1=386.77 m，H3=4.12 m，θ2=-5.21°，aycirc=2.71 m/s2，r=7 208.54 m，a=-580.23 m，b=7 230.74 m，R1=-2 843.66 m，R2=-1 234.81 m，R3=-161.55 m，a1=8.83，a2=-1.54×10-3，a3=-7.21.
深下滑着陆轨迹和拉平着陆轨迹组成完整的进程着陆轨迹.
为检验本文的设计方法是否更优,将本文提出的方法与文献[3]的设计方法进行比较.文献[3]在设计着陆轨迹时没有考虑起落架的放下时间限制,同时也没有考虑着陆过程最大法向过载最小化的约束条件,所设计的着陆轨迹如图 5所示.
 |
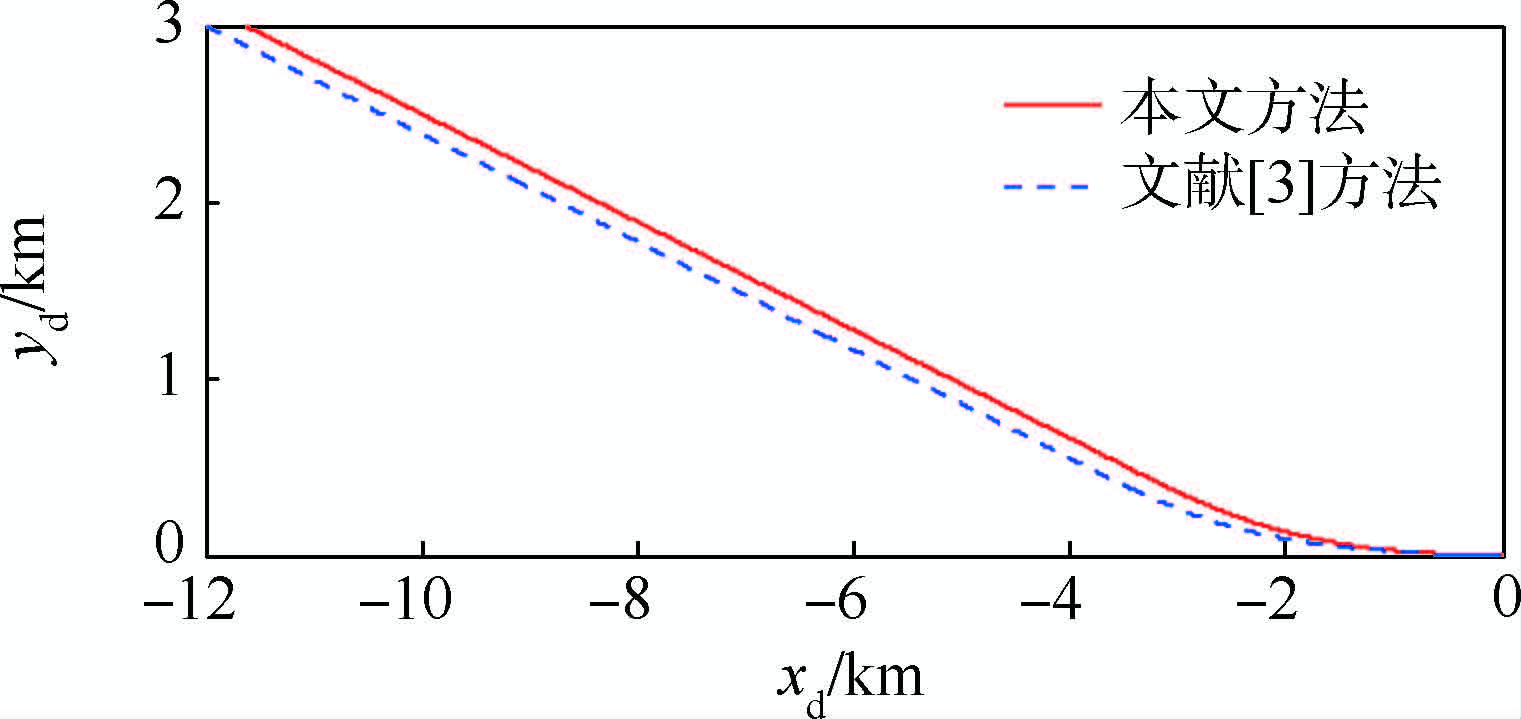| 图 5 进场着陆轨迹Fig. 5 Approach and landing trajectory |
| 图选项 |
分别对采用本文方法设计的着陆轨迹和采用文献[3]方法设计的着陆轨迹进行着陆轨迹推演,记录RLV动压q、地速Vd、升降速度Vy、迎角α、俯仰角
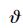、法向过载ny和起落开始架放下至RLV接地时间Tg等参数,并画出各参数的响应曲线,如图 6所示. |
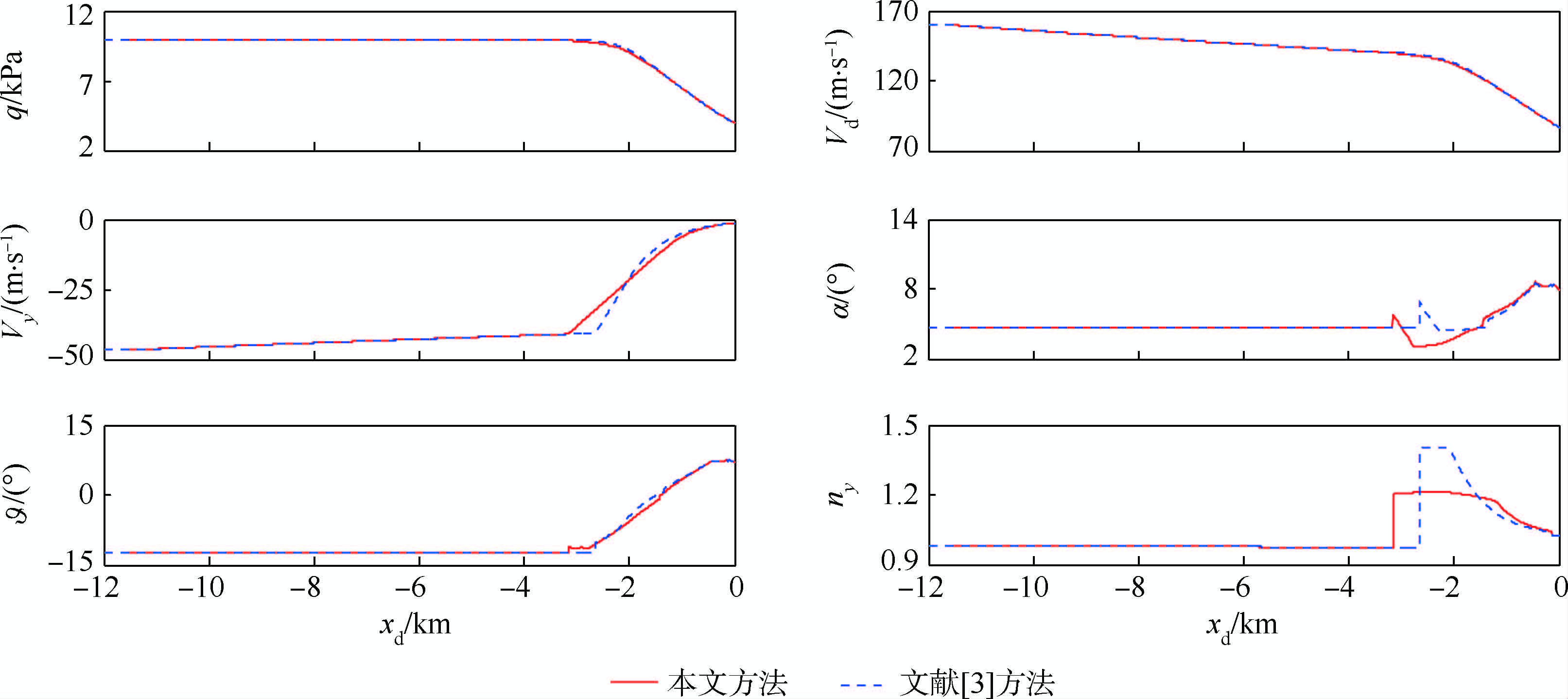| 图 6 RLV进场着陆响应曲线Fig. 6 Response curves of approach and landing for RLV |
| 图选项 |
由图 6可见,两条轨迹对应的接地状态相同,均达到设计要求,但本文方法设计的着陆轨迹对应的最大法向过载较小(本文设计过载1.21,文献[3]过载1.43),拉平过程更平稳.另外,RLV沿本文方法设计的着陆轨迹飞行,从起落架开始放至RLV接地的时间为21.7 s,满足设计要求,而沿文献[3]方法设计的着陆轨迹飞行对应的时间Tg仅为16.3 s,不满足设计要求.因此起落架放下时间限制在着陆轨迹设计过程中是必须考虑的因素.
6 结 论本文着陆轨迹设计方法全面考虑了RLV的实际舵面操纵限制、构型变化过程、放起落架时间约束,并保证着陆过程中过载最小.
1) 大的气动舵面调节余量有助于提高着陆过程飞行器对气动参数误差的适应能力,以及抵抗风干扰的控制能力.
2) 对起落架放下时间的限制,确保RLV接地前起落架释放到位.
3) 限制最大法向过载有利于提高RLV进场着陆的平稳性.
4) 考虑起落架角度及各气动舵面偏角的变化过程,使所设计的轨迹更符合实际情况.
参考文献
| [1] | Khapane P D.Simulation of asymmetric landing and typical ground maneuvers for large transport aircraft[J].Aerospace Science and Technology,2003,7(8):611-619 |
| Click to display the text | |
| [2] | Khapane P D.Gear walk instability studies using flexible multibody dynamics simulation methods in SIMPACK[J].Aerospace Science and Technology,2006,10(1):19-25 |
| Click to display the text | |
| [3] | Barton G H,Tragesser S G.Autolanding trajectory design for X-34[C]// AIAA Atmospheric Flight Conference and Exhibit.Reston:AIAA,1999:15-30 |
| Click to display the text | |
| [4] | Hanson J M,Jones R E.Test results for entry guidance methods for space vehicles[J].Journal of Guidance,Control,and Dynamics,2004,27(6):960-966 |
| Click to display the text | |
| [5] | Hanson J M.A plan for advanced guidance and control technology for 2nd generation reusable launch vehicles[C]//AIAA Guidance,Navigation and Control Conference and Exhibit.Reston:AIAA,2002:1-9 |
| Click to display the text | |
| [6] | Kluever C A,Horneman K R.Terminal trajectory planning and optimization for an unpowered reusable launch vehicle[C]// AIAA Guidance,Navigation and Control Conference and Exhibit. Reston:AIAA,2005:1-23 |
| Click to display the text | |
| [7] | Kluever C A.Unpowered approach and landing guidance with normal acceleration limitations[J].Journal of Guidance,Control,and Dynamics,2007,30(3):882-885 |
| Click to display the text | |
| [8] | 杨帆,张曙光.某RLV飞行器投放轨迹的设计与分析[J].北京航空航天大学学报,2005,31(8):843-847. Yang F,Zhang S G.Design and analysis on dropping trajectories of RLV configuration[J].Journal of Beijing University of Aeronautics and Astronautics,2005,31(8):843-847(in Chinese) |
| Cited By in Cnki (5) | Click to display the text | |
| [9] | 王宏伦,裴云峰,倪少波,等.飞行器无动力应急着陆域和着陆轨迹设计[J].航空学报,2014,35(5):1404-1415. Wang H L,Pei Y F,Ni S B,et al.Design of emergency landing reglon and landing trajectory for unpowered aircraft[J].Acta Aeronautica et Astronautica Sinica,2014,35(5):1404-1415(in Chinese) |
| Cited By in Cnki (3) | Click to display the text | |
| [10] | Das K,Purlupady C,Padhi R,et al.Optimal nonlinear control and estimation for a reusable launch vehicle during reentry phase[C]// Proceedings of 16th Mediterranean Conference on Control and Automation.Piscataway,NJ:IEEE Press,2008:47-52 |
| Click to display the text | |
| [11] | Song Y D.Guaranteed performance control of nonlinear systems with application to flexible space structures[J].AIAA Journal of Guidance,Control and Dynamics,1995,18(1):143-150 |
| Click to display the text | |
| [12] | Jiang Z S,Raul O.Trajectory generation on approach and landing for RLVs using motion primitives and neighboring optimal control[C]// Proceedings of 2007 American Control Conference.Piscataway,NJ:IEEE Press,2007:1091-1096 |
| Click to display the text | |
| [13] | Tsikalas G M.Space shuttle autoland design[C]// AIAA Guidance,Navigation and Control Conference and Exhibit.Reston:AIAA,1982,AIAA-1982-1604-CP:1-14. |
| [14] | Walyus K D,Dalton C.Approach and landing simulator for space shuttle orbiter touchdown conditions[J].Journal of Spacecraft and Rockets,1991,28(4):478-485 |
| Click to display the text | |
| [15] | Kluever C A.Unpowered approach and landing guidance using trajectory planning[J].Journal of Guidance,Control,and Dynamics,2004,27(6):967-974 |
| Click to display the text |
