从组成的个体来看,机械臂具有一定的局部感知能力、自治运动能力和对环境做出反应的能力.由于多机械臂系统与多智能体系统有着相同的结构特点,这样借助于多智能体的研究方法来研究多机械臂系统的协调控制问题可以简化问题的复杂性,能够设计出高效可行的系统控制协议.
对于多智能体的一致性问题,文献[2, 3, 4]研究了多智能体系统一致性问题,形成了多智能体系统一致性理论的框架,为解决多机械臂一致性问题提供理论支持.文献[5, 6, 7, 8]通过对领航机器人的控制使整个系统跟随它达到一致性,这种方法往往需要所有智能体都具有期望位置识别信息.但在实际应用中并不是系统中的每个个体都能具有期望的位置信息,因此运用文献[9, 10, 11, 12]中的协调方法,可以在只有一部分智能体具有期望轨迹信息的前提下使系统达到期望轨迹和一致性.
近年来,科研工作者在多机械臂系统的协调控制问题上取得了许多研究成果:Su[13]提出了一种自主式的机器人基座坐标系的标定方法;Kosuge等[14]提出了一种主从式的协调方法;然而在大多数情况下,机械臂动力学模型中的参数是很难被精确测定的,比如系统的哥氏力、转轴的转动惯量等.因此这些控制方法在实际应用中受到了很大的限制.2006年,Tayebi和Islam[15]针对单个机械臂提出了一种自适应迭代学习控制律(Adaptive Iterative Learning Control,AILC),实现了单个机械臂系统的轨迹跟踪问题.2008年,Chien和Tayebi[16]进一步提出了一种具有双参数开关结构的自适应迭代学习控制律,在实现轨迹跟踪的同时保证了跟踪误差与控制输入的有界性.这种AILC方法可以在机械臂动力学方程参数不能被精确测定的前提下使其达到期望轨迹,而不需要了解机械臂的过多先验信息.
文献[17]基于多智能体一致性的协调控制及单一机械臂的控制方法,针对具有无向连通图拓扑结构的多机械臂系统,提出的AILC使得整个系统达到一致性.然而该方法在对自适应不确定参数的迭代学习过程中只用到了一个机器人自身的状态信息,而并没有考虑到与周围相关邻居机器人的关系.因此在文献[16]的基础上本文对其控制协议进行了改进,在迭代学习过程中,同时运用了一个机器人和其相关邻居机器人的状态信息,使其具有更好的性能.
1 问题描述设G=(V,E,A)为具有n个节点的网络所对应的拓扑图,其中V={vii=1,2,…,n}表示由有限个顶点或节点组成的集合;E⊆{(vi,vj)vi,vj∈V}为边的集合,eij=(vi,vj)∈E称为边;A=[aij]∈Rn×n表示权重矩阵,其中aij表示连接权重,aij>0⇔(vj,vi)∈E.若节点出现重复,则定义其连接权重为0,即aii=0,∀i=1,2,…,n.若图G存在一个节点有达到所有其他节点的有向路径,则成图G包含一棵生成树.当aij=aji,∀i,j时,图G表示无向图.若无向图G中任意两个不同节点都可以通过有向路径连接起来,则称图G为连通的.
根据文献[3],L=[lij]∈Rn×n表示图G的Laplacian矩阵,其元素lij可定义为
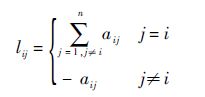
进一步,可得Laplacian矩阵L可表示为L=Δ-A
其中:Δ=diag(Δ11,Δ22,…,Δnn)
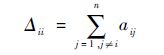
考虑拓扑结构由无向图G表示的多机械臂系统,并且其第i个机械臂的动力学方程[15]为
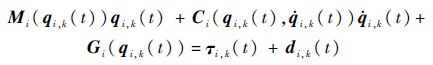
其中:i=1,2,…,n为各机器人的编号;k=1,2,…为迭代次数;t∈[0,T]为时间变量;qi,k(t)为m维状态向量;$\dot{q}$i,k(t)为m维速度向量;qi,k(t)为m维加速度向量;Mi(qi,k(t))为m×m维惯性矩阵;Ci(qi,k(t),$\dot{q}$i,k(t))为m×m维哥氏力和向心力矩阵;Gi(qi,k(t))为m维重力矩向量;τi,k(t)为m维输入向量;di,k(t)为m维未知的外部干扰.
为了便于分析,引入向量:
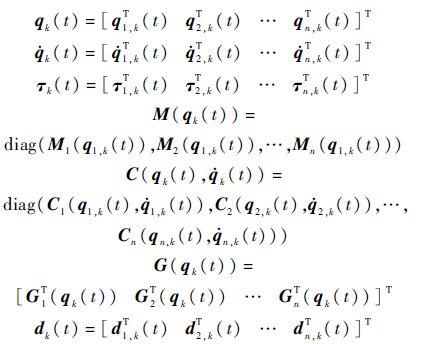
由此,可以将整个系统的动力学方程表示为
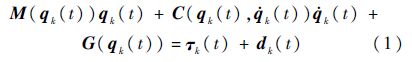
令qr(t)表示式(1)在有限时间t∈[0,T]内的期望参考轨迹.假定机械臂系统组成的拓扑为无向连通,整个机械臂系统内只有一部分机械臂可以获得qr(t)的信息.用ωi来表示第i个机械臂是否可以直接获得qr(t)的信息,即,若ωi=0则表示第i个机械臂不能直接获得期望参考轨迹的位置信息,若ωi>0则表示第i个机械臂可以直接获得期望参考轨迹的位置信息.可用正定对角矩阵Ω=diag(ω1,ω2,…,ωn)来表示各机械臂个体对qr(t)的识别情况.为了方便起见,假设qr(t)是一个虚拟机械臂领导者v0的轨迹,将v0引入无向图G中得到有向图G,并假设:
1) G有一个以v0为根节点的生成树.
2) qr(t)、$\dot{q}$r(t)、q¨r(t)有界,不失一般性,令‖qr(t)‖≤kr,‖$\dot{q}$r(t)‖≤k′r,‖qr(t)‖≤k″r.
3) qi,k(0)=qr(0),$\dot{q}$i,k(0)=$\dot{q}$r(0),∀k∈Z+.其中:kr、k′r、k″r为大于0的常数.
在假设1)~假设3)成立的前提下,一致性控制目标为设计分布式控制律使得
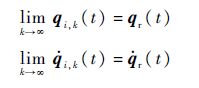
定义位置误差$\tilde{q}$i,k(t)和速度误差$\dot{\tilde{q}}$i,k(t)分别为
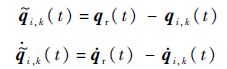
为了考察系统的稳定性以及所提出的自适应迭代学习控制方法的收敛性,在第2节讨论中,会用到‖x(t)‖pe的定义[15]:
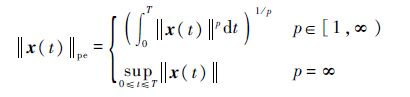
如果‖x(t)‖pe存在,那么x(t)∈Lpe.
除了假设与定义,还将用到一些机械臂系统的一些基本性质[17]:
1) M(qk(t))正定有界
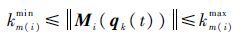
kminm(i)和kmaxm(i)是未知的有界正常数.
2) xT[$\dot{M}$i(qi,k)-2Ci(qi,k,$\dot{q}$i,k)]x=0,∀x∈Rm.
3) Ci(qi,k,$\dot{q}$i,k)≤kc(i)$\dot{q}$i,k,di,k≤kd(i)且
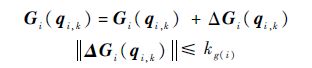
其中,kc(i)、kd(i)和kg(i)为未知有界正常数.
引理[17] 对于任意一个正定矩阵Γ∈Rm×m,(L+Ω)⊗Γ是正定的当且仅当假设1)成立.
2 多机械臂系统的一致性2.1 多机械臂分布式一致性控制律自适应迭代学习控制律设计为
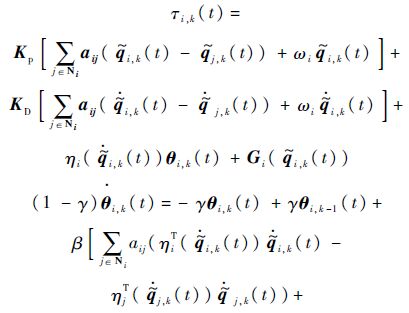
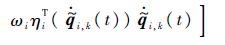
其中:Kp、KD为m×m维正定增益矩阵,0<Γ<1和β>0为标量增益;ηi($\dot{\tilde{q}}$i,k(t))为不确定性估计(具体形式将在定理1的证明中给出);θ^i,k(t)为参数估计.
经整理,上述自适应迭代学习控制律可写成向量形式:
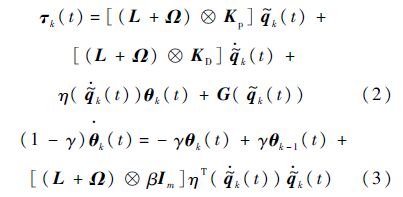
式中:
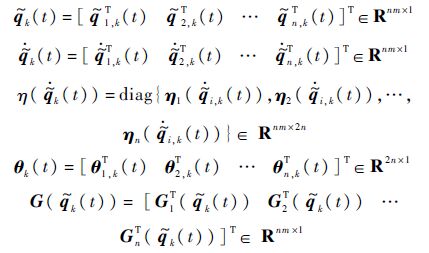
Im为m×m的单位矩阵.
容易看出,所提自适应迭代学习控制律只需了解每个机械臂及其邻居机械臂的相对信息,而不需要过多的先验知识.因此,与文献[17]中的控制律相比,具有更好的分布式结构特点.
2.2 收敛性分析下面结合单个机械臂系统自适应迭代学习控制的分析方法[15, 16],给出所提多机械臂系统分布式自适应迭代学习控制过程的收敛性结论.
定理1 式(1)中多机械臂系统,假设其满足性质1)~性质3)的前提下.若假设1)~假设3)成立,则当采用自适应迭代控制律式(2)和式(3)时,可以得到
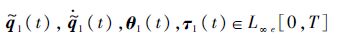
证明 由假设2)、性质1)和性质3)可得

式中:
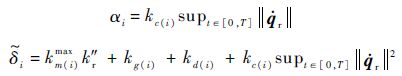
这样存在一个正常数δi∈R使得
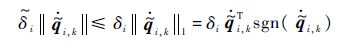
结合式(4),可进一步得到
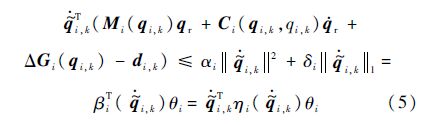
式中:
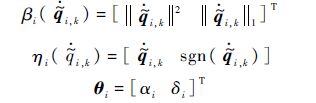
考虑如下李雅普诺夫函数:
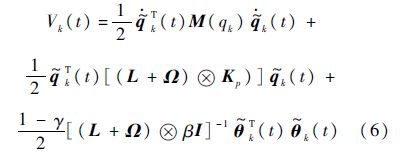
式中:$\tilde{\theta }$k(t)=θ^k(t)-θ为参数估计误差.
运用性质2),Vk(t)对于时间t的导数为
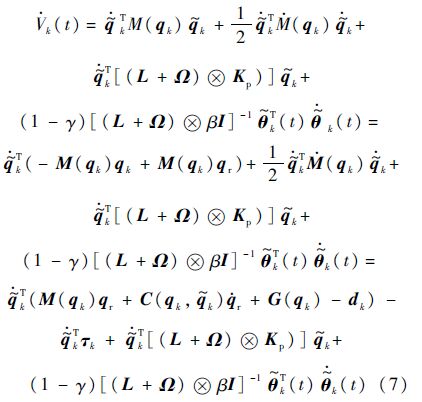
将式(2)和式(5)代入式(7)中可得
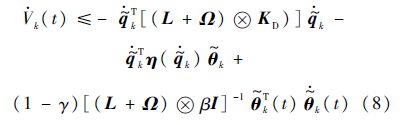
运用式(3)以及-Γθk+Γθ^k-1=-Γ$\tilde{\theta }$k+Γ$\tilde{\theta }$k-1,式(8)可以写成
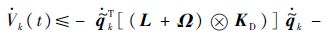
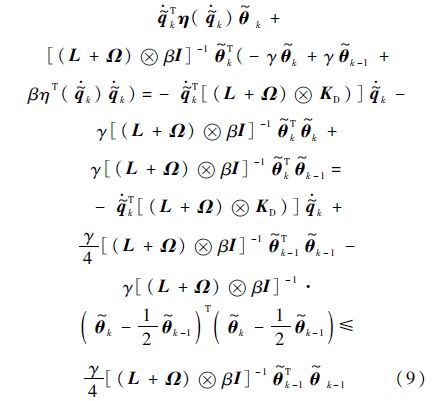
由于θ^0(t)=θini(∀t∈[0,T]),可得
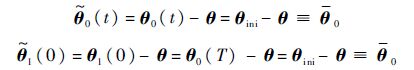
考虑初始情况
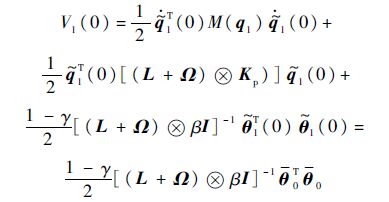
根据假设2),则V1(0)有界.由此根据式(9)可得
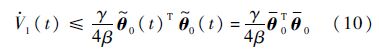
故有$\dot{V}$1(t),$\tilde{q}$1(t),$\dot{\tilde{q}}$1(t),θ1(t)∈L∞e[0,T],因此,τ1(t)∈L∞e[0,T].
定理2 考虑在自适应迭代学习控制律(式(2)和式(3))作用下的多机械臂系统(式(1)).若定理1中的所有条件成立,则$\dot{\tilde{q}}$k(T),$\tilde{q}$k(t),$\tilde{\theta }$k(T),$\tilde{\theta }$Tk(T)$\tilde{\theta }$k(T),∫0T$\dot{\tilde{q}}$Tk$\dot{\tilde{q}}$kdt有界,且$\underset{x\to \infty }{\mathop{\lim }}\,$ $\dot{\tilde{q}}$k(t)=$\underset{x\to \infty }{\mathop{\lim }}\,$ $\tilde{q}$k(t)=$\underset{x\to \infty }{\mathop{\lim }}\,$ ∫0T$\dot{\tilde{q}}$Tk>$\dot{\tilde{q}}$kdt=0.
证明 考虑函数
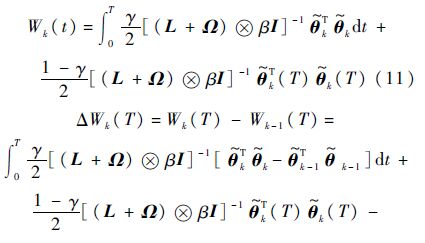
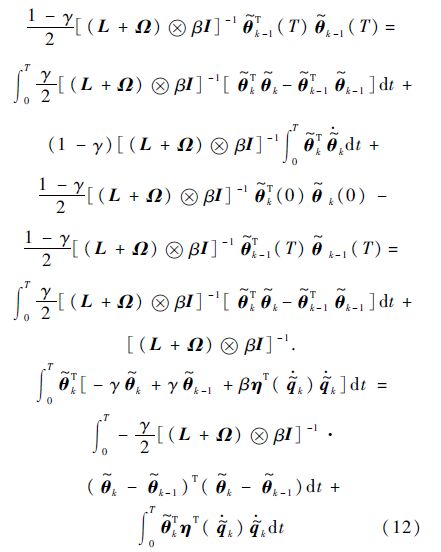
定义另一个正定的函数Uk:
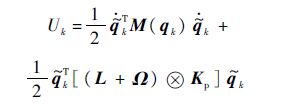
则
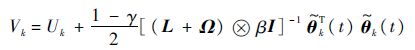
并且Uk对于时间t的导数满足
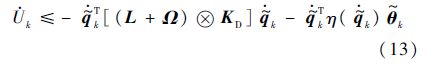
对式(13)两边同时积分得
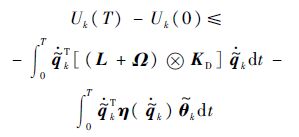
由假设3)有Uk(0)=0,因此
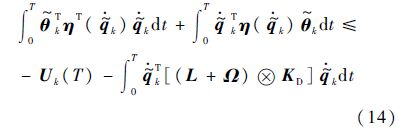
将式(14)代入式(12)可得
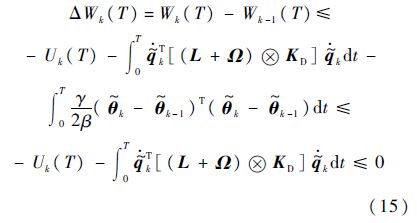
由W1(t)有界可知$\tilde{\theta }$Tk(T)$\tilde{\theta }$k(T)和∫0T$\tilde{\theta }$Tk(T)$\tilde{\theta }$k(T)dt是有界的.同时,式(15)可变形为
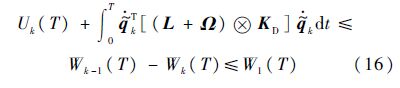
由式(16)可知,Uk(T),$\dot{\tilde{q}}$k(T),$\tilde{q}$k(T),∫0T$\dot{\tilde{q}}$Tk$\dot{\tilde{q}}$kdt有界,并且式(15)也可变形为

或
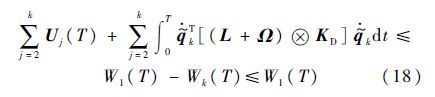
综上,由式(15)~式(17)可得
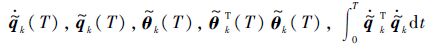
有界,并且$\underset{x\to \infty }{\mathop{\lim }}\,$ $\dot{\tilde{q}}$k(T)=$\underset{x\to \infty }{\mathop{\lim }}\,$ $ilde{q}$k(T)=$\underset{x\to \infty }{\mathop{\lim }}\,$ ∫0T$\dot{\tilde{q}}$Tk$\dot{\tilde{q}}$kdt=0,定理得证.证毕
3 仿真实例对于给出的自适应迭代学习分布式控制律式(2)和式(3),这里将给出一个具体的实例来验证该方法的有效性.
考虑一个由4个机械臂组成的系统,其中每个机械臂具有相同的动力学特性,即4个机械臂的M矩阵、C矩阵、G向量彼此相同,即
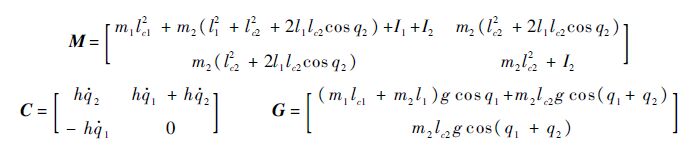
各机械臂的机构参数为
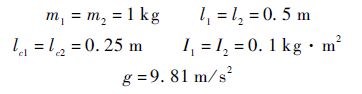
第i个机械臂的干扰设为
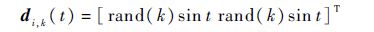
rand(k)为0~1之间的一个随机数.设各机械臂的期望参考轨迹为
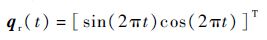
取KD=Kp=20×I2×2,β=20,Γ=0.5.
此外,4个机械臂的拓扑结构如图 1所示.
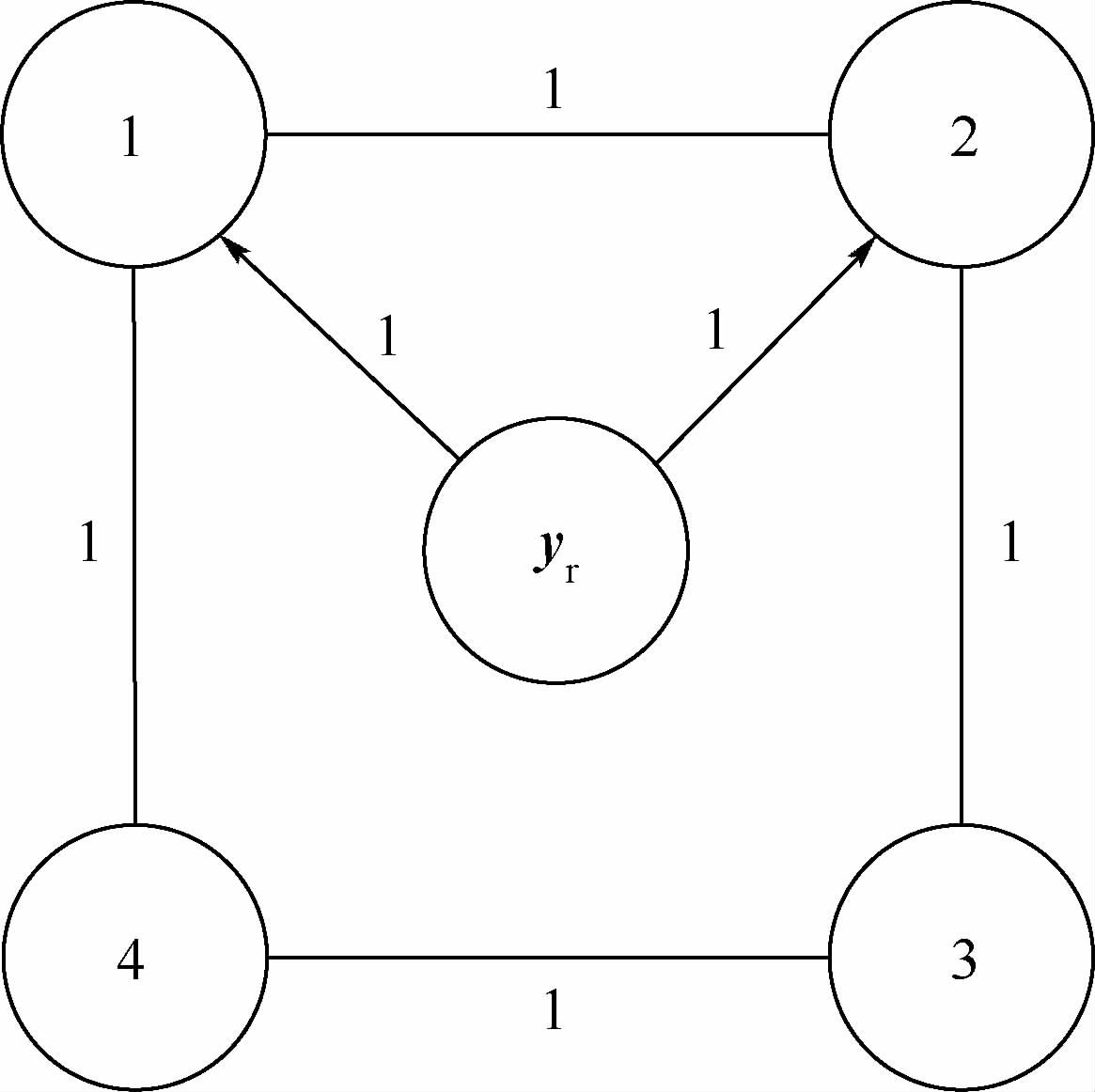 |
| 图 1 机械臂系统的拓扑结构 Fig. 1 Topology structure of robot manipulators |
| 图选项 |
可以看出,机械臂1和机械臂2可识别期望轨迹信息,机械臂3和机械臂4不能识别期望轨迹信息.因此,
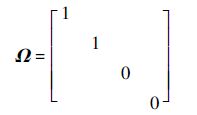
对系统进行50次自适应迭代之后,在式(2)和式(3)的自适应迭代学习控制协议作用下,所有机械臂的位置如图 2所示以及整个机械臂系统的跟踪误差曲线如图 3所示.
 |
| 图 2 机械臂的位置Fig. 2 Position of robot manipulators |
| 图选项 |
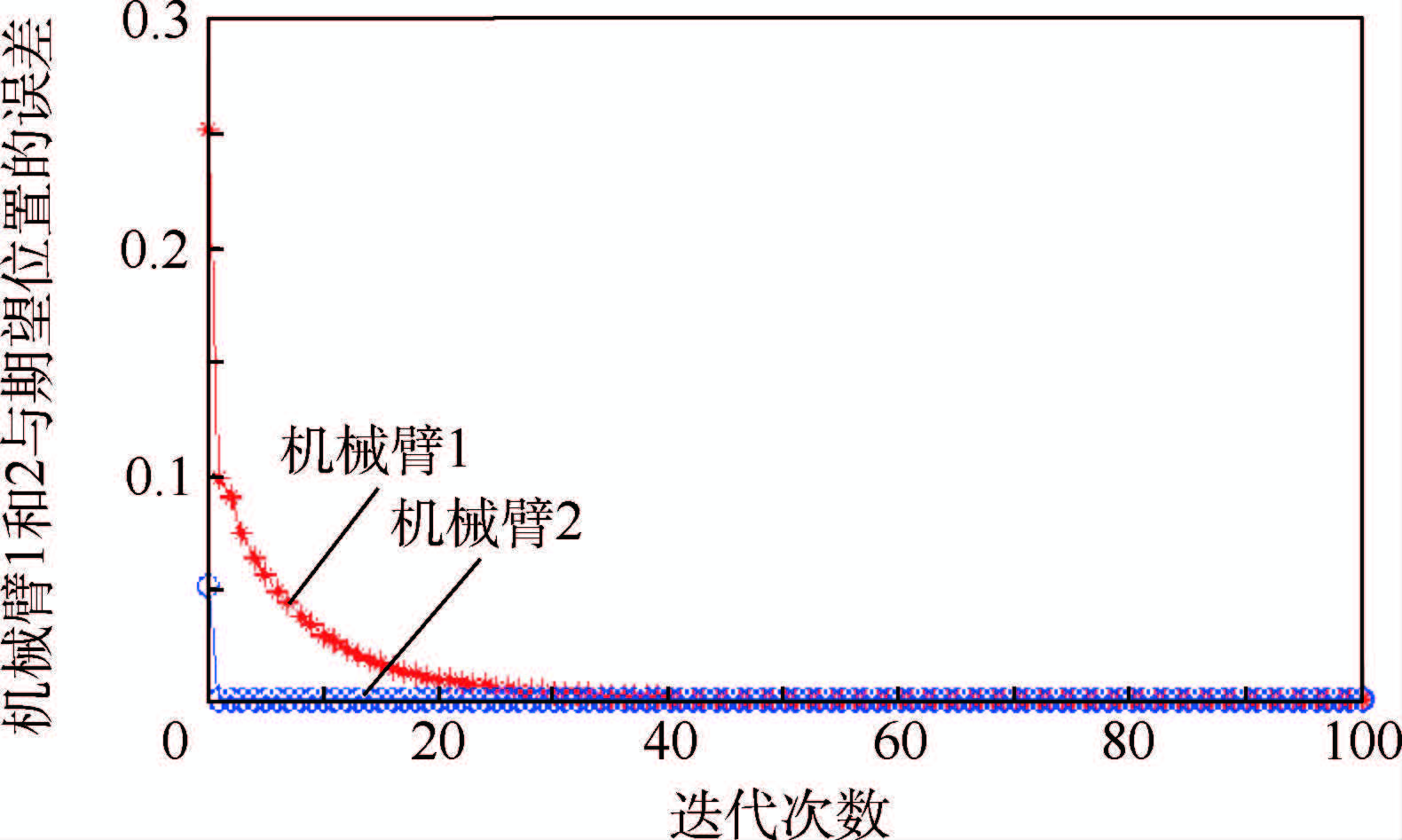 |
| 图 3 跟踪误差 Fig. 3 Tracking errors |
| 图选项 |
从图 2和图 3可以看出,所有机械臂在进行50次迭代学习之后,位置达到了期望轨迹.特别地,从图 3知,随着迭代次数的增加,多机械臂系统的跟踪误差不断减小.
4 结 论本文针对基于连通拓扑结构的多机械臂系统一致性问题,得到了一种分布式的自适应控制与迭代学习控制相结合的控制协议,能够使得多个机械臂实现一致性跟踪.该协议优点为:
1) 只须有限次迭代,每个机械臂能够趋近于期望轨迹.相较于已有的控制协议[17],具有更好的分布式结构.
2) 不需要精确的系统参数,克服多个运动机械臂难以精确建模的难题,便于实际应用.
参考文献
| [1] | 吴振彪.工业机器人[M].武汉:华中理工出版社,2004:6-10. Wu Z B.Industrial robot[M].Wuhan:Huazhong Institute of Technology Press,2004:6-10(in Chinese). |
| [2] | Ren W,Beard R W.Consensus seeking in multi-agent systems under dynamically changing interaction topologies[J].IEEE Transactions on Automatic Control,2005,50(5):655-661 |
| Click to display the text | |
| [3] | Olfati-Saber R,Murray R M.Consensus problems in networks of agents with switching topology and time-delays[J].IEEE Transactions on Automatic Control,2004,49(9):1520-1533 |
| Click to display the text | |
| [4] | Olfati-Saber R.Ultrafast consensus in small-world networks[C]//Proceedings of the 2005 American Control Conference.Piscataway,NJ:IEEE Press,2005,4:2371-2378 |
| Click to display the text | |
| [5] | Hong Y G,Hu J P,Gao L X.Tracking control for multi-agent consensus with an active leader and variable topology[J].Automatica,2006,42(7):1177-1182 |
| Click to display the text | |
| [6] | Hu J P,Hong Y G.Leader-following coordi-nation of multi-agent systems with coupling time delays[J].Physica A:Statistical Mechanics and Its Applications,2007,374(2):853-863 |
| Click to display the text | |
| [7] | Ni W,Cheng D Z.Leader-following consensus of multi-agent systems under fixed and switching topologies[J].Systems & Control Letters,2010,59(3-4):209-217 |
| Click to display the text | |
| [8] | Zhang H W,Frank L.Optimal design for synchronization of cooperative systems:State feedback,observer and output feedback[J].IEEE Transactions on Automatic Control,2011,56(8):1948-1952 |
| Click to display the text | |
| [9] | Ren W.Multi-vehicle consensus with a time-varying reference state[J].Systems & Control Letters,2007,56(7-8):474-483 |
| Click to display the text | |
| [10] | Liu S,Xie L H,Lewis F L.Synchronization of multi-agent systems with delayed control input information from neighbors[J].Automatica,2011,47(10):2152-2164 |
| Click to display the text | |
| [11] | Li J,Li J.Adaptive iterative learning control for consensus of multi-agent systems[J].IET Control Theory and Applications,2013,7(1):136-142 |
| Click to display the text | |
| [12] | Meng D Y,Jia Y M.Iterative learning approaches to design finite-time consensus protocols for multi-agent systems[J].Systems & Control Letters,2012,61(1):187-194 |
| Click to display the text | |
| [13] | Su J B.Base calibration for dual robot system[J].Control Theory & Applications,1998,15(4):575-582 |
| Click to display the text | |
| [14] | Kosuge K,Ishikawa J,Furuta K,et al.Control of single master multi-slave manipulator system using VIM[C]//Proceeding of IEEE International Conference on Robotics and Automation.Piscataway,NJ:IEEE Press,1990:1172-1177 |
| Click to display the text | |
| [15] | Tayebi A,Islam S.Adaptive iterative learning control for robot manipulators: Experimental results[J].Control Engineering Practice,2006,14(7):843-851 |
| Click to display the text | |
| [16] | Chien C J,Tayebi A.Further results on adaptive iterative learning control of robot manipulators[J].Automatica,2008,44(3):830-837 |
| Click to display the text | |
| [17] | 孙继鹏,孟德元.多机器人手臂系统一致性的自适应迭代学习控制[C]//第十届中国智能系统会议(CISC'14).北京:智能空天系统专业委员会,2014:346-351. Sun J P,Meng D Y.Adaptive iterative learning control for consensus tracking of multi-manipulator systems[C]//The 10th Chinese Intelligent System Conference(CISC'14).Beijing:Society of Intelligent Aerospace Systems,2014:346-351(in Chinese). |
