计算机技术的迅速发展为数据搜集和存储提供了极大的便利,使得数据观测的频率越来越高,甚至可以认为是连续观测,这类数据统称为函数型数据^[1]。函数型数据分析已具有众多研究成果,许多多元统计方法均可扩展到函数型数据的统计分析中^{[2, 3, 4, 5]}。关于函数型线性回归模型的研究成果众多,主要有:基于函数型主成分的最小二乘估计量的最优收敛速度^[6]、基于核函数的非参数M估计^[7]、函数型线性模型的分位数估计^[8]、线性模型中函数型数据的光滑化预处理^[9]、函数型线性模型的变量选择^[10]等。这些结果所涉及的回归模型大多数含有函数型协变量和数值型响应变量,主要研究函数型协变量对应的函数型系数的统计性质。但在实际数据分析中,在回归模型中经常会遇到数值型多元变量和函数型变量混杂的协变量。在对模型进行估计时,既需要估计多元数值型协变量对应的系数向量,又需要对函数型数据对应的函数型系数进行估计。虽然估计比较复杂,但这种混合数据回归模型具有更广泛的适用性,因而具有研究的意义。此外,普通线性回归模型要求响应变量是连续型随机变量,而在数据处理过程中经常会遇到响应变量为离散型随机变量甚至是属性数据的情形。为扩展函数型线性模型的实用性,需要考虑含有函数型协变量的广义函数型线性模型,对响应变量的类型不局限于连续型随机变量,可进一步扩展模型的实用性。基于此,本文提出含有函数型协变量的广义线性模型并对其进行估计,在指数分布族的假设下,分别得到参数部分和非参数部分的极大似然估计量,并对因变量为离散型随机变量或属性数据的情形进行具体分析。最后,通过数值模拟来验证本文所提出方法的可行性和正确性。1 函数型广义线性模型本节引入含有普通数值型数据和函数型数据的广义线性模型,并在指数分布族的假设下给出其极大似然估计。假设Z∈R^p为数值型多元随机变量,p为维数,{X(t):t∈T}为定义在概率空间(Ω,F,P)上的期望为零的二阶随机过程。令Y为一元数值型响应变量,记μ=E(Y|Z,X(t)),η=Z_γ+〈X,β〉,其中〈X,β〉=∫_TX(t)β(t)dt。考虑模型:
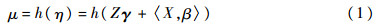
式中:h(·)为连接函数,严格单调且充分光滑;γ和β(t)分别为协变量Z,X(t)的待估未知参数和未知函数。进一步假设给定Z,X(t)时响应变量Y的条件分布属于指数分布族,其密度为
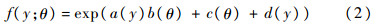
其中:若a(y)=y,称其为标准指数分布族(以下考虑标准指数分布族)。常见的许多分布均属于指数分布族,如正态分布、伽马分布、逆高斯分布、泊松分布和二项分布等。例如,令c(θ)=-μ²/(2σ²)-ln(2πσ<sup>2)/2,b(θ)=μ/σ²,d(y)=-y²/(2σ²)，即可得到期望方差分别为μ,σ²的正态分布的密度函数;令b(θ)=lnλ,c(θ)=-λ,d(y)=-ln(y!)可以得到期望为λ的泊松分布的密度函数。式(1)模型可看作是多元数据广义线性模型和函数型数据广义线性模型的推广。若γ≡0,式(1)模型则成为文献^[11]所研究的广义函数型线性回归模型^[12],若β(t)≡0,则式(1)模型退化为通常的广义线性模型。2 模型中〈X,β〉的处理本节通过选择基函数对式(1)模型中的〈X,β〉进行展开,通过准则函数的选择进行截断后转化为多元数据的形式。不失一般性地假设T=[0,1],从而有〈X,β〉=∫₀¹X(t)β(t)dt。事实上,对于函数型协变量X(t)而言,在实际观测时观测点{t_i}即使非常密集也是离散的,需要通过线性插值或者其他常用的非参数办法进行光滑,得到一条连续的曲线。同时,一般也对函数型系数β(t)的光滑性进行假设。通常在函数型数据分析中使用的基函数有两种类型:①预先给定基函数类型基于数据对基函数个数进行选择,例如B样条和Fourier基函数等^[13];②完全基于数据构造基函数,例如函数型主成分基函数^[6],函数型偏最小二乘基函数等。这里重点介绍函数型主成分基函数。2.1 函数型主成分基函数设n个独立同分布的样本观测值分别为{Z_i,X_i(t),Y_i}_i=1ⁿ。定义函数型数据X(t)的协方差函数和样本协方差函数分别为
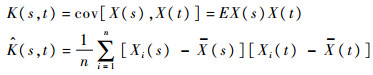
式中:。
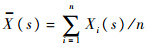根据 Mercer 定理,对如上定义的算子K具有谱分解的形式:
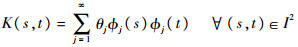
式中:θ₁≥θ₂≥…≥0为算子K的各个特征值；φ_j为对应的特征函数；I为区间。相应地,对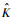(s,t)也可以进行类似分解得到特征值{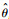_j}和对应的特征函数{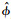_j}。将X(t),β(t)在{φ_j}_j=1^∞所展成的空间进行展开可得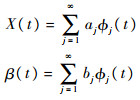
进一步利用基函数之间的正交性质可以得到
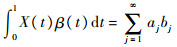
2.2 〈X,β〉的处理在实际数据分析中,第2.1节中的无穷求和不具备操作性,通常会根据某些准则对基函数个数进行选择,然后进行估计。这里函数型主成分基函数的个数可以通过方差占比进行选择,例如设定选取基函数的个数能保留85%的方差信息,根据
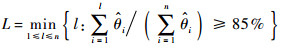
来选择L个函数型主成分基函数,其中:l为基函数数量可选的范围。如果采用的是B样条基函数,基函数个数可通过Schwartz和Bayes Information Criterion(BIC)等类型的准则进行选择。假设选定了L个函数型主成分基函数对X_i(t)和β(t)进行展开,则模型转化为
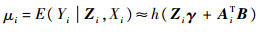
式中：A_i=[a_i1 a_i2 … a_iL]^T；B=[b₁ b₂ … b_L]^T。3 模型估计本节采用极大似然估计法对模型中的未知参数和未知函数型系数进行估计,并针对因变量是二元属性数据情形的Logistic回归和因变量为离散型整值变量情形的泊松回归进行详细分析。由式(2)可以写出对数似然的形式为
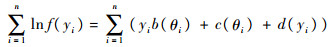
式中：θ_i通常依赖于模型中的未知参数,可根据具体模型进行表示。3.1 Logistic 回归以下考虑一种特殊情形,令因变量Y为0-1型随机变量,取值为1的概率为π且h(x)=exp(x)/(1+exp(x))。这时b(π)=ln(π/(1-π))。如果记Pr(Y_i=1)=E(Y_i)=π_i则似然函数可以表示为
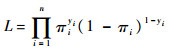
对数似然函数可以表示为
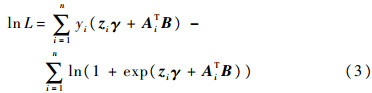
通过极大化式(3)可以得到极大似然估计(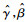),然后根据所选择基函数可重构得到β(t)的估计量。对于0-1型因变量,单位概率回归模型也是常见的广义线性模型之一,其使用的连接函数是标准正态分布的累积分布函数,在此不再详细叙述。3.2 泊松回归对于因变量为离散型数值变量的情形,尤其是因变量表示某类事件发生的次数等整值随机变量(计数变量)时,不可以进行普通回归。通过选择指数函数为连接函数,可得到泊松回归^[14]。假设给定协变量Z,X(t)时,因变量Y服从参数为λ的泊松分布,即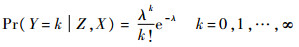
式中:λ=exp(Z_γ+〈X,β〉),则对数似然函数
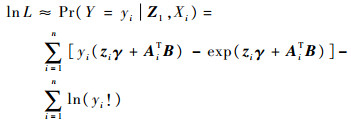
式中:ln(y_i!)项与参数无关,在极大化对数似然函数可略去不考虑。对lnL关于(γ,B)求导,并给定初值通过重加权算法等可以得到极大似然估计。以γ,B均为一维参数为例描述重加权算法。假设(γ^(m),B^(m))为在第m步迭代中得到的值。对对数似然函数求导可得
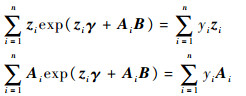
使用重加权算法,可以由以下公式更新得到(γ^(m+1),B^(m+1))。
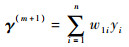
式中:
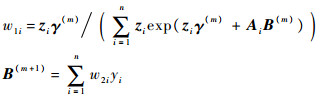
其中:
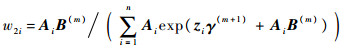
由以上重加权算法,只需给定初值(γ⁽⁰⁾,B⁽⁰⁾)反复迭代直至收敛为止,即可得到极大似然估计值。对于参数维数多元情形,可对每一个参数逐一进行迭代更新,过程类似。以上是针对泊松回归进行分析,事实上对于伽马分布和逆高斯分布等连续性分布,都具有类似结论。总之,指数型分布族都可以通过选择连接函数和极大化对数似然函数得到对应的极大似然估计,具体细节在此不再赘述。4 数值模拟本节通过第3.2节所提出的重加权算法对二项分布和泊松分布情形的广义线性模型的未知参数和函数型系数进行估计,考查其有限样本性质。同时列出普通二乘回归(对应正态分布)的结果便于进行比较。关于函数型数据及其函数型系数,仿照文献^[6]进行如下设计:

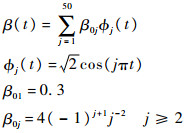
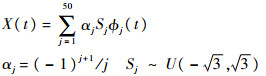
式中:U(a,b)为[a,b]区间上的均匀分布。多元数值型变量Z由以下二元正态分布随机生成：Z~N((0,0),Σ),其中Σ的4个元素为Σ₁₁=Σ₂₂=1,Σ₁₂=Σ₂₁=0.3，其系数γ=[0.5 0.5]^T。随机生成样本,样本容量取为200,重复进行200次,计算γ=[γ₁ γ₂]^T估计值的均值和标准差,如表 1所示,其中σ表示误差的标准差,表中数值不带括号的为200次模拟估计量的均值,括号内为200次模拟得到估计量的标准差。在正态、Logistic和泊松3种情形下,估计量的均值都在参数真值附近波动,随着σ的增大,估计量的方差都随着增大。在σ相同时,正态情形的估计方差最小,泊松情形次之,Logistic情形最大。正态分布情形就是普通回归模型因变量为连续的,泊松回归中因变量为计数变量,Logistic回归中因变量只取0,1,因变量的取值范围越来越小,因此从中提取的信息依次越来越少。由表 1可见,含函数型协变量的广义线性模型中多元系数的极大似然估计具有良好的效果。表 1 不同广义线性模型下对多元系数估计的结果Table 1 Estimators for multivariate coefficients in different generalized linear models

误差水平	估计量	正态	Logistic	泊松
σ=0.2	γ1	0.5012	0.5138	0.5042
		(0.0172)	(0.1803)	(0.0576)
	γ2	0.4999	0.5325	0.4910
		(0.0168)	(0.1662)	(0.0556)
σ=0.5	γ1	0.5013	0.4955	0.5297
		(0.0364)	(0.1961)	(0.0870)
	γ2	0.5020	0.5399	0.5214
		(0.0381)	(0.1609)	(0.0908)
σ=1.0	γ1	0.5093	0.4313	0.6148
		(0.0724)	(0.1574)	(0.1464)
	γ2	0.4959	0.4280	0.5696
		(0.0663)	(0.1618)	(0.1586)

表选项


以下考查对模型中函数型系数的估计效果。这里采用均方误差MSE作为衡量估计效果的指标^[15]:
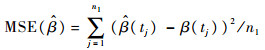
式中:{t_j,1≤j≤n₁}为在区间上取定的具有等间隔的格子点。MSE越小,估计效果越好。表 2以泊松回归为例,展示了在不同误差水平和不同样本容量下模拟200次得到的MSE均值和标准差(括号内为标准差)。随着样本容量的增大,MSE的均值和标准差都越来越小。相同样本容量情形下,误差的标准差越大,MSE的均值和标准差也越大。相对表 1而言,表 2选取的误差的方差都较小,这是因为当噪声水平较高即σ较大时,MSE都比较大,从图 1也可以看出这一点。函数型系数的估计对噪声较为敏感。表 2 泊松回归的均方误差Table 2 MSEs for Possion regression

样本容量	σ=0.2	σ=0.4	σ=0.6
100	0.1456	0.2145	1.1189
	(0.1146)	(0.1543)	(0.8696)
200	0.0751	0.1180	0.7030
	(0.0554)	(0.0853)	(0.6449)
300	0.0494	0.0826	0.6335
	(0.0318)	(0.0655)	(0.6884)
500	0.0296	0.0410	0.4461
	(0.0209)	(0.0242)	(0.5886)

表选项


图 1为不同误差水平下对函数型系数的估计效果比较,所使用的样本容量为200。当噪声的方差较大σ=1时,对函数型系数的估计效果很不好。方差较小时,估计得到的函数型系数具有较高的精度。

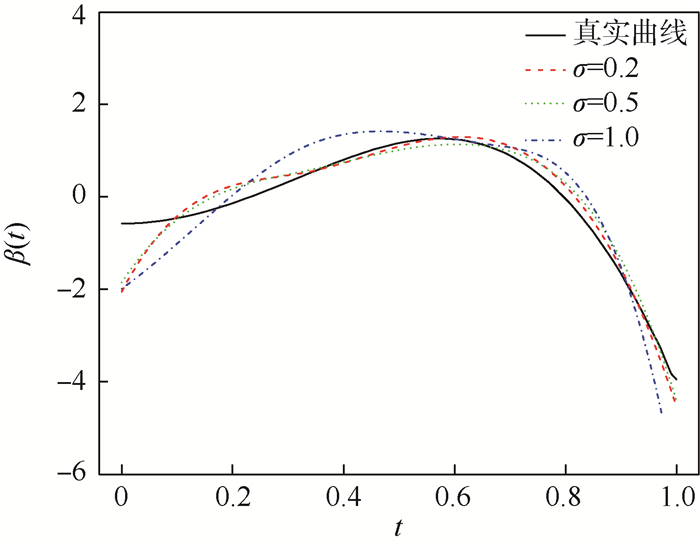图 1 不同误差水平下对函数型系数的估计Fig. 1 Estimation for functional coefficient under different variances of error

图选项

5 结 论本文对含有函数型变量的混合数据广义线性模型进行研究,尤其针对因变量为离散变量或者属性数据情形,经数值模拟验证表明:1) 所提出的估计方法不需要对误差分布进行假设,扩大了适用范围。2) 模型可以解决因变量为离散型或者属性数据的回归问题。3) 将函数型数据分析方法引入了广义线性模型。
参考文献

[1]	RAMSAY J O.When the data are functions[J].Psychometrika,1982,47(4):379-396.
	Click to display the text
[2]	MULLER H,WU Y,YAO F.Continuously additive models for nonlinear functional regression[J].Biometrika,2013,100(3):607-622.
	Click to display the text
[3]	DELSOL L,FERRATY F,VIEU P.Structural test in regression on functional variables[J].Journal of Multivariate Analysis,2011,102(3):422-447.
	Click to display the text
[4]	HE G,MULLER H,WANG J,et al.Functional linear regression via canonical analysis[J].Bernoulli,2010,16(3):705-729.
	Click to display the text
[5]	DELAIGLE A,HALL P.Classification using censored functional data[J].Journal of the American Statistical Association,2013,108(504):1269-1283.
	Click to display the text
[6]	HALL P,HOROWITZ J L.Methodology and convergence rates for functional linear regression[J].The Annals of Statistics,2007,35(1):70-91.
	Click to display the text
[7]	GHERIBALLAH A,LAKSACI A,SEKKAA S.Nonparametric M-regression for functional ergodic data[J].Statistics & Probability Letters,2013,83(3):902-908.
	Click to display the text
[8]	KATO K.Estimation in functional linear quantile regression[J].The Annals of Statistics,2012,40(6):3108-3136.
	Click to display the text
[9]	FERRATY F,GONZÁLEZ-MANTEIGA W,MARTÍNEZ-CALVO A,et al.Presmoothing in functional linear regression[J].Statistica Sinica,2012,22(1):69-94.
	Click to display the text
[10]	LIAN H.Shrinkage estimation and selection for multiple functional regression[J].Statistica Sinica,2013,23(1):51-74.
	Click to display the text
[11]	CANTONI E,RONCHETTI E.Robust inference for generalized linear models[J].Journal of the American Statistical Association,2001,96(455):1022-1030.
	Click to display the text
[12]	BOENTE G,HE X,ZHOU J.Robust estimates in generalized partially linear models[J].The Annals of Statistics,2006,34(6):2856-2878.
	Click to display the text
[13]	JAMES G M,WANG J,ZHU J.Functional linear regression that's interpretable[J].The Annals of Statistics,2009,37(5A):2083-2108.
	Click to display the text
[14]	CAMERON A C,TRIVEDI P K.Regression-based tests for overdispersion in the Poisson model[J].Journal of Econometrics,1990,46(3):347-364.
	Click to display the text
[15]	KIM M.Quantile regression with varying coefficients[J].The Annals of Statistics,2007,35(1):92-108.
	Click to display the text