文献[2]提出了在比例导引律的基础上加了一个时变偏置项,用来满足末端攻击角度约束的要求,此制导律形式简单,但仅限于固定目标.文献[3, 4, 5, 6]提出了满足攻击角度要求的最优控制导引律,选取不同的加权函数对制导性能有很大的影响,该方法能得到显式制导律,但对模型精度要求较高.由于对包含建模误差及不确定性具有很强的鲁棒性[7],滑模控制被用于制导律的设计[8, 9, 10].该方法使系统状态趋近并保持在根据末端攻击角约束设计的滑动模态上,最终达到期望落角,具有较强的鲁棒性,但抖振现象会降低性能.而文献[11, 12]基于滑模控制技术设计了滑模制导律,同时采用了非线性扰动观测器对目标机动加速度进行观测和控制量补偿,降低了控制量的高频振荡,提高了制导的精度.文献[13, 14]提出了考虑自动驾驶仪动态条件下拦截机动目标的带攻击角约束的制导律,通过零化弹目相对法向速度将攻击角约束转化为视线角约束,并把期望的视线角视为定值.文献[15, 16, 17, 18]通过零化弹目相对法向速度,将攻击角约束转化为视线角约束,目标机动状态下,期望的视线角是时变的,且变化率正比于目标加速度.文献[15]中设计的制导律存在奇异问题,而文献[16]提出了非奇异终端滑模带攻击角约束的制导律,但打击目标仅限于固定和匀速运动目标,但都未给出未知目标加速度的处理方法.在此基础上,文献[17, 18]针对机动目标提出了带攻击角约束的制导律,并采用观测器估计未知目标加速度,同时文献[18]考虑了导弹自驾仪的动态特性,采用非奇异终端滑模和动态面控制方法设计制导律.以上制导律在性能上都满足期望的角度,但是对于制导系统的收敛时间问题基本没有考虑.在有些情况下,人们希望导弹的弹道倾角在命中目标以前也收敛到约束的入射角度,因此就需要考虑系统收敛的快速性,设计有限时间收敛的导引律.在文献[19]中,由于在到达滑模面阶段使用幂次趋近律,导致系统轨迹在远离平衡点的时候收敛速度较慢,不具有全局快速收敛的特性.文献[20]提出了非奇异终端滑模导引律,并对奇异问题做了相关处理,但是采用等速趋近律,滑模面只能收敛到边界层,不能严格收敛到零,视线角难以严格收敛到期望的视线角,无法获得高精度的攻击角跟踪性能.文献[21]中采用快速终端滑模函数设计趋近律,可以期望获得更高精度的视角角跟踪性能,但是该制导律所需调整的参数较多且敏感,在跟踪的初始阶段控制量容易饱和.
上述的制导律都能满足末端零控脱靶量和期望角度约束,但是在设计过程中增加了系统的复杂度,同时对于导弹运动过程中的未知量(导弹速度的未知时变不确定性和目标加速度)无法实时地测量,或者由于系统和外界的不确定性,导致假设的目标机动加速度上限无法准确获得,对模型的依赖度较高,并且由于假设的上界过大导致控制量过大出现高频震颤现象.自文献[22]提出干扰观测器(DO)的概念以来,基于非线性干扰观测器(NDO)的控制方法因其计算结构简单、鲁棒性好且不依赖于精确模型等优点引起许多****的关注[22, 23, 24].DO的独特优势在于不需要假设干扰上界已知,同时可以估计出系统的总扰动,且观测器增益的整定有一套成熟的公式可供参考[22].
本文结合扩张干扰观测器(EDO)和有限时间稳定控制技术提出一种适用于目标机动逃逸情况的终端攻击角约束的有限时间稳定制导律.采用EDO对系统的总干扰(导弹速度的未知时变、未知的目标加速度等)进行估计,并把估计值用于设计非奇异终端滑模面的设计.保证视线角可以很好地跟踪时变的期望视线角,进而精确地达到预先给定的攻击角.同时,引入跟踪微分器解决了制导律中所需的期望视线角速率无法量测的问题,因此,该制导律需要的状态量较少,便于工程应用.最后通过导弹不同的机动形式、不同攻击场景条件下的数值仿真验证了该制导律的良好性能.通过对比仿真,相对于仅利用非奇异终端滑模控制设计的制导律,本文提出的制导律具有较小的过载和更好的鲁棒性.
1 导弹拦截模型为了便于描述,考虑攻击角约束的弹目拦截问题采用二维平面交战模型,其结果可以应用到三维场景中.导弹-目标二维平面拦截示意图如图 1所示.
为了简化问题,假设导弹和目标均为质点,忽略导弹和目标所受的重力.弹目相对运动方程以极坐标形式表示:
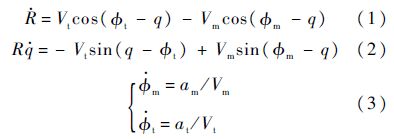
式中:R和$\dot{R}$分别为弹目相对距离及其变化率;q和$\dot{q}$分别为视线角及其变化率;am和at分别为导弹和目标的法向加速度;$\phi $m和$\phi $t分别表示导弹和目标的航迹角;Vm和Vt分别为导弹和目标的速度.
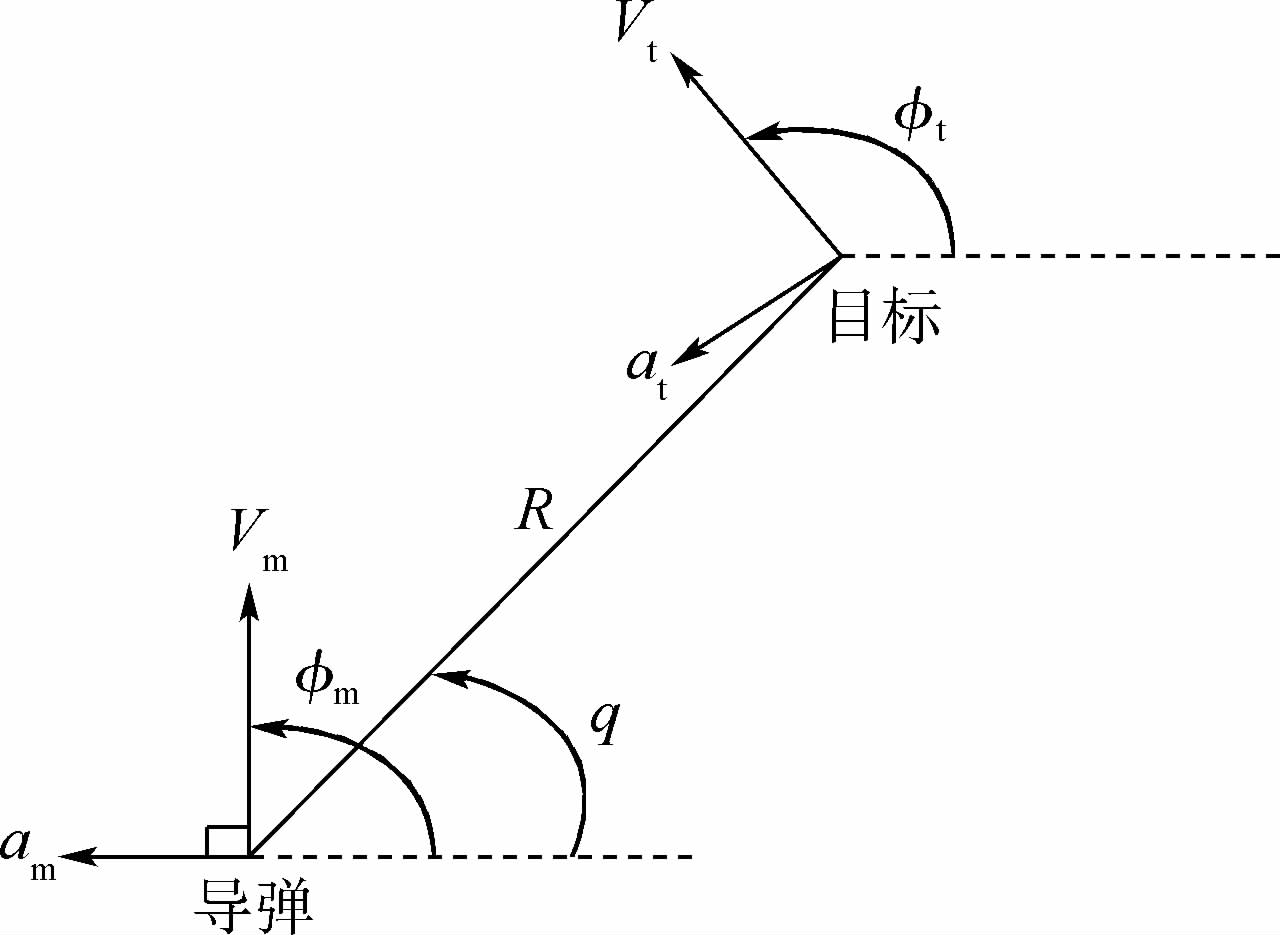 |
| 图 1 导弹-目标平面拦截几何Fig. 1 Missile-target engagement geometry |
| 图选项 |
对式(2)两边对时间t求导并将式(1)代入,可得
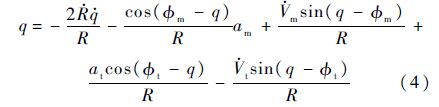
令atλ=atcos($\phi $t-q),atλ为目标法向加速度沿垂直视线方向的分量.在实际工程应用中,目标的法向加速度at是未知的,因此如何实时准确快速估算出at的值是制导律设计的关键.
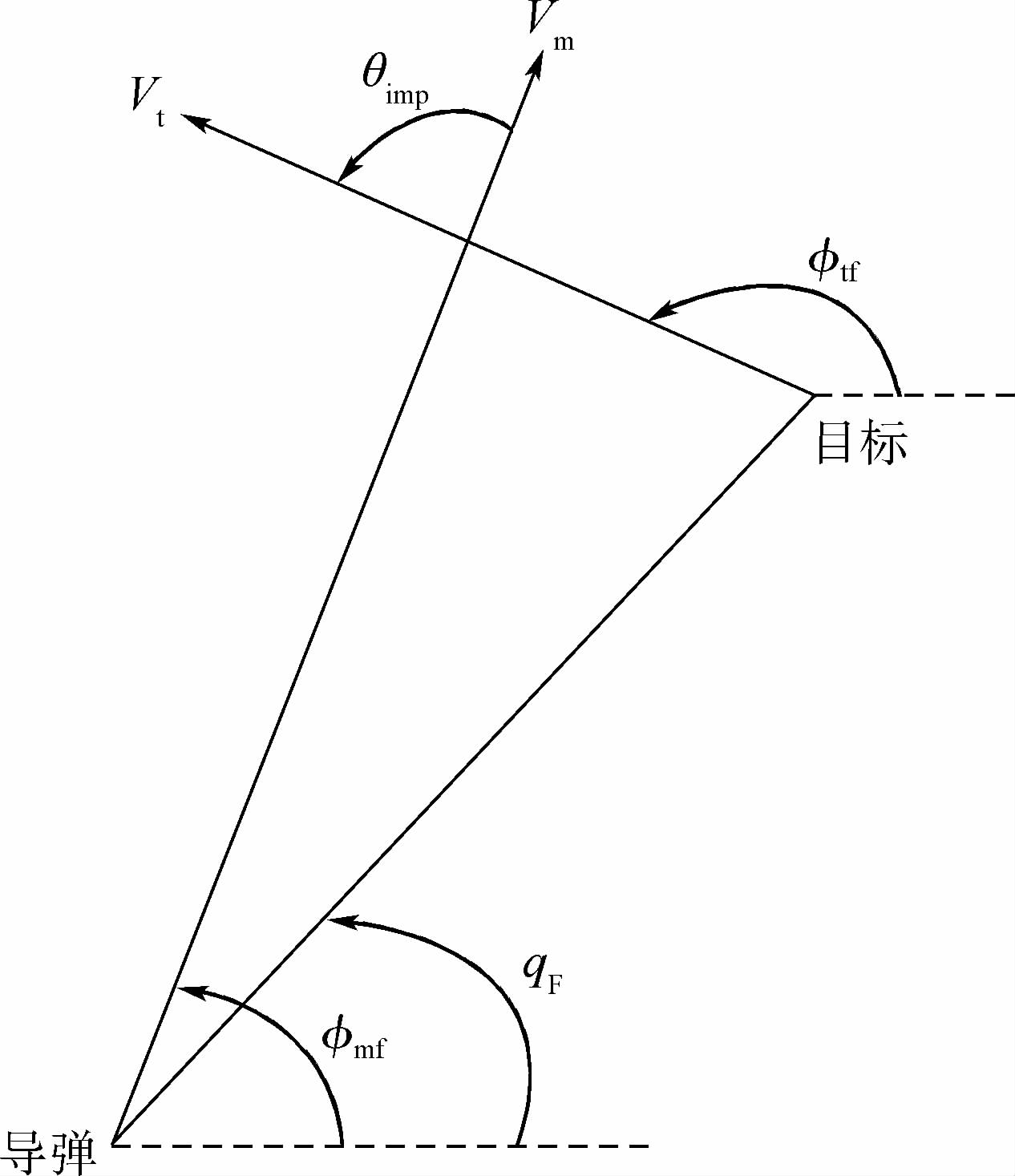
在这里定义攻击角θimp为在碰撞时刻导弹与目标速度向量的夹角[15],如图 2所示.
攻击角约束制导问题就是指导弹击中目标的同时要满足期望的攻击角度,以提高杀伤效力.即在终端时刻tf,满足条件:

式中:$\phi $tf和$\phi $mf分别表示碰撞时刻导弹与目标的航迹角.其中,式(5)物理含义是在制导的过程中确保目标在导引头视场角范围内.
当导弹和目标位于碰撞三角形航迹线上时,有R$\dot{q}$=0,则存在
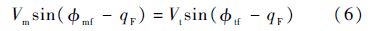
式中:qF为导弹碰撞时刻的期望视线角.
 |
| 图 2 导弹和目标碰撞航迹Fig. 2 Missile and target on collision course |
| 图选项 |
假设1 系统中变量R、q、Vt、Vm、$\phi $t、$\phi $m可以直接得到.
假设2 对于给定的$\phi $t和$\phi $m,式(6)的解qF*存在且唯一;同样,对于给定的qF和$\phi $t,有且只有一个$\phi $m*满足式(6).
假设3 目标与导弹的速度比近似为一个常值,且满足:

求解式(6)可得
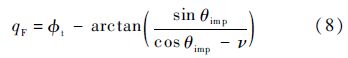
即在制导过程结束前,视线角满足约束q=qF.式(8)描述的是导弹碰撞时刻的期望视线角与目标航迹角之间的关系.为了使导弹击中目标时获取给定的攻击角度,从制导开始时刻就满足式(8)的条件,而不仅仅是在碰撞时刻才成立.
由式(8)可知,当θimp=nπ,n=±1,±2,…时,期望视线角qF与目标与导弹的速度比ν无关.从文献[15]可知,攻击角θimp与期望视线角qF是一一对应的关系,故攻击角约束就转化为视线角约束问题.当目标机动时,目标航迹角$\phi $t随时间变化,因此期望视线角qF是时间变化的量,其一阶和二阶导数分别为
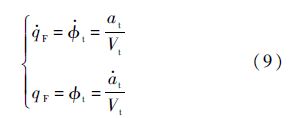
由式(9)可知,期望视线角的变化率$\dot{q}$F正比于目标加速度.
定义状态变量x1=q-qF,x2=$\dot{q}$-$\dot{q}$F,同时考虑式(4),则有
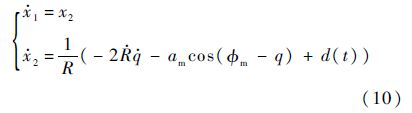
式中:
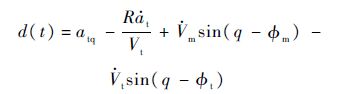
其中am为系统的控制量,d(t)为系统的总扰动,体现了导弹速度未知时变、目标的机动逃逸等引起的扰动.
假设4 假设d(t)是有界的并存在一个常数M>0,则有
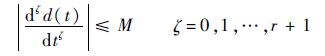
式中:r为EDO扩张的阶数,将在下文详细分析.
2 复合制导律设计导弹飞行过程中控制系统容易受到参数变化和外界环境干扰,因此制导律的设计必须考虑系统的鲁棒性.
为了使导弹实现上述拦截策略,本文采用滑模控制理论设计有限时间收敛制导律.采用EDO对闭环系统式(10)的总干扰d(t)进行实时的观测和动态补偿.控制器设计目标为:在系统外部干扰存在的条件下,设计控制器u使得x1和x2有限收敛于零.复合制导律结构框图如图 3所示.
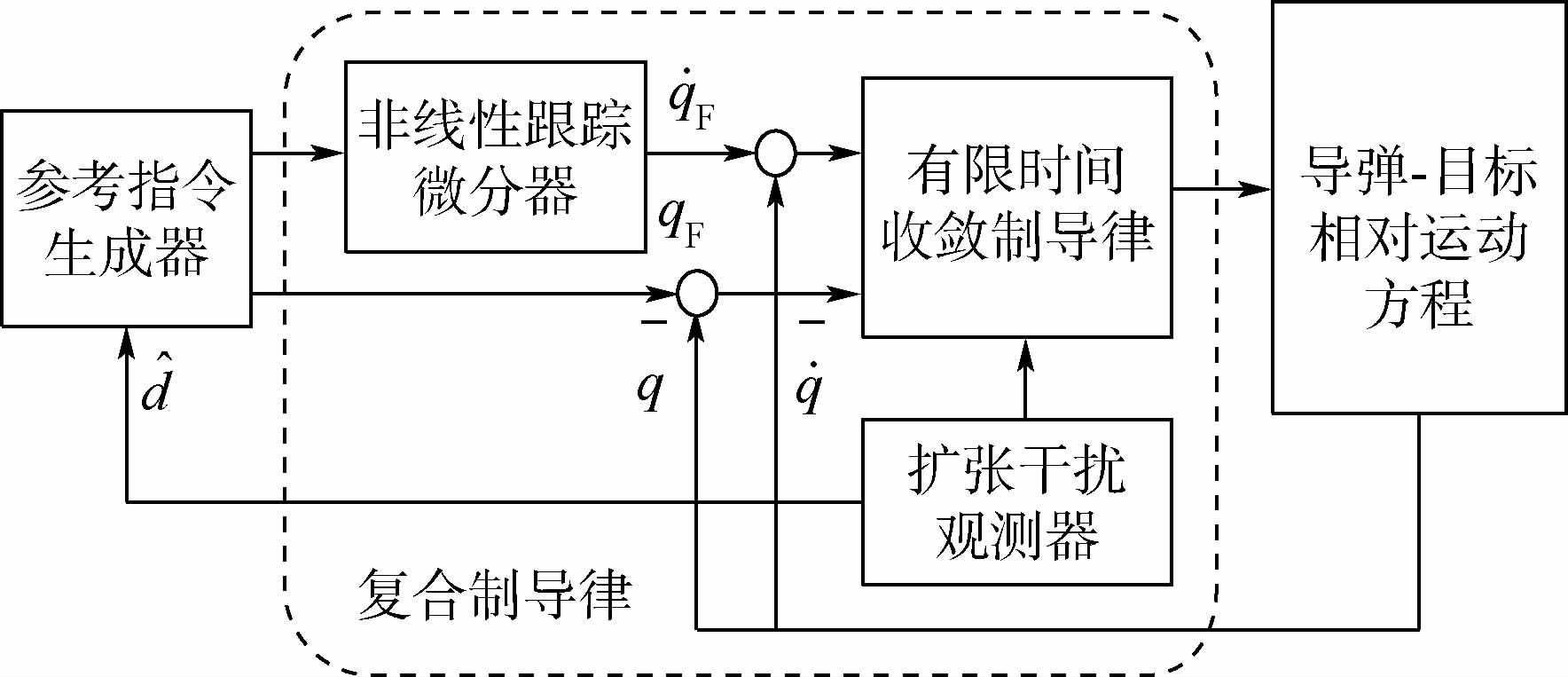 |
| 图 3 复合制导律结构框图Fig. 3 Structure block diagram of compound guidance law |
| 图选项 |
2.1 扩张干扰观测器文献[22]提出DO的思想,因其参数少,便于调试,通过调节观测增益改变DO的收敛速度等优点,得到了广泛的应用.综合考虑系统模型不确定性及输入扰动对制导律的影响,基于高阶泰勒多项式逼近重构扰动的原理,提出具有扩张状态的EDO,该观测器不仅可以对干扰真值进行观测,而且可对其任意阶导数进行估计,有效提高观测精度.
定义新的变量:

则式(4)变为
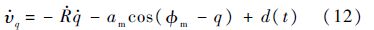
构造EDO估计式(10)中的总扰动d(t),其数学模型为

式中:d为d(t)的估计值,d(i-1)(i=2,3,…,r)为d(t)各阶导数的估计;pi∈R(i=1,2,…,r+1)和li∈R(i=1,2,…,r+1)分别为辅助变量和观测增益参数,可调参数li采用基于带宽的配置方法,可以改变观测器的收敛速度或带宽,则满足如下的特征多项式:
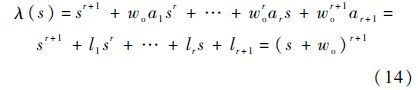
式中:li=αi/εi,i=1,2,…,r+1,ε=1/wo,wo>0为观测器带宽,且为EDO唯一需要调整的参数.系统的干扰估计可表示为
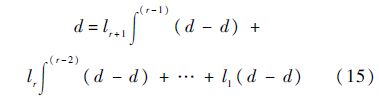
式中:
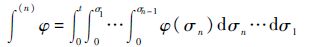
为了说明EDO的收敛性(即估计误差渐进稳定),有如下定理.
定理1 若假设4条件满足,且选取观测器增益li∈R(i=1,2,…,r+1)使得观测器误差方程特征多项式Hurwitz稳定,那么误差向量Eo指数收敛并有界,且收敛域为
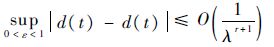
证明 根据系统(13),定义
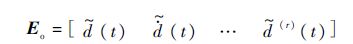
则系统观测误差动态方程可以表示为

式中:

求解式(16),可得
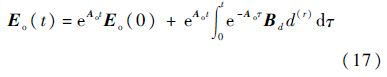
由于矩阵Ao满足Hurwitz,即Ao的所有特征值λi均具有负实部,因此,式(17)第1项可得
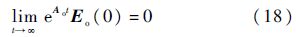
则式(17)变为如下形式:
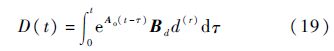
在假设4满足的前提下,根据矩阵函数的相关理论,可得D(t)的上界为
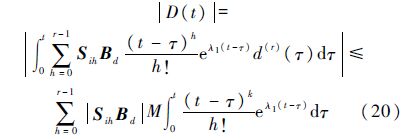
式中:Sih为由矩阵Ao决定的常数矩阵,h为积分步长.
同样,由于矩阵Ao满足Hurwitz,λi<0(i∈p),p为特征根的重数,则有
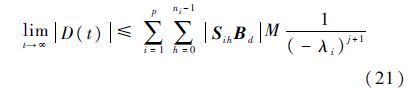
因此,由式(17)、式(18)及式(21)可知,系统观测误差是有界的.
进一步,可以获得EDO的观测误差收敛域.考虑当矩阵Ao有相同的特征根,则有
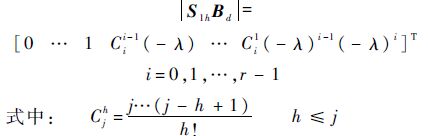
因此,观测误差的上界满足如下关系:

当i=1时,系统的总干扰d(t)的估计误差为
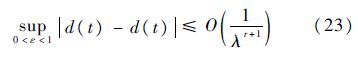
证毕
从定理1可知,当特征值λ足够大时,系统式(13)可以渐进跟踪d(t)及其任意阶导数.此外,各状态的估计误差随着扩张阶数的增加而减小.当扩张阶数逐渐增加时,假设1中对干扰的约束条件越来越苛刻,即当扩张阶数为r时,干扰的r阶导数存在且有界.因此,扩张阶数并不能随意增加.
2.2 有限时间收敛制导律设计对于系统式(10),为满足式(5)所示的约束条件,控制器设计目标为:在系统总干扰d(t)存在的条件下,设计控制器u使得状态x1和x2有限时间收敛于零.
首先,选取如下的滑模面:
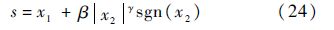
式中:β>0;1<γ=a/b<2,a、b且为奇数.
对式(24)求导可得
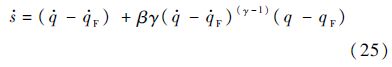
根据如下滑模到达条件:

选取趋近律为
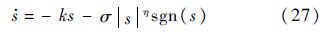
式中:k>0;σ>0;0<η<1.该趋近律能够保证系统式(10)的状态轨迹以有限时间收敛到滑模面s的邻域内.
由式(4)、式(12)和式(14)可以得到

由式(28)可知,当|$\phi $m-q|=π/2时,导弹的法向加速度am→∞,故采用如下的函数对其进行限幅处理

式中:am_max为导弹所能提供的最大过载.
2.3 快速跟踪微分器由式(9)和式(28)描述的控制算法中不难看出,$\dot{q}$F正比于目标加速度,由于目标加速度未知,而无法直接给出,因此需要对指令信号求导.若直接采用数值微分的方法,当存在量测噪声时,噪声很容易被放大.根据文献[25],利用快速跟踪微分器(TD)来实现从弹载传感器输出的信号中获取$\dot{q}$F,采用的TD的形式如下所示:
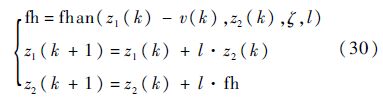
式中:fhan(z1(k)-v(k),z2(k),r,l)[25]为二阶最速离散跟踪微分器输入;l为微分器的积分步长;ζ为决定跟踪过程快慢的因子,且r越大,其跟踪速度越快;z2(k)为参考指令qF的微分信号的估计值,即z2(k)=$\dot{q}$F.TD的收敛性证明可以参考文献[26],TD具有良好的收敛跟踪特性.
3 稳定性分析基于非线性系统有限时间稳定性理论有如下引理[27].
考虑如下系统:
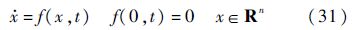
式中:向量场f:U0×R→Rn在U0×R连续,U0为原点x=0的一个开邻域.
引理1 考虑非线性系统(31),系统原点x=0为有限时间稳定平衡点:假定存在一个定义在原点的邻域U$\subset $U0$\subset $Rn上的C1光滑函数V(x),并且存在实数c>0以及0<a<1,使得V(x)在U上正定和$\dot{V}$(x)+cVa(x)在U上半负定,则系统(24)的原点是有限时间稳定的.同时,若Tr为V(x)收敛至原点的时间,则
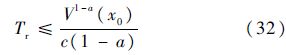
式中:x0为原点某一开邻域中的任何一点.
下面证明系统式(10)在有限时间收敛.在整个系统中,非线性跟踪微分器是相对独立的一个环节.因此,这里考虑在EDO(式(13))、滑模面(式(24))与控制律(式(28))作用下的闭环系统的收敛特性.
针对系统式(10)构造正定Lyapunov函数:

对式(33)按时间t求导可得

式中:x2=$\dot{q}$-$\dot{q}$F;ρ(x2)=βγ|x2|γ-1/R.当x2≠0,即$\dot{q}$≠$\dot{q}$F时,$\overset{\cdot }{\mathop{ss}}\,$≤0,满足滑模面到达条件.假设存在一个权数0<ζ≤1,使得不等式(34)可以写成
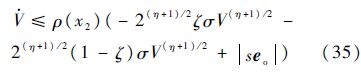
显然,如果V(η+1)/2>|se1|/2(η+1)/2(1-ζ)σ成立,则有$\dot{V}$≤-2(η+1)/2ρ(x2)ζσV(η+1)/2,根据引理1,随着V的减小,闭环系统的轨迹满足V(η+1)/2≤|se1|/2(η+1)/2(1-ζ)σ,闭环系统在有限时间到达滑模面邻域p:
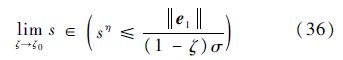
式中:0<ζ0<1.同时,有限收敛时间可以表示为

进一步分析系统状态在域s≤p内,对平衡点的稳态收敛精度.考虑
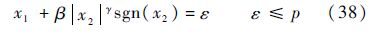
即
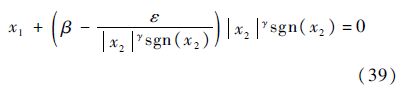
当β-(ε/|x2|γsgn(x2))>0时,式(38)仍保持非奇异终端滑模面的形式,且x2的收敛区域为
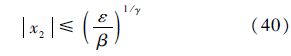
同理,x1的收敛区域为
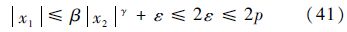
滑动模态阶段,系统的收敛时间表示为
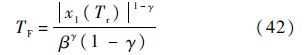
综上所述,在观测器稳定的前提下,通过调节控制律(28)中的参数k、σ,可以保证系统的轨迹有限时间收敛于s=0的邻域p内,即视线角q将在有限时间内跟踪上期望视线角qF,但是存在稳态收敛误差.稳态收敛误差的收敛域与系统观测器的观测误差成正比.但是,观测器的带宽将增大,引入的观测噪声会降低观测器的估计能力.同样,在实际工程应用中,参数k、σ过大,会使得控制量过大超过了导弹所能提供的过载.因此,在整定系统参数时,应权衡设计方法和实际应用条件的限制.
4 仿真结果分析将本文设计的复合制导律应用于拦截空中机动目标的数学仿真中,以验证所设计制导律的性能.当满足一定的条件时,启动末制导,采用带攻击角约束的制导律,导引头在导弹进入视场后捕捉及跟踪目标,输出导引信号.选取导弹在惯性坐标系下的初始位置为xm(0)=0 m,ym(0)=0 m,初始弹目距离R0=10 km,初始视线角q0=π/6 rad,导弹和目标的初始航迹角分别为$\phi $m0=π/4 rad和$\phi $t0=2π/3 rad,导弹和目标的速度分别为Vm=450 m/s,Vt=250 m/s.考虑目标不同的机动形式,不同的打击场景下,导弹制导律的性能.同时,将本文提出的基于扩张干扰观测器的复合制导律(EFTCG)与文献[15]提出的基于TSMC的制导律(TSMG)对比,考察各种制导律末端脱靶量、期望视线角跟踪情况以及控制量大小.
为了获得连续的制导律,减弱开关函数sgn()引起的高频抖振现象.故采用sigmoid函数代替控制量(28)中的开关函数,即
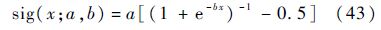
式中:参数a为幅值增益,用于调节sig(x)函数的幅值;参数b为指数因子,负责调节sig(x)函数的近似线性工作区间的范围.
4.1 打击场景分析在制导律仿真中,需要对不同的打击场景所对应的攻击角及期望视线角进行分析讨论.
1) 当导弹采用垂直拦截时,所对应的攻击角为:θimp1=π/2 rad,由式(8)可得初始的期望视线角为qF0=3.201 rad.根据式(5)的约束条件则有qF0-$\phi $m0=2.416 rad>π/2 rad,使得目标不在导引头的视场范围内.因此,需将式(8)修改为
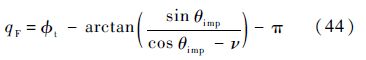
2) 当导弹采用追击拦截时,所对应的攻击角为:θimp2=0 rad,由式(8)可得初始的期望视线角为qF0=2.093 rad.根据式(5)的约束条件可知,目标在导引头的视场范围内,即可以采用式(12)计算期望视线角.
3) 上述给出了在两种特殊攻击角约束的情况下,期望视线角的计算.当选取其他任意攻击角约束时可以参考上述方法计算期望的视线角.
4.2 滑模捕获能力分析当闭环系统在Tr时刻到达滑模面,从滑模捕获能力角度分析制导律的鲁棒性.根据第3节中稳定性分析,当系统到达滑模面,得到如下结果:

此时,制导律为
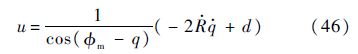
即在到达滑模面后,系统将保持式(46)的制导律直到拦截成功.在任意t=TF>Tr时刻,为保证拦截成功,需要满足条件:在(υR,υq)坐标空间内,导弹运动轨迹在t=TF时刻满足$\dot{R}$(TF)<0或不穿过υq轴.该结论的详细证明可以参照文献[15].
4.3 仿真算例对比及分析为了验证该制导律的有效性,考虑系统的外部扰动及不确定性.系统仿真步长为0.001 s,EFTCG的参数统一取为:h=0.001,r=50,w1=20,β=10,γ=1.2,k=2,σ=20,η=1,a=2,b=3.导弹加速度的最大值am=200 m/s2.同时在弹体反馈环节引入3(°)/s、方差为0.1的随机白噪声,仿真按照如下方式进行.
算例1 目标作法向加速度为恒值at=10 m/s2的机动.
1) 考虑垂直攻击的场景,即θimp1=π/2 rad.
针对这种情况,导弹与目标的相对运动曲线如图 4所示.其中,A和D分别为末制导开始时刻和结束时刻.导弹拦截目标的攻击时间为19.04 s,最后的攻击角度为88.1°.
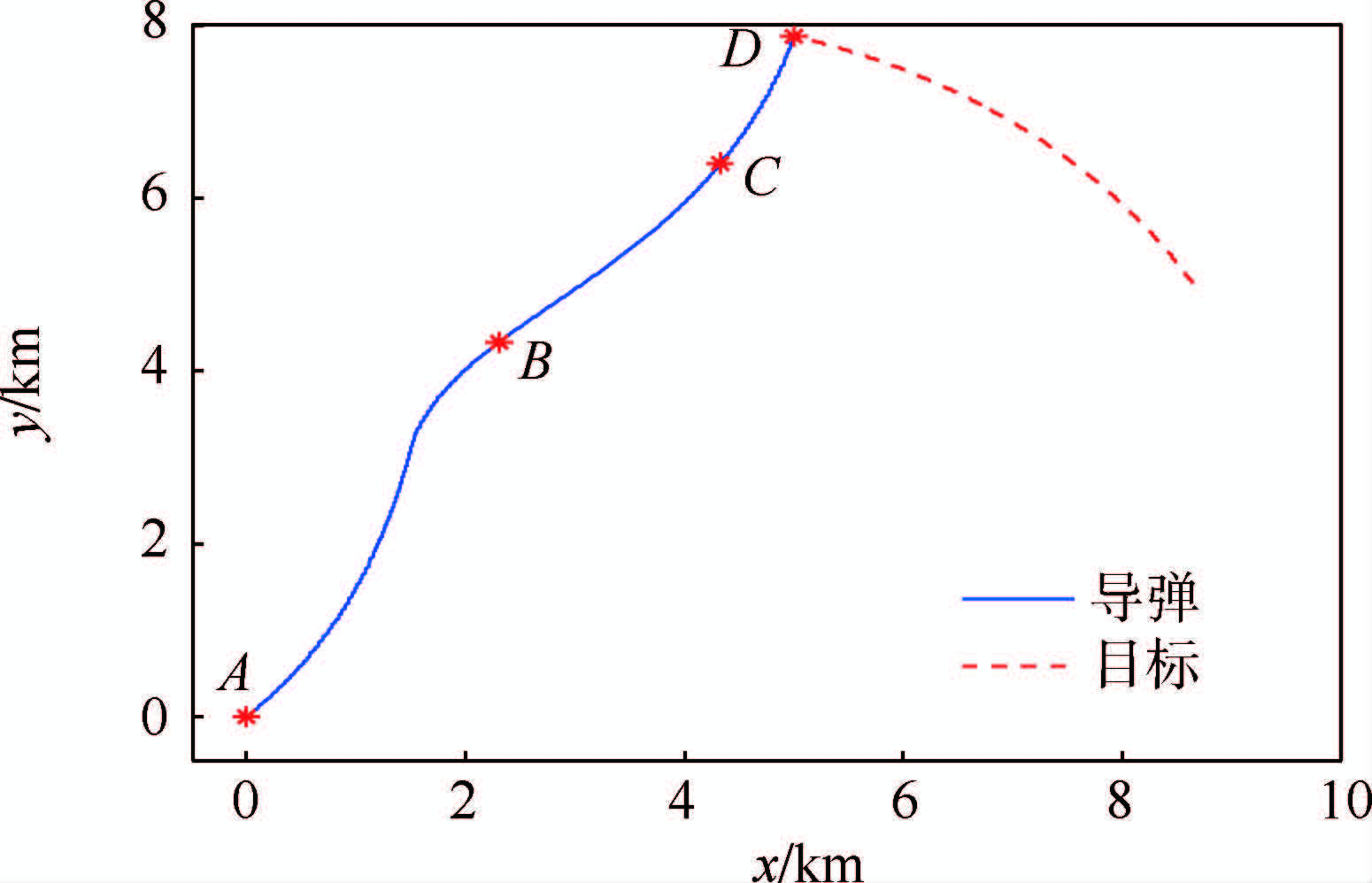 |
| 图 4 算例1中弹目相对运动轨迹(θimp1=π/2)Fig. 4 Curves of relative motion between missile and target in case 1(θimp1=π/2) |
| 图选项 |
由图 5(a)可知,系统在t=Tr时刻到达B点,即到达滑模面s=0.在滑模面上的运动时,根据快速非奇异终端滑模面的特性,在t=TF时刻到达C点,此时,满足式(43)的结论,如图 5(c)、图 5(d)所示.导弹所需的过载平滑且无抖振现象,如图 5(b)所示.导弹在两个阶段所需的过载较大:即初始阶段和将要到达滑模面阶段.即使到达滑模面,导弹所需过载也不会减小到零,此时导弹将保持式(44)的制导律实施拦截.为保证拦截成功,必须满足第4.2节中的条件:即在t=TD时刻到达D点,满足$\dot{R}$(TD)<0,此时υq≈0,即拦截成功.如图 6所示,验证了上述的结论.
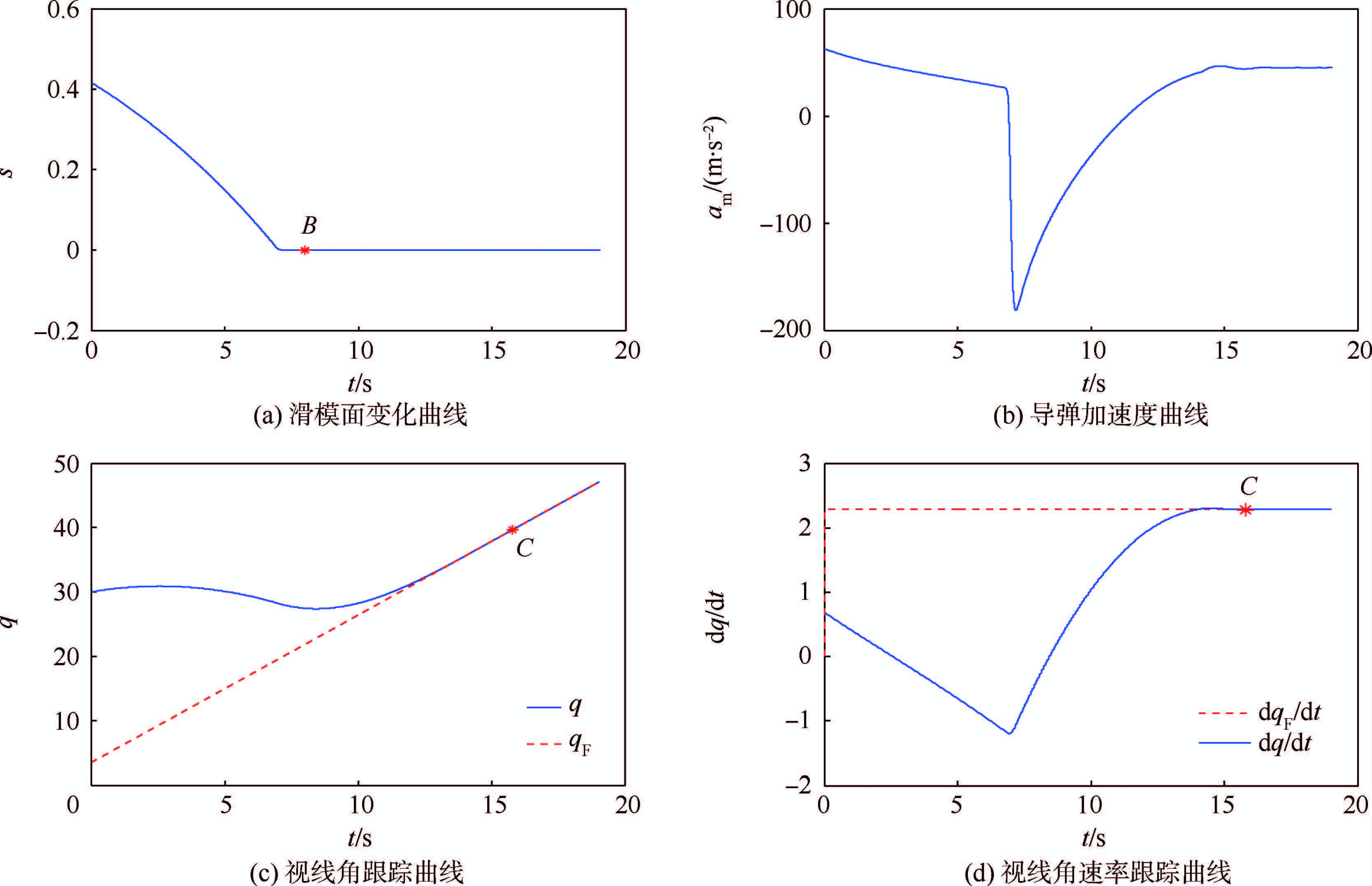 |
| 图 5 恒值机动目标的仿真结果(θimp1=π/2)Fig. 5 Simulation results of constant maneuver target (θimp1=π/2) |
| 图选项 |
 |
| 图 6 算例1中弹目相对运动在(υR,υq)空间内的轨迹(θimp1=π/2)Fig. 6 Trajectory of relative motion between missile and target in (υR,υq) space in case 1 (θimp1=π/2) |
| 图选项 |
2) 考虑尾追攻击的场景,即θimp2=0 rad.
针对这种情况,导弹与目标的相对运动曲线如图 7所示.导弹成功拦截目标时,攻击角度为0.8°,攻击时间为28.4 s.其中,A和D分别为末制导开始时刻和结束时刻.
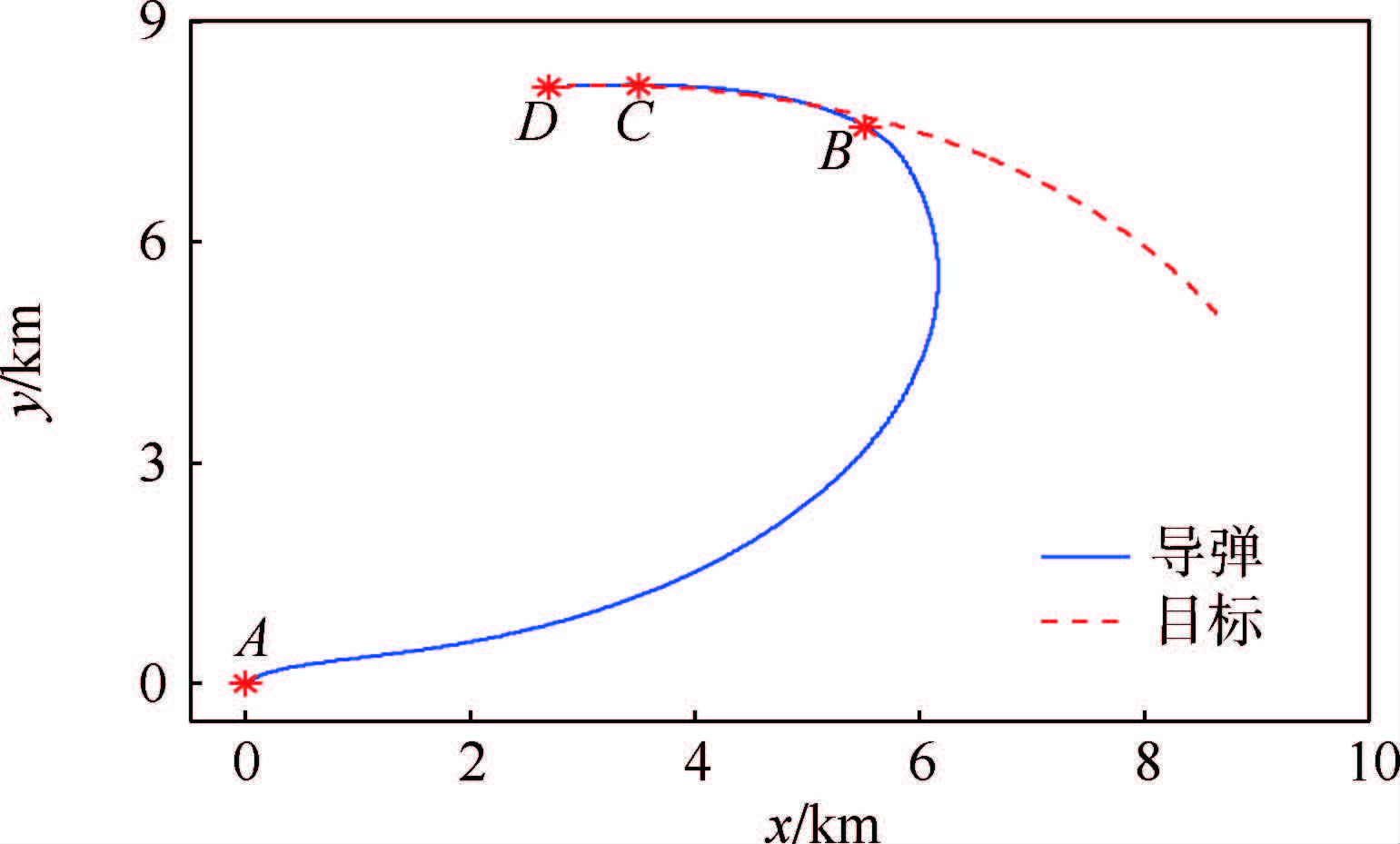 |
| 图 7 算例1中弹目相对运动轨迹(θimp2=0)Fig. 7 Curves of relative motion between missile and target in case 1 (θimp2=0) |
| 图选项 |
由图 8(a)可知,系统在t=Tr时刻到达B点,即滑模面s=0.在滑模面上运动时,在t=TF时刻到达C点,并满足式(45)的结论,如图 8(c)、图 8(d)所示.导弹所需的过载平滑且无抖振现象,如图 8(b)所示.在D点,满足$\dot{R}$(TD)<0,此时υq≈0,即拦截成功,如图 9所示.相对于垂直攻击的场景,攻击时间增加,同时在初始时刻和到达滑模面时刻的过载增大,并在拦截过程中过载有明显的饱和现象,降低了该制导律的鲁棒性.
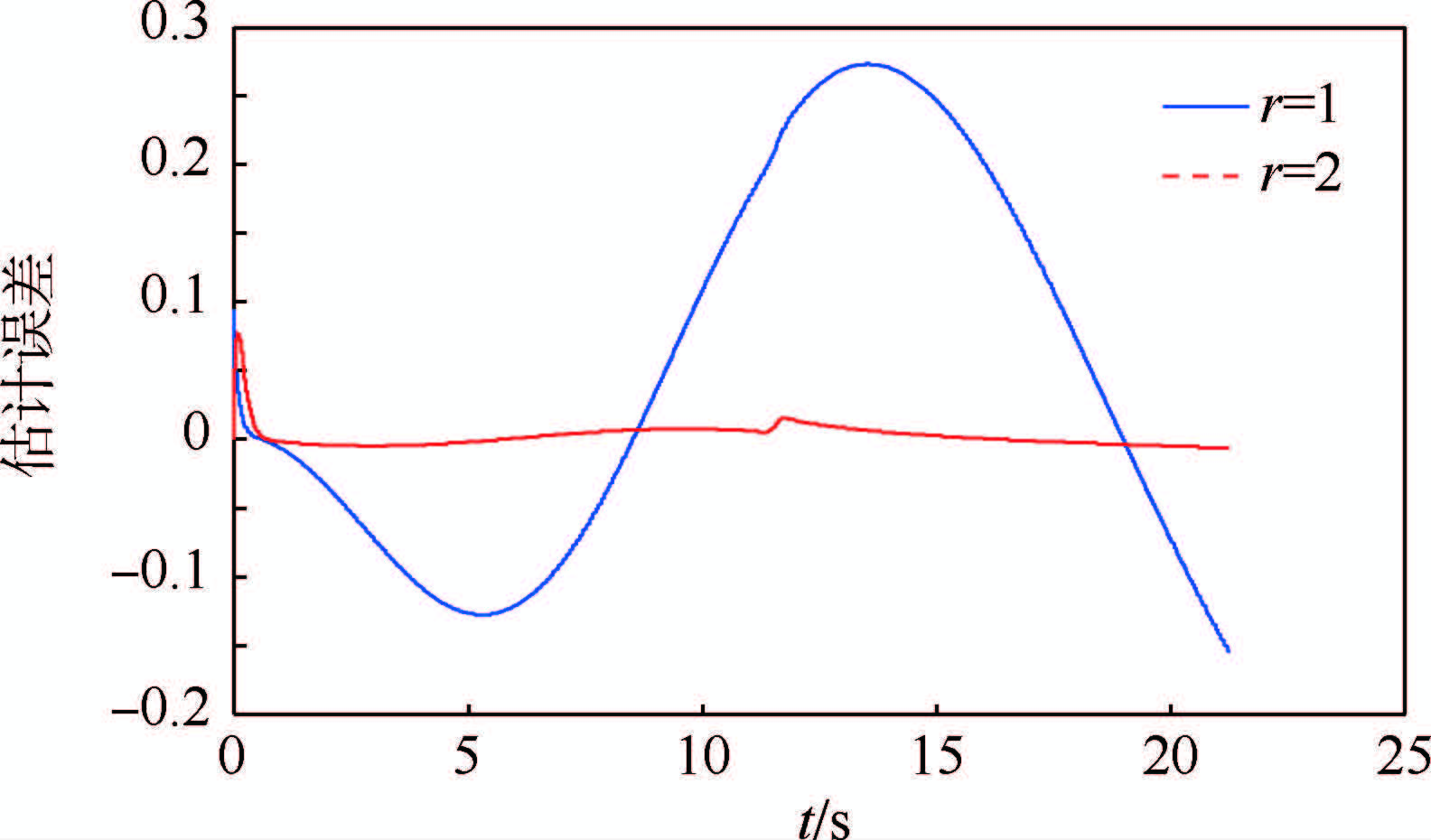
针对该算例,考察EDO对系统(10)中的干扰d(t)的估计能力,在这里考虑目标逃逸的加速度atq的估计即假设$\dot{V}$m=0,$\dot{V}$t=0的情况,及扩张阶数r=1,2的情况,且保持观测器的带宽wo=10 rad/s不变.扩张阶数对干扰估计能力的影响如图 10所示.EDO具有很好的干扰估计能力.同时,在相同观测带宽下,系统干扰的估计误差随着扩张阶数的增加而减小,与稳定性证明中的定理1的结论一致.
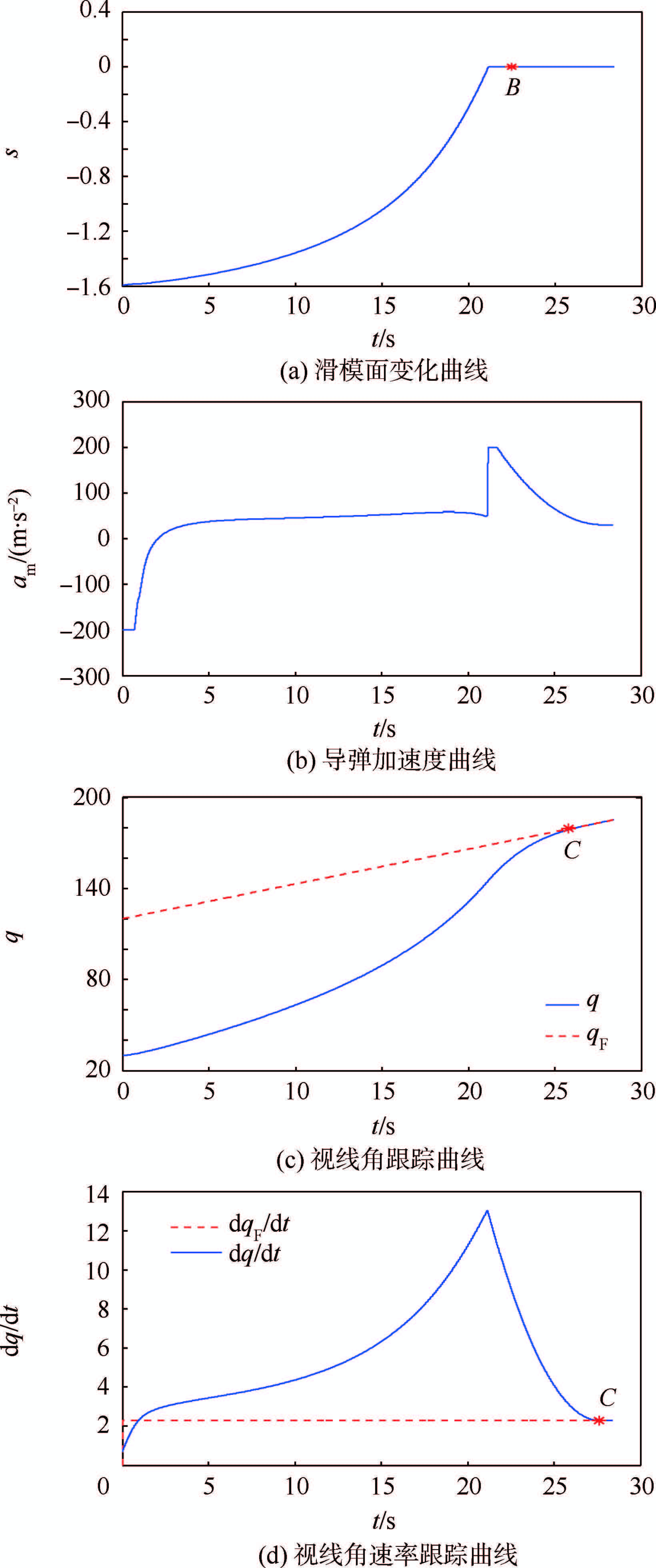 |
| 图 8 恒值机动目标的仿真结果(θimp2=0)Fig. 8 Simulation results of constant maneuver target (θimp2=0) |
| 图选项 |
 |
| 图 9 算例1中弹目相对运动在(υR,υq)空间内的轨迹(θimp2=0)Fig. 9 Trajectory of relative motion between missile and target in (υR,υq) space in case 1 (θimp2=0) |
| 图选项 |
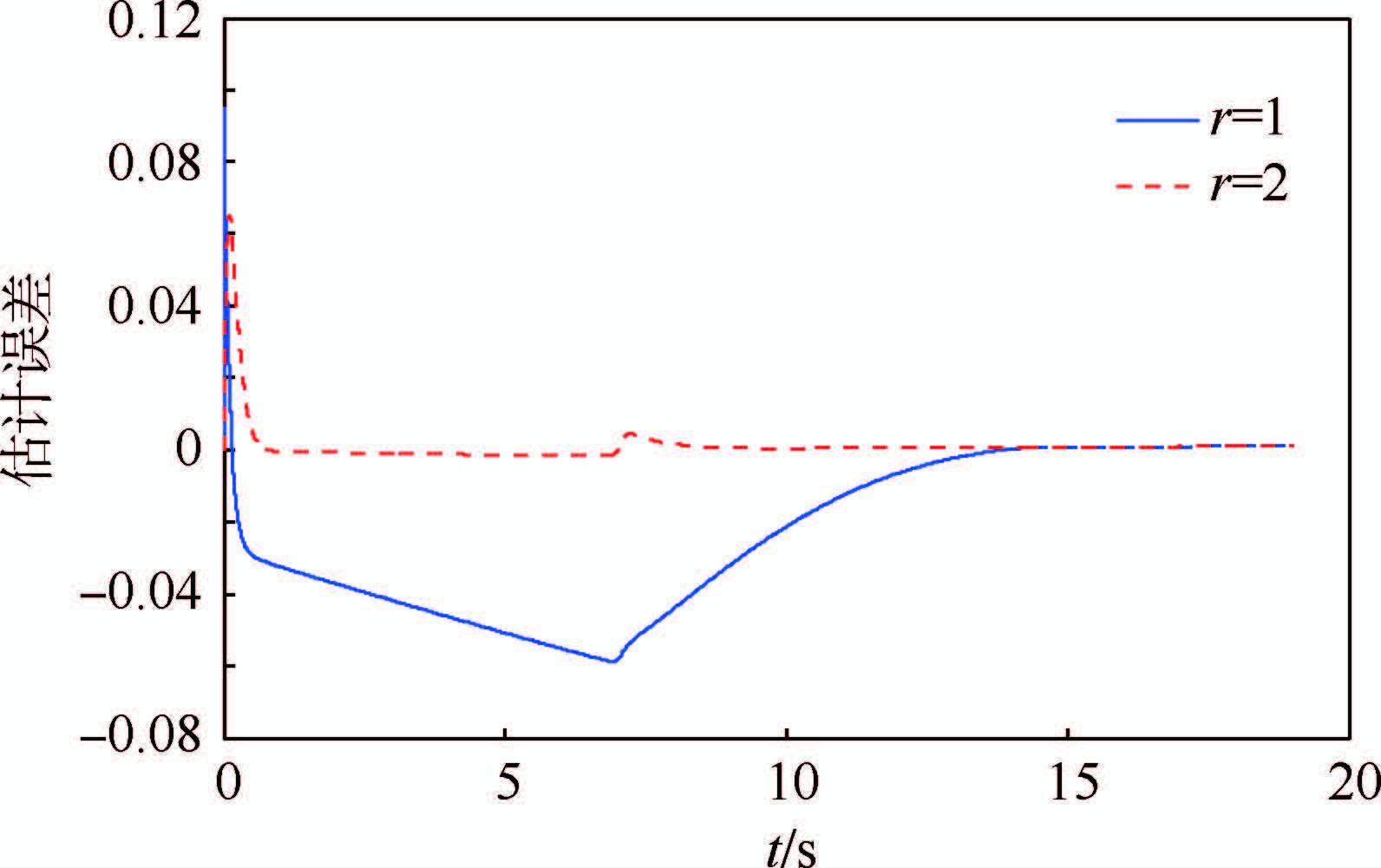 |
| 图 10 算例1中不同扩张阶数时的估计误差Fig. 10 Estimation error with different extended orders in case 1 |
| 图选项 |
算例2 目标作加速度为at=Am sin(πt/10)m/s2的蛇形机动.
针对这种情况,当Am=15时,分别考虑垂直攻击和尾追攻击的场景,导弹与目标的相对运动曲线分别如图 11(a)和图 12(a)所示.在垂直攻击场景中最后的攻击角度为88.16°,相应的攻击时间为19.06 s;在尾追攻击场景中最后的攻击角度为1.3°,相应的攻击时间为29.27 s.在两种攻击场景下,都能满足拦截成功的条件,即在D点满足$\dot{R}$(TD)<0,υq≈0.二者对比可知,在垂直攻击中到达B点的时间较短,同时,整个攻击时间也较短.在整个拦截过程中,垂直攻击所需的过载较小,并且对制导律参数的敏感度低,鲁棒性较高.
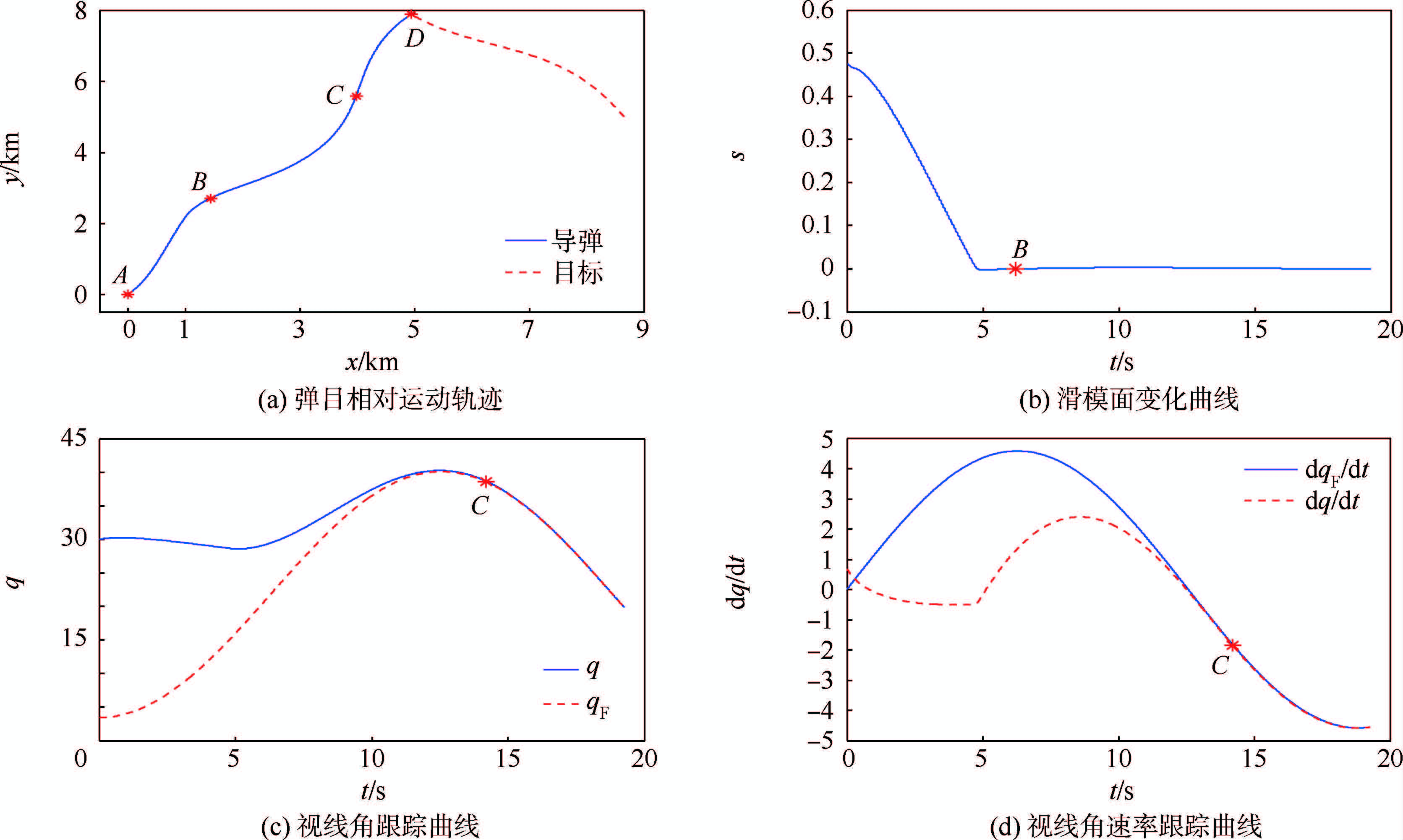 |
| 图 11 算例2中蛇行机动目标的仿真结果(θimp1=π/2)Fig. 11 Simulation results of weaving maneuver target in case 2 (θimp1=π/2) |
| 图选项 |
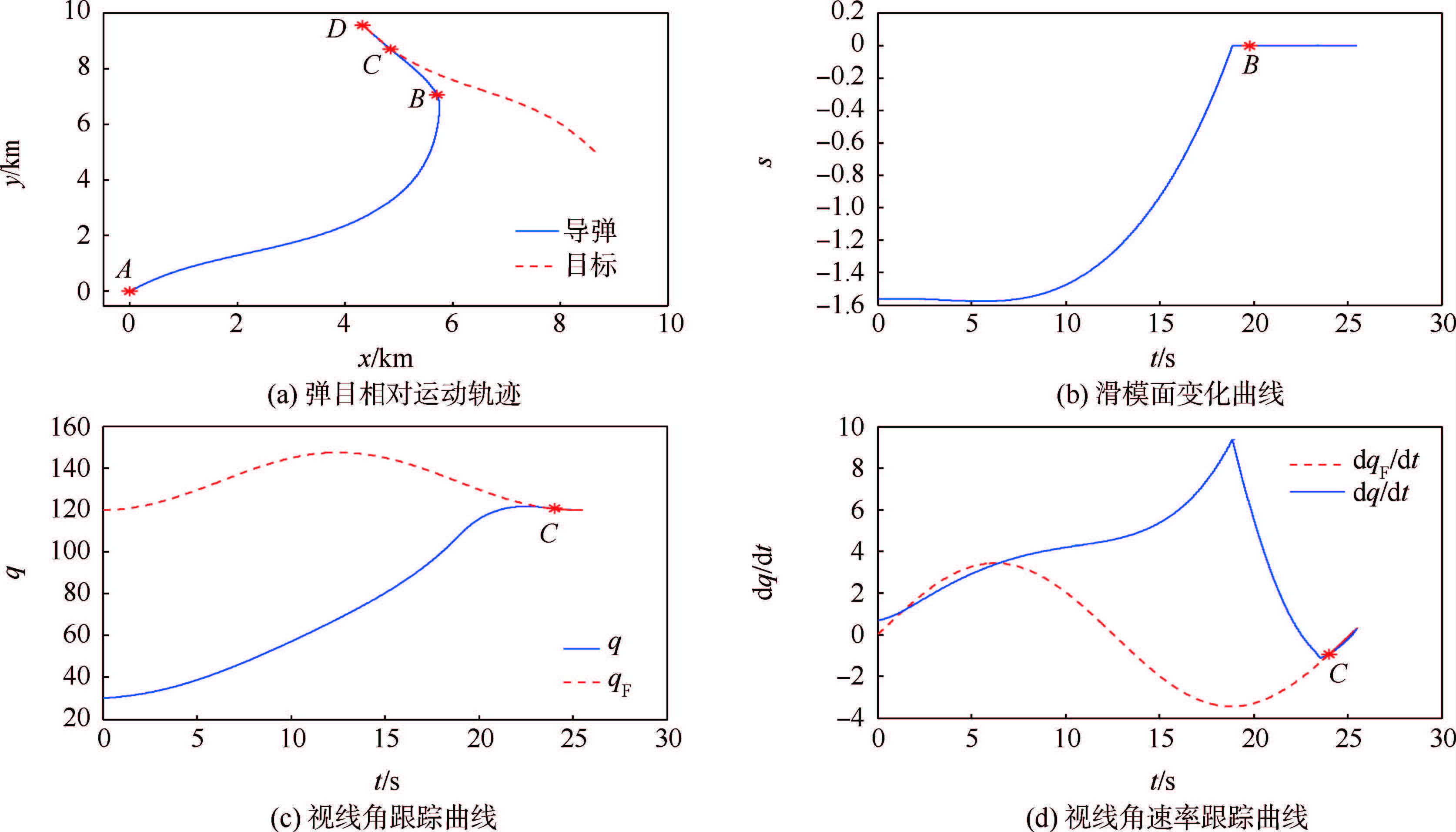 |
| 图 12 算例2中蛇形机动目标的仿真结果(θimp2=0)Fig. 12 Simulation results of waving maneuver target in case 2 (θimp2=0) |
| 图选项 |
为了进一步考察EFTCG制导律在拦截机动目标时的性能,考虑目标加速度的幅值Am=1g,1.5g,2g,2.5g,3g时,导弹拦截目标的仿真结果如图 13所示.由图 13(a)可知,导弹都能按照期望的攻击角约束完成对目标的拦截.随着目标加速度的幅值的增加,导弹所需的过载增大,同时系统收敛到滑模面s=0的时间缩短,仿真结果如图 13(b)和图 13(c)所示.
 |
| 图 13 目标加速度幅值不同时的仿真结果Fig. 13 Simulation results of weaving target with different amplitudes of weave maneuver |
| 图选项 |
当保持目标机动加速度的幅值不变,即Am=15,考察导弹在不同攻击角约束时该制导律的性能,仿真结果如图 14所示.当攻击角约束θimp=π/3,π/2,2π/3时,相应的攻击时间分别为:23.23、19.98、21.27 s,系统在初始时刻和到达滑模面时需要的过载较大.
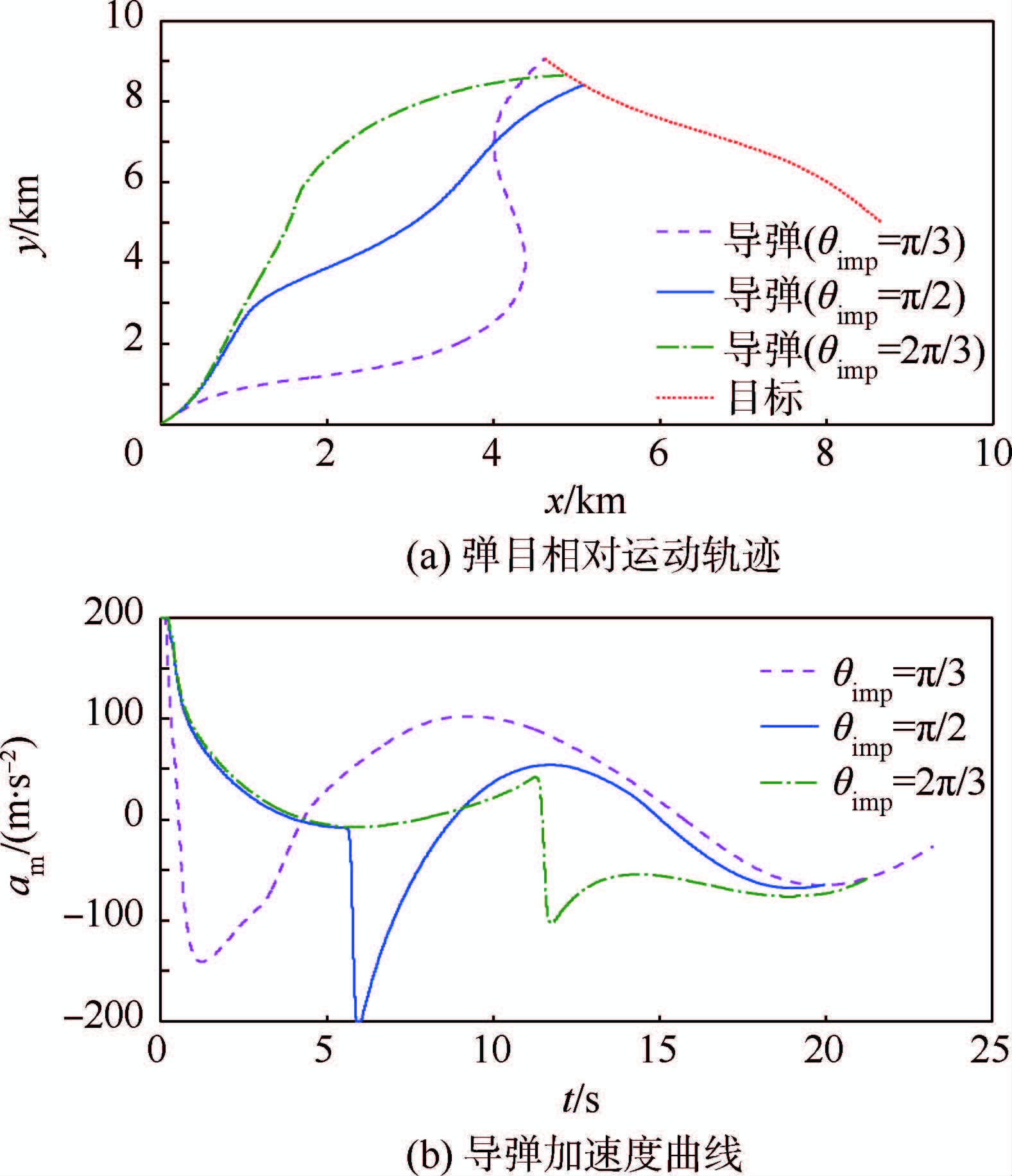 |
| 图 14 不同攻击角时拦截蛇行机动目标的仿真结果Fig. 14 Simulation results of interception of a weaving maneuver target with various impact angles |
| 图选项 |
针对该算例,考察EDO对系统(10)中的总干扰d(t)的估计能力,假设$\dot{V}$m=5 m/s,$\dot{V}$t=10 m/s,体现了导弹速度时变及目标加速度未知的情况.在这里考虑扩张阶数n=1、2的情况,且保持观测器的带宽wo=10 rad/s不变.干扰估计结果如图 15所示,EDO具有很好的干扰估计能力.当观测带宽相同时,系统干扰的估计误差随着扩张阶数的增加而减小.
 |
| 图 15 算例2中不同扩张阶数时的估计误差Fig. 15 Estimation error with different extended order in case 2 |
| 图选项 |
同时,期望视线角速率信号依靠对弹载传感器的反馈信号微分获取.采用常规的微分方法易于受噪声的影响,降低系统的鲁棒性.因此,本文采用TD获取$\dot{q}$F,同时在仿真的过程中加入方差为0.1的高斯白噪声.对比仿真结果如图 16所示.仿真结果表明,TD具有良好的跟踪性能和明显的抑制噪声的作用.
 |
| 图 16 跟踪微分器仿真结果Fig. 16 Simulation results of tracking differentiator |
| 图选项 |
为了对比制导律性能,将本文的制导律与文献[15]提出的制导律进行对比仿真分析.假设目标机动加速度为at=15 sin(0.25t)m/s2,文献[15]的制导律为

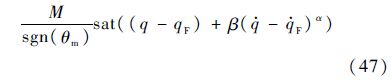
式中:M=500;β=10;α=5/3.该制导律详细的分析请参考文献[15].
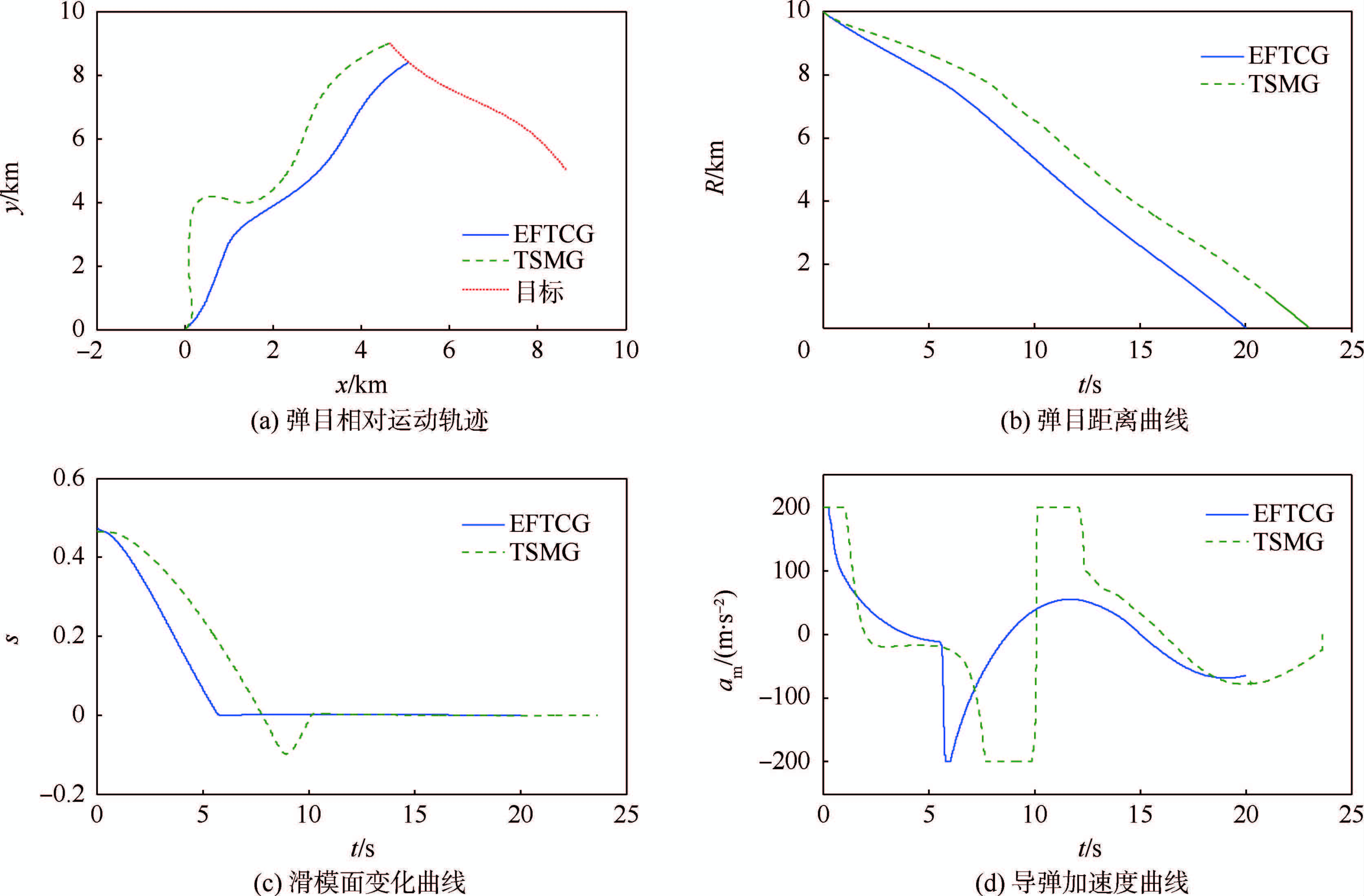
对于EFTCG和TSMG制导律,在垂直攻击场景下,导弹的攻击时间分别为19.98 s和23.17 s;最后的攻击角度分别为89.2°和85.4°,与期望的攻击角度相比,误差分别为0.8°和4.6°.由图 17(a)和图 17(d)可知,EFTCG制导律的弹道轨迹较平滑,攻击时间较短,所需的过载较小.
 |
| 图 17 不同制导律拦截蛇形机动目标的仿真结果(θimp1=π/2)Fig. 17 Simulation results of interception of weaving maneuver target with different guidance law(θimp1=π/2) |
| 图选项 |
由图 17(c)和图 17(d)可知,在初始时刻,TSMG所需的过载明显饱和,且初始时刻的变化率较快.EFTCG所需的过载较小,且其变化率较平缓.EFTCG收敛到滑模面s=0的时间较短,且在该时刻所需的过载较小,而TSCG有明显的饱和现象,在接近目标的末端时刻会出现发散现象.TSCG对参数的敏感度较高,鲁棒性较差.
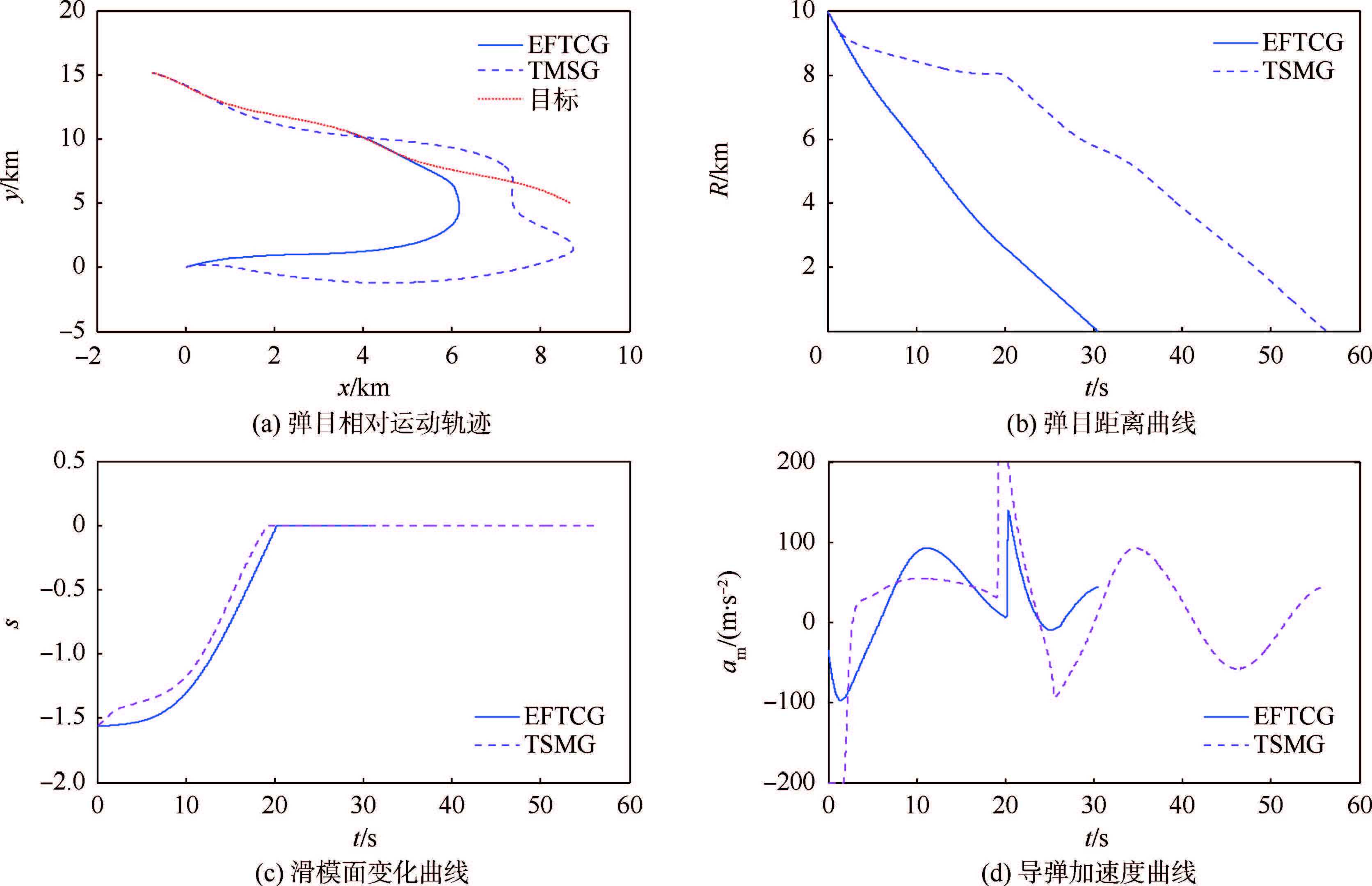
在尾追攻击场景下,导弹的攻击时间分别为30.52 s和56.27 s;最后的攻击角误差分别为0.365°和1.267°.由图 18(b)可知,EFTCG的相对距离变化率相对平滑,攻击的时间约为TSMG的一半.在整个制导过程中,TSMG所需的过载较大,同时,TSMG到达滑模面的时间较短,但是所需的过载较大并有明显的饱和现象,降低了系统的鲁棒性.在该场景下,TSMG不仅对制导律参数较为敏感,而且对舵机环节的延时也更加敏感,不具有工程实用的价值.本文提出的制导律不仅在整个制导过程中未出现饱和现象,而且在有限时间内跟踪上期望的视线角.
 |
| 图 18 不同制导律拦截蛇形机动目标的仿真结果(θimp2=0)Fig. 18 Simulation results of interception of weaving maneuver target with different guidance laws (θimp2=0) |
| 图选项 |
5 结 论针对目标机动且加速度不可测、导弹速度时变的情况,本文基于扩张干扰观测器和有限时间收敛控制技术提出了一种末端攻击角约束制导律.
1) 借鉴干扰观测器的设计思想,设计了扩张干扰观测器,并给出其稳定性证明及误差收敛域,同时,给出了基于带宽的调参方法,便于工程应用及推广.
2) 在制导律设计过程中,引入快速跟踪微分器解决了制导律中所需的期望视线角速率无法直接给出的问题.同时,推导了该复合制导律的收敛时间及收敛域,为参数的整定提供指导.
3) 将该复合制导律应用于不同攻击场景、目标不同的机动形式的仿真,引入滑模捕捉能力的概念.对比仿真结果表明,导弹在垂直攻击场景中拦截快速高机动目标时,本文提出的制导律能够保证导弹以更短的时间、更小的需用过载和更精确的攻击角度实现对目标的精度打击.
参考文献
| [1] | Kim M,Grider K V.Terminal guidance for impact attitude angle constrained flight trajectories[J].IEEE Transactions on Aerospace and Electronic Systems,1973,9(6):852-859. |
| Click browse the original | |
| [2] | Kim B S,Lee J G,Han H S.Biased PNG law for impact with angular constraint[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(1):277-288. |
| Click browse the original | |
| [3] | Ryoo C K,Cho H,Tahk M J.Optimal guidance laws with terminal impact angle constraint[J].Journal of Guidance,Control,and Dynamics,2005,28(4):724-732. |
| Click browse the original | |
| [4] | Ryoo C K,Cho H,Tahk M J.Time-to-go weighted optimal guidance with impact angle constraints[J].IEEE Transactions on Control Systems Technology,2006,14(3):483-492. |
| Click browse the original | |
| [5] | Ohlmeyer E J,Philips C A.Generalized vector explicit guidance[J].Journal of Guidance,Control,and Dynamics,2006,29(2):261-268. |
| Click browse the original | |
| [6] | Jeon I S,Lee J I.Optimality of proportional navigation based on nonlinear formulation[J].IEEE Transactions on Aerospace and Electronic Systems,2010,46(4):2051-2055. |
| Click browse the original | |
| [7] | Utkin V.Variable structure systems with sliding modes[J].IEEE Transactions on Automatic Control,1977,22(2):212-222. |
| Click browse the original | |
| [8] | 贾庆忠,刘永善,刘藻珍.电视制导侵彻炸弹落角约束变结构反演制导律设计[J].宇航学报,2008,29(1):208-214. Jia Q Z,Liu Y S,Liu Z Z.Variable-structure backstepping guidance law with terminal angular constraint for video guided penetrating bomb[J]. Journal of Astronautics, 2008, 29(1): 208-214(in Chinese). |
| Cited By in Cnki (28) | Click to display the text | |
| [9] | Harl N,Balakrishnan S N.Impact time and angle guidance with sliding mode control[J].IEEE Transactions on Control Systems Technology, 2012, 20(6): 1436-1449. |
| Click browse the original | |
| [10] | Sun W M,Zheng Z Q.3D variable structure guidance law based on adaptive model-following control with impact angular constraint[C]// Proceedings of the 26th Chinese Control Conference.Piscataway, NJ:IEEE Press,2007: 61-66. |
| [11] | Zhang Z X,Li S H,Luo S.Terminal guidance laws of missile based on ISMC and NDOB with impact angle constraint[J]. Aerospace Science and Technology, 2013, 31(1): 30-41. |
| Click browse the original | |
| [12] | 王晓芳,郑艺裕,林海.基于扰动观测器的终端角约束滑模导引律[J].系统工程与电子技术,2014,36(1): 111-116. Wang X F,Zheng Y Y, Lin H.Sliding mode guidance law with impact angle constraint based on disturbance observer[J].Systems Engineering and Electronics,2014,36(1):111-116(in Chinese). |
| Cited By in Cnki (4) | Click to display the text | |
| [13] | 孙胜,张华明,周荻.考虑自动驾驶仪动特性的终端角度约束滑模导引律[J].宇航学报,2013,34(1):69-78. Sun S,Zhang H M,Zhou D.Sliding mode guidance law with autopilot lag for terminal angle constrained trajectories[J].Journal of Astronautics,2013,34(1):69-78(in Chinese). |
| Cited By in Cnki (17) | Click to display the text | |
| [14] | Zhou D,Qu P P,Sun S.A guidance law with terminal impact angle constraint accounting for missile autopilot[J].Journal of Dynamic Systems Measurement and Control,2013,135(5):051009. |
| Click browse the original | |
| [15] | Kumar S R,Rao S,Ghose D.Sliding-mode guidance and control for all-aspect interceptors with terminal angle constraints[J].Journal of Guidance,Control,and Dynamics,2012,35(4):1230-1246. |
| Click browse the original | |
| [16] | Kumar S R,Rao S,Ghose D.Nonsingular terminal sliding mode guidance with impact angle constraints[J].Journal of Guidance,Control,and Dynamics,2014,37(4):1114-1130. |
| Click browse the original | |
| [17] | Xiong S F,Wang W H,Liu X D,et al.Guidance law against maneuvering targets with intercept angle constraint[J].ISA Transactions,2014,53(4):1332-1342. |
| Click browse the original | |
| [18] | 熊少锋,王卫红,刘晓东,等.考虑导弹自动驾驶仪动态特性的带攻击角度约束制导律[J].控制与决策,2014,30(4):585-592. Xiong S F,Wang W H,Liu X D,et al.Impact angle guidance law considering missile's dynamics of autopilot[J].Control and Decision,2014,30(4):585-592(in Chinese). |
| Cited By in Cnki (0) | |
| [19] | 张运喜,孙明玮,陈增强.滑模变结构有限时间收敛制导律[J].控制理论与应用,2012,29(11):1413-1418. Zhang Y X,Sun M W,Chen Z Q.Sliding mode variable structure finite-time convergence guidance law[J].Control Theory & Applications,2012,29(11):1413-1418(in Chinese). |
| Cited By in Cnki (5) | Click to display the text | |
| [20] | 王钊,李世华,费树岷.非奇异终端滑模导引律[J].东南大学学报,2009,39(1):87-90. Wang Z,Li S H,Fei S M.Nonsingular terminal sliding mode guidance law[J].Journal of Southeast University,2009,39(1):87-90(in Chinese). |
| Cited By in Cnki (11) | Click to display the text | |
| [21] | 熊少锋,王卫红,王森.带攻击角度约束的非奇异快速终端滑模制导律[J].控制理论与应用,2014,31(3):269-278. Xiong S F,Xang W H,Wang S.Nonsingular fast terminal sliding-mode guidance with intercept angle constraint[J].Control Theory & Applications,2014,31(3):269-278(in Chinese). |
| Cited By in Cnki (2) | Click to display the text | |
| [22] | Chen W H.Nonlinear disturbance observer-enhanced dynamic inversion control of missiles[J].Journal of Guidance,Control,and Dynamics,2003,26(1):161-166. |
| Click browse the original | |
| [23] | Chen X S,Yang J,Li S H,et al.Disturbance observer based multi-variable control of ball mill grinding circuits[J].Journal of Process Control,2009,19(7):1205-1213. |
| Click browse the original | |
| [24] | Xia Y Q,Chen R F,Pu F,et al.Active disturbance rejection control for drag tracking in mars entry guidance[J].Advances in Space Research,2014,53(5):853-861. |
| Click browse the original | |
| [25] | 韩京清.自抗扰控制技术[M].北京:国防工业出版社,2008:56-66. Han J Q.Active disturbance rejection control technique[M].Beijing:National Defence Industry Press,2008:56-66(in Chinese). |
| [26] | Guo B Z,Zhao Z L.On convergence of tracking differentiator[J].International Journal of Control,2011,84(4):693-701. |
| Click browse the original | |
| [27] | Bhat S P,Bernstein D S.Finite-time stability of continuous autonomous systems[J].SIAM Journal of Control and Optimization,2000,38(8):751-766. |
| Click browse the original |
