基于贝叶斯网络的故障诊断系统性能评价

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2021-12-25

贝叶斯网络是智能诊断领域中发展成熟的不确定推理方法,采用有向图及条件概率表达随机变量之间复杂的概率关系^[1],因其具有强大的不确定性问题处理能力和较为准确的推理能力,而被广泛地运用于军事^[2]、医疗^[3]和经济^[4]等各个领域,是现阶段不确定知识表达和推理领域最有效的理论模型之一。目前有大量研究着眼于优化故障诊断模型的推理能力,通常由诊断准确度衡量其改进结果^{[5, 6]},由于准确度指标易受到模型及数据影响而产生误差,部分故障诊断系统引入了置信度这一指标用于估计其性能^{[7, 8]},但现有置信区间评价指标是基于测试数据组诊断推理结果符合正态分布的假设,在数据规模较小(通常小于100组)的情况下将产生较大误差,并且因该方法所得置信区间上限不随准确度的增加而收敛于1,而是会超出概率界限而失去意义,所以不能适用于诊断准确度高的应用。在上述研究基础上,考虑故障诊断系统输出结果真实分布情况,提出新的置信区间计算方法,能够对贝叶斯网络诊断模型的性能提供更客观的评价,并采用机载燃油系统故障诊断模型应用实例进行了对比验证,证明本文所提方法有效。1 贝叶斯网络诊断模型的性能评价贝叶斯网络由模型结构和相关参数共同组成,通过在网络节点上进行的概率计算,可以由已知的部分节点(实际系统中称为故障征兆节点)概率推理出其他节点(实际系统中称为故障状态节点)概率^[9]。模型结构建立不准确或者参数关系存在误差都将导致诊断结果的不准确,而模型诊断结果将直接影响使用系统的维护策略,如何对输出结果可信度进行有效预测和评估成为了系统使用的关键。部分面向贝叶斯网络的优化策略通过诊断准确度的提升来说明其模型性能的提升,故障诊断准确度定义如下:系统对设备已知故障征兆节点数据进行诊断测试,获得故障状态节点的诊断结果,故障诊断准确度是该诊断结果与设备真实工作状态间相符合程度的期望值^[10]。准确度可以评价模型诊断性能,但是作为对样本数据多次测定的估计值,准确度不等于真值,无法准确衡量系统诊断结果与真实状态的一致程度。由于实际系统不可避免地存在数据噪声、建模误差等不确定因素,而有限的测试数据不足以全面反映故障系统诊断准确度,导致准确度期望值与真实值出现偏差,对此可以采用期望与方差的概率论思想来解决。计算偏差大小来获得更加准确的结果,这一结果称为准确度期望值的置信区间指标,可以有效地反应故障诊断系统单次诊断能力。置信区间是对模型输出范围的预测,它的物理意义是^{[7, 11, 12]}:置信度水平1－α是公认真值包含在置信区间内的概率,一旦选取置信水平1－α,则真实值落在该置信区间的概率为1－α。对故障诊断系统估计准确度求解置信区间,那么理论上,系统进行一次诊断,该置信区间涵盖系统真实诊断准确度的概率为1－α。通过判断准确度期望是否落在置信区间可以初步检验准确度的正确性,由准确度期望和置信区间共同构成的故障诊断系统性能评价指标可以反映系统真实诊断能力,指示系统每次诊断结果的可信程度。2 诊断准确度计算贝叶斯诊断模型的建立通常依赖于先验知识和对训练样本的学习,训练数据的完整性和准确性会直接影响诊断系统的性能,面对建模系统,通常需要利用其历史工作数据及故障维护数据作为样本进行学习,确定合适的贝叶斯网络拓扑结构及各节点处的条件概率密度,建立贝叶斯诊断网络。贝叶斯网络诊断系统准确度计算公式为^[13]

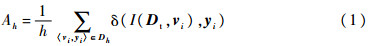
式中：D_t为训练数据集；D_h为测试数据集；h为测试数据集规模；<v_i,y_i>∈D_h(i∈[1,h])为测试集中的一组数据；v_i为各故障征兆节点所构成的向量；y_i为各故障状态节点构成的向量。使用训练数据建立贝叶斯网络推理机I,对测试数据集中的每组观察值v_i,可获得对故障状态节点的诊断结果,克罗内克函数δ(i,j)仅在i=j时输出为1,其余情况下输出均为0,因此准确度A_h实际就是贝叶斯网络诊断正确的次数与总测试次数的比值。尽管贝叶斯网络的建立仅取决于训练数据,但根据式(1)可以看出,准确度A_h的计算结果与测试数据同样有关,过小的测试数据规模可能导致不准确的计算结果;贝叶斯网络对故障状态节点的诊断概率是对故障可能性的度量,通常需要与预先设定的故障概率阈值进行比较以判定是否故障^[14],因此阈值设定同样会影响A_h计算中的诊断结果;此外,δ(I(D_t,v_i),y_i)反映所有故障状态节点诊断结果的正确程度,过多的故障状态节点也会影响准确度的计算结果,合理地将系统拆分为多个子系统分别诊断将有效提高贝叶斯系统诊断准确度。3 置信区间计算3.1 传统置信区间计算方法故障诊断系统通过计算系统准确度期望的置信区间来消除准确度估计误差对评价指标的影响,对于诊断结果,仅存在诊断正确或错误2种情况,因此准确度A_h满足0-1分布。已知二项分布的期望和方差分别为

当样本数据足够大时可以采用中心极限定理进行估计,样本结果近似遵循正态分布,即

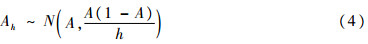
采用文献^[7]所述计算方法,求得系统置信区间如式(5)所示,其中z_α/2为置信度1－α下的临界值,可通过查询标准正态分布表得到

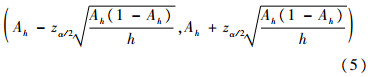
3.2 改进的置信区间计算方法第3.1节中所述方法将测试样本近似为正态分布,其前提条件是测试样本足够大,对实际诊断系统而言,该近似方法将存在2个问题:首先,测试样本必须有其倍数规模的训练样本存在,不必要地增加训练样本会导致系统训练时间和空间复杂度的增加,并且增加了诊断系统的建模代价;其次,由于历史数据通常有限,增加测试样本必然会牺牲训练样本数量,进而降低系统诊断准确度。此外,由式(5)可以看出,该置信区间受到准确度A_h的直接影响,A_h误差将会被置信区间所继承,因此上述方法求得置信区间可信程度低。本文采用改进的二项分布参数估计方法,并结合β分布与F分布对置信区间进行求解,过程如下:定义置信水平为1－α的可靠度置信区间满足P{p_L≤p≤p_H}=1－α(p为概率值;p_L为置信区间下限;p_H为置信区间上限),对概率分布函数P[p|h,m](h为样本大小,m为诊断正确样本数,

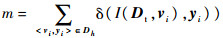,在置信区间[p_L,p_H]上积分得^[15]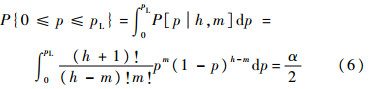

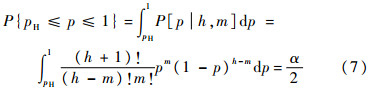
根据Γ(n+1)=n!,式(6)可转化为

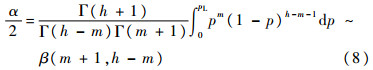
式(8)将二项分布参数p构建为β分布,该变化被称之为信任分布,此时n=h+1,再令v₁=m+1,v₂=n－m,对该β分布进一步变形,得到F分布^[16],即

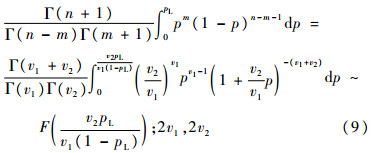
式(9)表示参数p的信任分布符合F(2v₁,2v₂)分布在v₂p_L/[v₁(1－p_L)]处的值,结合式(8)与式(9)得到

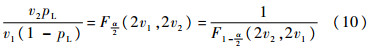
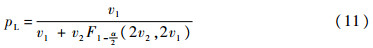
同理求得

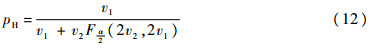
得到参数p的置信区间为

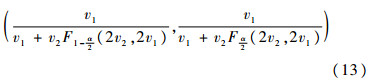
取置信水平0.95,样本规模h分别为100、1000和10000,对期望为0.01~0.99之间的诊断准确度求取置信区间,图 1(a)为第3.1节所述传统方法求得的置信范围,图 1(b)为改进方法所得置信范围。表 1选取若干组关键数据,对图 1中置信区间的区间大小进行了详细对比。通过对比图 1与表 1中各组数据,可以得出以下结论:1) 在相同置信水平下改进方法所求得的置信区间相较于传统方法更狭窄。2) 尽管在h=100时传统方法所得边界处置信区间要窄于改进方法,但传统方法的置信上下限超出了概率值的有效范围[0,1],不符合置信区间含义。3) 随着实验样本的增加,置信区间会趋于狭窄,并且2种方法的区间范围也会更加接近。

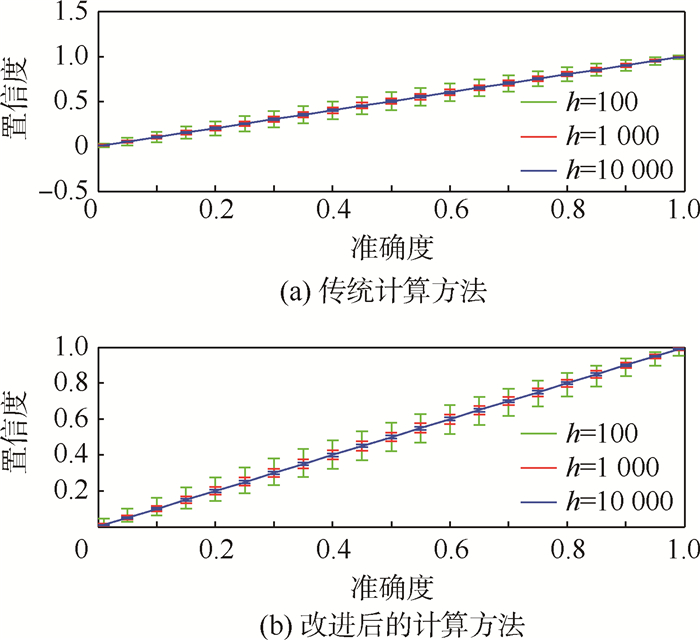图 1 2种方法求得的置信区间对比Fig. 1 Comparison of confidence intervals calculated from two methods

图选项

表 1 2种方法求得的置信区间对比Table 1 Comparison of confidence intervals calculated from two methods

h	方法	准确度
h	方法	0.01	0.10	0.30	0.50	0.70	0.90	0.99
100	传统方法	0.0390	0.1176	0.1796	0.1960	0.1796	0.1176	0.0390
100	改进方法	0.0426	0.0999	0.1491	0.1622	0.1491	0.0999	0.0426
1000	传统方法	0.0123	0.0372	0.0568	0.0620	0.0568	0.0372	0.0123
1000	改进方法	0.0107	0.0312	0.0476	0.0519	0.0476	0.0312	0.0107
10000	传统方法	0.0039	0.0118	0.0180	0.0196	0.0180	0.0118	0.0039
10000	改进方法	0.0033	0.0099	0.0151	0.0164	0.0151	0.0099	0.0033

表选项

置信区间是对诊断准确度可信程度的反映,在相同置信水平下,置信区间狭窄表明诊断结果可靠性高、鲁棒性好^[17],可以认为系统诊断能力更好,因此,当样本数据较小时,改进后的置信区间计算方法得到诊断性能更加准确。特别在实际系统中,往往更关心诊断准确度接近100%时的置信区间,此时传统方法得到的置信区间不能用于衡量系统诊断能力。反观改进方法,置信区间不直接受准确度A_h的影响,但准确度估计值均落在置信区间范围内,并且随着准确度的变化置信区间的分布情况也会有所改变,而不是如传统方法所示准确度始终位于置信区间中点,因此,改进方法所求置信区间可以用于验证准确度,并且更加符合实际工程情况。4 实例验证图 2所示诊断模型为机载燃油系统结构,其中机身油箱与机翼油箱为2个供给油箱,供给油箱交替向消耗油箱供油,每个油箱具有相应的传感器。对系统组件/子系统分别编号建立贝叶斯网络模型,其中节点(1)~(14)为故障节点(以白色椭圆表示),节点(15)~(21)为测试节点(以灰色矩形表示)。数据来源于贝叶斯网络开发工具Hugin Expert A/S对系统进行的建模仿真^[18],模型结构与条件概率遵循专家知识,诊断过程将测试节点数据作为证据输入,获取各故障节点的故障概率。本文考虑贝叶斯网络常见误差来源于数据完整性的缺乏,故分别对完整及不同程度缺失的训练数据进行仿真,得到若干组不同规模的故障数据。最后采用Holdout验证方法估计模型的诊断准确度期望,该验证方法的思路是:随机从最初的样本中选择部分数据形成验证数据,剩下的数据作为训练数据。

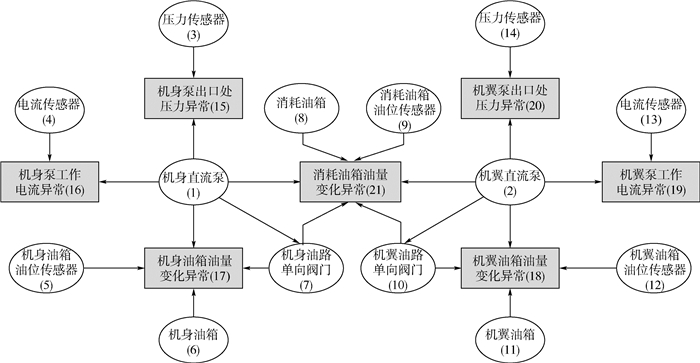图 2 燃油系统故障诊断模型Fig. 2 Fault diagnostic model for a fuel system

图选项

图 3为系统在不同训练数据下的诊断准确度。测试数据规模h=100,训练数据规模分别为300、3000和30000,所有训练数据下的测试数据完全相同,系统置信水平设置为95%,故障概率阈值设定为0.5(故障概率大于0.5判定为故障节点),根据图 3所示数据可以看出,对于完整数据训练样本,当训练数据达到测试数据3倍时诊断准确度已经接近理想值;当数据规模大于3000,训练数据的增加对于诊断准确度的提高将不再明显,但是如果训练数据出现缺失,在300及3000数据规模下的准确度会有较大幅度下降。此外,当数据缺失程度达到10%以上时,即使训练数据规模为30000,诊断准确度也将低于60%。

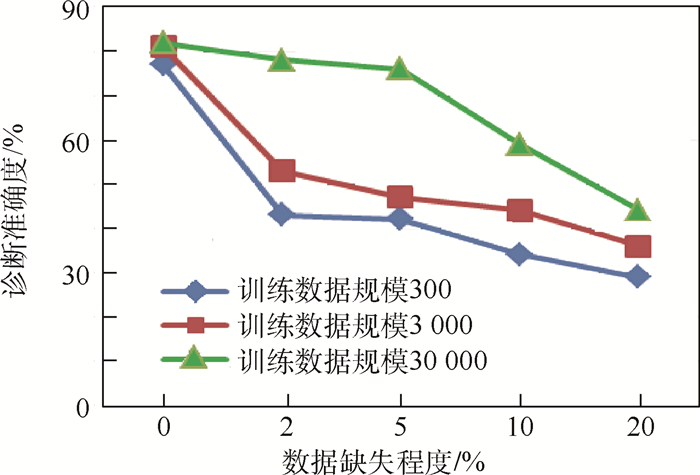图 3 缺失训练数据对诊断准确度的影响Fig. 3 Influence of missing training data on diagnostic accuracy

图选项

由此可以看出,诊断准确度能够作为评价训练是否充分的指标,随着数据缺失比例的上升,要获得较好的诊断准确度就必须增加训练数据规模。当准确度不再随训练数据规模增加而上升时,说明该准确度已接近系统真实值,此时若想进一步提高系统诊断准确度,只能从系统设计角度进行优化。图 4是对置信区间的验证,离散点代表测试数据规模为10、50、100、500和1000时的若干组测试准确度期望值,阴影区域在x轴方向所对应的概率上下限代表该训练数据下的置信区间计算值,以300训练数据为例,根据式(13)求得诊断准确度的置信区间范围是68.8%~85.2%(置信区间③所在区域),意味着该系统真实诊断准确度处于该范围内的概率为95%,通过训练数据规模为300的离散点的分布可以看出,诊断准确度基本符合该区间,并且随着训练数据和测试数据规模的增加,符合程度逐渐增加。因此可以验证第3.2节中对置信区间计算方法的合理性。

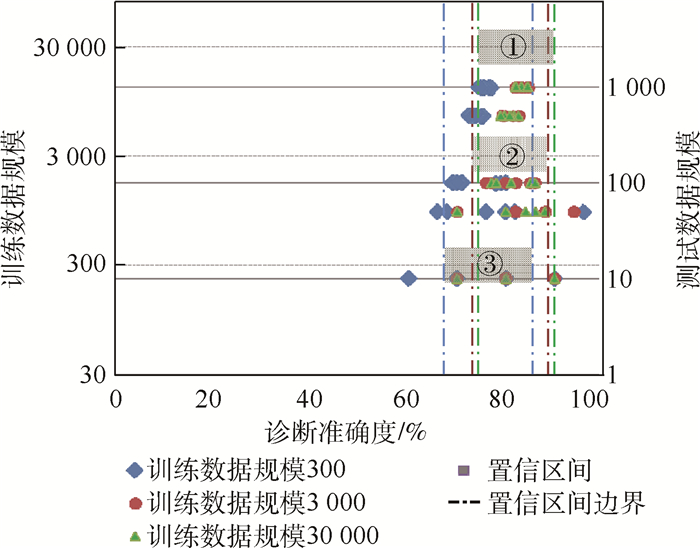图 4 置信区间验证Fig. 4 Verification of confidence interval

图选项

5 结论本文研究并改进了基于贝叶斯网络的故障诊断系统性能评价方法,通过实验证明:1) 采用准确度与置信区间相结合的指标计算方法可以较为客观和全面地衡量贝叶斯网络的故障诊断性能,运用该指标能够观察到训练数据规模以及数据缺失程度对于诊断系统性能的影响。2) 对已有置信区间的计算方法进行改进,放宽了置信区间对测试数据规模的限制条件,减小准确度指标因受测试数据制约而造成的误差,计算所得指标可靠性更高,并且更加符合工程实际应用。3) 通过燃油系统故障诊断实例对诊断准确度和置信区间组成的综合评价指标体系进行验证评估,证明该指标能够实现实际故障诊断系统的评价及改进优化。该方法可以进一步推广到其他故障诊断模型,成为故障诊断技术性能分析的评价指标。
参考文献

[1]	HECKERMAN D.Learning in graphical models[M].Berlin:Springer Netherlands,1998:301-354.

[2]	LUXHØJ J T,COIT D W.Modeling low probability/high consequence events:An aviation safety risk model[C]//Proceedings of the Reliability & Maintainability Symposium (RAMS).Washington,D.C.:IEEE Computer Society,2006:215-220.
	Click to display the text
[3]	徐璡,许朝霞,许文杰,等.基于贝叶斯网络原理的835例冠心病病例中医证候分类研究[J].上海中医药杂志,2014,48(1):10-13. XU J,XU Z X,XU W J,et al.Classification of TCM syndromes in 835 cases of coronary heart disease:On the basis of Bayesian networks principle[J].Shanghai Journal of Traditional Chinese Medicine,2014,48(1):10-13(in Chinese).
	Cited By in Cnki (3)
[4]	DALLA V L,GIUDICI P.A Bayesian approach to estimate the marginal loss distributions in operational risk management[J].Computational Statistics,2008,52(6):3107-3127.
	Click to display the text
[5]	BASIR O,YUAN X H.Engine fault diagnosis based on multisensor information fusion using Dempster-Shafer evidence theory[J].Information Fusion,2007,8(4):379-386.
	Click to display the text
[6]	李业波,李秋红,黄向华,等.航空发动机气路部件故障融合诊断方法研究[J].航空学报,2014,35(6):1612-1622. LI Y B,LI Q H,HUANG X H,et al.Research on gas fault fusion diagnosis of aero-engine component[J].Acta Aeronautica et Astronautica Sinica,2014,35(6):1612-1622(in Chinese).
	Cited By in Cnki (1)
[7]	DAS S,HARRIS M.Estimating accuracy and confidence interval of an intelligent diagnostic reasoner system[C]//Proceedings of the 2009 IEEE Autotestcon.Piscataway,NJ:IEEE Press,2009:288-291.
	Click to display the text
[8]	WINTERBOTTOM A.The interval estimation of system reliability from component test data[J].Operations Research,1984,32(3):628-640.
	Click to display the text
[9]	CHOI A,DARWICHE A,ZHENG L,et al.Machine learning and knowledge discovery for engineering systems health management[M].Boca Raton,FL:Chapman and Hall/CRC Press,2011:39-66.

[10]	段荣行,董德存,赵时旻.采用动态故障树分析诊断系统故障的信息融合法[J].同济大学学报(自然科学版),2011,39(11):1699-1704. DUAN R X,DONG D C,ZHAO S M.Information fusion method for system fault[J].Journal of Tongji University(Natural Science),2011,39(11):1699-1704(in Chinese).
	Cited By in Cnki (3)
[11]	ZHANG J J.Empirical likelihood ratio confidence interval for positively associated series[J].Acta Mathematicae Applicatae Sinica,English Series,2007,23(2):245-254.
	Click to display the text
[12]	蒋灵,何小荣.BP神经网络的置信度分析[J].计算机与应用化学,1999,16(3):55-60. JIANG L,HE X R.Confidence bounds prediction for backpropagation neural network[J].Computers and Applied Chemsitry,1999,16(3):55-60(in Chinese).
	Cited By in Cnki (17)
[13]	KOHAVI R.A study of cross-validation and bootstrap for accuracy estimation and model selection[C]//Proceedings of the 14th International Joint Conference in Artificial Intelligence,Volof the International Joint Conference in Artificial Intelligence.San Francisco,CA:Morgan Kaufmann Publishers Inc.,1995,2:1137-1143.
	Click to display the text
[14]	李俭川,胡茑庆,秦国军,等.贝叶斯网络理论及其在设备故障诊断中的应用[J].中国机械工程,2003,14(10):896-900. LI J C,HU N Q,QIN G J,et al.Bayesian network theory and its application in equipment fault diagnosis[J].China Mechanical Engineering,2003,14(10):896-900(in Chinese).
	Cited By in Cnki (122)
[15]	李鸿.二项分布的参数估计问题研究[J].应用数学学报,2010,33(3):385-394. LI H.The research about binomial distribution parameter estimation problem[J].Acta Mathematicae Applicatae Sinica,2010,33(3):385-394(in Chinese).
	Cited By in Cnki (5)
[16]	孟昭为.二项分布参数的置信区间[J].工科数学,1995,11(4):169-171. MENG Z W.The confidence interval of the binomial distribution parameters[J].Journal of Mathematics for Technology,1995,11(4):169-171(in Chinese).
	Cited By in Cnki (5)
[17]	王正武,任喜风,张瑞平.置信区间分析法在BP神经网络中的应用研究[J].数理统计与管理,2006,25(2):156-160. WANG Z W,RENG X F,ZHANG R P.The research about the application of the confidence interval analysis in BP neural network[J].Application of Statistics and Management,2006,25(2):156-160(in Chinese).
	Cited By in Cnki (2)
[18]	MADSEN A L,LANG M,KJARULFF U B,et al.The Hugin Tool for learning Bayesian networks[M].Symbolic and Quantitative Approaches to Reasoning with Uncertainty.Berlin:Springer,2003:594-605.