Saeed[2, 3, 4]采用标准半圆凹曲面替代翼型防冰腔进行了三维热气阵列射流冲击凹曲面的传热特性仿真研究,得出射流孔间距、射流孔距离前缘冲击壁面的距离、射流孔阵列结构和射流马赫数是影响热气防冰腔换热性能的关键参数[2],并且指出单排射流孔与叉排射流孔排间在笛形管上的圆周交角为20°的阵列冲击换热性能明显好于圆周交角为10°的阵列冲击换热性能[3];射流孔间距越大,射流孔距离前缘冲击壁面的距离越小,马赫数越大,越能获得明显的换热性能[4]。Planquart等[5]利用红外温度记录仪和反向热流实验方法测得叉排直喷式热气防冰腔蒙皮内表面换热系数分布情况,得出其换热性能与供气雷诺数、射流孔的展向和弦向分布距离相关,并总结了笛形管冲击前缘内壁面驻点区的平均对流换热系数与上述参数的实验关联式,其中笛形管相对于前缘的距离与孔径比(简称相对管壁距)Zn/d > 20,3 000 < 喷孔射流出口雷诺数(Rej) < 41 000。Papadakis和Wong[6, 7, 8]研究了射流孔排列结构、笛形管放置位置、防冰腔几何结构、热气温度和流量对系统的性能影响,指出一旦射流孔供气达到壅塞状态,供气流量的增加对防冰壁面温度的影响相较于供气温度提高的影响要小很多,而笛形管的放置位置、射流孔的周向排列对前缘壁面的传热性能至关重要,但腔体形式的改变对壁面温度分布几乎没有影响等。Brown等[9]通过实验得出了笛形管冲击热气防冰腔前腔的平均对流换热系数关于孔间距、供气雷诺数的准则关系式,其中所有射流孔供气均处于壅塞状态,且笛形管相对管壁距Zn/d=5。
目前,国内多数采用计算流体力学方法对腔内的热气流动换热[10, 11, 12, 13, 14, 15]或防冰系统的防冰性能[16]进行数值模拟,亦或是通过实验研究防冰系统的总体防冰性能[10]。关于热气防冰腔内复杂射流冲击翼型凹表面的传热研究还很欠缺,特别是缺乏对防冰腔内局部换热特性的关注,细致的实验研究工作尚未开展。基于此,本文将通过实验深入研究热气防冰系统前缘内表面局部传热性能的分布特性。
1 实验方案实验系统如图 1所示。实验采用反向热流测量技术(inverse flux technique)[5],即和实际防冰系统工作时表面热流方向相反。实际情况是外表面冷空气吹袭,内部防冰系统供热气。本文通过对防冰腔防冰壁面加以恒定的加热流密度,用恒温300 K的压缩空气作为冷却介质输送至防冰腔内,射流冲击腔体前缘防冰壁面并带走热量,以此模拟防冰腔内的流动传热过程。此方法成本较低,方便开展,且能准确预测防冰腔内部流动换热情况[5]。
 |
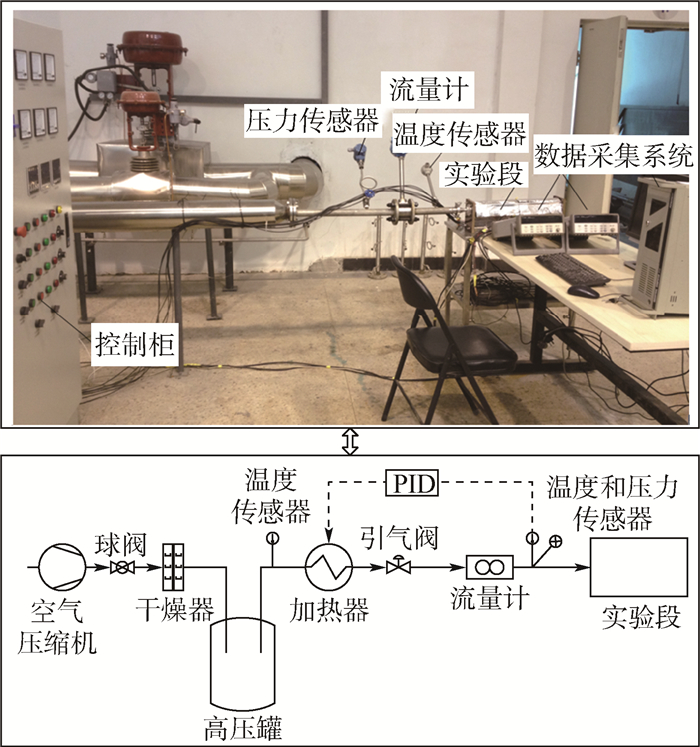| 图 1 实验系统 Fig. 1 Experiment system |
| 图选项 |
实验用热气防冰腔的腔体模型选用某飞机机翼防冰腔的二维弦向截面原型(见图 2)等比例(1:1)加工而成,腔体材质为防锈铝5A06,铝板厚3 mm,腔体的展向长度取为500 mm。该模型具有的笛形管射流结构及腔内空气流动换热形式有普遍代表性,压缩空气通过笛形管上的射流孔喷射进入防冰腔前腔,射流冲击到前缘壁面带走壁面热量,乏气通过高度为1 mm的狭缝加速形成贴壁射流进入后腔,并与后腔防冰壁面热交换,最终由排气孔排出。腔内笛形管采用不锈钢圆管加工制成,笛形管上的射流孔阵列形式采用图 3所示的3排顺排阵列。实验关注的结构参数及其值的范围由表 1详细列出,基本能够覆盖现役各型带笛形管结构的机翼热气防冰系统。
 |
| 图 2 防冰腔结构及温度测点布置 Fig. 2 Anti-icing cavity structure and thermocouples distribution |
| 图选项 |
 |
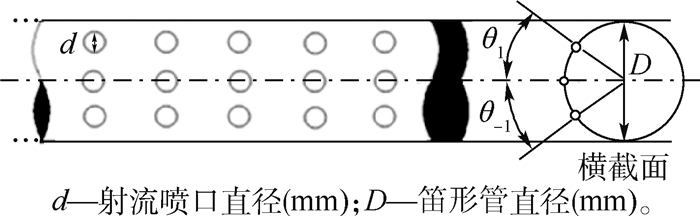| 图 3 笛形管射流孔阵列示意图 Fig. 3 Sketch of jet hole layout on piccolo tube |
| 图选项 |
表 1 防冰腔结构参数的取值范围 Table 1Range of anti-icing cavity structure parameters
| 结构参数 | 范围 |
| d/mm | 2 |
| θ -1, θ 0, θ 1/(°) | θ -1:(-60 ~ -15), θ 0:(0 ~ 0), θ1:(15 ~ 60) |
| Z n/ d | 1.736 ~ 27.5 |
| r/ d | 13.21 ~ 61.5 |
| 注：θ0、θ-1和θ1为孔偏转角。 | |
表选项
热气防冰腔前缘外壁面通过贴合特制的康铜加热膜进行加热。加热膜的电阻值几乎不随温度变化,且发热均匀。加热量由功率表直接测出。加热膜外布置高热阻橡塑海绵保温材料防止热量往外散失,使得热量几乎全部能传导进入腔体内,漏热量不大于5%。
防冰腔前缘蒙皮内表面温度(即防冰面内表面温度)由经过精确校准的T型热电偶线(测量误差为±0.5℃)测量,热电偶线温感探头布置在距外蒙皮2.5 mm深度的盲孔内,以导热绝缘胶固定,这样不会影响防冰腔的内部流动,同时温度探头距离内表面只有0.5 mm,测得温度数据可以认为就是相应内表面温度。同时选择了射流孔正前方的一个弦向位置进行了图 2所示的热电偶布置,共43个温度测量点,其中换热情况复杂的射流冲击区布置了较其他区域更高密度的温度测量点。所有测量信号由数据采集仪Agilent34970A的34901A模块进行采集并传送给计算机存储和二次处理。
2 数据处理基于本文的实验原理,局部对流换热系数hx计算公式为
式中:q为防冰壁面加载的热流密度;qloss为漏热量;Twx为前缘防冰壁面内表面的局部温度;Tin为供气温度。
局部对流换热努谢尔数Nux计算公式为
式中:λ为空气导热系数。
考虑在不同的供气工况和结构参数下,壁面局部换热努谢尔数Nux的值和分布规律不尽相同,而本文主要研究目标区域的局部换热性能的分布规律,与具体的Nux数值无关,为了方便研究,本文定义新参数ξx替代Nux。如式(3)所示,ξx为当地x/d处努谢尔数Nux与前缘驻点处努谢尔数Nustag的数值百分比,表示当地换热与驻点处换热的弱化程度。这样,所有ξx的分布曲线在前缘驻点处的取值均为100%,只有从驻点处向两侧的衰减程度不同。故而用ξx替代Nux既能够保留局部换热性能的分布规律,又能够简化研究的问题。
3 结果与讨论本文针对弦向3排喷孔,且中央喷孔正对前缘驻点的射流结构,开展了喷孔射流出口雷诺数Rej、笛形管相对管壁距Zn/d和射流冲击驻点区弦向弧长与孔径比(简称相对冲击驻点区弧长)r/d对射流腔内表面局部换热性能分布及衰减的影响研究。所设计的所有工况覆盖以下选值范围:Rej:2.5×104~1×105;Zn/d:1.736~27.5;r/d:13.21~61.5。以上范围较好地涵盖了目前热气防冰系统的笛形管射流结构尺寸范围和防冰热气流量范围。
3.1 笛形管喷孔射流出口雷诺数Rej的影响图 4为不同喷孔射流出口雷诺数Rej下的ξx值弦向分布曲线,其线型均近似为从驻点开始向两侧衰减的钟形曲线。横坐标x/d取负值的区域表示为下表面,正值为上表面。可以定性地认为,ξx-x/d曲线从驻点开始向两侧的衰减过程经过了衰减较缓慢的稳定段、迅速衰减的下降段以及衰减减缓的结束段3部分,其中下降段和结束段间的界定明显,由下降段进入结束段可见明显的ξx曲线衰减减缓的现象,而稳定段和下降段间则不好定量地描述其界定原则,考虑到研究结论需要具备推广性,本文定义稳定段为ξx值从驻点处向两侧衰减5%的弦向范围,图中以虚线间隔这2个部分。
 |
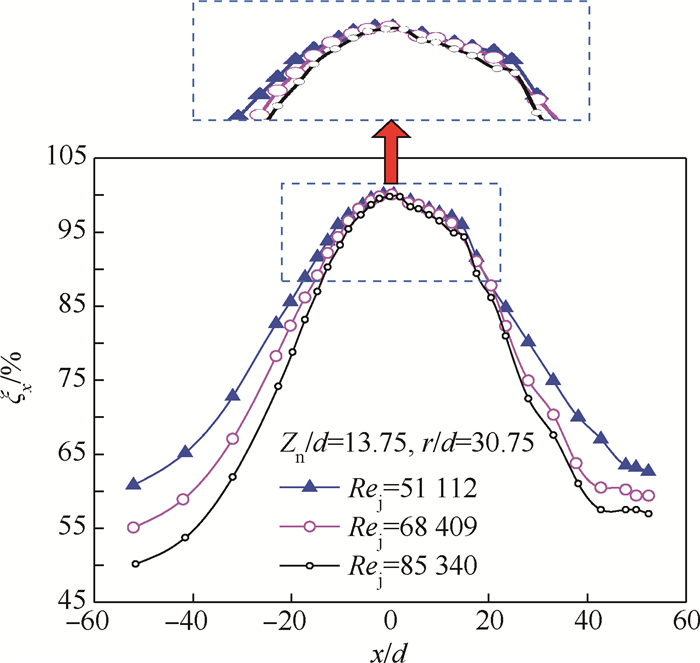| 图 4 喷孔射流出口雷诺数Rej对ξx的影响 Fig. 4 Effect of jet Reynolds number Rej on ξx |
| 图选项 |
由图 4可知:① ξx分布曲线稳定段的放大区明显可见,不同Rej对应的稳定段曲线几乎重合,差别较小。② Rej能够明显影响ξx-x/d曲线的下降段,Rej越大,下降段的衰减速率越快,下降段的总下降幅度也越大,当Rej由51 112增长至85 340时,下表面下降段的总下降幅度增大近14%。 ③ 3喷孔对称射流结构正前缘的驻点两侧ξx分布曲线不尽相同,主要是受到图 2中的狭缝结构作用,使得上表面的ξx-x/d曲线下降段衰减速率明显比下表面小,衰减总幅度也随之降低,下降段提前转变为结束段,这一方面说明狭缝结构有明显改善上表面换热性能的作用,另一方面,虽然ξx分布曲线在驻点两侧不对称,但是稳定段、下降段和结束段受喷孔出口雷诺数的影响作用是一致的。
3.2 相对管壁距Zn/d的影响图 5为相对管壁距Zn/d对ξx值弦向分布规律的影响。可以明显看出,参数Zn/d的影响特性类似于参数Rej,主要作用在ξx弦向分布曲线的下降段。① Zn/d取值越小,下降段的衰减速率越快,下降段的总下降幅度也越大。② 针对ξx-x/d曲线稳定段,如图 5中放大区域所示,不同的Zn/d取值只是在上表面略有不同,但是最大相差也仅2%左右,此时Zn/d的影响作用较微弱,几乎可以忽略。
 |
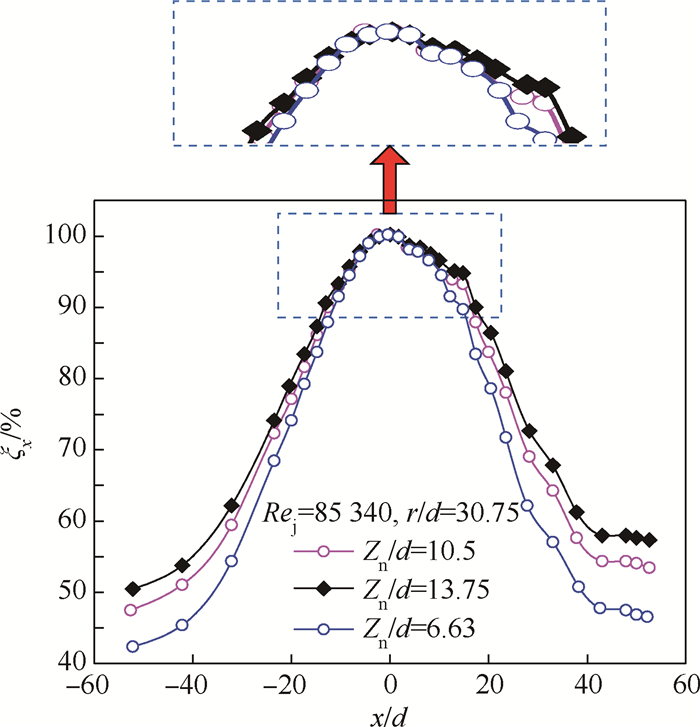| 图 5 相对管壁距Zn/d对ξx的影响 Fig. 5 Effect of relative piccolo tube to surface distance Zn/d on ξx |
| 图选项 |
3.3 相对冲击驻点区弧长r/d的影响图 6显示了相对冲击驻点区弧长r/d对ξx值弦向分布规律的影响。可以发现,参数r/d的作用规律与参数Rej和Zn/d明显不同。① 参数r/d能够明显影响ξx-x/d曲线的稳定段,r/d取值越大,稳定段越宽;反之,稳定段越窄,并且提前进入下降段。② 参数r/d能够影响下降段,但是作用效果仅体现在下降段的下降速率,几乎不改变下降段的总下降幅度。r/d取值减小,下降段的下降速率会加大,上、下表面下降段的总下降幅度均无明显变化。
 |
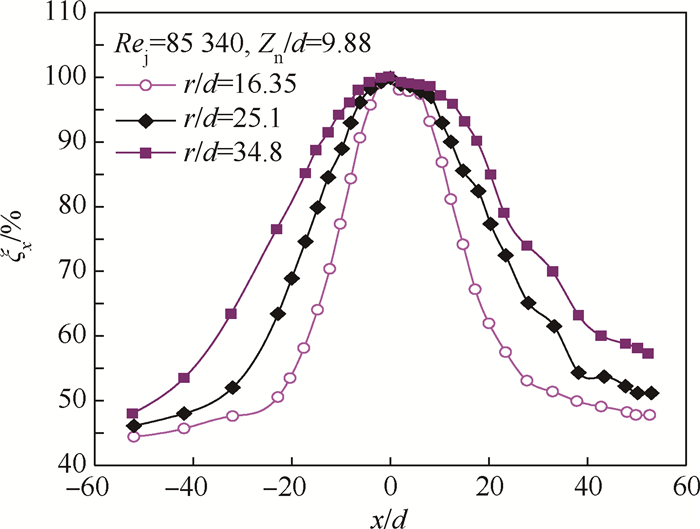| 图 6 相对冲击驻点区弧长r/d对ξx的影响 Fig. 6 Effect of relative chordwise arc length in the jet impingement zone r/d on ξx |
| 图选项 |
4 换热性能衰减分布曲 线的实验关 联式 考虑到防冰区域外表面的局部水收集系数随撞击位置发生变化,外表面防冰热载荷也不尽相同,为了在防冰系统设计时就能够预先匹配优化防冰热量的供给,若能够获得射流冲击防冰腔壁面的换热性能分布的通用模型,则能更加快捷准确地实现这一重要需求。所以,本文针对弦向3排喷孔,且中央喷孔正对前缘驻点的射流结构,建立冲击换热性能ξx-x/d曲线的实验关联式。
通过第3节可知,ξx-x/d曲线为从驻点向上、下表面两侧衰减的近似钟形曲线,但狭缝结构会影响驻点向上表面侧的换热性能衰减分布。 本文拟合工作中不考虑狭缝的影响,用驻点向下表面的换热性能衰减分布曲线替代上表面的实际曲线,形成驻点向两侧完全对称的换热性能衰减分布钟形曲线,并选择高斯拟合公式(4)对射流孔前缘冲击换热性能分布曲线进行描述,如图 7所示。
式中:xstag为驻点处坐标,本文取值为0;ξ0为ξx离驻点最远端的值(即衰减终止量);A/(w×
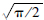)为衰减高度H;w为半衰高度H/2处高斯曲线宽值的1/
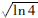倍。  |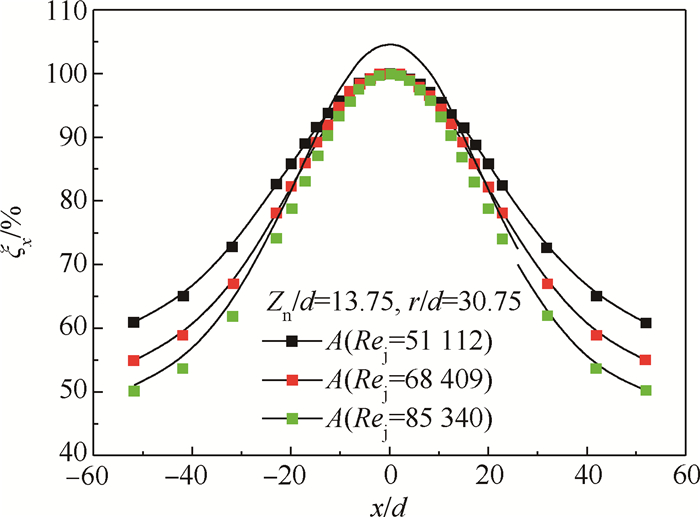
| 图 7 ξx弦向分布的高斯方程拟合 Fig. 7 Gauss equation fitting of ξx in chordwise direction |
| 图选项 |
定义衰减系数M=2/w2,代入式(4)得
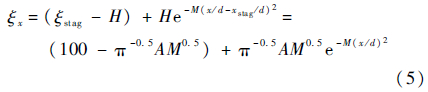
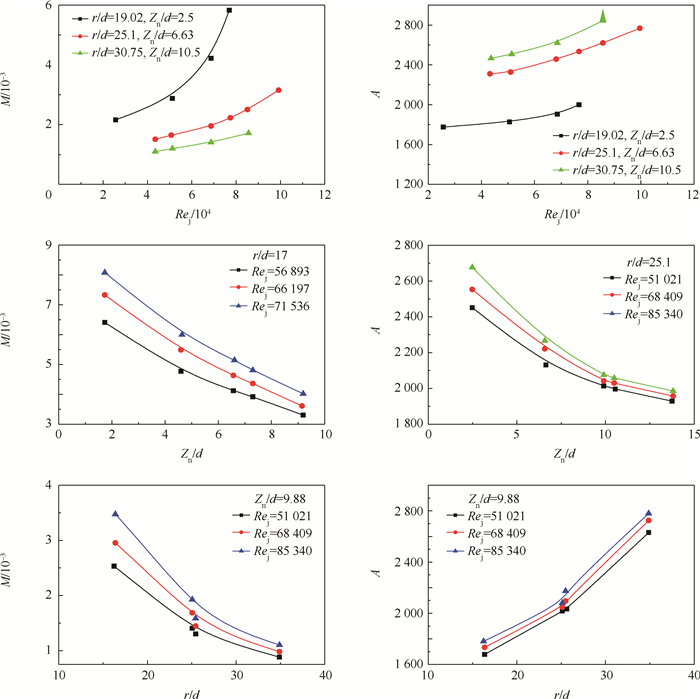
根据式(5)应用非线性拟合技术对所有实验样本点进行拟合,每一个实验样本点曲线对应一对确定的A、M值,拟合的相关系数R为0.980～0.996。进一步分析,式(5)中的衰减系数M和系数A都与参数Rej、Zn/d和r/d有关,并主要由这3个参数决定。图 8为参数Rej、Zn/d和r/d对衰减系数M和系数A的一元影响,均符合幂乘函数关系,故而均采用幂乘函数方程式分别拟合衰减系数M随Rej、Zn/d和r/d变化的关联式(6)和系数A随Rej、Zn/d和r/d变化的关联式(7),式(6)相关系数R=0.96,式(7)相关系数R=0.98。
 |
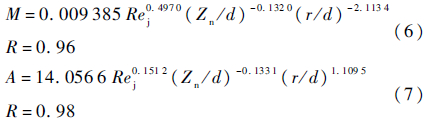
| 图 8 M、A随影响参数Rej、Zn/d和r/d的变化关系 Fig. 8 Relations of M,A with its factors Rej,Zn/d and r/d |
| 图选项 |
将关联式(6)和关联式(7)代入式(5),经过化简得到关联式(8)。关联式(8)便是弦向3排喷孔结构冲击射流前缘换热性能衰减分布曲线的通用拟合模型,适用于2.5×104≤Rej≤ 1×105、1.736 ≤Zn/d≤ 27.5和13.21 ≤r/d≤ 61.5的工况和结构。
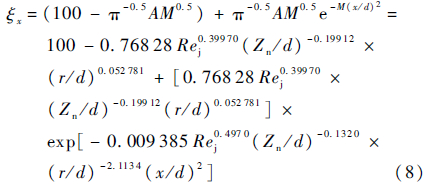
最后,选取参与关联式(8)拟合的所有实验样本点外的结构进行实验,并将关联式(8)推导出的ξx弦向分布曲线与实验结果进行比较,如图 9所示,最大相差为2%。可见,关联式(8)在限定工况和结构范围内,能够较准确地预测防冰腔内弦向3排喷孔结构冲击射流前缘换热性能的分布规律,辅助并指导热气防冰系统的设计和性能评估工作。
 |
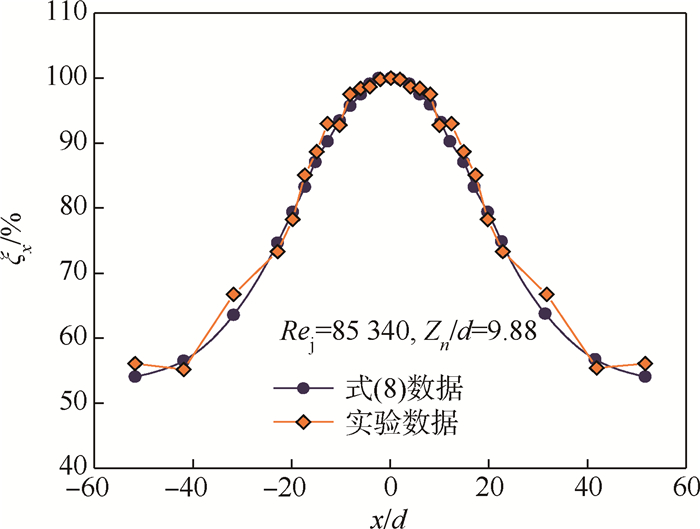| 图 9 ξx拟合模型的实验验证 Fig. 9 Experimental validation of fitting model of ξx |
| 图选项 |
5 结 论针对弦向3排喷孔,且中央喷孔正对前缘驻点的射流结构,本文详细研究了参数Rej、Zn/d和r/d对射流腔内表面传热性能的影响作用规律,总结如下:
1) 局部换热性能分布曲线从驻点开始向两侧的衰减过程经过了衰减较缓慢的稳定段、迅速衰减的下降段以及衰减减缓的结束段3部分。
2) 换热性能分布的稳定段仅受参数r/d的影响,参数Rej和Zn/d则几乎没有影响作用。r/d取值越大,稳定段越宽;反之,稳定段越窄,且提前进入下降段。
3) 参数Rej、Zn/d和r/d均能够明显影响换热性能分布的下降段。Rej越大或者Zn/d取值越小,下降段的衰减速率均加快,且下降段的总下降幅度也越大;参数r/d取值减小,下降段的下降速率也越大,但几乎不会改变下降段的总下降幅度。
4) 拟合并验证了弦向3排喷孔结构射流冲击防冰壁面的换热性能衰减分布曲线通用模型,该模型适用于2.5×104≤Rej≤1×105、1.736≤Zn/d≤27.5和13.21≤r/d≤61.5的工况和结构。
参考文献
| [1] | SAEED F,MORENCY F,PARASCHIVOIU I.Numerical simulation of a hot-air anti-king system[C]//38th Aerospace Sciences Meeting and Exhibit.Reston:AIAA,2000. |
| Click to display the text | |
| [2] | SAEED F.Numerical heat transfer correlation for array of hot-air jets impinging on 3-dimensional concave surface[J].Journal of Aircraft,2005,42(3):665-670. |
| Click to display the text | |
| [3] | SAEED F.Numerical simulation of surface heat transfer from an array of hot-air jets[J].Journal of Aircraft,2008,45(2):700-714. |
| Click to display the text | |
| [4] | FREGEAU M,GABR M,PARASCHIVOIU I,et al.Simulation of heat transfer from hot-air jets impinging a three-dimensional concave surface[J].Journal of Aircraft,2009,46(2):721-726. |
| Click to display the text | |
| [5] | PLANQUART P,BORRE G V,BUCHLIN J M.Experimental and numerical optimization of a wing leading edge hot air anti-icing system:AIAA-2005-1277[R].Reston:AIAA,2005. |
| Click to display the text | |
| [6] | PAPADAKIS M,WONG S H J.Parametric investigation of a bleed air ice protection system:AIAA-2006-1013[R].Reston:AIAA,2006. |
| Click to display the text | |
| [7] | PAPADAKIS M,WONG S H,YEONG H W,et al.Icing tunnel experiments with a hot air anti-icing system:AIAA-2008-444[R].Reston:AIAA,2008. |
| Click to display the text | |
| [8] | PAPADAKIS M,WONG S H,YEONG H W,et al.Icing tests of a wing model with a hot-air ice protection system:AIAA-2010-7833[R].Reston:AIAA,2010. |
| [9] | BROWN J,WATTERSON J K,RAGHUNATHAN S,et al.Heat transfer correlation for de-icing systems:AIAA-2001-0837[R].Reston:AIAA,2001. |
| Click to display the text | |
| [10] | 潘旭云.某型飞机防冰系统机翼防冰腔性能研究[D].南京:南京航空航天大学,2006. PAN X Y.Performance analysis of micro-ejector anti-icing tunnel[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2006(in Chinese). |
| Cited By in Cnki (5) | Click to display the text | |
| [11] | 马辉,陈维建,孟繁鑫,等.发动机导向叶片热气防冰腔结构改进[J].南京航空航天大学学报,2013,45(1):70-74. MA H,CHEN W J,MENG F X,et al.Improvement of hot-air anti-icing structure of engine inlet vane[J].Journal of Nanjing University of Aeronautics and Astronautics,2013,45(1):70-74(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [12] | 周玉洁.热气腔结构的优化设计与数值模拟[D].南京:南京航空航天大学,2010. ZHOU Y J.Optimal design and numerical simulation of the hot air cavity structure[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2010(in Chinese). |
| Cited By in Cnki (2) | Click to display the text | |
| [13] | 彭珑,卜雪琴,林贵平,等.热气防冰腔结构参数对其热性能影响研究[J].空气动力学学报,2014,32(6):848-853. PENG L,BU X Q,LIN G P,et al.Influence of the structural parameters on thermal performance of the hot air anti-icing system[J].Acta Aerodynamica Sinica,2014,32(6):848-853(in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [14] | 卜雪琴,陈雨晨,林贵平,等.热气防冰腔中短小销钉强化传热数值模拟[J].北京航空航天大学学报,2013,39(8):1053-1057. BU X Q,CHEN Y C,LIN G P,et al.Investigation of heat transfer enhancement of short pin fins in hot air anti-icing system[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(8):1053-1057(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [15] | 卜雪琴,林贵平,郁嘉.三维内外热耦合计算热气防冰系统表面温度[J].航空动力学报,2009,24(11):2495-2500. BU X Q,LIN G P,YU J.Three-dimensional conjugate heat transfer simulation for the surface temperature of wing hot-air anti-icing system[J].Journal of Aerospace Power,2009,24(11):2495-2500(in Chinese). |
| Cited By in Cnki (9) | Click to display the text | |
| [16] | 卜雪琴,郁嘉,林贵平,等.机翼热气防冰系统设计[J].北京航空航天大学学报,2010,36(8):927-930. BU X Q,YU J,LIN G P,et al.Investigation of the design of wing hot-air anti-icing system[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(8):927-930(in Chinese). |
| Cited By in Cnki (9) | Click to display the text |
