在圆柱绕流流场中加入隔板是一种典型且较为成熟的被动控制技术。这项技术在过去的几十年里已经被科研人员进行了广泛的研究,例如Anderson和Szewczyk[8],Hwang等[9],Kwon和Choi[10],Ozono[11]。但其中大多数研究的关注点都在于把隔板放在圆柱下游,从而影响尾迹区的流动情况。早在1955年,Roshko[12]就注意到圆柱尾部的隔板对流场具有重要影响。他们在Re=1.45×104的实验条件下发现,当尾部隔板长度大于5倍圆柱直径时,将不再有旋涡从圆柱剪切层中脱落,同时圆柱的阻力系数会大大降低。当隔板长度等于圆柱直径时,隔板对旋涡脱落的影响主要依赖于隔板与圆柱后缘点之间的距离:当这一间距小于4倍圆柱直径时,绕流的Strouhal数随间距的增大而减小,圆柱尾迹区的压力随间距增大而增加,此时圆柱阻力不断减小;而当这一间距太大时,隔板对旋涡脱落几乎没有影响。
受上述研究的启发,科研人员将隔板放置于钝体上游,探讨前置隔板对钝体绕流的影响。不难发现,圆柱后置隔板的作用多在于阻断圆柱两侧卡门涡的相互作用,进而抑制尾迹涡的生成。对于前置隔板而言,Hwang和Yang[13]利用数值方法在较低雷诺数的条件下(Re=30~160)发现,前置隔板给流体带来的摩擦阻力有助于减小圆柱前驻点的压力。在计算过程中,前置隔板被设定为完全刚性,而隔板的长度与圆柱直径相同,此外他们还试图通过改变隔板与圆柱的相对距离,找到一个能使圆柱阻力最小的最优间距。由于平板边界层流动的临界雷诺数(从层流转捩到湍流)Rex=2×105~6×105[14]远远大于实验工况的雷诺数,保证了流体在经过上游隔板时依旧为层流状态。计算结果显示,当间距等于1.5倍的圆柱直径时,阻力值达到最小,阻力降幅约14.7%。2014年,Qiu等[14]在风洞中开展了类似的研究工作,发现当Re<3.0×105时,阻力系数相较于未加隔板控制的工况有明显的下降,下降幅度最高可达到50%。这是由于气流流经圆柱时背风面的分离点向下游运动,导致尾迹区的宽度变窄,从而使圆柱阻力下降,并且前置隔板产生的湍流边界层会加快圆柱下游分离剪切层的转捩。
本实验圆柱绕流雷诺数Re=1 800,利用粒子图像测速(Particle Image Velocimetry,PIV)技术研究不同刚度的前置隔板对固定圆柱流场特性和流动结构的影响。
1 实验装置及数据处理方法本实验在北京航空航天大学自循环水槽中进行,实验段长度为3 m,横截面积为0.6 m×0.6 m,水槽侧壁及底部均为透明有机玻璃,便于进行实验观测和拍摄。该水槽的来流速度在0~400 mm/s范围内连续可调,湍流度σ<0.8%,流场品质良好。实验装置如图 1所示(图 1(a)中间四方区域为PIV测量区域,图中数字单位均为mm)。
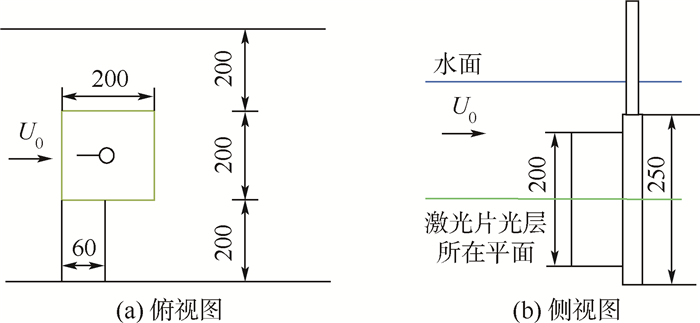 |
| 图 1 实验装置示意图Fig. 1 Sketch of experimental set-up |
| 图选项 |
实验中由2个半圆形铝制长杆拼接而成的圆柱模型的直径D=12 mm,长度W=250 mm。在附加隔板的控制中,分别在圆柱的前端加上柔性和刚性2种隔板,它们均采用透明聚酯薄膜制成。柔性隔板厚度hF=0.1 mm;刚性隔板厚度hR=1 mm,2种隔板的长度均为L=3D。实验过程中来流速度U0=156 mm/s,基于圆柱直径的雷诺数Re=1 800。柔性隔板和刚性隔板的有效弯曲刚度П的定义如式(1)所示[15, 16]:

式中:E为聚酯薄膜的弹性模量;ρf为流体密度。根据以上参数可得柔性隔板的有效弯曲刚度ΠF=1.22;刚性隔板的有效弯曲刚度ΠR=1 220。流场速度利用PIV系统进行测量,粒子为空心玻璃微珠,平均直径为5 μm,密度为1.05 g/cm3。1台Nd:Yag连续激光器作为片光源,激光器输出功率为1.5 W,片光厚度为1 mm。采集图像所用的高速CCD相机分辨率为2 048像素×2 048像素,视野范围约为200 mm×200 mm,图像采样频率为250 Hz,曝光时间为1 ms,每种工况各采集5 000帧。图像采用多通道迭代Lucas-kanade(Multi-pass Iterative Lucas-kanade,MILK)算法进行处理,过程中用到互相关计算方法。查询窗口采用32像素×32像素,x方向和y方向的平移步长均为16像素,保证有50%的重叠率。
2 流场特性2.1 时均流向速度分布图 2和图 3给出了单独圆柱绕流、圆柱前缘安装柔性隔板和刚性隔板3种实验情况下圆柱下游流场流向速度U分布和流向速度亏损最大值Umin沿流向的变化。可以看出,由于圆柱的存在以及剪切层的分离,圆柱尾迹区会产生一个较为明显的速度亏损。在近尾迹区x/D=2~6范围内,刚性隔板的速度亏损量最大,柔性隔板则经历了由亏损大于单独圆柱绕流到小于单独圆柱绕流的情况。在x/D=6的流向位置处,2种控制工况的速度亏损基本相当,并且在x/D=7处,控制工况的速度亏损基本与单独圆柱绕流相同。此后,2种控制情况下尾迹速度的恢复均比单独圆柱绕流情况快。
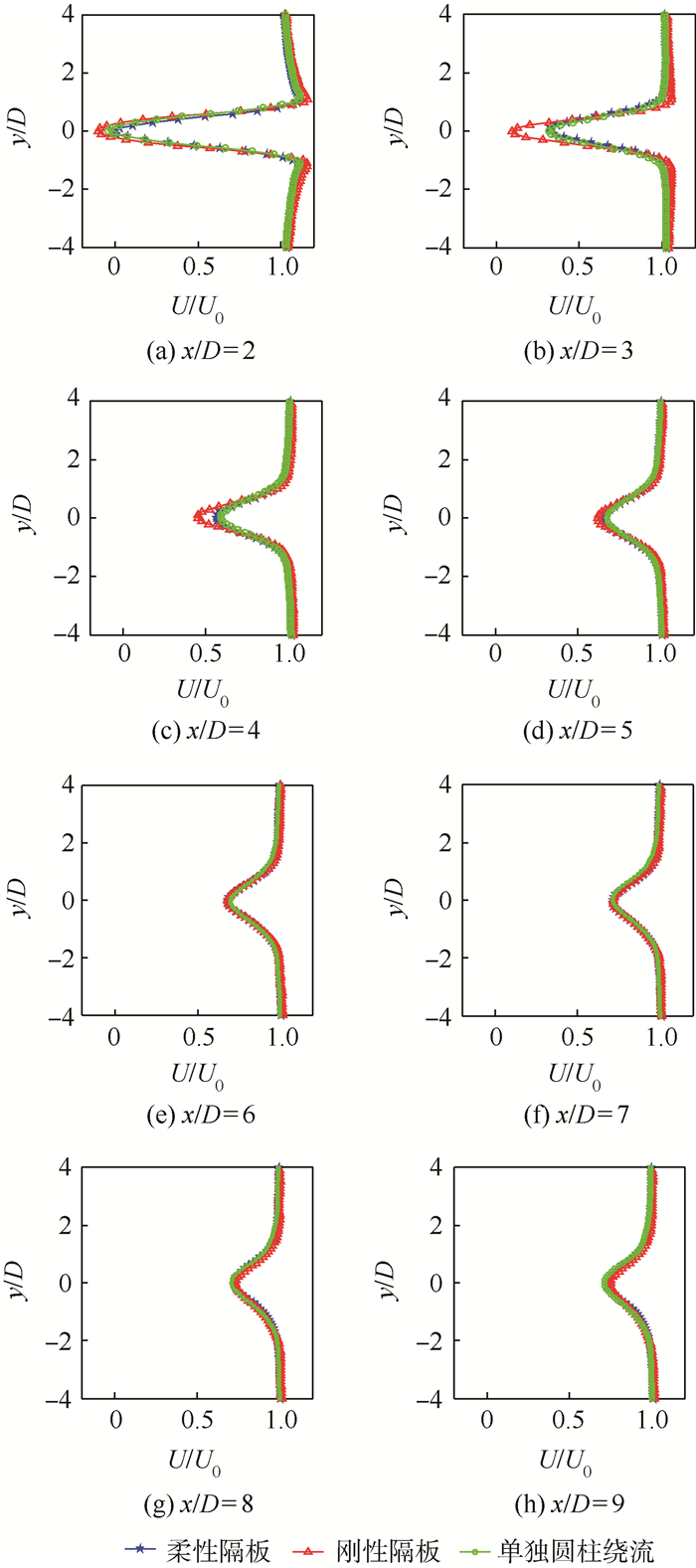 |
| 图 2 时均流向速度分布Fig. 2 Profiles of mean streamwise velocity |
| 图选项 |
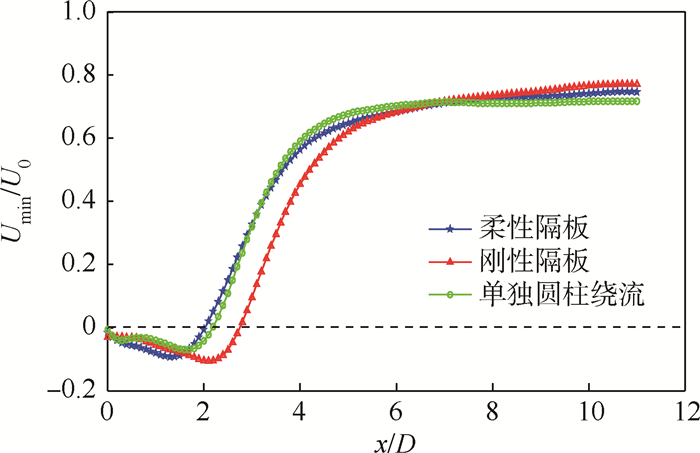 |
| 图 3 对称面流向速度变化Fig. 3 Variation of streamwise velocity at y/D=0 |
| 图选项 |
从图 3可以看出,在圆柱下游,对称面上的流向速度会在一定范围内小于0,表明这个区域实际上是回流区,并且回流区的长度就定义为圆柱后缘到对称面速度恢复到0时(图中曲线与Umin/U0=0虚线相交处)的这段距离。单独圆柱绕流与柔性隔板情况下对称面上U=0的流向位置相近,而刚性隔板情况下对称面上U=0的点则靠后,说明单独圆柱绕流与柔性隔板情况的回流区长度相当,刚性隔板情况下回流区则更长一些。这些流场特性的差异,预示着流动结构的不同演化。
2.2 时均脉动量垂向脉动量所展现出的是一种单峰结构,这是由上下2排尾迹脱落涡相互作用形成的。从3种实验情况的垂向脉动量v分布(见图 4)来看,柔性隔板的垂向速度脉动在近尾迹区(x/D=4之前)要大于刚性隔板工况,这是由自由来流条件下柔性隔板的变形及振动所致。在x/D=5及之后的流向位置处,2种控制工况的脉动量曲线基本重合,说明柔性隔板变形的影响已经衰减。但是,增加隔板控制都使圆柱近尾迹区垂向脉动降低。
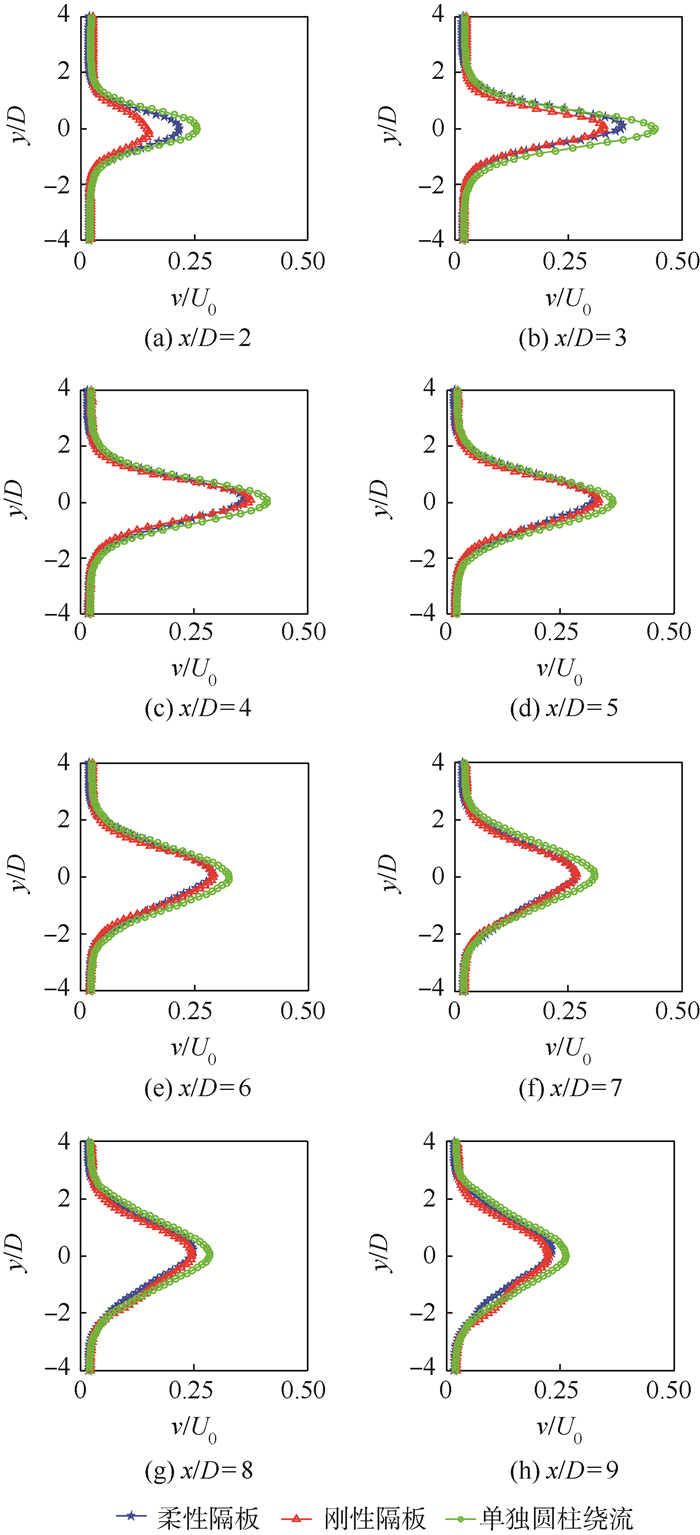 |
| 图 4 垂向脉动量分布Fig. 4 Profiles of vertical velocity fluctuation |
| 图选项 |
从图 5关于垂向速度脉动量最大值vmax沿流向的变化中可以发现,在流体流经圆柱之后,脉动量会出现一个大幅的增长,这是由于剪切层的增
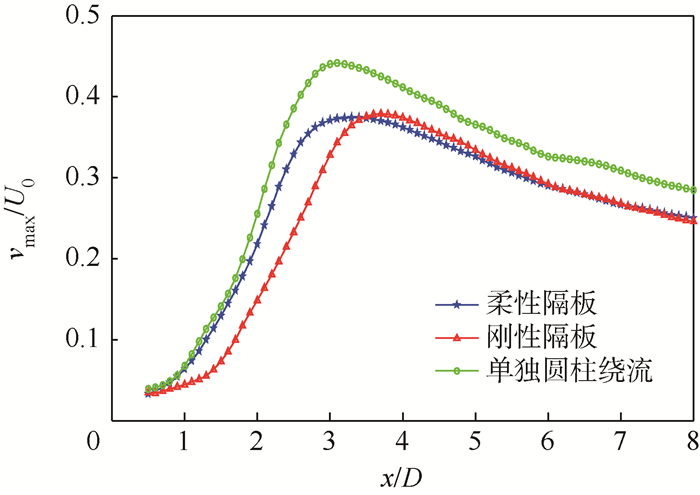 |
| 图 5 垂向脉动量最大值变化Fig. 5 Variation of the maximum of vertical velocity fluctuation |
| 图选项 |
长以及尾迹涡的形成。在近尾迹区x/D=1附近,单独圆柱绕流与柔性隔板工况的增长速度较快,而刚性隔板工况的增长速度则较慢,但在流向位置x/D=1.5处,刚性隔板工况的增速有一个大幅的提高,随后达到与前2种工况增速相当的程度。另外从图 5中可以看到,单独圆柱绕流和柔性隔板工况的峰值都出现在x/D=3处,而刚性隔板的峰值位置则相对靠后,出现在x/D=3.7处。此外,柔性隔板和刚性隔板工况垂向脉动量所达到的峰值大小几乎相同,都在vmax/U0≈0.37,而单独圆柱绕流工况的峰值则达到了vmax/U0≈0.45。
3 阻力特性阻力系数的计算采用了Antonia和Rajagopalan[17]给出的计算公式如式(2)所示:
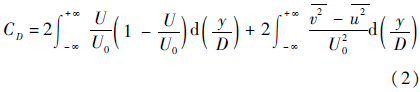
式中:u、v分别为流向和垂向的速度脉动值。式(2)右边第1项为动量积分,第2项为雷诺正应力对阻力的贡献。
由于拍摄视野所限,拍摄区域最下游流向位置x/D稍大于10。因此,取x/D=10处流场信息对阻力进行了估算。得到单独圆柱绕流、圆柱前缘加柔性隔板、圆柱前缘加刚性隔板3种情况下的阻力系数分别为1.06、1.01和0.99,柔性隔板和刚性隔板工况的阻力系数与原始工况相比分别降低了4.7%和6.6%。
4 流场结构在讨论流场结构前,首先应用快速傅里叶变换(Fast Fourier Transformation,FFT)对流场主频进行分析。得到柔性隔板工况下圆柱涡脱落的主频为2.75 Hz,由此得到基于圆柱直径的Strouhal数StF=0.21,刚性隔板和单独圆柱绕流的脱落涡主频均为2.6 Hz,StR=0.20,柔性隔板影响了涡脱落频率,约增加5%。由此也可看出,与后置隔板相比,在圆柱前缘放置隔板并没有显著降低尾迹区流场的Strouhal数,说明在此工况下,前置隔板(尤其是刚性隔板)对尾迹区卡门涡的脱落没有造成实质性的影响。但与此同时,在隔板长度L=3D的条件下,柔性隔板的自由端在来流的作用下会发生偏移变形,并伴随小幅度的振动,生成周期性的诱导涡,改变了圆柱近尾迹区脱落涡的主频。其中诱导涡的脱落频率与主频的关系会在后文做进一步分析。
4.1 相位平均流场本节利用λci方法来表征当地涡量[18]。图 6给出各工况圆柱下游相位平均λci场,其中每种工况4幅图分别代表0°、90°、180°以及270°相位角。由图 6(a)中可以看出,单独圆柱绕流工况下尾迹区会产生周期性脱落的卡门涡,且卡门涡刚好脱落时(以第1幅图中下方的脱落涡为例),涡核处于x/D=2.5的流向位置;另一方面,从λci的数值大小来看,圆柱两侧脱落涡的强度相当,没有明显的不对称现象出现。
 |
| 图 6 相位平均λci场Fig. 6 Phase averaged λci field |
| 图选项 |
对于柔性隔板工况来说(见图 6(b)),由于柔性隔板前缘受到流场的扰动向一侧偏转,从而引发了诱导涡的产生,诱导涡流经平板并与圆柱剪切层中生成的涡融合。圆柱下游卡门涡脱落时,涡核也处于x/D=2.5的位置,可见涡的形成长度并没有明显变化。对比单独圆柱绕流工况来看,圆柱下方脱落涡的强度在数值上要明显小于上方的脱落涡,这可能是由于柔性隔板偏转而造成的,但是这种差距会随着流向距离的增大而减弱。
刚性隔板(见图 6(c))有一定的厚度,自由来流流经隔板自由端时存在流动分离并产生涡,但该涡结构强度较弱,没有柔性隔板情况产生的诱导涡强度大。另外,此种工况下卡门涡脱落时,涡核的流向位置较之前2种工况后移,处于x/D≈3.5的流向位置处,导致涡的形成长度变长。另一方面,圆柱两侧脱落涡的强度差距相较于柔性隔板工况也有所减小。
4.2 涡动力学模态分解柔性隔板前缘由于自身刚度较低,受到流场的扰动向一侧偏转,从而引发了诱导涡的产生。图 7(a)~图 7(c)表示间隔一段时间内,诱导涡沿着平板向下游运动的过程,从图中可以看到,平板前端处有一个λci值较大的区域,这是流体在经过柔性隔板时,由于隔板自由端偏转而产生的诱导涡。脱落的涡沿着平板一直向下游运动,直到撞击圆柱迎风面。
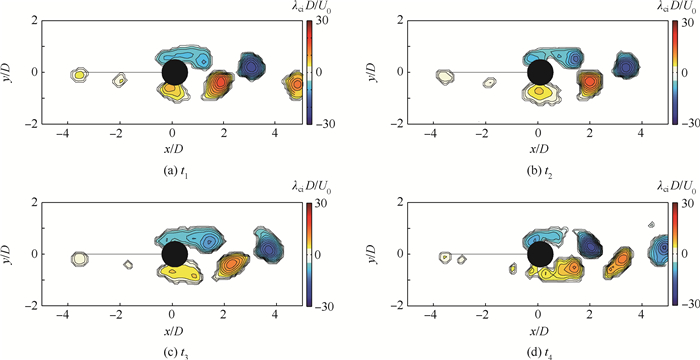 |
| 图 7 柔性隔板工况瞬时λci场Fig. 7 Instantaneous λci field for flexible plate condition |
| 图选项 |
通过本征正交分解(Proper Orthogonal Decomposition,POD)模态分解的结果可以看出,1、2阶模态的主频主要展现的是卡门涡街的频率,也就是圆柱本身对流场的影响。图 8为柔性隔板工况各模态的流场频率。对于柔性隔板情形,对应的主频为2.751 Hz(见图 8(a)),这与之前全流场的FFT分析结果也相符。另一方面,如果想知道柔性隔板自由端诱导涡对整个流场的影响,则需要对更高阶模态进行分析。在对柔性隔板工况下速度场的FFT分析中,发现柔性隔板自由端附近存在一个较为明显的涡脱落频率f1=2.2 Hz。同时,在对比了该工况下流场前6阶模态之后,发现在4、5阶模态中,能量在2.15 Hz处达到一个峰值(见图 8(b)),据此判断这2阶模态对应柔性隔板自由端诱导涡对全流场的影响。此外从能量的数量级来看,柔性隔板自由端诱导涡的能量仅为卡门涡街所占能量的10%。在刚性隔板工况中,由于之前用FFT方法分析得到的平板自由端诱导涡的脱落频率不是很明显,所以在POD分解中也找不到与之相对应的高阶模态。
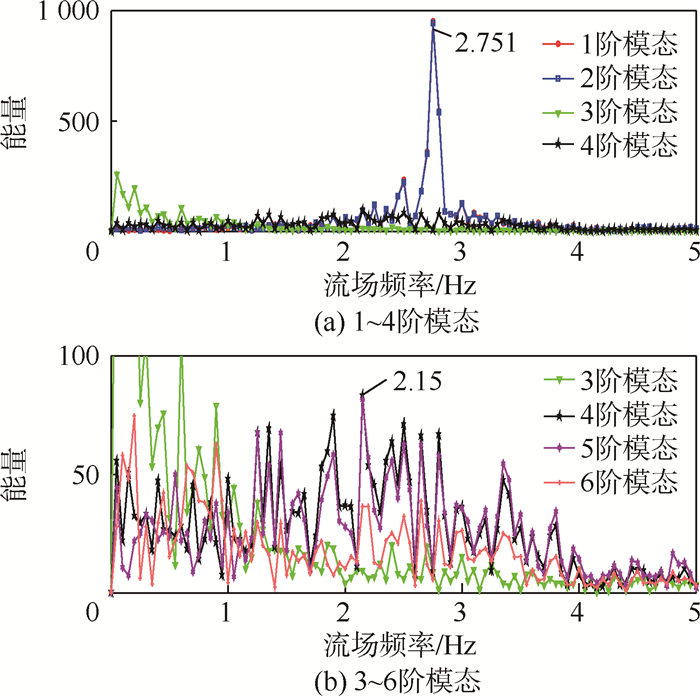 |
| 图 8 柔性隔板工况1~6阶模态的流场频率Fig. 8 Flow field frequency in 1~6 modality for flexible plate condition |
| 图选项 |
5 结 论前置隔板控制方法对于圆柱绕流来讲,目前实验研究方面的工作较少。通过本次实验可以看到,在雷诺数Re=1 800的条件下,2种刚度的隔板对圆柱流场的控制作用主要体现在:
1) 圆柱加前置柔性和刚性隔板后阻力可分别减少4.7%和6.6%。在圆柱下游,单独圆柱绕流工况与前置柔性隔板工况的回流区长度相当,前置刚性隔板工况的回流区则更长一些。在涡结构的演化方面,由于柔性隔板自由端的变形及振动,使流场增加了额外的扰动,影响了圆柱剪切层的发展,从而改变了近尾迹区内卡门涡街的脱落频率。
2) 单独圆柱绕流及圆柱安装前置刚性隔板2种工况下绕流尾迹区产生的卡门涡脱落的Strouhal数均为0.20。在安装柔性隔板的工况下,柔性隔板自由端弯曲变形诱导产生脱落涡的Strouhal数为0.17。该涡结构沿隔板向下游移动,并影响圆柱剪切层中涡结构的形成,导致尾迹流场的Strouhal数变为0.21,相较于单独圆柱绕流工况增加了5%。
参考文献
| [1] | 赵军圣,庄光明,王增桂.极大似然估计方法介绍[J].长春理工大学学报,2010,5(6):53-54. ZHAO J S,ZHUANG G M,WANG Z G.An introduction about maximum likelihood estimation[J].Journal of Changchun University of Science and Technology,2010,5(6):53-54(in Chinese). |
| Cited By in Cnki (11) | |
| [2] | BO R.The maximum spacing method:An estimation method related to the maximum likelihood method[J].Scandinavian Journal of Statistics,1984,11(2):93-112. |
| Click to display the text | |
| [3] | EKSTRÖM M.On the consistency of the maximum spacing method[J].Journal of Statistical Planning and Inference,1998,70(2):209-224. |
| Click to display the text | |
| [4] | GHOSH K,JAMMALAMADAKA S R.A general estimation method using spacings[J].Journal of Statistical Planning and Inference,2001,93(1):71-82. |
| Click to display the text | |
| [5] | EKSTROM M.Consistency of generalized maximum spacing estimates[J].Scandinavian Journal of Statistics,2001,28(2):343-354. |
| Click to display the text | |
| [6] | 孙振东,王喜山.一种计算电子元器件工作寿命的方法——最好线性无偏估计(BLUE)法[J].烟台大学学报(自然科学与工程版),1994(4):10-17. SUN Z D,WANG X S.A method to calculate lifetime of electronic devices-the best linear undistorted estimation[J].Journal of Yantai University(Natural Science and Engineering),1994(4):10-17(in Chinese). |
| Cited By in Cnki (1) | |
| [7] | 徐安.BLUE和GLUE及主要点估计方法的评价[J].济南交通高等专科学校学报,1994(1):37-44. XU A.Assessment of BLUE and GLUE and the main point estimation method[J].Journal of Jinan Communications College,1994(1):37-44(in Chinese). |
| Cited By in Cnki (1) | |
| [8] | SHAO Y.Consistency of the maximum product of spacing method and estimation of a unimodal distribution[J].Statistica Sinica,2001,11(4):1125-1140. |
| Click to display the text | |
| [9] | EKSTRÖM M.Alternatives to maximum likelihood estimation based on spacings and the Kullback-Leibler divergence[J].Journal of Statistical Planning and Inference,2008,138(6):1778-1791. |
| Click to display the text | |
| [10] | RANNEBY B,JAMMALAMADAKA S R,TETERUKOVSKIY A.The maximum spacing estimation for multivariate observations[J].Journal of Statistical Planning and Inference,2005,129(1):427-446. |
| Click to display the text | |
| [11] | EL HAJE HUSSEIN F,GOLUBEV Y.On entropy estimation by m-spacing method[J].Journal of Mathematical Sciences,2009,163(3):290-309. |
| Click to display the text | |
| [12] | GOMES A E,DA SILVA C Q,CORDEIRO G M.The beta Burr III model for lifetime data[J] Brazilian Journal of Probability and Statistics,2013,27(4):502-543. |
| Click to display the text | |
| [13] | BADSHA MD.B,MOLLAH MD.N H,JAHAN N,et al.Robust complementary hierarchical clustering for gene expression data analysisby β-divergence[J].Journal of Bioscience and Bioengineering,2013,116(3):397-407. |
| Click to display the text | |
| [14] | CORDEIRO G M,NADARAJAH S,ORTEGA E M M.General results for the beta Weibull distribution[J].Journal of Statistical Computation and Simulation,2013,83(6):1082-1114. |
| Click to display the text | |
| [15] | CORDEIRO G M,LEMONTE A J.The β-Birnbaum-Saunders distribution:An improved distribution for fatigue life modeling[J].Computational Statistics and Data Analysis,2011,55(3):1445-1461. |
| Click to display the text | |
| [16] | PARANAÍBA P F,ORTEGA E M M,CORDEIRO G M,et al.The beta Burr XII distribution with application to lifetime data[J].Computational Statistics and Data Analysis,2011,55(2):1118-1136. |
| Click to display the text | |
| [17] | SILVA G O,ORTEGA E M M,CORDEIRO G M.The beta modified Weibull distribution[J].Lifetime Data Analysis,2010,16(3):409-430. |
| Click to display the text | |
| [18] | 赵宇,杨军,马小兵.可靠性数据分析教程[M].北京:北京航空航天大学出版社,2009:150-151. ZHAO Y,YANG J,MA X B.Data analysis of reliability[M].Beijing:Beihang Uuiversity Press,2009:150-151(in Chinese). |
| [19] | 周品,赵新芬.MATLAB数理统计分析[M].北京:国防工业出版社,2009:200-204. ZHOU P,ZHAO X F.MATLAB statistics analysis[M].Beijing:National Defense Industry Press,2009:200-204(in Chinese). |
