则系统在时刻t的瞬时可用度定义为A(t)=P(X(t)=1),即时刻t系统处于正常状态的概率。定义2[20] 系统在[0,t]时间内系统平均可用度为
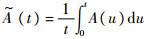。若极限
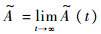存在,则称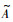
为系统极限平均可用度。而若极限
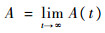存在,则称其为系统稳态可用度。注:若系统稳态可用度存在,则极限平均可用度必存在,且A=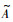,其中A和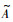与定义2中相同。引理1[20] 假设系统由一个部件组成,其故障时间X遵从一般概率分布F(t),修复时间Y遵从一般概率分布G(t),则系统稳态可用度为A==
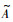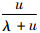;其中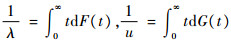
。1.2 模型引入根据文献[20]中的模型,假设系统由一个部件组成,其故障时间X遵从一般概率分布F(t),部件(系统)故障后,立即由修理设备进行修理,修复时间Y遵从一般概率分布G(t),修复后,部件立即转入工作状态。进一步假设故障部件经修复后,其工作寿命分布如新部件一样,且X和Y相互独立。在上述假设下,有模型构建的系统瞬时可用度A(t)满足更新方程:
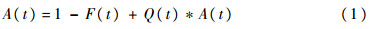
其中:
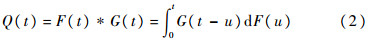
式中:*表示函数的卷积。下面对X和Y服从均匀分布情况下,系统瞬时可用度A(t)进行分析,主要通过把更新方程(1)转化为时滞或常微分方程,得到解析解。判断其是否存在小于稳态可用度的点来说明是否存在波动性,并通过仿真进行验证。2 均匀分布下系统瞬时可用度分析本节所讨论的是系统部件故障时间和修复时间都为均匀分布的情况。均匀分布是指随着时间增长,故障发生时间X和修复完成时间Y的概率成正比例增长,这种分布较为符合实际工程背景,所以需要对在这种分布下系统的瞬时可用度进行分析和研究。2.1 X和Y都服从相同均匀分布设故障时间X服从的均匀分布为F(t),修复时间Y服从的均匀分布为G(t),其分布函数为
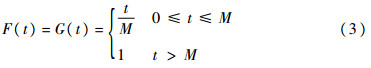
式中:M为均匀分布参数。从式(3)可以得到:定理1 设系统故障时间X服从的均匀分布为F(t),修复时间Y服从的均匀分布为G(t),其中F(t)=G(t),则瞬时可用度A(t)在t∈[0,3M]的解析表达式为
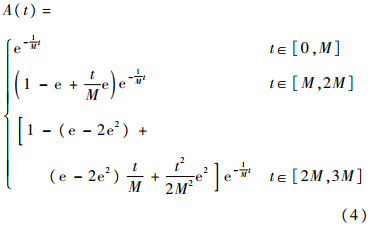
证明 把分布函数式(3)代入式(2),可以得到的分段函数为
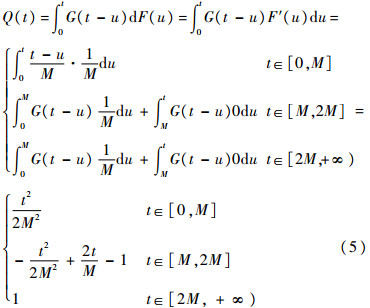
再把式(5)的Q(t)代入更新方程(1),可以得到
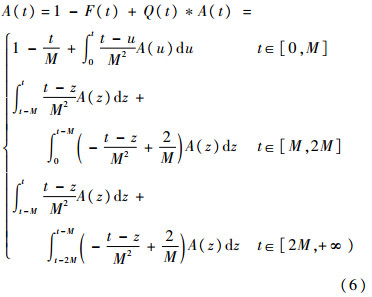
对方程(6)两边求导,得到二阶分段时滞微分方程:
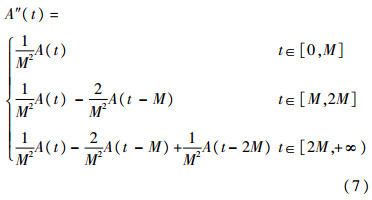
对上述得到的时滞微分方程(7),由A(t)的连续性及A′(t)在分段点的值,得到可用度A(t)在t∈［0,3M]的分段解析表达式如下:
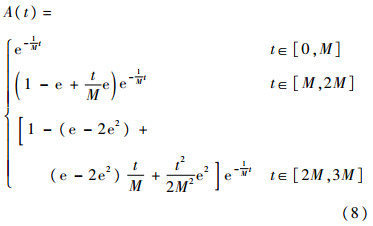
证毕根据定理1中得到的瞬时可用度A(t)的解析表达式,可以给出波动是否存在的方法。具体地说,根据式(5),容易证明Q′(t)是连续的,则根据更新方程(1)可知,1－F(t)有界,则A(t)也是连续的[21]。因此容易给出如下判断波动是否存在的方法:若A(t)在有限时间内存在小于稳态可用度的点,结合稳态可用度的极限理论[20]及引理1可知:
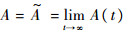,可知系统瞬时可用度存在波动性。下面根据定理1给出判断波动存在性的步骤。首先选取定理1中式(4)在t∈[0,M]的解析表达式,如果存在小于稳态可用度的点,则波动存在。否则考虑t>M情况,具体步骤为:步骤1 计算稳态可用度。由引理1及式(3)可得:A=
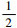。步骤2 判断A(t)在t∈[0,M]是否存在小于稳态可用度的点。由式(4)知:A(t)=e－t/M,t∈[0,M],则有A(M)=e－1<A=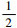,即存在小于稳态可用度的点,即波动存在。下面通过仿真来说明所用方法的有效性。对于式(8),分别令M=1,5,10,15,20,A=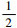;仿真得到图 1中的各条曲线。从图 1中曲线可以看出,当故障时间X和修复时间Y服从相同均匀分布时,瞬时可用度A(t)在t=M时小于稳态可用度A。结合波动存在的理论分析,说明A(t)确实存在波动性(选取的M只是为了保证曲线对比时清晰完整,实际?M都具有波动性)。2.2 X和Y服从不同均匀分布设故障时间X服从的均匀分布为F(t),修复时间Y服从的均匀分布为G(t),其分布函数为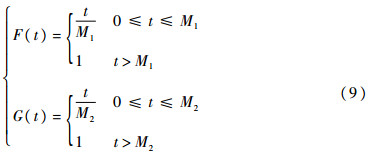
式中:M1和M2为均匀分布的参数。选取参数为M1、M2，满足M1<M2(M2<M1可类似证明)。
 |
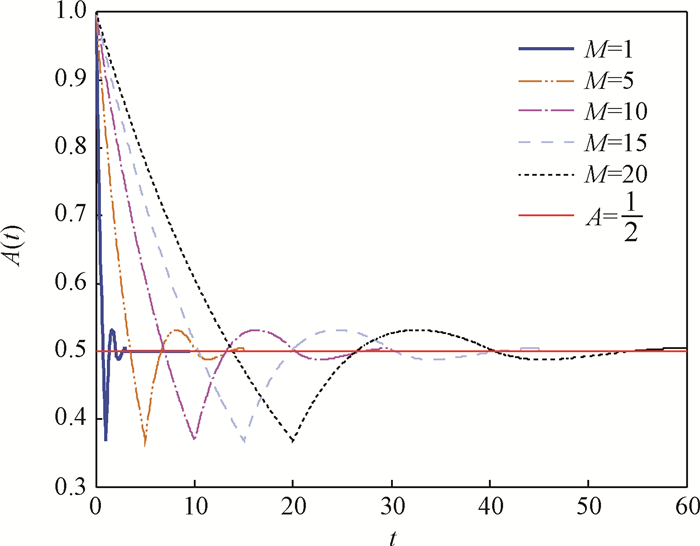| 图 1 X和Y服从相同均匀分布时瞬时可用度对比曲线Fig. 1 Comparative curves of instantaneous availability when X and Y obey the same uniform distributions |
| 图选项 |
从式(9)可以得到:定理2 设故障时间X服从的均匀分布为F(t),修复时间Y服从的均匀分布为G(t),其中F(t)≠G(t);则瞬时可用度A(t)在t∈[0,M1]的解析表达式为
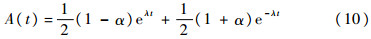
式中:
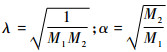证明 把分布函数式(9)代入式(2),可以得到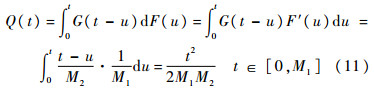
把Q(t)代入更新方程(1),得到如下的瞬时可用度的积分方程：
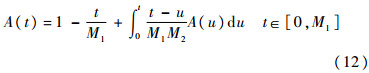
对方程(12)两边求导,得到常微分方程:
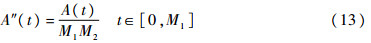
求解t∈[0,M1]的二阶常微分方程(13),可得
式中:
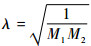;C1和C2为待定系数。根据初值A(0)=1及A′(0)=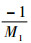
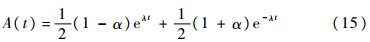
式中:
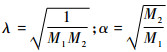证毕由定理2给出了故障时间X和修复时间Y在服从不同均匀分布下,系统瞬时可用度A(t)在t∈[0,M1]的解析表达式。为了进一步研究波动存在性,给出如下结论。定理3 在t∈(0,1)上,函数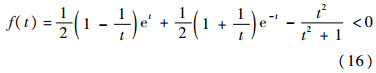
证明 整理式(16)中的f(t)有
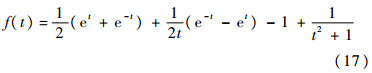
则只需要证明在t∈(0,1)上,式(17)中f(t)<0。首先et及e－t在(0,1)上的泰勒公式为
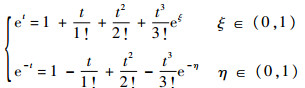
故
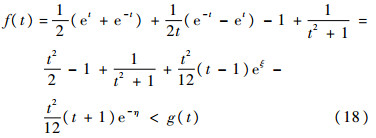
式中:
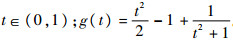根据式(18)可知,若g(t)<0,t∈(0,1),则f(t)<0。
则当t∈(0,1),
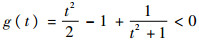,结合式(18),即可得到在t∈(0,1)上,f(t)<0恒成立。证毕作出函数f(t)的图像(Z为纵坐标),如图 2所示。 |
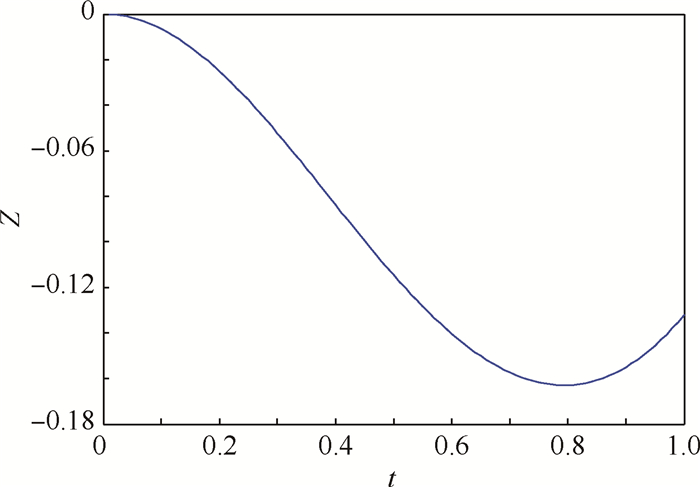| 图 2 函数f(t)的图像Fig. 2 Image of function f(t) |
| 图选项 |
从图 2中也可以看出:f(t)<0,t∈(0,1)。类似于第2.1节判断波动性存在的方法,下面根据定理2和定理3给出判断波动性存在的步骤。步骤1 计算稳态可用度。由引理1,计算可得
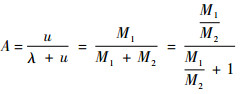
步骤2 判断A(t)在t∈[0,M1]是否存在小于稳态可用度的点。由式(10)结合定理 3及
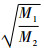<1可知:
故波动存在。下面通过仿真验证所给方法的有效性。结合式(15),分别令M1=20;M2=40,60,80,100,则A=
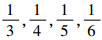,仿真得到图 3所示的服从不同均匀分布可用度比较曲线。从图 3中4组曲线变化情况分析,由于系统瞬时可用度A(t)在t=M1小于稳态可用度A,由连续性和极限稳定性知,随后A(t)必存在一次波动。所以在这种均匀分布情况下,理论分析与仿真验证说明依然存在波动性(实际对?M1,M2成立)。 |
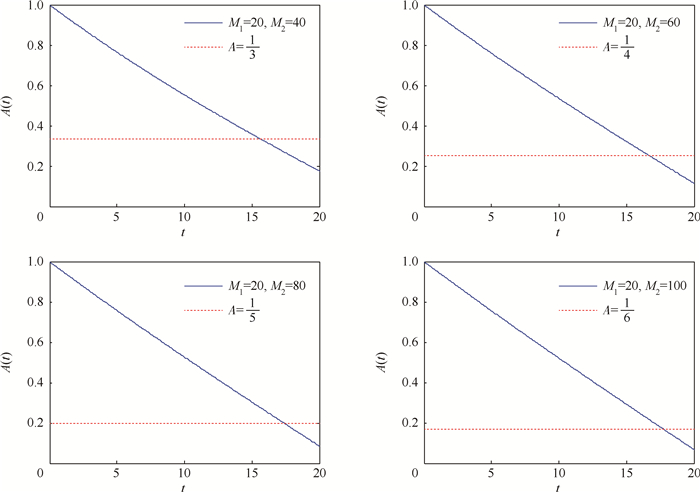| 图 3 X和Y服从不同均匀分布瞬时可用度比较曲线Fig. 3 Comparative curves of instantaneous availability when X and Y obey different uniform distributions |
| 图选项 |
3 结 论本文对单部件可修系统模型中瞬时可用度的波动现象进行了理论分析。通过把积分方程转化为微分方程方法研究瞬时可用度A(t)的波动性问题。通过理论分析和仿真验证,得到:1) 当故障时间X和修复时间Y服从相同的均匀分布时,瞬时可用度在第1个分段函数中存在小于稳态可用度的点,所以由可用度的稳定性可以说明A(t)至少存在一次波动。2) 当故障时间X和修复时间Y服从不同的均匀分布时,瞬时可用度在第1个分段函数中也存在小于稳态可用度的点,所以说明A(t)至少存在一次波动。综上所述,当故障时间X和修复时间Y服从均匀分布时,瞬时可用度均存在波动性,与均匀分布参数M1、M2的选取无关。
参考文献
| [1] | 杨懿.一般概率分布下系统瞬时可用度离散时间建模分析与应用[D].南京:南京理工大学,2008:20-47. YANG Y.The instantaneous availability of the systems under discrete time modeling analysis and application in general probability distribution[D].Nanjing:Nanjing University of Science and Technology,2008:20-47(in Chinese). |
| Cited By in Cnki (2) | |
| [2] | 康锐,于永利.我国装备可靠性维修性保障性工程的理论与实践[J].中国机械工程,1998,9(12):3-6. KANG R,YU Y L.The theory and practice of engineering of our equipment reliability and maintainability and security[J].China Mechanical Engineering,1998,9(12):3-6(in Chinese). |
| Cited By in Cnki (23) | |
| [3] | 杨为民,阮镰,屠庆慈.可靠性系统工程——理论与实践[J].航空学报,1995,16(8):1-8. YANG W M,RUAN L,TU Q C.The theory and practice of reliability system engineering[J].Acta Aeronautica et Astronautica Sinica,1995,16(8):1-8(in Chinese). |
| Cited By in Cnki (4) | |
| [4] | 康锐,王自立.可靠性系统工程的理论与技术框架[J].航空学报,2005,26(5):633-636. KANG R,WANG Z L.Framework of theory and technique on reliability system engineering[J].Acta Aeronautica et Astronautica Sinica,2005,26(5):633-636(in Chinese). |
| Cited By in Cnki (23) | |
| [5] | 杨为民.可靠性维修性保障性总论[M].北京:国防工业出版社,1995:328-389. YANG W M.The general introduction of reliability maintainability and supportability[M].Beijing:National Defense Industry Press,1995:328-389(in Chinese). |
| [6] | 马绍民.综合保障工程[M].北京:国防工业出版社,1995:31-76. MA S M.Integrated support engineering[M].Beijing:National Defense Industry Press,1995:31-76(in Chinese). |
| [7] | 杨为民,屠庆慈.21世纪初装备可靠性维修性保障性工程发展框架研究[J].中国机械工程,1998,9(12):45-48. YANG W M,TU Q C.Framework for the study of the development of equipment reliability maintainability supportability engineering at the beginning of twenty-first century[J].China Mechanical Engineering,1998,9(12):45-48(in Chinese). |
| Cited By in Cnki (28) | |
| [8] | 王正元,刘靖旭,谭跃进,等.基于作战仿真的装甲车辆作战效能评估方法[J].国防科技大学学报,2004,26(2):106-109. WANG Z Y,LIU J X,TAN Y J,et al.Method of efficiency evaluation of armored vehicle combat simulation[J].Journal of National University of Defense Technology,2004,26(2):106-109(in Chinese). |
| Cited By in Cnki (8) | |
| [9] | 康建设,张森林,王亚彬.自行火炮保障性要求及可用度预计方法研究[C]//第一届维修工程国际学术会议论文集.北京:科学出版社,2006:632-636. KANG J S,ZHANG S L,WANG Y B.The security requirements of self-propelled gun and the method for prediction of availability[C]//Proceedings of the First International Conference on Maintenance Engineering.Beijing:Science Press,2006:632-636(in Chinese). |
| [10] | 徐廷学.导弹武器系统的使用可用度[J].航空科学技术,2000(3):34-35. XU T X.The system availability of missile weapon[J].Aeronautical Science and Technology,2000(3):34-35(in Chinese). |
| Cited By in Cnki (4) | |
| [11] | AMIRI M,PRENOSIL V.General solution for MTTF and steady-state availability of NMR system[C]//2014 9th International Symposium on Reconfigurable and Communication-Centric Systems-on-Chip.Piscataway,NJ:IEEE Press,2014:1-4. |
| Click to display the text | |
| [12] | 王立超,杨懿,邹云,等.离散Weibull分布下实现系统可用度的最小波动[J].控制理论与应用,2010,27(5):575-581. WANG L C,YANG Y,ZOU Y,et al.Achieving the minimum volatility of the system availability under the discrete Weibull distribution[J].Control Theory and Applications,2010,27(5):575-581(in Chinese). |
| Cited By in Cnki (1) | |
| [13] | SUN H R,HAN J J.The failure of MTTF in availability evaluation[C]//Proceedings of the Annual Reliability and Maintainability Symposium.Piscataway,NJ:IEEE Press,2002:279-284. |
| Click to display the text | |
| [14] | 王立超.系统可用度匹配化分析与设计[D].南京:南京理工大学,2008:13-50. WANG L C.The analysis and design of system availability[D].Nanjing:Nanjing University of Science and Technology,2008:13-50(in Chinese). |
| Cited By in Cnki (2) | |
| [15] | WANG K Y,LIU Y,YIN M Y,et al.Analysis on the instantaneous availability of series repairable systems in cyber warfare environment[C]//2014 33rd Chinese Control Conference.Piscataway,NJ:IEEE Press,2014:3001-3005. |
| Click to display the text | |
| [16] | TILLMAN F A,WAY K,NASSAR R F,et al.Numerical evaluation of instantaneous availability[C]//IEEE Transactions on Reliability.Piscataway,NJ:IEEE Press,1983,R32(1):119-123. |
| [17] | XUE A C,JING Q,LUO L,et al.Instantaneous availability for the protection devices based on non-homogeneous Markov model and a case study[C]//2014 33rd Chinese Control Conference.Piscataway,NJ:IEEE Press,2014:6524-6527. |
| Click to display the text | |
| [18] | REZENDE R,DITTRICH A,MALEK M.User-perceived instantaneous service availability evaluation[C]//2013 19th Pacific Rim International Symposium on Dependable Computing.Piscataway,NJ:IEEE Press,2013:273-282. |
| Click to display the text | |
| [19] | CHA J H.Sequential confidence interval estimation for system availability[J].Quality and Reliability Engineering International,2005,22(2):165-176. |
| Click to display the text | |
| [20] | 曹晋华,程侃.可靠性数学引论[M].2版.北京:高等教育出版社,2006:250-261. CAO J H,CHENG K.A mathematical introduction to reliability[M].2nd ed.Beijing:Higher Education Press,2006:250-261(in Chinese). |
| [21] | 林元烈.应用随机过程[M].北京:清华大学出版社,2002:66-68. LIN Y L.Applied stochastic processes[M].Beijing:Tsinghua University Press,2002:66-68(in Chinese). |
