为了准确获得不同飞行状态下蜻蜓的飞行参数以及飞行特征,研究者使用了不同的实验方法和手段。1997年,Wakeling和Ellington[2-4]使用2台光轴垂直的高速摄像机,拍摄得到滑翔和自由前飞状态下蜻蜓和豆娘的翅膀及身体运动参数,并用准定常分析法计算了飞行过程中的升力系数和阻力系数。2003年,Wang等[5]使用投影梳状条纹插值法测量了蜻蜓前飞和转弯状态下的运动参数以及飞行过程中翅膀的变形情况。2008年,Cheng等[6]使用投影栅线法测量了蜻蜓前飞和转弯状态下翅膀的变形。2010年,Dong团队用3台摄像机拍摄了自由飞行的蜻蜓,并提出用拱形变形量与弦长的比值来表示翅膀拱形变形情况[7]。
以上研究主要针对蜻蜓悬停、前飞和转弯等飞行状态进行观察和研究,对于蜻蜓实际飞行中,特别是在紧急逃避或者抓捕猎物时经常出现的一种典型飞行状态——爬升的研究却鲜有文献公开报道。与其他飞行状态不同的是,爬升过程蜻蜓需要克服自身重力向上飞行,因此需要翅膀提供更大的气动载荷。在实际飞行中,蜻蜓很少出现垂直爬升,斜向上爬升飞行较为常见。对于斜向上的爬升飞行,需要蜻蜓翅膀提供竖直向上的升力和水平向前的推力。因此爬升角度不同,需要翅膀提供的上升力和推力就不同,相应的身体和翅膀运动参数就有所差别。
本文采用2台光轴相互垂直的高速摄像机对蜻蜓进行活体拍摄,利用蜻蜓的趋光性引导其进行爬升飞行,获取了蜻蜓不同爬升角爬升时身体和翅膀的运动细节。通过整理实验结果发现,蜻蜓的爬升飞行主要有2种情况:大于50°的大爬升角爬升和小于30°的小爬升角爬升。本文针对2种情况,选取不同的飞行序列,使用特征点匹配和三维重构方法对其进行运动参数分析和对比,探究了不同爬升角下蜻蜓身体和翅膀的运动规律和气动特征,为仿生流体力学理论探索和微型飞行器工程应用提供了数据基础和指导。
1 实验方案 1.1 实验系统 蜻蜓扑翼飞行实验观测系统如图 1所示,包括2台高速摄像机及其配套控制器显示装置(CDU)、2盏摄影灯和1个观察箱。
 |
| 图 1 实验室高速摄像系统布置 Fig. 1 High-speed camera system setup in lab |
| 图选项 |
高速摄像机是实验观测系统中最关键的设备。在昆虫活体拍摄实验中,为了获取更准确的飞行规律,通常要求所使用摄像机的拍摄频率不小于昆虫扑翼频率的20倍[8]。根据目前所有研究结论可知,蜻蜓的扑翼频率基本都在30~40 Hz范围内,本实验所选用的摄像机拍摄频率为1 000帧/s,分辨率为1 280像素×1 024像素,完全能够满足实验测试精度要求。拍摄过程中,2台高速摄像机呈光轴正交放置,使用1个按压式触发开关实现2台高速摄像机的同时触发。
实验中所使用的观察箱是利用透光性足够好的玻璃制成,尺寸为780 mm×780 mm×1 000 mm,可以实现蜻蜓的自由飞行。观察箱上方为2盏功率为1 000 W的石英灯,一方面可为拍摄提供照明补偿,另一方面也可作为利用蜻蜓趋光性引导蜻蜓向上爬升的诱导光源。
1.2 实验对象 实验对象选取蜻蜓种类中的黄蜻。捕捉到的蜻蜓被放置在不透光的纸盒中,黑暗的环境有助于蜻蜓恢复平静,以避免其受到光线刺激而奋力扑动造成翅膀损伤及活力下降。因为在非自然环境中蜻蜓无法通过进食恢复体力,因此自捕获之时起,蜻蜓的活力开始衰减。为保证获得蜻蜓的真实飞行状态,本实验所有蜻蜓的拍摄均在捕获后6 h内完成。
实验前对蜻蜓的形态参数进行测量,包括:身体和翅膀的质量和,身体头尾之间的距离(身长),两翅尖的距离(翼展),翅根到翅尖的距离(翅长),翅前缘到尾缘的距离(弦长)。本次实验共捕获了53只蜻蜓,所测得的参数平均值如表 1所示。实验前,用黑墨水在蜻蜓翅膀上进行标记,可以避免由于翅膀表面对强光的反射作用造成翅膀表面拍摄模糊,同时标记点将作为翅膀三维重构过程中的参考点[7]。为了得到较为完整的运动参数,标记点覆盖翅膀前缘、尾缘以及中间弦向位置,其具体尺寸及分布如图 2所示,标记点质量占整个蜻蜓身体质量的比例不超过千分之三,对蜻蜓飞行情况的影响可以忽略不计。
表 1 蜻蜓形态参数 Table 1 Morphological parameters of dragonfly
| 参数 | 数值 | |
| 身体参数 | 质量/g | 0.342 |
| 身长/mm | 49 | |
| 翅膀参数 | 前翼展/mm | 88.4 |
| 前翅长/mm | 43.6 | |
| 前翅弦长/mm | 9.7 | |
| 后翼展/mm | 83.8 | |
| 后翅长/mm | 41.2 | |
| 后翅弦长/mm | 11.9 | |
表选项
 |
| 图 2 翅膀标记点分布 Fig. 2 Distribution of marked points of wings |
| 图选项 |
1.3 测试方法 在进行实验前,需要对高速摄像机进行标定,本文采用了一种基于共面法的分布线性标定法。该方法利用共面点约束,只需借助二维标定物即可完成标定,操作简单,容易实现;通过分步思想,避免了求解的非线性迭代。此外,该标定方法还考虑了对必要的摄像机径向变形以及透镜变形等因素的修正,精度较高。对高速摄像机进行标定的目的主要是获得从拍摄的图像坐标到世界坐标的转化参数,包括摄像机的主点坐标(u0,v0)、图像元素比例因子Sx、有效焦距fr和径向畸变系数ki等由摄像机内部光学组件性质决定的内部参数;旋转矩阵R和平移矩阵T等表征摄像机在世界坐标系中具体位置和方位的外部参数。所使用的标定物是一个已知尺寸和位置的二维棋盘标定板,通过高速摄像机拍摄得到的标定物特征点图像坐标和相应特征点的已知世界坐标值,求解含有内外参数的矩阵方程就可以求得所有摄像机参数,具体过程参见文献[9]。
上述标定过程完成以后,要实现从图像坐标到三维世界坐标的转换还需要知道2台高速摄像机的场深。本实验中,2台高速摄像机呈光轴正交放置,从而相互提供场深信息。实验前基于数字图像处理方法,采用1个环形标定板对2台高速摄像机光轴的垂直度进行了校准[10]。最后利用标定得到的摄像机参数矩阵和2台高速摄像机场深信息,可以对拍摄对象进行三维重构,即根据2台高速摄像机的二维图像坐标计算得到相应的三维世界坐标。
利用一个已知坐标信息的棋盘标定板对上述测量系统进行了准确性验证。标定板上相邻标定点间距约为100 mm,三维重构结果最大误差为1.134 mm,即最大相对误差为1.13%。该误差包含了标定板印刷误差、摄像机标定误差、图像坐标提取误差和三维重构计算误差等,结合本文蜻蜓飞行观测实验的具体情况,认为该精度能够满足实验要求。
2 运动参数提取 基于三维重构得到的特征点三维坐标值,即可提取蜻蜓身体和翅膀的运动参数。身体运动参数包括:质心轨迹和身体姿势。翅膀运动参数包括:扑翼频率、相位差、拍动角、攻角、扭转角、偏离角和拍动平面倾角。提取运动参数前需要建立坐标系,包括固定于空间一点的世界坐标系和固定于蜻蜓身体质心的相对坐标系。世界坐标系主要描述蜻蜓的质心轨迹和身体姿势,相对坐标系则用以描述翅膀的运动参数[5]。
图 3为世界坐标系和相对坐标系的定义。利用蜻蜓头部、尾部以及翼根的位置确定相对坐标系(Xb,Yb,Zb)的坐标原点,蜻蜓头部和尾部的连线称为身体轴线,2个前翅翼根连线的中点在身体轴线上的投影点Ob即为相对坐标系的原点。Xb轴指向蜻蜓的尾部,Zb轴垂直Xb轴并指向蜻蜓身体的左侧。2套坐标系的建立都满足右手法则。根据此方法建立的相对坐标系的原点位置接近蜻蜓的身体质心[5],因此相对坐标系原点Ob的运动轨迹即可认为是蜻蜓的飞行轨迹。
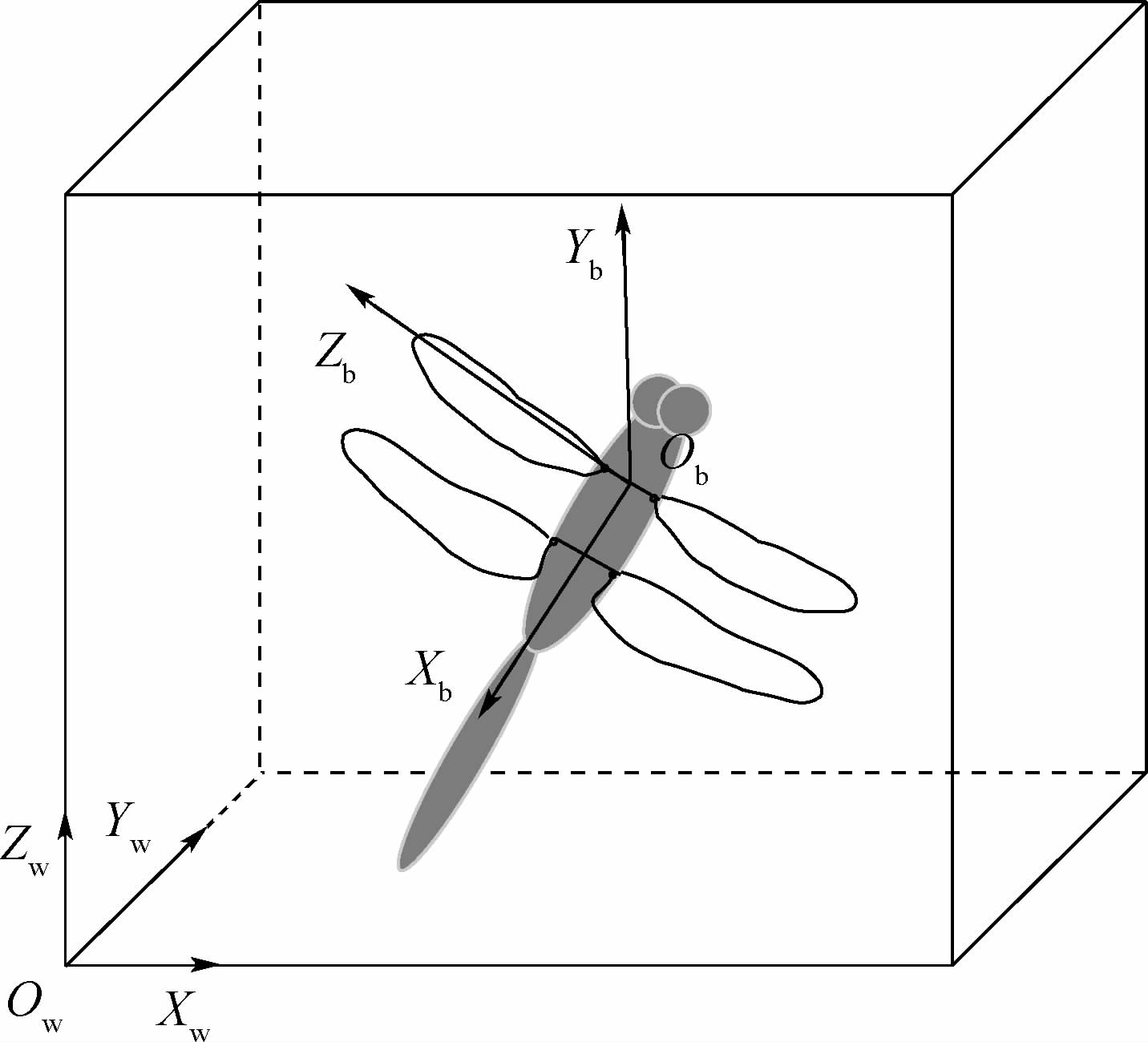 |
| 图 3 世界坐标系与相对坐标系的定义 Fig. 3 Definition of world coordinate system and relative coordinate system |
| 图选项 |
昆虫扑翼飞行时,可近似认为翅膀是在同一个平面内拍动,该平面即为拍动平面。描述翅膀位置和姿态的各个参数都是基于拍动平面来定义的。拍动平面的具体定义方法如下[11]:将蜻蜓翅尖在若干拍动周期内的轨迹投影到身体的对称平面XbYb上,并利用最小二乘方法求得上述投影点的线性回归线,则可将蜻蜓的拍动平面定义为过翅根一点且平行于该线性回归线并垂直于身体对称面的平面[12]。该平面与身体轴线(Xb轴)的夹角称为拍动平面倾角β(见图 4(a))。图 4(b)为为基于拍动平面定义的翅膀拍动过程中的几个角度参数,L1表示翅膀翅根与翅尖的连线,L2为L1在拍动平面内的投影。定义L2与相对坐标轴Zb的夹角为拍动角Ф,L1与L2的夹角为翅膀偏离角θ。拍动角用来描述翅膀拍动的幅值大小,偏离角用来描述翅膀偏离拍动平面的情况[5]。另外,本文中涉及到的其他几个运动参数定义如下:爬升角定义为身体质心飞行速度与水平方向的夹角;爬升率定义为单位时间内蜻蜓质心上升高度;身体俯仰角定义为蜻蜓身体轴线与水平方向的夹角。
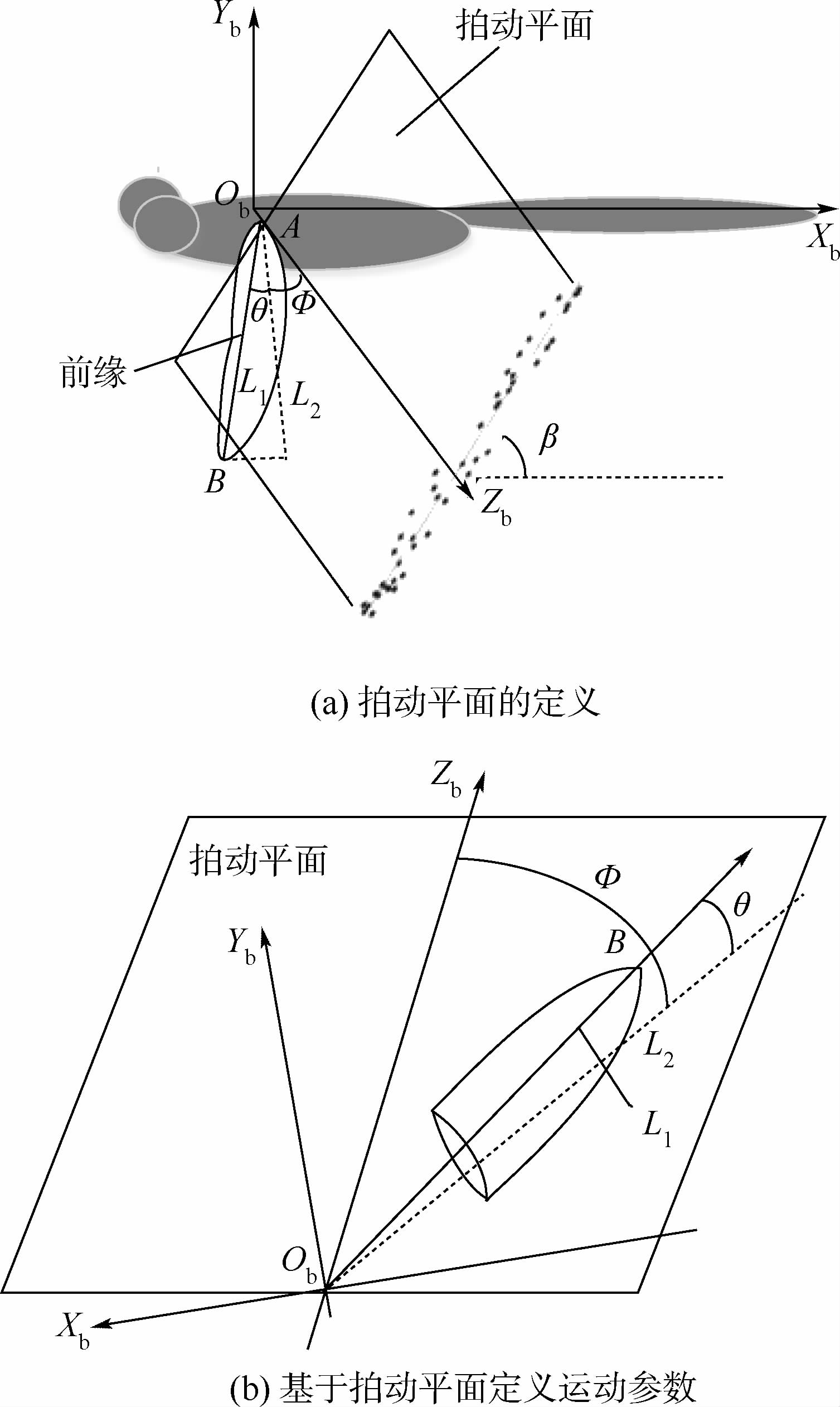 |
| 图 4 翅膀的飞行参数定义方式 Fig. 4 Definition of wing kinematics |
| 图选项 |
3 爬升飞行特征分析 实验共拍得若干蜻蜓自由飞行序列,本文重点关注爬升状态,为保证实验数据的有效性,提取分析的飞行序列满足以下条件:①飞行序列包括2个以上的拍动周期;②飞行轨迹为近似竖直向上或斜向上的直线运动;③绕身体轴线几乎没有旋转运动。基于以上条件,在进行翅膀运动参数测量时可以使用“对称性”假设,即认为蜻蜓左右翅膀的拍动规律完全相同。基于此,由于遮挡原因导致的信息不完整性可以通过左右翅膀的信息进行一定程度的弥补。基于以上原则和处理方式,选取了多组蜻蜓爬升状态的飞行序列进行处理和参数提取。发现由于不同爬升角飞行时需要气动力不同,蜻蜓的扑翼频率、前后翅相位差、翅膀拍动幅度、翅膀偏离角和身体俯仰角等参数有明显差别。本文针对同一蜻蜓的2种不同爬升角飞行状态进行飞行规律对比和动力学分析。
3.1 蜻蜓爬升过程中的质心运动 图 5(a)和图 5(b)分别给出了蜻蜓2种爬升角度飞行时身体质心位移随时间的变化关系。可以看出,2种情况下蜻蜓质心在3个方向上的位移均近似为直线。对于大爬升角爬升(见图 5(a)),蜻蜓在Xb和Yb方向上的位移变化较小,主要是沿正Zb方向作爬升运动。而对于小爬升角爬升(见图 5(b)),沿竖直方向(Zb向)的位移远远小于Yb方向的位移。从图 6(a)和图 6(b)给出的2种情况的爬升速度可以看出,2种情况下蜻蜓沿3个方向的飞行速度都近似周期性波动,波动周期约为蜻蜓的扑翼周期;大爬升角爬升(见图 6(a))时蜻蜓的爬升率约为0.9 m/s(即Zb方向爬升速度);而小爬升角爬升飞行(见图 6(b))时爬升率只有0.4 m/s,不到前者的一半。对于大爬升角爬升飞行来说,需要翅膀提供的竖直向上的升力大于水平方向的推力,而对于小爬升角爬升飞行,需要向前的推力大于向上的升力。
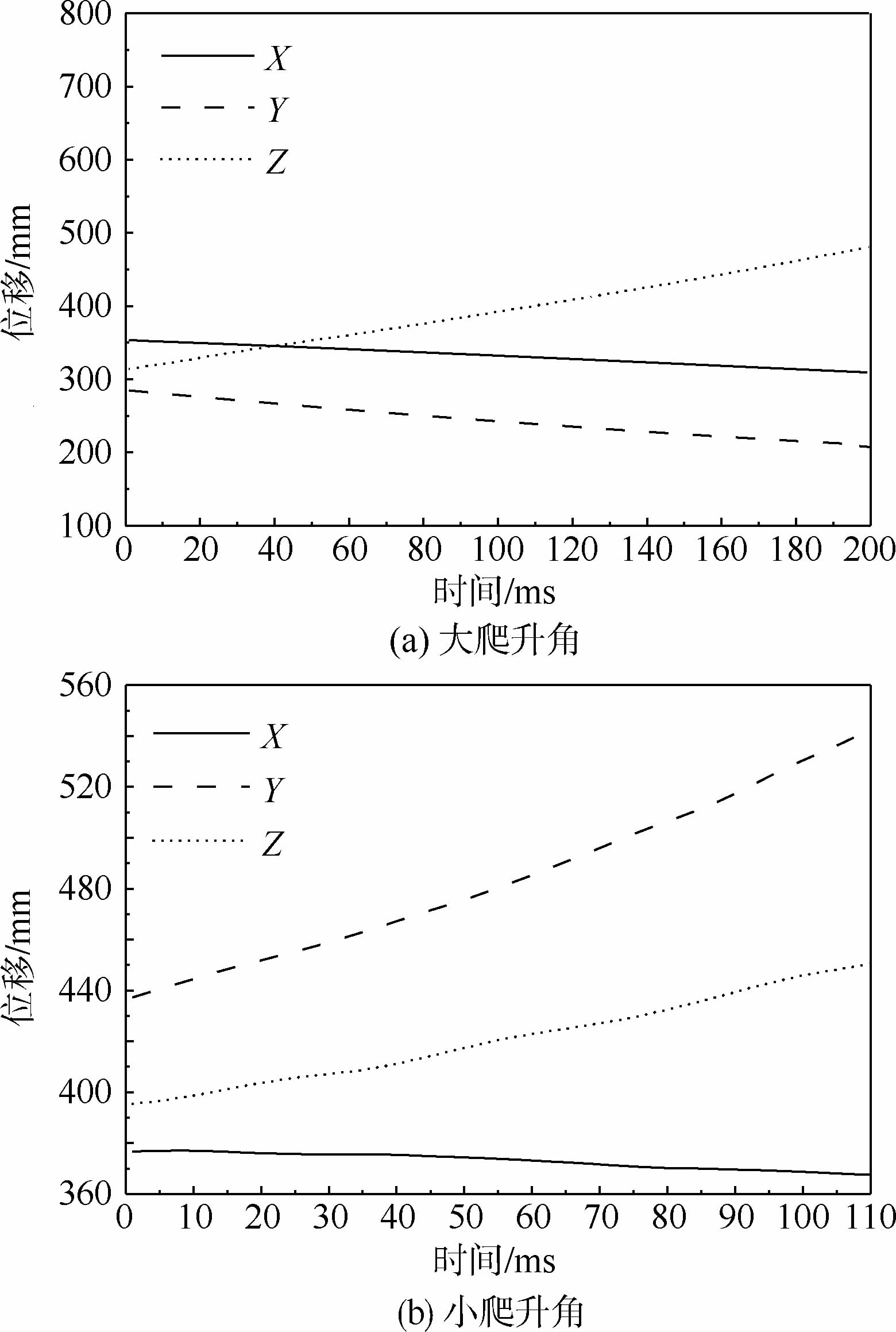 |
| 图 5 蜻蜓爬升过程质心位移随时间变化 Fig. 5 Centroid displacement changed over time of dragonfly during climbing |
| 图选项 |
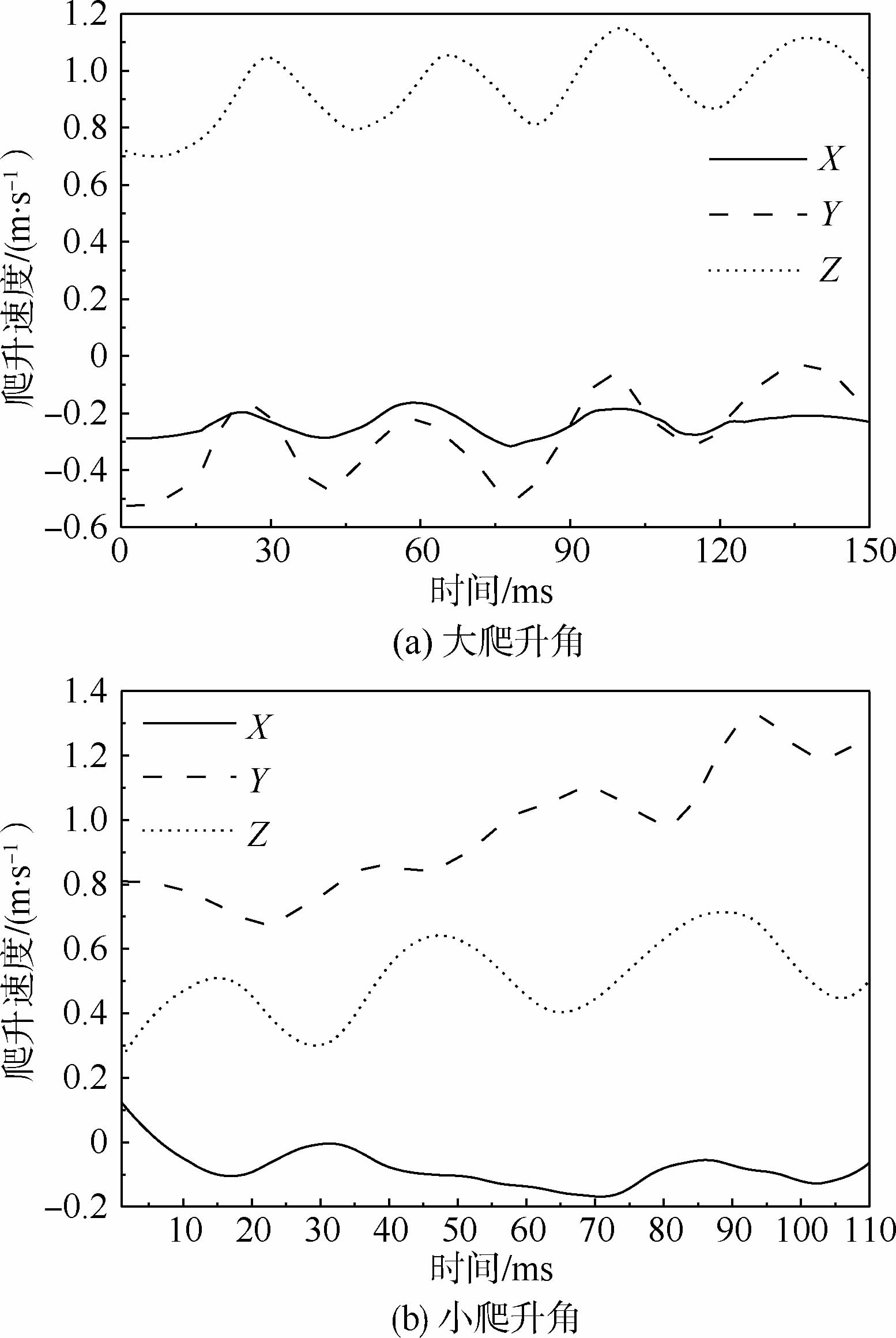 |
| 图 6 蜻蜓爬升速度随时间变化关系 Fig. 6 Dragonfly climbing speed changed over time |
| 图选项 |
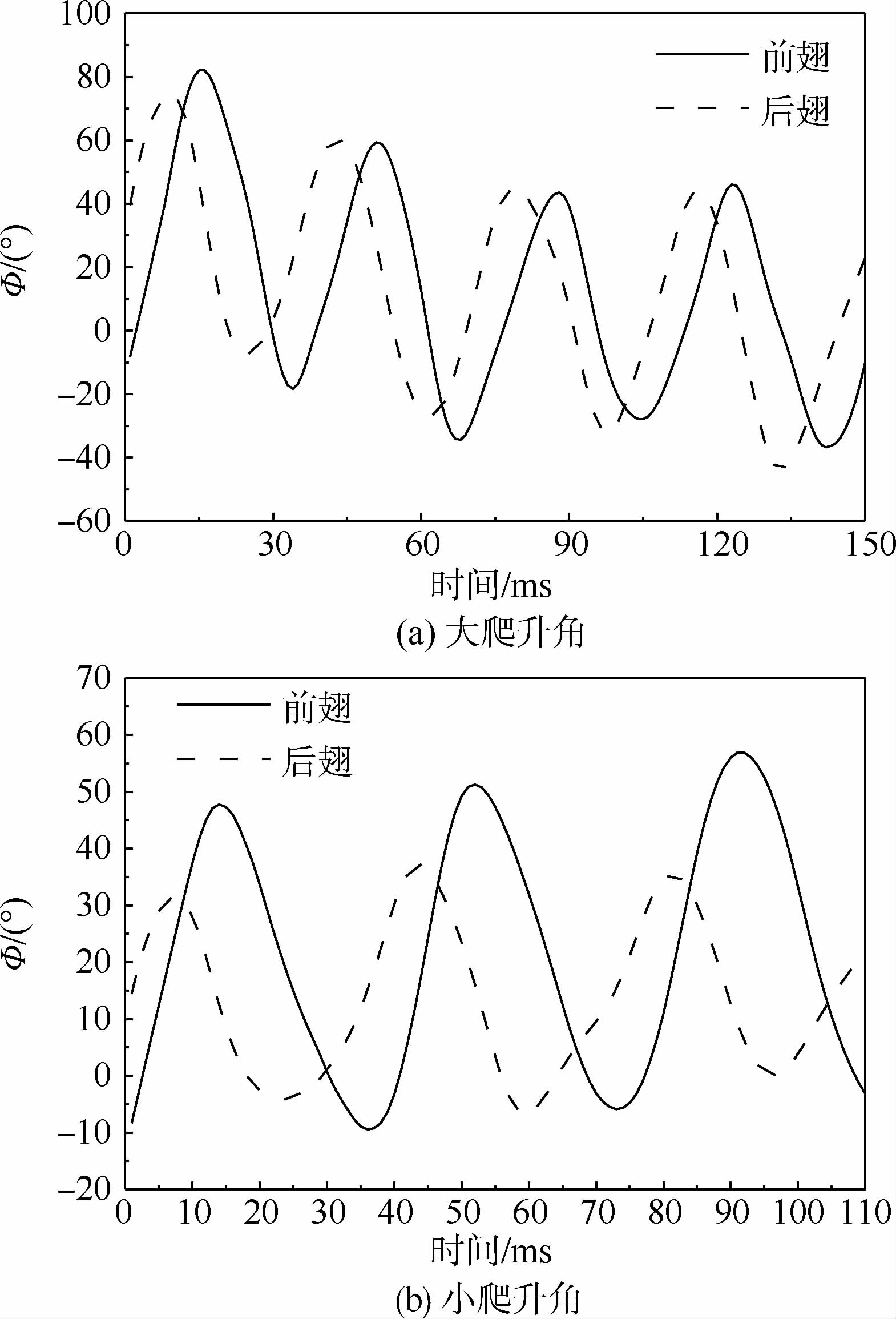
3.2 扑翼频率和翅膀拍动角 图 7(a)和图 7(b)分别为蜻蜓2种爬升角爬升飞行时前后翅拍动角随时间的变化。对2种情况下的数据分别进行傅里叶变换,可以发现,用1级谐波(k=1)的分量即可近似模拟拍动角的变化趋势,如式(1)所示形式。2种爬升角下蜻蜓前后翅拍动角各参数值见表 2。
 |
| 图 7 爬升过程中蜻蜓前后翅拍动角随时间变化关系 Fig. 7 Flapping angles of fore-hind wings changed over time of dragonfly during climbing |
| 图选项 |
表 2 不同爬升角下蜻蜓前后翅拍动角参数值 Table 2 Parameters of flapping angle of fore-hind wings of dragonfly during different climbing angles
| 状态 | Ф0/( ) | 2Ф1/( ) | f/Hz | δ/(°) | |
| 大爬升角 | 前翅 | 17.5 | 65.2 | 30.5 | 0 |
| 后翅 | 18 | 60 | 30.5 | 76.7 | |
| 小爬升角 | 前翅 | 22.3 | 56 | 27.2 | 0 |
| 后翅 | 13.9 | 36 | 27.2 | 102.3 | |
| 注:Ф0—扑翼中心值;Ф1—拍动幅值的一半;f—扑翼频率;δ—前后翅相位差。 | |||||
表选项
从表 2中可以发现,对于大爬升角爬升飞行,其前后翅的扑翼频率均为30.5 Hz,前后翅为稳定异步拍翅且后翅领先前翅,相位差约为76.7°。而对于小爬升角爬升,其前后翅扑翼频率只有27.2 Hz,比前者小3.3 Hz,前后翅相位差比大爬升角爬升时大26°左右。结合文献[13]对于蜻蜓前后翅相位差与气动载荷关系的研究进行分析,大爬升角爬升时要克服自身重力且产生较高的爬升率,比小爬升角爬升需要更大的上升力,因此大爬升角爬升状态时前后翅的相位差更小。另外发现,大爬升角爬升时双翅的拍动幅度均在60°以上,而小爬升角爬升时前后翅的拍动幅度差别较大,前翅拍动幅度为56°,后翅拍动幅度只有36°。可见,大爬升角爬升时蜻蜓通过前后翅较大的拍动幅度来获得更大的爬升率。
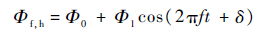 | (1) |
式中:Фf,h为前(后)翅的拍动角。
3.3 爬升飞行身体姿势 通过基于蜻蜓身体质心建立的相对坐标系与世界坐标系的位置关系,可以得到蜻蜓爬升过程中的身体姿势。一般来说,蜻蜓飞行过程中身体姿势包括3个方向的旋转,然而由于本文在处理飞行序列时满足本节提到的3个条件,使身体姿势由3个参数简化为只有身体俯仰角1个参数。图 8(a)和图 8(b)分别给出了蜻蜓大爬升角爬升和小爬升角爬升过程中的爬升角和身体俯仰角。可以发[CM(18]现,2种情况下蜻蜓的爬升角和身体俯仰角都随时间呈周期性波动,波动周期约为蜻蜓的扑翼周期。为了更清楚地看出两者关系,表 3列出了2种状态下爬升角和身体俯仰角的波动中心值。可以发现,较大的爬升角下身体俯仰角也比较大,均为65°左右;而对于爬升角只有27°的小爬升角爬升飞行,身体俯仰角只有13°。另外从大爬升角爬升的时间变化(见图 8(a))中也可以发现,爬升角和身体俯仰角有着一致的上升趋势。由此得出结论:身体俯仰角和蜻蜓的爬升角有着直接的正相关关系。
 |
| 图 8 蜻蜓爬升飞行时身体俯仰角和爬升角 Fig. 8 Pitch angles of body and flying angles of dragonfly during climbing |
| 图选项 |
表 3 2种状态的爬升角和身体俯仰角 Table 3 Pitch angles of body and flying angles of dragonfly during climbing
| 状态 | 爬升角/(°) | 身体俯仰角/(°) |
| 大爬升角 | 65 | 63 |
| 小爬升角 | 27 | 13 |
表选项
从产生气动力的角度对上述结论进行分析,以蜻蜓翅膀中间弦线为分析对象,其在某一个拍动瞬间产生的气动力几乎垂直弦线向上[14]。上拍和下拍过程中在同一个位置的攻角几乎相同,因此一个拍动周期以后该弦线产生的沿拍动平面方向的气动力基本抵消,产生的气动合力基本垂直拍动平面。因而翅膀拍动平面与水平方向夹角越小越容易产生竖直向上的升力,越有利于爬升飞行。图 9(a)和图 9(b)为蜻蜓2种爬升状态的飞行姿态示意图和实拍图。向上的粗箭头表示蜻蜓前翅拍动一个周期产生的气动合力F(只表示近似理论结果)。可以发现,对于大爬升角爬升(见图 9(a)),较大的身体俯仰角可以使翅膀拍动平面更接近水平面,从而更容易产生竖直向上的升力。而对于小爬升角爬升飞行来说,需要翅膀提供的向前的推力大于向上的升力,因此蜻蜓在进行小爬升角爬升(见图 9(b))时身体需要保持较小的身体俯仰角。
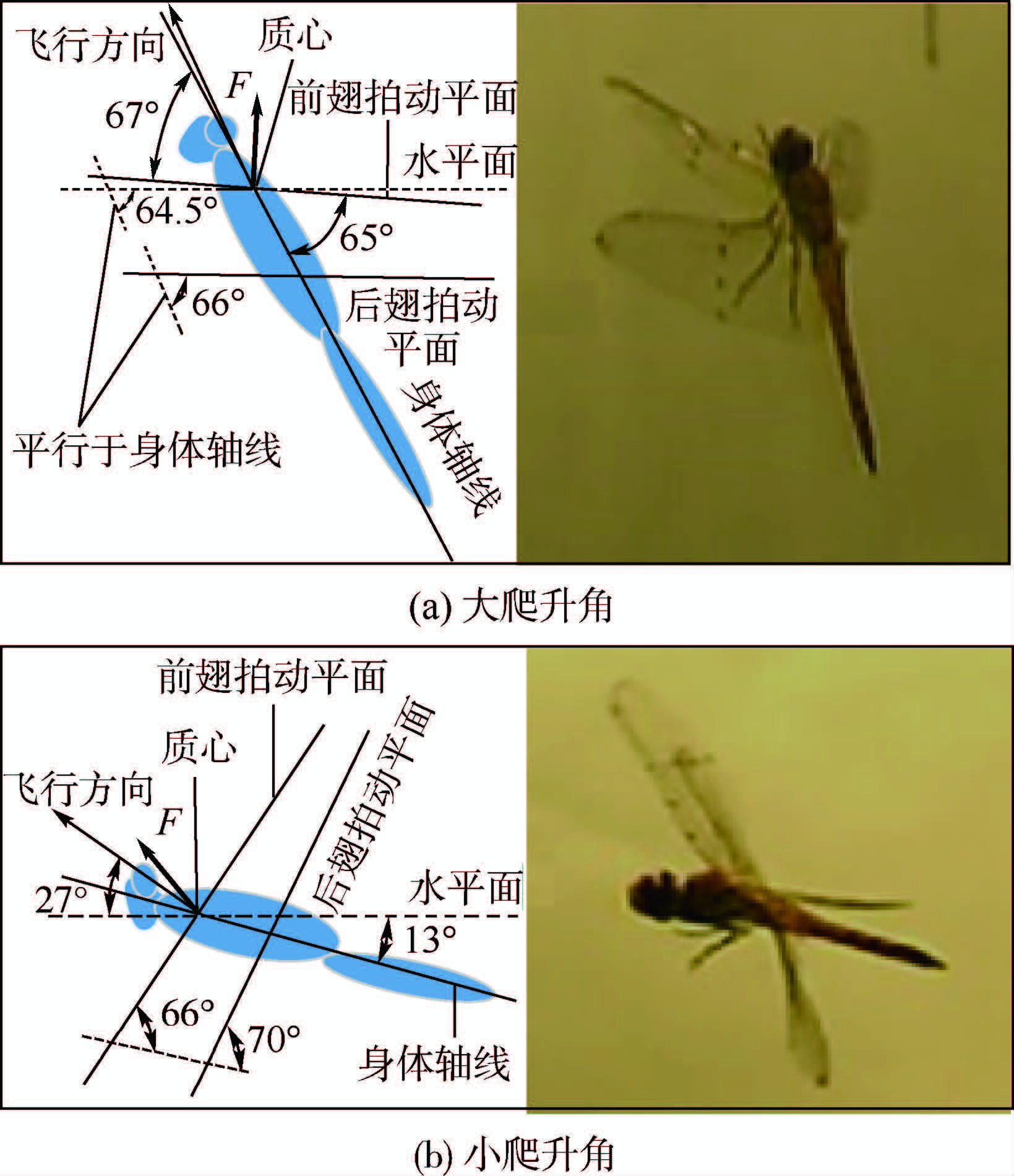 |
| 图 9 蜻蜓爬升状态飞行姿势示意图和实拍图 Fig. 9 Schematic diagrams and photographs of dragonfly’s flying posture during climbing |
| 图选项 |
3.4 翅膀偏离角 图 10(a)和图 10(b)给出了蜻蜓大、小爬升角爬升飞行时2对翅膀的偏离角变化规律。可以发现,不同爬升角爬升状态下蜻蜓前后翅的偏离角均在一个范围内周期性波动,波动周期近似为扑翼频率;对于大爬升角爬升(见图 10(a)),前翅波动的中心值大约为19°,而后翅在2°波动;对于小爬升角爬升(见图 10(b)),前翅波动的中心值约为6°,后翅约为1°。文献[15]通过数值计算得出昆虫飞行过程中翅膀的偏离角与身体俯仰角有直接的关系。由此对蜻蜓爬升过程进行分析发现,蜻蜓主要通过控制前翅的偏离角来控制身体俯仰角;大爬升角爬升过程,前翅大约前倾19°从而使身体可以保持约65°的身体俯仰角;小爬升角爬升时,由于身体俯仰角较小,前翅前倾角度也较小;而后翅偏离角与爬升角几乎无关,基本垂直身体拍动。
 |
| 图 10 蜻蜓爬行飞行时前后翅偏离角 Fig. 10 Deviation angles of fore-hind wings of dragonfly during climbing |
| 图选项 |
另外,对比大爬升角爬升时的翅膀偏离角(见图 10(a))和身体俯仰角(见图 8(a))变化趋势可发现,两者呈一致的上升趋势,此结果也可说明蜻蜓翅膀偏离角与身体俯仰角有正相关关系。
4 结 论 本文采用2台高速摄像机对自由飞行的蜻蜓进行了活体拍摄实验,并选取2种不同爬升角爬升飞行的运动序列对蜻蜓的身体和翅膀运动参数进行分析,研究结论如下:
1) 相比小爬升角爬升飞行,大爬升角爬升时,蜻蜓在较高的扑翼频率、较小的前后翅相位差以及较大的拍动幅度下可获得更大的爬升率。
2) 蜻蜓爬升飞行时,较大的身体俯仰角有助于翅膀获得更大的上升力。因而身体俯仰角与爬升角平均值趋势一致,但由于拍动引起的推力和升力的周期变化,爬升角也呈周期变化。
3) 蜻蜓主要通过控制前翅偏离角来控制身体俯仰角,且有正相关的关系。因此在大爬升角爬升时,也具有较大的前翅偏离角。
参考文献
| [1] | SUN M. Insect flight dynamics:Stability and control[J]. Reviews of Modern Physics,2014, 86(2): 615–646. |
| Click to display the text | |
| [2] | WAKELING J M, ELLINGTON C P. Dragonfly flight.Ⅱ.Velocities, accelerations and kinematics of flapping flight[J]. Journal of Experimental Biology,1997, 200(3): 557–582. |
| Click to display the text | |
| [3] | WAKELING J M, ELLINGTON C P. Dragonfly flight.I.Gliding flight and steady-state aerodynamic forces[J]. Journal of Experimental Biology,1997, 200(3): 543–556. |
| Click to display the text | |
| [4] | WAKELING J M, ELLINGTON C P. Dragonfly flight.Ⅲ.Lift and power requirements[J]. Journal of Experimental Biology,1997, 200(3): 583–600. |
| Click to display the text | |
| [5] | WANG H, ZENG L J, LIU H, et al. Measuring wing kinematics,flight trajectory and body attitude during forward flight and turning maneuvers in dragonflies[J]. Journal of Experimental Biology,2003, 206(4): 745–757. |
| Click to display the text | |
| [6] | CHENG P, HU J, ZHANG G, et al. Deformation measurements of dragonfly's wings in free flight by using windowed Fourier transform[J]. Optics and Lasers in Engineering,2008, 46(2): 157–161. |
| Click to display the text | |
| [7] | DONG H,KOEHLER C,LIANG Z,et al.An integrated analysis of a dragonfly in free flight:AIAA-2010-4390[R].Reston:AIAA,2010. |
| Click to display the text | |
| [8] | 魏榛.扑翼非定常气动力实验研究及相关应用探索[D].合肥:中国科学技术大学,2010:4. WEI Z.Experimental study of unsteady aerodynamics for flapping flight and exploration on their related application[D].Hefei:University of Science and Technology of China,2010:4(in Chinese).(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [9] | 邹凤娇.摄像机标定及相关技术研究[D].成都:四川大学,2005:38-42. ZOU F J.Research on camera calibration and related technique[D].Chengdu:Sichuan University,2005:38-42(in Chinese).(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [10] | 龚昊, 吕乃光, 娄小平, 等. 二维视觉测量中光轴与载物台垂直度调节方法[J]. 北京机械工业学院学报,2006, 21(3): 35–38.GONG H, LV N G, LOU X P, et al. A method of verticality adjusting between optical axis and carrier in two-dimensional vision measurement[J]. Journal of Beijing Institute of Machinery,2006, 21(3): 35–38.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [11] | ELLINGTON C P. The aerodynamics of hovering insect flight.Ⅲ[J]. Philosophical Transactions of the Royal Society of London B:Biological Sciences,1984, 305(1122): 41–78. |
| Click to display the text | |
| [12] | CHEN M W, ZHANG Y L, SUN M. Wing and body motion and aerodynamic and leg forces during take-off in droneflies[J]. Journal of the Royal Society Interface,2013, 10(89): 20130808. |
| Click to display the text | |
| [13] | WANG J K, SUN M. A computational study of the aerodynamics and forewing-hindwing interaction of a model dragonfly in forward flight[J]. Journal of Experimental Biology,2005, 208(19): 3785–3804. |
| Click to display the text | |
| [14] | SANE S P. The aerodynamics of insect flight[J]. Journal of Experimental Biology,2003, 206(23): 4191–4208. |
| Click to display the text | |
| [15] | MINAMI K, SUZUKI K, INAMURO T. Free flight simulations of a dragonfly-like flapping wing-body model using the immersed boundary-lattice Boltzmann method[J]. Fluid Dynamics Research,2015, 47(1): 015505. |
| Click to display the text | |
