20世纪90年代初,关于立体视觉的研究开始趋于成熟。1992年,卡内基梅隆大学Tomasi和Kanade[1]在假定相机为正交投影模型的条件下,利用仿射分解的方法构建了第一个基于图像的三维重构系统。Shum等[2]、Cipolla等[3]通过人为确定几何约束的方法分别提出了2种人工交互的三维重建系统。Pritchett和Zisserman[4]、Faugeras等[5]分别利用分层重建的思想,完成了视觉导航系统和对建筑物的三维重建。
21世纪以来,运动法(Structure From Motion,SFM)成为了基于序列图像三维重建的主流方法。基于SFM方法,Nistér[6, 7, 8]开发了基于未标定视频序列的自动稠密重构系统;Pollefeys等[9, 10, 11]开发并完善了基于连续拍摄的图像序列的三维场景自动建模系统;Snavely等[12, 13]开发了Photo Tourism和Photosynth 2个三维重建系统。在SFM方法中,集束调整(Bundle Adjustment,BA)技术[14]是一个重要的优化方法,而针对集束调整方法运算量大、不适于大规模重建的问题,又有研究者分别提出了稀疏集束调整(Sparse Bundle Adjustment,SBA)[15]等改进方法。在稠密重建方法中,Furukawa和Ponce[16]提出的基于面片的多视几何重建(Path-based Multi-View Stereo,PMVS)算法利用立体匹配技术在目标的表面生成一层稠密的面片,能够很好地表达目标的三维结构及细节。
针对空间目标三维重建的研究少有公开报道,尚处于起步阶段。国内方面,傅丹[17]针对空间目标中存在的大量直线元素开展了基于直线特征的空间目标三维重建研究;唐永鹤[18]考虑到卫星发射过程对相机参数的影响,重点开展了在线标定技术的研究,仅重建生成了稀疏点云;曾蔚等[19]则提出了利用红外图像获取空间目标三维信息的红外-自阴影重建(Infrared-Shape From Shading,IR-SFS)算法。本文则重点研究基于SFM方法重建空间目标的稠密点云,以获得更精细的目标三维数据。
空间目标存在结构对称、纹理重复的特点,使得拍摄角度间隔较大(如接近180°)的2帧图像容易出现较多错匹配点,从而导致重建错误。针对此问题,本文对SFM方法提出改进措施,将序列目标图像的成像时间顺序作为迭代时的先验信息,顺序地加入新图像,直到添加完所有图像,再通过集束调整进行优化;同时针对空间目标成像数据匮乏,进行了空间目标可见光图像的仿真,并开展了地面模拟成像实验,为空间目标三维重建研究提供数据支撑;在空间目标图像仿真数据上进行了实验测试,探讨空间目标三维重建的边界条件,测试方法对噪声的鲁棒性。
1 本文方法图 1为本文空间目标三维重建方法的流程。首先通过特征点检测和匹配建立特征点匹配集合,然后利用SFM方法进行运动分析及稀疏点云重构,求出相机的运动信息后利用基于面片的目标稠密重建方法进行稠密重建,最后获得目标的稠密点云模型。
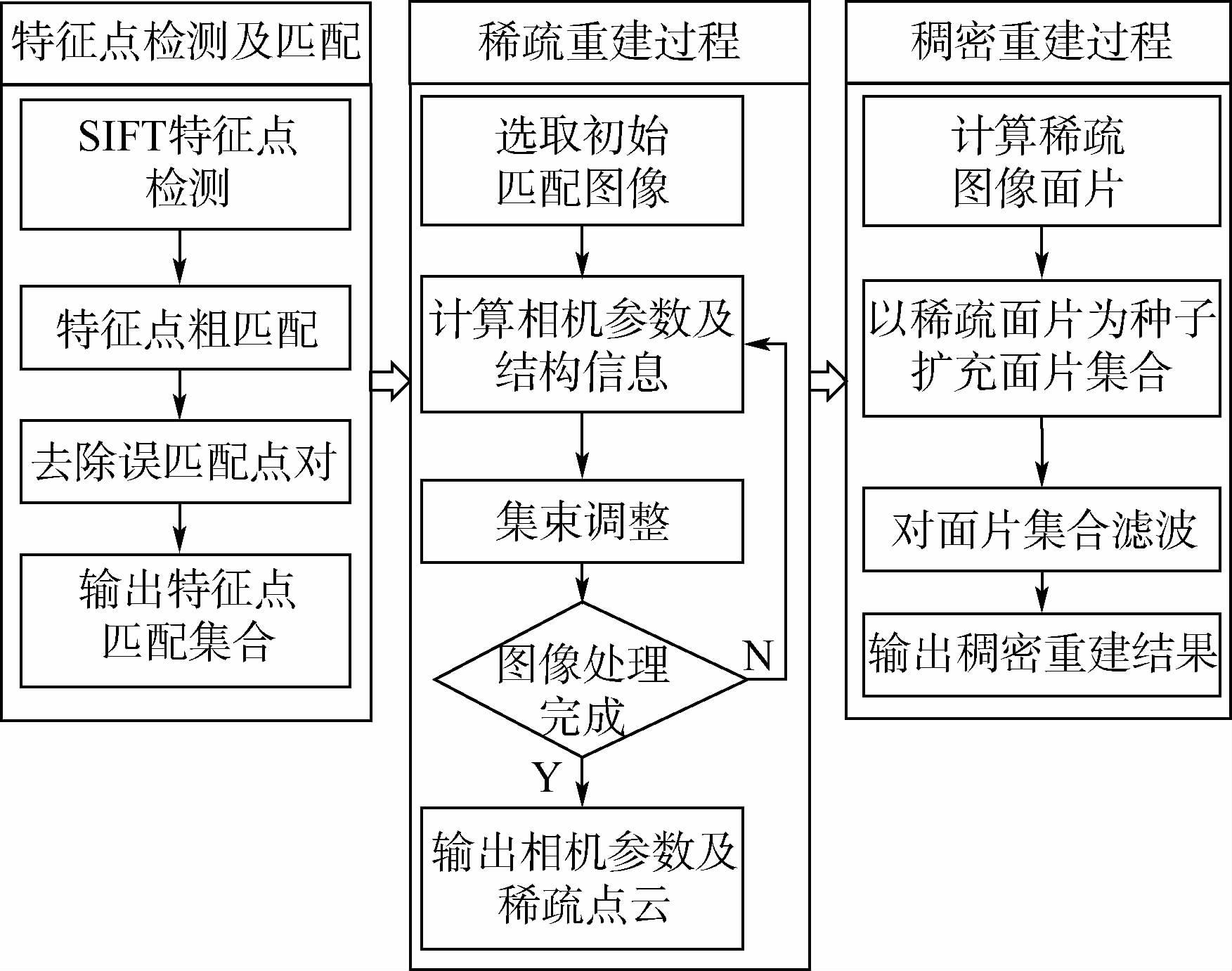 |
| 图 1 三维重建方法流程 Fig. 1 Flowchart of 3D reconstruction method |
| 图选项 |
1.1 特征点检测与匹配图像匹配是基于图像序列进行三维重建的第1步,本文利用Lowe[20]提出的尺度不变特征变换(Scale Invariant Feature Transform,SIFT)特征进行图像特征点的检测和匹配。该特征具有局部性、特殊性、多量性和高效性等优点,且具有对图像缩放、旋转甚至仿射变化的不变性。
匹配过程中,先基于图像中各特征点的128维SIFT特征描述之间的欧氏距离进行粗匹配;之后又利用图像间的极线约束,通过随机采样一致(Random Sample Consensus,RANSAC)算法[21]排除误匹配点,从而得到最终匹配结果。
1.2 稀疏重建方法1.2.1 SFM方法SFM方法是一个迭代计算的过程。参考文献[22]的方法,首先,选取匹配点多和内点率高的图像作为初始图像对I1、I2,计算得到初始的相机运动信息及目标结构信息;然后,通过I1、I2之间的匹配点对的三角化过程得到目标的初始三维点云Mj;最后,通过最小化三维点云的反投影误差(即式(1)),优化目标的三维结构及相机投影矩阵。
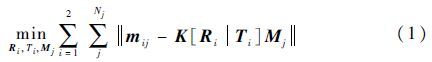
式中:m1j、m2j为三维点集Mj对应在2帧图像I1、I2中的匹配点对;Nj为Mj中点云数目;K[RiTi]为相机参数矩阵;Ri为第i幅图的旋转矩阵;Ti为第i幅图像对应的平移矩阵。
得到初始的相机运动信息及目标的三维结构后,再逐个加入剩余的图像进行SFM迭代。
1.2.2 集束调整优化方法SFM方法中每加入一帧图像就可以获得该图像所对应的相机的参数及新的目标结构信息,然后可利用集束调整的方法来进行参数优化。集束调整优化方法实际上是通过调整所有的光束与相机的位置,从而使得总误差最小。对于N幅图像和M个特征点,集束调整的目标函数为
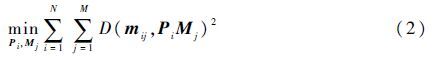
式中:Pi为第i帧图像的投影矩阵;D为欧氏距离。
1.2.3 SFM方法改进 利用文献[22]中的SFM策略对第2.1节中卫星仿真图像序列进行稀疏重建时,出现图 2所示的错误结果。原本均匀分布于一个圆周上的成像视点被错误地恢复成了2个半圆周,而重建出的稀疏点云则出现了类似于镜像对称的现象。
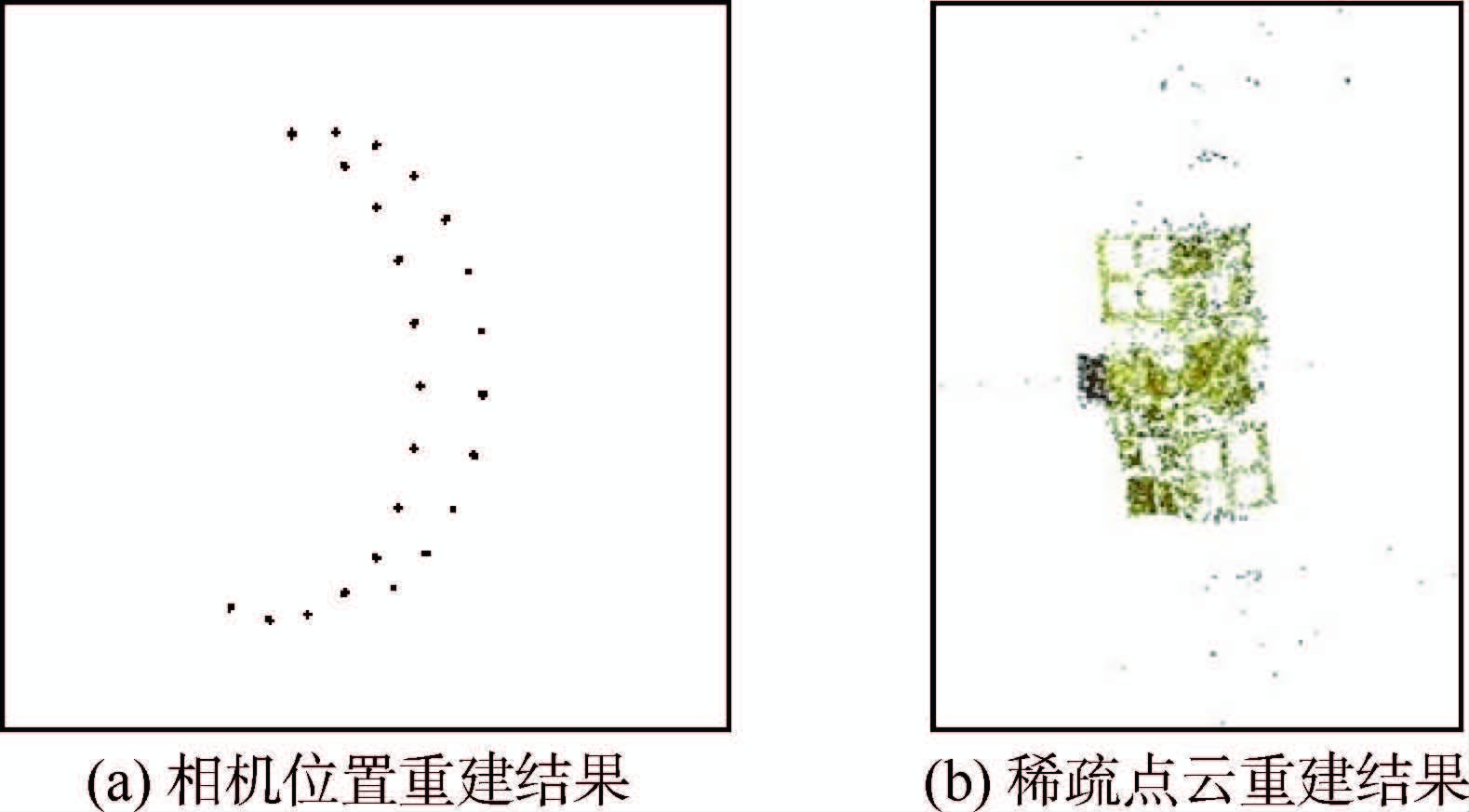 |
| 图 2 文献[22]中SFM方法的重建结果 Fig. 2 Reconstruction results by SFM method from Ref.[22] |
| 图选项 |
造成以上错误的原因在于该SFM方法中添加新图像的策略仅考虑了图像间的特征点匹配的多少,而未考虑相机之间的相对位置关系。由于Helios 2A目标结构对称、纹理重复,因此角度间隔较大的2帧图像也可能出现较多匹配点对。图 3为成像角度间隔为180°的2帧图像之间的匹配信息。从图 3中可以看出,这2帧图像之间存在着较多的匹配点,而在进行SFM过程中,这些匹配点对是不应该被考虑的。
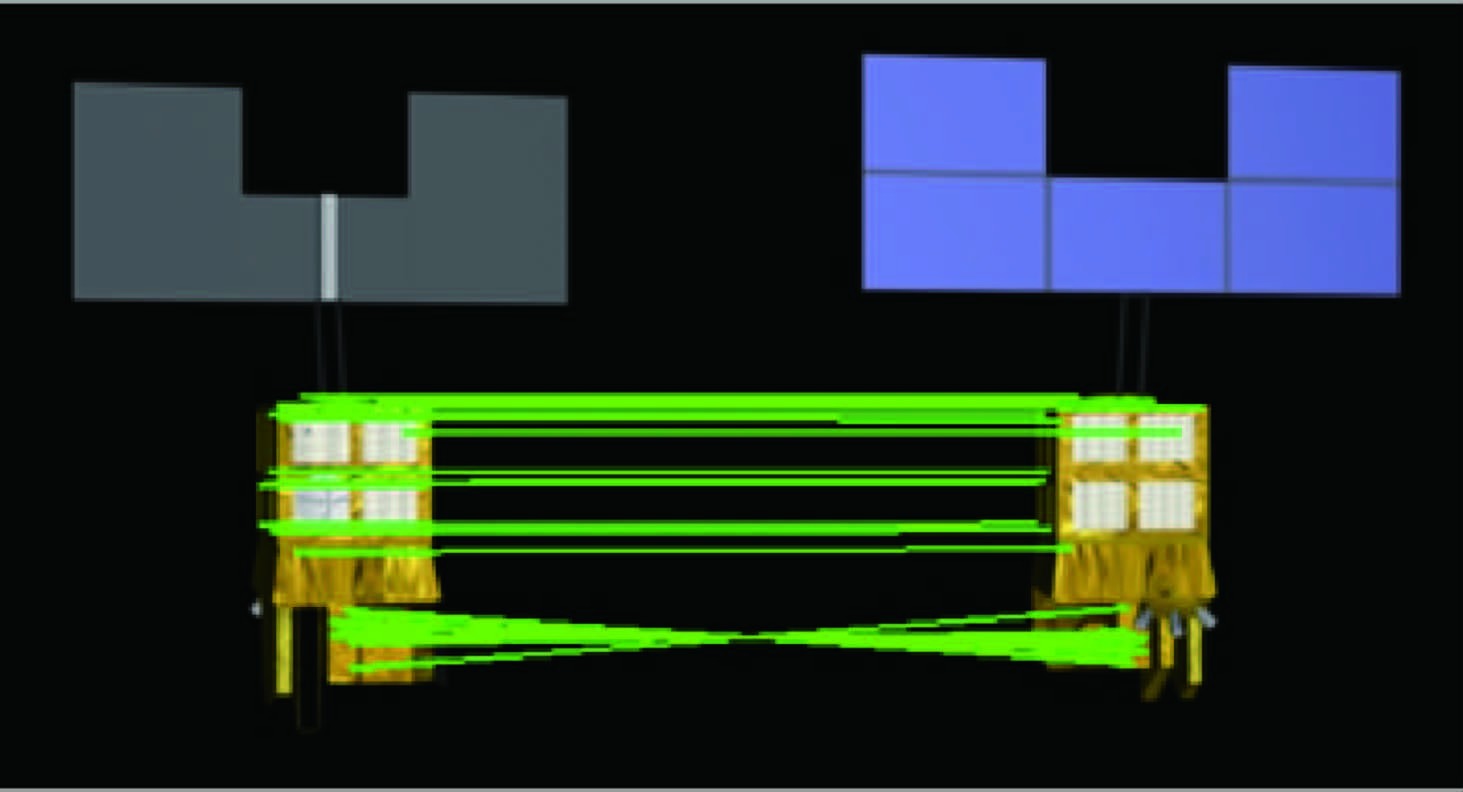 |
| 图 3 成像角度间隔相差180°的2帧图像匹配结果 Fig. 3 Match results of two frames imaged with angle difference of 180° |
| 图选项 |
对此,本文通过将目标成像的先后顺序作为先验信息对SFM方法进行改进。设有空间目标图像序列Ii(i=1,2,…,N),以及该序列图像对应的成像时刻ti(i=1,2,…,N)。首先选取t1、t22个时刻对应的2帧图像作为初始图像帧I1、I2,计算初始的相机运动信息及目标结构信息,进行集束调整;然后顺序添加下一时刻t3对应的图像I3,计算新图像对应的相机参数及新的目标结构,进行集束调整;最后按照成像时间顺序迭代添加新图像,直到添加完所有图像。
图 4为改进后的SFM方法对Helios 2A仿真图像序列进行重建获得的相机位置及稀疏点云。从图 4中可以看出,改进后的SFM方法解决了纹理重复问题,获得了正确的重建结果。
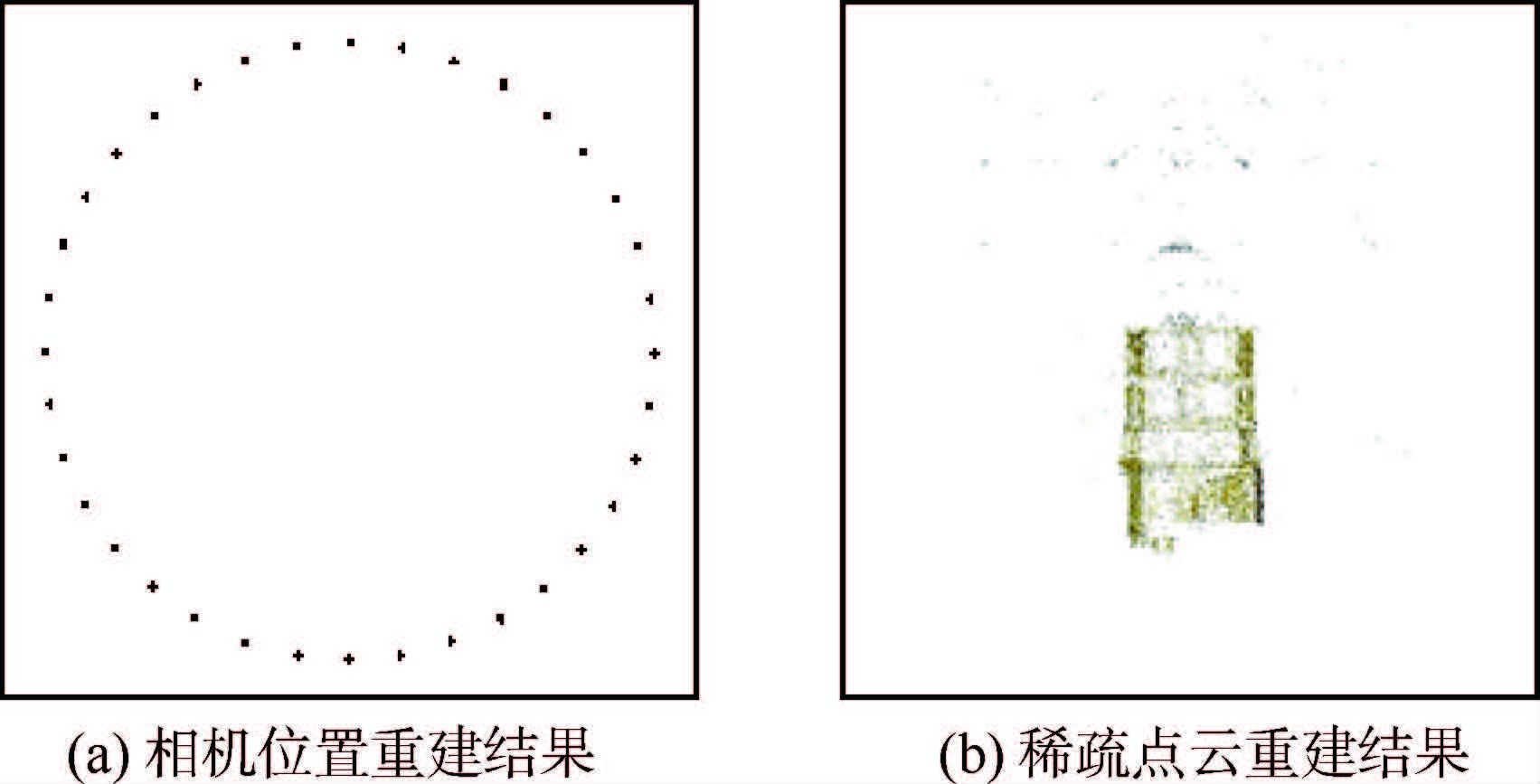 |
| 图 4 改进SFM方法重建结果 Fig. 4 Reconstruction results by improved SFM method |
| 图选项 |
1.3 基于面片的目标稠密重建方法PMVS算法[16]针对已标定的多视图图像,无需深度和包围盒等初始化信息,只需要估计点的深度,然后通过局部光学连续性估计点的法向。空间目标图像序列背景简单,仅包含单个目标,通过PMVS算法能取得较好的三维重建效果。
PMVS算法实质是扩散与滤波的过程。该算法将稀疏重建获得的相机参数信息及稀疏点云作为输入,将初始特征点匹配得到的种子面片投影到对应的图像平面中,在投影的邻域内进行面片扩散,得到新的面片,然后对获取的面片进行优化,并进行滤波以去除错误的面片。迭代地进行扩散与滤波的过程,从而得到最终的目标面片模型。
2 实验与分析成像角度间隔和噪声等是影响空间目标三维重建效果的主要因素。本文通过实验研究,探讨了空间目标三维重建的边界条件,测试了方法对噪声的鲁棒性,并在此基础上获得了空间目标成像时的相机参数、空间目标稀疏点云以及稠密点云。
2.1 实验数据参考文献[23]中的仿真方法,选取BUAA-SID1.0库中的Helios 2A卫星模型进行成像仿真。设置成像相机焦距为24 mm,像元尺寸为10 μm,面阵大小为1 024×1 024。将相机设置在距离目标200 m的圆上,从纬度为零的视点开始,设置等间隔的视点组,得到绕卫星一周的可见光图像序列。图 5给出了角度间隔为5°时Helios 2A卫星72个视点图像中的4帧,从左至右旋转角度依次为10°、30°、60°和150°。
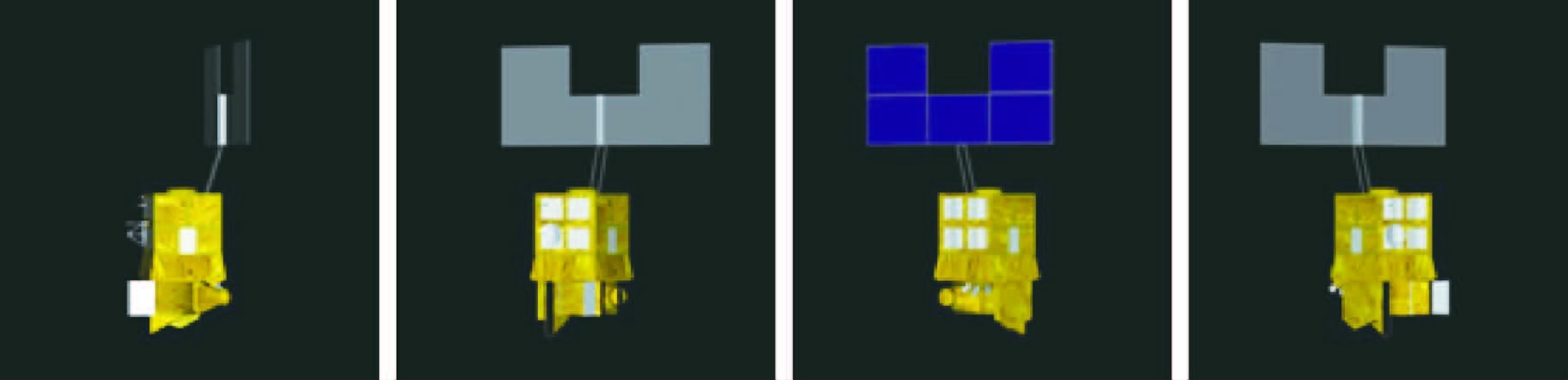 |
| 图 5 Helios 2A多视点图像 Fig. 5 Multi-view images of Helios 2A |
| 图选项 |
为了测试方法对噪声的鲁棒性,利用MATLAB中的imnoise (I,‘gaussian’,m,v)函数对仿真出的图像加高斯白噪声。其中均值m设为0,方差v取值范围为0.001~0.010,这里的方差与真实噪声方差var之间的关系为var=v×2552。
为了进一步测试三维重建方法的有效性,设计了地面模拟实验方法以获取空间目标可见光图像。采用支架搭建暗室并覆盖吸光布、遮光布以遮挡环境光线,防止反射灯光对目标造成干扰;用平行光源模拟太阳光照;用“神舟”飞船和“天宫一号”的缩比模型模拟空间目标;将目标置于一维转台上,转台以10°间隔旋转一周,在固定位置用相机对模型进行拍摄,以模拟获取空间目标图像的过程。另外,对拍摄图像进行预处理,去除背景噪声,分割出目标图像,以避免背景干扰。
图 6为地面实验获取的“神舟”飞船和“天宫一号”图像序列中的4帧,旋转角度依次为10°、40°、170°和260°。
 |
| 图 6 地面仿真实验获取的图像序列 Fig. 6 Image sequences from ground imaging simulation experiments |
| 图选项 |
2.2 结果与分析2.2.1 成像角度间隔由左至右以5°、10°、15°、20°和25°的成像角度间隔分别获得72帧、36帧、24帧、18帧和15帧图像序列。对这5组不同成像角度间隔的图像序列进行三维重建,获取的相机位置信息及相机旋转角误差分别如图 7和图 8所示。
 |
| 图 7 不同成像角度间隔下稀疏重建的相机位置信息Fig. 7 Camera position information obtained from sparse reconstruction of images imaged with different angle separation |
| 图选项 |
从图 7可以看出,在成像角度间隔为25°的情况下,稀疏重建仅得到了6个相机的位置信息,说明成像角度间隔为25°时已不能有效地对目标进行稀疏重建;从图 8中可以看出,随着成像角度间隔的增大,获取的相机旋转角的精度逐渐下降,但是仍然比较精确。
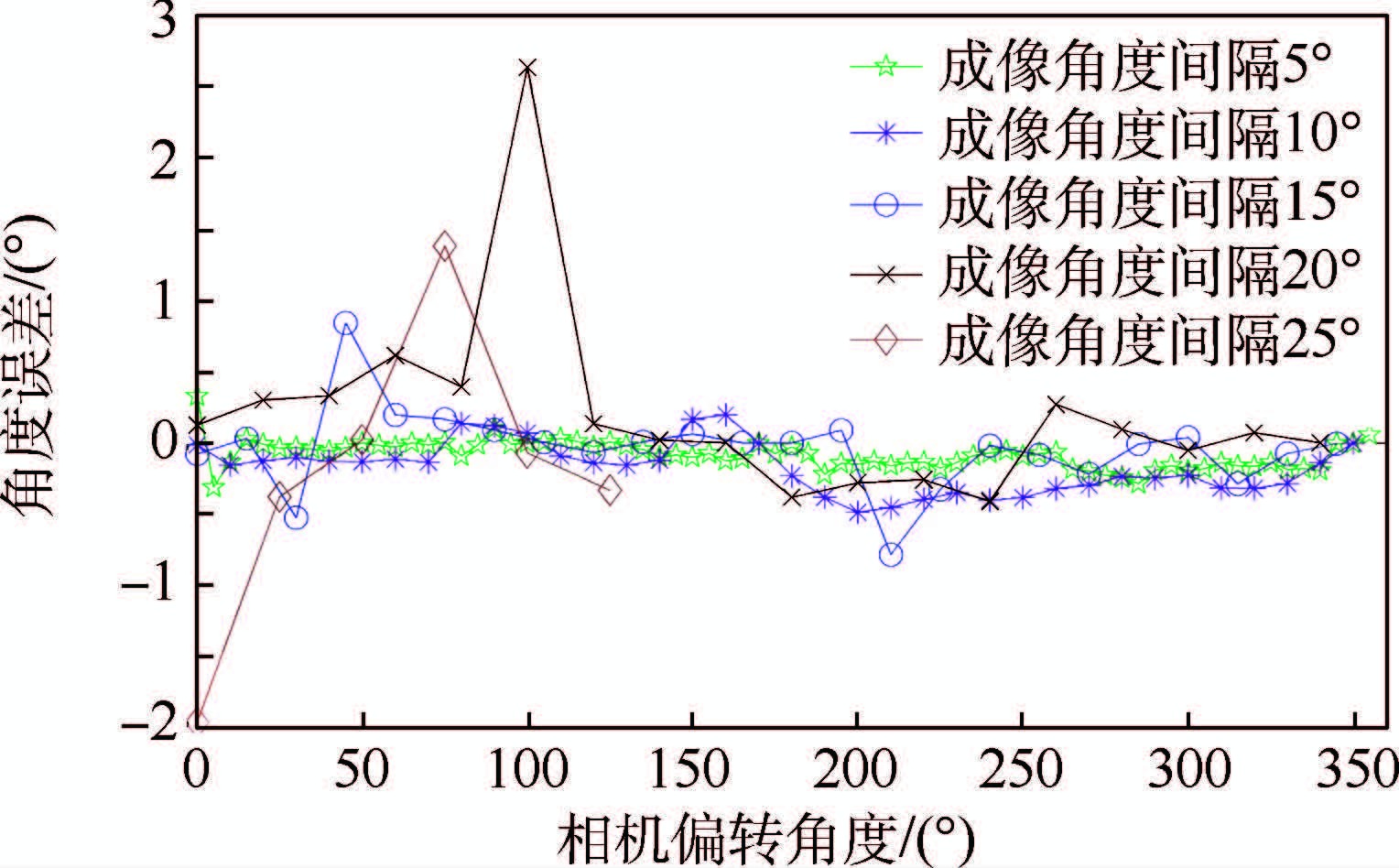 |
| 图 8 不同成像角度间隔下稀疏重建的相机旋转角误差 Fig. 8 Errors of camera rotation angle obtained from sparse reconstruction of images imaged with different angle separation |
| 图选项 |
图 9、图 10则分别给出了不同成像角度间隔(由左至右分别为5°、10°、15°、20°和25°)下三维重建方法获得的目标稀疏点云及稠密点云。从视觉效果上看,随着成像角度间隔的增加,三维重建方法获取的目标点云数目逐渐降低,但是在成像角度间隔小于20°时目标的整体结构均较为清晰,而在成像角度间隔为25°时,目标的稀疏点云结构缺失,而稠密重建方法仅恢复出目标的一个表面。
 |
| 图 9 不同成像角度间隔下重建的目标稀疏点云 Fig. 9 Sparse point cloud reconstructed from images imaged with different angle separation |
| 图选项 |
 |
| 图 10 不同成像角度间隔下重建的目标稠密点云 Fig. 10 Dense point cloud reconstructed from images imaged with different angle separation |
| 图选项 |
表 1给出了对目标稀疏点云及稠密点云的定量描述。在成像角度间隔为25°时,目标的稀疏点云个数及稠密点云个数急剧减少,已不能正确地表达目标的三维结构。
表 1 不同成像角度间隔下重建的稀疏点云及 稠密点云个数 Table 1 Number of sparse point clouds and dense point clouds reconstructed from images imaged with different angle separation
| 成像角度间隔/(°) | 5 | 10 | 15 | 20 | 25 |
| 稀疏点云个数 | 12 007 | 7 226 | 4 611 | 3 861 | 538 |
| 稠密点云个数 | 26 899 | 23 199 | 16 788 | 17 155 | 3 673 |
表选项
综上分析,可以得到如下结论:在对空间目标进行三维重建时,成像角度间隔对最后的重建结果影响较大,当成像角度间隔大于20°时,三维重建方法不能有效地恢复目标的三维结构,因此对目标进行绕飞成像时,成像角度间隔应小于20°。
2.2.2 鲁棒性选取成像角度间隔为10°的图像序列,分别添加方差为0.002、0.004、0.006、0.008和0.010的高斯白噪声生成噪声图像序列。同时由于太阳能帆板表面纹理匮乏,特征点检测算法将噪声检测为纹理从而影响了特征点匹配的正确性,因此考虑将所有噪声图像序列中的帆板去除,只对目标的本体部分进行三维重建。
图 11、图 12分别给出了进行稀疏重建得到的相机旋转角信息和角度误差的平均值随噪声的变化情况。可以看出,对于添加噪声的图像,相机旋转角误差值相对于无噪声图像明显增加,最大角度误差在6°左右;当噪声方差达到0.006时,恢复出的某些视点的旋转角误差明显增大,但角度误差平均值随噪声的变化较为平稳,说明方法在去除太阳能帆板后的图像序列上对噪声具有一定的鲁棒性。
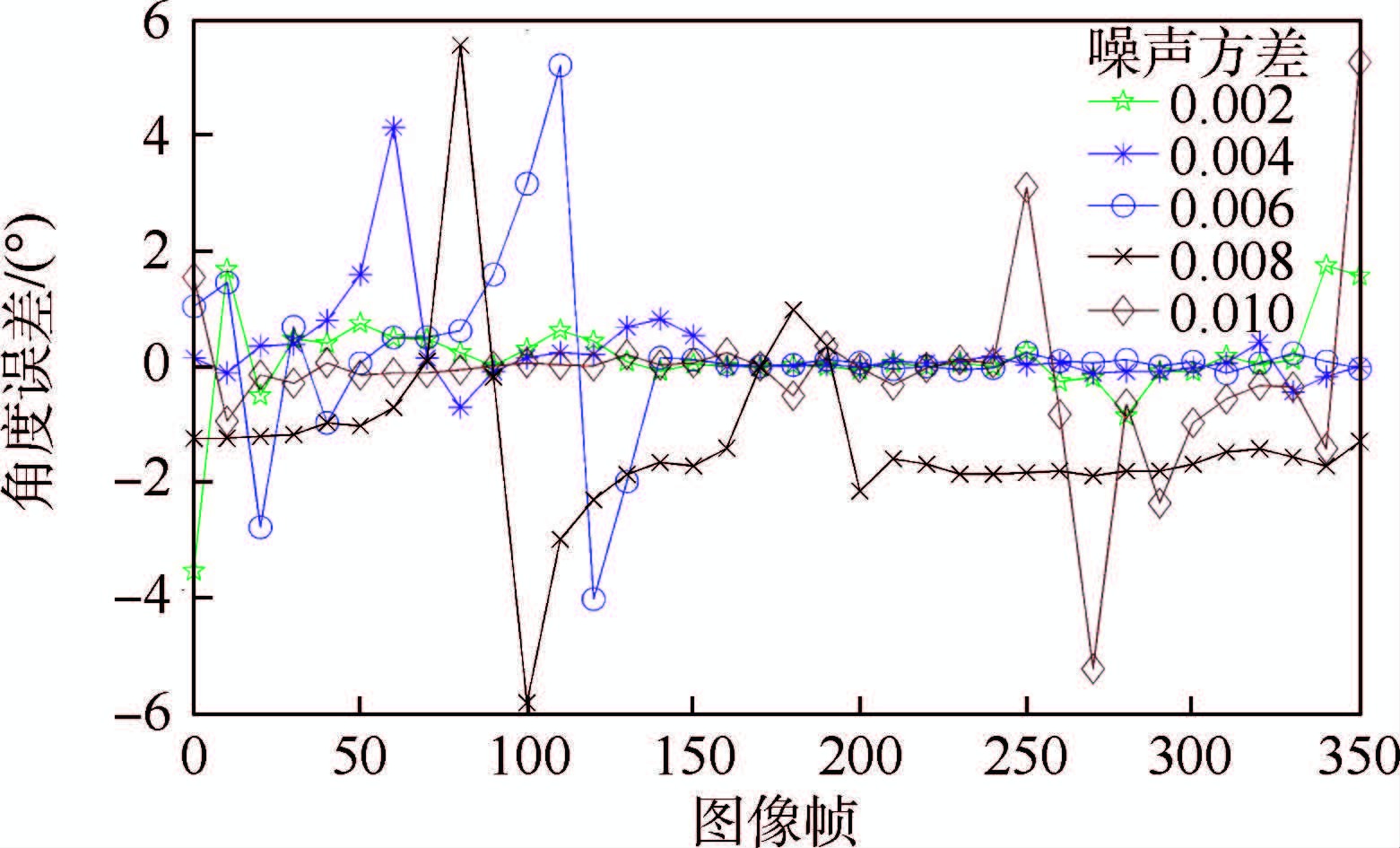 |
| 图 11 不同噪声水平下的角度误差Fig. 11 Angle errors under different noise levels |
| 图选项 |
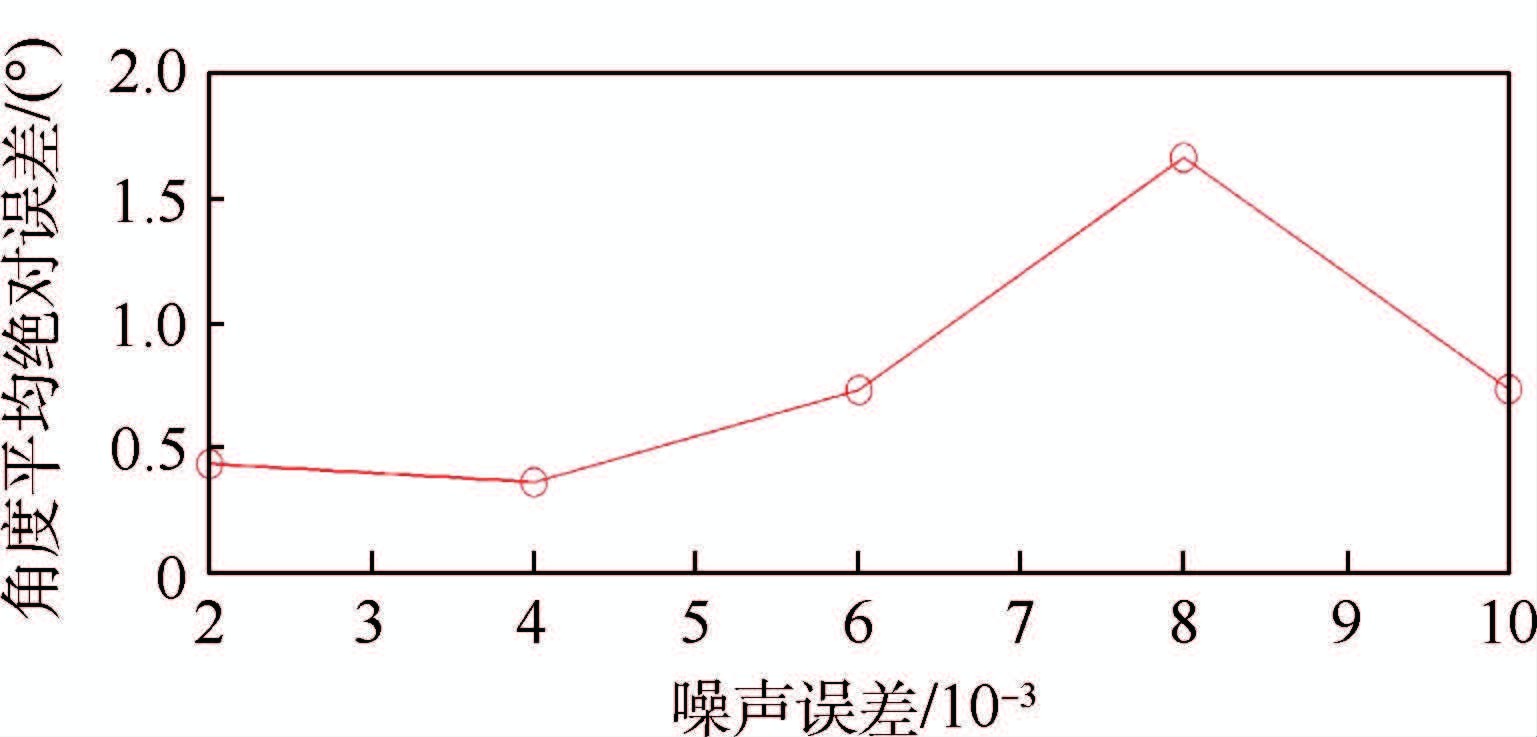 |
| 图 12 不同噪声水平下的角度平均绝对误差 Fig. 12 Mean absolute errors on angle under different noise levels |
| 图选项 |
2.2.3 地面实验图像上的测试结果图 13为对“神舟”飞船和“天宫一号”仿真图像序列进行稠密重建的结果。从图 13中可以看出,获取的神舟模型结构完整,细节清晰,而天宫模型则效果较差,这是由于天宫模型表面纹理不丰富,并且在成像时光照反射强烈,出现了过饱和的现象。
 |
| 图 13 “神舟”飞船和“天宫一号”的稠密重建结果 Fig. 13 Dense reconstruction results of spacecraft Shenzhou and Tiangong-1 |
| 图选项 |
在地面拍摄的图像序列上进行的实验表明:三维重建方法能够有效地获取相机参数信息及目标的结构信息,同时光照条件及目标表面纹理的丰富程度对三维重建方法的影响较大。
3 结 论1) 在成像距离较近、图像分辨率较高的情况下,成像角度间隔是影响空间目标三维重建结果的主要因素。
2) 对仿真图像序列的实验表明,在成像角度间隔20°以下时,三维重建方法能够较好地恢复目标三维结构。
3) 噪声实验结果表明,三维重建方法对噪声有一定的鲁棒性。
4) 在地面实验图像序列上的实验表明,三维重建方法得到的相机参数信息准确,目标的三维模型结构完整、细节清晰。
总的来说,本文针对空间目标图像序列的三维重建问题,结合实验分析,给出了实现空间目标三维重建的边界条件,估计了目标成像时的相机位置信息、目标的稀疏点云及稠密点云,能够为空间目标的识别、测量等任务提供数据支撑,同时对天基监视系统的设计也具有一定的参考意义。
参考文献
| [1] | TOMASI C,KANADE T.Shape and motion from image streams under orthography:A factorization method[J].International Journal of Computer Vision,1992,9(2):137-154. |
| Click to display the text | |
| [2] | SHUM H Y,HAN M,SZELISKI R.Interactive construction of 3D models from panoramic mosaics[C]//CVPR '98 Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Los Alamitos:IEEE Computer Society,1998:427-433. |
| Click to display the text | |
| [3] | CIPOLLA R,ROBERTSON D,BOYER E.Photobuilder-3D models of architectural scenes from uncalibrated images[C]//IEEE International Conference on Multimedia Computing and Systems.Los Alamitos:IEEE Computer Society,1999,1:25-31. |
| Click to display the text | |
| [4] | PRITCHETT P,ZISSERMAN A.Matching and reconstruction from widely separated views[C]//Proceeding of the European Workshop on 3D Structure from Multiple Images of Large-Scale Environments.Berlin:Springer,1998:92. |
| Click to display the text | |
| [5] | FAUGERAS O,ROBERT L,LAVEAU S,et al.3-D reconstruction of urban scenes from image sequences[J].Computer & Image Understanding,1997,69(3):292-309. |
| Click to display the text | |
| [6] | NISTÉR D.Reconstruction from uncalibrated sequences with a hierarchy of trifocal tensors[C]//European Conference on Computer Vision 2000.Berlin:Springer,2000,1842:649-663. |
| Click to display the text | |
| [7] | NISTÉR D.Calibration with robust use of cheirality by quasi-affine reconstruction of the set of camera projection centres[C]//8th IEEE International Conference on Computer Vision(ICCV 2001).Los Alamitos:IEEE Computer Society,2001:116-123. |
| Click to display the text | |
| [8] | NISTÉR D.Frame decimation for structure and motion[C]//2nd European Workshop on 3D Structure from Multiple Images of Large-Scale Environments.Berlin:Springer,2000:17-34. |
| Click to display the text | |
| [9] | POLLEFEYS M,KOCH R,VERGAUWEN M,et al.Automated reconstruction of 3D scenes from sequences of images[J].ISPRS Journal of Photogrammetry and Remote Sensing,2000,55(4):251-267. |
| Click to display the text | |
| [10] | POLLEFEYS M,GOOL L V,VERGAUWEN M,et al.Visual modeling with a hand-held camera[J].International Journal of Computer Vision,2004,59(3):207-232. |
| Click to display the text | |
| [11] | POLLEFEYS M,NISTÉR D,FRAHM J M,et al.Detailed real-time urban 3D reconstruction from video[J].International Journal of Computer Vision,2008,78(2-3):143-167. |
| Click to display the text | |
| [12] | SNAVELY N,SEITZ S M,SZELISKI R.Photo tourism:Exploring photo collections in 3D[J].ACM Transactions on Graphics,2006,25(3):835-846. |
| Click to display the text | |
| [13] | SNAVELY N,SEITZ S M,SZELISKI R.Modeling the world from internet photo collections[J].International Journal of Computer Vision,2008,80(2):189-210. |
| Click to display the text | |
| [14] | TRIGGS B,MCLAUCHLAN P F,HARTLEY R I,et al.Bundle adjustment:A modern synthesis[M]//TRIGGS B,ZISSERMAN A,SZELISKI R.Vision algorithms:Theory and practice.Berlin:Springer,2000:298-372. |
| [15] | LOURAKIS M I A,ARGYROS A A.SBA:A software package for generic sparse bundle adjustment[J].ACM Transactions on Mathematical Software(TOMS),2009,36(1):1-30. |
| Click to display the text | |
| [16] | FURUKAWA Y,PONCE J.Accurate,dense,and robust multiview stereopsis[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(8):1362-1376. |
| Click to display the text | |
| [17] | 傅丹.基于直线特征的空间目标三维结构重建和位姿测量方法研究[D].长沙:国防科学技术大学,2008:17-126. FU D.Researches on three-dimensional structure reconstruction and pose measurements based on line feature for space targets[D].Changsha:National University of Defense Technology,2008:17-126(in Chinese). |
| Cited By in Cnki (12) | |
| [18] | 唐永鹤.基于序列图像的空间非合作目标三维重建关键技术研究[D].长沙:国防科学技术大学,2012:13-36. TANG Y H.Researches on 3D reconstruction technologies for non-cooperative space targets using image sequences[D].Changsha:National University of Defense Technology,2012:13-36(in Chinese). |
| Cited By in Cnki (0) | |
| [19] | 曾蔚,王汇源,刘莹奇,等.基于IR-SFS算法空间目标红外影像3D重建[J].中国光学,2014,7(3):376-388. ZENG W,WANG H Y,LIU Y Q,et al.3D reconstruction of space target IR image based on IR-SFS algorithm[J].Chinese Optics,2014,7(3):376-388(in Chinese). |
| Cited By in Cnki (4) | |
| [20] | LOWE D G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision,2004,60(2):91-110. |
| Click to display the text | |
| [21] | FORSYTH D A,PONCE J.Computer vision:A modern approach[M].Upper Saddle River:Prentice-Hall,2003:294-299. |
| [22] | SNAVELY N.Bundler:Structure from motion(SfM) for unordered image collectionshttp[EB/OL].(2014-11-17)[2015-02-10].http://www.cs.cornell.edu/-snavely/bundler/. |
| Click to display the text | |
| [23] | ZHANG W,JIANG Z G,LUO J W,et al.Optical image simulation system for space surveillance[C]//International Conference on Image and Graphics.Piscataway,NJ:IEEE Press,2013:721-726. |
| Click to display the text |
