无论哪种算法,在进行图像处理时,都是将图像分为连续和离散(数字的)两种.当图像函数为连续时,通常采用偏微分方程进行处理;当图像离散时,多采用随机理论和小波分析进行处理.本文提出的一种算法[12]是对电荷耦合器件(CCD)传感器的物理描述,CCD传感器在采样点处数字化,形成像素栅格,这些像素在空间上是分立的,但像素之间的信息结构是相互联系的,文中利用像素在空间上分立、在信息结构上相联系的特性,建立了像素之间的时间演化方程.当空间结构信息是非线性时,可得到图像像素的非线性微分差分方程,分析证明该演化方程具有孤波解的形式,该孤波解在研究中被称作图像孤波.首先借助文献[12]建立时间演化方程,对方程进行分析求解,提出基于孤波的图像处理模型,并应用于图像滤波处理.
1 图像孤波模型的建立图 1和图 2分别建立了一维和二维图像像素栅格动力系统模型.
 |
| 图 1 一维图像像素栅格动力系统模型Fig. 1 One-dimensional image pixel grid power system model |
| 图选项 |
 |
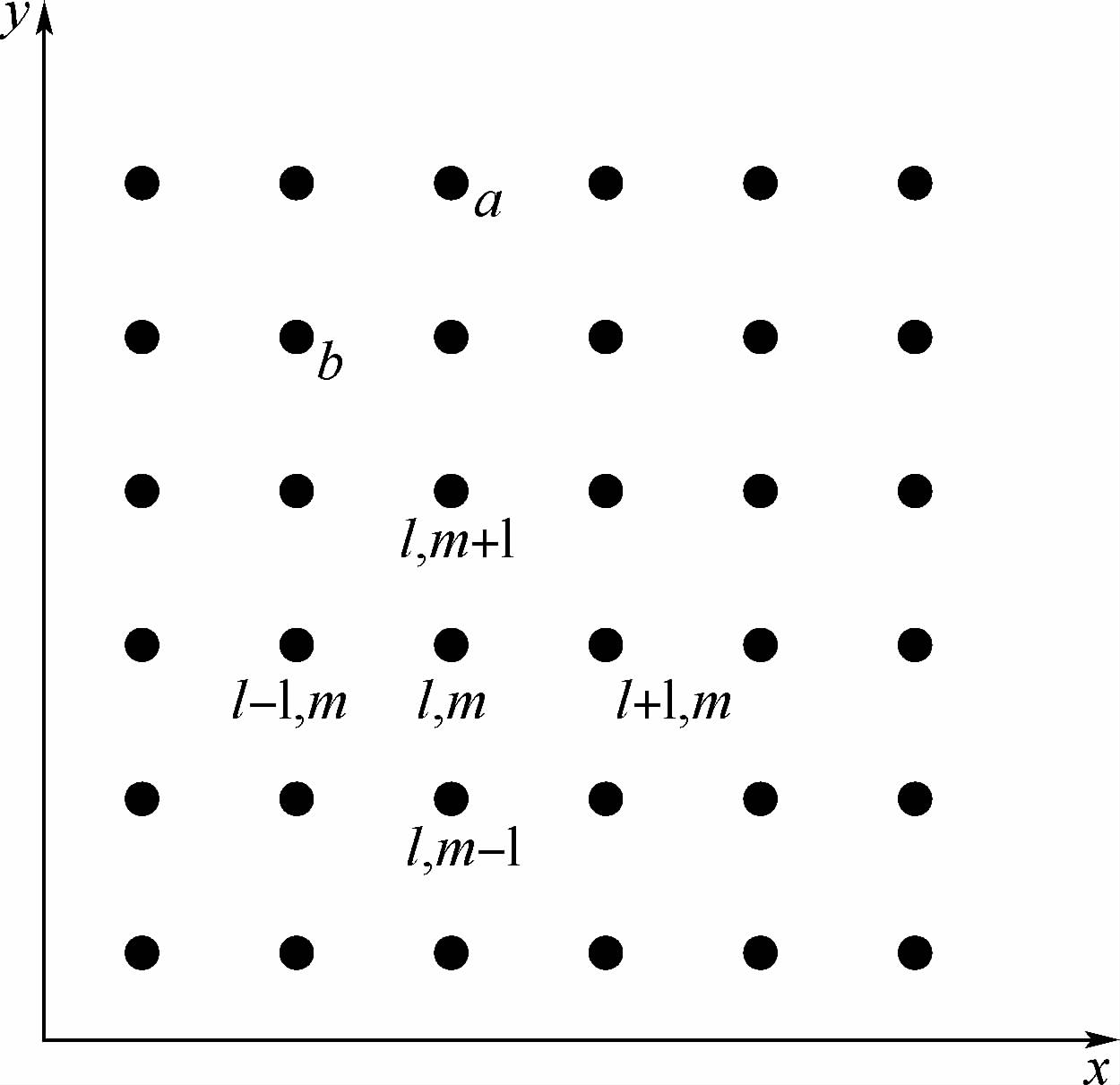| 图 2 二维图像像素栅格Fig. 2 Two-dimensional image pixel grid |
| 图选项 |
图 1表示的是一维非线性像素栅格动力学方程,设xn(t)表示第n个像素值为M的像元受到相邻像元影响所产生的效应,F(r)=a(1－e－br)为像素相互之间的影响效果[12],其中:r为连续变量,a为图像的性质参数,b为图像集群性质,集群近景则b值小,反之则b值大,而其他像素对它的影响可以忽略不计,则像素作用时间演化方程为[13, 14]
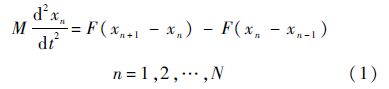
式中:n为单行像素栅格中像素点的分布,故为整数;N为行像素的最大值;xn为第n个像素的影响效应.r离散为变量rn,令相对作用效果为
结合式(1)则:
进一步化简:
结合公式F(r)=a(1－e－br)对式(3)进行化简:
进一步推导,式(3)可化为
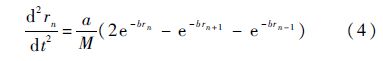
式(4)是标准的非线性微分差分方程,由于式(4)中n为整数,其表明像素作用的时间演化方程有孤波形式的解析解,即图像孤波解[15]:
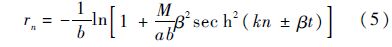
式中:
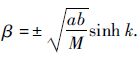
根据图 2的二维像素栅格方程,考察某像素点受四邻域像素的影响.利用Hamilton理论建立四次非线性相互作用下的二维像素影响方程,该方程的Hamilton为[16]
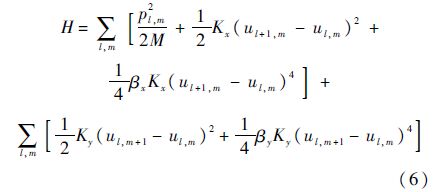
式中:M、pl,m和ul,m分别为像素的大小、第l列第m行像素的动量和作用效果;Kx和Ky分别为x轴方向和y轴方向的作用效果常数.结合文献[12]可知,式(6)等价于二维非线性薛定锷方程[17]:
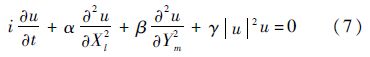
式中:u为像素间影响效果;Xl为x轴方向上的影响;Ym为y轴方向上的影响;γ和α为对应的影响系数.
式(7)也具有孤波解,并可简化方程组:
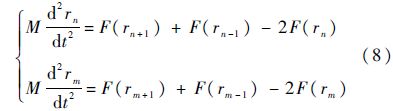
当m,n代表x轴和y轴时,方程组(8)表示孤波在笛卡儿坐标系中横向和纵向的传播.由式(1)可知,二维图像像素影响方程的解可以根据一维模型的解直接推出,这就是图像的二维模型.
2 孤波图像处理模型性能分析根据像素动力学方程,本节对模型性能进行分析并应用此动力学方程来对图像进行处理.像素栅格方程实际上是一个非线性微分-差分方程,若按照偏微分方程在图像处理中的方法,直接利用演化方程对图像进行处理,将会出现很多问题.考虑到方程是非线性且解不唯一的特性,文中详细分析了孤波性能并根据模型性能对图像进行处理.
分析孤波间的相互作用,可知像素栅格方程具有多孤波解.实际应用中主要考察2孤子解的相互作用,具体分析如下:
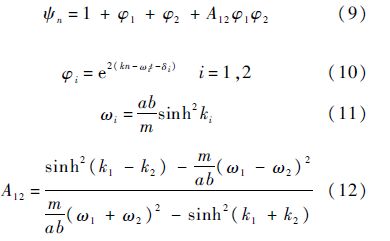
式(10)中φ1和φ2分别对应参数为k1和k2的孤立子解的像素孤波,ω1和ω2的正负性代表像素孤波之间不同的行进方向,文中主要分析像素孤波相对行进的情况,此时ω1和ω2异号.
相对作用的情况下,ω1=ab/msinh k1 和 ω2=－ab/msinh k2,则
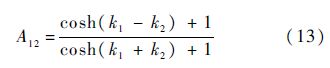
引入由fn所表示的波形.注意到fn=m/b·(ln(1+φ1))tt 与 fn=m/b(ln(1+φ2))tt分别表示参数k1与k2的像素孤波,下标tt表示对时间的二阶导数,且(ln φ1)tt=(ln φ2)tt=0,k1>k2>0,考虑φ1与φ2取值范围不同时fn所表示的波形,孤立波有如下4条性质:
1) φ2≈1,φ1≤1时,ψn=1+φ2,相应于k2波;当φ2≈1,φ1≥1时,ψn=φ1(1+A12φ2),fn=mb·(ln ψn)tt=mb(ln(1+φ~2))tt,其中φ~2=A12φ2·exp2k2n－ω2t－δ2+12ln A12这也相应于k2波,但相位有所移动,由δ2变到δ′2=δ2－12ln A12.
2) 同理,当φ1≈1,φ2≤1时,ψn=1+φ1,相应于k1波;当φ1≈1,φ2≥1时,这也相应于k1波,但相位有所移动,相应δ1改变为δ′1=δ1－12ln A12.
3) 当φ1≤1,φ2≤1时,ψn≈1,(ln ψn)tt≈0,即fn＜＜1;当φ1＞＞1,φ2＞＞1时,ψn≈A12φ1φ2,(ln ψn)tt=(ln φ1)tt+(ln φ2)tt≈0,即fn＜＜1;当φ1＞＞1,φ1φ2≈1时,ψn≈φ2,而φ2＜＜1,φ1φ2≈1时,ψn≈φ1,均有(ln ψn)tt≈0,即fn＜＜1;均表示没有像素孤波.
4) 当φ1≈1,φ2≈1时,两个像素孤波非线性叠加.
利用上面像素孤波的存在情况来分析在整个时间轴演化时波形的变化情况进行讨论:
1) 在k2n－ω2t－δ2=0附近,φ2≈1,而φ1=
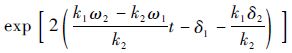,k1ω2－k2ω1=
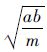(k1sinh k2－k2sinh k1)<0,故φ1→∞,由上述像素孤波存在性质可知在k2n－ω2t－δ2=0附近ψn→∞,fn近似于k2波,中心位置在δ2－12ln A12.2) 在k1n－ω1t－δ1=0附近,φ1≈1,而φ2=
,k2ω1－k1ω2=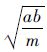(k2sinh k1－k1sinh k2)>0,故φ2→0,可知在k1n－ω1t－δ1=0附近,fn近似于k1波.3) 除去上述的其他地方,φ1、φ2很小或者是很大,fn≈0,即表示没有像素孤波.
当t很大时,φ1≈1与φ2≈1都不同时成立;所以当t→－∞或t→∞时,k1波与k2波都是彼此分离地独立运动着,没有相互作用.但当t在[－∞,∞]演化时,参数k1的波逐渐追赶上参数k2对应的波,当达到φ1≈1,φ2≈1的位置时,两个像素孤波便会发生相互作用,作用后参数k1波将超前于参数k2的波,两个像素孤波又相互分开各自独立运动.
两个像素孤波发生相互作用的具体位置n和时间t则由k1n－ω1t－δ1=k2n－ω2t－δ2=0来求解,结果为
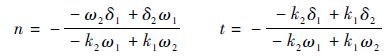
两个像素孤波发生相互影响后,像素孤波不会发生改变,只是波的中心位置分别由δ′2和δ1移到δ2和δ′1,即参数为k1像素孤波在原基础上向前平移12ln A1/2,像素参数为k2孤波则对应向后平移1/2ln A1/2.
说明模型存在两个像素孤波,且两个孤波可以相互影响,影响过后又可恢复到各自的原来状态,这样稳定的孤波具有原子性,对其他像素产生影响自身却并不发生改变,因此可以用孤波代替图像的像素.
相互作用后的两个孤波形状和速度都没有改变,只是像素孤波的相位发生了改变.因此从相位改变中提取图像的方位信息,建立一种映射将相位偏移转化为方位信息Ψ′=Ψ+ψ,其中Ψ为孤波的前进方向,ψ为相位的偏移方向,Ψ′为相位改变后的方向.同时,两个孤波产生碰撞时像素孤波的幅值是非线性叠加的,这个非线性叠加的幅值即像素之间相互影响的大小.
3 模型在图像滤波中应用由第2节的论述可知,像素栅格方程有很多孤波解,但众多的孤波解并不能直接用于方程演化,文中利用方程的解直接作用到像素上也就是用孤波代替像素.应用文中的模型对图像进行滤波处理,主要注意如下几点:
1) 孤波模型具有解析解,可以直接代替像素,孤波幅值的变化与参数k1和k2有关且与波的宽度成反比,不同的参数值可以得到不同尺度的孤波,处理中将归一化的像素值作为孤波初始值,本文利用像素归一化的灰度值作为初始化的参数,通过乘以相应的系数k来改变参数得到像素孤波.
2) 处理图像时只需考虑初始相位的孤波解.
3) 虽然像素栅格方程是随时间演化的,但图像处理时只考虑相对碰撞发生时刻.
4) 处理时给出像素孤波碰撞产生相互影响的方向信息.
5) 建立4邻域孤波模板,将1)~4)放在一个处理模板里.
6) 所建立的模板利用幅值的变化范围和方向判断某像素点是否是噪声.若不能判定则改变孤波的参数值,得到不同尺度的孤波重新进行判断,重复操作直到得到不同尺度下的图像的细节.
结合MATLAB,利用上述方法对椒盐噪声进行图像处理的仿真,给出了以k为参数的图像滤波,结果如图 3所示,其中图 3(c)的k1值为1,图 3(d)的k2值为0.8.
 |
| 图 3 基于孤波的图像滤波算法仿真Fig. 3 Algorithm simulation of image filtering based on solitary waves |
| 图选项 |
4 结 论本文对像素栅格动力学方程的性能进行分析,给出了利用孤波来进行图像处理的原因和方法,可以得到:
1) 像素栅格方程可以提供图像的幅值和方向信息,图像的像素可以用像素孤波来代替.
2) 文中采用的算法包含图像的方向信息,在滤波处理时可以更清晰地突出图像的边缘.
3) 文中算法处理得到的图像平滑度低于最优算子,但边缘和细节信息保留较好,高于一般的滤波算法.
4) 处理过程中参数设置不当,算法的非线性效应会造成数值计算的溢出,在对溢出进行归一化时产生的干扰噪声,有待进一步深入研究.
参考文献
| [1] | Vese L,Osher S.The level set method links active contours,mumford-shah segmentation,and total variation restoration,CAM-report 02-05[R].Los Angeles,CA:CAM Report,2002. |
| [2] | Perona P,Malik J.Scale-space and edge detection using anisotropic diffusion[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1990,12(7):629-639. |
| Click to display the text | |
| [3] | Xiao Z T,Xu Z B,Zhang F,et al.ESPI filtering method based on anisotropic coherence diffusion and Perona-Malik diffusion[J].Chinese Optics Letters,2013,11(10):43-46. |
| Click to display the text | |
| [4] | Shapiro J M.Embedded image coding using zero-tree of wavelet coefficients[J].IEEE Transactions on Signal Processing,1993,41(12):3445-3462. |
| Click to display the text | |
| [5] | Mallat S,Zhong S F.Characterization of signals from multiscale edges[J].IEEE Transactions on PAMI,1992,14(7):710-732. |
| Click to display the text | |
| [6] | Mallat S.Multiresolution representation and wavelets[D].Philade,PA:University of Pennsylvania,1988. |
| [7] | Rafiullah C,Asifullah K,Adnan I.Wavelet based image authentication and recovery[J].Journal of Computer Science & Technology,2007(6):795-804. |
| Click to display the text | |
| [8] | 晁锐,张科,李言俊.一种基于小波变换的图像融合算法[J].电子学报,2004,32(5):750-753. Chao R,Zhang K,Li Y J.An image fusion algorithm using wavelet transform[J].Acta Electronica Sinica,2004,32(5):750-753(in Chinese). |
| Cited By in Cnki (253) | Click to display the text | |
| [9] | 郭亮.基于偏微分方程的图像滤波方法研究[D].沈阳:大连海事大学,2013. Guo L.PDE-based research on image filtering methods[D].Shenyang:Dalian Maritime University,2013(in Chinese). |
| Cited By in Cnki (1) | |
| [10] | 蔡超.基于小波和偏微分方程的图像处理方法与应用[D].武汉:华中科技大学,2005. Cai C.Wavelet and partial differential equation based image processing methods and their applications[D].Wuhan:Huazhong University of Science and Technology,2005(in Chinese). |
| Cited By in Cnki (16) | |
| [11] | 董卫军.基于小波变换的图像处理技术研究[D].西安:西北大学,2006. Dong W J.Image processing technique research based on wavelet transform[D].Xi'an:Northwest University,2006(in Chinese). |
| Cited By in Cnki (43) | |
| [12] | Zhu Z M,Liu R Q,Cao Y W,et al.Image processing algorithm based on solitary wave[J].Applied Mechanics and Materials,2014(539):126-130. |
| Click to display the text | |
| [13] | 田强.晶格振动简正坐标的具体表述及其讨论[J].大学物理,1999(8):7-8. Tian Q.Discussions on some relations about ortho-coordinate[J].College Physics,1999(8):7-8(in Chinese). |
| Cited By in Cnki (3) | Click to display the text | |
| [14] | 陈登远.孤子引论[M].北京:科学出版社,2006:39-41. Chen D Y.An introduction to soliton[M].Beijing:Science Press,2006:39-41(in Chinese). |
| [15] | Hirota R.Exact solutions of Kortewerg-de veris equation for multiple collisions of solutions[J].Physical Review Letters,1971,27(18):1192-1194. |
| Click to display the text | |
| [16] | Remoissenet M.Waves called solitons[M].2nd ed.Berlin Heidelberg:Springer,1999:138-204. |
| [17] | Sulem C,Sulem P L.The nonlinear Schrodinger equation:Self-focusing and wave collapse[M].New York:Springer New York Inc.,1999:57-92. |
