国内外对磁悬浮高速转子的热-结构耦合分析文献较少,其中文献[3]对磁悬浮飞轮转子组件进行了热-结构耦合分析,首先计算出飞轮组件工作状态下的温度场,随后在温度场的基础上进行静力分析,但是由于该模型仅为二维有限元模型,导致温度场分析结果误差较大。因此,获得相对精确的温度场是进行热-结构耦合分析的基础。在进行航天器温度场分析时,经常采用等效热网络法,它采用网络拓扑模型能够直观地反映结构部件之间复杂的热量交换关系[4]。文献[5, 6]中建立变速箱传动系统的热网络模型,采用热路法计算出传动系统处于热平衡时各重要部件的温度;文献[7]对高速储能飞轮中永磁同步电机的功耗进行了分析计算,并建立飞轮的热网络模型,分析了其工作时的热特性;文献[8]采用热网络法对行星轮传动系统建立热传递模型,分析了系统达到稳态时的温度分布。随着有限元分析软件的迅速发展,有限元法被广泛地应用于温度场的分析中,文献[9]建立了磁悬浮飞轮转子组件的二维有限元模型,对模型施加热传导与热辐射边界条件,计算出飞轮转子组件的温度场,该文献仅建立了飞轮转子组件模型,没有建立整体模型,在进行温度场分析时,会出现较大的误差。文献[10]建立了磁悬浮直线运动平台的二维有限元模型,分析了发热部件的功耗,计算得到真空条件下平台的温度云图。文献[11]对磁悬浮铣床主轴温度场进行了分析,建立有限元二维模型,计算出铣床主轴在高速旋转时的温度场,但是其工作环境为普通环境,热传递方式为热传导与热对流,没有考虑热辐射。文献[12]建立了磁悬浮反作用飞轮的热网络模型,列出了热网络方程,并且建立磁悬浮反作用飞轮的二维有限元模型,计算出飞轮工作时的温度场,最后根据热网络模型提出优化措施,有效地降低了飞轮工作温度,但没有进行飞轮的热-结构耦合分析。
有限元法计算精度高、速度快,适于定量计算,但进行优化时,陀螺的复杂结构使得优化变量过多,运算量大,计算时间过长;热网络法求解精度低于有限元法,但其能够直观地反映热量传递关系,易于通过网络拓扑模型确定影响各部件温度的主要因素。因此,本文采用有限元法定量计算磁悬浮控制力矩陀螺的温度场,并进行热-结构耦合分析,针对温度过高的部件,采用等效热网络模型定性分析其主要影响因素,并提出相应的优化措施,以提高陀螺结构的可靠性。
1 结构及功耗分析1.1 磁悬浮控制力矩陀螺结构由于全主动磁轴承系统较复杂,且在输出力矩状态下产生大量的热,难以满足空间应用需求;而主被动磁轴承系统相对简单,产热少,因此,对主被动磁悬浮控制力矩陀螺的研究备受重视。本文以一种主被动磁悬浮控制力矩陀螺为研究对象,其主要组件包括上下端陀螺房、一体化磁轴承、转子轮体和高速电机和框架。主被动磁悬浮控制力矩陀螺本身结构过于复杂,在热分析之前需对其结构进行简化,以利于有限元模型的建立,简化后的主被动磁悬浮控制力矩陀螺结构如图 1所示。
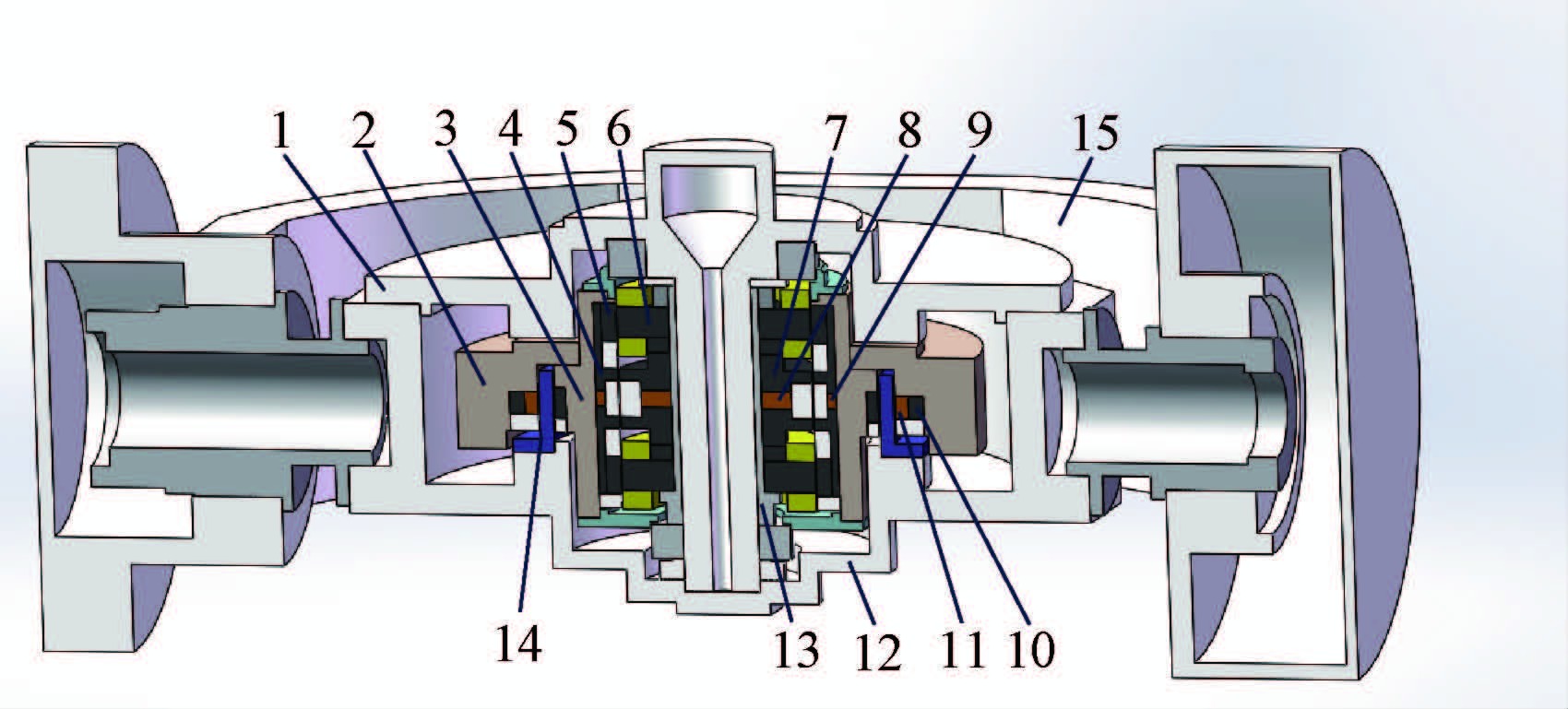 |
| 1—上端陀螺房;2—转子外轮毂;3—转子内轮毂;4—转子导磁环;5—转子铁心;6—定子铁心;7—定子导磁环;8—定子永磁体;9—转子永磁体;10—电机铁心;11—电机永磁体;12—下端陀螺房;13—磁轴承套筒;14—电机定子;15—框架。图 1 主被动磁悬浮控制力矩陀螺三维模型Fig. 1 3D model of active-passive MSCMG |
| 图选项 |
主被动磁悬浮控制力矩陀螺的主要产热部件为磁轴承与高速电机,损耗主要包括铁损与铜损。磁轴承转子铁心高速旋转时由于其表面不均匀的磁密分布会产生涡流损耗;磁轴承定子铁心由于控制线圈中电流的不断变化会产生涡流损耗;电机定子中电流脉宽调制(PWM)分量在电机内外转子铁心及永磁体中会产生涡流损耗;磁轴承控制线圈电流与电机定子电流会产生铜损。
1.2 发热部件功耗计算1.2.1 铜 损磁轴承的铜损是由控制电流流经绕组电阻引起的,电机的铜损是由电机定子电流流经绕组电阻引起的,两者的铜损可根据欧姆定律由式(1)计算:

式中:I为通入磁轴承控制线圈或电机定子线圈电流的有效值;R为磁轴承控制线圈或电机定子线圈的总电阻。
1.2.2 铁 损铁损包括涡流损耗和磁滞损耗,磁轴承的涡流损耗是由铁心中磁通密度变化引起的,转子的高速旋转及控制线圈中电流的不断变化都会产生涡流损耗,其计算公式[13, 14]为

式中:ρ为铁心电阻率;e为叠片厚度;fu为再磁化频率;Bm为最大磁通密度;Vfe为铁心体积。
磁滞损耗是由导磁材料被反复交变磁化,磁畴相互摩擦产生,磁滞损耗可由式(3)计算[15]:

式中:kh为材料常数。
电机定子中相电流的PWM分量在电机内外转子铁心与永磁体中产生的涡流损耗可由式(2)计算。
1.3 功耗测试为准确计算发热部件的功耗,对主被动磁悬浮控制力矩陀螺进行功耗测试。将陀螺升速到10000r/min,分别测出磁轴承线圈和电机定子线圈的电流,根据式(1)计算出相应的铜损,其值分别为1W和0.4W。定子铁损可根据直流电源的输出功率确定,直流电源的输出功率为控制板损耗、铜损与定子铁损三者之和,经计算定子铁损为6W。转子铁损可由陀螺降速曲线确定,其值为17W,降速曲线如图 2所示。通过式(2)、式(3)对铁损的计算以及定转子铁损的合理分配,最终可确定各发热部件的功耗值。
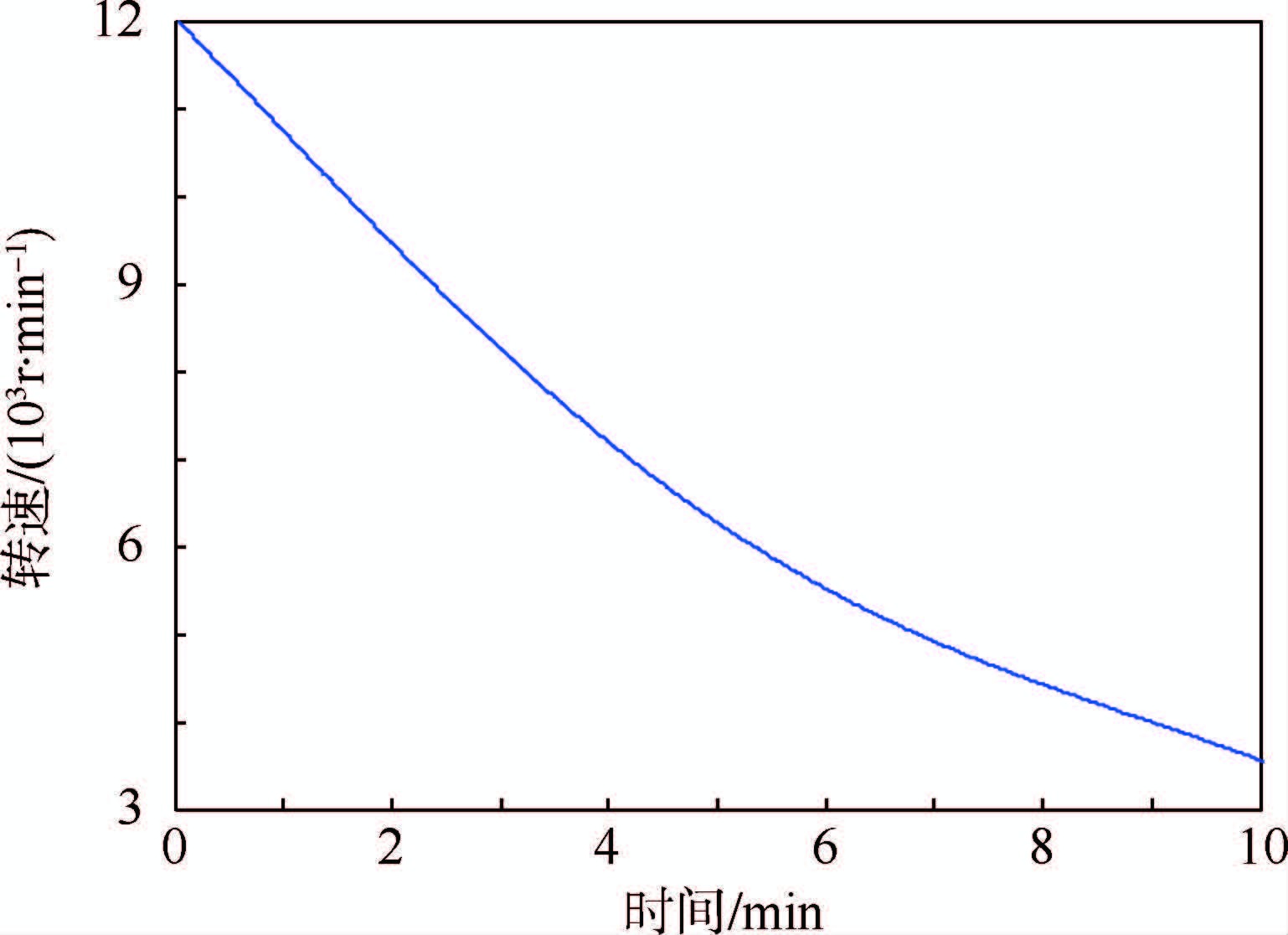 |
| 图 2 降速曲线Fig. 2 Curve of speed down |
| 图选项 |
2 温度场的计算与实验采用ANSYS建立磁悬浮控制力矩陀螺的有限元模型,施加相应的热分析边界条件,进行陀螺温度场的计算。
2.1 有限元模型建立主被动磁悬浮控制陀螺框架结构、下端陀螺房以及磁轴承定子铁心都是非轴对称结构,因此无法使用二维有限元模型进行等效计算,为计算得到相对精确的温度场,建立如图 3所示的主被动磁悬浮控制力矩陀螺三维有限元模型。
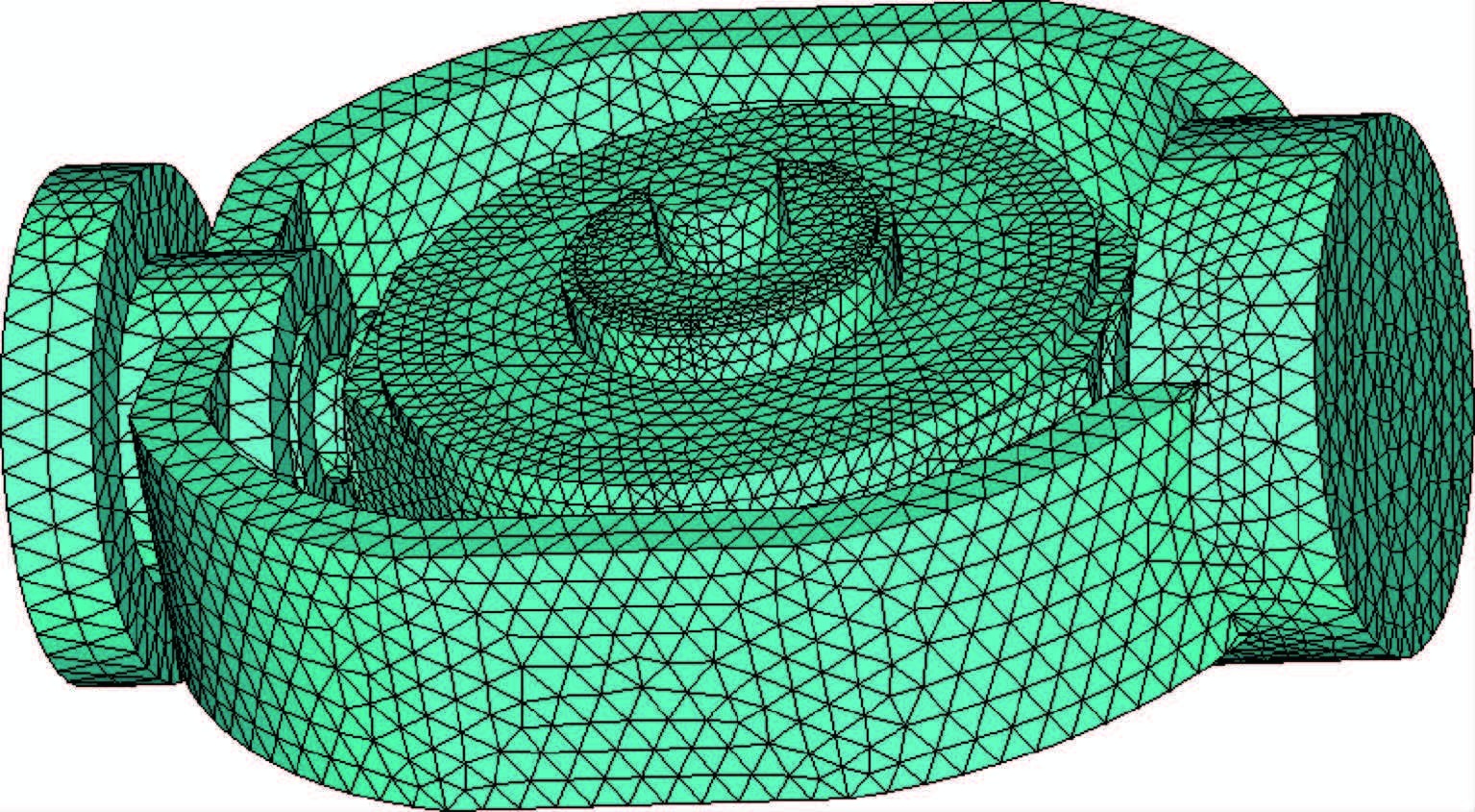 |
| 图 3 主被动磁悬浮控制力矩陀螺三维有限元模型Fig. 3 3D finite element model of active-passive MSCMG |
| 图选项 |
为精确分析陀螺内部热传导过程,在接触部件之间创建接触单元,接触面采用CONTA173单元,目标面采用TARGE170单元。在接触单元中设置接触热导,用以等效接触部件之间的接触热阻。如定子铁心、定子导磁环以及定子永磁体与定子安装套筒之间的接触,转子铁心、转子导磁环、转子永磁体以及电机内转子铁心与转子内轮毂之间的接触,电机永磁体、电机外转子铁心与转子外轮毂之间的接触,定子安装套筒与上端陀螺房之间的接触等。
磁悬浮控制力矩陀螺工作时,会向周围环境辐射热量,因此在进行热辐射计算时,需要定义空间节点,用于吸收陀螺辐射的热量,确保能量守恒,空间节点的温度为空间环境的温度。此外,热辐射求解过程中需要计算辐射角系数,ANSYS提供2种计算辐射角系数的方法:非隐藏法和隐藏法。采用非隐藏法计算辐射角系数时,必须确保辐射面之间完全可见,否则辐射角系数计算结果不正确。由于陀螺内部结构复杂,很难保证所选辐射面之间完全可见,这样会导致温度场计算误差过大。因此,定义辐射边界条件时,选用隐藏法计算辐射角系数,隐藏法首先自动判断2个单元之间是否“完全可见”,之后计算出辐射热量,避免了因辐射角系数不准确而引起的温度场计算误差。
2.2 温度场仿真根据主被动磁悬浮控制力矩陀螺功耗测试及式(1)~式(3)计算出的功耗值如表 1所示,陀螺结构部件材料的热性能参数如表 2所示。
表 1 磁悬浮控制力矩陀螺发热部件功耗值Table 1 Losses of heating components in MSCMG
| 发热部件 | 功耗/W | 生热速率/(kW·m-3) |
| 电机定子 | 0.4 | 20 |
| 电机内转子铁心 | 1.2 | 192 |
| 电机外转子铁心 | 0.8 | 100 |
| 电机永磁体 | 1 | 154 |
| 径向磁轴承定子铁心 | 6 | 289 |
| 径向磁轴承转子铁心 | 10 | 702 |
| 径向磁轴承永磁体 | 2.4 | 530 |
| 径向磁轴承线圈 | 1 | 38 |
| 轴向被动磁轴承转子导磁环 | 1.2 | 317 |
| 轴向被动磁轴承永磁体 | 0.4 | 72 |
表选项
表 2 磁悬浮控制力矩陀螺结构部件材料热性能参数Table 2 Thermal performance parameters for materials of structural components in MSCMG
| 材料 | 导热系数/(W·(m·K)-1) | 辐射率 |
| 2014铝合金 | 160 | 0.6 |
| 锻制不锈钢 | 16.3 | 0.7 |
| 钛合金 | 7.2 | 0.4 |
| 铜线 | 100 | 0.8 |
| 聚砜 | 0.26 | 0.9 |
| 1J50 | 17 | 0.5 |
| Sm2Co17 | 11 | 0.5 |
| DT4c | 50 | 0.4 |
表选项
根据表 1对有限元模型施加生热速率条件,根据表 2赋予有限元模型相应的材料属性,环境温度为20℃。经计算,主被动磁悬浮控制力矩陀螺工作达到热稳态时的温度云图如图 4所示。
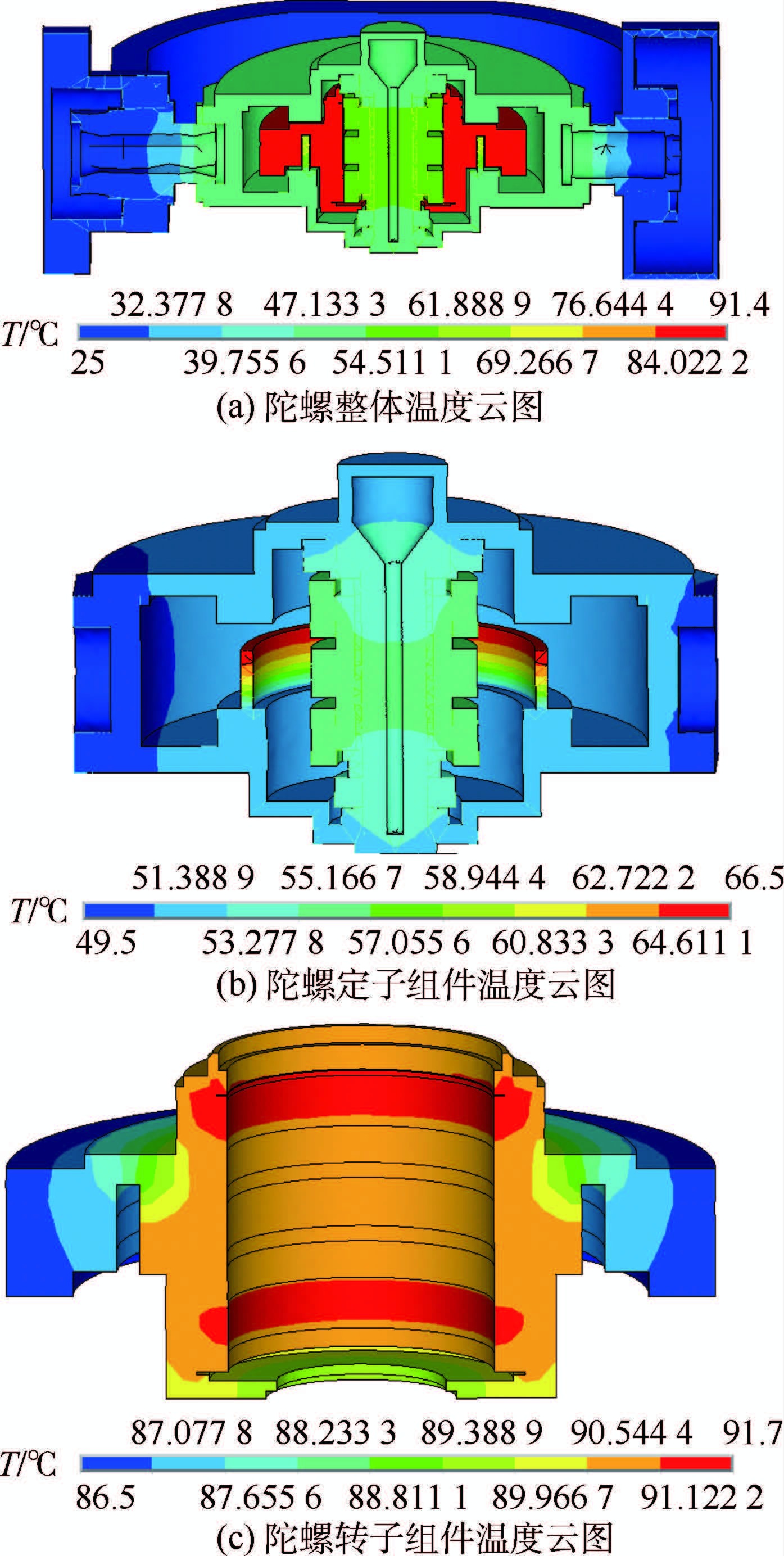 |
| 图 4 主被动磁悬浮控制力矩陀螺温度云图Fig. 4 Temperature contours of active-passive MSCMG |
| 图选项 |
由图 4(b)可见,定子组件温度最高点在电机定子上,温度值为66.5℃,由材料的热性能可知,电机定子的传导系数很小,产生的热量无法及时地传递到下端陀螺房,导致其温度较高。由图 4(a)、图 4(c)可见,转子组件整体温度较高,转子组件温度最高点在磁轴承转子铁心上,温度值为91.7℃,由产热部件的功耗值可知,磁轴承转子铁心功耗较大,产热量多,从而导致其自身温度过高。
2.3 样机温度实验主被动磁悬浮控制力矩陀螺样机如图 5所示,实验时将其置于真空度为4.5Pa的真空罩内。取上端陀螺房、下端陀螺房、框架和电机定子作为温度测试对象,分别安装温度传感器。待陀螺样机工作达到热稳态后,测得上端陀螺房、下端陀螺房、框架和电机定子的温度分别为54.7、53.2、28.2和68.6℃。由图 4可知,有限元法计算出的温度分别为52.8、52.2、26.6和66.5℃,与实验结果相比,其最大误差为5.7%,在热分析误差允许范围内,从而验证了有限元法分析磁悬浮控制力矩陀螺温度场的准确性。
 |
| 图 5 主被动磁悬浮控制力矩陀螺样机Fig. 5 Prototype of active-passive MSCMG |
| 图选项 |
3 热-结构耦合分析在温度场的基础上进行定子组件与转子组件的静力学分析,计算出磁悬浮控制力矩陀螺工作状态下各结构部件的应力,确定陀螺组件的强度安全系数。热-结构耦合分析过程中,将ANSYS温度分析环境更改为结构分析环境,结构单元代替温度单元,施加相应的静力边界条件。表 3为陀螺结构部件材料的力学性能参数。
表 3 磁悬浮控制力矩陀螺结构部件材料力学性能参数Table 3 Mechanical performance parameters for materials of structural components in MSCMG
| 材料 | 弹性模量/GPa | 泊松比 | 膨胀系数/(10-6℃) |
| 2014铝合金 | 73 | 0.33 | 21.5 |
| 锻制不锈钢 | 200 | 0.30 | 16.6 |
| 钛合金 | 110 | 0.30 | 9.1 |
| 铜线 | 108 | 0.32 | 9.1 |
| 聚砜 | 2.7 | 0.42 | 0.71 |
| 1J50 | 211 | 0.31 | 9.2 |
| Sm2Co17 | 77.8 | 0.30 | 7 |
| DT4c | 206 | 0.30 | 12 |
表选项
3.1 定子组件静力分析磁悬浮控制力矩陀螺工作时,由于陀螺房整体转动缓慢,对定子组件的结构应力影响很小,因此,进行定子组件静力分析时,忽略陀螺房的转动,将求解的陀螺温度场作为边界条件施加到有限元模型上。图 6为定子组件热-结构耦合分析结果。
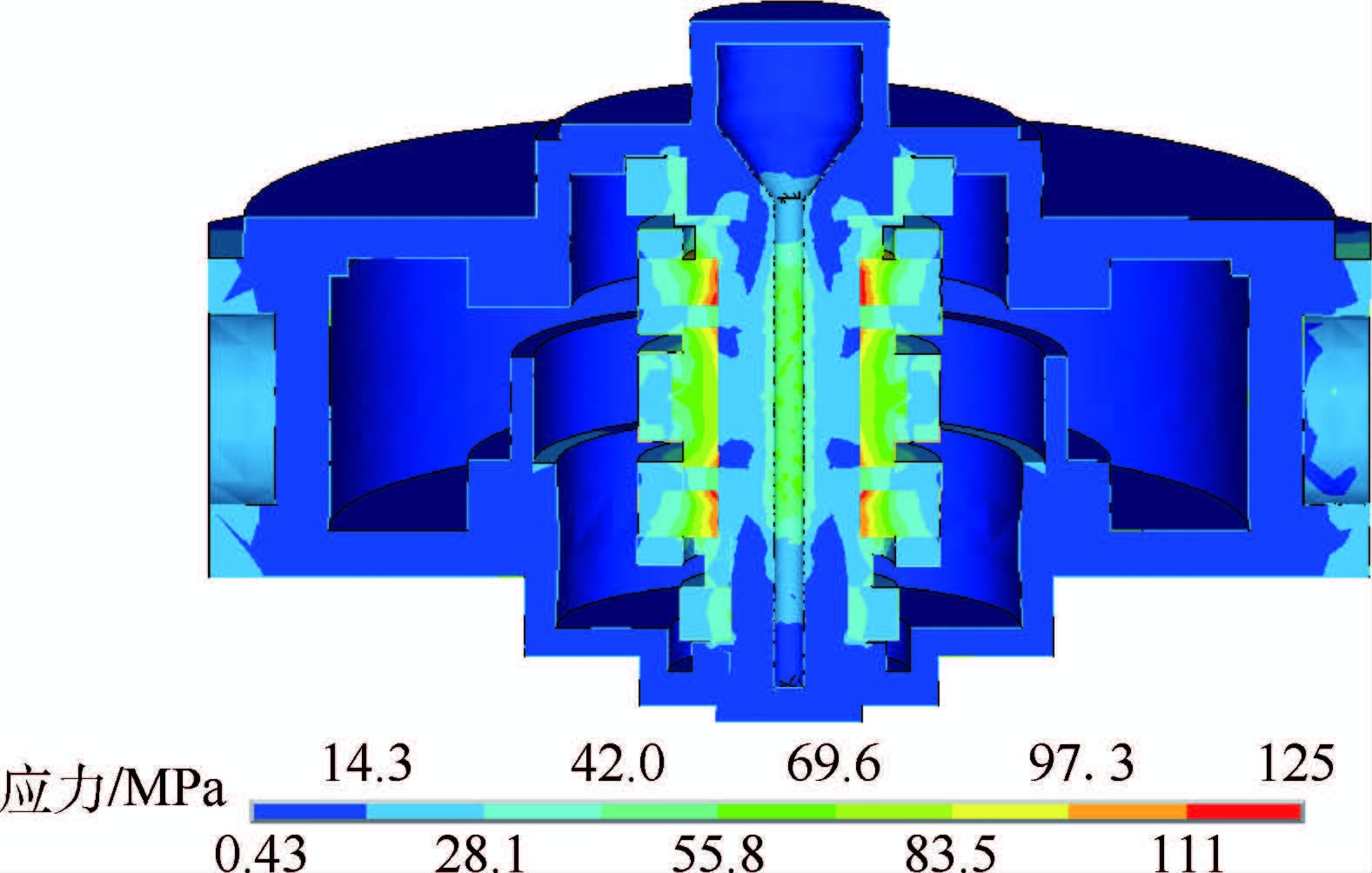 |
| 图 6 磁悬浮控制力矩陀螺定子组件等效应力Fig. 6 Von Mises stress of MSCMG stator assembly |
| 图选项 |
由图 6可以看出,在温度场的影响下,定子组件会产生热应力,磁轴承定子铁心处应力最大,应力值为125MPa,定子组件主要结构部件的最大应力与屈服强度如表 4所示。
表 4 定子结构部件最大应力与屈服强度Table 4 Maximum stress and yield strength of structural components in stator
| 定子结构部件 | 最大应力/MPa | 屈服强度/MPa |
| 定子铁心 | 125 | 686.0 |
| 定子导磁环 | 111 | 264.6 |
| 定子永磁体 | 83.5 | 127.4 |
| 磁轴承套筒 | 42 | 440.0 |
| 上下端陀螺房 | 55.8 | 440.0 |
表选项
强度安全系数为部件屈服强度与最大应力之比,定子组件的强度安全系数为各部件强度安全系数中的最小值。通过表 4计算可知,定子结构部件中定子永磁体的强度安全系数最小,值为1.52。因此,定子组件的强度安全系数为1.52。
3.2 转子组件静力分析磁悬浮控制力矩陀螺工作时,转子组件处于高速旋转状态,转速为10000r/min,因此,转子组件的应力是温度场产生的热应力与转子组件高速旋转产生的结构应力共同作用的结果。进行静力分析时,将求解的陀螺温度场与转速作为边界条件施加到有限元模型上。图 7为转子组件热-结构耦合分析结果。
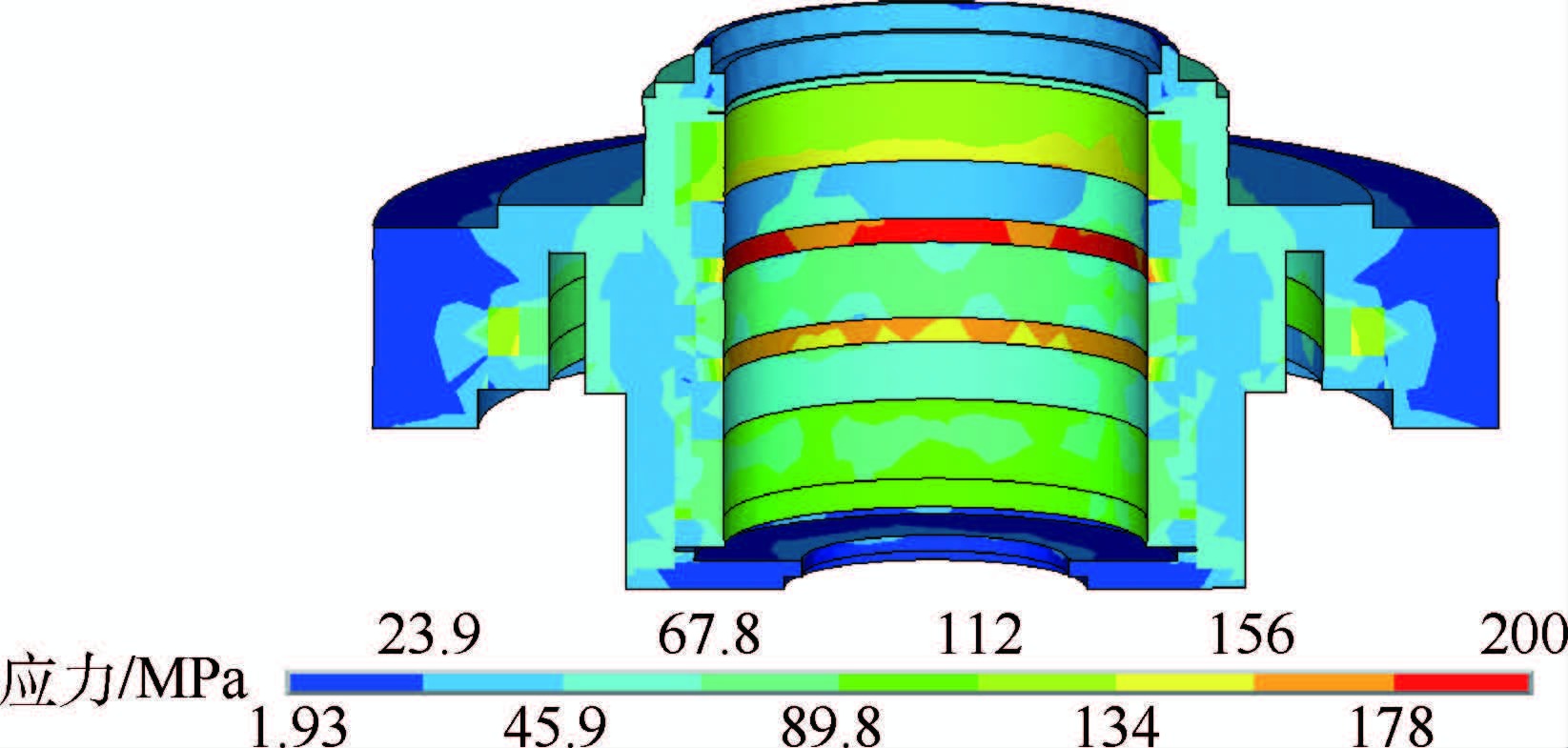 |
| 图 7 磁悬浮控制力矩陀螺转子组件等效应力Fig. 7 Von Mises stress of MSCMG rotor assembly |
| 图选项 |
由图 7可以看出,在温度场与转速共同作用下,转子组件会产生较高的应力,磁轴承转子导磁环处应力最大,应力值为200 MPa,转子组件主要结构部件的最大应力与屈服强度如表 5所示。
表 5 转子结构部件最大应力与屈服强度Table 5 Maximum stress and yield strength of structural components in rotor
| 转子结构部件 | 最大应力/MPa | 屈服强度/MPa |
| 转子铁心 | 156.0 | 685.0 |
| 转子导磁环 | 200.0 | 264.6 |
| 转子永磁体 | 45.9 | 127.4 |
| 转子内轮毂 | 67.8 | 895.0 |
| 转子外轮毂 | 67.8 | 520.0 |
| 电机铁心 | 156.0 | 685.0 |
| 电机永磁体 | 89.8 | 127.4 |
表选项
通过表 5计算可知,转子结构部件中转子导磁环的强度安全系数最小,值为1.32。因此,转子组件的强度安全系数为1.32。
4 温度场的分析与优化通过温度场与热-结构耦合分析结果可以看出,磁悬浮控制力矩陀螺在工作状态下,转子组件温度较高,结构部件产生较大的热应力,导致其结构强度安全系数较低。为提高陀螺结构的可靠性,采用热网络法建立磁悬浮控制力矩陀螺的热网络模型,分析影响部件温度过高的主要因素,从而对陀螺工作状态下的温度场进行优化。
4.1 热网络模型的建立利用等效热网络法分析陀螺热量的传递路径,即将陀螺各重要部件等效成节点,节点包含自身的功耗及热参数,部件间的热量传递关系则用节点间的热阻或热导值表示。如果节点为热源,其输入能量为相应产热部件的功耗;如果节点为非热源,其输入能量为0。各节点之间通过热阻相连,形成整个陀螺系统的等效热网络模型。主被动磁悬浮控制力矩陀螺各结构部件的等效节点及传热路径如图 8所示。
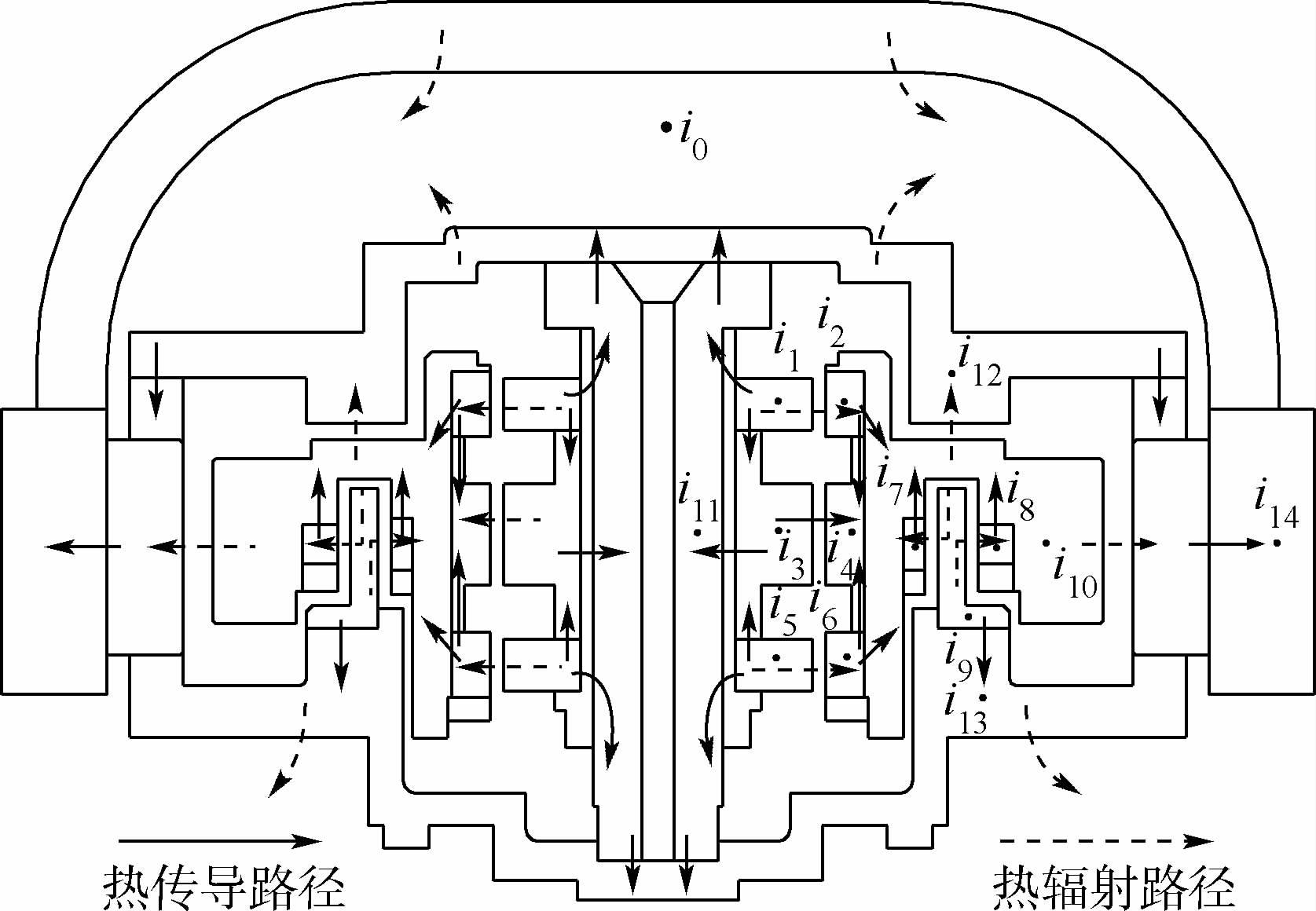 |
| i0—空间节点;i1—径向磁轴承上端定子;i2—径向磁轴承上端转子;i3—轴向被动磁轴承定子;i4—轴向被动磁轴承转子;i5—径向磁轴承下端定子;i6—径向磁轴承下端转子;i7—电机内转子;i8—电机外转子;i9—电机定子;i10—转子轮体;i11—心轴;i12—上端陀螺房;i13—下端陀螺房;i14—陀螺框架。图 8 主被动磁悬浮控制力矩陀螺等效节点及传热路径Fig. 8 Equivalent nodes and heat flux path of active-passive MSCMG |
| 图选项 |
根据各节点之间的传热关系建立主被动磁悬浮控制力矩陀螺热网络模型,如图 9所示。
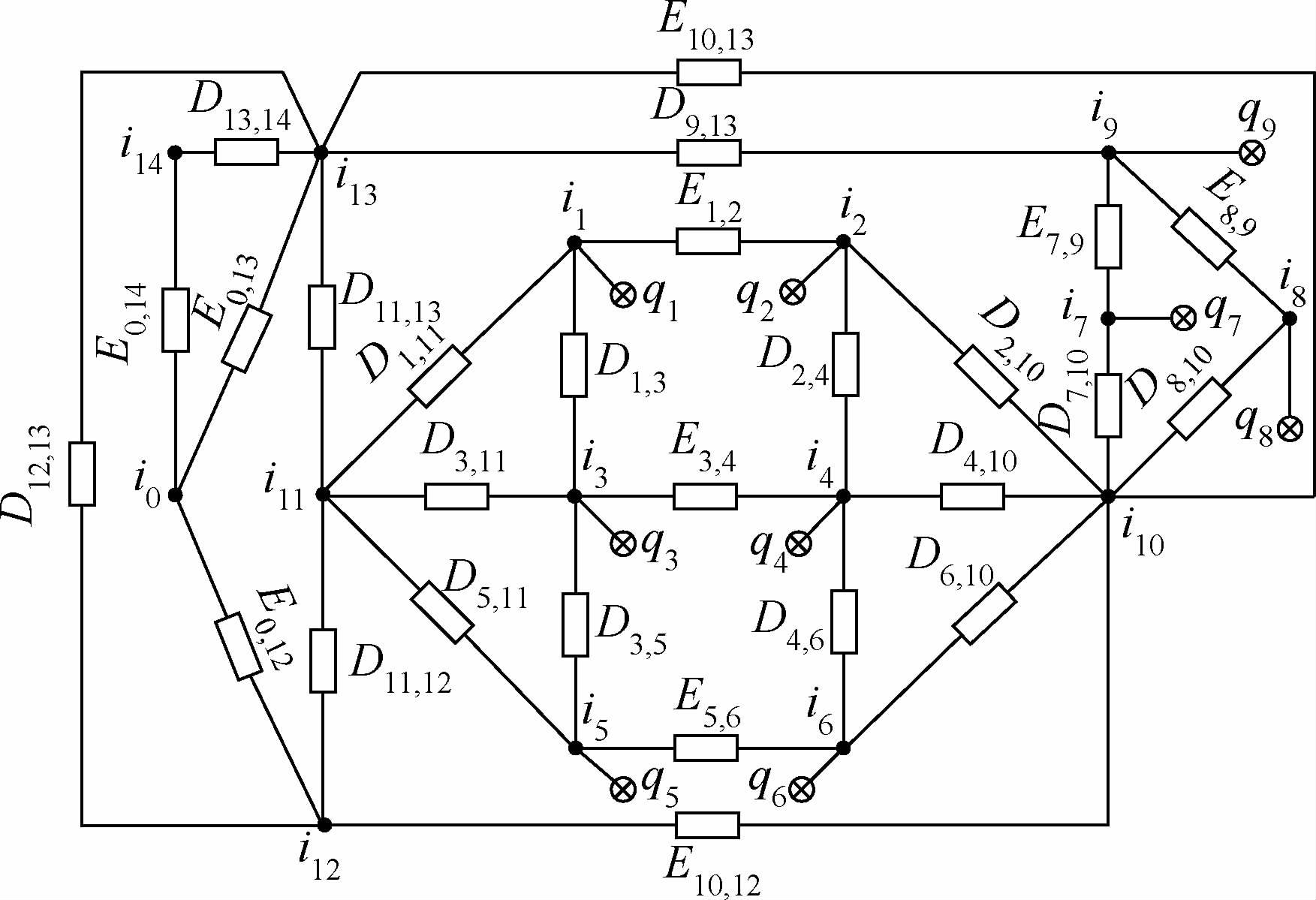 |
| 图 9 主被动磁悬浮控制力矩陀螺等效热网络模型Fig. 9 Equivalent thermal network model of active-passive MSCMG |
| 图选项 |
该模型的热网络方程为
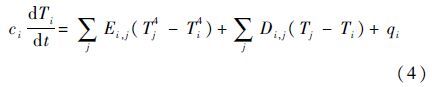
式中:ci为节点i的比热容;Ti为节点i的温度值;t为时间;qi为节点i的功耗;Ei,j为节点i与j间的热辐射系数,其表达式为
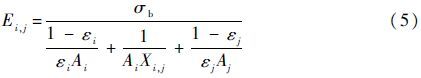
其中:Di,j为节点i和j间的热传导系数,其表达式为

σb=5.67×10-8W/(m2·K4)为黑体辐射常数;εi和εj为2个辐射面各自的辐射率;Ai和Aj为2个辐射面各自的面积;Xi,j为2个辐射面之间的角系数;λi为导热系数;Ai,j为相邻2个结构件的接触面积;δi,j为热传导的距离。
陀螺工作达到热稳态时的热网络方程为
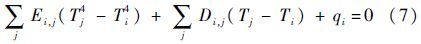
通过温度场分析结果可知,陀螺工作状态下温度较高的结构部件为磁轴承上下转子铁心、电机定子和转子轮体,其等效节点对应的热网络方程为
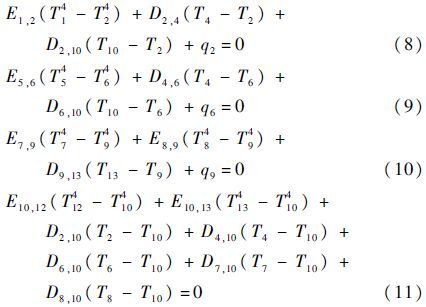
由式(8)和式(9)可以看出,磁轴承转子铁心产生的热量部分辐射到定子铁心,部分传导到转子导磁环,部分传导到转子轮体。因此,影响磁轴承转子铁心温度的因素有磁轴承转子铁心与磁轴承定子铁心之间的辐射系数E1,2和E5,6、磁轴承转子铁心与转子导磁环之间的热传导系数D2,4和D4,6、磁轴承转子铁心与转子轮体之间的热传导系数D2,10和D6,10以及磁轴承转子铁心功耗q2和q6。由有限元温度分析结果可知,转子组件整体温度较高且温度梯度较小,热传导系数与辐射系数对磁轴承转子铁心温度的影响很小,所以导致磁轴承转子铁心温度较高的主要原因是其功耗q2和q6过大;由式(10)可以看出,电机定子产生的热量部分传导到下端陀螺房,部分辐射到电机内转子和永磁体。因此,影响电机定子温度的因素有电机定子与下端陀螺房之间的热传导系数D9,13、电机定子与电机内转子之间的辐射系数E7,9、电机定子与电机永磁体之间的辐射系数E8,9以及电机定子的功耗q9。由于电机定子通过辐射散出的热量很少,所以导致电机定子温度较高的主要原因是电机定子与下端陀螺房之间的热传导系数D9,13过小。由式(11)可以看出,磁轴承转子铁心、转子导磁环、电机内转子与电机永磁体产生的热量都以热传导的方式传递到转子轮体,而转子轮体的散热方式仅为热辐射,通过辐射将热量传递给上下端陀螺房,所以导致转子轮体温度较高的主要原因是磁轴承转子铁心功耗q2和q6过大以及转子轮体与上下端陀螺房的热辐射系数E10,12和E10,13过小。
4.2 优化措施通过上述分析,确定了影响陀螺部件温度的主要因素,针对这些因素进行温度场优化,提出下述3种优化措施:
1) 改变磁轴承定子铁心形状,将其4个磁极设计成极靴,使一周内的气隙磁密变化尽可能小,定子铁心形状如图 10所示;在磁轴承满足性能要求的前提下,减小永磁体,使气隙磁密幅值Bm减小;同时极靴结构可减小定子铁心的体积Vfe;由式(2)可知,该方法能有效降低转子、定子铁心的功耗。经优化,转子铁心功耗由10W降为6W,生热速率为4.21×105W/m3,定子铁心功耗由6W降为4.5W,生热速率为2.17×105W/m3。
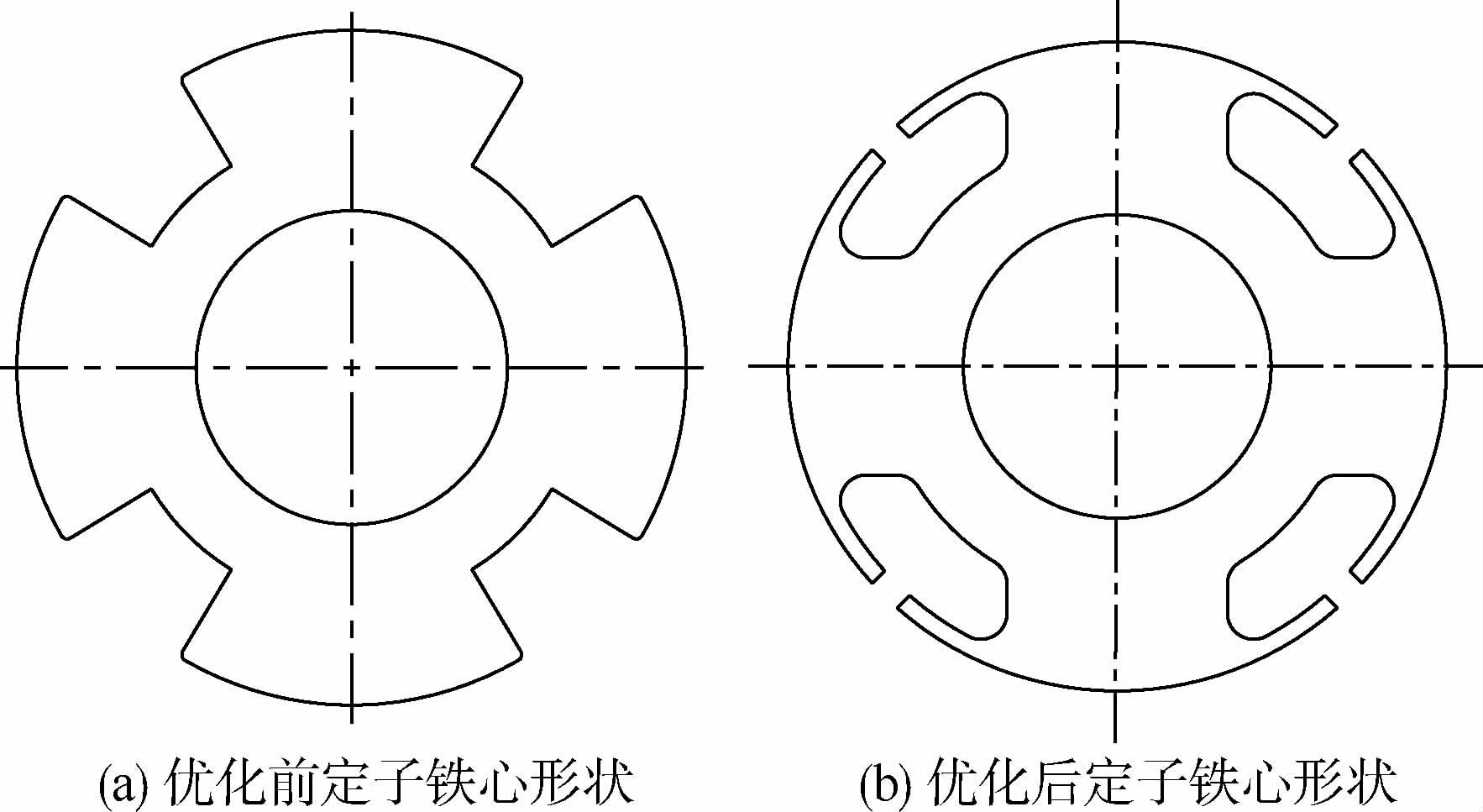 |
| 图 10 磁轴承定子铁心形状Fig. 10 Shape of stator iron core of magnetic bearing |
| 图选项 |
2) 电机定子材料为聚砜,导热系数仅为0.26W/(m·K),在电机定子灌封时,添加适量的铝粉,将其导热系数增大到2W/(m·K)。
3) 提高转子轮体表面、上下端陀螺房内外表面、框架表面的辐射率,通过黑色阳极氧化、表面涂层等表面处理技术可增大材料辐射率。经处理,转子轮体内轮毂表面辐射率由0.4增加到0.6,转子轮体外轮毂表面辐射率由0.7增加到0.9;上下端陀螺房内外表面、框架表面辐射率由0.6增加到0.85。
4.3 优化结果经过优化,陀螺工作达到热稳态时的温度云图如图 11所示。
 |
| 图 11优化后主被动磁悬浮控制力矩陀螺温度云图Fig. 11 Temperature contours of active-passive MSCMG |
| 图选项 |
由图 11可见,由于磁轴承定子铁心功耗降低以及电机定子传导系数增大,使得定子组件最高温度降至49℃,电机定子最高温度降至47.5℃;此外,由于磁轴承转子铁心功耗降低以及转子轮体辐射率增加,使得磁轴承转子铁心的最高温度降至76.9℃,转子组件整体温度降低。
温度场优化后,陀螺结构部件的等效应力如图 12所示。
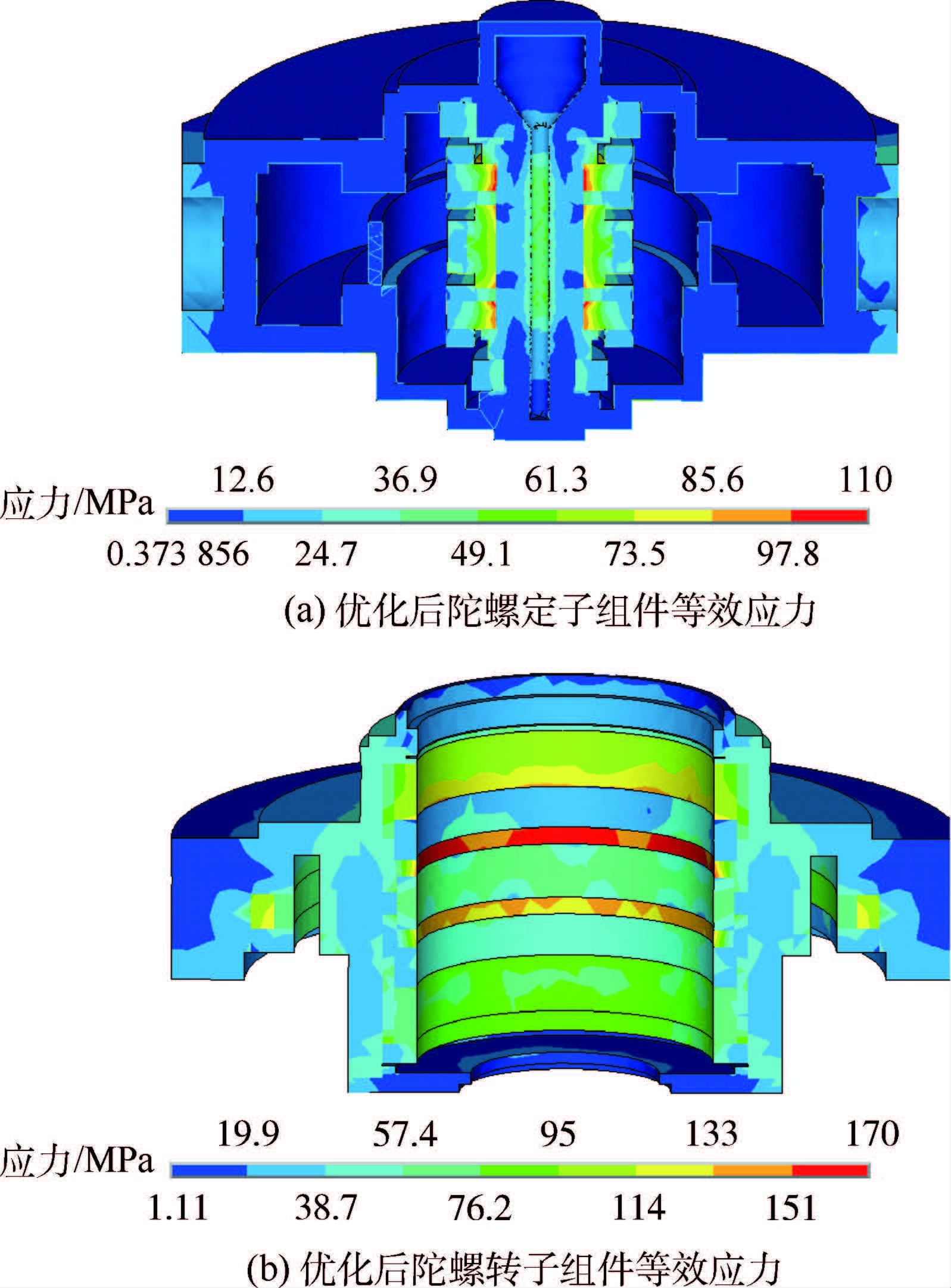 |
| 图 12 优化后主被动磁悬浮控制力矩陀螺等效应力Fig. 12 Von Mises stress of active-passive MSCMG after optimization |
| 图选项 |
由图 12可见,陀螺定子和转子组件的应力与优化前相比有所减小。经计算,定子组件的强度安全系数升至1.73,转子组件的强度安全系数系数升至1.56。优化前后陀螺组件的最高温度与强度安全系数如表 6所示。
表 6 优化前后磁悬浮控制力矩陀螺组件最高温度与强度安全系数Table 6Maximum temperature and safety factor of MSCMG before and after optimization
| 组件名称 | 优化前 | 优化后 | ||
| 最高温度/℃ | 安全系数 | 最高温度/℃ | 安全系数 | |
| 定子 | 66.5 | 1.52 | 49 | 1.73 |
| 转子 | 91.7 | 1.32 | 76.9 | 1.56 |
表选项
5 结 论本文以主被动磁悬浮控制力矩陀螺为研究对象,对其进行了热-结构耦合分析,可得到以下结论:
1) 采用有限元法分析了基于温度场的陀螺结构部件的应力分布,明确了温度场对陀螺结构强度的影响。
2) 采用热网络法分析了陀螺热量传递路径以及影响陀螺结构部件温度的主要因素,并对其温度场进行优化。
3) 经优化,定子组件最高温度降低了26.3%,转子组件最高温度降低了16.1%;定子组件的强度安全系数提高了13.8%,转子组件的强度安全系数提高了18.2%。
由此可见,磁悬浮控制力矩陀螺热-结构耦合分析与研究,对陀螺系统的热设计与结构设计有着重要意义。
参考文献
| [1] | FANG J C,SUN J J,XU Y L,et al.A new structure for permanent-magnet-biased axial hybrid magnetic bearings[J].IEEE Transactions on Magnetics,2009,45(12):5319-5325. |
| Click to display the text | |
| [2] | FANG J C,SUN J J,LIU H,et al.A novel 3-DOF axial hybrid magnetic bearing[J].IEEE Transactions on Magnetics,2010,46(12):4034-4045. |
| Click to display the text | |
| [3] | ZHANG S A,HAN B C,LI H,et al.Thermal and structural coupling analysis of magnetically suspended flywheel rotor[C]//6th International Symposium on Instrumentation and Control Technology:Sensors,Automatic Measurement,Control,and Computer Simulation.Bellingham,WA:SPIE,2006,5368:561-568. |
| [4] | 周超,杨洪波,王成彬.热传导及其在航天器系统中的计算方法[J].计算机仿真,2010,27(1):60-62. ZHOU C,YANG H B,WANG C B.Thermal conductivity and calculation methods for spacecraft[J].Computer Simulation,2010,27(1):60-62(in Chinese). |
| Cited By in Cnki (5) | |
| [5] | 周廷美,何庆,周浩,等.基于热网络法的汽车变速器热平衡分析[J].机械传动,2014,38(3):143-146. ZHOU T M,HE Q,ZHOU H,et al.Heat balance analysis of the automobile transmission based on the thermal network method[J].Mechanical Transmission,2014,38(3):143-146(in Chinese). |
| Cited By in Cnki (1) | |
| [6] | 张启胤,连晋毅,吴新,等.基于热网络法的工程车辆传动箱稳态热分析[J].机械科学与技术,2012,31(6):977-981. ZHANG Q Y,LIAN J Y,WU X,et al.Analysis steady-state heat balance of construction vehicle's transmission gearbox using thermal network method[J].Mechanical Science and Technology for Aerospace Engineering,2012,31(6):977-981(in Chinese). |
| Cited By in Cnki (1) | |
| [7] | CO H,ZHENG L P,MCMULLEN P.Thermal performance evaluation of a high-speed flywheel energy storage system[C]//Proceedings of the 33rd Annual Conference of the IEEE Industrial Electronics Society,IECON.Piscataway,NJ:IEEE Press,2007:163-171. |
| Click to display the text | |
| [8] | 黄飞,马希直.基于热网络法的行星减速器温度场研究[J].机械传动,2011,35(4):19-22. HUANG F,MA X Z.Study on temperature field of planetary reduction gear based on thermal network[J].Mechanical Transmission,2011,35(4):19-22(in Chinese). |
| Cited By in Cnki (12) | |
| [9] | 张姝娜,房建成,韩邦成,等.磁悬浮飞轮转子组件温度场分析与研究[J].中国惯性技术学报,2007,15(1):67-71. ZHANG S N,FANG J C,HAN B C,et al.Thermal analysis and research on magnetically suspended flywheel rotor[J].Journal of Chinese Inertial Technology,2007,15(1):67-71(in Chinese). |
| Cited By in Cnki (14) | Click to display the text | |
| [10] | 段吉安,郭宁平,周海波.一种新型磁悬浮直线运动平台的热分析[J].中国电机工程学报,2011,31(15):114-120. DUAN J A,GUO N P,ZHOU H B.Thermal analysis of a novel linear maglev transportation platform[J].Proceeding of the CSEE,2011,31(15):114-120(in Chinese). |
| Cited By in Cnki (5) | Click to display the text | |
| [11] | RO S K,KYUN J H.Study on the thermal characteristics of a magnetically suspended high speed machine tool spindle[C]//9th International Symposium on Magnetic Bearing.London:the British Library Board,2004:278-282. |
| [12] | 王春娥,房建成,汤继强,等.磁悬浮反作用飞轮热设计方法与实验研究[J].航空学报,2011,32(4):598-607. WANG C E,FANG J C,TANG J Q,et al.Thermal design method and experimental research of magnetically suspended reaction flywheel[J].Acta Aeronautica et Astronautica Sinica,2011,32(4):598-607(in Chinese). |
| Cited By in Cnki (2) | |
| [13] | TODA H,XIA Z P,WANG J B,et al.Rotor eddy-current loss in permanent magnet brushless machines[J].IEEE Transactions on Magnetics,2004,40(4):2104-2106. |
| Click to display the text | |
| [14] | YOSHIDA K,HITA Y,KESAMARU K.Eddy-current loss analysis in PM of surface-mounted-PM SM for electric vehicles[J].IEEE Transactions on Magnetics,2000,36(4):1941-1944. |
| Click to display the text | |
| [15] | MEEKER D C,FILATORV A V,MASLEN E H.Effect of magnetic hysteresis on rotational losses in heteropolar magnetic bearings[J].IEEE Transactions on Magnetics,2004,40(5):3302-3307. |
| Click to display the text |
