在以往的高超声速飞行器姿态控制系统研究设计工作中,为了简单起见,通常忽略其中的一些耦合现象,或把实际存在的耦合效应加以简化并解耦。文献[5]采用多变量频域理论对轴对称十字布局飞行器的耦合问题进行了研究,采用反向传播(Back Propagation,BP)神经网络对气动数据进行了解耦补偿。文献[6]在分析气动交叉耦合对导弹飞行特性影响后,提出了导弹的偏航/滚转通道解耦控制算法。文献[7]采用变结构鲁棒补偿控制方法设计了导弹在大攻角再入时的姿态控制系统。文献[8]提出一种基于动态逆的双阶段设计方法为倾斜转弯(Bank to Turn,BTT)导弹设计了三通道解耦控制律。但随着系统的复杂程度的增加和要求性能的提高,这种解耦设计常被证明是不合适的[9]。RLV的再入段要求侧滑角保持在零值附近,所以纵向通道可以独立于其他通道,而偏航通道和滚转通道严重耦合,并且在一定程度上受俯仰通道的耦合影响[10],因此研究RLV飞行器耦合现象的机理和产生条件,并针对其耦合特性设计姿态控制策略是十分必要的。目前还鲜见针对此类飞行器的耦合控制策略的研究。与常见的解耦控制策略不同,本文基于对飞行器耦合特性的分析,将设计一种横侧向协调控制的姿态控制策略。首先介绍该飞行器的气动布局与反作用力控制系统(Reaction Control System,RCS)的分布,并建立飞行器运动模型。针对此飞行器制导与姿态控制系统的特点分析了此类飞行器常见的几种耦合的产生原因和作用机理,并给出相应的耦合规避对策。然后设计考虑飞行器耦合特性、以简化控制律结构和节省RCS燃料消耗为目的的姿态控制策略。最后通过六自由度(6-DOF)仿真验证控制策略的可行性。
1 RLV气动外形与模型建立RLV的外形如图 1所示。该飞行器为升力体外形,气动控制面为一对体襟翼。通过两片体襟翼实现对3个通道的姿态控制,因此该飞行器为一典型的欠驱动系统。左右舵面偏角δfl、δfr与生成的等效升降舵偏角δe和等效副翼舵偏角δa的关系分别为
 |
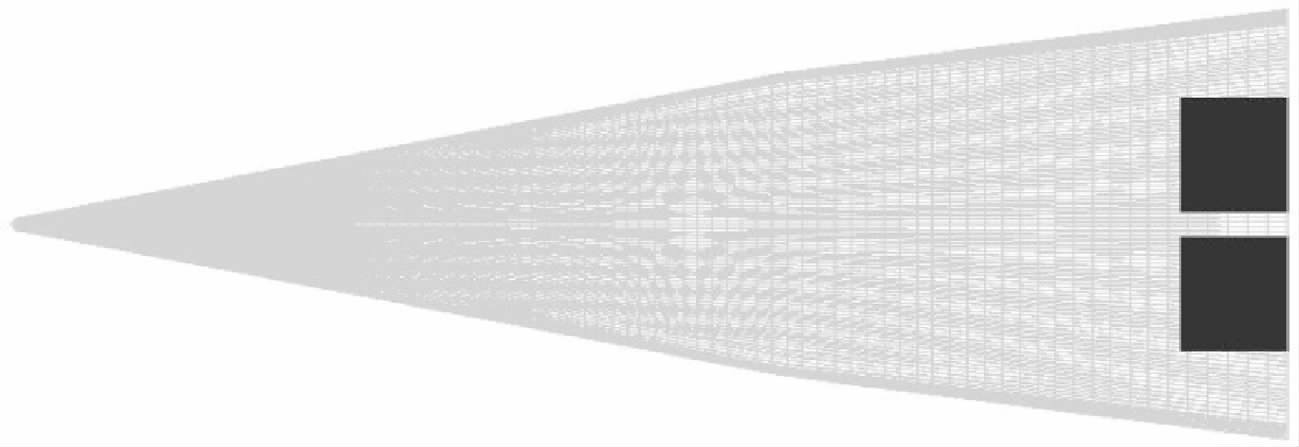| 图 1 RLV外形示意图(仰视图)Fig. 1 Shape of RLV (upward view) |
| 图选项 |
飞行器气动力参数(包括升力系数CL、阻力系数CD、侧力系数CY、绕飞行器质心的滚转力矩系数Cl、俯仰力矩系数Cm、偏航力矩系数Cn)是高度H、马赫数Ma、攻角α、侧滑角β、右体襟翼偏转角δfr、左体襟翼偏转角δfl、滚转角速率p、俯仰角速率q和偏航角速率r的函数。气动力参数在飞行器飞行包线内可认为是线性的,由以下形式表示:
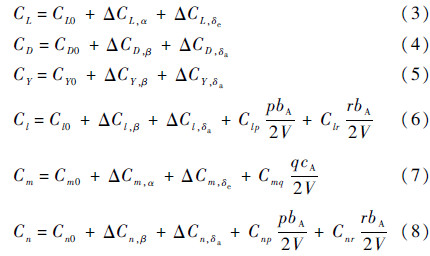
以偏航力矩系数为例,其中Cn0为零攻角零侧滑角并且无舵面偏转时的偏航力矩系数;ΔCn,β为由侧滑角带来的偏航力矩系数增量;ΔCn,δa为副翼偏转生成的偏航力矩系数增量;CnppbA/(2V)和CnrrbA/(2V)分别为滚转和偏航运动引起的阻尼力矩系数,bA为机翼展长，V为飞行速度；cA为平均气动弦长，其他力和力矩系数的表达式与此类似。
在低动压稀薄大气段,气动舵面舵效较低,此时使用RCS进行姿态控制。RCS由位于飞行器尾部垂直截面上的4个喷管组成,为非冗余设计,其布局如图 2所示。当使用RCS进行姿态控制时,将姿态控制器输出经控制分配逻辑转化成4喷管的开关指令,不同的喷管开启组合生成不同的三轴力矩,再与气动力矩分别叠加,即为姿态控制力矩。
 |
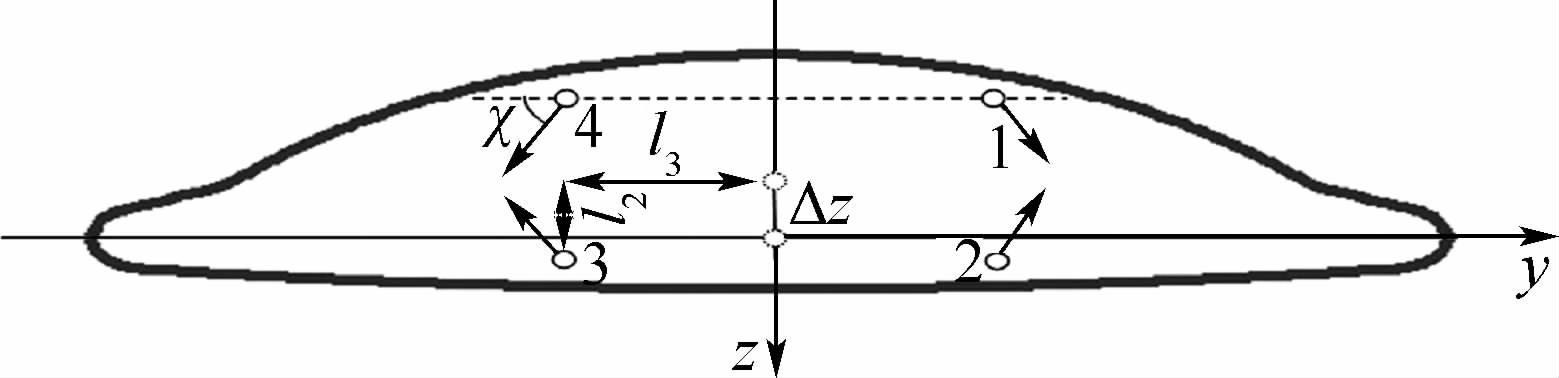| 图 2 RLV的RCS喷管示意图(尾视图)Fig. 2 RCS jets configuration of RLV (end view) |
| 图选项 |
无动力再入飞行器刚体姿态动力学方程如式(9)所示。定义状态向量x=[αβμpqr]T,其中μ为倾侧角;控制输入向量为u=[δeδaLRCSMRCSNRCS]T,其中LRCS、MRCS和NRCS分别为RCS的输出力矩在飞行器本体坐标系滚转、俯仰和偏航3个通道上的投影。由于重力加速度、航迹倾斜角和航迹速度变化得比姿态和姿态角速率慢的多,因此将它们视为常量。模型中忽略了操纵面产生的侧力和升力,即形如Yδ和Lδ的导数都置为零,这对于高超声速飞行状态下的升力体飞行器来说是可取的假设[11]。
式中：g为重力加速度；Y为侧力；γ为滚转角；Φ为俯仰角；L为升力；Ix、Iy和Iz为转动惯量；Ixy、Ixz和Iyz为惯量积；LA、MA和NA分别为气动舵面产生的滚转力矩、俯仰力矩和偏航力矩。
通常情况下,再入飞行器制导系统给出的横侧向指令是倾斜角,倾斜角为飞行器对称平面与包含速度矢量的铅垂面之间的夹角,该定义中的速度矢量必须严格限定在飞行器对称平面内(侧滑角为零),即绕稳定坐标系x轴的滚转角。在飞行器对倾斜角指令的跟踪过程中,显然不能保证侧滑角一直为零,此时应通过考查飞行器的倾侧角μ的变化情况来体现对制导指令的跟踪精度。倾侧角(bank angle)定义为飞行器对称平面与包含速度矢量的铅垂面之间的夹角,式(9)中给出了μ的动态方程。而执行机构安装在飞行器本体坐标系下,通过偏转舵面或者开启RCS喷管使飞行器绕本体坐标系转动从而改变飞行器姿态,因此在描述飞行器滚转姿态(横侧向运动模态)时常用姿态滚转角Φ,定义为飞行器对称平面与包含机体坐标系x轴的铅垂面之间的夹角。补充Φ的动态方程:
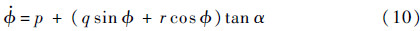
可见姿态滚转角Φ与倾侧角μ存在差别,并且当攻角和侧滑角较大时,差异较为明显,如式(11)所示,因此在控制器设计与仿真中,倾侧角和滚转角并不能等同视之。
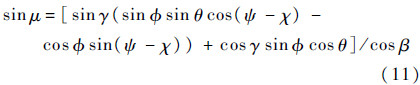
由于飞行器响应的是本体坐标系3个方向上的指令,而制导系统给出的是稳定轴系下的指令,本文的横侧向控制策略设计为通过使飞行器跟踪制导指令在本体系中的投影来实现对倾斜角的精确跟踪。图 3为稳定轴系与本体轴系在飞行器对称平面上的位置关系。从坐标系之间的相对位置关系可以看出,对于大攻角再入的飞行器来说,由于稳定轴与体轴不重合,倾斜角和滚转角之间的差异不可忽略,若要响应横侧向的侧滑角和倾侧角指令,则本体坐标系的滚转通道需响应的指令分别为－βsinα、μcosα,偏航通道需要响应的指令为βcosα、μsinα。而对于纵向通道来说,由于再入飞行器侧滑角通常很小(小于3°),因此可认为稳定轴系和本体轴系的y轴近似重合,所以本体坐标系俯仰通道需响应的指令为αcosβ≈α。
 |
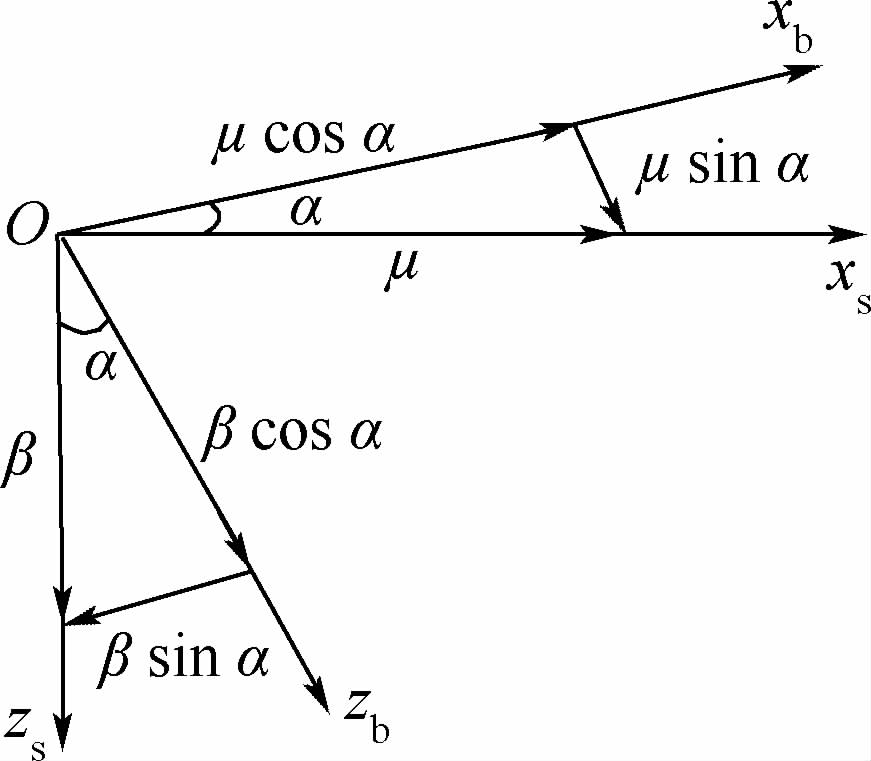| 图 3 稳定轴系(s)与本体轴系(b)的位置关系与角度投影Fig. 3 Position relation of stable coordinate system (s) and body coordinate system (b) and angle projection |
| 图选项 |
2 横侧向耦合机理RLV姿态控制面临的众多挑战之一是多种耦合作用极易诱发失稳,而在这些耦合因素中,由滚转机动所产生的惯性耦合是其中的重要因素。过大的倾侧角角速率很容易导致飞行器绕体轴而不是稳定轴滚转,进一步诱发运动耦合,出现攻角与侧滑角的快速交替变化,最终导致飞行器整体性能的急剧下降,甚至失稳。因此在控制律设计之前,本节将介绍此类飞行器常见耦合的作用机理与规避方式。
2.1 惯性耦合惯性耦合是指当飞行器不绕其某一惯性主轴旋转时会产生不利惯性力矩。根据式(12),俯仰和偏航通道在滚转角速率p很大的情况下,会产生额外的俯仰惯性力矩(Ix－Iz)pr和偏航惯性力矩(Iy－Ix)pq,抵消掉部分原有的静稳定力矩,从而产生不利影响。类似的,当存在俯仰角速率q时,在滚转和偏航通道也会产生附加的不利滚转力矩(Iz－Iy)qr和偏航力矩(Iy－Ix)pq。
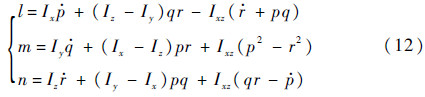
式中：l为滚转力矩；m为俯仰力矩；n为偏航力矩。
假设飞行器以滚转角速率p*绕水平直线定常滚转,并且在滚转过程中飞行速度保持不变,得到机体轴系下的绕质心转动的动力学方程组和质心运动的动力学方程组,将其线性化,并忽略惯性积与较小分量,可以得到特征方程:
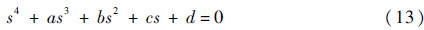
忽略阻尼项Mq、Nr,则特征方程可简化为s4+bs2+d=0,易知急滚稳定条件为b>0且d>0。通常情况下由于此类飞行器具有偏航静稳定性,并且在再入过程中高马赫数情况下具有纵向静稳定性,因此能保证b>0。令d>0得到定常滚转的必要条件为
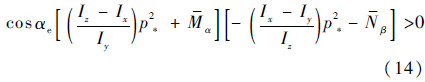
令
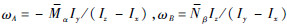,即 
或
如果飞行器的纵向与航向同时具有静稳定性,则满足关系式(15)可以保证飞行器近似绕主惯性轴旋转,而满足关系式(16)则可以保证飞行近似绕速度轴旋转[12]。因此,为减弱运动耦合应该保证满足关系式(16),最终得到滚转角速率幅值上限计算方法,即在ωA与ωB中取较小的数并开根号作为倾侧角角速率幅值上限(假设将滚转轴的角速率近似看作滚转角的角速率)。在再入轨迹上,选取纵向静稳定的工作点,分别计算ωA、ωB,如图 4所示。
 |
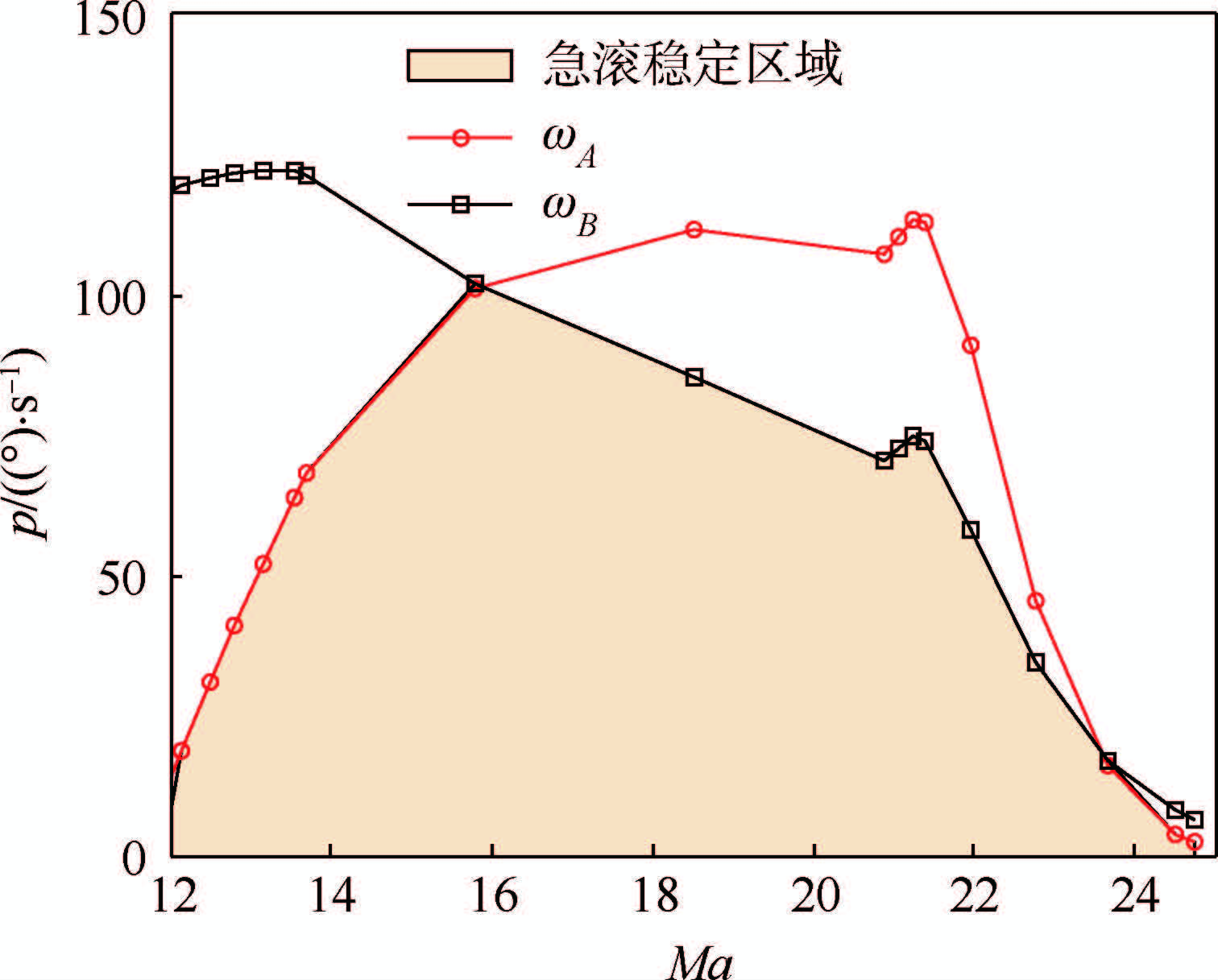| 图 4 RLV再入轨迹上的急滚稳定边界Fig. 4 Fast roll stability boundary along the RLV’s reentry trajectory |
| 图选项 |
根据前面的分析,滚转角速率应小于min(ωA,ωB)。因此图 4中阴影部分即为飞行器的急滚稳定边界。从图中可以看出,在初始下降段(高空),纵向通道要求的滚转角速率约束起主导作用,且允许的滚转角速率较小,因此,应尽量避免进行滚转机动;而在高马赫数滑翔段,航向通道要求的滚转角速率约束起主导作用,即偏航通道更易因滚转产生发散。因此在飞行器控制律设计中可以考虑通过滚转角速率限幅来改善惯性耦合。例如,航天飞机的控制律中对滚转角速率进行了限幅处理,且滚转角速率与图 4有着类似的规律,在再入初期都随着马赫数降低而逐渐增大。
表 1为RLV不同质量特性参数表。在每种质量特性下沿标称轨迹计算急滚稳定边界,如图 5所示。从图中可以看出,不同的质量特性下的急滚稳定边界的趋势大体类似,较大质量与惯量下的滚转角速率上限也较小。实际控制律设计时,可根据此计算结果对指令角速率进行限幅,以减弱惯性耦合。
表 1 RLV不同质量特性参数Table 1 Different quality characteristic parameters of the RLV
| 参数 | 质量特性① | 质量特性② | 质量特性③ | 质量特性④ |
| m/kg | 500 | 900 | 2200 | 4500 |
| I x/(kg·m 2) | 100 | 200 | 500 | 1000 |
| I y/(kg·m 2) | 700 | 1400 | 3500 | 7000 |
| I z/(kg·m 2) | 800 | 1500 | 3600 | 8000 |
| I xz/(kg·m 2) | -20 | -40 | -100 | -200 |
表选项
 |
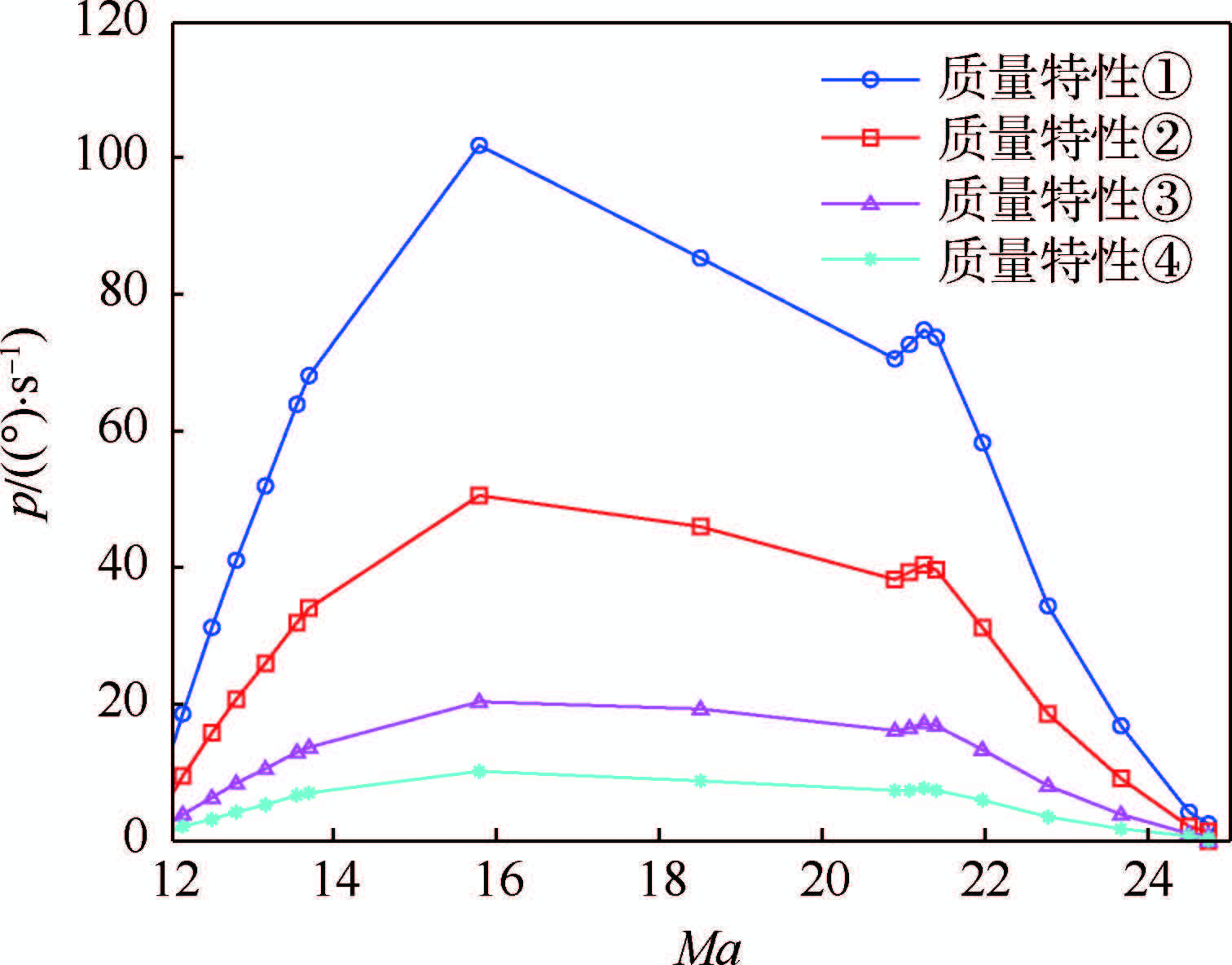| 图 5 不同质量特性飞行器的急滚稳定边界Fig. 5 Fast roll stability boundaries of vehicles with different quality characteristic |
| 图选项 |
2.2 稳定性耦合通常飞行器的横侧向运动具有3个模态:荷兰滚模态、滚转收敛模态和螺旋模态。其中荷兰滚模态是滚转运动与航向运动的耦合形成的震荡模态,在大攻角时使用动态偏航稳定性导数Cβn,dyn表征航向动态稳定性(即荷兰滚稳定性),Cβn,dyn>0则具有航向动态稳定性。Cβn,dyn的计算公式为
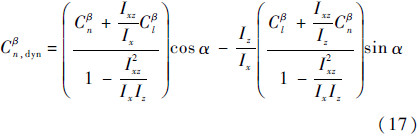
从式(17)可以看出,Cβn,dyn同时考虑了上反效应、攻角和惯量比对荷兰滚的影响。Cβn,dyn可以根据式(18)预测荷兰滚频率,但不能表征荷兰滚阻尼。本文提出一种荷兰滚阻尼预测式,通过此式预测荷兰滚稳定性,以在控制律中根据不同需求设定控制增益。
式中：ωd为荷兰滚模态的自然频率；Q为动压；S为参考面积;bA为机翼展长。
忽略阻尼力矩项以及角速率对侧力的影响,由横侧向线性模型得到横侧向特征行列式[13]:
由于以上简化,使得滚转和螺旋模态的根退化为零[14],因此,式(19)中的常数项即为荷兰滚频率的平方。由此可见Cβn,dyn>0只是荷兰滚稳定的充分条件,并不能保证荷兰滚稳定。
令ξd为荷兰滚模态的阻尼比,－d1和－d2分别为滚转收敛和螺旋模态的特征根,因此横侧向运动的特征行列式为
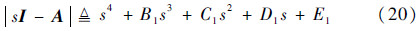
式中:
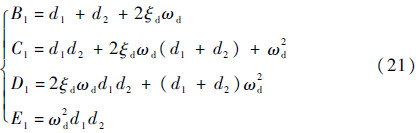
通常不考虑姿态角速率对侧力的影响,即Yp和Yr为0,因此由横侧向线性化模型得到的特征行列式为
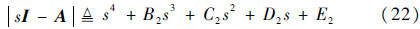
由于
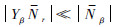且
,因此式(22)中B2、C2、D2和E2可化简为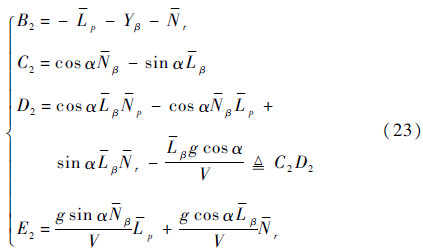 
式中:
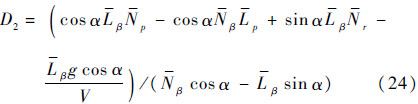
显然应有B1=B2、C1=C2、D1=D2、E1=E2。由于螺旋模态为一阶模态,且时间常数较大,特征根很小,通常情况下d2«min(d1,ωd),因此D1≌d1ω2d,并且d2≌E1/D1。然后将特征行列式写成:
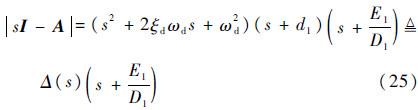
式中:
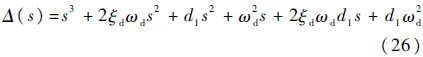
因此令
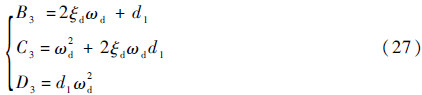
由于D2≈D3,所以有
且由
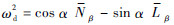可知d1=D2。因此可得荷兰滚模态阻尼为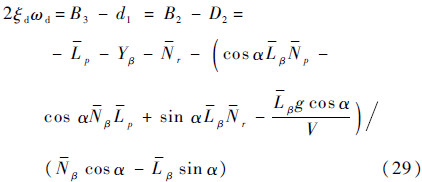 
图 6为荷兰滚阻尼预测式分解，从图中可以看出,使用式(29)得到的荷兰滚阻尼预测结果与模态分析的结果一致,能预测荷兰滚模态的稳定性。当阻尼力矩较小时,式(29)可简化为
 |
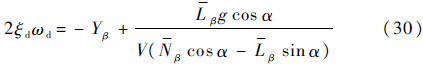
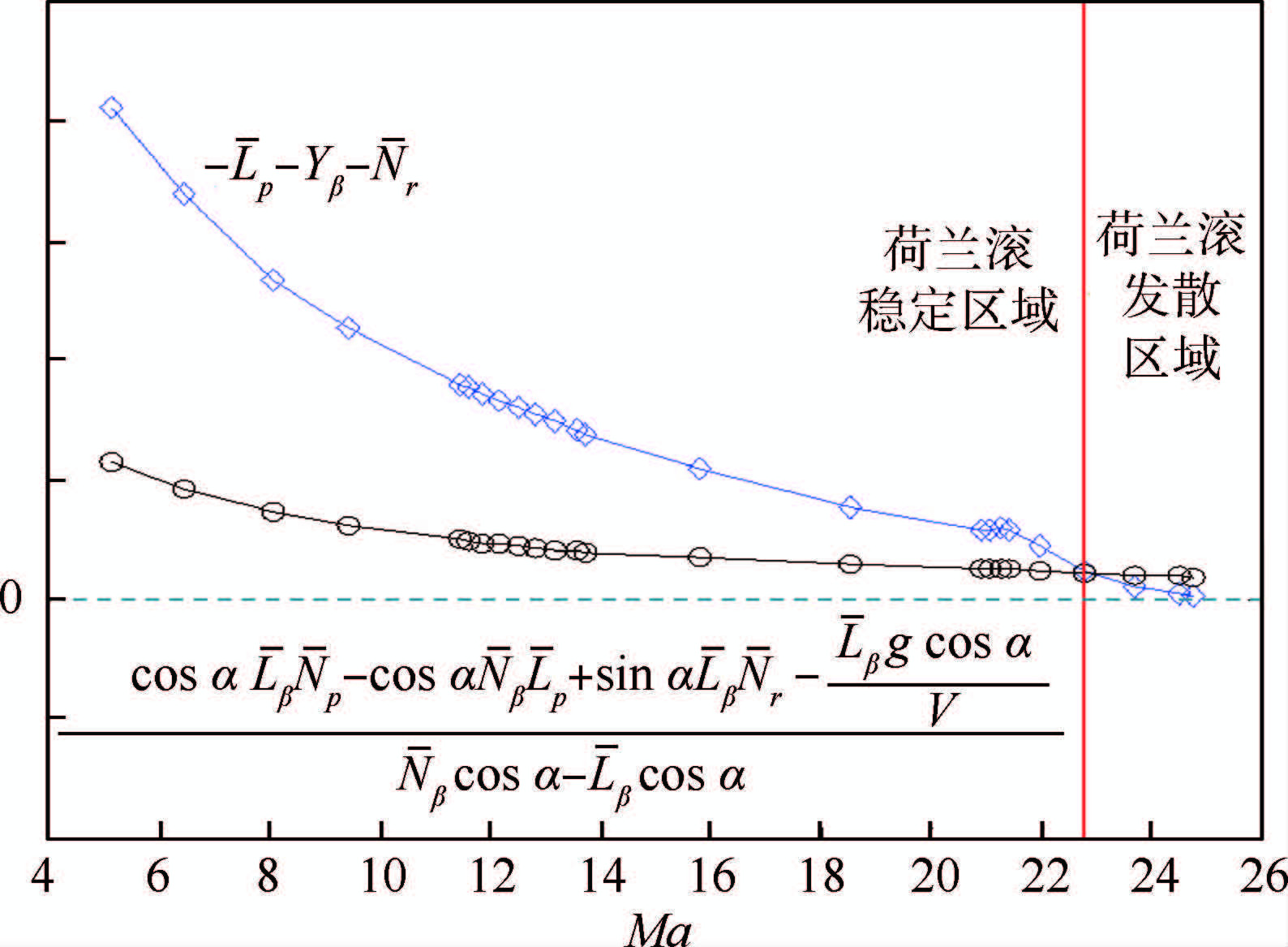| 图 6 荷兰滚阻尼预测式分解Fig. 6 Decomposition of the forecast formula of the damping of Dutch roll motion |
| 图选项 |
因此幅值较大的Yβ和更强烈的上反效应有利于稳定荷兰滚模态。
3 控制策略设计以简化控制系统结构和节省RCS燃料为目的,本节针对再入过程中不同阶段动压、舵效和模态特性的特点,设计低动压下机身襟翼-RCS复合控制策略以及高动压时机身襟翼单独作用的横侧向协调控制策略。
3.1 纵向控制律设计在此类飞行器再入过程中,马赫数大于12时,纵向运动稳定,阻尼较小,需要增加纵向阻尼。本文的制导律为保持常值攻角即可,姿态控制系统仅需要对干扰进行抑制,即需用姿态控制力矩通常较小。经考查,升降舵的舵效在再入过程中足够提供需要的纵向阻尼,因此设计如图 7所示的纵向通道控制策略。
 |
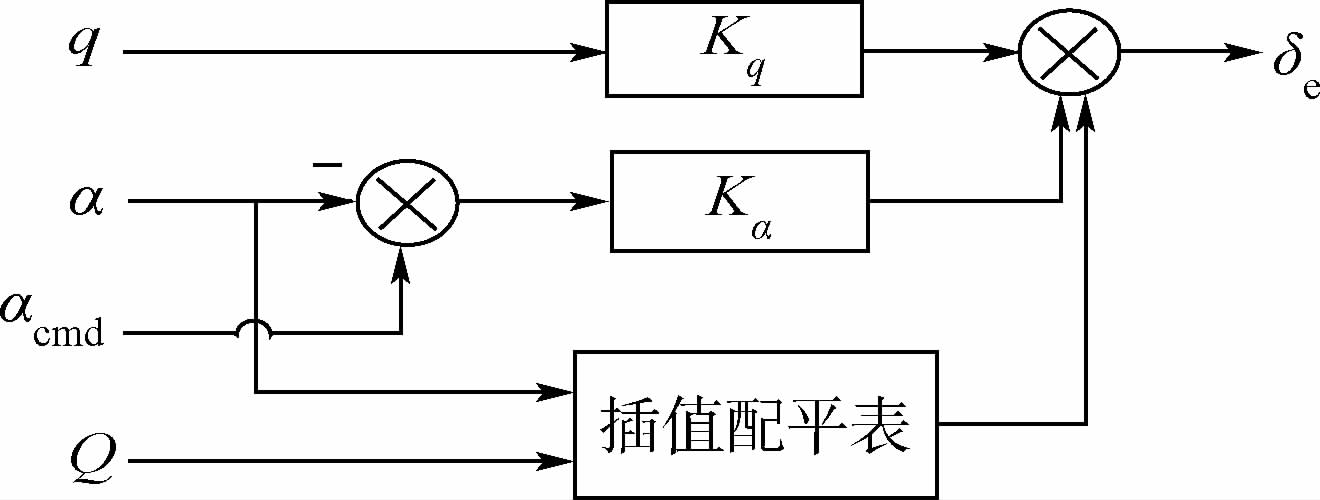| 图 7 纵向通道控制策略Fig. 7 Control strategy of longitude channel |
| 图选项 |
使用升降舵控制时,根据当前攻角和动压,通过在线插值方式得到配平升降舵偏角,从而实现纵向的舵面配平;通过攻角指令偏差eΔα实现对攻角制导指令的跟踪;通过反馈俯仰角速率q实现纵向增稳,调节控制参数Kq和Kα为短周期模态提供适当的自然频率和阻尼比。俯仰角速率到升降舵的反馈能提供足够的阻尼,因此纵向仅使用升降舵面配平并进行姿态控制,从而节省RCS燃料的消耗。但RCS控制通道应该保留,以备在故障以及飞行器受到较大扰动时提供足够的姿态控制力矩。
3.2 横侧向控制律设计3.2.1 低动压下的机身襟翼-RCS控制策略通过对飞行器运动模态的分析发现,本文研究对象的横侧向运动中荷兰滚模态在高动压马赫数大于22时不稳定,且整个再入过程中阻尼很小。因此横侧向姿态控制需解决的问题为高空高动压下的荷兰滚稳定与再入过程中的荷兰滚增稳。
当飞行器做快速大滚转机动并且飞行速度远大于重力加速度(即V》g)时,式(9)中攻角动态方程中的重力与升力项(cosμcosγ－L/mg)g/(Vcosβ)、侧滑角动态方程中的重力项gsinΦcosα/V数值很小,可以忽略不计,与此同时忽略侧力的影响,得到如下简化方程:
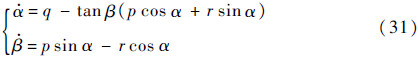
由式(31)可知,高超声速飞行器大攻角下进行滚转时,由于运动耦合的存在,攻角和侧滑角会相互转化,这种转化是造成急滚不稳定的原因之一。运动耦合的大小一般取决于滚转角速率[15]。若想保持α不变,应该使侧滑角为零,若要保持β不变,应使飞行器绕稳定轴的x轴旋转。因此希望绕速度轴进行滚转而不是体轴,同时保持在速度坐标系下的偏航角速率为零,即ra=rcosα－psinα=0,因此本体坐标系下的滚转角速率pb和偏航角速率rb需满足如下关系:
即当本体坐标系下的滚转角速率是偏航角速率的cotα倍时,不会发生运动耦合。因此在控制律中,将偏航角速率反馈至滚转阻尼通道,使滚转角速率保持与偏航角速率的倍数关系,以削弱运动耦合。
再入初期会出现荷兰滚模态不稳定的情况,且阻尼很低。由于荷兰滚模态中滚转运动占主要地位,因此考虑由滚转角速率到副翼的反馈提供滚转阻尼,根据式(29)预测荷兰滚模态的稳定性并以此调节增益K1,从而稳定荷兰滚模态。
为避免惯性耦合的发生,采用图 4生成的急滚稳定边界对指令角速率进行限幅,从而控制滚转角速率维持在急滚稳定边界之内,使飞行器近似绕速度轴旋转,同时也能避免运动耦合的产生。
当体襟翼差动产生副翼偏角操纵滚转的同时会产生不利偏航运动,从而引起副翼控制滚转反极性现象:操纵副翼绕机体轴左滚,飞行器却是绕机体轴右滚。通常使用横向控制偏离判据 (Lateral Control Departure Parameter,LCDP)预测副翼操纵性能[16, 17]:
一般情况下当LCDP>0时滚转通道稳定,当LCDP < 0时,原系统为非最小相位系统,滚转指令不能精确跟踪。LCDP出现负值的原因主要有2个,航向不稳定或稳定度不够,或者Cnδa>0。由于航天飞机不具有航向静稳定性,即Cnβ < 0,因此不利偏航力矩引起的侧滑角持续发散,再由于强烈的上反效应,使得侧滑角产生的滚转力矩阻碍副翼的滚转操纵。而对于此类飞行器,如图 8所示,由于其具有航向静稳定性,且Cnδa>0,此时正副翼在产生期望的负滚转力矩的同时,会附加正的不利偏航力矩引起负侧滑,而Clβ负值较大时,负侧滑将产生正滚转力矩,此横向静稳定力矩会降低副翼的操纵效果,阻碍副翼的滚转操纵甚至引起正滚转。
 |
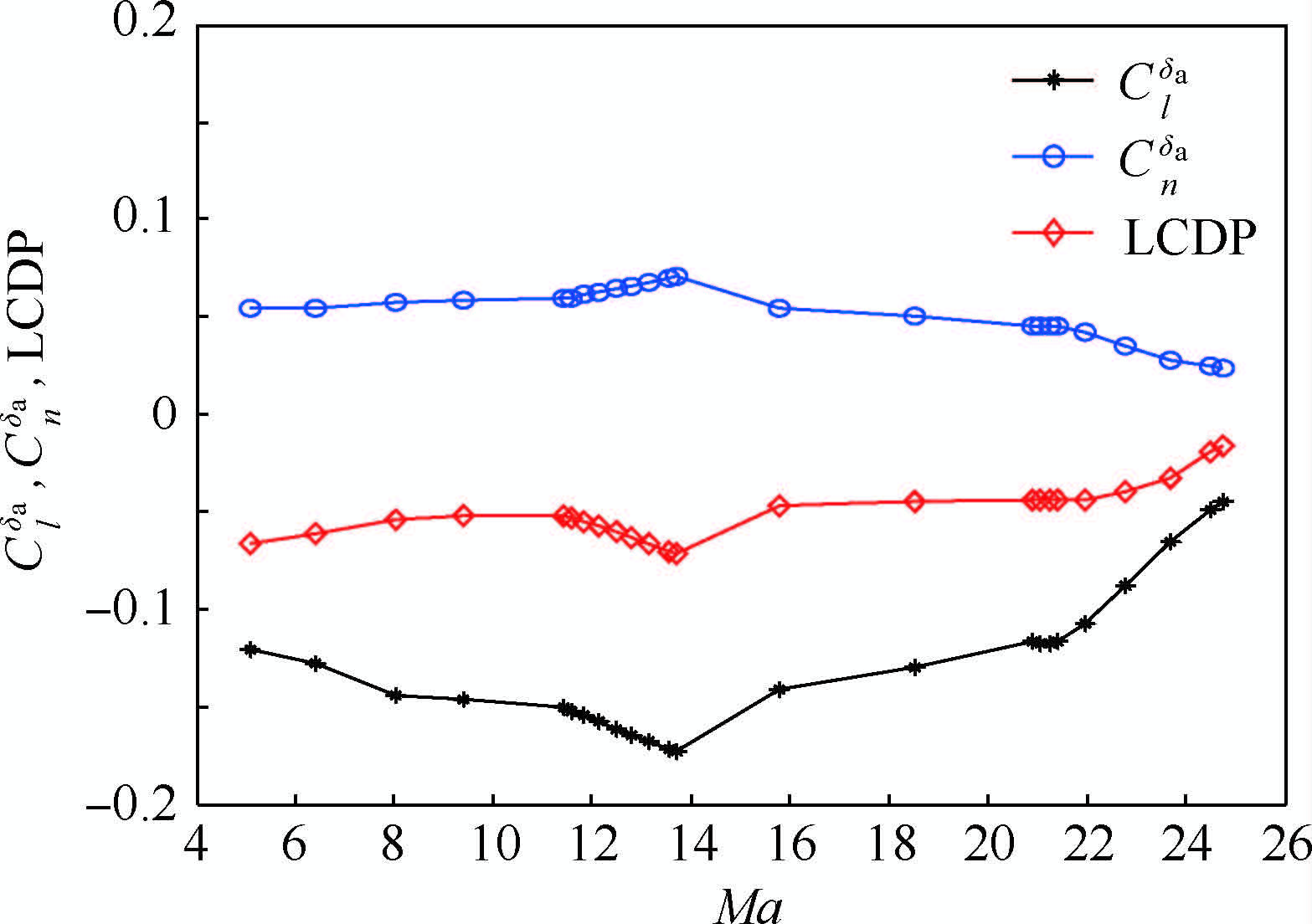| 图 8 再入轨迹工作点上的横侧向操纵系数Fig. 8 Lateral/directional operating coefficients of equilibrium points on reentry trajectory |
| 图选项 |
LCDP随攻角与马赫数变化趋势明显,如图 9所示,在高度为80km左右、攻角为10°左右时,LCDP会由负变正,不会发生副翼反效。为避免LCDP不确定带来的控制器失效的隐患,本文不采取常见的副翼控制滚转的方式。由于此类飞行器具有强烈的上反效应,因此采取由偏航RCS产生一定的偏航力矩,使飞行器产生侧滑角,再由此侧滑角激发与期望方向相同的滚转力矩的方式实现对指令的跟踪。
 |
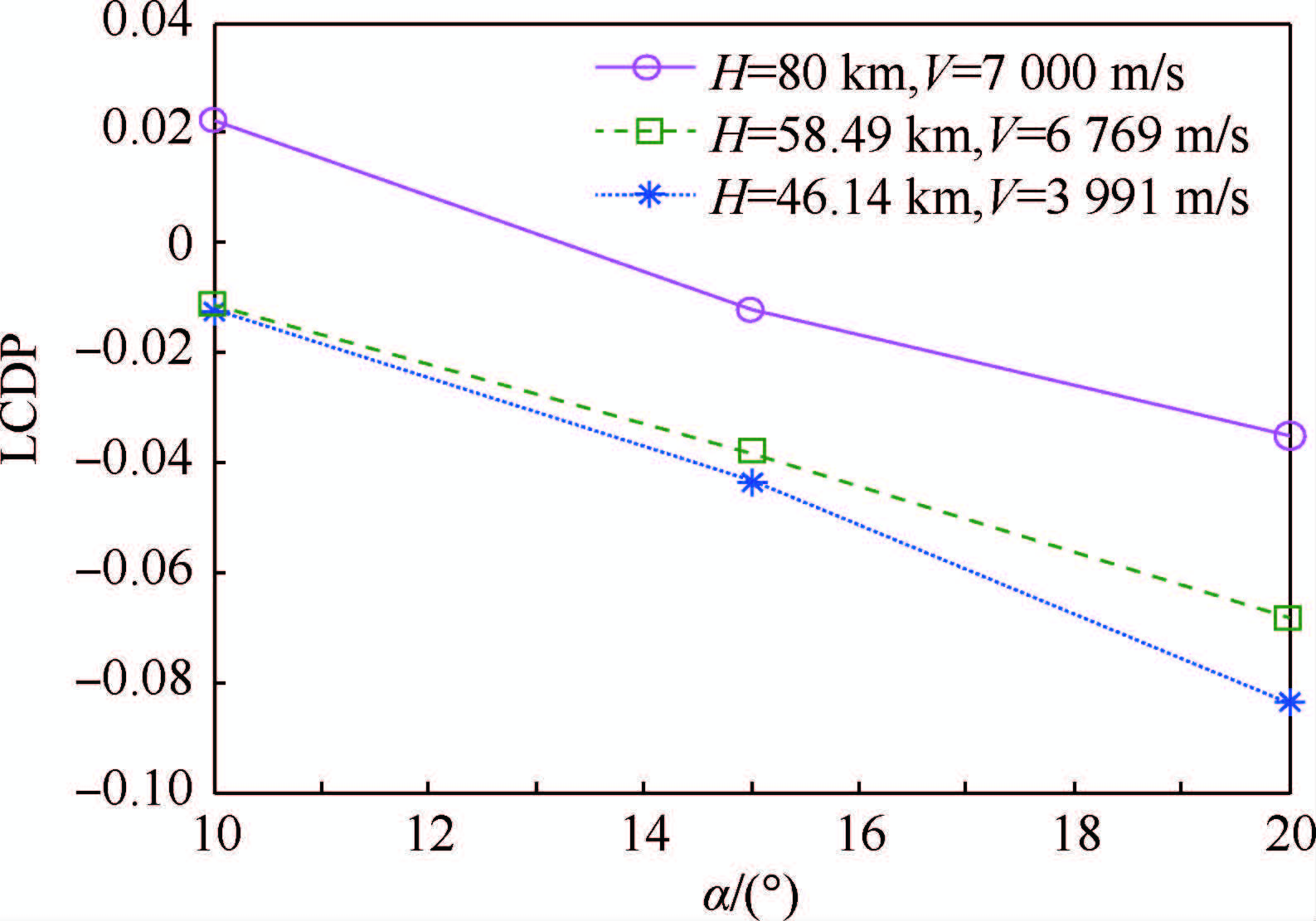| 图 9 LCDP随攻角变化Fig. 9 LCDP curves change with angle of attack |
| 图选项 |
综上,大攻角低动压下的横侧向控制策略如图 10和图 11所示。
 |
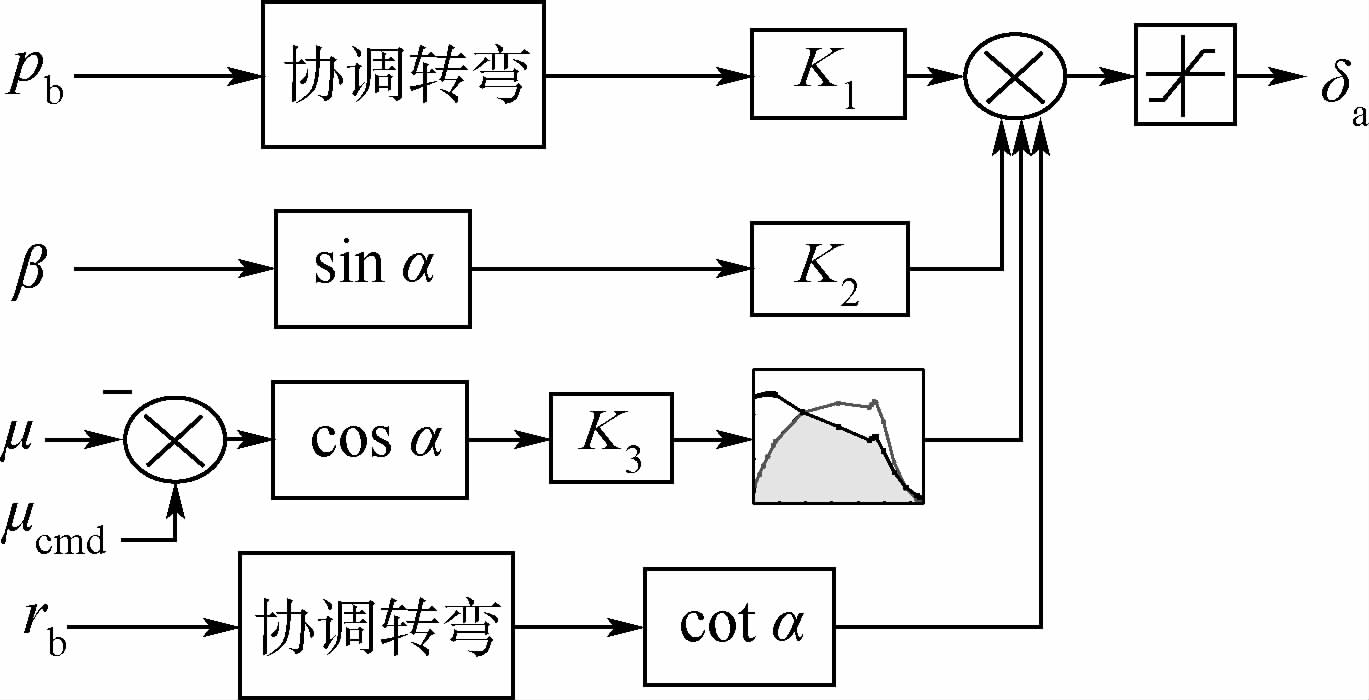| 图 10 低动压下的滚转通道控制策略Fig. 10 Control strategy of roll channel (low dynamic pressure) |
| 图选项 |
 |
| 图 11 低动压下的偏航通道控制策略Fig. 11 Control strategy of yaw channel (low dynamic pressure) |
| 图选项 |
3.2.2 高动压下的机身襟翼单独作用控制策略根据对横侧向运动的模态分析可知,随着高度降低,荷兰滚模态保持稳定,但阻尼一直很小。当高度降低,LCDP虽然随攻角变化明显,但始终保持为负,且随着动压增大,副翼的舵效也明显增大。因此在这一阶段直接断开RCS回路,使用副翼生成侧滑产生滚转力矩的方式控制滚转运动,并通过偏航角速率反馈使其抵消掉一部分滚转角速率在稳定轴系的投影,以削弱运动耦合。同时通过反馈滚转角速率稳定荷兰滚模态。其控制策略示意图如图 12所示。
 |
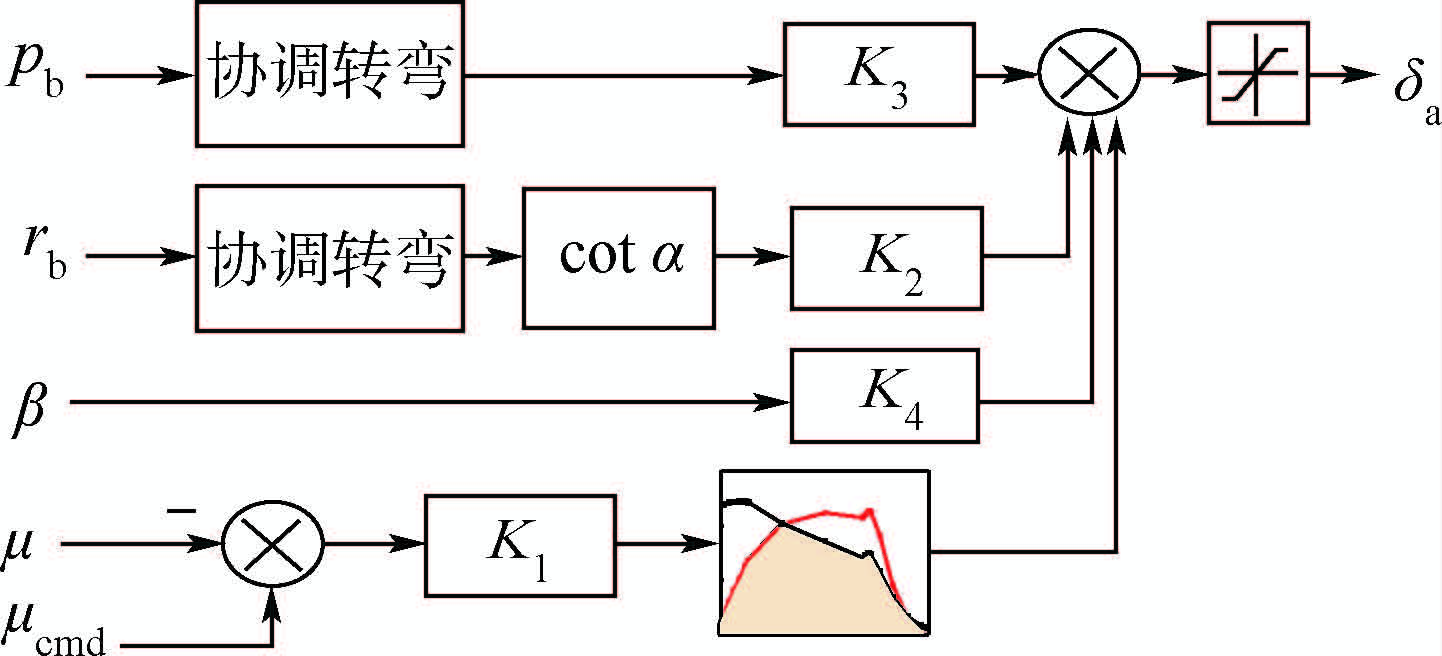| 图 12 高动压下的横侧向控制策略Fig. 12 Control strategy of lateral/directional channel (high dynamic pressure) |
| 图选项 |
4 仿真结果在高超声速飞行器再入段仿真模型中,制导指令代表了飞行器在再入段可能进行的姿态机动,包括纵向的攻角指令αcmd和横侧向的倾侧角指令μcmd,与此同时需要控制侧滑角在0°左右。本节通过对再入标称轨迹的跟踪仿真验证控制策略的可行性。六自由度仿真结果见图 13～图 17。仿真起始点H=80km,V=7000m/s,再入过程中需保持16°常值攻角,倾侧角指令如图 15中虚线所示。仿真周期为0.005s,仿真终止条件为H < 32km。
 |
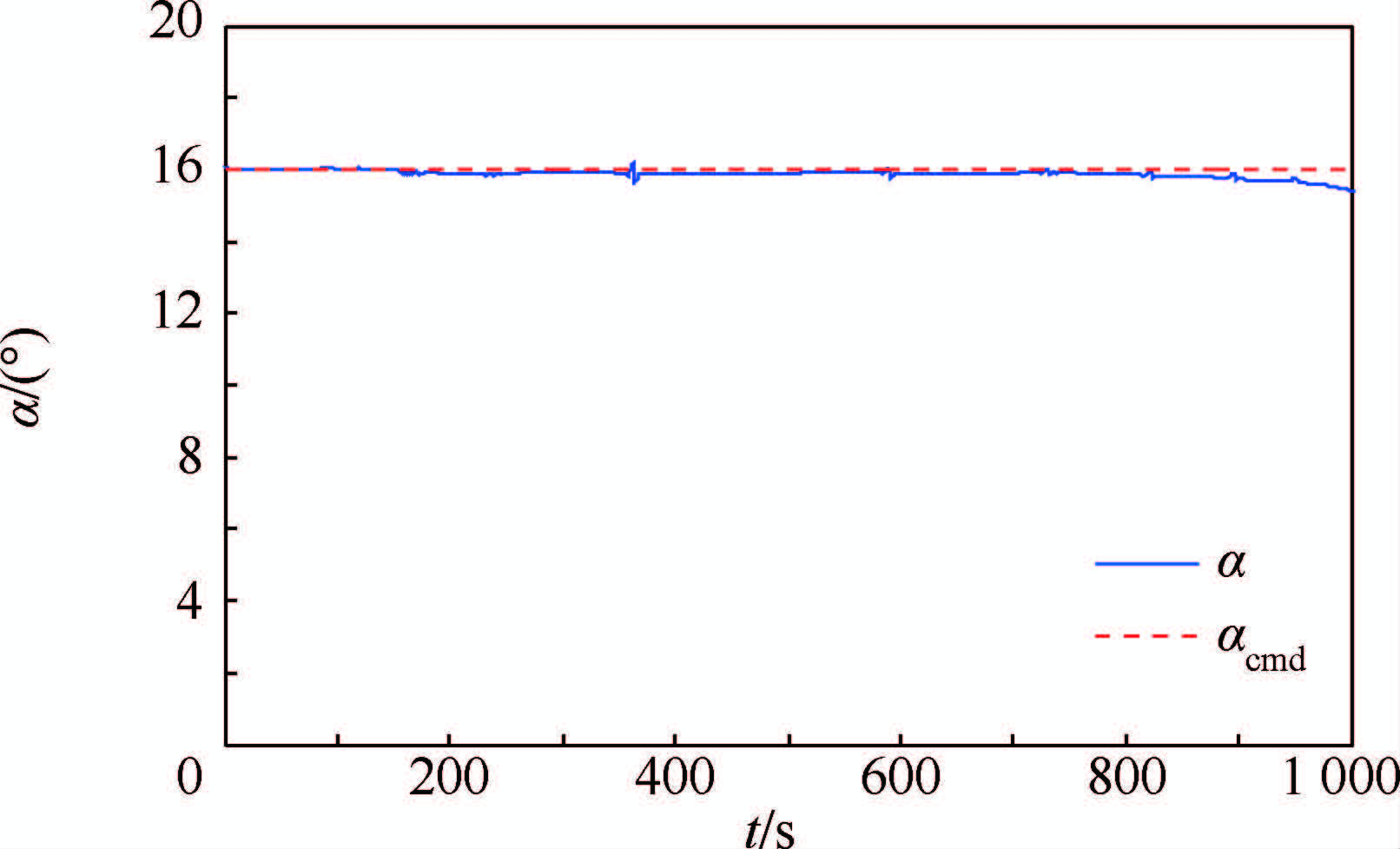| 图 13 六自由度模型跟踪标称轨迹:攻角响应曲线Fig. 13 Angle of attack response curves in 6-DOF simulation of tracking nominal trajectory |
| 图选项 |
 |
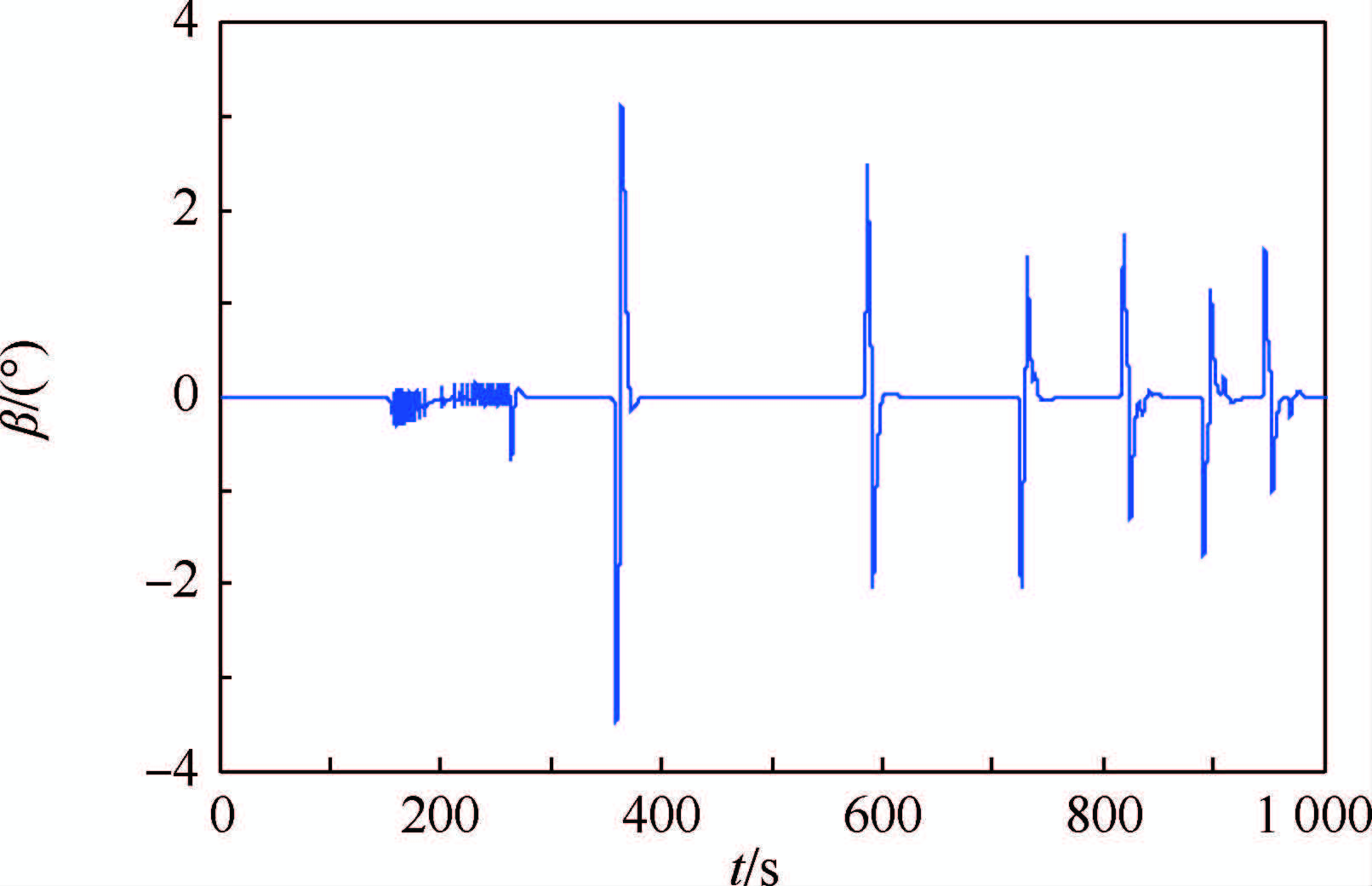| 图 14 六自由度模型跟踪标称轨迹:侧滑角响应曲线Fig. 14 Sideslip angle response curve in 6-DOF simulation of tracking nominal trajectory |
| 图选项 |
 |
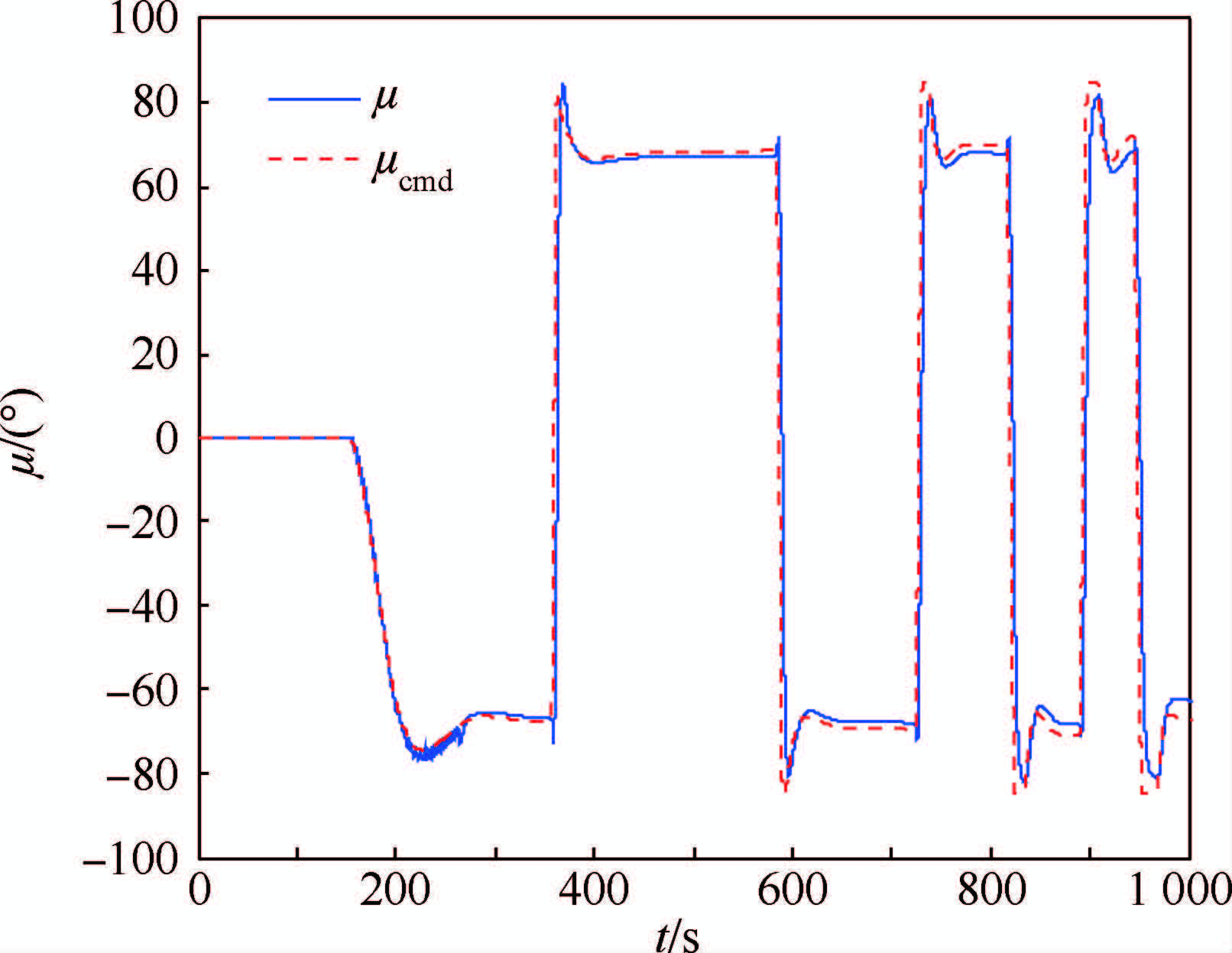| 图 15 六自由度模型跟踪标称轨迹:滚转角响应曲线Fig. 15 Bank angle response curves in 6-DOF simulation of tracking nominal trajectory |
| 图选项 |
 |
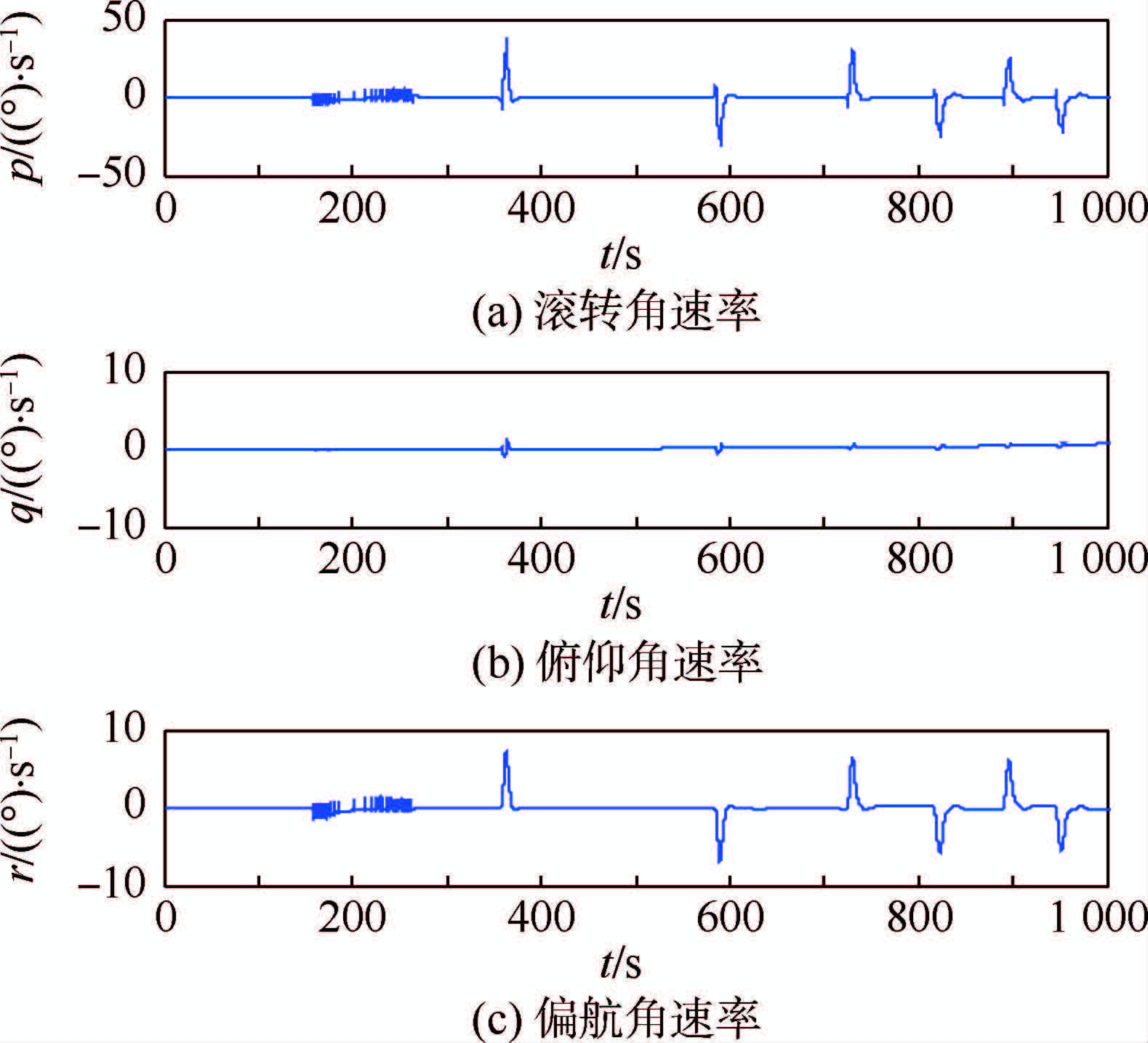| 图 16 六自由度模型跟踪标称轨迹:姿态角速率变化曲线Fig. 16 Attitude angular rates changing curves in 6-DOF simulation of tracking nominal trajectory |
| 图选项 |
 |
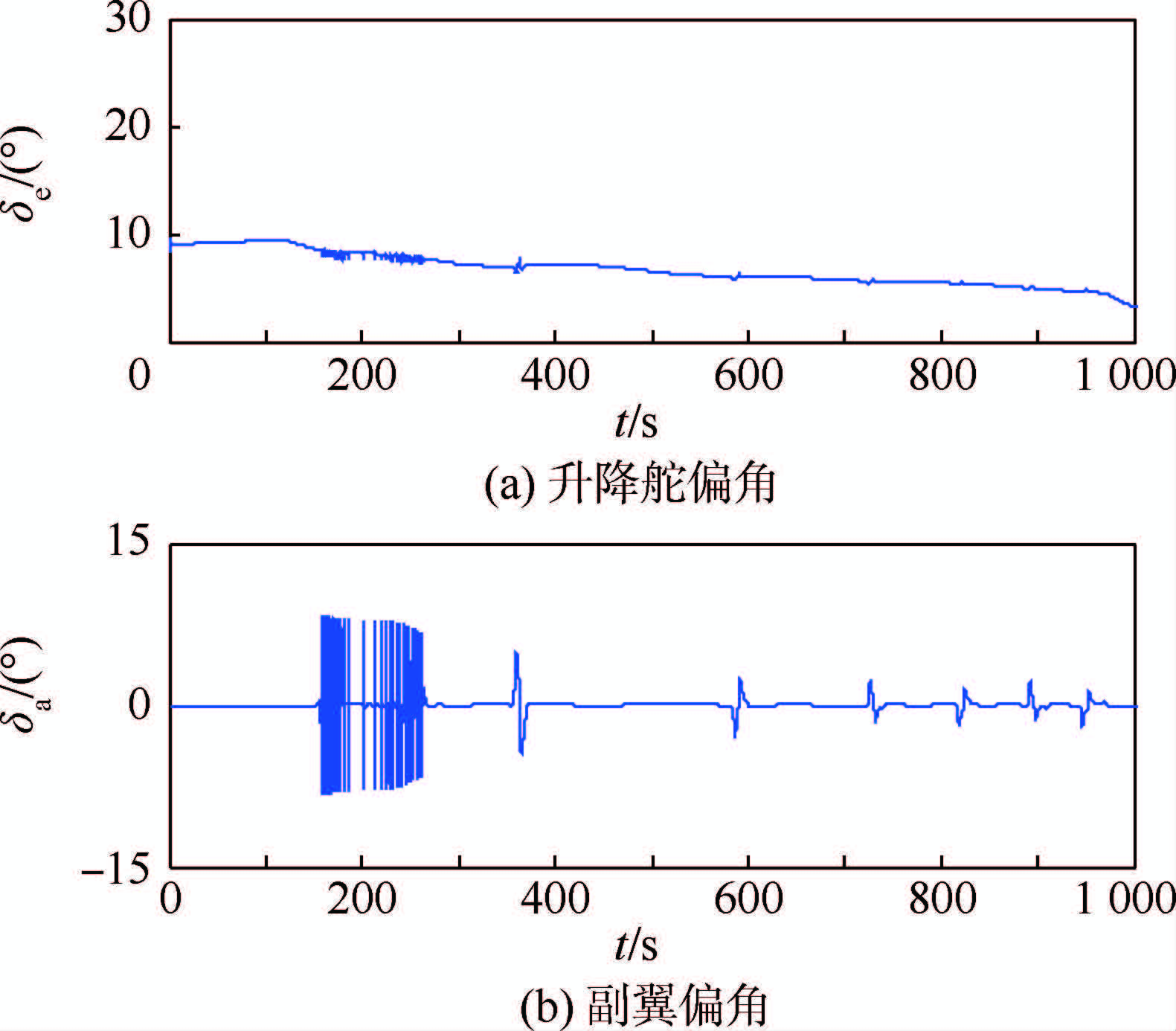| 图 17 六自由度模型跟踪标称轨迹:舵偏角变化曲线Fig. 17 Aerodynamic control surface responses in 6-DOF simulation of tracking nominal trajectory |
| 图选项 |
在仿真中采用根据当前动压选择控制策略的切换模式,在飞行器再入初期使用机身襟翼-RCS复合控制策略,当动压逐渐增大舵效增强,RCS退出控制,仅使用气动舵面进行姿态控制。
从仿真结果可以看出,攻角和滚转角能精确跟踪制导指令,侧滑角基本保持在±3°之内,气动舵面偏转未发生饱和,具有一定的控制裕度。姿态角速率控制在合理范围内。经统计4个RCS喷管的开启时间共计为13.7s,燃料消耗在合理范围内。仿真结果验证了控制策略的有效性。
5 结论1) 结合制导与姿态控制系统的特点详细介绍了倾斜角、倾侧角与滚转角的区别,并给出了横侧向高精度姿态控制要求下对这3个角的处理方法。
2) 计算了不同质量特性下沿轨迹的飞行器的急滚稳定边界,在再入过程中进行横侧向机动时控制滚转角速率在此稳定边界之内能较好地抑制惯性耦合。
3) 针对此类飞行器常见的稳定性耦合推导了一种新的荷兰滚频率预测式,使用此式可有效地判断荷兰滚稳定性并切换控制器增益。
4) 根据对飞行器耦合特性的分析设计了此类欠驱动飞行器的横侧向耦合控制策略,即在高空低动压阶段,采用偏航RCS使飞行器生成侧滑角,利用上反效应产生与期望滚转同向的滚转力矩,从而避免由副翼控制滚转带来的副翼反效不确定现象,与此同时由副翼提供滚转阻尼以稳定荷兰滚模态;在高动压阶段,随着舵效增大RCS逐步退出控制环,使用副翼对横侧向进行耦合控制,此时通过调节控制增益来保证生成的滚转力矩与期望方向相同。对标称轨迹跟踪的六自由度仿真验证了该控制策略的有效性,达到了节省RCS燃料和简化控制系统结构的目的。
参考文献
| [1] | THOMPSON R A.Reviewof X-33 hypersonic aerodynamic and aerothermodynamic development[C]//Independent Component Analysis.Hampton,Virginia:National Aeronautics and Space Administration Langley Research Center,2000:323.1-323.19. |
| Click to display the text | |
| [2] | HORVATH T J,O'CONNELL T F,CHEATWOOD F M,et al.Experimental hypersonic aerodynamic characteristics of Mars surveyor 2001 precision lander with flap[J].Journal of Spacecraft and Rockets,2006,43(2):270-281. |
| >Click to display the text | |
| [3] | RODRIGUEZ A A,DICKESON J J,CIFDALOZ O,et al.Modeling and control of scramjet-powered hypersonic vehicle:Challengers,trends,& tradeoffs[C]//AIAA Guidance,Navigation and Control Conference and Exhibit.Reston:AIAA,2008:18-21. |
| Click to display the text | |
| [4] | 牛文,董婧,李文杰,等.2012年上半年世界高超声速动态[J].飞航导弹,2012(10):13-21. NIU W,DONG J,LI W J,et al.Worldwide news of hypersonic in the first half of 2012[J].Aerodynamic Missile Journal,2012(10):13-21(in Chinese). |
| Cited By in Cnki (7) | |
| [5] | 张珂珂.飞行器耦合机理及耦合补偿研究[D].武汉:华中科技大学,2013:31-38. ZHANG K K.Coupling mechanism and decoupling study of vehicle[D].Wuhan:Huazhong University of Science and Technology,2013:31-38 (in Chinese). |
| Cited By in Cnki | |
| [6] | 雷延花,陈士橹.导弹气动耦合分析与解耦算法研究[J].弹道学报,2003,15(1):11-16. LEI Y H,CHEN S L.The missile aerodynamic coupling analysis and decoupling arithmetic study[J].Journal of Ballistics,2003,15(1):11-16(in Chinese). |
| Cited By in Cnki (15) | Click to display the text | |
| [7] | 周军,刘玉玺,周凤岐.动态解耦和变结构鲁棒补偿的导弹再入控制[J].系统仿真学报,2009,21(10):3071-3073. ZHOU J,LIU Y X,ZHOU F Q.Study of missile reentry dynamic decoupling control based on variable structure robustness compensating[J].Journal of System Simulation,2009,21(10):3071-3073(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [8] | 张艳,段朝阳,张平,等.基于动态逆的BTT导弹自动驾驶仪设计[J].北京航空航天大学学报,2007,33(4):422-426. ZHANG Y,DUAN C Y,ZHANG P,et al.BTT missile autopilot design based on dynamic inversion[J].Journal of Beijing University of Aeronautics and Astronautics,2007,33(4):422-426(in Chinese). |
| Cited By in Cnki (19) | Click to display the text | |
| [9] | 黄琳,段志生,杨莹.现代飞行器控制的几个科学问题[J].科技导报,2008,26(20):92-98. HUANG L,DUAN Z S,YANG Y.Several problems on control of modern aerocraft[J].Science & Technology Review,2008,26(20):92-98(in Chinese). |
| Cited By in Cnki (12) | Click to display the text | |
| [10] | 尹佳杰,都延丽,陆宇平.近空间飞行器滑翔再入控制的研究方法与进展[J].飞行力学,2013,31(3):203-208. YIN J J,DU Y L,LU Y P.Research methods and development of gliding reentry control for near space vehicles[J].Flight Dynamics,2013,31(3):203-208(in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [11] | WALLNER E M,WELL K H.Attitude control of a reentry vehicle with internal dynamics[J].Journal of Guidance,Control,and Dynamics,2003,26(6):846-854. |
| Click to display the text | |
| [12] | 方振平,陈万春,张曙光.航空飞行器飞行动力学[M].北京:北京航空航天大学出版社,2005:351-353. FANG Z P,CHEN W C,ZHANG S G.Aircraft flight dynamics[M].Beijing:Beihang University Press,2005:351-353(in Chinese). |
| [13] | MENGALI G,GIULIETTI F.Unified algebraic approach to approximation of lateral-directional modes and departure criteria[J].Journal of Guidance,Control and Dynamics,2004,27(4):724-728. |
| Click to display the text | |
| [14] | LUTZE F H,DURHAM W C,MASON W H.Unified development of lateral-directional departure criteria[J].Journal of Guidance,Control,and Dynamics,1996,19(2):489-493. |
| Click to display the text | |
| [15] | DAY R E.Coupling dynamics in aircraft:A historical perspective:Vol.532[R].Washington,D.C.:NASA,1997:32-33. |
| Click to display the text | |
| [16] | LEE H P,CHANG M,KAISER M K.Flight dynamics and stability and control characteristics of the X-33 technology demonstrator vehicle[C]//AIAA Guidance,Navigation and Control Conference and Exhibit.Reston:AIAA,1998:1-11. |
| Click to display the text | |
| [17] | CALHOUN P.An entry flight controls analysis for a reusable launch vehicle[C]//Proceedings of the AIAA Aerospace Sciences Meeting.Reston:AIAA,2000:1-12. |
| Click to display the text |
